MetaTrader 5 / 统计分析
English Русский Español Deutsch 日本語
preview
基于主成分的特征选择与降维

基于主成分的特征选择与降维

MetaTrader 5 — 统计分析 |
106 1
Francis Dube
Francis Dube

概述

金融时间序列预测通常涉及对众多特征的分析，其中许多特征可能高度相关。主成分分析（Principal Component Analysis，PCA）等降维技术有助于以更紧凑的形式表示这些特征。然而，PCA存在局限性，尤其是在存在高度相关变量的情况下。在这种情况下，PCA往往表现出分组效应，即一组高度相关的变量共同对某一主成分产生贡献。PCA并非突出单个变量，而是将影响相对均匀地分布在相关组中的所有变量上。

这种均匀分布有利于抑制噪声，因为主成分强调的是共同模式，而非单个变量特有的随机波动。然而，这种噪声抑制是有代价的：它往往会稀释每个主成分中单个变量的贡献。某些变量本身可能具有重要意义，但在转换后的空间中，其重要性可能降低，因为它们的影响被吸收到了该组所捕捉的更广泛结构中。在变量选择等任务中，这可能是一个重大缺陷，因为变量选择的目的是识别最具影响力的特征；在根源分析中，了解特定变量的直接影响也至关重要。

此外，这一特性还使模型解释变得复杂。由于每个主成分代表的是所有原始变量的组合，因此将这些成分的贡献转换回原始变量的上下文中可能颇具挑战性。使用者可能难以从主成分中得出清晰的见解，因为很难确定哪些原始变量驱动了观察到的模式。为解决这一问题，我们引入了前向选择成分分析（FSCA）的实现方法，该方法受Luca Puggini和Sean McLoone的研究启发，旨在避免PCA在处理高度相关特征时存在的缺陷。


前向选择成分分析（FSCA）

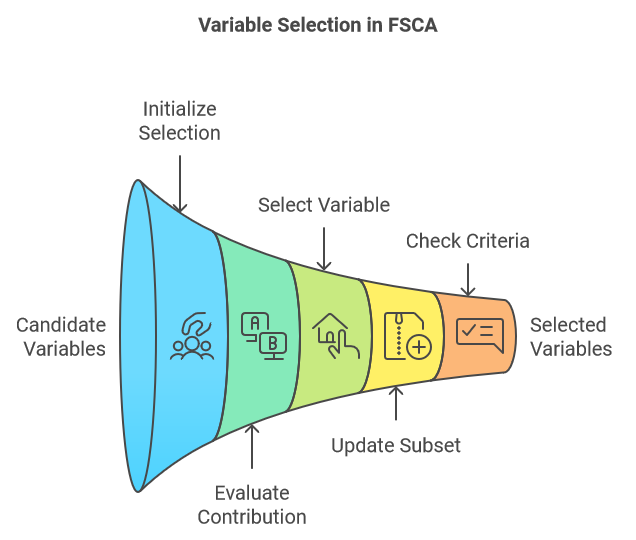
前向选择成分分析（FSCA）是一种降维技术，它通过识别最具信息量的变量来解释原始数据，从而将降维与特征选择相结合。FSCA采用贪婪策略，根据变量捕捉数据剩余方差的能力，逐个选择变量。以下是FSCA流程中涉及的核心步骤概述：

  1. 初始化：
    • 从选定的变量空集和完整的候选变量全集开始。
    • 计算数据集的总方差。
    • 开始迭代过程，选择能够最优预测所有其他变量值的变量，确保这一选择能够捕捉到最大程度的可解释方差。
  2. 迭代选择：
    • 在每一步中，评估每个剩余候选变量在加入当前选定变量集时，对可解释方差的贡献。
    • 选择在加入子集后能使可解释方差增加最多的变量。
  3. 更新：
    • 将选定的变量加入已选变量的子集。
    • 从候选变量集中移除已选定的变量。
    • 在考虑了选定变量的贡献后，重新计算剩余方差（即未解释方差）。
  4. 停止准则：
    • 继续该过程，直到满足预定的停止准则。可以是选定的变量数量达到指定值、可解释方差达到总方差的目标比例，或是添加新变量所解释的增量方差达到阈值。


      FSCA流程概述

给定一组原始变量，我们将它们排列成一个矩阵，其中每一列代表一个不同的特征，每一行代表一个样本。首先，通过标准化对原始值进行转换。从这一刻起，任何提及原始变量均指标准化后的变量集，我们称之为矩阵X。该矩阵X有v列（即v个变量）。FSCA算法至少会生成三组新的变量集：

  • 矩阵Z：该矩阵由X中的k列（k<v）组成，这些列是根据它们对X重建的贡献程度进行排序的。这些列被称为前向选择变量（Forward Selection Variables，FSV）。
  • 矩阵M：该矩阵的列被称为前向选择成分（Forward Selection Components，FSC）。每个成分都是Z中对应列以及（如果存在的话）其前面列的函数。
  • 矩阵U：该矩阵包含系数或载荷，这些系数或载荷与FSV相结合可生成FSC。

该算法的目标是获得一个最优的变量子集，该子集能最好地表示X中的独特变化。然而，这是一个具有挑战性的优化问题。根据所定义的优化标准，FSCA并不总能找到最优的变量子集。在处理大型数据集时，搜索所有可能的子集或许不切实际，因此FSCA提供了一种更为务实的做法。尽管如此，它有时仍无法找到最优子集，因为在早期迭代中选择的变量可能会随着新变量的加入而变得冗余。为了解决这一局限性，本文开头提及的研究论文的作者提出在FSCA过程中引入一个后向精炼步骤。


带后向精炼的FSCA

后向精炼是一种允许移除和替换先前选定变量的过程。该过程涉及重新评估每个选定变量对整体可解释方差的贡献，并考虑可能提供更好匹配的替代变量。尽管这可以提高最终变量集的质量，但它牺牲了纯前向选择所保持的严格重要性顺序。

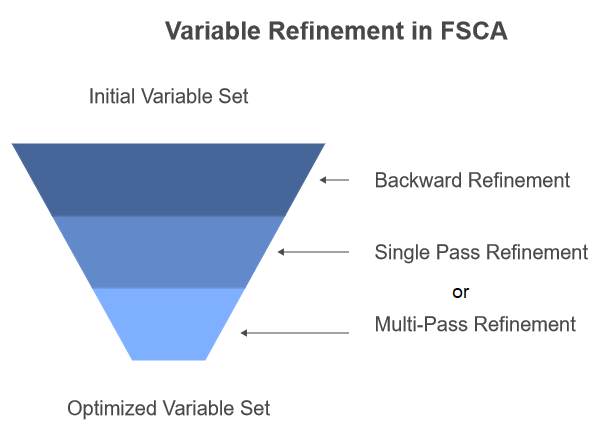
该研究论文概述了两种引入后向精炼的方法。第一种方法是在完成FSCA的所有步骤后，作为后处理步骤应用后向精炼。第二种方法称为递归后向精炼，涉及在FSCA算法第3步结束时每次向Z中添加新变量后，都进行后向精炼。本文后面的部分所展示的代码，就是用于实现的该方法。

精炼步骤本身也有两种变体。第一种称为单次后向精炼（Single Pass Backward Refinement，SPBR），它按顺序评估每个变量的相关性，从最旧的到最新的。第二种称为多次后向精炼（Multi-Pass Backward Refinement，MPBR），它认为最初被认定相关的变量可能会随着对序列中后面变量的调整而变得不再相关。在MPBR中，该过程会重复进行，直到完整遍历一次而没有进行任何进一步的精炼为止。请注意，本文后面提供的代码仅实现了SPBR。

后向精炼示意图

在接下来的章节中，我们将借助一些数学公式和代码，更详细地描述FSCA算法的各个步骤。所有引用的代码段均摘自本文末尾附件中的fsca.mqh文件。


主成分

FSCA算法依赖于使用主成分来初步识别数据集X中独特的变异来源。这一步骤还为Z矩阵的成分变量最大数量提供了指示，从而确定了k值（如前文所定义）。在研究论文中，该算法使用用户指定的k值。然而，在我们的实现中，k始终设置为等于主成分的数量。主成分是通过对X的相关矩阵进行特征值分解得到的。以下列表展示了使用compute_factor_structure()函数计算因子结构的程序。

//+------------------------------------------------------------------+
//| computes the factor structure of a correlation matrix            |
//+------------------------------------------------------------------+
matrix            compute_factor_structure(matrix &covar,matrix &eigenvectors,vector &eigenvalues,vector &cumeigenvalues)
  {
   if(!covar.EigenSymmetricDC(EIGVALUES_V,eigenvalues,eigenvectors))
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return matrix::Zeros(1,1);
     }
   double sum = 0.0;


   if(!np::reverseVector(eigenvalues) ||  !np::reverseMatrixCols(eigenvectors))
     {
      Print(__FUNCTION__, " reverse operation error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   double cumulate[];
   for(ulong i=0 ; i<eigenvalues.Size() ; i++)
     {
      if(eigenvalues[i]>1.e-8)
        {
         sum += eigenvalues[i] ;
         if(!cumulate.Push(sum))
           {
            Print(__FUNCTION__," error adding element ", GetLastError());
            return matrix::Zeros(1,1);
           }
        }
     }

   if(!cumeigenvalues.Assign(cumulate))
     {
      Print(__FUNCTION__," vector assignment error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   cumeigenvalues/=cumeigenvalues[cumeigenvalues.Size()-1];

   cumeigenvalues*=100.0;

   matrix structmat=eigenvectors;

   for(ulong i = 0; i<structmat.Cols(); i++)
      if(!structmat.Col(eigenvectors.Col(i)*sqrt(eigenvalues[i]>=0.0?eigenvalues[i]:0.0),i))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return matrix::Zeros(1,1);
        }

   if(!structmat.Clip(-1.0,1.0))
     {
      Print(__FUNCTION__, "error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   return structmat;
  }
//+------------------------------------------------------------------+
//| computes the factor structure of a correlation matrix            |
//+------------------------------------------------------------------+
matrix compute_factor_structure(matrix &covar, matrix &eigenvectors, vector &eigenvalues, vector &cumeigenvalues) {
    if (!covar.EigenSymmetricDC(EIGVALUES_V, eigenvalues, eigenvectors)) {
        Print(__FUNCTION__, " error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    double sum = 0.0;

    if (!np::reverseVector(eigenvalues) || !np::reverseMatrixCols(eigenvectors)) {
        Print(__FUNCTION__, " reverse operation error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    double cumulate[];
    for (ulong i = 0; i < eigenvalues.Size(); i++) {
        if (eigenvalues[i] > 1.e-8) {
            sum += eigenvalues[i];
            if (!cumulate.Push(sum)) {
                Print(__FUNCTION__, " error adding element ", GetLastError());
                return matrix::Zeros(1, 1);
            }
        }
    }

    if (!cumeigenvalues.Assign(cumulate)) {
        Print(__FUNCTION__, " vector assignment error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    cumeigenvalues /= cumeigenvalues[cumeigenvalues.Size() - 1];
    cumeigenvalues *= 100.0;

    matrix structmat = eigenvectors;

    for (ulong i = 0; i < structmat.Cols(); i++) {
        if (!structmat.Col(eigenvectors.Col(i) * sqrt(eigenvalues[i] >= 0.0 ? eigenvalues[i] : 0.0), i)) {
            Print(__FUNCTION__, "error ", GetLastError());
            return matrix::Zeros(1, 1);
        }
    }

    if (!structmat.Clip(-1.0, 1.0)) {
        Print(__FUNCTION__, "error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    return structmat;
}

该函数以相关矩阵covar作为输入，并返回一个包含因子载荷的矩阵。它使用EigenSymmetricDC函数对相关矩阵进行特征值分解。所得的特征值存储在eigenvalues向量中，而特征向量则存储在eigenvectors矩阵中。随后，该函数将特征值和特征向量的顺序反转，以确保它们按降序排列。它通过迭代求和计算累积特征值，并将这些值存储在cumeigenvalues向量中。累积特征值经过标准化处理，用于表示总方差的百分比。

接下来，该函数通过将每个特征向量乘以其对应特征值的平方根来计算因子载荷，并将结果存储在structmat矩阵中。为确保因子载荷保持在合理范围内，其值被限制在-1到1之间。最后，该函数返回包含计算所得因子载荷的structmat矩阵。

从相关矩阵中推导出的因子结构由因子载荷组成，这些载荷表示变量与潜在隐含因子之间的关系。这些载荷有助于解释隐含因子的含义，并评估每个变量在解释数据方差时的重要性。

compute_factor_structure() 的输出用于compute_principal_components() 函数中，用于计算主成分。

//+------------------------------------------------------------------+
//|   calculates the principal components                            |
//+------------------------------------------------------------------+
matrix compute_principal_components(void) {
    matrix out(m_data.Rows(), ulong(m_num_comps));
    vector drow, eigcol, nv;
    double sum;

    for (ulong i = 0; i < m_data.Rows(); i++) {
        drow = m_data.Row(i);
        for (ulong j = 0; j < m_num_comps; j++) {
            sum = 0.0;
            for (ulong k = 0; k < m_data.Cols(); k++) {
                sum += drow[k] * m_eigvectors[k][j] / sqrt(m_eigvalues[j]);
            }
            out[i][j] = sum;
        }
    }

    return out;
}

compute_principal_components()函数无需输入参数，返回一个包含主成分的矩阵。初始化一个输出矩阵out用于存储主成分，其维度与输入数据的行数以及期望的主成分数量相等。该函数遍历输入数据矩阵的每一行，通过计算该行与协方差矩阵对应特征向量的点积，再除以相关特征值的平方根，来得到每个主成分。计算得到的主成分存储在out矩阵中。此函数采用标准公式将数据点投影到主成分子空间，从而计算主成分。

主成分的基本概念是，利用一组数量减少的成分变量，对包含众多变量的原始数据矩阵 X 进行近似表示。这种近似是通过线性变换实现的。

主成分

我们可以通过计算原始数据矩阵X与其近似值之间差异的平方和，来评估这种近似的误差。

近似误差

或者，我们也可以通过计算成分变量所能解释的X总方差的比例，来评估近似的质量。

可解释方差

为了实现最优近似，我们必须从X中策略性地选择一部分列来构成矩阵Z，这些列将用于计算成分变量。需要注意的是，主成分与最终由矩阵M表示的成分变量是不同的。


最大化可解释方差

FSCA算法的一个关键步骤是，从现有子集中选择要添加的最优变量。为此，我们为每个潜在变量分配一个分数，并选择分数最高的那个。正如研究论文所述，该评分标准（分数）的计算相对复杂。然而，作者提供了数学证明，表明对于竞争变量，该评分标准的排名顺序与它们可解释方差的排名顺序相匹配。意味着，分数最高的变量也能使可解释方差最大化。

以下方程式提供了一种更简单的方法，用于描述每个潜在变量的分数计算方式。对公式数学推导感兴趣的读者可参考研究论文。

中间项公式

评分标准公式

Z(i) 是将矩阵X的第i列添加到矩阵Z后所得到的新矩阵。
变量x(j)是矩阵X的第j列
项v表示矩阵X中变量（列）的数量
中间项q是一个长度为k的列向量

以下是实现该评分标准计算过程的代码。

//+------------------------------------------------------------------+
//|  calculates the criterion for assessing a component              |
//+------------------------------------------------------------------+
double compute_criterion(matrix &covar, ulong &keptcols[], ulong nkept, ulong trial_col) {
    ulong i, j, k, irow, new_kept;
    double sum, crit, dtemp;
    new_kept = nkept + 1;
    matrix mt(new_kept, new_kept);

    for (i = 0; i < new_kept; i++) {
        if (i < nkept)
            irow = keptcols[i];
        else
            irow = trial_col;

        for (j = 0; j < nkept; j++)
            mt[i][j] = covar[irow][keptcols[j]];

        mt[i][nkept] = covar[irow][trial_col];
    }

    matrix mtinv = mt.Inv();
    vector vec(new_kept);

    crit = 0.0;
    for (j = 0; j < m_preds; j++) {
        for (i = 0; i < nkept; i++)
            vec[i] = covar[j][keptcols[i]];

        vec[nkept] = covar[j][trial_col];

        sum = 0.0;
        for (i = 0; i < new_kept; i++)
            sum += vec[i] * vec[i] * mtinv[i][i];

        crit += sum;

        sum = 0.0;
        for (i = 1; i < new_kept; i++) {
            dtemp = vec[i];
            for (k = 0; k < i; k++)
                sum += dtemp * vec[k] * mtinv[i][k];
        }

        crit += 2.0 * sum;
    }

    return crit;
}

compute_criterion()函数用于计算一个评估标准，以便在特征选择过程中评估某个成分。该函数接收以下输入：一个相关矩阵covar、已选变量数组keptcols、已选变量数量nkept，以及待评估试验变量的索引。

函数首先创建一个新矩阵mt，该矩阵将现有已选变量与试验变量合并。接着，函数计算这个扩展矩阵mt的逆矩阵。随后，函数遍历原始数据集中的所有变量，根据每个变量与已选变量之间的协方差（以mt矩阵的逆矩阵加权）计算一个评估标准值。计算得到的评估标准值累加到变量crit中。

该函数的目的是评估向已选变量集中添加一个新变量的影响程度。评估标准值越高，表明该新变量可能有助于提高模型性能；而评估标准值越低，则表明该新变量可能无益。此函数可在特征选择算法中使用，以识别对给定模型最具信息量的变量。


递归反向精炼

反向精炼是前向选择的一种变体，如以下backward_refinement()代码示例所示。

//+------------------------------------------------------------------+
//| backward refinement routine                                      |
//+------------------------------------------------------------------+
ulong backward_refinement(matrix &covar, ulong &kept_columns[], ulong nkept, double &best_crit) {
    ulong i, old_col, new_col, best_col, refined;
    double crit;

    best_crit = substvar(covar, kept_columns, nkept, 0, kept_columns[0]);
    refined = 0;

    for (old_col = 0; old_col < nkept; old_col++) {

        if (old_col == nkept - 1 && !refined)
            break;

        best_col = ULONG_MAX;
        for (new_col = 0; new_col < m_preds; new_col++) {

            for (i = 0; i < nkept; i++) {
                if (new_col == kept_columns[i])
                    break;
            }

            if (i < nkept)
                continue;

            crit = substvar(covar, kept_columns, nkept, old_col, new_col);

            if (crit > best_crit) {
                best_crit = crit;
                best_col = new_col;
            }
        }

        if (best_col != ULONG_MAX && best_col >= 0) {
            // Print(__FUNCTION__,"  Replaced predictor at column ",kept_columns[old_col], " with ",best_col," to get criterion = ", best_crit);
            kept_columns[old_col] = best_col;
            refined = 1;
        }
    }
    return refined;
}

这段MQL5代码实现了一种用于特征选择的反向精炼算法。该算法会迭代评估移除每个已选变量对特定评估标准的影响。通过在移除每个变量后计算评估标准，函数能够确定移除哪个变量对评估标准造成的变化最小。如果变化低于预设阈值，则该变量会从已选集合中移除，并重复此过程，直至无法再进行进一步精炼。如果进行了精炼操作，函数会返回1；否则返回0。

backward_refinement()函数中调用的substvar()例程实现了一种变量替换机制，该机制根据相关矩阵和一组已选变量计算评估标准。在特征选择算法中，此例程用于评估用一个变量替换另一个变量的影响。

//+------------------------------------------------------------------+
//| variable substitution routine                                    |
//+------------------------------------------------------------------+
double substvar(matrix &covar, ulong &keptcols[], ulong nkept, ulong old_col, ulong new_col) {
    ulong i, j, k, irow, saved_col;
    double sum, crit, dtemp;
    matrix mt(nkept, nkept);

    saved_col = keptcols[old_col];
    keptcols[old_col] = new_col;

    for (i = 0; i < nkept; i++) {
        irow = keptcols[i];
        for (j = 0; j < nkept; j++) {
            mt[i][j] = covar[irow][keptcols[j]];
        }
    }

    matrix mtinv = mt.Inv();
    vector vec(nkept);

    crit = 0.0;
    for (j = 0; j < m_preds; j++) {

        for (i = 0; i < nkept; i++) {
            vec[i] = covar[j][keptcols[i]];
        }

        sum = 0.0;
        for (i = 0; i < nkept; i++) {
            sum += vec[i] * vec[i] * mtinv[i][i];
        }
        crit += sum;

        sum = 0.0;
        for (i = 1; i < nkept; i++) {
            dtemp = vec[i];
            for (k = 0; k < i; k++) {
                sum += dtemp * vec[k] * mtinv[i][k];
            }
        }
        crit += 2.0 * sum;
    }

    keptcols[old_col] = saved_col;

    return crit;
}

该函数接收以下输入参数：相关矩阵covar、已选变量数组keptcols、已选变量数量nkept，以及待替换的旧变量和新变量的索引。函数首先创建一个临时矩阵mt，用于存储covar矩阵中与已选变量对应的子矩阵。随后，使用Inv()函数计算矩阵mt的逆矩阵。接着，遍历原始数据集中的所有变量，根据每个变量与已选变量之间的协方差（以mt矩阵的逆矩阵加权）计算一个评估标准值。计算得到的评估标准值累加到变量crit中。计算完评估标准后，函数将 keptcols 数组中的原始变量恢复，并返回计算得到的评估标准值。

该函数的目的是评估用一个变量替换另一个变量对整体模型的影响程度。评估标准值越高，表明替换操作可能有助于提升模型性能；评估标准值越低，则表明替换可能无益。此函数可集成到特征选择算法中，以确定给定模型的最佳变量组合。


成分的正交性

仅通过严格的前向选择（不结合反向精炼）来选择变量，会根据变量的重要性建立一个层次顺序，从最具影响力的变量开始，重要性逐渐递减。这种排序在实际应用中往往具有重要价值。虽然可以直接使用原始值，但以原始变量的线性组合构建的正交成分变量具有显著优势。这些成分之间不相关，有助于简化模型训练并减少冗余。此外，这些变量内部不存在冗余，可以简化对其贡献的解释。

为了在保留原始排序的同时实现成分变量的正交化，可采用格拉姆-施密特（Gram-Schmidt）正交化方法。该方法首先将第一个成分定义为缩放后的第一个已选变量。对于后续成分，则减去其在现有成分上的投影。通过系统地减去这些投影并进行单位长度标准化，确保成分之间的正交性。最后，重新缩放至单位标准差以便保持一致性。本质上讲，格拉姆-施密特正交化将已选变量转换为一组正交成分，这些成分保留了原始的重要性顺序，为模型的可解释性和效率提供了潜在优势。
以下是格拉姆-施密特变换的实现代码。该函数的输出是一个新矩阵，其中每一列代表一个正交化向量。

//+------------------------------------------------------------------+
//|   Gram Schmidt routine                                           |
//+------------------------------------------------------------------+
matrix gram_schmidt(matrix &input_) {
    ulong irow, icol, inner;
    double dtemp, sum;
    ulong nrows = input_.Rows();
    ulong ncols = input_.Cols();
    matrix output = input_;

    sum = 0.0;

    vector colsum = output.Col(0);
    colsum = MathPow(colsum, 2.0);
    sum = colsum.Sum();
    sum = sqrt(sum);

    if (sum == 0.0) {
        Print(__FUNCTION__, " sum == 0.0 ");
        return matrix::Zeros(0, 0);
    }

    if (!output.Col(output.Col(0) / sum, 0)) {
        Print(__FUNCTION__, " failed column insertion ", GetLastError());
        return matrix::Zeros(0, 0);
    }

    for (icol = 1; icol < ncols; icol++) {
        for (inner = 0; inner < icol; inner++) {
            sum = 0.0;
            for (irow = 0; irow < nrows; irow++)
                sum += (output[irow][icol] * output[irow][inner]);

            for (irow = 0; irow < nrows; irow++)
                output[irow][icol] -= (sum * output[irow][inner]);
        }

        sum = 0.0;
        for (irow = 0; irow < nrows; irow++) {
            dtemp = output[irow][icol];
            sum += dtemp * dtemp;
        }

        sum = sqrt(sum);

        if (sum == 0.0) {
            Print(__FUNCTION__, " sum == 0.0 ");
            return matrix::Zeros(0, 0);
        }

        if (!output.Col(output.Col(icol) / sum, icol)) {
            Print(__FUNCTION__, " failed column insertion ", GetLastError());
            return matrix::Zeros(0, 0);
        }
    }

    return output;
}

该算法通过迭代方式，将输入矩阵的每一列相对于先前已正交化的列进行正交化处理。算法通过将当前列投影到由先前列张成的子空间上，并从当前列中减去该投影来实现。随后，对结果向量进行标准化处理，使其长度为1（单位长度）。代码中包含多项优化以提高效率，例如采用向量运算进行计算，并避免不必要的重复计算。此外，函数还集成了错误处理机制，用于检测潜在问题（如零长度向量或列插入失败等情况）。

在介绍了前向选择（可选结合反向精炼）的所有核心例程后，下一节将展示这些例程如何在FSCA算法的完整实现中被调用。


CFsca类

CFsca类封装了针对数据集执行前向选择成分分析的功能。该类的完整定义位于fsca.mqh文件中，同时包含一个名为stdmat()的简单标准化变换例程。此函数接收一个矩阵作为输入，并返回标准化后的矩阵。

//+------------------------------------------------------------------+
//| standardize a matrix                                             |
//+------------------------------------------------------------------+
matrix stdmat(matrix &in) {
    vector mean = in.Mean(0);
    vector std = in.Std(0);
    std += 1e-10;
    matrix out = in;

    for (ulong row = 0; row < out.Rows(); row++) {
        if (!out.Row((in.Row(row) - mean) / std, row)) {
            Print(__FUNCTION__, " error ", GetLastError());
            return matrix::Zeros(in.Rows(), in.Cols());
        }
    }

    return out;
}

stdmat() 函数通过调用Mean和Std函数，计算输入矩阵中每一列的均值和标准差。随后，创建一个与输入矩阵维度相同的输出矩阵out。该函数遍历输入矩阵的每一行，通过减去对应列的均值并除以该列的标准差，对行数据进行标准化处理。标准化后的行数据存储在输出矩阵out中，最终由函数返回。此函数独立于CFsca类定义，以便单独调用和使用。


CFsca类首先定义其私有成员变量，这些变量用于存储中间计算结果以及FSCA算法所需的数据结构。 

//+------------------------------------------------------------------+
//| fsca class implementation                                        |
//+------------------------------------------------------------------+
class CFsca
  {
private:
   bool              m_fitted;              //flag showing if principal factors were extracted
   matrix m_corrmat,             //correlation matrix
          m_covar,               //altered correlation matrix
          m_data,                //standardized data is here
          m_eigvectors,          //matrix of eigen vectors of m_corrmat matrix
          m_structmat,           //factor loading matrix of m_corrmat matrix
          m_principal_components,             //principal components
          m_fscv_struct,        //fsca factor structure
          m_fscv_eigvects,      //fsca eigen structure
          m_Fsca,        //ordered fsca variables
          m_coeffs,      //fsca component coefficients
          m_Fscv;        //refined fsca variables
   vector m_eigvalues,           //vector of eigen values of m_corrmat matrix
          m_sqcorr,              //mean squared correlation matrix
          m_fscv_eigvals,        //fsca eigen values
          m_fscv_cumeigvals,     //fsca cumulative variance contribution
          m_cumeigvalues;        //cumulative variance contributions of m_corrmat matrix
   ulong             m_num_comps;           //unique instances of redundent variation in m_data
   ulong             m_preds;               //number of variables (columns) in dataset (m_data)
   ulong  m_keptorderedcolumns[],//indices of columns upon which components are calculated for ordered fsca
          m_keptrefinedcolumns[],//indices of columns upon which components are calculated for backward refined fsca
          m_keptcolumns[],
          m_bestcolumn;          //index of first selected column in analysis
   double            m_best_crit;           //best criterion value

接下来是CFsca类的私有方法，其中部分方法已在本文的前文部分有过介绍。其余方法将在讨论该类的公有方法时简要提及。

公有方法定义在CFsca类的末尾部分。在初始化该类的实例后，应首先调用fit()方法。该方法对原始数据集执行前向选择成分分析，接收一个包含原始数据的矩阵作为输入，并返回一个布尔值，指示拟合过程是否成功完成。

//+------------------------------------------------------------------+
//| perform forward selection component analysis on a raw dataset    |
//+------------------------------------------------------------------+
bool fit(matrix &data) {
    m_preds = data.Cols();
    m_fitted = false;
    m_sqcorr = vector::Zeros(m_preds);

    m_data = stdmat(data);
    m_corrmat = m_data.CorrCoef(false);

    m_structmat = compute_factor_structure(m_corrmat, m_eigvectors, m_eigvalues, m_cumeigvalues);

    if (m_structmat.Rows() == 1)
        return false;

    m_num_comps = m_cumeigvalues.Size();

    if (ArrayResize(m_keptorderedcolumns, int(m_num_comps)) < 0 || 
        ArrayResize(m_keptrefinedcolumns, int(m_num_comps)) < 0 ||
        ArrayResize(m_keptcolumns, int(m_num_comps)) < 0 || 
        ArrayInitialize(m_keptcolumns, ULONG_MAX) < 0) {
        Print(__FUNCTION__, " array error ", GetLastError());
        return false;
    }

    m_principal_components = compute_principal_components();

    for (ulong i = 0; i < m_preds; i++)
        m_sqcorr[i] = (compute_criterion(m_corrmat, m_keptcolumns, 0, i) - 1.0) / double(m_preds - 1);

    vector evd_vals = m_eigvalues;
    while (evd_vals[m_preds - 1] <= 0.0) {
        for (ulong j = 1; j < m_preds; j++) {
            for (ulong k = 0; k < j; k++) {
                m_corrmat[j][k] *= 0.99999;
                m_corrmat[k][j] = m_corrmat[j][k];
            }
        }

        matrix empty;
        if (!m_corrmat.EigenSymmetricDC(EIGVALUES_N, evd_vals, empty)) {
            Print(__FUNCTION__, " failed eig decomp ", GetLastError());
            return false;
        }
    }

    m_Fsca = compute_fsca_components(m_data);
    m_Fscv = compute_fscv_components(m_data);

    m_fitted = (m_Fsca.Rows() > 1 && m_Fscv.Rows() > 1);

    return m_fitted;
}

fit()函数负责初始化FSCA流程中使用的各类变量和矩阵。首先，它对输入数据矩阵进行标准化处理，确保数据均值为0且方差为1。随后，函数计算标准化数据的相关矩阵，并将其存储在m_corrmat中。接着，通过调用compute_factor_structure函数计算相关矩阵的因子结构，该结构包含相关矩阵的特征向量（m_eigvectors）、特征值（m_eigvalues）及累积特征值（m_cumeigvalues）。函数会检查因子结构矩阵（m_structmat）是否仅有一行；若如此，则表明因子结构评估出错，函数将返回false。

成分数量（m_num_comps）被设置为非0特征值的个数。随后，函数初始化FSCA流程中使用的各类数组。通过调用compute_principal_components函数计算标准化数据的主成分，并计算各变量与第一主成分的平方相关系数。此外，函数还会检查是否存在负特征值。若发现负值，则对相关矩阵进行微调并重新计算特征值，直至所有特征值均为正。最后，函数分别通过compute_fsca_components和compute_fscv_components函数计算FSCA成分和FSCV成分。若两类成分均成功计算，函数将m_fitted标识设为true。

CFsca类的定义以一系列getter函数收尾，这些函数提供对FSCA分析过程中各类计算结果的访问接口。

//+------------------------------------------------------------------+
//| get the principal components                                     |
//+------------------------------------------------------------------+
matrix get_principal_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_principal_components;
}

//+------------------------------------------------------------------+
//| get the ordered fsca components                                  |
//+------------------------------------------------------------------+
matrix get_fsca_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_Fsca;
}

//+------------------------------------------------------------------+
//| get the backward refined fsca components                         |
//+------------------------------------------------------------------+
matrix get_fscv_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_Fscv;
}

//+------------------------------------------------------------------+
//| get indices of variables defining the ordered fsca components    |
//+------------------------------------------------------------------+
bool get_fsca_var_indices(ulong &indices[]) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    return (ArrayCopy(indices, m_keptorderedcolumns, 0, 0, int(m_num_comps)) > 0);
}

//+---------------------------------------------------------------------------+
//| get indices of variables defining the backward refined fsca components    |
//+---------------------------------------------------------------------------+
bool get_fscv_var_indices(ulong &indices[]) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    return (ArrayCopy(indices, m_keptrefinedcolumns, 0, 0, int(m_num_comps)) > 0);
}

//+-------------------------------------------------------------------+
//| get cumulative variance contribution based on principal components|
//+-------------------------------------------------------------------+
vector get_principal_components_cumulative_variance_contribution(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_cumeigvalues;
}

//+-------------------------------------------------------------------+
//| get cumulative variance contribution based on fscv components     |
//+-------------------------------------------------------------------+
vector get_fscv_cumulative_variance_contribution(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_fscv_cumeigvals;
}

//+-------------------------------------------------------------------+
//| get eigen structure of principal components                       |
//+-------------------------------------------------------------------+
bool get_principal_components_eigstructure(matrix &vectors, vector &values) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    vectors = m_eigvectors;
    values = m_eigvalues;

    return true;
}

//+-------------------------------------------------------------------+
//| get eigen structure of backward refined FSCs                      |
//+-------------------------------------------------------------------+
bool get_fscv_eigstructure(matrix &vectors, vector &values) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    vectors = m_fscv_eigvects;
    values = m_fscv_eigvals;

    return true;
}

//+-------------------------------------------------------------------+
//| get principal components factor structure                         |
//+-------------------------------------------------------------------+
matrix get_principal_components_factorstructure(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_structmat;
}

//+-------------------------------------------------------------------+
//| get the factor structure of FSC with backward refinement          |
//+-------------------------------------------------------------------+
matrix get_fscv_factorstructure(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_fscv_struct;
}

//+------------------------------------------------------------------+
//| get mean squared correlations                                    |
//+------------------------------------------------------------------+
vector get_avg_correlations(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_sqcorr;
}

//+-------------------------------------------------------------------+
//| get forward selection component coefficients matrix               |
//+-------------------------------------------------------------------+
matrix get_fsca_component_coeffs(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_coeffs;
}

这些函数使用户能够获取关键分析结果，例如标准化数据、相关矩阵、因子结构、主成分及成分变量，从而为结果的进一步分析与解释提供便利。本文的阐述至此告一段落，最后将通过一个示例展示如何运用CFsca类。


示例

以下代码清单定义了一个名为FSCA_Demo.mq5的MQL5脚本，该脚本对随机生成的数据集执行前向选择成分分析（FSCA）。脚本中引入了fsca.mqh头文件，其中包含用于FSCA分析的CFsca类定义。

//+------------------------------------------------------------------+
//|                                                    FSCA_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<fsca.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   MathSrand(120);
//---
   matrix mat(100,9);
//---
   mat.Random(0.0,1.0);
//---
   vector var1 = mat.Col(0) + mat.Col(1);
// ---
   vector var2 = mat.Col(2) + mat.Col(3);
//---
   vector var3 = var1 + var2;
//---
   if(!mat.Col(var1,6) || !mat.Col(var2,7) || !mat.Col(var3,8))
     {
      Print("failed column assignment ", GetLastError());
      return;
     }
//---
   CFsca fsca;
//---
   if(!fsca.fit(mat))
      return;
//---
   ulong index[];
   Print("Principal components cumulative variance conributions \n", fsca.get_principal_components_cumulative_variance_contribution());
   Print(" Principal components factor structure \n", fsca.get_principal_components_factorstructure());
   Print("Mean squared correlation of each variable with all others \n", fsca.get_avg_correlations());
//---
   if(fsca.get_fsca_var_indices(index))
     {
      Print(" Ordered FSCA components based on variables located in column indices ");
      ArrayPrint(index);
     }
//---
   Print(" Ordered FSCA component coefficients matrix \n", fsca.get_fsca_component_coeffs());
//---
   if(fsca.get_fscv_var_indices(index))
     {
      Print(" Backward refined FSCA components based on variables located in column indices ");
      ArrayPrint(index);
     }
//---
   matrix vects;
   vector vals;
//---
   if(fsca.get_fscv_eigstructure(vects,vals))
     Print("Backward refined fsca component eigenvalues \n", vals);
//---
   Print(" Backward refined cumulative variance contributions \n", fsca.get_fscv_cumulative_variance_contribution());
//---
   Print(" Backward refined fsca components factor structure \n", fsca.get_fscv_factorstructure());
  }
//+------------------------------------------------------------------+

脚本首先设置随机种子，并创建一个包含随机值的矩阵。随后，通过对矩阵中现有列求和生成三个新向量。接着，脚本尝试将矩阵数据拟合至FSCA模型，并提取多项分析结果，包括累积方差贡献率、因子结构及均方相关性等。此外，脚本分别执行标准FSCA和反向精炼FSCA分析，输出排序后的变量索引和成分系数。以及反向精炼FSCA成分的因子结构。该脚本仅生成一个包含100个样本和9个特征的随机变量数据集。其中后3个变量被设定为依赖于其他变量，其余变量则相互独立。 

运行脚本并分析主成分特征后发现，在9个变量中仅存在6个独立的变异来源。 

DG      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   Principal components cumulative variance conributions 
RM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [31.72121326219056,54.98374706330443,70.21399790786099,82.34742379766755,91.9067775629936,100]
CM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Principal components factor structure 
MH      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [[-0.5430877600903072,0.4698851388299595,-0.02139789374204959,0.5468988095320395,-0.4254498037566715,-0.06082703269184352,-1.3842452210817e-09,-7.527559895073524e-10,0]
RH      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5283294988376427,0.4246506210338227,-0.1190026606589024,-0.6285471675075863,0.3351428244532062,0.1377893424956133,-1.351333204556555e-09,-7.34858353171856e-10,0]
ES      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5563230307728618,-0.3632156082945803,0.4770295070287525,0.3051596297191441,0.4575827252246154,-0.1688715686919785,-1.694159101189325e-09,2.164855665400724e-10,0]
NF      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.2379617600470182,-0.6943076552356867,-0.4580766878219635,-0.2737307249578351,-0.4112051990027778,0.08636320534609224,-1.769139142521297e-09,2.260667780777343e-10,0]
DO      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [0.02487447101754412,-0.08203927651647476,-0.6079889924620585,0.4701685445643955,0.3604839483405348,0.5215295442601863,1.313244252124911e-25,1.228203109452781e-25,0]
IP      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.07016546285360215,-0.110242984252018,0.7306990214221818,-0.07491798042552207,-0.2276538908363994,0.6257501374625694,4.158606798395552e-25,-7.369218656716687e-26,0]
NE      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.7598477338270035,0.6346843827822741,-0.09872272409405579,-0.04786755450396145,-0.0705236166963274,0.05287812507625003,-1.359967783374346e-10,1.333715775589249e-09,0]
NO      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5934182368659159,-0.8024046895986707,-0.000973814713973191,0.01424096330384607,0.02077689502375221,-0.05801790712583575,2.667167815186452e-10,-1.355042254629964e-11,0]
RM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.9897757278036692,-0.1138316306178367,-0.07343616940955985,-0.02494592427830717,-0.03690113231990194,-0.0030829919659495,2.802923111601039e-09,-3.865027968054199e-10,0]]

这是符合预期的，因为其中三个变量是其他变量的组合。观察各变量的累积方差贡献率可以发现，第一个主成分约占总变异的三分之一。因子结构显示，第一主成分与第0至3列及第6至8列的变量呈中度至强负相关，而第4列和第5列的变量则呈现相反趋势。第二个主成分则反映了第0、1列变量与第2、3列变量之间的差异。综合来看，前两个主成分共同解释了超过55%的总变异。

QK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   Mean squared correlation of each variable with all others 
GK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [0.09874555673359317,0.09196664871445229,0.09678803260182336,0.08640965168371836,0.009232616218980055,0.01341075732654295,0.1892345119240549,0.1695472310064176,0.2291509382521983]

接下来分析每个变量与全体变量集合的均方相关系数向量，该向量按原始数据集中变量的出现顺序列出了相关系数。结果显示，最后三个变量的平均相关系数最高，而第4列和第5列变量的相关系数最低。

LR      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Ordered FSCA components based on variables located in column indices 
QQ      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   8 6 2 4 1 5

接下来，我们分析通过调用get_fscv_var_indices()获得的前向选择变量索引。这些索引按变量对数据集总变异的贡献程度降序排列，即贡献最大的变量排在首位。结果显示，最后一个变量（因其出现在索引首位）捕获了数据中最多的变异信息。

QJ      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Ordered FSCA component coefficients matrix 
DM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [[0.9999999989356357,-0.9551778313323678,-1.196676438579672,-0.163265209103464,-0.1301792726137802,0.0741114239785734]
IR      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [7.62883988565579e-10,1.382882745177175,0.7080052470472653,0.1327136589445282,-0.8962870520067646,-0.01038862969019799]
LF      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [6.044914586250671e-10,-1.162965671680505e-09,1.327736785211269,0.1291890234653878,0.1244453203448803,-0.2315140872599129]
EM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [5.84342504938995e-11,-9.115276242144255e-11,-1.685031073006549e-10,1.005785752630206,0.08917398176616295,0.2288955899392838]
JM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [6.626278020206711e-11,8.05911615654048e-10,2.135397240976555e-10,-3.939133914887538e-11,1.404086244047662,0.03569800251260542]
KK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-2.859616016204214e-11,3.48387846349496e-11,2.600743786995707e-10,-1.479500966183878e-10,-3.333024481411151e-11,1.048952273510343]]

接下来，我们研究计算六个主成分所需的系数表。变量按照前文分析的索引数组（即变量重要性排序）依次排列。可以看到，作为最后一个也是最重要的变量，其对应系数非常接近1。继续观察该系数矩阵，会发现越靠后的变量系数越小，直至趋近于0。

CM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Backward refined FSCA components based on variables located in column indices 
ND      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   3 0 2 4 1 5

最后，我们分析通过前向选择与反向精炼相结合的方式筛选出的变量索引。需要强调的是，在这种改进版FSCA方法中，所选变量的顺序并不具有实际意义。然而，相较于严格排序的前向选择方法，这种组合筛选策略能生成更具解释性的变量集合——其仅保留独立的随机变量，而自动剔除存在依赖关系的变量。这一点通过对比标准前向选择与反向精炼前向选择的结果可清晰验证。


结论

本文实现了基于MQL5的前向选择成分分析（FSCA）算法，验证了其在降维与特征选择任务中的有效性。该工具同样适用于探索性数据分析的场景。算法的附加产品之一——数据集的因子结构，为理解潜在作用机制提供了重要的参考。文中提及的所有代码均附于下方。
文件名
 描述
MQL5/include/np.mqh
 通用向量与矩阵工具函数的头文件
MQL5/include/fsca.mqh
 包含实现前向选择成分分析（FSCA）的CFsca类定义的头文件
MQL5/scripts/FSCA_Demo.mq5
 一份用于演示CFsca类使用方法的 MetaTrader 5脚本

本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/16190

附加的文件 |
下载ZIP
np.mqh (74.16 KB)
fsca.mqh (26.89 KB)
FSCA_Demo.mq5 (2.46 KB)
Mql5.zip (16.32 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

最近评论 | 前往讨论 (1)
Aleksey Vyazmikin
Aleksey Vyazmikin | 11 7月 2025 在 12:07

当然，这个话题是永恒的，而且始终具有现实意义。

最好能在文章中介绍不同的方法，以比较它们的有效性，不是在合成数据上，而是在真实数据上。

我曾尝试将特征数增加到 5000，行数增加到 10000，结果等了三天也没等到结果。所以我在想，如果我们把特征数量分成几组，比如每组 100 个例子，然后把每组的优胜者集中起来进行最终筛选，质量是否会大打折扣？

如何使用 MetaTrader 和 Google Sheets 创建交易日志 如何使用 MetaTrader 和 Google Sheets 创建交易日志
使用 MetaTrader 和 Google Sheets 创建交易日志！您将学习如何通过 HTTP POST 同步您的交易数据，并使用 HTTP 请求来获取它。最后，您有一个交易日志，可以帮助您有效地跟踪您的交易。
交易中的神经网络：对比形态变换器（终章） 交易中的神经网络：对比形态变换器（终章）
在本系列的上一篇文章中，我们考察了“原子-基序对比变换器”（AMCT）框架，其用对比学习来发现各个级别的关键形态，从基本元素到复杂结构。在本文中，我们将继续利用 MQL5 实现 AMCT 方式。
构建K线趋势约束模型（第九部分）：多策略EA（2） 构建K线趋势约束模型（第九部分）：多策略EA（2）
理论上，可以集成至EA中的策略数量没有上限。然而，每新增一种策略都会提升算法复杂度。通过融合多策略架构，EA能够更灵活地适应不同市场环境，从而可能提升整体盈利能力。今天，我们将探讨如何通过MQL5实现理查德·唐奇安（Richard Donchian）的经典通道突破策略，以此进一步拓展我们的趋势约束型EA功能体系。
如何将“聪明钱”概念（OB）与斐波那契指标相结合，实现最优进场策略 如何将“聪明钱”概念（OB）与斐波那契指标相结合，实现最优进场策略
SMC（订单块）是机构交易者发起大规模买入或卖出的关键区域。当价格出现显著波动后，借助斐波那契数字可识别从近期波段高点至波段低点的潜在回撤，从而锁定最佳进场位。