MetaTrader 5 / Statistics and analysis
Русский 中文 Español Deutsch 日本語
preview
Feature selection and dimensionality reduction using principal components

Feature selection and dimensionality reduction using principal components

MetaTrader 5 — Statistics and analysis |
1 042 1
Francis Dube
Francis Dube

Introduction

Financial time series prediction often involves analyzing numerous features, many of which may be highly correlated. Dimensionality reduction techniques like Principal Component Analysis (PCA) can help create a more compact representation of these features. However, PCA has limitations, especially in the presence of highly correlated variables. In such cases, PCA tends to exhibit the grouping effect, wherein a set of highly correlated variables collectively contributes to a given principal component. Instead of highlighting any single variable, PCA distributes the influence relatively evenly across all variables in the correlated group.

This even distribution can be beneficial for noise suppression because the principal components emphasize common patterns rather than the random fluctuations unique to individual variables. However, this noise suppression comes at a cost: it often dilutes the contribution of individual variables to each principal component. Variables that might be significant on their own can appear less important within the transformed space, as their influence is absorbed into the broader structure captured by the group. This can be a significant drawback in tasks like variable selection, where the goal is to identify the most influential features, or in root-cause analysis, where understanding the direct impact of specific variables is crucial.

Additionally, this characteristic complicates model interpretation. Since each principal component represents a combination of all the original variables, translating the contribution of these components back into the context of the original variables can be challenging. Practitioners may struggle to draw clear insights from the principal components, as it becomes difficult to determine which original variables drive the observed patterns. To address this issue, we introduce an implementation of Forward Selection Component Analysis (FSCA), a method inspired by the work of Luca Puggini and Sean McLoone, which aims to avoid the pitfalls of PCA when dealing with highly correlated features.


Forward Selection Component Analysis

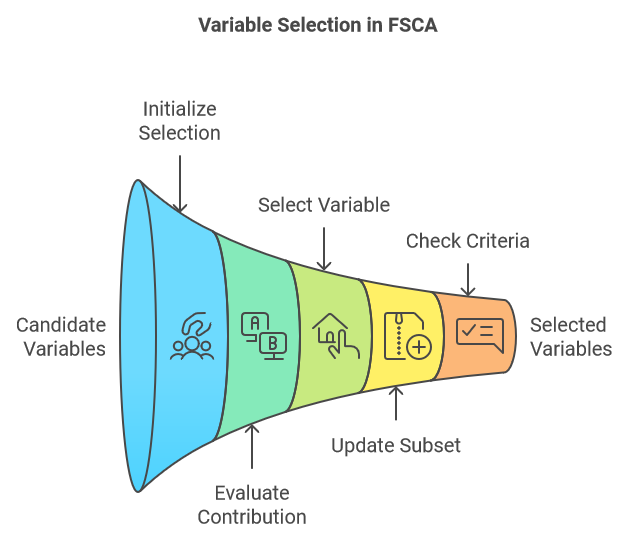
Forward Selection Component Analysis (FSCA) is a dimensionality reduction technique that combines dimensionality reduction and feature selection by identifying the most informative variables to explain the original data. FSCA uses a greedy approach, selecting variables one at a time based on their ability to capture the remaining variance in the data. Below is an outline of the core steps involved in the FSCA procedure:

  1. Initialization:
    • Start with an empty set of selected variables and a full set of candidate variables.
    • Calculate the total variance of the dataset.
    • Begin the iterative process by selecting the variable that best predicts the values of all other variables, ensuring that this choice captures the maximum amount of explained variance.
  2. Iterative Selection:
    • At each step, evaluate the contribution of each remaining candidate variable to the explained variance when added to the current set of selected variables.
    • Select the variable that results in the greatest increase in explained variance when added to the subset.
  3. Update:
    • Add the selected variable to the subset of chosen variables.
    • Remove the selected variable from the set of candidate variables.
    • Recompute the residual variance, or the remaining unexplained variance, after accounting for the contributions of the selected variables.
  4. Stopping Criteria:
    • Continue the process until a predetermined stopping criterion is met. This could be a specified number of selected variables, a target proportion of the total variance explained, or a threshold for the incremental variance explained by adding a new variable.


      FSCA outline

Given a set of raw variables, we arrange them into a matrix, with each column representing a distinct feature and each row representing a single sample. The raw values are first transformed through standardization. From this point forward, any reference to the original variables refers to the set of standardized variables, which we will call matrix X. This matrix X has v columns (variables). The FSCA algorithm produces at least three new sets of variables:

  • Matrix Z: This matrix consists of a subset k (where k<v) of the columns of X, ranked according to how well they contribute to the reconstruction of X. These columns are known as the Forward Selection Variables (FSV).
  • Matrix M: The columns of this matrix are referred to as Forward Selection Components (FSC). Each component is a function of the corresponding column in Z, as well as those that precede it, if any.
  • Matrix U: This matrix contains the coefficients or loadings that, when combined with the FSVs, produce the FSCs.

The goal of the algorithm is to obtain an optimal subset of variables that best represent the unique variation in X. However, this is a challenging optimization problem. FSCA is not always guaranteed to find the optimal subset of variables according to the defined optimization criteria. When dealing with large datasets, it may be impractical to search over all possible subsets, so FSCA offers a more pragmatic approach. Nonetheless, it sometimes fails to find the optimal subset because variables selected in early iterations can become redundant as additional variables are added. To address this limitation, the authors of the research paper referenced at the beginning of this article propose introducing a backward refinement step in the FSCA procedure.


FSCA with backward refinement

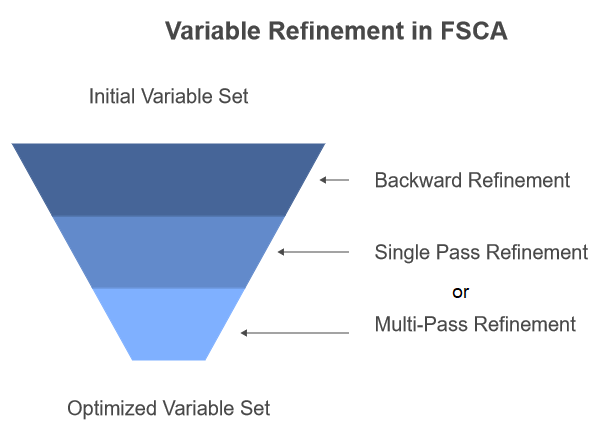
Backward refinement is a procedure that allows for the removal and replacement of previously selected variables. This process involves re-evaluating the contribution of each selected variable to the overall explained variance and considering alternative variables that might provide a better fit. While this can improve the quality of the final variable set, it sacrifices the strict order of importance maintained by pure forward selection.

The research paper outlines two approaches for incorporating backward refinement. The first approach applies backward refinement after all steps of FSCA are completed, as a post-processing step. The second approach, called recursive backward refinement, involves conducting backward refinement each time a new variable is added to Z at the end of step 3 in the FSCA algorithm. This approach is the one implemented in the code that will be presented in a later section of this text.

There are also two variations of the refinement step itself. The first, called Single Pass Backward Refinement (SPBR), evaluates the relevance of each variable in sequence, moving from the oldest to the newest. The second, Multi-Pass Backward Refinement (MPBR), acknowledges that variables initially deemed relevant may become irrelevant as adjustments are made to variables later in the sequence. In MPBR, the process repeats until a full pass occurs without any further refinements. Note that the code provided later in this article implements only SPBR.

Illustration of Backward refinement

In the sections that follow, we will describe the steps of the FSCA algorithm in more detail, using some mathematics and code. All the code snippets referenced are extracted from fsca.mqh, which can be found attached at the end of this article.


Principal components

The FSCA algorithm relies on using principal components to initially identify the unique sources of variation in the dataset X. This step also provides an indication of the maximum number of component variables for the Z matrix, determining the value of k (as defined earlier). In the research paper, the algorithm uses a user-specified k value. However, in our implementation, k is always set equal to the number of principal components. The principal components are derived by decomposing the eigenvalues of the correlation matrix of X. The following listing shows the routine that calculates the factor structure using the compute_factor_structure() function.

//+------------------------------------------------------------------+
//| computes the factor structure of a correlation matrix            |
//+------------------------------------------------------------------+
matrix            compute_factor_structure(matrix &covar,matrix &eigenvectors,vector &eigenvalues,vector &cumeigenvalues)
  {
   if(!covar.EigenSymmetricDC(EIGVALUES_V,eigenvalues,eigenvectors))
     {
      Print(__FUNCTION__, " error ", GetLastError());
      return matrix::Zeros(1,1);
     }
   double sum = 0.0;


   if(!np::reverseVector(eigenvalues) ||  !np::reverseMatrixCols(eigenvectors))
     {
      Print(__FUNCTION__, " reverse operation error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   double cumulate[];
   for(ulong i=0 ; i<eigenvalues.Size() ; i++)
     {
      if(eigenvalues[i]>1.e-8)
        {
         sum += eigenvalues[i] ;
         if(!cumulate.Push(sum))
           {
            Print(__FUNCTION__," error adding element ", GetLastError());
            return matrix::Zeros(1,1);
           }
        }
     }

   if(!cumeigenvalues.Assign(cumulate))
     {
      Print(__FUNCTION__," vector assignment error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   cumeigenvalues/=cumeigenvalues[cumeigenvalues.Size()-1];

   cumeigenvalues*=100.0;

   matrix structmat=eigenvectors;

   for(ulong i = 0; i<structmat.Cols(); i++)
      if(!structmat.Col(eigenvectors.Col(i)*sqrt(eigenvalues[i]>=0.0?eigenvalues[i]:0.0),i))
        {
         Print(__FUNCTION__, "error ", GetLastError());
         return matrix::Zeros(1,1);
        }

   if(!structmat.Clip(-1.0,1.0))
     {
      Print(__FUNCTION__, "error ", GetLastError());
      return matrix::Zeros(1,1);
     }

   return structmat;
  }
//+------------------------------------------------------------------+
//| computes the factor structure of a correlation matrix            |
//+------------------------------------------------------------------+
matrix compute_factor_structure(matrix &covar, matrix &eigenvectors, vector &eigenvalues, vector &cumeigenvalues) {
    if (!covar.EigenSymmetricDC(EIGVALUES_V, eigenvalues, eigenvectors)) {
        Print(__FUNCTION__, " error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    double sum = 0.0;

    if (!np::reverseVector(eigenvalues) || !np::reverseMatrixCols(eigenvectors)) {
        Print(__FUNCTION__, " reverse operation error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    double cumulate[];
    for (ulong i = 0; i < eigenvalues.Size(); i++) {
        if (eigenvalues[i] > 1.e-8) {
            sum += eigenvalues[i];
            if (!cumulate.Push(sum)) {
                Print(__FUNCTION__, " error adding element ", GetLastError());
                return matrix::Zeros(1, 1);
            }
        }
    }

    if (!cumeigenvalues.Assign(cumulate)) {
        Print(__FUNCTION__, " vector assignment error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    cumeigenvalues /= cumeigenvalues[cumeigenvalues.Size() - 1];
    cumeigenvalues *= 100.0;

    matrix structmat = eigenvectors;

    for (ulong i = 0; i < structmat.Cols(); i++) {
        if (!structmat.Col(eigenvectors.Col(i) * sqrt(eigenvalues[i] >= 0.0 ? eigenvalues[i] : 0.0), i)) {
            Print(__FUNCTION__, "error ", GetLastError());
            return matrix::Zeros(1, 1);
        }
    }

    if (!structmat.Clip(-1.0, 1.0)) {
        Print(__FUNCTION__, "error ", GetLastError());
        return matrix::Zeros(1, 1);
    }

    return structmat;
}

This function takes a correlation matrix, covar, as input and returns a matrix containing the factor loadings. It performs eigenvalue decomposition on the correlation matrix using the EigenSymmetricDC function. The resulting eigenvalues are stored in the eigenvalues vector, while the eigenvectors are stored in the eigenvectors matrix. The function then reverses the order of the eigenvalues and eigenvectors to ensure they are sorted in descending order. It computes the cumulative eigenvalues by iteratively summing them and stores these in the cumeigenvalues vector. The cumulative eigenvalues are normalized to represent the percentage of the total variance.

Next, the function calculates the factor loadings by multiplying each eigenvector by the square root of its corresponding eigenvalue, storing the result in the structmat matrix. To ensure that the factor loadings remain within a reasonable range, they are clipped between -1 and 1. Finally, the function returns the structmat matrix containing the calculated factor loadings.

The factor structure derived from the correlation matrix consists of factor loadings that represent the relationships between the variables and the underlying latent factors. These loadings help interpret the latent factors' meaning and assess each variable's importance in explaining the variance in the data.

The output from compute_factor_structure() is used in the compute_principal_components() function to calculate the principal components.

//+------------------------------------------------------------------+
//|   calculates the principal components                            |
//+------------------------------------------------------------------+
matrix compute_principal_components(void) {
    matrix out(m_data.Rows(), ulong(m_num_comps));
    vector drow, eigcol, nv;
    double sum;

    for (ulong i = 0; i < m_data.Rows(); i++) {
        drow = m_data.Row(i);
        for (ulong j = 0; j < m_num_comps; j++) {
            sum = 0.0;
            for (ulong k = 0; k < m_data.Cols(); k++) {
                sum += drow[k] * m_eigvectors[k][j] / sqrt(m_eigvalues[j]);
            }
            out[i][j] = sum;
        }
    }

    return out;
}

The compute_principal_components() function takes no input parameters and returns a matrix containing the principal components. An output matrix out is initialized to store the principal components, with dimensions equal to the number of rows in the input data and the number of desired principal components. The function iterates over each row of the input data matrix, calculating each principal component by taking the dot product of the row with the corresponding eigenvector of the covariance matrix, divided by the square root of the associated eigenvalue. The resulting principal component is stored in the out matrix. This function calculates the principal components using the standard formula for projecting data points onto the principal component subspace.

The fundamental concept underlying principal components is the approximation of the original data matrix X, which contains many variables, using a reduced set of component variables. This approximation is achieved through a linear transformation.

Principal Components

We can evaluate the error in this approximation by calculating the sum of squared differences between X and its approximation.

Error of Approximation

Alternatively, we can assess the quality of the approximation by computing the fraction of X's total variance that is explained by the component variables.

Explained Variance

To achieve an optimal approximation, we must strategically select a subset of columns from X to form Z, which will be used to calculate the component variables. It is important to note that the principal components and the final component variables, represented by the matrix M, are distinct.


Maximizing explained variance

One of the key steps in the FSCA algorithm is selecting the optimal variable to add to the existing subset. To do this, we assign a score to each potential variable and select the one with the highest score. The computation of this criterion (score), as described in the research paper, is relatively complex. However, the authors provide a mathematical proof that the rank order of this criterion for competing variables matches the rank order of their explained variance. This means that the variable with the highest score also maximizes the explained variance.

A simpler way to describe the score calculation for each potential variable is with the equation provided below. Readers interested in the mathematical derivation of the formula can refer to the research paper.

Formula for Intermediate term

Formula for the criterion

Z(i) is the matrix Z with column i of X added to it.
The variable x(j) is column j of X
The term v is the number of variables (columns) in X
The intermediate term q is a column vector k elements long

Below is the code that implements the calculation of the criterion.

//+------------------------------------------------------------------+
//|  calculates the criterion for assessing a component              |
//+------------------------------------------------------------------+
double compute_criterion(matrix &covar, ulong &keptcols[], ulong nkept, ulong trial_col) {
    ulong i, j, k, irow, new_kept;
    double sum, crit, dtemp;
    new_kept = nkept + 1;
    matrix mt(new_kept, new_kept);

    for (i = 0; i < new_kept; i++) {
        if (i < nkept)
            irow = keptcols[i];
        else
            irow = trial_col;

        for (j = 0; j < nkept; j++)
            mt[i][j] = covar[irow][keptcols[j]];

        mt[i][nkept] = covar[irow][trial_col];
    }

    matrix mtinv = mt.Inv();
    vector vec(new_kept);

    crit = 0.0;
    for (j = 0; j < m_preds; j++) {
        for (i = 0; i < nkept; i++)
            vec[i] = covar[j][keptcols[i]];

        vec[nkept] = covar[j][trial_col];

        sum = 0.0;
        for (i = 0; i < new_kept; i++)
            sum += vec[i] * vec[i] * mtinv[i][i];

        crit += sum;

        sum = 0.0;
        for (i = 1; i < new_kept; i++) {
            dtemp = vec[i];
            for (k = 0; k < i; k++)
                sum += dtemp * vec[k] * mtinv[i][k];
        }

        crit += 2.0 * sum;
    }

    return crit;
}

The compute_criterion() function calculates a criterion for assessing a component in the feature selection process. It takes as input a correlation matrix, covar, an array of selected variables, keptcols, the number of selected variables, nkept, and the index of the trial variable to be evaluated.

The function begins by creating a new matrix, mt, which augments the existing set of selected variables with the trial variable. It then calculates the inverse of this augmented matrix, mt. The function iterates over all variables in the original dataset, calculating a criterion for each variable based on the covariance between that variable and the selected variables, weighted by the inverse of the mt matrix. The calculated criterion is accumulated in the crit variable.

The purpose of this function is to evaluate the impact of adding a new variable to the set of selected variables. A higher criterion value indicates that the new variable is likely to improve the model's performance, while a lower criterion value suggests it may not be beneficial. This function can be used within a feature selection algorithm to identify the most informative variables for a given model.


Recursive backward refinement

Backward refinement is a variation of forward selection, as illustrated by the backward_refinement() code listing below.

//+------------------------------------------------------------------+
//| backward refinement routine                                      |
//+------------------------------------------------------------------+
ulong backward_refinement(matrix &covar, ulong &kept_columns[], ulong nkept, double &best_crit) {
    ulong i, old_col, new_col, best_col, refined;
    double crit;

    best_crit = substvar(covar, kept_columns, nkept, 0, kept_columns[0]);
    refined = 0;

    for (old_col = 0; old_col < nkept; old_col++) {

        if (old_col == nkept - 1 && !refined)
            break;

        best_col = ULONG_MAX;
        for (new_col = 0; new_col < m_preds; new_col++) {

            for (i = 0; i < nkept; i++) {
                if (new_col == kept_columns[i])
                    break;
            }

            if (i < nkept)
                continue;

            crit = substvar(covar, kept_columns, nkept, old_col, new_col);

            if (crit > best_crit) {
                best_crit = crit;
                best_col = new_col;
            }
        }

        if (best_col != ULONG_MAX && best_col >= 0) {
            // Print(__FUNCTION__,"  Replaced predictor at column ",kept_columns[old_col], " with ",best_col," to get criterion = ", best_crit);
            kept_columns[old_col] = best_col;
            refined = 1;
        }
    }
    return refined;
}

This MQL5 code implements a backward refinement algorithm for feature selection. It iteratively evaluates the impact of removing each selected variable on a specified criterion. By calculating the criterion with each variable removed, the function identifies which variable’s removal results in the least significant change to the criterion. If the change is below a predefined threshold, the variable is removed from the selected set, and the process is repeated until no additional refinements can be made. The function returns 1 if a refinement was made and 0 otherwise.

The substvar() routine, called within the backward_refinement() function, implements a variable substitution mechanism that calculates a criterion based on the correlation matrix and a set of selected variables. This routine is utilized in a feature selection algorithm to evaluate the impact of replacing one variable with another.

//+------------------------------------------------------------------+
//| variable substitution routine                                    |
//+------------------------------------------------------------------+
double substvar(matrix &covar, ulong &keptcols[], ulong nkept, ulong old_col, ulong new_col) {
    ulong i, j, k, irow, saved_col;
    double sum, crit, dtemp;
    matrix mt(nkept, nkept);

    saved_col = keptcols[old_col];
    keptcols[old_col] = new_col;

    for (i = 0; i < nkept; i++) {
        irow = keptcols[i];
        for (j = 0; j < nkept; j++) {
            mt[i][j] = covar[irow][keptcols[j]];
        }
    }

    matrix mtinv = mt.Inv();
    vector vec(nkept);

    crit = 0.0;
    for (j = 0; j < m_preds; j++) {

        for (i = 0; i < nkept; i++) {
            vec[i] = covar[j][keptcols[i]];
        }

        sum = 0.0;
        for (i = 0; i < nkept; i++) {
            sum += vec[i] * vec[i] * mtinv[i][i];
        }
        crit += sum;

        sum = 0.0;
        for (i = 1; i < nkept; i++) {
            dtemp = vec[i];
            for (k = 0; k < i; k++) {
                sum += dtemp * vec[k] * mtinv[i][k];
            }
        }
        crit += 2.0 * sum;
    }

    keptcols[old_col] = saved_col;

    return crit;
}

The function takes as input a correlation matrix, covar, an array of selected variables, keptcols, the number of selected variables, nkept, and the indices of the old and new variables to be substituted. It creates a temporary matrix, mt, to store the submatrix of covar corresponding to the selected variables. The function then calculates the inverse of the mt matrix using the Inv() function. It iterates over all variables in the original dataset, calculating a criterion for each variable based on the covariance between the variable and the selected variables, weighted by the inverse of the mt matrix. The calculated criterion is accumulated in the crit variable. After calculating the criterion, the function restores the original variable in the keptcols array and returns the calculated criterion.

The purpose of this function is to evaluate the impact of replacing a variable with another on the overall model. A higher criterion value indicates that the replacement is likely to improve the model's performance, while a lower criterion value suggests that it may not be beneficial. This function can be integrated into a feature selection algorithm to identify the optimal combination of variables for a given model.


Orthogonalization of components

Selecting variables through strictly forward selection, without incorporating backward refinement, establishes a hierarchical order based on their significance, starting with the most influential and progressively decreasing in importance. This ordering is often invaluable in practical applications. While raw values can be used directly, orthogonal component variables—constructed as linear combinations of the original variables—offer distinct advantages. These components are uncorrelated, which facilitates model training and minimizes redundancy. Additionally, the absence of redundancy within these variables can simplify the interpretation of their contributions.

To achieve orthogonal component variables while preserving the original ordering, the Gram-Schmidt orthogonalization method is suitable. This procedure begins by defining the initial component as the scaled first selected variable. For subsequent components, projections onto existing components are subtracted. By systematically subtracting these projections and normalizing to unit length, the orthogonality of the components is ensured. Finally, rescaling to unit standard deviation maintains consistency. In essence, Gram-Schmidt orthogonalization transforms the selected variables into a set of orthogonal components that retain the original order of importance, offering potential benefits in model interpretability and efficiency.

The following is an implementation of the Gram-Schmidt transformation. The output of the function is a new matrix where each column represents an orthogonalized vector.

//+------------------------------------------------------------------+
//|   Gram Schmidt routine                                           |
//+------------------------------------------------------------------+
matrix gram_schmidt(matrix &input_) {
    ulong irow, icol, inner;
    double dtemp, sum;
    ulong nrows = input_.Rows();
    ulong ncols = input_.Cols();
    matrix output = input_;

    sum = 0.0;

    vector colsum = output.Col(0);
    colsum = MathPow(colsum, 2.0);
    sum = colsum.Sum();
    sum = sqrt(sum);

    if (sum == 0.0) {
        Print(__FUNCTION__, " sum == 0.0 ");
        return matrix::Zeros(0, 0);
    }

    if (!output.Col(output.Col(0) / sum, 0)) {
        Print(__FUNCTION__, " failed column insertion ", GetLastError());
        return matrix::Zeros(0, 0);
    }

    for (icol = 1; icol < ncols; icol++) {
        for (inner = 0; inner < icol; inner++) {
            sum = 0.0;
            for (irow = 0; irow < nrows; irow++)
                sum += (output[irow][icol] * output[irow][inner]);

            for (irow = 0; irow < nrows; irow++)
                output[irow][icol] -= (sum * output[irow][inner]);
        }

        sum = 0.0;
        for (irow = 0; irow < nrows; irow++) {
            dtemp = output[irow][icol];
            sum += dtemp * dtemp;
        }

        sum = sqrt(sum);

        if (sum == 0.0) {
            Print(__FUNCTION__, " sum == 0.0 ");
            return matrix::Zeros(0, 0);
        }

        if (!output.Col(output.Col(icol) / sum, icol)) {
            Print(__FUNCTION__, " failed column insertion ", GetLastError());
            return matrix::Zeros(0, 0);
        }
    }

    return output;
}

The algorithm works by iteratively orthogonalizing each column of the input matrix regarding the previously orthogonalized columns. This is accomplished by projecting the current column onto the subspace spanned by the previous columns and subtracting this projection from the current column. The resulting vector is then normalized to have unit length. The code includes several optimizations to improve efficiency, such as using vector operations for calculations and avoiding unnecessary computations. Additionally, the function incorporates error handling to check for potential issues, such as zero-length vectors or failed column insertions.

Having covered all the core routines for performing forward selection with optional backward refinement, the next section will demonstrate how these routines are utilized in the full implementation of the FSCA algorithm.


The CFsca class

The class named CFsca encapsulates the functionality for performing forward selection component analysis on a dataset. The full class is defined in fsca.mqh, alongside a simple standardization transformation routine called stdmat(). This function takes a matrix as input and returns a standardized matrix.

//+------------------------------------------------------------------+
//| standardize a matrix                                             |
//+------------------------------------------------------------------+
matrix stdmat(matrix &in) {
    vector mean = in.Mean(0);
    vector std = in.Std(0);
    std += 1e-10;
    matrix out = in;

    for (ulong row = 0; row < out.Rows(); row++) {
        if (!out.Row((in.Row(row) - mean) / std, row)) {
            Print(__FUNCTION__, " error ", GetLastError());
            return matrix::Zeros(in.Rows(), in.Cols());
        }
    }

    return out;
}

The stdmat() function calculates the mean and standard deviation of each column in the input matrix using the Mean and Std functions. It then creates an output matrix out with the same dimensions as the input matrix. The function iterates over each row of the input matrix, standardizing it by subtracting the mean of the corresponding column and dividing by the column's standard deviation. The standardized row is stored in the output matrix out, which is returned at the end of the function. This function is placed outside the CFsca class to allow for independent utilization.


The CFsca class begins by defining its private members, which are used to store intermediate results and the data structures required for FSCA. 

//+------------------------------------------------------------------+
//| fsca class implementation                                        |
//+------------------------------------------------------------------+
class CFsca
  {
private:
   bool              m_fitted;              //flag showing if principal factors were extracted
   matrix m_corrmat,             //correlation matrix
          m_covar,               //altered correlation matrix
          m_data,                //standardized data is here
          m_eigvectors,          //matrix of eigen vectors of m_corrmat matrix
          m_structmat,           //factor loading matrix of m_corrmat matrix
          m_principal_components,             //principal components
          m_fscv_struct,        //fsca factor structure
          m_fscv_eigvects,      //fsca eigen structure
          m_Fsca,        //ordered fsca variables
          m_coeffs,      //fsca component coefficients
          m_Fscv;        //refined fsca variables
   vector m_eigvalues,           //vector of eigen values of m_corrmat matrix
          m_sqcorr,              //mean squared correlation matrix
          m_fscv_eigvals,        //fsca eigen values
          m_fscv_cumeigvals,     //fsca cumulative variance contribution
          m_cumeigvalues;        //cumulative variance contributions of m_corrmat matrix
   ulong             m_num_comps;           //unique instances of redundent variation in m_data
   ulong             m_preds;               //number of variables (columns) in dataset (m_data)
   ulong  m_keptorderedcolumns[],//indices of columns upon which components are calculated for ordered fsca
          m_keptrefinedcolumns[],//indices of columns upon which components are calculated for backward refined fsca
          m_keptcolumns[],
          m_bestcolumn;          //index of first selected column in analysis
   double            m_best_crit;           //best criterion value

Next, are the private methods of the CFsca class, some of which we have covered in previous sections of this text. Other methods will be briefly mentioned when we discuss the public methods of the class.

The public methods are defined at the end of the CFsca class. The fit() method should be called first after initializing an instance of the class. This method performs forward selection component analysis on the raw dataset. It takes as input a matrix containing the original raw data and returns a boolean value indicating whether the fitting process was successful.

//+------------------------------------------------------------------+
//| perform forward selection component analysis on a raw dataset    |
//+------------------------------------------------------------------+
bool fit(matrix &data) {
    m_preds = data.Cols();
    m_fitted = false;
    m_sqcorr = vector::Zeros(m_preds);

    m_data = stdmat(data);
    m_corrmat = m_data.CorrCoef(false);

    m_structmat = compute_factor_structure(m_corrmat, m_eigvectors, m_eigvalues, m_cumeigvalues);

    if (m_structmat.Rows() == 1)
        return false;

    m_num_comps = m_cumeigvalues.Size();

    if (ArrayResize(m_keptorderedcolumns, int(m_num_comps)) < 0 || 
        ArrayResize(m_keptrefinedcolumns, int(m_num_comps)) < 0 ||
        ArrayResize(m_keptcolumns, int(m_num_comps)) < 0 || 
        ArrayInitialize(m_keptcolumns, ULONG_MAX) < 0) {
        Print(__FUNCTION__, " array error ", GetLastError());
        return false;
    }

    m_principal_components = compute_principal_components();

    for (ulong i = 0; i < m_preds; i++)
        m_sqcorr[i] = (compute_criterion(m_corrmat, m_keptcolumns, 0, i) - 1.0) / double(m_preds - 1);

    vector evd_vals = m_eigvalues;
    while (evd_vals[m_preds - 1] <= 0.0) {
        for (ulong j = 1; j < m_preds; j++) {
            for (ulong k = 0; k < j; k++) {
                m_corrmat[j][k] *= 0.99999;
                m_corrmat[k][j] = m_corrmat[j][k];
            }
        }

        matrix empty;
        if (!m_corrmat.EigenSymmetricDC(EIGVALUES_N, evd_vals, empty)) {
            Print(__FUNCTION__, " failed eig decomp ", GetLastError());
            return false;
        }
    }

    m_Fsca = compute_fsca_components(m_data);
    m_Fscv = compute_fscv_components(m_data);

    m_fitted = (m_Fsca.Rows() > 1 && m_Fscv.Rows() > 1);

    return m_fitted;
}

The fit() function initializes various variables and matrices used in the FSCA process. First, it standardizes the input data matrix, ensuring it has zero mean and unit variance. The function then calculates the correlation matrix of the standardized data, storing it in m_corrmat. Next, it computes the factor structure of the correlation matrix using the compute_factor_structure function. This factor structure includes the eigenvectors (m_eigvectors), eigenvalues (m_eigvalues), and cumulative eigenvalues (m_cumeigvalues) of the correlation matrix. The function checks whether the factor structure matrix (m_structmat) has only one row; if so, this indicates an error in evaluating the factor structure, and the function returns false.

The number of components (m_num_comps) is set equal to the number of non-zero eigenvalues. The function then initializes various arrays used in the FSCA process. It computes the principal components of the standardized data using the compute_principal_components function and calculates the squared correlations between each variable and the first principal component. Additionally, the function checks for any negative eigenvalues. If any are found, it makes slight adjustments to the correlation matrix and recalculates the eigenvalues until all are positive. Finally, the function computes the FSCA components using the compute_fsca_components function and the FSCV components using the compute_fscv_components function. If both the FSCA and FSCV components are successfully calculated, the function sets the m_fitted flag to true.

Concluding the definition of the CFsca class are getter functions that provide access to various aspects of the analytic computations performed during the FSCA process.

//+------------------------------------------------------------------+
//| get the principal components                                     |
//+------------------------------------------------------------------+
matrix get_principal_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_principal_components;
}

//+------------------------------------------------------------------+
//| get the ordered fsca components                                  |
//+------------------------------------------------------------------+
matrix get_fsca_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_Fsca;
}

//+------------------------------------------------------------------+
//| get the backward refined fsca components                         |
//+------------------------------------------------------------------+
matrix get_fscv_components(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_Fscv;
}

//+------------------------------------------------------------------+
//| get indices of variables defining the ordered fsca components    |
//+------------------------------------------------------------------+
bool get_fsca_var_indices(ulong &indices[]) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    return (ArrayCopy(indices, m_keptorderedcolumns, 0, 0, int(m_num_comps)) > 0);
}

//+---------------------------------------------------------------------------+
//| get indices of variables defining the backward refined fsca components    |
//+---------------------------------------------------------------------------+
bool get_fscv_var_indices(ulong &indices[]) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    return (ArrayCopy(indices, m_keptrefinedcolumns, 0, 0, int(m_num_comps)) > 0);
}

//+-------------------------------------------------------------------+
//| get cumulative variance contribution based on principal components|
//+-------------------------------------------------------------------+
vector get_principal_components_cumulative_variance_contribution(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_cumeigvalues;
}

//+-------------------------------------------------------------------+
//| get cumulative variance contribution based on fscv components     |
//+-------------------------------------------------------------------+
vector get_fscv_cumulative_variance_contribution(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_fscv_cumeigvals;
}

//+-------------------------------------------------------------------+
//| get eigen structure of principal components                       |
//+-------------------------------------------------------------------+
bool get_principal_components_eigstructure(matrix &vectors, vector &values) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    vectors = m_eigvectors;
    values = m_eigvalues;

    return true;
}

//+-------------------------------------------------------------------+
//| get eigen structure of backward refined FSCs                      |
//+-------------------------------------------------------------------+
bool get_fscv_eigstructure(matrix &vectors, vector &values) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return false;
    }

    vectors = m_fscv_eigvects;
    values = m_fscv_eigvals;

    return true;
}

//+-------------------------------------------------------------------+
//| get principal components factor structure                         |
//+-------------------------------------------------------------------+
matrix get_principal_components_factorstructure(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_structmat;
}

//+-------------------------------------------------------------------+
//| get the factor structure of FSC with backward refinement          |
//+-------------------------------------------------------------------+
matrix get_fscv_factorstructure(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_fscv_struct;
}

//+------------------------------------------------------------------+
//| get mean squared correlations                                    |
//+------------------------------------------------------------------+
vector get_avg_correlations(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return vector::Zeros(0);
    }

    return m_sqcorr;
}

//+-------------------------------------------------------------------+
//| get forward selection component coefficients matrix               |
//+-------------------------------------------------------------------+
matrix get_fsca_component_coeffs(void) {
    if (!m_fitted) {
        Print(__FUNCTION__, " either analyze() returned an error or it was not called ");
        return matrix::Zeros(0, 0);
    }

    return m_coeffs;
}

These functions allow users to retrieve important results, such as the standardized data, correlation matrix, factor structure, principal components, and component variables, facilitating further analysis and interpretation of the results. We conclude this exposition with a demonstration of how to employ the CFsca class.


An Example

The code listing below defines an MQL5 script named FSCA_Demo.mq5 that performs Forward Selection Component Analysis (FSCA) on a randomly generated dataset. The script includes the fsca.mqh header file, which contains the definition of the CFsca class used for FSCA analysis.

//+------------------------------------------------------------------+
//|                                                    FSCA_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include<fsca.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   MathSrand(120);
//---
   matrix mat(100,9);
//---
   mat.Random(0.0,1.0);
//---
   vector var1 = mat.Col(0) + mat.Col(1);
// ---
   vector var2 = mat.Col(2) + mat.Col(3);
//---
   vector var3 = var1 + var2;
//---
   if(!mat.Col(var1,6) || !mat.Col(var2,7) || !mat.Col(var3,8))
     {
      Print("failed column assignment ", GetLastError());
      return;
     }
//---
   CFsca fsca;
//---
   if(!fsca.fit(mat))
      return;
//---
   ulong index[];
   Print("Principal components cumulative variance conributions \n", fsca.get_principal_components_cumulative_variance_contribution());
   Print(" Principal components factor structure \n", fsca.get_principal_components_factorstructure());
   Print("Mean squared correlation of each variable with all others \n", fsca.get_avg_correlations());
//---
   if(fsca.get_fsca_var_indices(index))
     {
      Print(" Ordered FSCA components based on variables located in column indices ");
      ArrayPrint(index);
     }
//---
   Print(" Ordered FSCA component coefficients matrix \n", fsca.get_fsca_component_coeffs());
//---
   if(fsca.get_fscv_var_indices(index))
     {
      Print(" Backward refined FSCA components based on variables located in column indices ");
      ArrayPrint(index);
     }
//---
   matrix vects;
   vector vals;
//---
   if(fsca.get_fscv_eigstructure(vects,vals))
     Print("Backward refined fsca component eigenvalues \n", vals);
//---
   Print(" Backward refined cumulative variance contributions \n", fsca.get_fscv_cumulative_variance_contribution());
//---
   Print(" Backward refined fsca components factor structure \n", fsca.get_fscv_factorstructure());
  }
//+------------------------------------------------------------------+

It starts by setting a random seed and creating a matrix of random values. Three new vectors are created by summing existing columns in the matrix. The script then attempts to fit the matrix data to the FSCA model and retrieves various FSCA results, including cumulative variance contribution, factor structure, and mean squared correlations. It also performs both standard FSCA and backward refined FSCA, printing the ordered variable indices and component coefficients. As well as the factor structure of the Backward refined FSCA components. The script simply generates a dataset of random variables with 100 samples and 9 features. The last 3 variables of the dataset are set up to be dependent on other variables, whilst the rest are independent. 

When we run the script and analyze the characteristics of the principal components, we find that there are only six unique sources of variation out of the nine. 

DG      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   Principal components cumulative variance conributions 
RM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [31.72121326219056,54.98374706330443,70.21399790786099,82.34742379766755,91.9067775629936,100]
CM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Principal components factor structure 
MH      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [[-0.5430877600903072,0.4698851388299595,-0.02139789374204959,0.5468988095320395,-0.4254498037566715,-0.06082703269184352,-1.3842452210817e-09,-7.527559895073524e-10,0]
RH      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5283294988376427,0.4246506210338227,-0.1190026606589024,-0.6285471675075863,0.3351428244532062,0.1377893424956133,-1.351333204556555e-09,-7.34858353171856e-10,0]
ES      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5563230307728618,-0.3632156082945803,0.4770295070287525,0.3051596297191441,0.4575827252246154,-0.1688715686919785,-1.694159101189325e-09,2.164855665400724e-10,0]
NF      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.2379617600470182,-0.6943076552356867,-0.4580766878219635,-0.2737307249578351,-0.4112051990027778,0.08636320534609224,-1.769139142521297e-09,2.260667780777343e-10,0]
DO      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [0.02487447101754412,-0.08203927651647476,-0.6079889924620585,0.4701685445643955,0.3604839483405348,0.5215295442601863,1.313244252124911e-25,1.228203109452781e-25,0]
IP      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.07016546285360215,-0.110242984252018,0.7306990214221818,-0.07491798042552207,-0.2276538908363994,0.6257501374625694,4.158606798395552e-25,-7.369218656716687e-26,0]
NE      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.7598477338270035,0.6346843827822741,-0.09872272409405579,-0.04786755450396145,-0.0705236166963274,0.05287812507625003,-1.359967783374346e-10,1.333715775589249e-09,0]
NO      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.5934182368659159,-0.8024046895986707,-0.000973814713973191,0.01424096330384607,0.02077689502375221,-0.05801790712583575,2.667167815186452e-10,-1.355042254629964e-11,0]
RM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-0.9897757278036692,-0.1138316306178367,-0.07343616940955985,-0.02494592427830717,-0.03690113231990194,-0.0030829919659495,2.802923111601039e-09,-3.865027968054199e-10,0]]

This is expected because three of the variables are combinations of the others. Looking at the cumulative variance contributions of each variable, we see that the first component accounts for about one-third of the total variation. The factor structure indicates a moderate to strong inverse correlation between the first principal component and the variables in columns 0 to 3 and 6 to 8, inclusive, while variables in columns 4 and 5 show the opposite trend. The second component depicts the differences between variables 0 and 1 versus 2 and 3. Together, the first two components explain over 55 percent of the total variation.

QK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   Mean squared correlation of each variable with all others 
GK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [0.09874555673359317,0.09196664871445229,0.09678803260182336,0.08640965168371836,0.009232616218980055,0.01341075732654295,0.1892345119240549,0.1695472310064176,0.2291509382521983]

Moving on to the vector of mean square correlations of each variable with the combined collection of all variables, this vector lists the correlations in the order the variables appear in the original dataset. The last three variables have the largest average correlations, while variables in columns 4 and 5 have the lowest.

LR      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Ordered FSCA components based on variables located in column indices 
QQ      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   8 6 2 4 1 5

Next, we look at the forward-selected values, which are obtained by calling get_fscv_var_indices(). It shows the indices of variables that best capture the majority of the variation in the dataset, arranged in descending order in terms of which variable contributes the most to the overall variation in the data. Here, we see that the last variable captures the most variation in the data, as it appears first.

QJ      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Ordered FSCA component coefficients matrix 
DM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   [[0.9999999989356357,-0.9551778313323678,-1.196676438579672,-0.163265209103464,-0.1301792726137802,0.0741114239785734]
IR      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [7.62883988565579e-10,1.382882745177175,0.7080052470472653,0.1327136589445282,-0.8962870520067646,-0.01038862969019799]
LF      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [6.044914586250671e-10,-1.162965671680505e-09,1.327736785211269,0.1291890234653878,0.1244453203448803,-0.2315140872599129]
EM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [5.84342504938995e-11,-9.115276242144255e-11,-1.685031073006549e-10,1.005785752630206,0.08917398176616295,0.2288955899392838]
JM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [6.626278020206711e-11,8.05911615654048e-10,2.135397240976555e-10,-3.939133914887538e-11,1.404086244047662,0.03569800251260542]
KK      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    [-2.859616016204214e-11,3.48387846349496e-11,2.600743786995707e-10,-1.479500966183878e-10,-3.333024481411151e-11,1.048952273510343]]

Next, we study the table of coefficients needed to compute the six components. The variables are depicted in the same order of importance given by the indices of the array we just examined. Here, we see that with the last variable being the most important, the corresponding coefficient is very close to 1. Moving down this matrix, note how the coefficients become so small that they are practically zero.

CM      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)    Backward refined FSCA components based on variables located in column indices 
ND      0       07:16:46.014    FSCA_Demo (BTCUSD,D1)   3 0 2 4 1 5

Finally, we examine the indices of variables selected through a combination of forward selection and backward refinement. It's important to note that in this variation of FSCA, the order of the selected variables does not carry significance. However, the resulting set of selected variables is more meaningful than the strict ordering approach, as it retains only the independent random variables, discarding those that exhibit some dependency. This is clearly shown by comparing the results from both standard forward selection and backward refined forward selection.


Conclusion

In conclusion, we have presented an implementation of Forward Selection Component Analysis in MQL5, showcasing its efficacy as a tool for both dimensionality reduction and feature selection. The tool can also be used for exploratory data analysis. One of the byproducts of the algorithm is the factor structure of the dataset, which can be useful when trying to understand the effects at play. All the code referenced in this article is attached below.
File Name
 Description
MQL5/include/np.mqh
 header file of generic vector and matrix utility functions
MQL5/include/fsca.mqh
 header file containing definition of CFsca class that implement Forward Selection Component Analysis
MQL5/scripts/FSCA_Demo.mq5
 a MetaTrader 5 script demonstrating the use of the CFsca class
Attached files |
Download ZIP
np.mqh (74.16 KB)
fsca.mqh (26.89 KB)
FSCA_Demo.mq5 (2.46 KB)
Mql5.zip (16.32 KB)
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

Other articles by this author

Last comments | Go to discussion (1)
Aleksey Vyazmikin
Aleksey Vyazmikin | 11 Jul 2025 at 12:07

The topic is, of course, eternal and always relevant.

It would be good to have different methods in the article to compare their effectiveness, not on synthetic data, but on real data.

I tried to increase the number of features to 5000 and rows to 10000 - I waited three days for the result - no result. So I wonder if the quality would suffer significantly if we split the number of features into groups, say 100 examples each, and then bring together the winners from each group for a final selection?

Creating a Trading Administrator Panel in MQL5 (Part V): Two-Factor Authentication (2FA) Creating a Trading Administrator Panel in MQL5 (Part V): Two-Factor Authentication (2FA)
Today, we will discuss enhancing security for the Trading Administrator Panel currently under development. We will explore how to implement MQL5 in a new security strategy, integrating the Telegram API for two-factor authentication (2FA). This discussion will provide valuable insights into the application of MQL5 in reinforcing security measures. Additionally, we will examine the MathRand function, focusing on its functionality and how it can be effectively utilized within our security framework. Continue reading to discover more!
Developing a Replay System (Part 49): Things Get Complicated (I) Developing a Replay System (Part 49): Things Get Complicated (I)
In this article, we'll complicate things a little. Using what was shown in the previous articles, we will start to open up the template file so that the user can use their own template. However, I will be making changes gradually, as I will also be refining the indicator to reduce the load on MetaTrader 5.
MQL5 Wizard Techniques you should know (Part 44): Average True Range (ATR) technical indicator MQL5 Wizard Techniques you should know (Part 44): Average True Range (ATR) technical indicator
The ATR oscillator is a very popular indicator for acting as a volatility proxy, especially in the forex markets where volume data is scarce. We examine this, on a pattern basis as we have with prior indicators, and share strategies & test reports thanks to the MQL5 wizard library classes and assembly.
Neural networks made easy (Part 89): Frequency Enhanced Decomposition Transformer (FEDformer) Neural networks made easy (Part 89): Frequency Enhanced Decomposition Transformer (FEDformer)
All the models we have considered so far analyze the state of the environment as a time sequence. However, the time series can also be represented in the form of frequency features. In this article, I introduce you to an algorithm that uses frequency components of a time sequence to predict future states.