离散哈特莱变换
概述
1942年,Ralph Hartley在他的文章“应用于传输问题的更对称傅立叶分析”中提出了傅立叶变换的模拟。
就像傅立叶变换(FT)一样,哈特莱变换(HT)将原始信号转换为三角函数的和。但它们之间有一个显著的区别。FT将实数转换为复数,而HT仅提供实数结果。由于这种差异,哈特莱变换并没有流行起来——科学家和技术人员没有看到它的任何优点,继续使用通常的傅立叶变换。1983年,Ronald Bracewell提出了Hartley变换的离散版本。
一点理论
离散哈特莱变换(DHT)可用于离散时间序列的分析和处理。它可以过滤信号,分析它们的频谱等等。DHT的能力不亚于离散傅立叶变换的能力。然而,与DFT不同的是,DHT只使用实数,这使得它在实践中更方便实现,并且其应用结果更直观。
让我们有N个实数h[0]…h[N-1]。利用离散哈特莱变换,我们得到了N个实数H[0]…H[N-1]。
这种变换使我们能够将信号从时域转移到频域。在它的帮助下,我们可以估计原始信号中特定谐波的影响有多大。b0>H[0]数字包含有关信号的基本信息。H[1]…H[N-1]数字提供了额外的数据。这些数字显示了原始信号中特定谐波的强度。这些数字的索引显示了该谐波的多少个周期将适合于原始信号。换句话说,指数越高,谐波频率就越高。
逆哈特莱变换用于从频域转到时域。它的方程式是这样的。
在这两个方程中,cas(cos和sin)函数表示三角函数的和。
尽管如此,它也可以用不同的东西来代替。变换的本质不会改变。现在,让我们看看如何将DHT付诸实践。
引入离散哈特莱变换
因此,DHT将信号从时域转换到频域。但有可能从中获得任何实际利益吗?
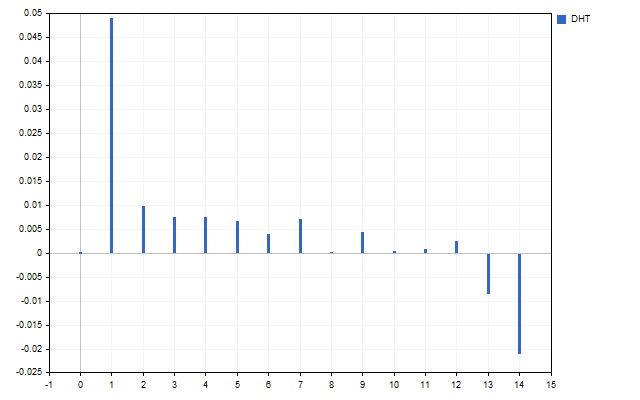
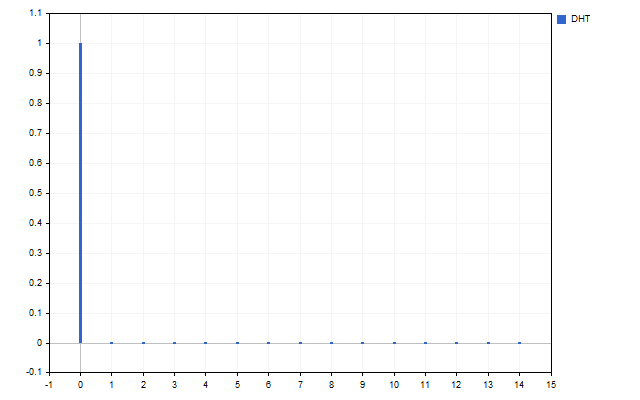
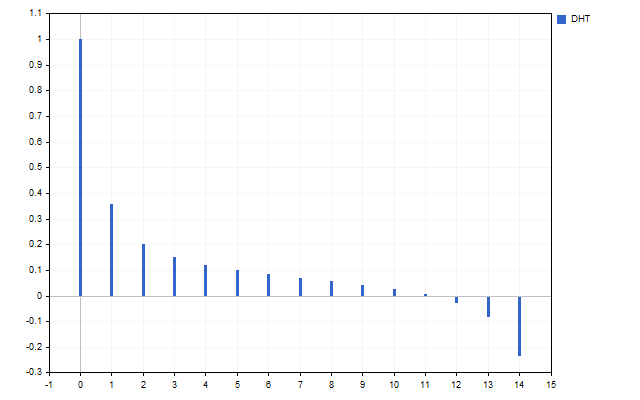
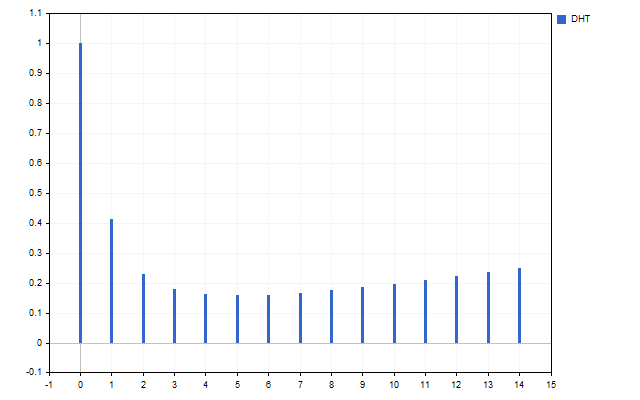
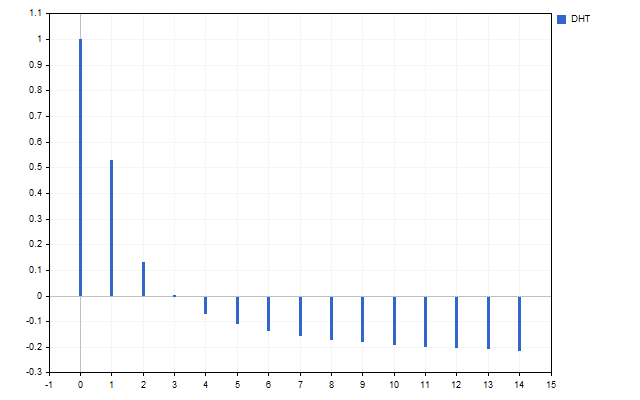
让我们以15开盘价格为信号。这就是这个时间序列的频谱的样子(由于比例差异,不显示H[0])。
该图清楚地表明,不同的谐波具有不同的强度。但是这个光谱能做些什么呢?
让我们以简单移动平均线为例。它的方程式非常简单。
如果我们将其中一个价格设置为零,指标会发生什么变化?我们不太可能得到什么好东西。但在频域中,这是可能的。我们可以将任意数量的谐波归零。
这就是原始信号的样子。
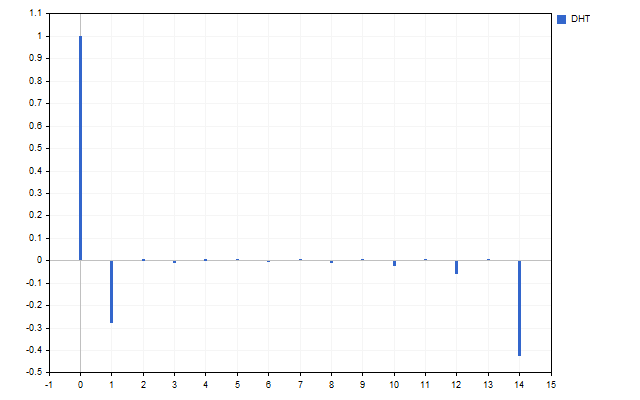
现在,让我们将所有H[1]–H[14]谐波设置为零。现在我们只有关于原始信号的基本信息。让我们将逆哈特莱变换应用于这个频谱。
现在移除具有最高频率H[10]–H[14]的谐波。哈特莱变换将提供以下结果。
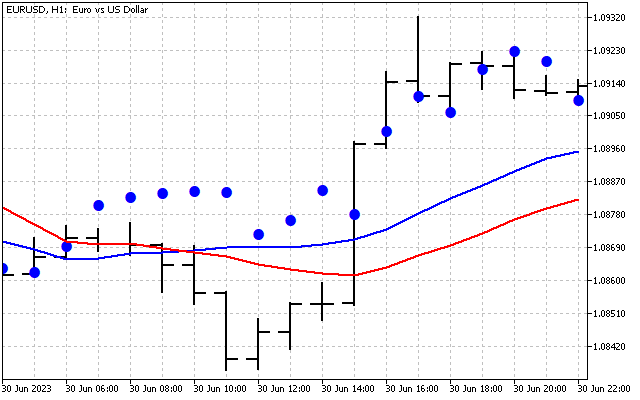
我们已经对原始信号进行了平滑处理。这是在实践中应用哈特莱变换的第一种方法。首先,我们可以在频域中平滑时间序列。之后,所获得的值被转移到常用指标的输入。让我们以两条移动平均线为例。其中一个像往常一样应用于价格(红线)。第二个应用于DHT值(蓝线)。
消除某些谐波并不是处理信号频谱的唯一方法。我们可以一次衰减所有谐波,例如通过将它们除以给定的数字。
或者,我们可以根据每个谐波的频率来衰减它——频率越高,衰减就越大。
在任何情况下,我们都会得到一个平滑的时间序列。这就是谐波衰减2倍的信号的样子。
处理频谱的另一种方法是只留下最强的谐波。要做到这一点,我们必须找到所有谐波的平均值。
我们将只留下其中超过该平均值绝对值的那些。
那么我们将只得到主信号加上最强谐波。
另一个信号处理选项是,我们可以反转谐波值。那么重构的信号将处于相反的相位。
在这种情况下,我们将收到信号的镜像反射——上升趋势被下降趋势所取代,反之亦然。这种方法在计算支撑和阻力水平时非常有用。
用于处理源信号的频谱的所有选项可以单独使用,也可以彼此组合使用。例如,可以先只保留最强的谐波,然后将它们的符号改为相反的符号。在这种情况下,结果将显示出一种可能的反趋势冲动。
具有最佳频谱的指标
任何线性指标都是一组系数。如果我们将哈特莱变换应用于这些系数,我们就获得了指标的光谱特性。
我们知道SMA是一个低通滤波器。让我们检查一下这句话。该指标的所有系数都等于1/N。哈特莱变换提供了这种指标光谱。
如我们所见,SMA仅通过主信号H[0],但所有其他谐波都被完全抑制。
光谱(指标的频率特性)可能彼此有很大差异。例如,LWMA通过输入信号的所有谐波。
另一方面,SMMA仅允许一些谐波通过并抑制其余谐波。
每个指标都有自己独特的光谱。它可以用于处理价格序列。要做到这一点,我们需要首先找到原始信号H[]的频谱。然后我们将其逐项乘以指标I[]的光谱。
将逆哈特莱变换应用于所获得的结果。结果,我们获得了频域中的信号滤波。这就是基于LWMA指标的频率滤波器的操作。
但我们可以走另一条路,首先设置指标的频谱,然后获得其系数。让我们试着制作一个指标,其光谱特性将与信号的光谱相对应。
算法如下:首先,我们得到了DHT的信号频谱。然后我们需要使其规范化。为此,我们需要将所有谐波值除以D=H[0]。
注意,在规范化之后,当构造指标时,H[0]=1是强制性条件。
之后,我们需要应用逆变换,逆变换将提供指标的加权系数。
这些系数与SMA没有太大区别。但与移动平均线相比,这样的指标将具有较小的滞后性,这将使更准确地跟踪市场动态成为可能。
噪声和颜色
在处理金融时间序列时,术语“噪声”通常指的是不需要的信号失真。为了消除这种噪声,可以使用各种滤波器,包括SMA。
随机或不可预测的信号也可以被认为是噪声。如果我们将市场价格波动表示为噪声的总和,会发生什么?要做到这一点,我们需要转向彩色噪声的概念。彩色噪声是在不同频率范围内具有不同能量的噪声。它们的名字来源于不同颜色的可见光:红色是低频噪声,而紫色是高频噪声。
在分析金融时间序列时,将价格波动表示为有色噪声的总和可以给出有趣的结果。这种方法使我们能够考虑价格波动的各种频率分量。
每个彩色噪声都有自己独特的特性,反映了频谱中取决于f频率的能量分布。
噪音有五种原色。
| p 参数 | 噪声颜色 |
|---|---|
| -2 | 红色 |
| -1 | 粉色 |
| 0 | 白色 |
| +1 | 蓝色 |
| +2 | 紫色 |
每种噪音都与特定的价格波动有关。例如,红色噪声可以表示价格波动中存在长期趋势或周期。白噪音表示市场处于平盘状态。紫色噪声可以指示随机和不可预测的价格行为。在金融时间序列分析中使用有色噪声可以帮助识别隐藏的模式,以及在传统分析中不总是可见的模式。
现在让我们来看看不同的噪声在市场上是如何表现的。要做到这一点,我们需要采取几个简单的步骤。
首先,我们需要找到信号的频谱,用它我们可以估计每个谐波的能量。要做到这一点,我们需要将每个谐波的值平方。
现在,我们可以使用p参数来估计噪声的缩放因子的值。当使用该系数时,信号和噪声的总能量将相等。
知道了这个系数,我们就可以构造EN[]噪声的能谱。
现在我们可以找到HN[]噪声频谱。要做到这一点,我们需要取能谱的平方根。
几乎没有什么可以做的了——像原始信号的谐波一样,为噪声频谱的谐波分配+/-符号。在这种情况下,噪声和原始信号将处于相同的相位。
在这之后,我们需要执行逆哈特莱变换来获得价格图上的噪声值。这就是红色噪音在市场上的样子。
但我们也可以取谐波的相反符号。在这种情况下,噪声将相对于原始信号处于相反的相位。此外,我们可以严格取正调和值或负调和值。我们可以在频域中接受这样的方法,然后我们将能够看到市场中噪音运动的界限。
有色噪声的概念不仅可以用来描述市场动态,还可以用来开发指标。
为此,我们首先需要设置指标功率E>0。此参数决定指示器的灵敏度。在此之后,我们执行已经熟悉的程序。首先我们找到比例因子。
之后,我们找到了HI[]指标的光谱。不要忘记HI[0]应该等于1。
如有必要,我们所要做的就是为指示器频谱的谐波分配+/-号。然后我们需要应用逆哈特莱变换并获得指标系数。这就是具有不同谐波符号变体的红色噪声指示器的外观。
在制定指标时,我们不仅可以使用纯噪声,还可以使用它们的各种组合。例如,这就是红色和紫色噪声之和的频谱。
这就是红噪声和白噪声光谱之间的区别。
在接收到coefficient[]指标系数后,我们应该对它们进行规范化。要做到这一点,我们首先需要找到所有系数的和。
在这之后,我们需要将每个系数除以得到的量。
除了列出的主要噪音外,还有其他噪音。例如,黑色噪声的一个定义是参数为p<-2的噪声。让我们尝试一种不同的方法。让我们假设p噪声参数可以取分数值。让我们看看它是如何随着时间的推移而变化的。
为了计算噪声参数,我们首先需要找到信号E[]的能谱。之后,我们需要计算四个系数。
在所有方程中,k=1…N-1。可以使用该方程来计算最合适的噪声参数。
这就是这个参数在市场条件下的变化。
正如我们所看到的,在金融时间序列分析中使用有色噪声可以成为探索和理解市场动态的有用工具。这种方法可以帮助揭示隐藏的模式,并改进对价格走势的预测。
结论
离散哈特莱变换有自己的快速变换算法。但是,如果我们预先为cas值分配数组,我们可以显著加快数据处理速度。此数组的大小应等于(N-1)^2+1,其中N是一个指标周期。然后,此数组的值设置如下:
我在这篇文章中正是使用了这种方法。
文章附有以下指标。
| 符号 | 描述 |
|---|---|
| DHT | 该指标展示了处理信号谐波的能力。
|
| DHT LWMA | 该指标显示了LWMA指标在光谱区域中的价格处理 |
| Spectrum | 系数具有与原始信号相似的频谱特性的指示器 |
| Noise Levels | 指标显示彩色噪音的级别 Noise - 噪声颜色 Type - 改变原始信号的相位 |
| Noise Indicator | 指标选择与所选择的噪声颜色相对应的系数 E-噪声功率。 |
| Fractional Noise | 显示分数噪声参数的指标。 |
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/12984
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
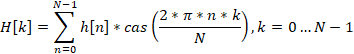
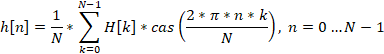
感谢您的文章!
就在昨天,我还在思考通过子样本中的统计指标来识别市场阶段的方法,我在文章中看到了类似的想法。
您在这个方向上做过更深入的研究吗?我想知道他们是以多快的速度(以多大的滞后期)和多大的误差来对趋势/扁平化进行分类的?
感谢您的文章!
就在昨天,我还在思考通过子样本中的统计指标来识别市场阶段的方法,我在文章中看到了类似的想法。
您在这个方向上做过更深入的研究吗?我想知道他们是以多快的速度(以多大的滞后期)和多大的误差来对趋势/扁平化进行分类的?
确定市场阶段可能是最简单的任务。我们将价格频谱(不含主要信号)通过聚类分析(Kohonen 地图)--这就是我们得到的市场阶段。但对于趋势而言,一切都非常复杂--变化/新趋势开始的标志是低频成分相对减弱,高频谐波相对增强。但不幸的是,我们有可能会严重错失趋势方向。