Transformada discreta de Hartley
Introducción
En 1942, Ralph Hartley en su artículo «A More Symmetrical Fourier Analysis Applied to Transmission Problems» propuso una transformada análoga a la de Fourier.
Al igual que la transformada de Fourier (FT), la transformada de Hartley (HT) convierte la señal original en una suma de funciones trigonométricas. Pero hay una diferencia significativa entre ambas. La FT convierte valores reales en números complejos, mientras que la HT solo ofrece un resultado de tipo real. Debido a esta diferencia, la transformada de Hartley no se hizo popular: los científicos y técnicos no vieron ninguna ventaja en ella y continuaron usando la transformada de Fourier habitual. No fue hasta 1983 que Ronald Bracewell introdujo una versión discreta de la transformada de Hartley.
Un poco de teoría
La transformada discreta de Hartley (DHT) se puede utilizar en el análisis y procesamiento de series temporales discretas. Con ella podremos filtrar señales, analizar su espectro y mucho más. Las capacidades de la DHT no son inferiores a las de la transformada discreta de Fourier. Sin embargo, a diferencia de esta, la DHT utiliza solo números reales, lo que hace su implementación más cómoda en la práctica; además, los resultados de su aplicación resultan más visuales.
Supongamos que tenemos N números reales h[0] ... h[N-1]. Usando la transformada discreta de Hartley, obtendremos de ellos N números reales H[0]…H[N-1].
Esta transformación permite transferir una señal del dominio del tiempo al dominio de la frecuencia. Con su ayuda podemos valorar cómo de grande es la influencia de un armónico particular en la señal original. El número H[0] contiene información básica sobre la señal, mientras que los números H[1]...H[N-1] suponen información adicional y aclaratoria. Estos números muestran cómo de fuerte es un armónico particular en la señal original, y el índice de estos números muestra cuántos ciclos de este armónico caben en la señal original. Es decir, cuanto mayor sea el índice, mayor será la frecuencia del armónico.
Para pasar del dominio de la frecuencia al dominio del tiempo, se usará la transformada inversa de Hartley. Su fórmula tiene el aspecto que sigue:
En ambas fórmulas, la función cas (cos y sin) es la suma de funciones trigonométricas.
Aunque también se puede sustituir por una diferencia. La esencia de la transformación no cambiará. Veamos ahora cómo podemos utilizar la DHT en la práctica.
Conociendo la transformada discreta de Hartley
Entonces, la DHT convierte una señal del dominio del tiempo al dominio de la frecuencia. ¿Pero es posible obtener algún beneficio práctico de ello?
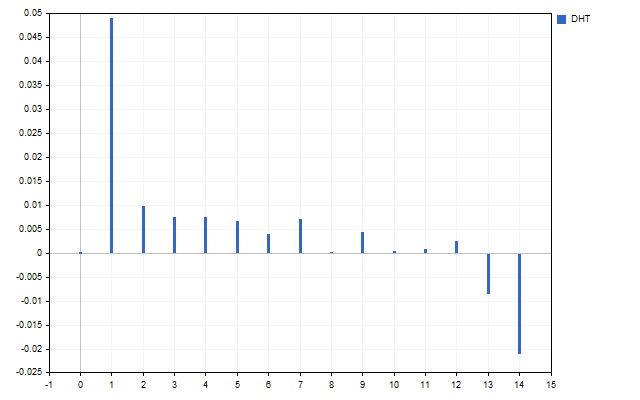
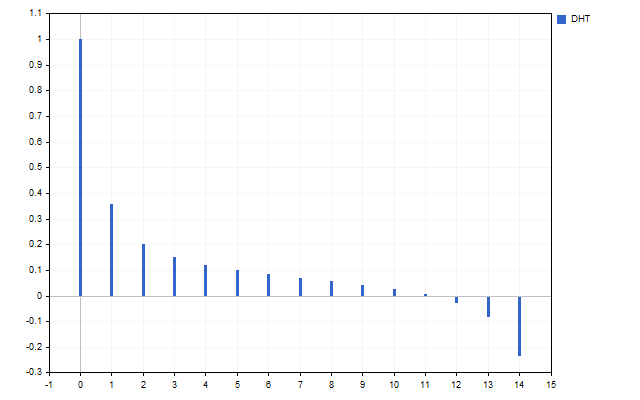
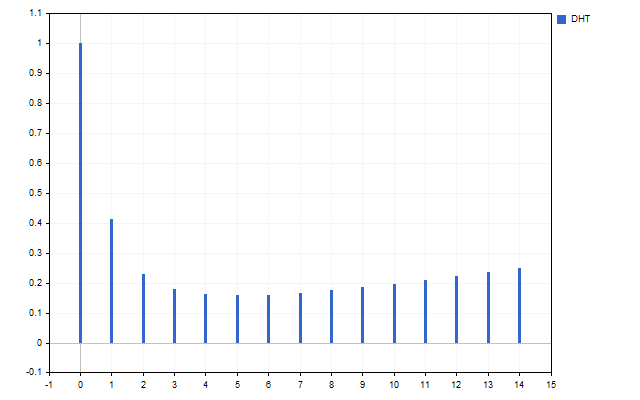
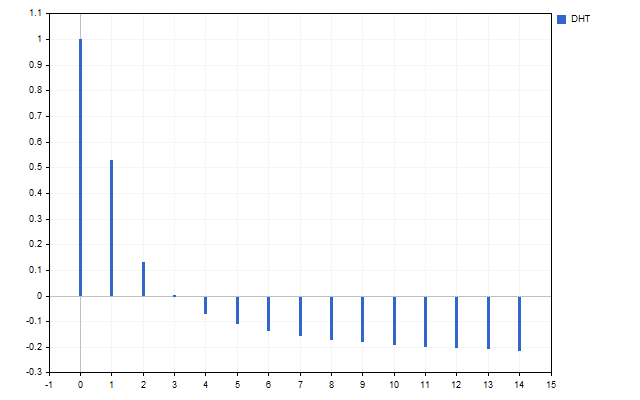
Como señal hemos tomado 15 precios de apertura. Este es el aspecto del espectro de esta serie temporal (el valor H[0] no se muestra debido a la diferencia de escalas).
La figura muestra claramente que diferentes armónicos poseen diferentes intensidades. Pero ¿qué podemos hacer con este espectro?
Tomaremos como ejemplo el indicador de media móvil simple. Su fórmula es muy sencilla.
¿Qué pasará con el indicador si ponemos uno de los precios a cero? Es poco probable que consigamos algo positivo, pero en el dominio de la frecuencia esto es posible: podemos poner a cero cualquier número de armónicos.
Así es como se verá la señal original.
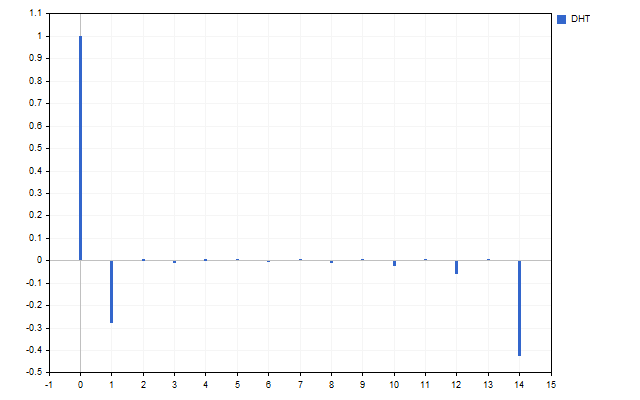
Ahora equipararemos todos los armónicos H[1] – H[14] a cero. Así solo tendremos la información básica sobre la señal original. A continuación, aplicaremos la transformada inversa de Hartley a este espectro.
Ahora eliminaremos los armónicos con las frecuencias más altas H[10] - H[14]. La transformada de Hartley nos dará este resultado.
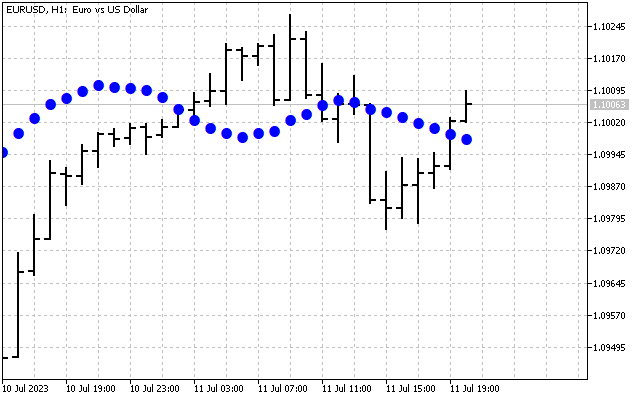
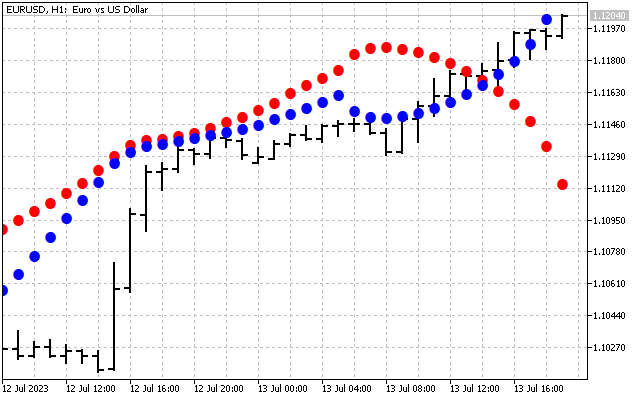
Es decir, hemos suavizado la señal original. Esta es la primera forma de aplicar la transformada de Hartley en la práctica. Primero podemos suavizar la serie temporal en el dominio de la frecuencia. Después de ello, los valores obtenidos se transferirán a la entrada de los indicadores habituales. Tomaremos como ejemplo dos medias móviles. Una de ellas se aplicará a los precios habituales (línea roja), mientras que la segunda la aplicaremos a los valores de la DHT (línea azul).
Anular algunos armónicos no es la única forma de procesar el espectro de la señal. Podemos atenuar todos los armónicos al mismo tiempo, por ejemplo, dividiéndolos por un número determinado.
O atenuar cada armónico según su frecuencia: cuanto mayor sea esta, mayor será la atenuación.
En cualquier caso, obtendremos una serie temporal suavizada. Así se verá una señal con armónicos atenuados 2 veces.
Otra forma de procesar el espectro es dejar solo los armónicos más fuertes: para ello tendremos que encontrar el promedio de todos los armónicos.
Y dejar solo aquellos de ellos que superen dicho promedio en su valor absoluto.
Entonces solo nos quedará la señal principal más los armónicos más fuertes.
Otra opción de procesamiento de la señal sería invertir los valores armónicos. Entonces la señal reconstruida se encontrará en la fase opuesta.
En este caso, obtendremos un reflejo especular de la señal: la tendencia alcista se verá reemplazada por una tendencia bajista y viceversa. Este enfoque puede resultar útil al calcular los niveles de apoyo y resistencia.
Todas las opciones disponibles para procesar el espectro de la señal original se pueden utilizar individualmente o combinadas entre sí. Por ejemplo, primero podemos dejar solo los armónicos más fuertes y luego cambiar su signo al opuesto. En este caso, el resultado mostrará un posible impulso contrario a la tendencia.
Indicador con espectro óptimo
Cualquier indicador lineal supone un conjunto de coeficientes. Si aplicamos la transformada de Hartley a dichos coeficientes, obtendremos la característica espectral del indicador.
Todos hemos oído que SMA es un filtro de frecuencias bajas. Vamos a comprobar esta afirmación. Todos los coeficientes de este indicador son iguales a 1/N. La transformada de Hartley nos ofrece dicho espectro de este indicador.
Como podemos ver, la SMA deja pasar solo la señal H[0] principal, pero todos los demás armónicos se suprimen por completo.
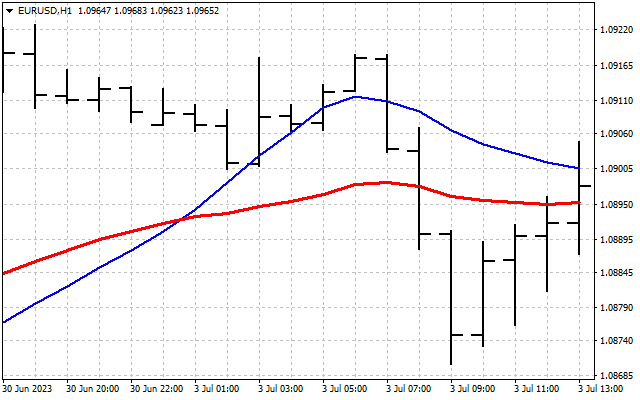
Los espectros, es decir, las características de frecuencia de los indicadores, pueden diferir mucho entre sí. Por ejemplo, LWMA transmite todos los armónicos de la señal de entrada.
Mientras que SMMA solo permite el paso de algunos armónicos y suprime el resto.
Cada indicador posee su propio espectro único, que podemos utilizar para procesar la serie de precios. Para hacer esto, primero necesitaremos encontrar el espectro de la señal original H[]. Luego lo multiplicaremos término por término por el espectro del indicador I[].
A continuación, aplicaremos la transformada inversa de Hartley al resultado obtenido. Como resultado, obtendremos un filtrado de señales en el dominio de la frecuencia. Así es como se verá el funcionamiento de un filtro de frecuencia integrado en el indicador LWMA.
Pero podemos ir por el otro lado, estableciendo primero el espectro del indicador y luego obteniendo sus coeficientes. Vamos a intentar crear un indicador cuya característica espectral se corresponda con el espectro de la señal.
El algoritmo de nuestras acciones será el siguiente. Primero, usando la DHT, obtendremos el espectro de la señal. Luego necesitaremos normalizarlo. Para hacer esto, deberemos dividir todos los valores de los armónicos entre D = H[0].
Tenga en cuenta que después de la normalización, el valor H[0] = 1 será una condición obligatoria al construir el indicador,
después de lo cual deberemos aplicar la transformación inversa, que nos ofrecerá los coeficientes de peso del indicador.
Estos coeficientes no son muy diferentes de la SMA, pero dicho indicador tendrá un retraso menor en comparación con la media móvil, lo cual permitirá monitorear con mayor precisión la dinámica del mercado.
Ruido y color
Al procesar series temporales financieras, el término ruido suele referirse a una distorsión de señal no deseada. Para combatir este tipo de ruido, podemos utilizar varios filtros: la SMA y muchos otros indicadores,
pero una señal aleatoria o impredecible también podría considerarse ruido. ¿Qué puede suceder si imaginamos los movimientos de precio en el mercado como una suma de ruido? Para ello, deberemos recurrir al concepto de ruido de color. El ruido de color son ruidos que tienen diferentes energías en diferentes rangos de frecuencia. Reciben su nombre de los diferentes colores de la luz visible: el rojo es un ruido de baja frecuencia, mientras que el violeta es un ruido de alta frecuencia.
Representar los movimientos de precio como una suma de ruido de color puede ofrecer resultados interesantes al analizar series temporales financieras. Este enfoque nos permitirá tener en cuenta varios componentes de frecuencia del movimiento de los precios.
Cada ruido de color posee su propia característica única que refleja la distribución de energía en el espectro dependiendo de la frecuencia f.
Existen cinco ruidos de color primarios.
| parámetro p | ruido de color |
|---|---|
| -2 | rojo |
| -1 | rosa |
| 0 | blanco |
| +1 | azul |
| +2 | violeta |
Cada ruido está asociado a un movimiento de precios específico. Por ejemplo, el ruido rojo puede indicar la presencia de tendencias o ciclos a largo plazo en los movimientos de precios. El ruido blanco puede indicar que el mercado se encuentra en un estado plano, mientras que el ruido violeta puede indicar un comportamiento de precios aleatorio e impredecible. El uso de ruido de color en el análisis de series temporales financieras puede ayudarnos a identificar patrones ocultos y patrones que no siempre resultan visibles en el análisis convencional.
Veamos ahora cómo se comportan los diferentes ruidos en el mercado. Para ello deberemos seguir unos sencillos pasos.
Primero necesitaremos encontrar un espectro de señal con el cual podamos estimar la energía de cada armónico. Para hacer esto, necesitaremos elevar al cuadrado el valor de cada armónico.
Ahora podremos estimar el valor del coeficiente de escala para el ruido con el parámetro p. Al usar este coeficiente, las energías totales de la señal y el ruido serán iguales.
Conociendo este coeficiente, podremos construir el espectro de energía del ruido EN[].
Ahora podemos encontrar el espectro de ruido HN[]. Para conseguirlo, necesitaremos extraer la raíz cuadrada del espectro de energía.
Ya queda muy poco por hacer: ahora asignaremos los signos +/- a los armónicos del espectro de ruido, al igual que los armónicos de la señal original. En este caso, el ruido y la señal original estarán en la misma fase.
Después de ello, deberemos realizar una transformada inversa de Hartley para obtener los valores de ruido en el gráfico de precios. Así es como se verá el ruido rojo en el mercado.
No obstante, también podemos tomar los signos opuestos de los armónicos. En este caso, el ruido estará en la fase opuesta respecto a la señal original. Además, podemos tomar valores armónicos estrictamente positivos o negativos; en el dominio de la frecuencia podemos permitirnos esto. Entonces podremos ver los límites de los movimientos de ruido en el mercado.
El concepto de ruido de color puede utilizarse no solo para describir la dinámica del mercado, sino también para desarrollar indicadores.
Para ello, primero deberemos configurar la potencia del indicador E > 0. Este parámetro determinará cómo de sensible será el indicador. Después de eso, realizaremos los procedimientos ya familiares. Primero encontraremos el factor de escala.
Después de esto, encontraremos el espectro del indicador HI[], pero sin olvidarnos de que HI[0] debe ser igual a 1.
Lo único que deberemos hacer es asignar los signos +/- a los armónicos del espectro del indicador, si fuera necesario. Luego tendremos que aplicar la transformada inversa de Hartley y obtener los coeficientes del indicador. Así es como se verá un indicador de ruido rojo con diferentes variantes de signos armónicos.
Al desarrollar indicadores, podemos utilizar no solo ruido puro, sino también sus diversas combinaciones. Por ejemplo, así es como se verá el espectro de la suma del ruido rojo y violeta.
Y así es como se verá la diferencia entre los espectros de ruido rojo y blanco.
Tras obtener los coeficientes del indicador coefficient[], deberemos normalizarlos. Para ello, primero tendremos que encontrar la suma de todos los coeficientes.
Después deberemos dividir cada coeficiente por la cantidad resultante.
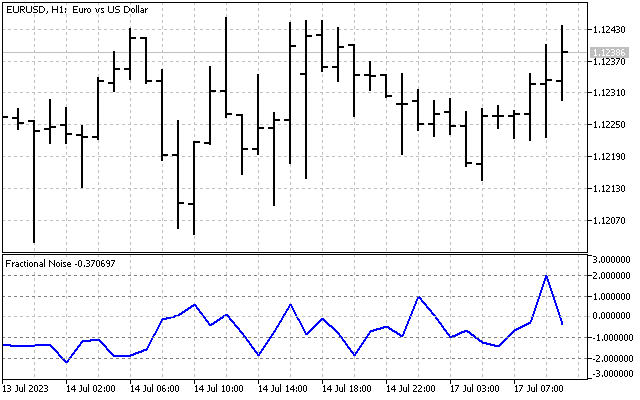
Además de los principales ruidos enumerados, existen otros. Por ejemplo, una definición de ruido negro sería un ruido con el parámetro p < -2. Ahora probaremos un enfoque diferente. Vamos a suponer que el parámetro de ruido p puede tomar valores fraccionarios y a ver cómo cambia con el tiempo.
Para calcular el parámetro de ruido, primero necesitaremos encontrar el espectro de energía de la señal E[]. Después de esto, deberemos calcular cuatro coeficientes.
En todas las fórmulas k = 1…N-1. El parámetro de ruido más adecuado se puede calcular usando la fórmula:
Y así es como este parámetro cambia en las condiciones del mercado:
Como hemos visto, el uso de ruidos de color en el análisis de series temporales financieras puede ser una herramienta útil a la hora de explorar y comprender la dinámica del mercado. Este enfoque puede ayudarnos a revelar patrones ocultos y mejorar la previsión de los movimientos de precio.
Conclusión
La transformada discreta de Hartley tiene sus propios algoritmos de transformación rápida, pero, si asignamos un array de antemano para los valores cas , podremos acelerar significativamente la velocidad de procesamiento de los datos. El tamaño de este array deberá ser igual a (N-1)^2+1, donde N será el periodo del indicador. Luego los valores de este array se establecerán de la siguiente manera:
Al escribir este artículo, hemos utilizado exactamente este enfoque.
Adjuntamos al artículo los siguientes indicadores.
| Nombre | Descripción |
|---|---|
| DHT | El indicador demuestra la capacidad de procesar armónicos de señales.
|
| DHT LWMA | El indicador muestra el procesamiento de precios por parte del indicador LWMA en el domino del espectro. |
| Spectrum | Los coeficientes de este indicador ofrecen una característica espectral similar a la de la señal original. |
| Noise Levels | El indicador muestra los niveles de ruido de color. Noise - ruido de color Type - cambiar la fase de la señal original |
| Noise Indicator | El indicador selecciona los coeficientes correspondientes al ruido de color seleccionado. E - potencia de ruido. |
| Fractional Noise | El indicador muestra el parámetro fraccionario del ruido. |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/12984
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
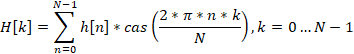
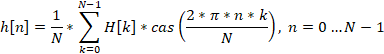
Gracias por el artículo.
Justo ayer estaba pensando en métodos para identificar etapas del mercado a través de indicadores estadísticos en una submuestra, y vi ideas similares en el artículo.
¿Han realizado alguna investigación más profunda en este sentido? Me pregunto con qué rapidez (con qué retardo) y con qué error consiguieron clasificar las tendencias\flats.
Gracias por el artículo.
Justo ayer estaba pensando en métodos para identificar etapas del mercado mediante indicadores estadísticos en una submuestra, y vi ideas similares en el artículo.
¿Han realizado alguna investigación más profunda en este sentido? Me pregunto con qué rapidez (con qué desfase) y con qué error consiguieron clasificar las tendencias\flats.
La identificación de las etapas del mercado es probablemente la tarea más fácil. Tomamos el espectro de precios (sin la señal principal) y lo pasamos por un análisis de conglomerados (mapas de Kohonen) - con eso obtenemos etapas de mercado. Pero todo es muy complicado con las tendencias - la señal de cambio/comienzo de una nueva tendencia es la debilidad relativa del componente de baja frecuencia y el fortalecimiento relativo de los armónicos de alta frecuencia. Pero, por desgracia, es posible errar gravemente en la dirección de la tendencia.