Die diskrete Hartley-Transformation
Einführung
Im Jahr 1942 schlug Ralph Hartley in seinem Artikel „A More Symmetrical Fourier Analysis Applied to Transmission Problems“ ein Analogon der Fourier-Transformation vor.
Genau wie die Fourier-Transformation (FT), wandelt die Hartley-Transformation (HT) das ursprüngliche Signal in eine Summe von trigonometrischen Funktionen um. Es gibt jedoch einen wesentlichen Unterschied zwischen ihnen. FT wandelt reelle Werte in komplexe Zahlen um, während HT nur reelle Ergebnisse liefert. Aufgrund dieses Unterschieds wurde die Hartley-Transformation nicht populär - Wissenschaftler und Techniker sahen darin keine Vorteile und verwendeten weiterhin die übliche Fourier-Transformation. Im Jahr 1983 stellte Ronald Bracewell eine diskrete Version der Hartley-Transformation vor.
Ein bisschen Theorie
Die diskrete Hartley-Transformation (DHT) kann bei der Analyse und Verarbeitung von diskreten Zeitreihen verwendet werden. Es ermöglicht die Filterung von Signalen, die Analyse ihres Spektrums und vieles mehr. Die Fähigkeiten von DHT stehen denen der diskreten Fourier-Transformation in nichts nach. Im Gegensatz zu DFT verwendet DHT nur reelle Zahlen, was die Umsetzung in der Praxis erleichtert, und die Ergebnisse ihrer Anwendung sind anschaulicher.
Wir wollen N reelle Zahlen h[0] ... h[N-1]. Die Verwendung der diskreten Hartley-Transformation erzeugt man N reelle Zahlen H[0]...H[N-1].
Diese Transformation ermöglicht es, ein Signal aus dem Zeitbereich in einen Frequenzbereich zu übertragen. Mit seiner Hilfe können wir abschätzen, wie groß der Einfluss einer bestimmten Schwingung im Originalsignal ist. Die Zahl in H[0] enthält grundlegende Informationen über das Signal. Die Zahlen H[1]...H[N-1] liefern zusätzliche Daten. Diese Zahlen geben an, wie stark eine bestimmte Schwingung im Originalsignal ist. Der Index dieser Zahlen gibt an, wie viele Zyklen diese Schwingung in das ursprüngliche Signal passen. Mit anderen Worten: Je höher der Index, desto höher die Frequenz der Schwingung.
Die inverse Hartley-Transformation wird verwendet, um vom Frequenzbereich in den Zeitbereich zu wechseln. Die Gleichung sieht wie folgt aus.
In beiden Gleichungen ist cas (cos and sin) die Summe der trigonometrischen Funktionen.
Sie kann jedoch durch eine Differenz ersetzt werden. Das Wesen der Transformation wird sich nicht ändern. Nun wollen wir sehen, wie wir DHT in die Praxis umsetzen können.
Einführung in die diskrete Hartley-Transformation
Also, DHT wandelt also ein Signal aus dem Zeitbereich in einen Frequenzbereich um. Aber ist es möglich, daraus einen praktischen Nutzen zu ziehen?
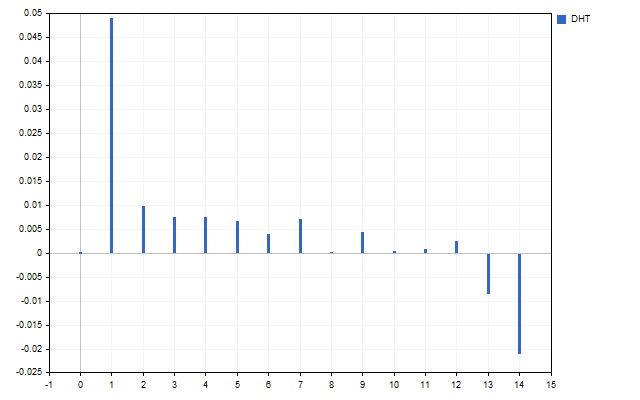
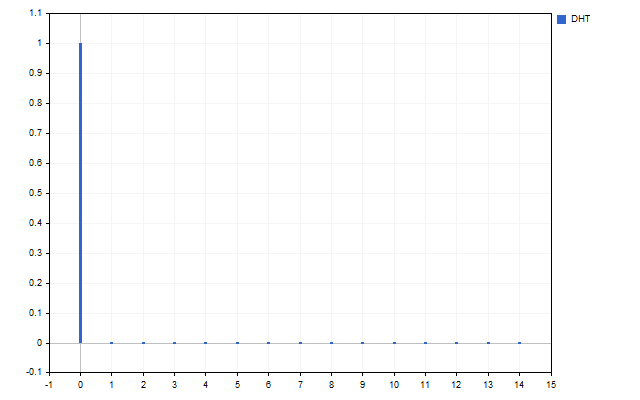
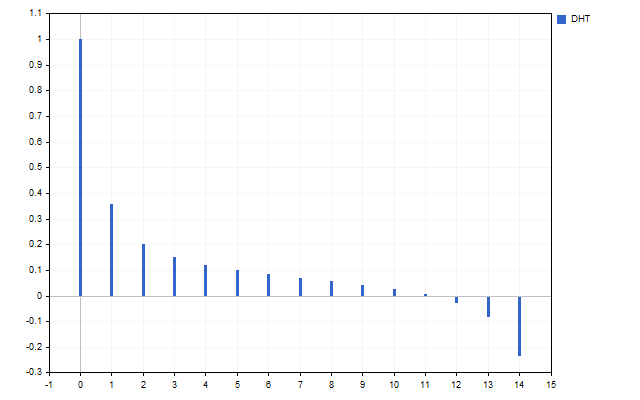
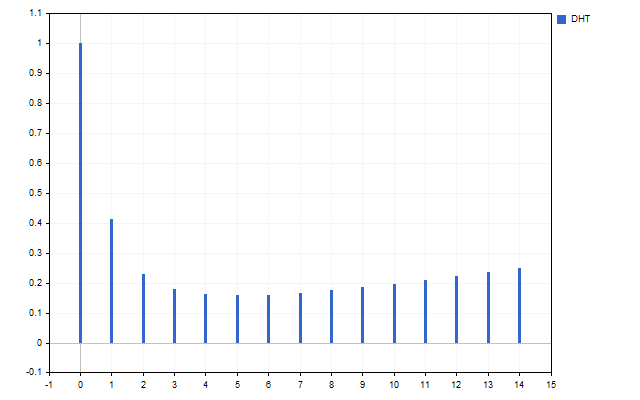
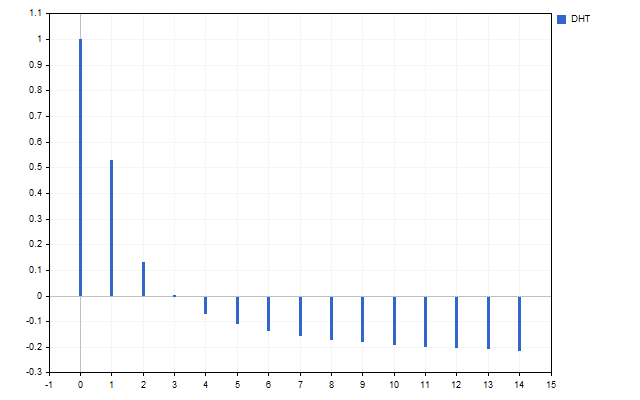
Wir nehmen 15 Eröffnungspreise als ein Signal. So sieht das Spektrum dieser Zeitreihe aus (H[0] wird aufgrund von Skalenunterschieden nicht angezeigt).
Die Abbildung zeigt deutlich, dass die verschiedenen Schwingungen unterschiedlich stark sind. Aber was kann man mit diesem Spektrum anfangen?
Nehmen wir zum Beispiel einen einfachen gleitenden Durchschnitt. Die Gleichung ist sehr einfach.
Was passiert mit dem Indikator, wenn wir einen der Preise auf Null setzen? Es ist unwahrscheinlich, dass wir etwas Gutes bekommen werden. Im Frequenzbereich ist dies jedoch möglich. Wir können eine beliebige Anzahl von Schwingungen ausschalten.
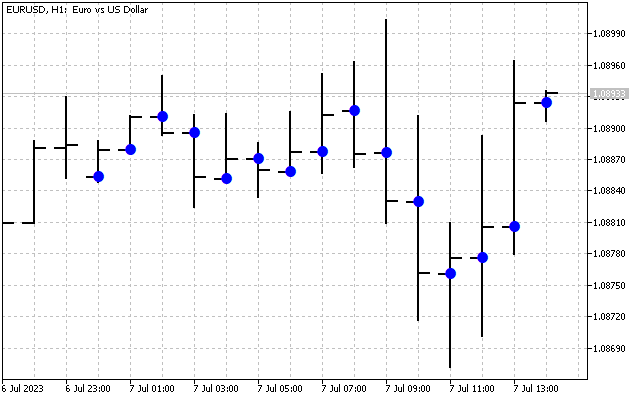
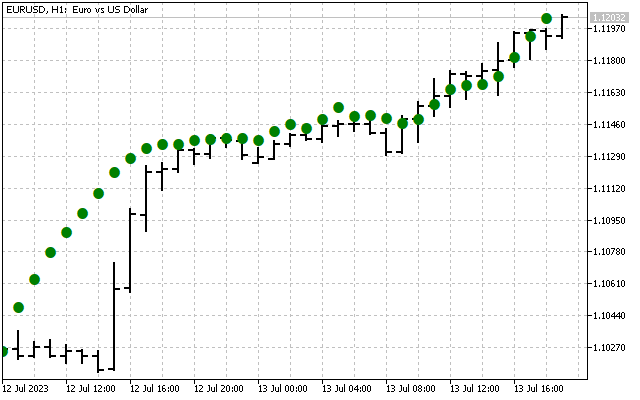
So sieht das Originalsignal aus.
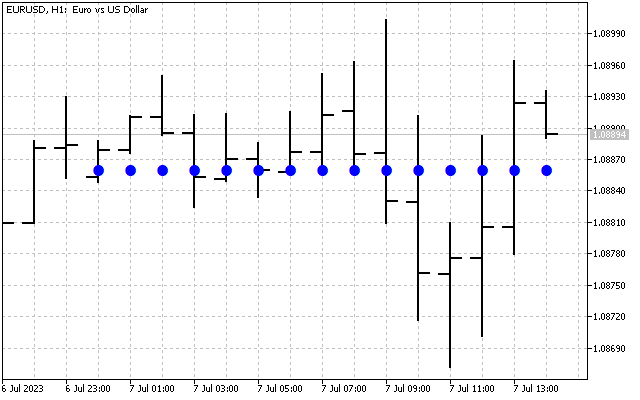
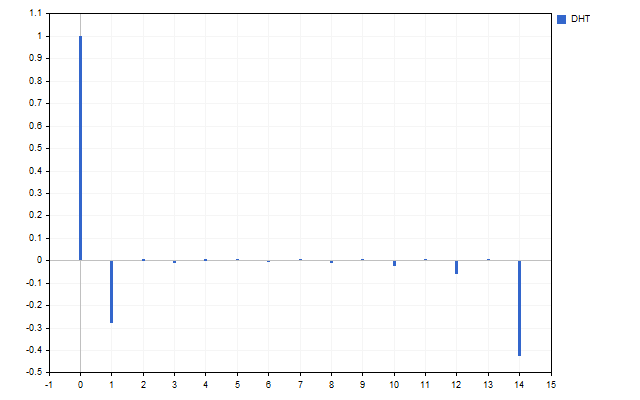
Setzen wir nun alle H[1] - H[14] Schwingungen auf Null. Jetzt haben wir nur grundlegende Informationen über das ursprüngliche Signal. Wenden wir nun die inverse Hartley-Transformation auf dieses Spektrum an.
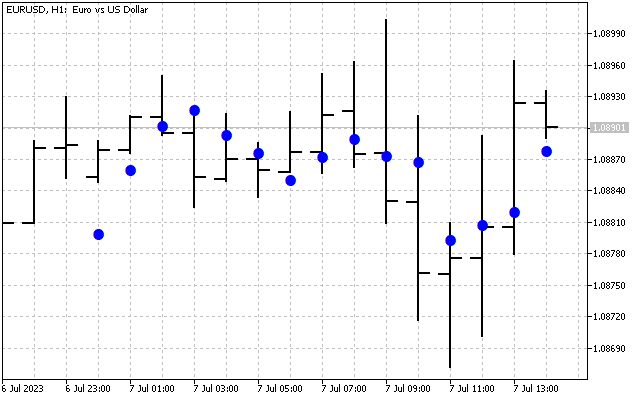
Entfernen wir nun die Schwingungen mit den höchsten Frequenzen H[10] - H[14]. Die Hartley-Transformation liefert das folgende Ergebnis.
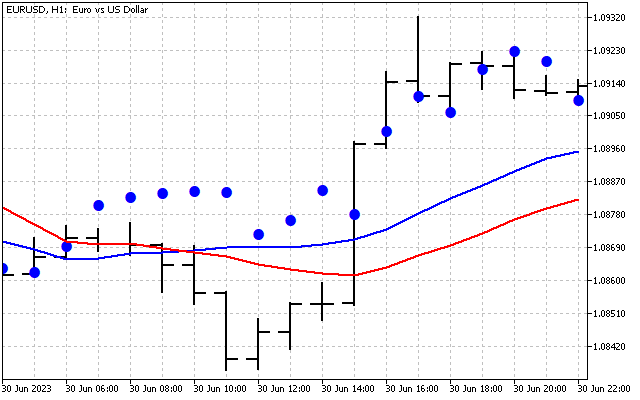
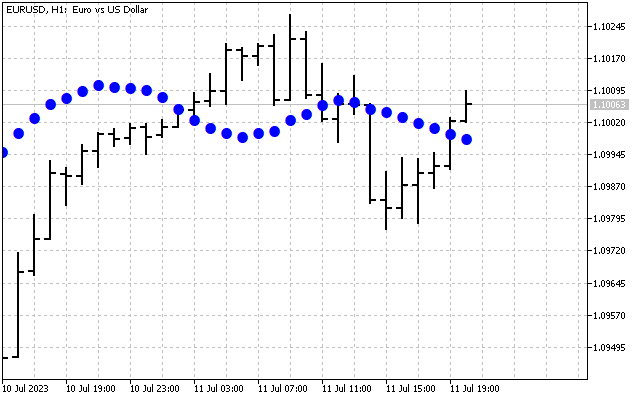
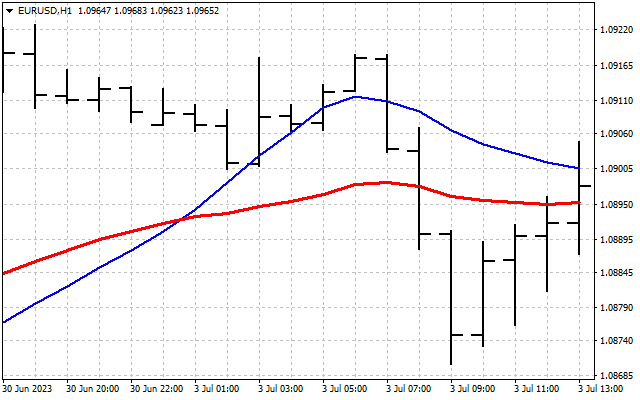
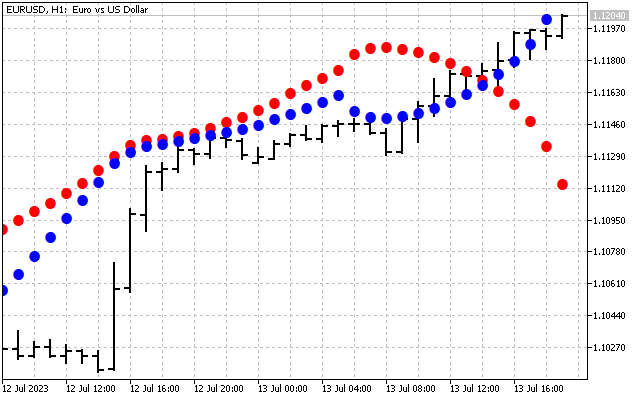
Wir haben das ursprüngliche Signal geglättet. Hier ist die erste Möglichkeit, die Hartley-Transformation in der Praxis anzuwenden. Zunächst können wir die Zeitreihen im Frequenzbereich glätten. Anschließend werden die ermittelten Werte in die Eingabe der üblichen Indikatoren übertragen. Nehmen wir als Beispiel zwei gleitende Durchschnitte. Eine davon wird wie üblich auf den Preis angewendet (rote Linie). Die zweite wird angewendet auf die Werte DHT (blaue Linie).
Das Ausblenden einiger Schwingungen ist nicht die einzige Möglichkeit, das Signalspektrum zu bearbeiten. Wir können alle Schwingungen auf einmal abschwächen, indem wir sie zum Beispiel durch eine bestimmte Zahl dividieren.
Alternativ können wir jede Schwingung entsprechend ihrer Frequenz abschwächen - je höher die Frequenz, desto größer die Abschwächung.
In jedem Fall erhalten wir eine geglättete Zeitreihe. So sieht ein Signal aus, bei dem die Schwingungen um den Faktor 2 abgeschwächt sind.
Eine andere Möglichkeit, das Spektrum zu bearbeiten, besteht darin, nur die stärksten Schwingungen zu behalten. Dazu müssen wir den Durchschnitt aller Schwingungen ermitteln.
Wir belassen nur diejenigen, die diesen Durchschnitt um ihren absoluten Wert übersteigen.
Dann haben wir nur das Hauptsignal plus die stärksten Schwingungen.
Eine weitere Möglichkeit der Signalverarbeitung ist die Umkehrung der Schwingungswerte. Dann hat das rekonstruierte Signal die entgegengesetzte Phase.
In diesem Fall erhalten wir eine Spiegelung des Signals - der Aufwärtstrend wird durch einen Abwärtstrend ersetzt und andersherum. Dieser Ansatz kann bei der Berechnung von Unterstützungs- und Widerstandsniveaus nützlich sein.
Alle Optionen zur Bearbeitung des Spektrums des Quellensignals können entweder einzeln oder in Kombination miteinander verwendet werden. Sie können zum Beispiel zunächst nur die stärksten Schwingungen belassen und dann ihr Vorzeichen umkehren. In diesem Fall wird das Ergebnis einen möglichen Gegentrendimpuls anzeigen.
Indikator mit optimalem Spektrum
Jeder lineare Indikator hat ein Reihe von Koeffizienten. Wendet man die Hartley-Transformation auf diese Koeffizienten an, erhält man die spektrale Charakteristik des Indikators.
Wir wissen, dass der SMA ein Tiefpassfilter ist. Aber überprüfen wir diese Aussage. Alle Koeffizienten dieses Indikators sind gleich 1/N. Die Hartley-Transformation liefert dieses Spektrum des Indikators.
Wie wir sehen können, SMA nur das Hauptsignal durch H[0]durch, aber alle anderen Schwingungen werden vollständig unterdrückt.
Die Spektren (Frequenzmerkmale von Indikatoren) können sich stark voneinander unterscheiden. Beispielsweise durchläuft LWMA alle Schwingungen des Eingangssignals.
Andererseits erlaubt SMMA nur einige Schwingungen und unterdrückt den Rest.
Jeder Indikator hat sein eigenes, einzigartiges Spektrum. Das kann zur Bearbeitung der Preisreihen verwendet werden. Zu diesem Zweck müssen wir zunächst das Spektrum des ursprünglichen Signals ermitteln H[]. Dann multiplizieren wir es Term für Term mit dem Spektrum des Indikators I[].
Die inverse Hartley-Transformation wird auf das erhaltene Ergebnis angewendet. Das Ergebnis ist eine Signalfilterung im Frequenzbereich. Dies ist die Funktionsweise eines Frequenzfilters, basierend auf der Grundlage des Indikators LWMA, sieht so aus.
Wir können aber auch den umgekehrten Weg gehen, indem wir zunächst das Spektrum des Indikators festlegen und dann seine Koeffizienten ermitteln. Versuchen wir, einen Indikator zu erstellen, dessen spektrale Charakteristik dem Spektrum des Signals entspricht.
Der Algorithmus wird folgendermaßen aussehen. Zunächst holen wir uns das Signalspektrum mit DHT. Dann müssen wir es normalisieren. Zu diesem Zweck müssen wir alle Schwingungswerte durch D = H[0] teilen.
Beachten Sie, dass nach der Normalisierung, H[0] = 1 eine zwingende Voraussetzung für die Konstruktion eines Indikators ist.
Danach müssen wir die inverse Transformation anwenden, die die Gewichtungskoeffizienten des Indikators liefern wird.
Diese Koeffizienten unterscheiden sich nicht wesentlich von SMA. Ein solcher Indikator hat jedoch eine geringere Verzögerung als der gleitende Durchschnitt, was eine genauere Verfolgung der Marktdynamik ermöglicht.
Rauschen und Farbe
Bei der Verarbeitung von Finanzzeitreihen bezieht sich der Begriff „Rauschen“ meist auf unerwünschte Signalverzerrungen. Um dieses Rauschen zu eliminieren, können verschiedene Filter verwendet werden, darunter SMA.
Ein zufälliges oder unvorhersehbares Signal kann auch als Rauschen betrachtet werden. Was passiert, wenn wir die Marktpreisbewegungen als eine Summe von Geräuschen darstellen? Dazu müssen wir uns mit dem Konzept der farbigen Geräusche befassen. Farben des Rauschens ist ein Rauschen, das in verschiedenen Frequenzbereichen unterschiedliche Energien haben. Ihren Namen haben sie von den verschiedenen Farben des sichtbaren Lichts: Rot ist niederfrequentes Rauschen, während Violett für hochfrequentes Rauschen steht.
Die Darstellung von Preisbewegungen als eine Summe von farbigem Rauschen kann bei der Analyse von Finanzzeitreihen interessante Ergebnisse liefern. Dieser Ansatz ermöglicht es uns, verschiedene Frequenzkomponenten der Preisbewegung zu berücksichtigen.
Jedes farbige Rauschen hat seine eigene, einzigartige Charakteristik, die die Verteilung der Energie im Spektrum in Abhängigkeit von der f Frequenz widerspiegelt.
Es gibt fünf Grundfarben des Rauschens.
| p Parameter | Rauschfarbe |
|---|---|
| -2 | rot |
| -1 | rosa |
| 0 | weiß |
| +1 | blau |
| +2 | violett |
Jedes Rauschen ist mit einer bestimmten Preisbewegung verbunden. So kann rotes Rauschen beispielsweise auf langfristige Trends oder Zyklen in den Kursbewegungen hinweisen. Weißes Rauschen zeigt an, dass sich der Markt in einem flachen Zustand befindet. Violettes Rauschen kann auf zufälliges und unvorhersehbares Preisverhalten hinweisen. Die Verwendung von farbigem Rauschen bei der Analyse von Finanzzeitreihen kann dazu beitragen, verborgene Muster zu erkennen, sowie Muster, die bei der herkömmlichen Analyse nicht immer sichtbar sind.
Nun wollen wir sehen, wie sich verschiedene Arten des Rauschens auf dem Markt verhalten. Dazu müssen wir ein paar einfache Schritte unternehmen.
Zunächst müssen wir das Spektrum des Signals ermitteln, mit dem wir die Energie jeder Schwingung schätzen können. Zu diesem Zweck müssen wir den Wert jeder Schwingung quadrieren.
Jetzt können wir den Wert des Skalierungsfaktors für Rauschen mit dem p Parameter schätzen. Bei Verwendung dieses Koeffizienten sind die Gesamtenergien von Signal und Rauschen gleich.
Mit Hilfe dieses Koeffizienten können wir das Energiespektrum EN[] des Rauschens konstruieren.
Jetzt können wir das Rauschspektrum HN[] finden. Dazu müssen wir die Quadratwurzel aus dem Energiespektrum ziehen.
Es bleibt nur noch wenig zu tun - den Schwingungen des Rauschspektrums müssen Vorzeichen +/- zugeordnet werden, genau wie den Schwingungen des ursprünglichen Signals. In diesem Fall sind das Rauschen und das ursprüngliche Signal in der gleichen Phase.
Danach müssen wir eine inverse Hartley-Transformation durchführen, um die Rauschwerte auf dem Preisdiagramm zu erhalten. So sieht das rote Rauschen auf dem Markt aus.
Wir können aber auch die entgegengesetzten Vorzeichen der Harmonischen nehmen. In diesem Fall ist das Rauschen im Vergleich zum Originalsignal gegenphasig. Darüber hinaus können wir streng positive oder negative Werte der Schwingung annehmen. Wir können uns das im Frequenzbereich leisten. Dann werden wir in der Lage sein, die Grenzen der durch das Rauschen verursachten Bewegungen auf dem Markt zu erkennen.
Das Konzept des farbigen Rauschens kann nicht nur zur Beschreibung der Marktdynamik, sondern auch zur Entwicklung von Indikatoren verwendet werden.
Dazu müssen wir zunächst die Indikatorleistung E > 0. Dieser Parameter bestimmt, wie empfindlich der Indikator sein soll. Danach führen wir die bereits bekannten Verfahren durch. Zunächst ermitteln wir den Skalierungsfaktor.
Danach finden wir das Spektrum des HI[] Indikators. Vergessen Sie nicht, dass HI[0] gleich 1 sein sollte.
Es genügt, den Schwingungen des Indikatorspektrums bei Bedarf Vorzeichen zuzuordnen. Dann müssen wir die inverse Hartley-Transformation anwenden und erhalten die Indikatorkoeffizienten. So sieht ein roter Rauschindikator mit verschiedenen Varianten der Vorzeichen der Schwingungen aus.
Bei der Entwicklung von Indikatoren können wir nicht nur reines Rauschen, sondern auch verschiedene Kombinationen davon verwenden. So sieht zum Beispiel das Spektrum der Summe aus rotem und violettem Rauschen aus.
So sieht der Unterschied zwischen den Spektren von rotem und weißem Rauschen aus.
Nachdem wir coefficient[], die Indikatorkoeffizienten, erhalten haben, müssen wir sie normalisieren. Dazu müssen wir zunächst die Summe aller Koeffizienten ermitteln.
Danach müssen wir jeden Koeffizienten durch den resultierenden Betrag teilen.
Neben dem aufgeführten „Hauptrauschen“ gibt es noch weitere. Eine Definition von schwarzem Rauschen ist zum Beispiel Rauschen mit dem Parameter p < -2. Versuchen wir einen anderen Ansatz. Gehen wir davon aus, dass die p Rauschparameter gebrochene Werte annehmen kann. Mal sehen, wie sie sich im Laufe der Zeit verändert.
Um den Rauschparameter zu berechnen, müssen wir zunächst das Energiespektrum des Signals ermitteln E[]. Danach müssen wir vier Koeffizienten berechnen.
Für alle Gleichungen: k = 1...N-1. Der am besten geeignete Rauschparameter kann mit Hilfe der folgenden Gleichung berechnet werden.
So verändert sich dieser Parameter unter Marktbedingungen.
Wie wir sehen, kann die Verwendung von farbigem Rauschen in der Finanzzeitreihenanalyse ein nützliches Instrument zur Erforschung und zum Verständnis der Marktdynamik sein. Dieser Ansatz kann dazu beitragen, verborgene Muster aufzudecken und die Vorhersage von Kursbewegungen zu verbessern.
Schlussfolgerung
Die diskrete Hartley-Transformation hat ihre eigenen schnellen Transformationsalgorithmen. Aber wenn wir im Vorhinein für das Array cas allozieren, können wir die Geschwindigkeit der Datenverarbeitung deutlich erhöhen. Die Größe dieses Arrays sollte gleich sein mit (N-1)^2+1sein, wobei N eine Indikatorperiode ist. Dann werden die Werte dieses Arrays wie folgt festgelegt:
Genau diesen Ansatz habe ich in diesem Artikel verwendet.
Die folgenden Indikatoren sind dem Artikel beigefügt.
| Symbol | Beschreibung |
|---|---|
| DHT | Der Indikator demonstriert die Möglichkeiten der Verarbeitung von Signalschwingungen.
|
| DHT LWMA | Der Indikator zeigt die Preisverarbeitung durch den LWMA-Indikator im Spektralbereich |
| Spectrum | Der Indikator, dessen Koeffizienten eine spektrale Charakteristik aufweisen, die der des Originalsignals ähnlich ist |
| Noise Levels | Der Indikator zeigt den Pegel der farbigen Rauschens an. Rauschen - Rauschfarbe Type - ändert die Phase des Originalsignals |
| Noise Indicator | Der Indikator wählt Koeffizienten aus, die der gewählten Rauschfarbe entsprechen. E - Rauschleistung. |
| Fractional Noise | Der Indikator, der den fraktionierten Rauschparameter anzeigt. |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/12984
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
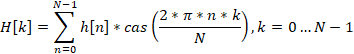
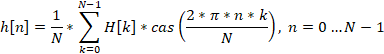
Vielen Dank für diesen Artikel!
Erst gestern habe ich über Methoden zur Identifizierung von Marktphasen durch statistische Indikatoren in einer Teilstichprobe nachgedacht, und ich habe ähnliche Ideen in dem Artikel gesehen.
Haben Sie in dieser Richtung weitergehende Untersuchungen angestellt? Ich frage mich, wie schnell (mit welcher Verzögerung) und mit welchem Fehler sie es geschafft haben, Trends zu klassifizieren?
Vielen Dank für den Artikel!
Erst gestern habe ich über Methoden zur Identifizierung von Marktphasen durch statistische Indikatoren in einer Teilstichprobe nachgedacht und ähnliche Ideen in diesem Artikel gesehen.
Haben Sie in dieser Richtung tiefergehende Untersuchungen angestellt? Ich frage mich, wie schnell (mit welcher Verzögerung) und mit welchem Fehler sie es geschafft haben, Trends zu klassifizieren?
Die Identifizierung von Marktphasen ist wahrscheinlich die einfachste Aufgabe. Wir nehmen das Preisspektrum (ohne das Hauptsignal) und lassen es durch eine Clusteranalyse (Kohonen Maps) laufen - so erhalten wir Marktphasen. Aber bei Trends ist alles sehr kompliziert - das Zeichen für einen Wechsel/Beginn eines neuen Trends ist eine relative Schwäche der niederfrequenten Komponente und eine relative Verstärkung der hochfrequenten Obertöne. Aber leider ist es möglich, die Trendrichtung ernsthaft zu verfehlen.