
Популяционные алгоритмы оптимизации
"Во всём, что происходит во Вселенной, проявляется действие
некоторого правила максимума или минимума"
Леонард Эйлер, XVIII век
Содержание:
- Историческая справка
- Классификация АО
- Сходимость и скорость сходимости. Устойчивость сходимости. Масштабируемость алгоритма оптимизации
- Тестовые функции, конструирование комплексного критерия оценки AO
- Тестовый стенд
- Простой пример АО с использованием ГСЧ
- Таблица результатов
1. Историческая справка
Алгоритмы оптимизации — алгоритмы, позволяющие находить экстремальные точки в области определения функции, на которых она достигает минимального или максимального значения.
Уже во времена античности, в древней Греции ученые мужи знали, что:
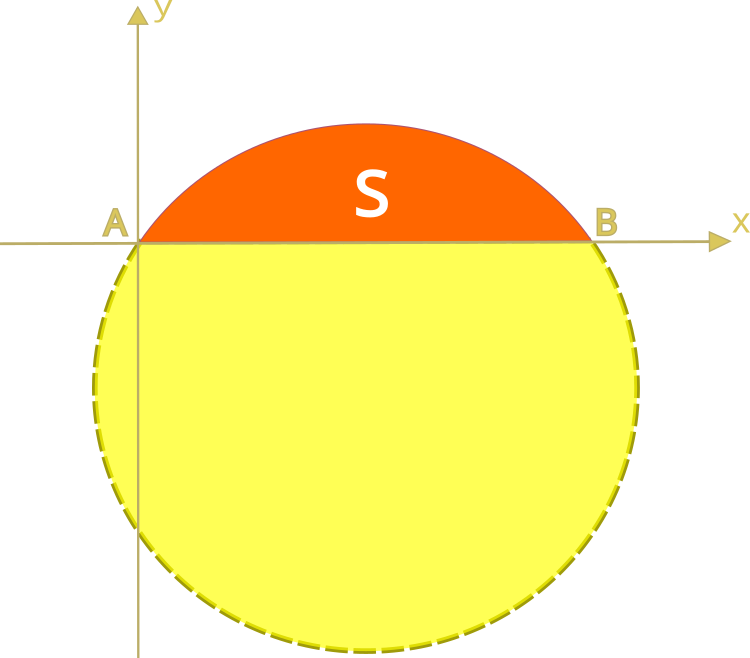
— Из всех фигур с заданным периметром наибольшую площадь имеет круг.
— Из всех многоугольников с заданным числом сторон и заданным периметром наибольшую площадь имеет правильный многоугольник.
— Из всех объемных фигур, имеющих заданную площадь, наибольший объем у шара.
Тогда же была сформулирована задача, имеющая первые вариационные решения. Это было, если верить легенде, около 825 года до нашей эры. Дидона, сестра царя финикийского города Тира, переселившись на южное побережье Средиземного моря, попросила у местного племени участок земли, который можно охватить шкурой быка. Местные жители предоставили шкуру, которую находчивая девушка разрезала на узкие ремни и связала их, получившимся канатом она охватила территорию у побережья, на котором основала город Карфаген.
Задача состоит в том, каким образом среди замкнутых плоских кривых, имеющих заданную длину, найти самую эффективную кривую, охватывающую максимальную площадь поверхности. Максимальную площадь в этой задаче представляет область, описанная полуокружностью.
К новому рассвету мысли, от античной культуры Средиземноморья, минуя гнет инквизиции с кострами и шарлатанством средних веков, перенесемся в эпоху ренессанса и возрождения, когда создавались свежие идеи и воплощались силой свободного полета мысли в новые теории. Так, Иоганн Бернулли публикует в июне 1696 года перед читателями Acta Eruditorum текст следующего содержания: "Я, Иоганн Бернулли, обращаюсь к самым блестящим математикам в мире. Нет ничего более привлекательного для интеллигентных людей, чем честная, сложная проблема, чье возможное решение принесет известность и навсегда останется памятником. Следуя примеру Паскаля, Ферма и т. д., я надеюсь заслужить благодарность всего научного сообщества, поставив перед лучшими математиками нашего времени задачу, которая проверит их методы и силу их интеллекта. Если кто-то сообщит мне решение предложенной проблемы, я публично объявлю его достойным похвалы".
Формулировка задачи И.Бернулли о брахистохроне:
"Учитывая две точки A и B в вертикальной плоскости, на какую кривую указывает точка, действующая только под действием силы тяжести, которая начинается в A и достигает B в кратчайшее время." Для уточнения, еще в 1638 году, задолго перед публикацией Бернулли, сам Галилей пытался решить аналогичную задачу для пути самого быстрого спуска. Ответ на эту задачу: самый быстрый путь из всех, из одной точки в другую - это не самый короткий путь, как представляется на первый взгляд, не прямая линия, а кривая — циклоида, которая определяет кривизну кривой в каждой точке.
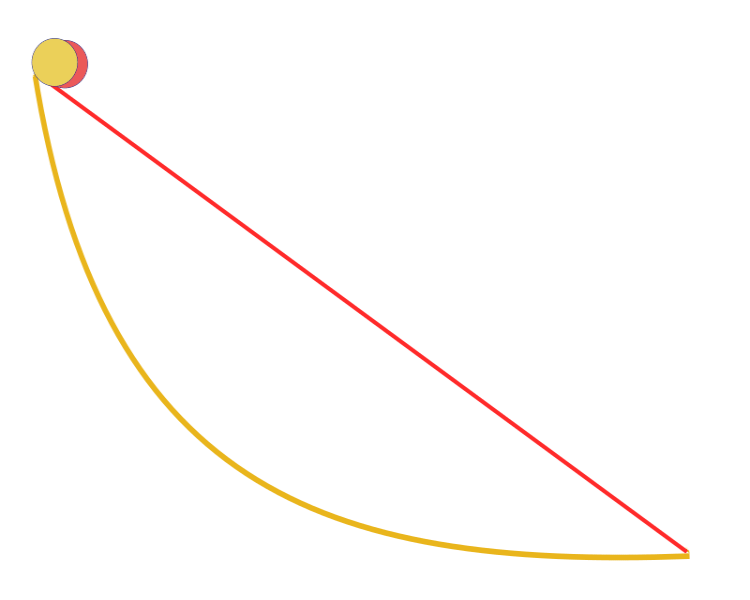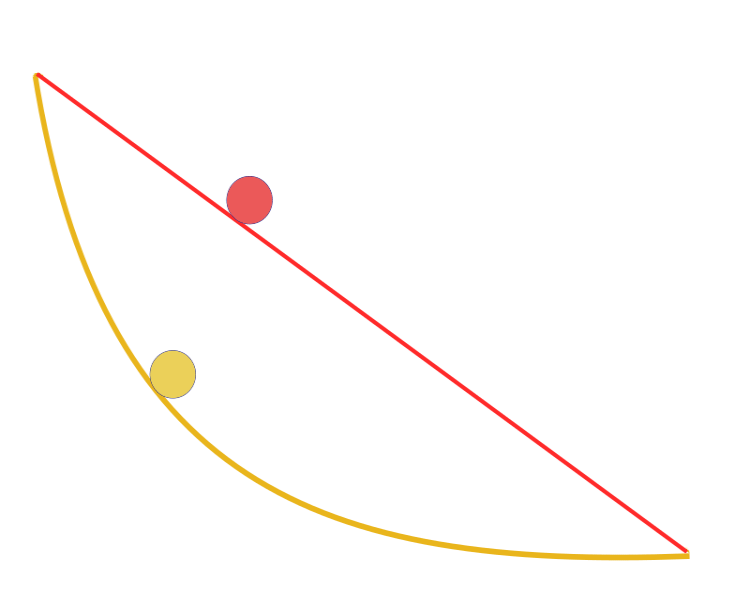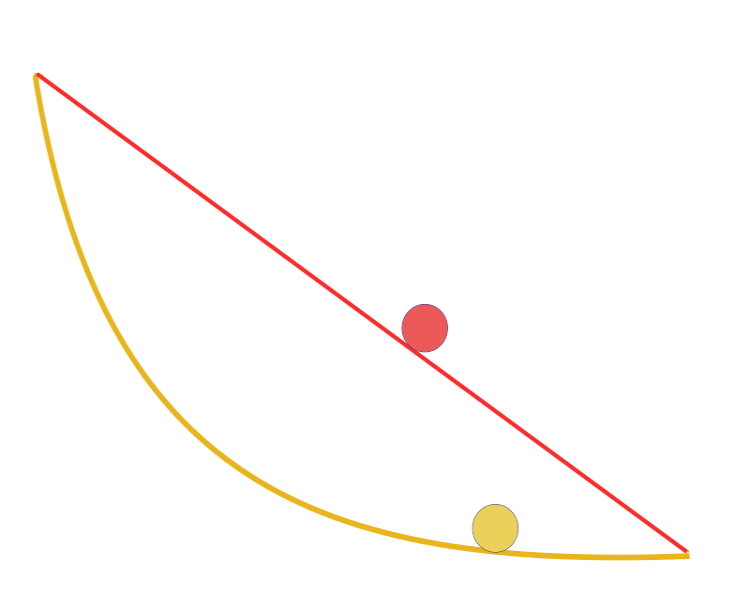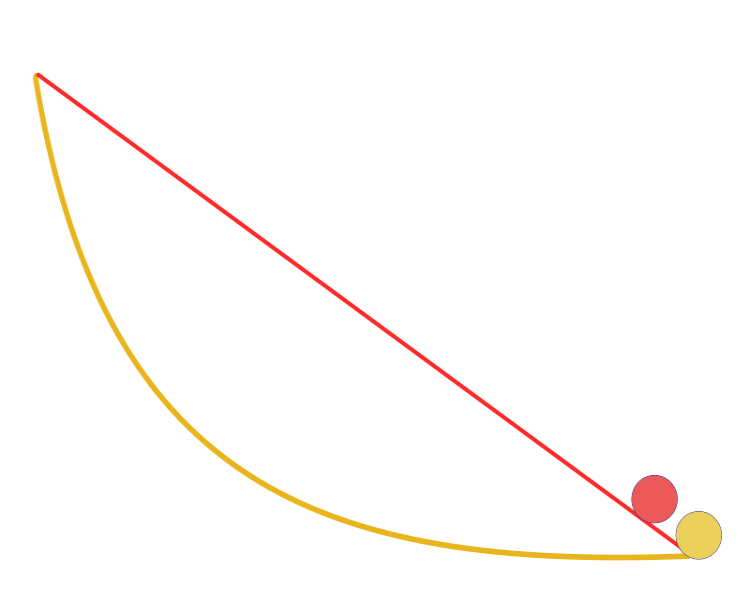
Brachistochrone curve
Все другие доказательства, включая доказательства Ньютона (которые не были раскрыты в то время), основаны на нахождении градиента в каждой точке. Важно также отметить, что метод решения, полученный Исааком Ньютоном, лёг в основу вариационного исчисления. Методы вариационного исчисления обычно используют для решения задач, в которых критерии оптимальности представляются в виде функционалов и решениями которых служат неизвестные функции. Такие задачи возникают обычно при статической оптимизации процессов с распределенными параметрами или в задачах динамической оптимизации.
Условия экстремума первого порядка в вариационном исчислении были получены Леонардом Эйлером и Жозефом Лагранжем (уравнения Эйлера — Лагранжа), эти уравнения широко используются в задачах оптимизации и совместно с принципом стационарности действия используются для вычисления траекторий в механике. Вскоре, однако, выяснилось, что решения этих уравнений не во всех случаях дают реальный экстремум, и встала задача найти достаточные условия, гарантирующие его нахождение. Работа была продолжена и выведены условия экстремума второго порядка учеными математиками— Лежандром и Якоби, затем его учеником Гессе. Вопрос о существовании решения в вариационном исчислении был впервые поставлен Вейерштрассом уже позднее, во второй половине XIX века.
Поиск и попытки оптимальных решений задач сформировали ко второй половине 18 века математические основы и принципы оптимизации. Однако к большому сожалению, на практике, до второй половины 20 века методы оптимизации во многих областях науки и техники фактически имели слабое применение, поскольку практическое использование математических методов требовало огромных вычислительных ресурсов и только с развитием технологий в современном мире ситуация изменилась, нашлись возможности реализации сложных методов оптимизации и создалось великое многообразие доступных алгоритмов.
В 1980-х годах началась интенсивная разработка класса стохастических алгоритмов оптимизации, которые стали результатом моделирования, заимствованного у природы.
2. Классификация АО
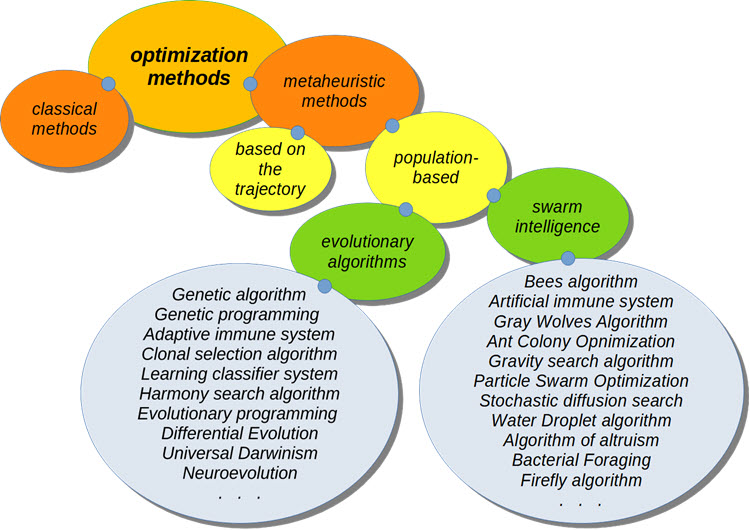
Classification AO
При оптимизации торговых систем наибольший интерес представляют метаэвристические алгоритмы оптимизации, которые не требуют знания формулы оптимизируемой функции и сходимость которых к глобальному оптимуму не доказана, но экспериментально установлено, что в большинстве случаев они дают достаточно хорошее решение и этого достаточно для ряда задач.
Очень много АО появились как модели, заимствованные у природы, их называют также поведенческими, роевыми, популяционными. Такие например, как поведение птиц в стае (алгоритм роя частиц) или принципы поведения колонии муравьев (алгоритм «колонии муравьев» или «муравьиный алгоритм»).
Популяционные алгоритмы предполагают одновременную обработку нескольких вариантов решения задачи оптимизации и представляют собой альтернативу классическим поисковым алгоритмам по траекториям движения, в области поиска которых эволюционирует только один кандидат при решении задачи.
3. Сходимость и скорость сходимости. Устойчивость сходимости. Масштабируемость алгоритма оптимизации
Для каждой алгоритмической реализации и для каждого класса задач оптимизации эффективность, быстродействие, сходимость, влияние условий задачи и параметров алгоритма требуют тщательного анализа.
3.1) Сходимость и скорость сходимости.
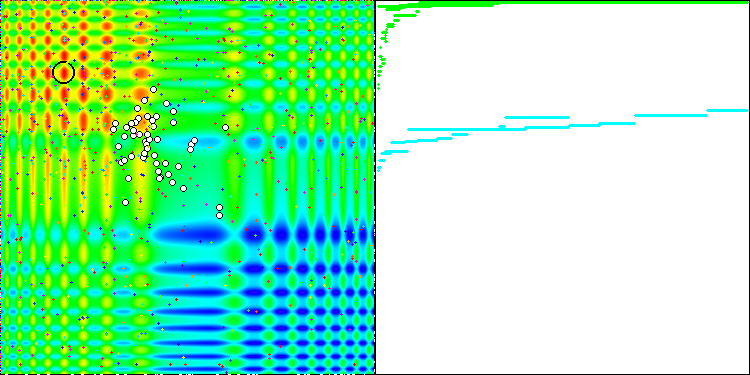
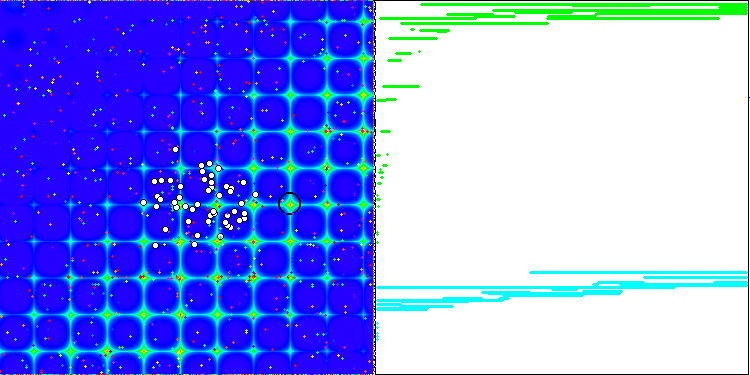
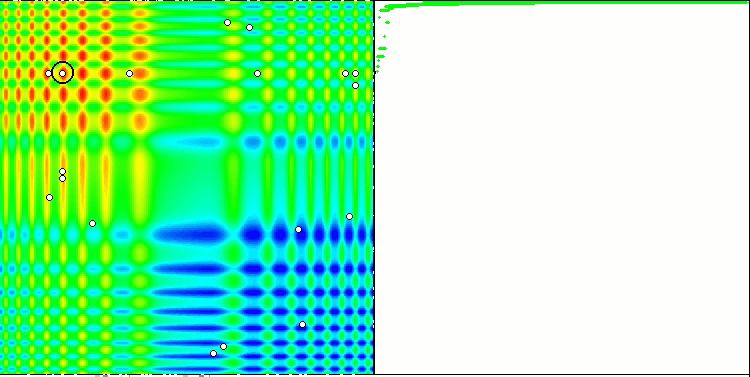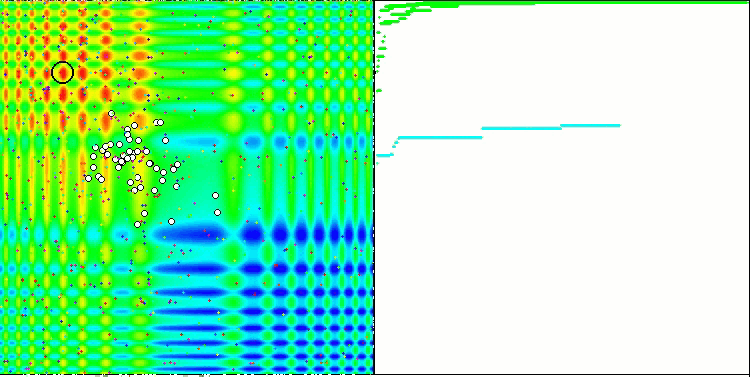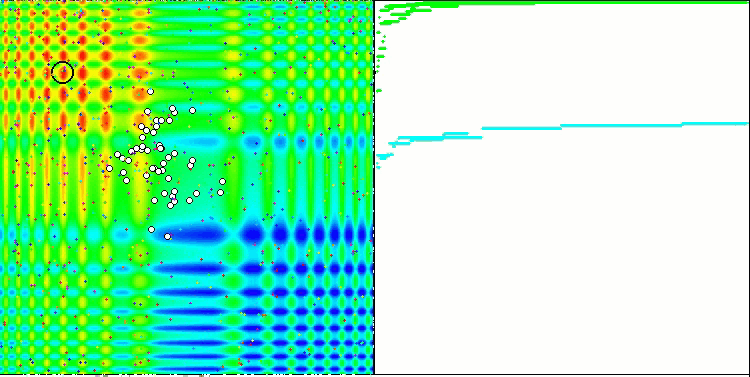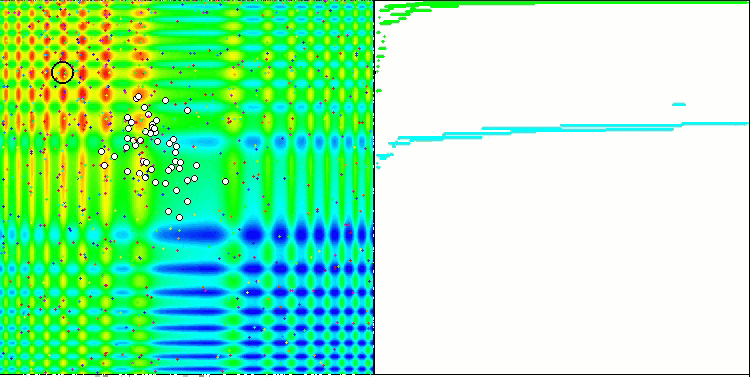
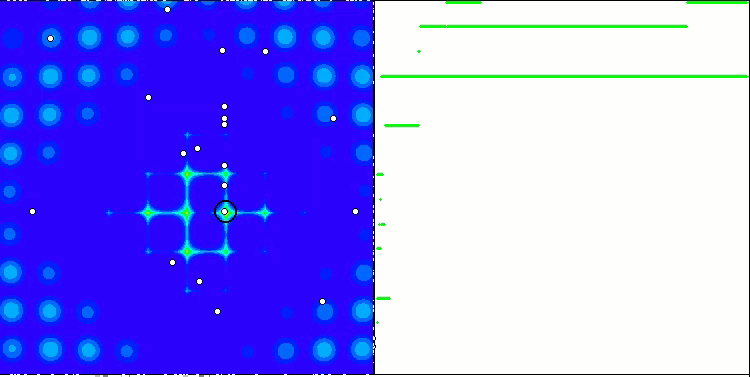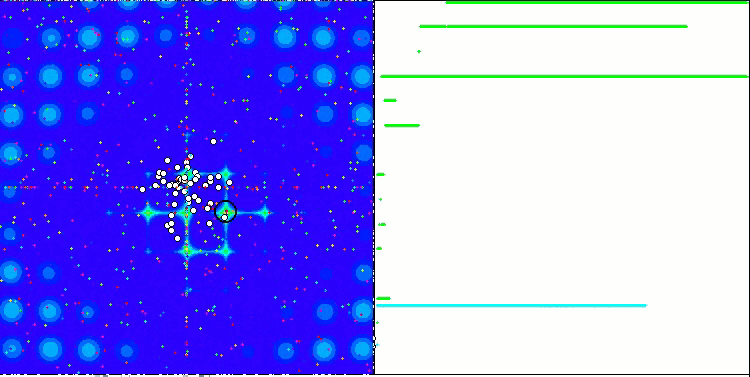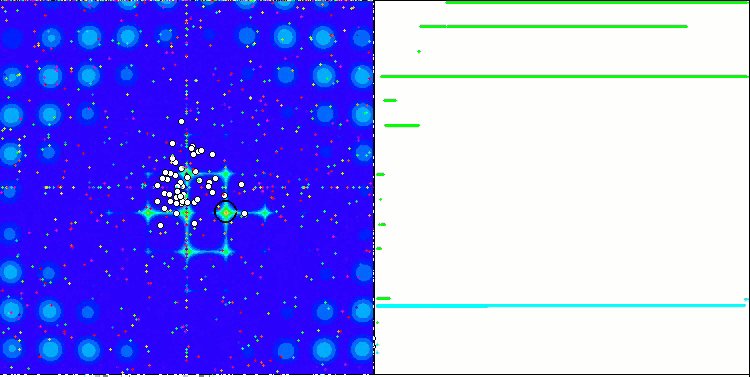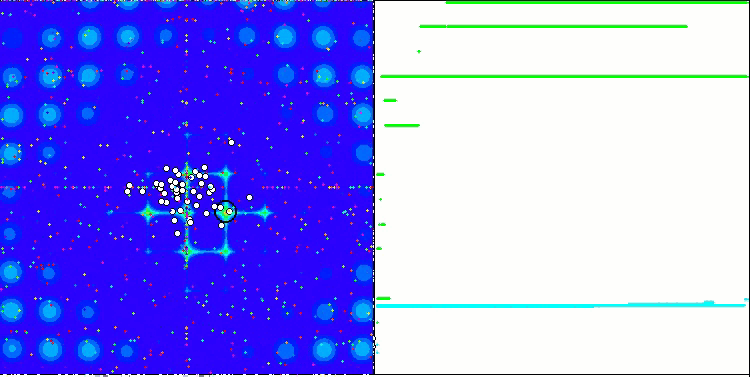
Свойство итерационного алгоритма достигать оптимума целевой функции или подходить достаточно близко к нему за конечное число шагов. Так, на скриншотах выше мы видим, в правой части итерационно построенный график результатов вычисленной тестовой функции. На основе представленных двух изображений, можно сделать вывод, что на сходимость влияет сложность поверхности исследуемой функции, чем она сложнее, тем труднее найти глобальный экстремум.
Скорость сходимости алгоритмов — один из важнейших показателей качества алгоритма оптимизации и является одной из основных характеристик методов оптимизации. Часто, когда говорят о том, что один алгоритм является более быстрым, чем другой, имеют в виду именно скорость сходимости. Чем ближе к глобальному экстремуму результат и чем быстрее он получен (имеется в виду более ранние итерации алгоритма), тем выше этот показатель. Отметим, что обычно скорость сходимости методов не превышает квадратичной. В редких случаях метод может обладать кубической скоростью сходимости.
3.2) Устойчивость сходимости.
Следует отметить, что количество итераций, требуемое для достижения результата, зависит не только от поисковой способности самого алгоритма, но и от исследуемой функции. Если функция характеризуется высокой сложностью поверхности (наличие изломов, дискретность, разрывы), то алгоритм может оказаться неустойчивым и вообще не сможет обеспечить приемлемой точности. Кроме того, устойчивость сходимости можно понимать как повторяемость результатов оптимизации при проведении нескольких подряд тестов. Если результаты имеют высокие расхождения в значениях, следовательно устойчивость алгоритма низкая.
3.3) Масштабируемость алгоритма оптимизации.
Масштабируемость алгоритма оптимизации — способность сохранять сходимость при увеличении размерности задачи, то есть при увеличении количества переменных оптимизируемой функции должна сохранятся сходимость на приемлемом для практических целей уровне. Популяционные алгоритмы поисковой оптимизации в сравнении с классическими алгоритмами имеют неоспоримые преимущества, прежде всего, при решении задач высокой размерности и плохо формализованных задач. В этих условиях популяционные алгоритмы могут обеспечить высокую вероятность локализации глобального экстремума оптимизируемой функции.
В случае гладкой и унимодальной оптимизируемой функции популяционные алгоритмы, как правило, менее эффективны, чем любой классический градиентный метод. Также к недостаткам популяционных алгоритмов следует отнести сильную зависимость их эффективности от значений степеней свободы (количества настроечных параметров), число которых в большинстве алгоритмов достаточно велико.
4. Тестовые функции, конструирование комплексного критерия оценки AO
Для тестирования алгоритмов оптимизации и сравнения их между собой не существует общепризнанной методики, но существуют множество тестовых функций, которые были придуманы в разные годы исследователями. Но мы будем использовать функции, которые были созданы мной перед публикацией первой статьи. Эти функции можно найти в папке терминала \MQL5\Experts\Examples\Math 3D\Functions.mqh и \MQL5\Experts\Examples\Math 3D Morpher\Functions.mqh. Данные функции удовлетворяют всем критериям сложности для тестирования АО. Дополнительно разработаны функции Forest и Megacity для обеспечения более разностороннего изучения поисковых возможностей AO.
Тестовая функция Skin:
![]()
Функция отличается гладкостью на всём своём определении и имеет множество локальных max/min, незначительно отличающихся по своему значению (ловушки сходимости), чем вызывают застревание алгоритмов, которые не достигают глобального экстремума.
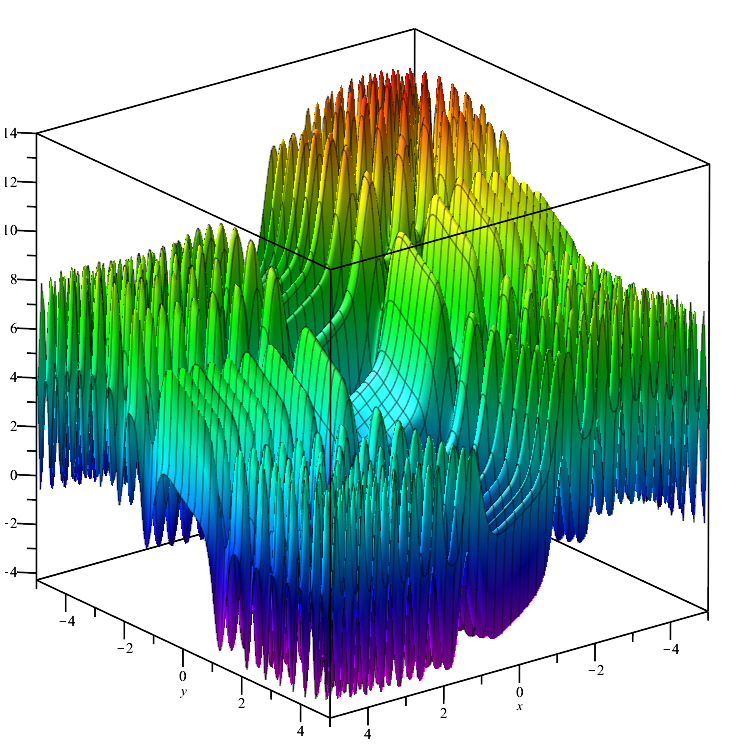
Тестовая функция Skin.
Тестовая функция Forest:
![]()
Функция представляет собой несколько максимумов, не имеющих дифференциала в своих точках, поэтому представляет сложность для алгоритмов оптимизации, робастность которых критична зависима от гладкости исследуемой функции.
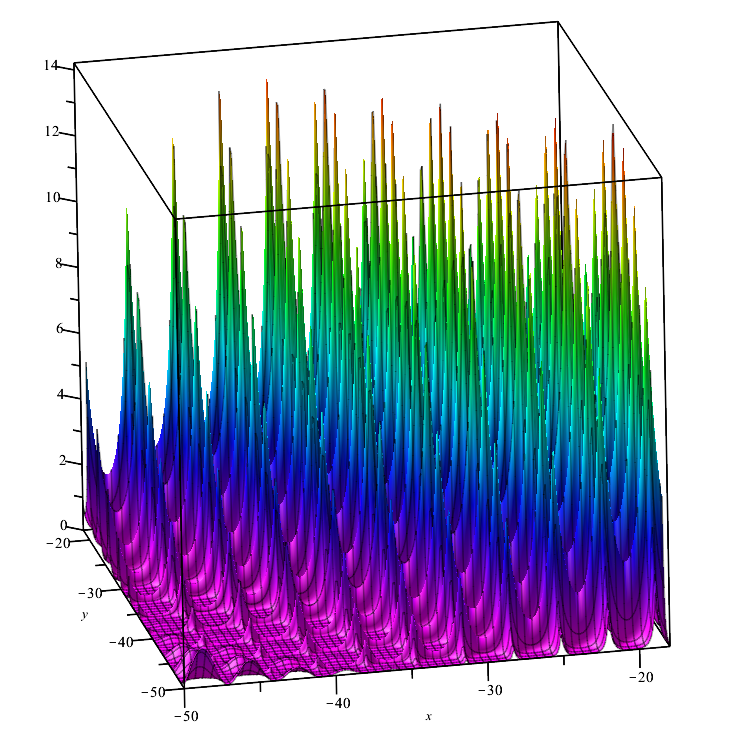
Тестовая функция Forest.
Тестовая функция Megacity:
![]()
Дискретная функция, образующая "площадки" (в таких местах изменение переменных не приводит к существенному изменению значения функции), поэтому сложная для алгоритмов, которые требуют наличие градиента.
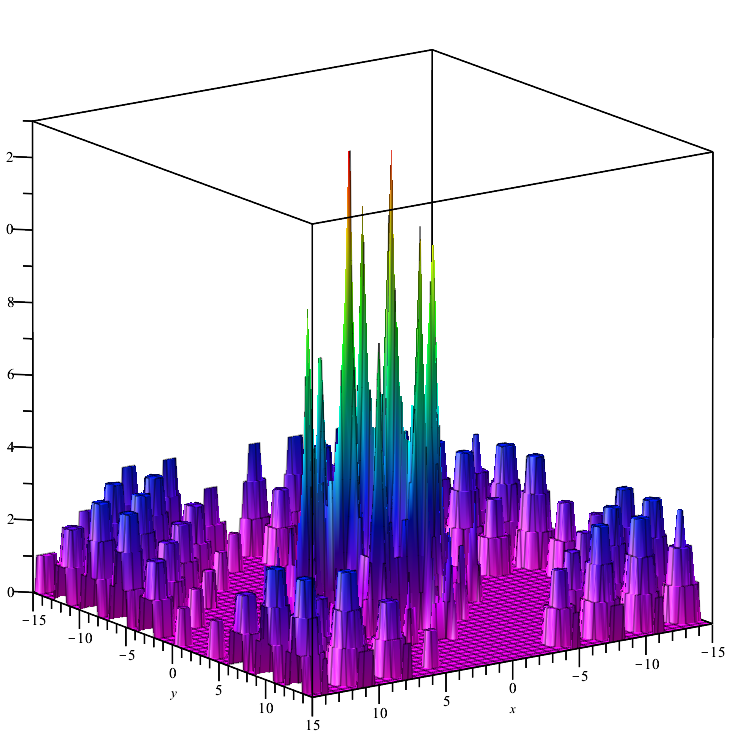
Тестовая функция Megacity.
5. Тестовый стенд
Для комплексного сравнения алгоритмов оптимизации предпринята попытка создания общего критерия оценки. Сложность этой затеи заключается в том, что непонятно, как сравнивать алгоритмы, ведь каждый из них по-своему хорош для соответствующего класса задач. Один, к примеру, быстро сходится, но плохо масштабируем, а другой масштабируется хорошо, но неустойчив.
- Сходимость: Для исследования сходимости используем три функции, представленные выше, максимум и минимум которых преобразованы в диапазон от 0.0 (худший результат) до 1.0 (лучший результат), что позволит оценить способность алгоритмов обеспечивать сходимость на разных типах задач.
- Скорость сходимости: Производятся замеры лучших результатов алгоритма на 1000-м и 10 000-м запуске тестируемой функции. Тем самым можно видеть, насколько быстро АО сходится. Чем быстрее сходимость, тем будет более изогнут график сходимости в сторону максимума.
- Устойчивость: Производим пять запусков оптимизации каждой из функций и сделаем расчет среднего значения в диапазоне от 0.0 до 1.0. Это необходимо, потому что от запуска к запуску результаты некоторых алгоритмов могут сильно отличаться. Чем выше сходимость в каждом из пяти тестов, тем показатель устойчивости выше.
- Масштабируемость: Некоторые АО могут показывать достойные практического применения результаты только на функциях с небольшим количеством переменных, например, не более двух, а некоторые даже не способны работать с количеством переменных больше чем 1. Кроме того, существуют алгоритмы способные работать с функциями при тысяче переменных, такие алгоритмы оптимизации могут быть использованы в качестве АО для нейронных сетей.
Для удобства использования тестовых функций напишем родительский класс и энумератор, который позволит нам в дальнейшем выбирать объект дочернего класса соответствующей тестовой функции:
//—————————————————————————————————————————————————————————————————————————————— class C_Function { public: //==================================================================== double CalcFunc (double &args [], //function arguments int amount) //amount of runs functions { double x, y; double sum = 0.0; for (int i = 0; i < amount; i++) { x = args [i * 2]; y = args [i * 2 + 1]; sum += Core (x, y); } sum /= amount; return sum; } double GetMinArg () { return minArg;} double GetMaxArg () { return maxArg;} double GetMinFun () { return minFun;} double GetMaxFun () { return maxFun;} string GetNamFun () { return fuName;} protected: //================================================================== void SetMinArg (double min) { minArg = min;} void SetMaxArg (double max) { maxArg = max;} void SetMinFun (double min) { minFun = min;} void SetMaxFun (double max) { maxFun = max;} void SetNamFun (string nam) { fuName = nam;} private: //==================================================================== virtual double Core (double x, double y) { return 0.0;} double minArg; double maxArg; double minFun; double maxFun; string fuName; }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— enum EFunc { Skin, Forest, Megacity }; C_Function *SelectFunction (EFunc f) { C_Function *func; switch (f) { case Skin: func = new C_Skin (); return (GetPointer (func)); case Forest: func = new C_Forest (); return (GetPointer (func)); case Megasity: func = new C_Megacity(); return (GetPointer (func)); default: func = new C_Skin (); return (GetPointer (func)); } } //——————————————————————————————————————————————————————————————————————————————
Тогда дочерние классы будут выглядеть так:
//—————————————————————————————————————————————————————————————————————————————— class C_Skin : public C_Function { public: //=================================================================== C_Skin () { SetNamFun ("Skin"); SetMinArg (-5.0); SetMaxArg (5.0); SetMinFun (-4.3182); //[x=3.07021;y=3.315935] 1 point SetMaxFun (14.0606); //[x=-3.315699;y=-3.072485] 1 point } private: //=================================================================== double Core (double x, double y) { double a1=2*x*x; double a2=2*y*y; double b1=MathCos(a1)-1.1; b1=b1*b1; double c1=MathSin(0.5*x)-1.2; c1=c1*c1; double d1=MathCos(a2)-1.1; d1=d1*d1; double e1=MathSin(0.5*y)-1.2; e1=e1*e1; double res=b1+c1-d1+e1; return(res); } }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— class C_Forest : public C_Function { public: //=================================================================== C_Forest () { SetNamFun ("Forest"); SetMinArg (-50.0); SetMaxArg (-18.0); SetMinFun (0.0); //many points SetMaxFun (15.95123239744); //[x=-25.132741228718345;y=-32.55751918948773] 1 point } private: //=================================================================== double Core (double x, double y) { double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0))); double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0)))); double f = a + b; double res = MathPow (f, 4); if (res < 0.0) res = 0.0; return (res); } }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— class C_Megacity : public C_Function { public: //=================================================================== C_Megacity () { SetNamFun ("Megacity"); SetMinArg (-15.0); SetMaxArg (15.0); SetMinFun (0.0); //many points SetMaxFun (15.0); //[x=`3.16;y=1.990] 1 point } private: //=================================================================== double Core (double x, double y) { double a = MathSin (MathSqrt (MathAbs (x - 1.13) + MathAbs (y - 2.0))); double b = MathCos (MathSqrt (MathAbs (MathSin (x))) + MathSqrt (MathAbs (MathSin (y - 2.0)))); double f = a + b; double res = floor (MathPow (f, 4)); return (res); } }; //——————————————————————————————————————————————————————————————————————————————
Для проверки действительности результатов тестирования АО, полученных на тестовом стенде, можем использовать скрипт, в котором производится полный перебор X и Y функции с размером шага Step. Необходимо быть внимательным с выбором шага, так как очень малая величина шага будет причиной слишком долгого выполнения расчетов. Для примера, функция Skin имеет диапазон аргументов [-5;5], при шаге 0.00001 по оси X будет (5-(-5))/0.00001=1'000'000 (миллион) шагов, столько же по оси Y, соответственно общее количество запусков тестовой функции для расчета значения в каждой из точек будет равным 1'000'000 х 1'000'000= 1'000'000'000'000 (10^12, триллион).
Необходимо понимать, насколько сложная задача стоит перед АО, так как требуется найти максимум всего лишь за 10'000 шагов (примерно такое значение используется в оптимизаторе MetaTrader 5). Следует учесть, что этот расчет сделан для функции с двумя переменными, а максимальное количество переменных, которое будет использовано в тестах составляет 1000.
Отдельно стоит выделить важный момент: тесты алгоритма в этой статье и последующих используют шаг 0.0! или минимально возможный для конкретной реализации для соответствующего АО.
//—————————————————————————————————————————————————————————————————————————————— input EFunc Function = Skin; input double Step = 0.01; //—————————————————————————————————————————————————————————————————————————————— void OnStart () { C_Function *TestFunc = SelectFunction (Function); double argMin = TestFunc.GetMinArg (); double argMax = TestFunc.GetMaxArg (); double maxFuncValue = 0; double xMaxFunc = 0.0; double yMaxFunc = 0.0; double minFuncValue = 0; double xMinFunc = 0.0; double yMinFunc = 0.0; double fValue = 0.0; double arg [2]; arg [0] = argMin; arg [1] = argMin; long cnt = 0; while (arg [1] <= argMax && !IsStopped ()) { arg [0] = argMin; while (arg [0] <= argMax && !IsStopped ()) { cnt++; fValue = TestFunc.CalcFunc (arg, 1); if (fValue > maxFuncValue) { maxFuncValue = fValue; xMaxFunc = arg [0]; yMaxFunc = arg [1]; } if (fValue < minFuncValue) { minFuncValue = fValue; xMinFunc = arg [0]; yMinFunc = arg [1]; } arg [0] += Step; if (cnt == 1) { maxFuncValue = fValue; minFuncValue = fValue; } } arg [1] += Step; } Print ("======", TestFunc.GetNamFun (), ", launch counter: ", cnt); Print ("MaxFuncValue: ", DoubleToString (maxFuncValue, 16), " X: ", DoubleToString (xMaxFunc, 16), " Y: ", DoubleToString (yMaxFunc, 16)); Print ("MinFuncValue: ", DoubleToString (minFuncValue, 16), " X: ", DoubleToString (xMinFunc, 16), " Y: ", DoubleToString (yMinFunc, 16)); delete TestFunc; } //——————————————————————————————————————————————————————————————————————————————
Напишем тестовый стенд:
#property script_show_inputs #property strict #include <Canvas\Canvas.mqh> #include <\Math\Functions.mqh> #include "AO_RND.mqh" #define AOname "C_AO_RND" //—————————————————————————————————————————————————————————————————————————————— input int Population_P = 50; input double ArgumentStep_P = 0.0; input int Test1FuncRuns_P = 1; input int Test2FuncRuns_P = 20; input int Test3FuncRuns_P = 500; input int Measur1FuncValue_P = 1000; input int Measur2FuncValue_P = 10000; input int NumberRepetTest_P = 5; input int RenderSleepMsc_P = 0; //—————————————————————————————————————————————————————————————————————————————— int WidthMonitor = 750; //monitor screen width int HeighMonitor = 375; //monitor screen height int WidthScrFunc = 375 - 2; //test function screen width int HeighScrFunc = 375 - 2; //test function screen height CCanvas Canvas; //drawing table C_AO_RND AO; //AO object C_Skin SkiF; C_Forest ForF; C_Megacity MegF; struct S_CLR { color clr []; }; S_CLR FunctScrin []; //two-dimensional matrix of colors double ScoreAll = 0.0; long TestCounter = 0; //—————————————————————————————————————————————————————————————————————————————— void OnStart () { //creating a table ----------------------------------------------------------- string canvasName = "AO_Test_Func_Canvas"; if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, WidthMonitor, HeighMonitor, COLOR_FORMAT_ARGB_RAW)) { Print ("Error creating Canvas: ", GetLastError ()); return; } ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN, false); ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true); ArrayResize (FunctScrin, HeighScrFunc); for (int i = 0; i < HeighScrFunc; i++) { ArrayResize (FunctScrin [i].clr, HeighScrFunc); } //============================================================================ //Test Skin################################################################### Print ("============================="); CanvasErase (); FuncTests (SkiF, Test1FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrLime); FuncTests (SkiF, Test2FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrAqua); FuncTests (SkiF, Test3FuncRuns_P, SkiF.GetMinFun (), SkiF.GetMaxFun (), -3.315699, -3.072485, clrOrangeRed); //Test Forest################################################################# Print ("============================="); CanvasErase (); FuncTests (ForF, Test1FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrLime); FuncTests (ForF, Test2FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrAqua); FuncTests (ForF, Test3FuncRuns_P, ForF.GetMinFun (), ForF.GetMaxFun (), -25.132741228718345, -32.55751918948773, clrOrangeRed); //Test Megacity############################################################### Print ("============================="); CanvasErase (); FuncTests (MegF, Test1FuncRuns_P, MegF.GetMinFun (), MegF.GetMaxFun (), 3.16, 1.990, clrLime); FuncTests (MegF, Test2FuncRuns_P, MegF.GetMinFun (), MegF.GetMaxFun (), 3.16, 1.990, clrAqua); FuncTests (MegF, Test3FuncRuns_P, MegF.GetMinFun (), MegF.GetMaxFun (), 3.16, 1.990, clrOrangeRed); Print ("============================="); Print ("All score for ", AOname, ": ", ScoreAll / TestCounter); } //—————————————————————————————————————————————————————————————————————————————— void CanvasErase () { Canvas.Erase (XRGB (0, 0, 0)); Canvas.FillRectangle (1, 1, HeighMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite)); Canvas.FillRectangle (HeighMonitor + 1, 1, WidthMonitor - 2, HeighMonitor - 2, COLOR2RGB (clrWhite)); } //—————————————————————————————————————————————————————————————————————————————— void FuncTests (C_Function &f, int funcCount, double minFuncVal, double maxFuncVal, double xBest, double yBest, color clrConv) { DrawFunctionGraph (f.GetMinArg (), f.GetMaxArg (), minFuncVal, maxFuncVal, f); SendGraphToCanvas (1, 1); int x = (int)Scale (xBest, f.GetMinArg (), f.GetMaxArg (), 0, WidthScrFunc - 1, false); int y = (int)Scale (yBest, f.GetMinArg (), f.GetMaxArg (), 0, HeighScrFunc - 1, false); Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack)); Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack)); Canvas.Update (); Sleep (1000); int xConv = 0.0; int yConv = 0.0; int EpochCmidl = 0; int EpochCount = 0; double aveMid = 0.0; double aveEnd = 0.0; //---------------------------------------------------------------------------- for (int test = 0; test < NumberRepetTest_P; test++) { InitAO (funcCount * 2, f.GetMaxArg (), f.GetMinArg (), ArgumentStep_P); EpochCmidl = Measur1FuncValue_P / (ArraySize (AO.S_Colony)); EpochCount = Measur2FuncValue_P / (ArraySize (AO.S_Colony)); // Optimization------------------------------------------------------------- AO.F_EpochReset (); for (int epochCNT = 1; epochCNT <= EpochCount && !IsStopped (); epochCNT++) { AO.F_Preparation (); for (int set = 0; set < ArraySize (AO.S_Colony); set++) { AO.A_FFcol [set] = f.CalcFunc (AO.S_Colony [set].args, funcCount); } AO.F_Sorting (); if (epochCNT == EpochCmidl) aveMid += AO.A_FFpop [0]; SendGraphToCanvas (1, 1); Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack)); Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack)); //draw a population on canvas for (int i = 0; i < ArraySize (AO.S_Population); i++) { if (i > 0) PointDr (AO.S_Population [i].args, f.GetMinArg (), f.GetMaxArg (), clrWhite, 1, 1, funcCount); } PointDr (AO.S_Population [0].args, f.GetMinArg (), f.GetMaxArg (), clrBlack, 1, 1, funcCount); Canvas.Circle (x + 1, y + 1, 10, COLOR2RGB (clrBlack)); Canvas.Circle (x + 1, y + 1, 11, COLOR2RGB (clrBlack)); xConv = (int)Scale (epochCNT, 1, EpochCount, 2, WidthScrFunc - 2, false); yConv = (int)Scale (AO.A_FFpop [0], minFuncVal, maxFuncVal, 1, HeighScrFunc - 2, true); Canvas.FillCircle (xConv + HeighMonitor + 1, yConv + 1, 1, COLOR2RGB (clrConv)); Canvas.Update (); Sleep (RenderSleepMsc_P); } aveEnd += AO.A_FFpop [0]; Sleep (1000); } aveMid /= (double)NumberRepetTest_P; aveEnd /= (double)NumberRepetTest_P; double score1 = Scale (aveMid, minFuncVal, maxFuncVal, 0.0, 1.0, false); double score2 = Scale (aveEnd, minFuncVal, maxFuncVal, 0.0, 1.0, false); ScoreAll += score1 + score2; TestCounter += 2; Print (funcCount, " ", f.GetNamFun (), "'s; Func runs ", Measur1FuncValue_P, " result: ", aveMid, "; Func runs ", Measur2FuncValue_P, " result: ", aveEnd); Print ("Score1: ", DoubleToString (score1, 5), "; Score2: ", DoubleToString (score2, 5)); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void InitAO (const int params, //amount of the optimized arguments const double max, //maximum of the optimized argument const double min, //minimum of the optimized argument const double step) //step of the optimized argument { AO.F_Init (params, Population_P); for (int idx = 0; idx < params; idx++) { AO.A_RangeMax [idx] = max; AO.A_RangeMin [idx] = min; AO.A_RangeStep [idx] = step; } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void PointDr (double &args [], double Min, double Max, color clr, int shiftX, int shiftY, int count) { double x = 0.0; double y = 0.0; double xAve = 0.0; double yAve = 0.0; int width = 0; int height = 0; color clrF = clrNONE; for (int i = 0; i < count; i++) { xAve += args [i * 2]; yAve += args [i * 2 + 1]; x = args [i * 2]; y = args [i * 2 + 1]; width = (int)Scale (x, Min, Max, 0, WidthScrFunc - 1, false); height = (int)Scale (y, Min, Max, 0, HeighScrFunc - 1, false); clrF = DoubleToColor (i, 0, count - 1, 0, 360); Canvas.FillCircle (width + shiftX, height + shiftY, 1, COLOR2RGB (clrF)); } xAve /= (double)count; yAve /= (double)count; width = (int)Scale (xAve, Min, Max, 0, WidthScrFunc - 1, false); height = (int)Scale (yAve, Min, Max, 0, HeighScrFunc - 1, false); Canvas.FillCircle (width + shiftX, height + shiftY, 3, COLOR2RGB (clrBlack)); Canvas.FillCircle (width + shiftX, height + shiftY, 2, COLOR2RGB (clr)); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void SendGraphToCanvas (int shiftX, int shiftY) { for (int w = 0; w < HeighScrFunc; w++) { for (int h = 0; h < HeighScrFunc; h++) { Canvas.PixelSet (w + shiftX, h + shiftY, COLOR2RGB (FunctScrin [w].clr [h])); } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void DrawFunctionGraph (double min, double max, double fMin, double fMax, C_Function &f) { double ar [2]; double fV; for (int w = 0; w < HeighScrFunc; w++) { ar [0] = Scale (w, 0, HeighScrFunc, min, max, false); for (int h = 0; h < HeighScrFunc; h++) { ar [1] = Scale (h, 0, HeighScrFunc, min, max, false); fV = f.CalcFunc (ar, 1); FunctScrin [w].clr [h] = DoubleToColor (fV, fMin, fMax, 0, 250); } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— //Scaling a number from a range to a specified range double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers = false) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return ((OutMIN + OutMAX) / 2.0); else { if (Revers) { if (In < InMIN) return (OutMAX); if (In > InMAX) return (OutMIN); return (((InMAX - In) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); } else { if (In < InMIN) return (OutMIN); if (In > InMAX) return (OutMAX); return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— color DoubleToColor (const double in, //input value const double inMin, //minimum of input values const double inMax, //maximum of input values const int loH, //lower bound of HSL range values const int upH) //upper bound of HSL range values { int h = (int)Scale (in, inMin, inMax, loH, upH, true); return HSLtoRGB (h, 1.0, 0.5); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— color HSLtoRGB (const int h, //0 ... 360 const double s, //0.0 ... 1.0 const double l) //0.0 ... 1.0 { int r; int g; int b; if (s == 0.0) { r = g = b = (unsigned char)(l * 255); return StringToColor ((string)r + "," + (string)g + "," + (string)b); } else { double v1, v2; double hue = (double)h / 360.0; v2 = (l < 0.5) ? (l * (1.0 + s)) : ((l + s) - (l * s)); v1 = 2.0 * l - v2; r = (unsigned char)(255 * HueToRGB (v1, v2, hue + (1.0 / 3.0))); g = (unsigned char)(255 * HueToRGB (v1, v2, hue)); b = (unsigned char)(255 * HueToRGB (v1, v2, hue - (1.0 / 3.0))); return StringToColor ((string)r + "," + (string)g + "," + (string)b); } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— double HueToRGB (double v1, double v2, double vH) { if (vH < 0) vH += 1; if (vH > 1) vH -= 1; if ((6 * vH) < 1) return (v1 + (v2 - v1) * 6 * vH); if ((2 * vH) < 1) return v2; if ((3 * vH) < 2) return (v1 + (v2 - v1) * ((2.0f / 3) - vH) * 6); return v1; } //——————————————————————————————————————————————————————————————————————————————
Для преобразования числа double из диапазона в цвет использован алгоритм преобразования из HSL в RGB (система цветов color MetaTrader 5).
Тестовый стенд выводит на график изображение, оно разделено пополам.
- В левой части отображается тестовая функция, трёхмерный график которой спроецирован на плоскость, где красный цвет означает максимум, а синий - минимум. Тут же выводим положение точек в популяции (цвет соответствует порядковому номеру тестовой функции с количеством переменных 40 и 1000, для функции с двумя переменными раскраска не производится), белом цветом обозначены точки, координаты которых усреднены, а черным - лучшая.
- В правую часть выводится график сходимости, зелёным цветом обозначены тесты с количеством переменных 2, синим - 40, а красным - 1000. Каждый из тестов проводится пять раз (по 5 графиков сходимости каждого цвета). Тут же можно наблюдать, насколько ухудшается сходимость AO с увеличением числа переменных.
6. Простой пример АО с использованием ГСЧ
Для примера тестирования реализуем самую простую стратегию поиска. Она не имеет практического значения, но будет в некотором роде эталоном, с которым в последующем мы будем сравнивать алгоритмы оптимизации и их между собой. Она заключается в генерации нового сета переменных функции в случайном выборе 50/50: либо скопируем переменную из случайно выбранного родительского сета из популяции, либо сгенерируем переменную из диапазона min/max. А после получения значений тестовых функций полученный новый набор сетов переменных копируем во вторую половину популяции, затем сортируем. Таким образом новые сеты постоянно заменяют одну половину популяции, а в другой концентрируются лучшие сеты.
А вот и сам код АO на ГСЧ:
//+————————————————————————————————————————————————————————————————————————————+ class C_AO_RND { public: //|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| struct ArrColony { double args []; }; //---------------------------------------------------------------------------- double A_RangeStep []; //Step ranges of genes double A_RangeMin []; //Min ranges of genes double A_RangeMax []; //Max ranges of genes ArrColony S_Population []; //Population ArrColony S_Colony []; //Colony double A_FFpop []; //Values of fitness of individuals in population double A_FFcol []; //Values of fitness of individuals in colony //---------------------------------------------------------------------------- // Initialization of algorithm void F_Init (int argCount, //Number of arguments int populationSize) //Population size { MathSrand ((int)GetMicrosecondCount ()); //reset of the generator p_argCount = argCount; p_sizeOfPop = populationSize; p_sizeOfCol = populationSize / 2; p_dwelling = false; f_arrayInitResize (A_RangeStep, argCount, 0.0); f_arrayInitResize (A_RangeMin, argCount, 0.0); f_arrayInitResize (A_RangeMax, argCount, 0.0); ArrayResize (S_Population, p_sizeOfPop); ArrayResize (s_populTemp, p_sizeOfPop); for (int i = 0; i < p_sizeOfPop; i++) { f_arrayInitResize (S_Population [i].args, argCount, 0.0); f_arrayInitResize (s_populTemp [i].args, argCount, 0.0); } ArrayResize (S_Colony, p_sizeOfCol); for (int i = 0; i < p_sizeOfCol; i++) { f_arrayInitResize (S_Colony [i].args, argCount, 0.0); } f_arrayInitResize (A_FFpop, p_sizeOfPop, -DBL_MAX); f_arrayInitResize (A_FFcol, p_sizeOfCol, -DBL_MAX); f_arrayInitResize (a_indexes, p_sizeOfPop, 0); f_arrayInitResize (a_valueOnIndexes, p_sizeOfPop, 0.0); } //---------------------------------------------------------------------------- void F_EpochReset () //Reset of epoch, allows to begin evolution again without initial initialization of variables { p_dwelling = false; ArrayInitialize (A_FFpop, -DBL_MAX); ArrayInitialize (A_FFcol, -DBL_MAX); } //---------------------------------------------------------------------------- void F_Preparation (); //Preparation //---------------------------------------------------------------------------- void F_Sorting (); //The settling of a colony in population and the subsequent sorting of population private: //||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||| //---------------------------------------------------------------------------- void F_PopulSorting (); //---------------------------------------------------------------------------- ArrColony s_populTemp []; //Temporal population int a_indexes []; //Indexes of chromosomes double a_valueOnIndexes []; //VFF of the appropriate indexes of chromosomes //---------------------------------------------------------------------------- template <typename T1> void f_arrayInitResize (T1 &arr [], const int size, const T1 value) { ArrayResize (arr, size); ArrayInitialize (arr, value); } //---------------------------------------------------------------------------- double f_seInDiSp (double In, double InMin, double InMax, double step); double f_RNDfromCI (double min, double max); double f_scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX); //---Constants---------------------------------------------------------------- int p_argCount; //Quantity of arguments in a set of arguments int p_sizeOfCol; //Quantity of set in a colony int p_sizeOfPop; //Quantity of set in population bool p_dwelling; //Flag of the first settling of a colony in population }; //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void C_AO_RND::F_Preparation () { //if starts of algorithm weren't yet - generate a colony with random arguments if (!p_dwelling) { for (int person = 0; person < p_sizeOfCol; person++) { for (int arg = 0; arg < p_argCount; arg++) { S_Colony [person].args [arg] = f_seInDiSp (f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]), A_RangeMin [arg], A_RangeMax [arg], A_RangeStep [arg]); } } p_dwelling = true; } //generation of a colony using with copying arguments from parent sets-------- else { int parentAdress = 0; double rnd = 0.0; double argVal = 0.0; for (int setArg = 0; setArg < p_sizeOfCol; setArg++) { //get a random address of the parent set parentAdress = (int)f_RNDfromCI (0, p_sizeOfPop - 1); for (int arg = 0; arg < p_argCount; arg++) { if (A_RangeMin [arg] == A_RangeMax [arg]) continue; rnd = f_RNDfromCI (0.0, 1.0); if (rnd < 0.5) { S_Colony [setArg].args [arg] = S_Population [parentAdress].args [arg]; } else { argVal = f_RNDfromCI (A_RangeMin [arg], A_RangeMax [arg]); argVal = f_seInDiSp (argVal, A_RangeMin [arg], A_RangeMax [arg], A_RangeStep [arg]); S_Colony [setArg].args [arg] = argVal; } } } } } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— void C_AO_RND::F_Sorting () { for (int person = 0; person < p_sizeOfCol; person++) { ArrayCopy (S_Population [person + p_sizeOfCol].args, S_Colony [person].args, 0, 0, WHOLE_ARRAY); } ArrayCopy (A_FFpop, A_FFcol, p_sizeOfCol, 0, WHOLE_ARRAY); F_PopulSorting (); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Ranging of population. void C_AO_RND::F_PopulSorting () { //---------------------------------------------------------------------------- int cnt = 1, i = 0, u = 0; int t0 = 0; double t1 = 0.0; //---------------------------------------------------------------------------- // We will put indexes in the temporary array for (i = 0; i < p_sizeOfPop; i++) { a_indexes [i] = i; a_valueOnIndexes [i] = A_FFpop [i]; } while (cnt > 0) { cnt = 0; for (i = 0; i < p_sizeOfPop - 1; i++) { if (a_valueOnIndexes [i] < a_valueOnIndexes [i + 1]) { //----------------------- t0 = a_indexes [i + 1]; t1 = a_valueOnIndexes [i + 1]; a_indexes [i + 1] = a_indexes [i]; a_valueOnIndexes [i + 1] = a_valueOnIndexes [i]; a_indexes [i] = t0; a_valueOnIndexes [i] = t1; //----------------------- cnt++; } } } // On the received indexes create the sorted temporary population for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (s_populTemp [u].args, S_Population [a_indexes [u]].args, 0, 0, WHOLE_ARRAY); // Copy the sorted array back for (u = 0; u < p_sizeOfPop; u++) ArrayCopy (S_Population [u].args, s_populTemp [u].args, 0, 0, WHOLE_ARRAY); ArrayCopy (A_FFpop, a_valueOnIndexes, 0, 0, WHOLE_ARRAY); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Choice in discrete space double C_AO_RND::f_seInDiSp (double in, double inMin, double inMax, double step) { if (in <= inMin) return (inMin); if (in >= inMax) return (inMax); if (step == 0.0) return (in); else return (inMin + step * (double)MathRound ((in - inMin) / step)); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— // Random number generator in the custom interval. double C_AO_RND::f_RNDfromCI (double min, double max) { if (min == max) return (min); double Min, Max; if (min > max) { Min = max; Max = min; } else { Min = min; Max = max; } return (double(Min + ((Max - Min) * (double)MathRand () / 32767.0))); } //—————————————————————————————————————————————————————————————————————————————— //—————————————————————————————————————————————————————————————————————————————— double C_AO_RND::f_scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0)); else { if (In < InMIN) return (OutMIN); if (In > InMAX) return (OutMAX); return (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); } } //——————————————————————————————————————————————————————————————————————————————
7. Таблица результатов
| AO | Runs | Skin | Forest | Megacity (discrete) | Final result | ||||||
| 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | |||
| RND | 1000 | 0,98744 | 0,61852 | 0,49408 | 0,89582 | 0,19645 | 0,14042 | 0,77333 | 0,19000 | 0,14283 | 0,51254 |
| 10000 | 0,99977 | 0,69448 | 0,50188 | 0,98181 | 0,24433 | 0,14042 | 0,88000 | 0,20133 | 0,14283 | ||
После проведения испытаний на тестовом стенде результаты AO RND оказались весьма неожиданными, алгоритм способен находить оптимум функций двух переменных с очень высокой точностью, хотя для функций Forest и Megacity результаты заметно хуже. Однако, с другой стороны, подтвердились догадки о слабых поисковых свойствах для функций со многими переменными, так уже на 40 аргументах результаты очень посредственные. Итоговый совокупный показатель составил 0.51254.
В последующих статьях разберём и протестируем известные и широко используемые алгоритмы оптимизации и продолжим таблицу, составляя рейтинг АО.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети — это просто (Часть 24): Совершенствуем инструмент для Transfer Learning
Нейросети — это просто (Часть 24): Совершенствуем инструмент для Transfer Learning
 Возможности Мастера MQL5, которые вам нужно знать (Часть 1): Регрессионный анализ
Возможности Мастера MQL5, которые вам нужно знать (Часть 1): Регрессионный анализ
 Машинное обучение и Data Science (Часть 04): Предсказание биржевого краха
Машинное обучение и Data Science (Часть 04): Предсказание биржевого краха
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Спасибо за ответ.
Есть ли быстрый метод для бинарных переменных/предикторов (общий объем в районе 5к) с длиной гена до 10 букв (или как там называется?)?
ответа у меня пока нет, буду его искать вместе с читателем в последующих статьях))
предстоит очень много исследовательской работы.
ответа у меня нет, буду его искать вместе с читателем в последующих статьях))
предстоит очень много исследовательской работы.
Если надо что посчитать - готов поделиться мощностями, ради науки! :)
Если надо что посчитать - готов поделиться мощностями, ради науки! :)
о, предложение очень кстати, спасибо.)
Не увидел байесовскую оптимизацию в перечислении. Или плохо смотрел?
В дереве классификации представлены далеко не все существующие методы оптимизации на сегодняшний день. Кроме того, будут рассматриваться только популяционные алгоритмы.