Discretização da série de preços, componente aleatória e "ruído"

Introdução

A maneira clássica de representar os movimentos de preços na forma de intervalos de tempo surgiu no augue dos mercados financeiros, quando ainda não existiam computadores e todas as negociações eram feitas em mercados reais com mercadorias de verdade. Naquela altura era difícil armazenar cada mudança do preço durante o dia, não fazendo muito sentido, uma vez que os preços não mudavam tão rápido. Por essa razão, era óbvio definir o valor do preço em intervalos de tempo regulares. Por exemplo, "o preço do trigo para hoje foi de 2 reais, já ontem era de 1,90". Tudo era muito claro, para hoje a demanda crescia e o preço das mercadorias sobia. Se compararmos com os padrões de hoje, havia poucas transações durante o dia, logo, o preço de uma mercadoria podia ser redefinido com relativa pouca frequência.

Com o desenvolvimento da análise de dados de preço, para tentar prever melhor o comportamento dos preços, e com o aumento do número de transações, para as pessoas se tornou importante entender qual preço era o mínimo e qual o máximo para um intervalo de tempo fixo. Ou seja, agora não bastava saber que ontem o preço era de 1,90 reais e hoje de 2, senão conhecer os valores máximos e os mínimos assumidos pelo preço num determinado intervalo de tempo. Surgiu uma necessidade e apareceram os conhecidos candles e barras que usamos ainda hoje.

A medida que o volume de transações aumentava, a discretização das séries de preços se tornou cada vez mais precisa. Agora já existe discretização de um minuto, ou mesmo de períodos menores, como de um segundo ou de dez segundos, conforme as necessidades da cada um.

As principais vantagens da discretização de tempo da série de preços são:

• Conveniência. Sabemos com precisão que após um minuto será gerada a próxima barra e receberemos novos valores de abertura, fechamento, alta e baixa de preços.
• Economia de recursos. Representar os dados como candles permite que sejam armazenados apenas 4 dígitos durante um intervalo de tempo, se não for necessária uma maior precisão. Se for armazenada cada variação do preço bid, ask, last, o histórico anual ficará com um volume significativo, exigindo cálculos em gigabytes e, em alguns casos, dezenas de gigabytes. Se for necessário armazenar (baixar) o histórico não de 1 ano, senão o de 10-20 anos, com base não num instrumento, senão em 200-500 instrumentos, isso se torna um problema. Além disso, o processamento de gigabytes de histórico para análise requer recursos de computação significativos. Por esse motivo, a análise e o processamento de candles parecem mais atraentes.
• Dimensionamento simples e análise visual. Se for necessário ter uma visão geral, podemos aumentar a escala de discretização (semanas ou até meses) para disponibilizar no monitor as alterações de preço com a quantidade de anos e número de alterações estabelecidos. Mas se for necessária precisão, reduzimos a escala de discretização e vemos o que acontece, por exemplo, num minuto. 
• Linearidade no tempo. Talvez a coisa mais conveniente nesta apresentação seja que visualmente o histórico ocupa a mesma quantidade de espaço na tela a cada ano. É fácil e intuitivo encontrar no gráfico o último ano, a última hora e assim por diante. Intuitivamente, a linearidade no tempo parece-nos um parâmetro muito importante, mas há momentos em que decisões "corretas" são contra-intuitivas.
• Facilidade ao comparar preços de diferentes instrumentos ao mesmo tempo.

Particularidades da discretização de sinais

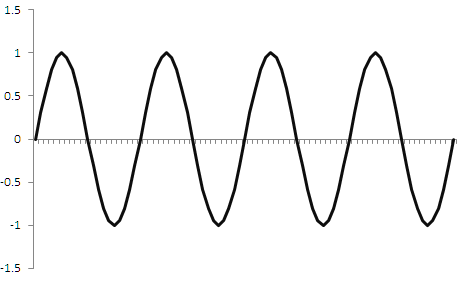
A necessidade de discretização de dados existe não apenas no trading, mas também em muitas outras áreas relacionadas ao processamento de sinais. Por exemplo, quando você ouve música, inicialmente o sinal contínuo é digitalizado usando discretização de tempo. Ou seja, a amplitude do sinal é obtido em intervalos regulares e armazenado na memória. Este sinal pode então ser transformado num sinal contínuo com ajuda de algum tipo de procedimentos. Ademais, a discretização de sinais contínuos tem sido bem estudada há muito tempo. Em particular, existe uma regra que vem do teorema de Kotelnikov (Nyquist–Shannon): um sinal pode ser completamente restaurado se a frequência de discretização exceder a frequência do sinal em 2 ou mais vezes. Isso significa que se tivermos uma frequência de sinal de 1 hertz, sua amplitude deve ser lida pelo menos 2 vezes por segundo (ou seja, com uma frequência de 2 hertz), só então, após a discretização, será possível obter sua forma original. A figura 1 abaixo mostra o que acontece se discretizarmos uma onda senoidal de 1 hertz com uma taxa de amostragem de 2 hertz. O sinal em si é mostrado em verde e o que é obtido após a discretização é mostrado em vermelho.

Fig. 1.

Após a discretização, a onda senoidal produz uma forma de onda triangular. É claro que há algum erro, mas com a ajuda de filtros passa-baixo podemos transformar esse sinal triangular de volta num seno. Ou seja, é possível restaurar o sinal original, sendo que o próprio sentido é preservado, o período é preservado, a amplitude também é preservada com algum erro. Se essas distorções são consideradas críticas para a música, então não são assustadoras para o trading. Mas o que acontece se a taxa de discretização for menor do que a do sinal original? Um exemplo é mostrado na figura 2 abaixo.

---->>

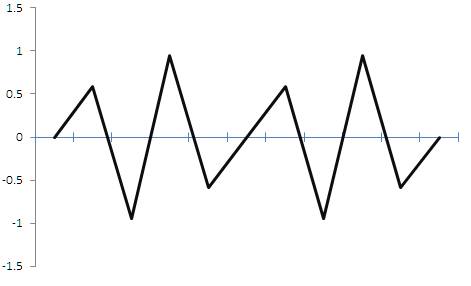
Fig. 2.

A figura mostra que se a frequência de discretização for menor que o dobro da frequência do sinal, então o sinal fica muito distorcido, na saída, e obtemos, de fato, um sinal aleatório que não tem nada a ver com o original. Se aplicado à negociação, no primeiro caso poderíamos vender quando encontrarmos o máximo e comprar quando encontrarmos o mínimo. Além disso, sabíamos a frequência, mas após uma discretização "errada", perdemos informações sobre a amplitude e a frequência do sinal. Assim, de um sinal periódico determinístico com características conhecidas, recebemos um sinal não periódico aleatório com características desconhecidas, errando apenas na escolha da frequência de discretização.

Sabendo de tudo isso, devem surgir duas questões: "será que erramos ao discretizar as séries de preços?" e "a série de preços é um sinal discreto ou contínuo e quais são seus parâmetros?" 

A resposta não é tão simples quanto pode parecer à primeira vista, mas é muito importante.

Série de preços é discreta ou contínua?

Podemos responder a essa pergunta se conhecermos o mecanismo de formação do preço de mercado. Não vou descrever em detalhes, acho que todo mundo sabe ou já leu o artigo "Princípios da precificação da bolsa tomando como exemplo o mercado de derivativos da bolsa de moscou (moex)" Alguns participantes colocam ordens no livro de ofertas e, em seguida, outros compram o volume necessário ao preço exigido; é assim que o gráfico de preços é formado. Os próprios níveis resultam ficar discretos, ou seja, podemos fazer uma ordem a um preço de 1, 2, 3 e assim por diante, com alguma precisão. O volume definido nas ordens e resgatado pelos compradores também é discreto, pois é possível comprar 1,2,3 unidades da mercadoria e assim por diante. A figura 3 abaixo mostra como exemplo um livro de ofertas, pode-se observar que preços e volumes possuem valores discretos. 

Figura 3.

Assim, podemos concluir que o gráfico da série de preços em si é de natureza discreta. O preço se move em níveis discretos depois que os participantes compram volumes discretos. 

O preço é função de que?

Já vimos que a série de preços em si é discreta, mas a mudança de preço é função de que parâmetro?

Discretizar um sinal de áudio em intervalos regulares é uma solução aceitável, porque o sinal de áudio é uma função que muda com o tempo. O sinal em si é uma amplitude que depende do tempo e essa propriedade nele é fundamental. É por isso que não há problemas neste ponto.

A natureza da série de preços é diferente, aqui a amplitude (preço), embora mude de tempos em tempos, este último não é a razão para a mudança de preço. Se pensarmos sobre qual é o motivo da mudança de preço, a pergunta não resulta tão simples. Podemos fazer várias suposições:

1. Preço em função das operações de negociação. Aqui, o preço muda a partir das operações de negociação realizadas, uma vez que são elas que movem o preço. Mas também é verdade que podem não levar a alterações de preços. Por exemplo, estão disponíveis 10 ações a um preço de 5 rublos por cada uma delas, o operador compra 4, 6 permanecem disponíveis a esse preço, indicando que foi realizada uma transação e o preço não mudou. Além disso, esta operação reduziu o volume disponível a este preço e pode causar novas alterações nele quando o próximo operador comprar a totalidade do volume a este preço. Os preços mudam apenas quando o volume disponível a um preço de 5 rublos por ação não foi suficiente para atender a demanda e todo o volume foi comprado a um preço de 5 rublos. Nesse caso, o preço ASK é alterado em 6 rublos, mas os outros participantes ainda tem uma chance de fazerem outra solicitação de 5 rublos e retornar o preço ASK ao seu local original.
2. Preço em função de todas as operações realizadas no mercado. O preço pode mudar não apenas pelo fato de os operadores comprarem o volume num determinado nível, mas também pelo fato de eles simplesmente retirarem suas ordens e recolocá-las em outros níveis. Desse modo, não ocorrerão operações de negociação e os preços BID e ASK irão se mover.
3. Preço em função do “benefício”. O preço pode mudar porque os operadores redefinem o valor do ativo para eles próprios, mas as razões para redefini-lo podem ser completamente diferentes. Em qualquer caso, tal redefinição está intimamente relacionada ao benefício dos operadores. Em teoria, o preço estabelecido sempre será o mais benéfico para todo o conjunto de operadores, tanto para compradores como para vendedores (mesmo que este benefício seja negativo). O mercado foi inicialmente criado precisamente para maximizar os benefícios e determinar o preço ideal, equilibrado e adequado para o comprador e o vendedor. Além disso, esse benefício pode nem estar associado a um ativo específico. Por exemplo, imaginemos um fundo de investimento que precisa sair com urgência de um ativo, e ele está disposto a fazer isso mesmo após receber prejuízo nesse ativo, pois considera que, tendo feito tal operação, receberia algum outro benefício, possivelmente comprando outro ativo ou até pagando lucros a seus clientes. A natureza do benefício aqui pode ser tão diversa quanto possível. Nesse caso, o preço é uma função de cada redefinição dos benefícios para cada operador.
4. Preço em função de si mesmo. Obviamente, toda mudança de preço certamente levará a uma mudança nos benefícios dos operadores. Os benefícios podem mudar sem alteração do preço, mas quando o preço muda, os benefícios dos operadores mudam. Essa pode não ser a maneira mais precisa de descrever as mudanças de preço, mas permite que nos aproximemos do modelo ideal e façamos uma série de suposições que não afetarão muito o resultado no futuro. Negociamos principalmente com base em mudanças de preços e mesmo se escolhermos estratégias de dividendos (sem prestar atenção ao preço de forma alguma), no final o pagamento de dividendos causa a mudança do preço. Aqui, tal mudança é um sinal para deslocar o gráfico para a esquerda. Fixamos o valor do preço somente quando ele passar de 1 ponto. Podemos definir qualquer incremento, depende da escala preferida, podemos fixar o valor do preço cada vez que ele passa n pontos verticalmente. 

Eu mesmo acredito que há uma terceira variante que é mais provável: o preço é uma função da redefinição dos benefícios. Mas é impossível calcular o benefício de cada operador para discretizar a série de preços. Nos dois primeiros casos, é realista calcular as operações comerciais e não comerciais nos mercados bolsistas, mas também podem surgir dificuldades. Por exemplo, um ativo pode ser negociado em duas ou mais bolsas diferentes, ou uma situação em que derivativos, como futuros e opções existem para o ativo subjacente, se é necessário contar todas as transações indiretamente relacionadas ao ativo ou não, não é uma questão simples e merece um amplo estudo. De qualquer forma, todos os quatro casos estão indiretamente relacionados entre si, e a quarta variante, em que o preço em função de si mesmo, permite pesquisas futuras, partindo do pressuposto de que será um modelo bruto.

A velocidade de variação do preço de um ativo depende exatamente do número de operações. Quanto mais operações de negociação, mais frequentemente muda o preço, o que significa que há uma correlação direta. Consequentemente, quantos mais operadores no mercado, mais transações e mais vezes é redefinido o benefício para cada um deles, portanto, cada participante tentará redefinir o preço com mais frequência, o que levará a um maior número de transações e quanto maior a frequência da alteração do preço do ativo...

Características de discretização da série de preços por intervalos de tempo e o componente aleatória

Tomemos como modelo bruto que o preço é uma função dele mesmo, ou seja, discretizamos o preço apenas quando ele muda num determinado número de pontos. Mesmo se este não for o caso, tal suposição permitirá desenvolver o tópico sem afetar muito o resultado final. Além disso, para ganhar dinheiro, interessa-nos exatamente o facto de o preço ter mudado e, para procurar padrões, é importante saber como muda. 

Cada mudança de preço em 1 ponto (por ponto entendemos a mudança de preço mínima possível) representará um passo e consideraremos o que acontece quando discretizamos tal série no tempo. Obviamente, o número de pontos que o preço vai passar por unidade de tempo depende da atividade de negociação. Quanto maior a atividade (o número de operações realizadas), mais passos irá eventualmente dar o preço. A atividade de negociação não está diretamente relacionada ao movimento do preço, mas de uma forma ou de outra, o movimento do preço depende da atividade de negociação e, quanto maior a atividade, mais movimentos haverá. A relação é indireta, mas a correlação é positiva. Por exemplo, assumamos que 1 passo são 10 pontos e que para exemplificar pegamos candles por hora. As duas figuras abaixo mostram uma representação do preço em blocos. Os blocos são semelhantes ao Renko, mas são construídos de uma maneira ligeiramente diferente. Os valores high e low são retirados dos candles clássicos. Eles mostram quais os valores máximo e mínimo assume o preço enquanto estava sendo formado o bloco. Assim como os candles, os blocos possuem 4 características: Open High Low Close. Ao contrário dos candles, a distância entre Open e Close é sempre definia e expressa em pontos. O bloco é fechado quando o preço passa N pontos verticalmente. Por exemplo, o tamanho do bloco é de 10 pips, enquanto assim que o preço se move 10 pips verticalmente, o bloco é fechado e começa a se formar um novo bloco.

Fig. 4.

Se assumirmos que um bloco é igual a um passo com um tamanho de N pontos, vamos ver o que acontece dentro do candle horário. As figuras 4 mostram os movimentos que ocorrem durante a formação do candle horário. Pode-se observar que na figura superior o preço ultrapassa 10 blocos verticalmente numa hora. Se os blocos tiverem 10 pontos cada, o tamanho do candle será de 100 pontos. Além disso, no total, durante a formação do candle, foram formados 25 blocos ou, em outras palavras, 25 passos. A figura abaixo mostra outro exemplo em que durante a formação do candle, o preço passa 0 blocos verticalmente e, portanto, 0 pontos. Além disso, o preço ultrapassa 40 blocos ou 40 passos durante a formação do preço. Agora vamos olhar um gráfico de tais candles, mostrado abaixo na figura 5. O candle é fechado uma vez por hora, já a série de preços definitivamente não é uma função do tempo, no caso simplificado é uma função das operações de trading, que, como escrevi acima, têm uma correlação positiva com o número de pontos passados. Como transformamos os pontos em blocos, o número de blocos tem uma correlação positiva com o número de operações de negociação. Dentro de cada vela (digamos de hora em hora), existe, de fato, um número aleatório de blocos, ou etapas por N pontos, e isso será ainda mais importante. Isso ocorre porque os candles simplesmente fecham com base no tempo, sem prestar atenção aos processos que ocorrem no mercado. O tempo aqui é obtido por um parâmetro externo que tem pouca relação com os processos que ocorrem com o preço. Ou seja, o preço muda não porque tenha passado uma hora, mas, sim, por motivos próprios, entre os quais pode estar o facto de ter passado uma hora.

Fig. 5.

A atividade de negociação pode mudar significativamente ao longo do tempo e é individual para cada instrumento. Além disso, com o desenvolvimento da negociação algorítmica, o número de negociações por unidade de tempo e o volume de transações cresce a cada ano, o que significa que seria errado comparar diretamente os candles horários para 2010 e hoje, porque dentro de cada um deles, na verdade, há um número diferente de operações.

A seguir, vamos fazer mais uma simplificação, vamos considerar o mercado como um passeio aleatório. Naturalmente, o mercado não é um errante aleatório, mas será mais fácil entendê-lo assim, portanto voltaremos aos mercados reais.

O teorema do limite central nos diz que a soma de um número suficientemente grande de variáveis aleatórias fracamente dependentes com aproximadamente as mesmas escalas (não domina nenhum dos termos, não faz uma contribuição determinante para a soma) tem uma distribuição próxima do normal. No que diz respeito ao nosso caso, a partir do teorema do limite central, podemos concluir que, em média, nosso processo aleatório passará em N passos uma distância proporcional à vertical, aproximadamente à raiz quadrada do número de passos. Se tivermos 1 bloco, isso é 1 passo, logo, para 100 blocos, o preço será em média 100^0,5 = 10 blocos verticalmente. Em algum lugar mais, em algum lugar menos, mas em média, nossa série de preços aleatórios obedecerá à lei da distribuição normal. Deve ser esclarecido que o número de passos para uma determinada série aleatória dependerá apenas ligeiramente do tempo, porque os passos são gerados pela atividade de negociação e muda muito com o tempo.

Acontece que o tamanho do candle horário para tal série de preços aleatória será, em média, proporcional ao número N^0,5, onde N é o número de passos dentro do candle. Ou seja, o tamanho do candle horário estará sujeito à lei de distribuição normal. Além disso, levando em consideração o fato de que dentro do candle haverá, de fato, um número aleatório de passos, podemos concluir que o tamanho do próprio candle estará sujeito à lei da distribuição normal. Ou seja, o tamanho do candle será igual à raiz do número de passos incluídos neste candle. Vamos verificar tal afirmação. Para isso, usarei os candles GBPUSD de 50.000 minutos para o período de 2020/05/18 a 2020.07.03.

1. Vamos encontrar o tamanho médio de um candle de minuto em valor absoluto, esse será o tamanho do passo. Para fazer isso, subtraímos o preço de fechamento do candle anterior do preço de fechamento de cada candle seguinte e calculamos o valor do módulo. Obtive o tamanho médio de um candle de minuto GBPUSD = 0,000170
2. Encontramos o tamanho médio do candle horário durante o mesmo período (no candle horário de 60 minutos). Para fazer isso, subtraímos o preço de fechamento de cada candle horário anterior do preço de fechamento de cada candle horário seguinte e calculamos o valor do módulo. Obtive o tamanho médio de um candle horário GBPUSD = 0,001117
3. Vamos descobrir quanto o preço deve passar em média por hora, se assumirmos que a série de preços é um passeio aleatório. Para fazer isso, multiplicamos o tamanho médio de um candle de minuto pela raiz do número de passos e multiplicamos pelo tamanho médio do passos. Temos 60 passos => 0,000170*(60^0,5) = 0,001315. O tamanho do candle horário tenderia a este tamanho médio se a série original obedecesse à lei da distribuição normal.
4. Comparamos o tamanho médio de um candle real e um candle de passeio aleatório (real 0,001117) ≈ (0,001315 teórico). A diferença é de apenas 0,0002. Pode-se concluir que a suposição de que o tamanho do candle está sujeito à lei da distribuição normal não é apenas verdadeira, mas também confirmada pelos dados de mercado do instrumento real. A diferença de 0,0002 não é significativa.

Além disso, usando as velas horárias obtidas, nós, de fato, combinamos e analisamos uma sequência de segmentos da série de preços cuja amplitude obedece à lei da distribuição normal. E não é surpreendente se, além disso, passando para períodos gráficos maiores, obtivermos todos os mesmos candles, cujo tamanho é proporcional à raiz do número de passos. Assim, voltamos à figura 2: se uma série é discretizada incorretamente, obtemos uma sequência aleatória na saída. Na verdade, usando a discretização do tempo, transformamos a série de preços numa sequência aleatória. Sim, os padrões ainda podem permanecer nas sequências com discretização de tempo, porque o mercado não é uma sequência aleatória e aqui estão presentes dependências indiretas do tempo, mas analisar tal série e identificar padrões se torna muito mais difícil. É justamente por causa da discretização de tempo que nas séries de preços aparecem os chamados "ruído" e não-estacionariedade, que muitos falam, mas não dizem de que tipo de ruído é e de onde vêm. Agora, o ruído pode ser entendido não apenas como ruído de discretização que ocorre durante a discretização do sinal, mas também como um componente aleatório que surge devido a parâmetros de discretização incorretos da série de preços, que por si só já é discreta.

Para ter certeza de que os resultados obtidos com os candles horários não foram uma coincidência, realizaremos uma operação semelhante para os candles diários. O dia tem 24 horas, uma vez que os pares de moedas são negociados 24 horas por dia, podemos dizer que o candle diário contém 1440 candles de minutos. Vamos cortar o mesmo intervalo de dados de minuto que usamos para plotar H1. Só que desta vez, por conveniência, irei exibir todos os dados como uma tabela.

Tamanho médio do candle m1	Tamanho real médio do candle H1	Tamanho teórico do candle D1 calculado como  0.000117*(60^0.5)	Tamanho real médio do candle D1	Tamanho teórico do candle D1 calculado como 0.00017*(1440^0.5)
0.000170	0.001117	0.001315	0.006547	0.006442

Como se pode ver, o tamanho médio real de um candle diário não difere muito do tamanho previsto teoricamente se não fosse um mercado real, mas, sim, um passeio aleatório. Anexarei um arquivo com dados históricos e cálculos ao artigo em formato Excel.

Antes disso, para calcular o tamanho médio do candle de um período gráfico maior, usamos os dados do período de um minuto. Mas e se descermos e usarmos dados de ticks, talvez obtenhamos resultados diferentes? Para fazer isso:

1. Vamos pegar os dados sobre o volume de ticks de candles de minuto (de uma conta real) para o mesmo período e encontrar o número médio de ticks num candle de minuto, o valor médio é 59,99 ticks por minuto. 
2. Agora vamos carregar os dados do tick e descobrir o tamanho médio do tick, resulta 0,000014378. 
3. Vamos calcular o tamanho teórico do candle de minuto como (59,99^0,5)*0,00014378=0,000111363
4. Vamos calcular o tamanho teórico do candle por hora como ((59,99*60)^0,5)*0,000014378=0,00086

Tamanho médio do tick	Tamanho real médio do candles m1	Tamanho teórico do candle m1, calculado como (59,99^0,5)*0,000014378	Tamanho real médio do candle H1	Tamanho teórico do candle H1, calculado como ((59,99*60)^0,5)* 0,000014378
0.000014378	0.00017	0.000111363	0.001117	0.00086

Como se pode ver, o tamanho médio do candle m1 e H1 não difere muito do teórico, que teria uma série de preços se fosse um passeio aleatório, com base nisto podemos concluir que por algum motivo a série de preços se comporta como um passeio aleatório e, talvez isso seja devido à discretização incorreta de intervalos de tempo.

Distribuição de frequências de incrementos da série de preços

A avaliação quantitativa tornou possível estimar aproximadamente como o tamanho dos candles da série de preços corresponde ao tamanho dos candles do passeio aleatório, mas é mais interessante construir a distribuição de frequências dos incrementos da série de preços a fim de avaliar visualmente as semelhanças ou diferenças com a distribuição de frequências dos incrementos para o passeio aleatório.

Preparar dados para análise é uma parte importante. Vamos construir a distribuição de frequências para o número de pontos que o preço pode passar em 60 minutos (numa hora), ou seja, em 60 passos. Para fazer isso, é preciso saber o tamanho médio de um candle de minuto e o número de passos (quantos candles de minuto existem num candle horário). Calculamos o tamanho médio de um candle de minuto antecipadamente, e ele é igual a 0,000170, o número de candles de minuto por hora é de 60. Isso significa que o preço pode dar 60 passos a 0,000170 por hora. Logo, haverá casos extremos em que o preço se moverá continuamente desde o ponto inicial 60 passos para cima ou 60 passos para baixo. Portanto, vamos estimar a distribuição de frequências no intervalo -0,00017*60=-0,0102 a 0,00017*60=0,0102. Em outras palavras, sabemos que se o preço apenas subir, em passos de 0,00017, então em 60 passos (por hora) atingirá o valor máximo de 0,0102. Além disso, para 60 passos, o preço pode ocupar apenas 0 níveis discretos; 0,00034; 0,00068; 0,00102 ... 0,0102 e valores negativos semelhantes. Para ilustrar por que exatamente o preço ocupará esses níveis, vejamos a figura 6.

Fig. 6.

A figura 6 mostra que se alguma função discreta deixa o ponto zero, seu passo é igual a 1, e ela dá 6 passos no total, logo, eventualmente ela pode ir ao longo da vertical 6; 4; 2; 0, das marcas de escala, só pode assumir valores discretos com um intervalo de passo duplo. Da mesma forma, para o nosso caso, se o tamanho médio de um candle de minuto for 0,00017, o preço pode ocupar níveis discretos com um intervalo igual a duas vezes o tamanho do candle. Na realidade, como os candles são de tamanhos diferentes, não apenas 0,00017, o preço pode assumir valores intermediários, então para a análise contaremos quantos eventos caem em intervalos com um tamanho médio de candle duplo. Para comparar o quanto difere a distribuição resultante para a série de preços, comparamos com a distribuição para um passeio aleatório. Para um passeio aleatório, é característico que a probabilidade de mudar a direção de cada passo seguinte seja de 50% e não haja memória. A figura 7 mostra as distribuições de densidade de probabilidade em preto para uma série de preços, em vermelho para um passeio aleatório.

Fig. 7.

Pela figura 7, pode-se observar que a densidade da distribuição de probabilidade da série de preços quase coincide com a densidade da distribuição de probabilidade para um passeio aleatório. A densidade de distribuição de probabilidade da série de preços tem um pico um pouco mais alto, um pouco mais estreito e um pouco deslocado para a direita, em relação à densidade de distribuição para um passeio aleatório. Isso sugere que a probabilidade de reversão de cada passo seguinte da série de preços está ligeiramente acima de 50%, e há uma pequena tendência de alta, mas essas diferenças não são grandes. Imediatamente há a tentação de ganhar dinheiro com esse desvio, parece que não é difícil fazer isso, mas no próximo artigo vamos olhar mais de perto esse padrão e a possibilidade de ganhar dinheiro com ele. Aqui é necessário entender que estamos falando de uma variável aleatória ideal, que, com uma amostra suficientemente grande, tenderá para a referência. O gráfico de densidade da distribuição de probabilidade para um passeio aleatório é construído usando uma tabela, parte da qual é mostrada na figura 8.

Fig. 8.

O gráfico da distribuição de densidade de probabilidade construído confirma as conclusões feitas anteriormente de que o tamanho dos candles (neste caso, por hora) tende para tal tamanho de candles, o que seria se a série de preços fosse um passeio aleatório, mas permite que avaliar esse fato visualmente e com mais precisão.

Todos os dados e cálculos que opero no artigo estão anexados ao artigo no formato xlsx, neste arquivo é possível encontrar todos os cálculos.

Áreas de alta e baixa volatilidade

Um operador atento pode replicar que nos gráficos muitas vezes vê como as velas no mercado são convencionalmente divididas em grupos de tamanhos "grandes" e "pequenos" (áreas com alta e baixa volatilidade), o que significa que o gráfico não é um passeio aleatório e há padrões. Se a discretização de tempo introduzisse distorções tão fortes, esse efeito não seria observado. Mas isso é justamente explicado pelo fato de que o tamanho das velas depende do número de operações de negociação realizadas dentro desse candle. Como podemos verificar isso? Basta olhar para o gráfico com volumes de tick e ver que os períodos com "pequenos candles" são acompanhados por períodos com baixos volumes de ticks, e os períodos com canldes grandes são acompanhados por períodos de grandes volumes de ticks. Se imaginarmos que um tick é um passo, o preço dará mais passos durante os períodos de "ticks grandes" e, consequentemente, terá um tamanho maior, mas o tamanho do candle em si permanecerá proporcional à raiz quadrada do número de passos multiplicado pelo tamanho médio do passo (figura 9). Os volumes de ticks, por sua vez, têm uma correlação direta com a atividade de negociação, quanto maior a atividade de negociação, mais ticks passam por unidade de tempo. Nos mercados bolsistas está disponível o histórico dos volumes reais, neles podemos observar que o tamanho dos volumes de ticks se correlaciona fortemente com os volumes reais, o que também indica a relação entre o número de ticks e a intensidade da negociação.

Fig. 9.

Este fato prova mais uma vez que a discretização por intervalos de tempo introduz fortes distorções na forma final da série de preços e complica significativamente a análise. Essa distorção levou ao surgimento de toda uma classe de sistemas de negociação, os chamados "scalpers noturnos". Não estou dizendo que eles sejam incapazes de obter lucro, mas durante o desenvolvimento de tais sistemas, é necessário levar em consideração essa peculiaridade relacionada com a apresentação da série de preços e realizar pesquisas adicionais que devem responder à pergunta: "a probabilidade de reversão nessas áreas é realmente maior do que a probabilidade de continuação da tendência?" e "será que as características estatísticas destes locais permitem obter lucro?", porque é este o padrão que é utilizado por sistemas deste tipo. 

Discretização alternativa da série de preços

Após a análise, finalmente podemos concluir que é melhor usar dados de tick para processamento e análise, de modo a não introduzir erros próprios de discretização na série de preços original, porque o preço vem discreto de qualquer maneira. Se precisarmos aumentar a escala, simplesmente faremos blocos de 10 ou 100 ticks. Mas o problema é que os próprios ticks também são uma forma de discretização. Acontece que esse método é estável e amplamente utilizado, mas pode distorcer o processo, pois o preço não é função dos ticks recebidos. O preço é pelo menos uma função das transações executadas, enquanto uma operação de negociação não pode gerar ticks. Na bolsa, os ticks estão de alguma forma conectados com a negociação real, já no FOREX, cada empresa pode transmitir quantos ticks quiser, e é impossível saber qual delas fornece os "corretos". Por isso, mesmo com uma suposição tão simples de que o preço é uma função das operações de negociação, fica claro que os ticks já distorcem a forma da série de preços e introduzem um componente aleatório, que pode causar erros em análises posteriores.

A questão sobre um discretização "correta" é uma parte importante da análise de dados. Por exemplo, a figura 10 abaixo mostra 2 gráficos do preço do Bitcoin em relação ao dólar. O gráfico superior é um regular construído a partir de candles semanais e o gráfico inferior é discretizado em blocos de N pontos. Este é o mesmo período, o mesmo número de blocos/candles, mas métodos de discretização diferentes. Pode-se ver o quanto diferem os gráficos para o mesmo ativo. Portanto, surge uma questão natural: "qual dos dois mapeamentos está correto?"

Fig. 10.

Cheguei à conclusão de que a exibição correta é aquela que leva em consideração a natureza da discretividade da série de preços. Mas, uma vez que a natureza da discretividade permanece desconhecida, será "mais correto" usar o método de discretização que for capaz de refletir o recebimento de lucro/prejuízo tanto por mim quanto por outros operadores. Consequentemente, é preferível analisar os dados com base nos quais são gerados nossos rendimentos. Ou seja, é melhor não considerar o movimento do preço com base no tempo, mas, em vez disso, levar em consideração apenas o tamanho da mudança no preço.

Uma discretização alternativa de tempo seria uma discretização de amplitude fixa, onde se supõe que o preço é uma função dele mesmo, ou seja, aqueles blocos sobre os quais escrevi acima. Consideramos que um bloco de N pips é fechado toda vez que o preço se move verticalmente N pips. Talvez esta não seja a melhor abordagem, mas durante a negociação, nós, como muitos outros operadores, estamos interessados em exatamente quantos pontos o preço se move, porque depende de quanto lucro ou perda obteremos. Além disso, é após o preço passar de N pontos na vertical que o lucro de cada operador muda. Ou seja, o modelo em que o preço é função dele mesmo é o que mais se aproxima do da negociação real. A figura 11 mostra como uma sinusóide é discretizada em blocos de tamanho fixo. Além disso, a forma é perdida, mas as principais características importantes para nós, como período e amplitude, são preservadas.

Fig. 11.

Mesmo se errarmos com os parâmetros de discretização, não acontecerá nada de terrível, os valores de amplitude e período serão salvos. A figura 12 abaixo mostra um exemplo do que acontece quando o tamanho do bloco é muito grande. Parte da informação que está dentro do bloco é perdida, ou seja, a precisão se deteriora e parte da informação é perdida (o que é inevitável ao comprimir dados), mas ao mesmo tempo a informação de amplitude e período é retida. Se o tamanho do bloco for maior do que a amplitude da série de preços, os blocos não serão exibidos. Como se pode ver, ao contrário do exemplo mostrado na figura 2, se o parâmetro de discretização for selecionado incorretamente, o sinal determinístico original não se transformará num sinal aleatório.

Fig. 12

Desta forma, é possível lidar com a componente aleatória introduzida pela discretização da série de preços no tempo e em situações em situações quando não se sabe função de qual parâmetro é a série original. Este método funciona melhor do que a discretização de tempo e permite dimensionar convenientemente o gráfico com uma precisão de escala de até 1 ponto.

Fim do artigo

• A natureza da série de preços é discreta, o que decorre da própria estrutura de formação de preços.
• O preço de mercado não é uma função do tempo, é uma função de processos econômicos intimamente relacionados e não é possível considerá-los todos no momento.
• A discretização da série de preços por intervalos de tempo introduz uma componente aleatória significativa, distorcendo a forma real do gráfico de preços, adicionando "ruído" e não-estacionariedade a um processo já complexo com parâmetros desconhecidos.
  
• Ao desenvolver métodos para discretizar uma série de preços, é necessário considerar "a mudança de preço é função de que parâmetro?".
• A não-estacionariedade da série de preços é formada, entre outras coisas, devido a parâmetros de discretização incorretos.
• É possível analisar gráficos de preços com discretização de tempo para descobrir padrões, mas os aspectos acima devem ser levados em consideração para compreender melhor a natureza de um determinado padrão.
• É necessário desenvolver formas de discretizar as séries de preços que introduzam muito menos distorção nos dados originais, uma delas é apresentada neste artigo.
• Ao desenvolver algoritmos de negociação e pesquisas estatísticas de mercado, é necessário levar em consideração as peculiaridades da discretização utilizada da série de preços.