Diskretisierung von Preisreihen, Zufallskomponente und das Rauschen

Einführung

Die klassische Methode, Preisreihen als Zeitintervalle (oder Zeitrahmen) darzustellen, erschien vor langer Zeit, zu Beginn der Entstehung von Finanzmärkten, als es noch keine Computer gab und reale Güter auf realen Märkten gehandelt wurden. Es war schwierig, jede Preisänderung während eines Tages zu speichern. Außerdem war es nutzlos, weil sich die Preise nicht schnell änderten. Daher lag es auf der Hand, die Preise in regelmäßigen Zeitabständen zu registrieren. Klingt logisch: "Heute kostet Weizen 90 Cent, während er gestern 80 Cent kostete". Alles ist ganz klar: Die Nachfrage ist gestiegen, und der Preis ist gestiegen. Im Vergleich zum heutigen Börsenhandel gab es nicht viele Geschäfte, deshalb wurde der Preis nur selten neu definiert.

Mit dem Aufkommen und der Entwicklung der Preisdatenanalyse, deren Ziel es war, das Preisverhalten besser vorherzusagen, und mit der Zunahme der Anzahl der Handelsoperationen wurde es für die Menschen wichtig, zu verstehen, welcher der höchste und welcher der niedrigste Preis für einen bestimmten Zeitraum war. Das heißt, Informationen über den gestrigen Preis von 80 Cent und über den heutigen Preis von 90 Cent reichten nicht mehr aus. Die Menschen wollten wissen, welche höchsten und niedrigsten Preise innerhalb des angegebenen Zeitraums erreicht wurden. Damals wurden die bekannten Kerzen und Balken erfunden.

Mit zunehmender Zahl der Handelsoperationen wurde die Diskretisierung der Preisreihen immer genauer. Heute verwenden wir bereits die Minuten-Diskretisierung oder manchmal sogar kleinere Frames, wie z.B. eine Sekunde und zehn Sekunden.

Die Hauptvorteile der Zeitdiskretisierung einer Preisreihe sind die folgenden:

• Praktikabilität. Wir wissen genau, dass in einer Minute der nächste Balken gebildet wird und wir neue Werte für Open, Close, High und Low erhalten werden.
• Ressourceneffizienz. Die Darstellung als Kerze erlaubt die Speicherung von nur 4 Zahlen über einen bestimmten Zeitraum, wenn keine größere Genauigkeit erforderlich ist. Wenn Sie jede Änderung von Bid, Ask und Last (Geld- und Brief- und letzter Preis) speichern, wäre das Volumen einer einjährigen Historie sehr groß, bis zu mehreren Gigabyte. Dies wäre ein echtes Problem, wenn Sie die Kurshistorie für 10-20 Jahre herunterladen und speichern müssen, oder wenn Sie nicht nur ein, sondern 200-500 Symbole verwenden. Außerdem wären riesige Computerressourcen erforderlich, um Gigabytes an Historie zu verarbeiten. Aus diesem Grund sehen die Analyse und Verarbeitung von Kerzen attraktiver aus.
• Einfache Skalierung und visuelle Analyse. Wenn es notwendig ist, ein größeres Bild zu betrachten, kann die Diskretisierungsskala auf Wochen oder sogar Monate erhöht werden, und die Anzeige zeigt Daten für so viele Jahre wie nötig. Wenn mehr Präzision erforderlich ist, können Sie die Skala verkleinern, um zu sehen, was innerhalb einer Minute passiert ist. 
• Zeitliche Linearität. Das vielleicht praktischste an dieser Präsentation ist die Tatsache, dass jedes einjährige Historienintervall visuell ungefähr die gleiche Bildschirmfläche einnimmt. Es ist einfach und intuitiv, auf einem Chart das Vorjahr oder die vorangegangene Stunde zu finden. Intuitiv scheint die zeitliche Linearität ein sehr wichtiger Parameter zu sein, aber es gibt Zeiten, in denen die "richtigen" Entscheidungen kontraintuitiv sind.
• Leichter Preisvergleich für verschiedene Instrumente.

Diskretisierungsfunktionen für Signale

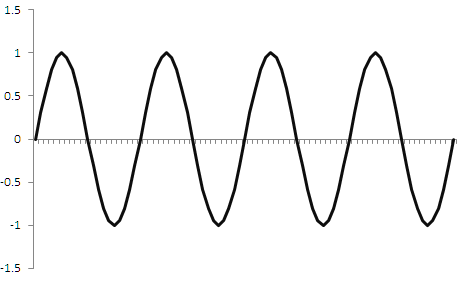
Die Diskretisierung von Daten ist nicht nur im Handel, sondern auch in vielen anderen Bereichen der Signalverarbeitung erforderlich. Zum Beispiel wird in der Musik das ursprünglich kontinuierliche Signal digitalisiert. Es wird mittels Zeitdiskretisierung kodiert. Der Signalamplitudenwert wird in regelmäßigen Zeitintervallen in den Speicher geschrieben. Dieses Signal kann dann durch bestimmte Manipulationen wieder in ein kontinuierliches Signal umgewandelt werden. Die Diskretisierung kontinuierlicher Signale ist ein gut untersuchtes Gebiet. Zum Beispiel die Regel, die sich aus dem Kotelnikov (Nyquist-Shannon)-Satz ergibt: "Ein Signal kann vollständig wiederhergestellt werden, wenn die Diskretisierungsfrequenz das Zwei- oder Mehrfache der Signalfrequenz beträgt. Wenn also eine Signalfrequenz 1 Hertz beträgt, dann muss ihr Amplitudenwert mindestens 2 Mal pro Sekunde ausgelesen werden (d.h. mit einer Frequenz von 2 Hertz). Nur in diesem Fall wird es möglich sein, nach der Diskretisierung seine ursprüngliche Form zu erhalten. Abbildung 1 zeigt, was passiert, wenn wir eine Sinuswelle von 1 Hertz mit einer Abtastrate von 2 Hertz diskretisieren. Das Signal ist grün dargestellt, und das Ergebnis der Diskretisierung ist rot.

Abb. 1.

Nach der Diskretisierung wird die Sinuskurve in eine dreieckige Wellenform umgewandelt. Es gibt natürlich einen gewissen Fehler, aber dieses Dreiecksignal kann mit Tiefpassfiltern wieder in eine Sinuskurve umgewandelt werden. Das bedeutet, dass wir ein Signal wiederherstellen können, wobei seine Idee, Periode und Amplitude erhalten bleiben, wenn auch mit einem gewissen Fehler. Solche Verzerrungen werden in der Musik als kritisch angesehen, aber sie sind für den Handel nicht so relevant. Was aber, wenn die Diskretisierungsrate geringer ist als die ursprüngliche Signalrate? Ein Beispiel ist in Abbildung 2 unten dargestellt.

---->>

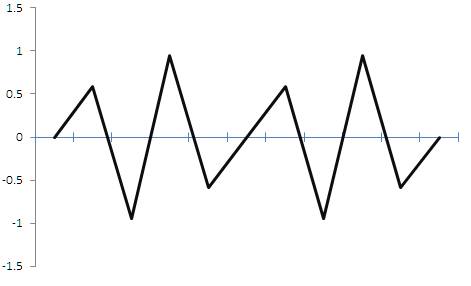
Abb. 2.

Die Abbildung zeigt, dass, wenn die Diskretisierungsfrequenz kleiner als eine doppelte Signalfrequenz ist, das resultierende Signal stark verzerrt wird und wir tatsächlich ein zufälliges Signal erhalten, das nichts mit dem ursprünglichen Signal zu tun hat. Bei der Anwendung im Handel würde uns der erste Fall erlauben, zu verkaufen, wenn wir das Hoch finden, und zu kaufen, wenn wir ein Tief sehen. Auch in diesem Fall kennen wir die Frequenz. Nach der falschen Diskretisierung verlieren wir Informationen über die Amplitude und die Signalfrequenz. Ein deterministisches periodisches Signal mit bekannten Eigenschaften verwandelte sich aufgrund einer falsch gewählten Diskretisierungsrate in ein zufälliges nichtperiodisches Signal mit unbekannten Eigenschaften.

Aus den obigen Erkenntnissen ergeben sich zwei logische Fragen: "Machen wir nicht einen Fehler bei der Diskretisierung einer Preisreihe?" und "Ist die Preisreihe ein diskretes oder ein kontinuierliches Signal und was sind ihre Parameter?" 

Die Antwort ist nicht so einfach, und sie ist sehr wichtig.

Ist die Preisreihe ein diskretes oder ein kontinuierliches Signal?

Die Frage lässt sich beantworten, wenn wir den Mechanismus der Marktpreisbildung kennen. Ich werde ihn nicht im Detail beschreiben, da die Beschreibung in dem Artikel "Grundlagen der Börsenkursbildung am Beispiel des Terminhandelsbereichs der Moskauer Börse" erfolgt. Einige Teilnehmer erteilen Aufträge in der Markttiefe, und andere Teilnehmer kaufen die erforderliche Menge zum erforderlichen Preis. Dies geschieht, wenn ein Preis-Chart gebildet wird. Die Niveaus sind diskret, d.h. es ist möglich, eine Order zu einem Preis von 1, 2, 3 und so eins mit einer gewissen Genauigkeit zu platzieren. Das in den Geboten festgelegte und von den Käufern gekaufte Volumen ist ebenfalls diskret, d.h. es ist möglich, 1, 2, 3 oder mehr Einheiten zu kaufen. Abbildung 3 unten zeigt ein Beispiel für die Markttiefe; Sie können sehen, dass Preise und Volumen diskrete Werte haben. 

Abb. 3.

Daraus können wir schließen, dass das Chart der Preisreihen diskreter Natur ist. Der Preis bewegt sich auf diskreten Niveaus, nachdem die Teilnehmer diskrete Mengen gekauft haben. 

Die Funktion dessen, was der Preis ist

Wir haben herausgefunden, dass die Preisreihe selbst diskret ist, aber die Funktion welches Parameters ist die Preisänderung?

Die Diskretisierung eines Audiosignals in regelmäßigen Abständen ist eine akzeptable Lösung, da ein Audiosignal eine Funktion ist, die sich mit der Zeit ändert. Das Signal selbst ist eine Amplitude, die von der Zeit abhängt. Diese Signaleigenschaft ist fundamental. Deshalb gibt es hier keine Probleme.

Die Preisreihe hat einen anderen Charakter. Hier ändert sich die Amplitude (der Preis) im Laufe der Zeit, aber die Zeit ist nicht der Grund für die Preisänderung. Wenn Sie versuchen, den Grund für die Preisänderung herauszufinden, dann ist die Frage nicht so einfach. Es können mehrere Annahmen getroffen werden:

1. Der Preis als Funktion der Handelsgeschäfte. Er ändert sich in Übereinstimmung mit ausgeführten Handelsgeschäften, weil sie den Preis bewegen. Aber Handelsoperationen sollten nicht zu Preisänderungen führen. Zum Beispiel sind 10 Aktien zu einem Preis von 1 USD erhältlich. Ein Teilnehmer kauft 4 Aktien, und es bleiben 6 Aktien zum gleichen Preis übrig. Es wurde also eine Handelsoperation ausgeführt, aber der Preis hat sich nicht geändert. Durch den Vorgang hat sich jedoch das zu diesem Preis verfügbare Volumen verringert, was zu weiteren Preisänderungen führen kann, wenn der nächste Teilnehmer das gesamte Volumen kauft. Preise ändern sich nur dann, wenn die Menge der verfügbaren Bestände zu 1 USD nicht ausreicht, um die Nachfrage zu decken, und die gesamte verfügbare Menge aufgekauft wurde. In diesem Fall bewegt sich der ASK-Preis auf 1,1 USD. Andere Teilnehmer können jedoch weiterhin einen Auftrag zu 1 USD erteilen und den ASK-Preis zurück bewegen.
2. Der Preis in Abhängigkeit von allen Handelsoperationen auf dem Markt. Er kann sich nicht nur ändern, wenn die Teilnehmer das Volumen auf einem bestimmten Niveau aufkaufen, sondern auch, wenn sie ihre Aufträge einfach stornieren oder auf andere Ebenen verschieben. Es wird also keine Handelsoperationen geben, aber die BID- und ASK-Preise werden sich bewegen.
3. Der Preis als Funktion des "Nutzens". Er kann sich ändern, weil die Teilnehmer den Vermögenswert für sich selbst neu definieren. Es kann ganz unterschiedliche Gründe für eine Neudefinition des Vermögenswerts geben. In jedem Fall ist die Neudefinition des Vermögenswerts eng mit dem Nutzen der Teilnehmer verbunden. Theoretisch ist der festgelegte Preis für die gesamte Gruppe der Teilnehmer, einschließlich Käufer und Verkäufer, der günstigste (auch wenn dieser Nutzen negativ ist). Der Markt wurde ursprünglich geschaffen, um den Nutzen zu maximieren und den optimalen Gleichgewichtspreis zu bestimmen, der sowohl für den Käufer als auch für den Verkäufer akzeptabel ist. Dieser Vorteil ist nicht unbedingt an einen bestimmten Vermögenswert gebunden. Zum Beispiel muss ein Investmentfonds dringend einen Vermögenswert verkaufen. Er ist bereit, dies zu tun, auch wenn er Verluste erleiden wird, weil er durch die Durchführung dieser Operation möglicherweise einen anderen Vorteil erhält, z.B. die Möglichkeit, einen anderen Vermögenswert zu kaufen oder Gewinne an seine Kunden auszuzahlen. Die Art des Vorteils kann unterschiedlich sein. In einem solchen Fall ist der Preis eine Funktion der jeweiligen Neudefinition der Vorteile für jeden Teilnehmer.
4. Der Preis als eine Funktion seiner selbst. Es liegt auf der Hand, dass jede Preisänderung zu einer Änderung des Nutzens für die Marktteilnehmer führt. Der Nutzen kann sich ändern, ohne dass sich der Preis ändert, aber wenn sich der Preis ändert, ändert sich der Nutzen für die Teilnehmer. Dies ist nicht die genaueste Beschreibung von Preisänderungen, aber sie erlaubt es uns, uns einem idealen Modell grob anzunähern und einige Annahmen zu treffen, die in Zukunft keine großen Auswirkungen auf die Ergebnisse haben werden. Grundsätzlich handeln wir die Preisänderungen. Selbst wenn wir Dividendenstrategien wählen (und dabei den Preis ignorieren), wird die Zahlung von Dividenden letztlich zu Preisänderungen führen. In diesem Fall ist die Preisänderung ein Signal, das Chart nach links zu verschieben. Wir registrieren Preisänderungen nur dann, wenn sich der Preis um einen Punkt bewegt. Je nach der bevorzugten Skala kann jede beliebige Stufe verwendet werden: Preiswerte können jedes Mal registriert werden, wenn sich der Preis um n Punkte nach oben oder unten bewegt. 

Ich halte die dritte Option für die wahrscheinlichste, die besagt, dass der Preis eine Funktion eines neudefinierten Nutzens ist. Aber es ist unmöglich, den Nutzen jedes einzelnen Teilnehmers zu berechnen, um die Reihe zu diskretisieren. In den ersten beiden Fällen ist es möglich, Handels- und Nicht-Handelsgeschäfte an den Börsenmärkten zu berechnen, aber es kann auch Schwierigkeiten geben. Zum Beispiel kann ein Vermögenswert an zwei oder mehr verschiedenen Börsen gehandelt werden. Oder wenn es Derivate eines Vermögenswertes gibt, wie Futures und Optionen, müssen wir dann die Operationen berechnen, die indirekt mit dem Vermögenswert verbunden sind? Diese Fragen erfordern eine separate große Studie. In jedem Fall stehen alle vier Fälle in einem indirekten Zusammenhang miteinander. Die vierte Option, bei der der Preis eine Funktion von sich selbst ist, erlaubt weitere Untersuchungen, vorausgesetzt, wir gehen davon aus, dass es sich um ein grobes Modell handelt.

Die Änderungsrate des Vermögenspreises hängt von der Anzahl der Handelsgeschäfte ab. Je mehr Handelsoperationen, desto häufiger ändert sich der Preis, d.h. es besteht ein direkter Zusammenhang. Dementsprechend führen viele Marktteilnehmer, wenn es viele Marktteilnehmer gibt, viele Handelsoperationen durch, was zu einer häufigeren Neudefinition des Nutzens für jeden Teilnehmer führt. Jeder Teilnehmer wird also versuchen, den Preis häufiger neu zu definieren, was zu einer größeren Anzahl von Handelsgeschäften führt, und die Häufigkeit der Vermögenspreisänderung wird hoch sein.

Merkmale der Preisreihendiskretisierung nach Zeitintervallen und einer Zufallskomponente

Nach unserem groben Modell ist der Preis eine Funktion von sich selbst, und wir diskretisieren den Preis nur dann, wenn er sich um eine bestimmte Anzahl von Punkten ändert. Auch wenn dies nicht ganz zutrifft, ermöglicht diese Annahme ein weiteres Verständnis des Themas, ohne das Endergebnis zu beeinflussen. Darüber hinaus müssen wir, um da zu nutzen, wissen, dass sich der Preis geändert hat. Außerdem müssen wir wissen, wie er sich verändert hat, um nach Mustern zu suchen. 

Jede 1-Punkt-Preisänderung (hier ist ein Punkt die kleinstmögliche Preisänderung) entspricht einem Schritt. Lassen Sie uns sehen, was passiert, wenn eine solche Serie zeitdiskretisiert wird. Es liegt auf der Hand, dass die Anzahl der Punkte, die der Preis pro Zeiteinheit passiert, von der Handelsaktivität abhängt. Je höher die Handelsaktivität (die Anzahl der ausgeführten Handelsgeschäfte), desto mehr Schritte wird der Preis letztendlich durchlaufen. Die Handelsaktivität ist nicht direkt mit der Kursbewegung verbunden, aber die Kursbewegung hängt von der Handelsaktivität ab: je höher die Aktivität, desto mehr Kursbewegungen wird es geben. Die Abhängigkeit ist indirekt, aber die Korrelation ist positiv. Angenommen, 1 Schritt entspricht 10 Punkten. In diesem Beispiel werden Kerzen von einer Stunde verwendet. Die beiden folgenden Abbildungen zeigen Preise, die als Bocks dargestellt werden. Die Blöcke ähneln den Renko-Balken, sind aber nach einem etwas anderen Prinzip aufgebaut. Sie verwenden Hoch und Tief der klassischen Kerzen, die den höchsten und niedrigsten Preiswert für die Blockbildungszeit zeigen. Wie Kerzen haben auch die Blöcke 4 Merkmale: Open, High, Low und Close. Der Unterschied zu den Kerzen besteht darin, dass der Abstand zwischen Open und Close immer fest ist und in Punkten ausgedrückt wird. Der Block schließt, wenn der Preis N Punkte vertikal nach oben passiert. Die Blockgröße beträgt zum Beispiel 10 Punkte. Sobald sich der Preis vertikal um 10 Punkte nach oben bewegt, wird der Block geschlossen und ein neuer Block beginnt.

Abb. 4.

Wenn ein Block einem Schritt von N Punkten entspricht, dann schauen wir einmal, was innerhalb einer Einstundenkerze passiert. Die Abbildungen 4 zeigen die Bewegungen, die während der Bildung der 1-Stunden-Kerze stattfanden. In der oberen Abbildung passierte der Preis in einer Stunde vertikal 10 Blöcke. Wenn die Blockgröße 10 Punkte beträgt, dann beträgt die Größe der Kerze 100 Punkte. Insgesamt wurden 25 Blöcke für die gesamte Kerzenbildungszeit gebildet, was 25 Schritten entspricht. Ein weiteres Beispiel ist in der unteren Abbildung dargestellt, in der sich der Preis während der Kerzenbildungszeit um 0 Blöcke oder 0 Punkte bewegt hat. Insgesamt bewegte sich der Preis während der gesamten Preisbildungszeit um 40 Blöcke oder 40 Schritte. Betrachten wir nun ein Chart, das aus solchen Kerzen besteht. Es ist in Abbildung 5 dargestellt. Die Kerze schließt einmal pro Stunde, und die Preisreihe ist definitiv keine Funktion der Zeit. In einem vereinfachten Fall ist sie eine Funktion der Handelsgeschäfte, die eine positive Korrelation mit der Anzahl der durchlaufenen Punkte haben. Da wir die Punkte in Blöcke umgewandelt haben, hat die Anzahl der Blöcke eine positive Korrelation mit der Anzahl der Handelsgeschäfte. Tatsächlich entpuppt sich jede Kerze (angenommen eine Stunde) als eine zufällige Anzahl von Blöcken oder Schritten mit jeweils N Punkten. Weiter werden wir sehen, warum dies wichtig ist. Das liegt daran, dass Kerzen einfach nach einer bestimmten Zeit schließen, trotz der Prozesse, die auf dem Markt stattfinden. Die Zeit ist ein externer Parameter, der wenig mit preisbezogenen Prozessen zu tun hat. Mit anderen Worten, der Preis ändert sich nicht, weil eine Stunde vergangen ist, sondern aus anderen Gründen, von denen einer auch die verstrichene Zeit sein kann.

Bild 5.

Handelsgeschäfte können sich im Laufe der Zeit erheblich verändern. Darüber hinaus sind die Handelsgeschäfte der verschiedenen Handelsinstrumente unterschiedlich. Darüber hinaus führt die Entwicklung des Algo-Handels zu einem Anstieg der Anzahl der Operationen pro Zeiteinheit und des Handelsumsatzes, was bedeutet, dass der direkte Vergleich von Kerzen zwischen den Jahren 2010 und 2020 falsch wäre, da jede von ihnen eine unterschiedliche Anzahl von Operationen enthalten würde.

Lassen Sie uns nun eine weitere Vereinfachung vornehmen und den Markt nach dem Zufallsprinzip betrachten. Natürlich ist der Markt kein Random Walk, aber auf diese Weise wird er leichter zu verstehen sein. Später werden wir auf die realen Märkte zurückkommen.

Der Zentrale Grenzwertsatz besagt, dass die Summe einer ausreichend großen Anzahl von schwach abhängigen Zufallsvariablen mit ungefähr gleichen Skalen (keiner der Begriffe dominiert oder leistet einen bestimmenden Beitrag zu der Summe) ungefähr normalverteilt ist. Wie auf unseren Fall angewandt, können wir aus diesem Theorem schließen, dass unser Zufallsprozess im Durchschnitt für N Schritte eine Strecke durchläuft, die ungefähr vertikal proportional zur Quadratwurzel der Anzahl der Schritte ist. Wenn ein Block einem Schritt entspricht, dann wird der Preis für 100 Blöcke im Durchschnitt vertikal 100^0,5 = 10 Blöcke durchlaufen. In Einzelfällen kann dies mehr oder weniger der Fall sein, aber im Durchschnitt folgt die Zufallsreihe der Normalverteilungsregel. Die Anzahl der Schritte dieser Zufallsreihe wird leicht von der Zeit abhängen, da die Schritte durch die Preisaktivität generiert werden, die im Laufe der Zeit stark variieren kann.

Daher wird die Größe der 1-Stunden-Kerze für eine solche Zufallspreisreihe im Durchschnitt proportional zu N^0,5 sein, wobei N die Anzahl der Schritte innerhalb der Kerze ist. Das bedeutet, dass die Größe der 1-Stunden-Kerze dem Gesetz der Normalverteilung unterliegt. Unter Berücksichtigung der Tatsache, dass eine zufällige Anzahl von Schritten innerhalb einer Kerze existieren kann, können wir schlussfolgern, dass auch die Kerzengröße dem Normalverteilungsgesetz unterliegt. D.h. die Kerzengröße ist gleich der Quadratwurzel aus der Anzahl der Schritte innerhalb dieser Kerze. Lassen Sie uns diese Aussage überprüfen. Zu diesem Zweck werde ich 50.000 1-Minuten Kerzen von GBPUSD in dem Zeitraum zwischen 2020.05.18 und 2020.07.03 verwenden.

1. Lassen Sie uns den Modulo-Wert der durchschnittlichen Größe einer 1-Minuten-Kerze finden - dies wird die Schrittgröße sein. Dazu subtrahieren wir den Schlusskurs jeder vorherigen Kerze vom Schlusskurs jeder nächsten Kerze und nehmen den Modulo-Wert. Ich habe die durchschnittliche Größe einer 1-Minuten GBPUSD-Kerze = 0,000170
2. Lassen Sie uns nun die durchschnittliche Größe einer 1-Stunden-Kerze für den gleichen Zeitraum ermitteln (eine 1-Stunden-Kerze enthält 60 1-Minuten-Kerzen). Dazu subtrahieren wir den Schlusskurs jeder vorherigen 1-Stunden-Kerze vom Schlusskurs jeder nächsten 1-Stunden-Kerze und ermitteln den Modulo-Wert. Dann ergibt sich die durchschnittliche Größe einer 1-Stunden GBPUSD-Kerze = 0,001117
3. Lassen Sie uns nun herausfinden, um wie viel der Preis pro Stunde im Durchschnitt sich verändert, wenn wir davon ausgehen, dass die Preisreihe ein Random Walk ist. Um dies herauszufinden, multiplizieren wir die durchschnittliche Größe einer 1-Minuten-Kerze mit der Quadratwurzel aus der Anzahl der Schritte und multiplizieren Sie sie mit der durchschnittlichen Schrittgröße. Wir haben 60 => 0,000170*(60^0,5) = 0,001315. Die Größe einer 1-Stunden-Kerze würde zu dieser Durchschnittsgröße tendieren, wenn die ursprüngliche Serie dem Normalverteilungsgesetz folgen würde.
4. Vergleichen wir die durchschnittliche Größe einer realen Kerze und einer Random-Walk-Kerze (real 0,001117) ≈ (theoretisch 0,001315). Der Unterschied beträgt nur 0,0002. es kann gefolgert werden, dass unsere Annahme, dass die Größe der Kerze dem Gesetz der Normalverteilung unterliegt, wahr ist und durch die realen Symbolmarktdaten bestätigt wird. Ein Unterschied von 0,0002 ist nicht signifikant.

Darüber hinaus kombinieren und analysieren wir mit den erhaltenen 1-Stunden-Kerzen tatsächlich eine Sequenz von bestimmten Segmenten einer Preisreihe, deren Amplitude dem Normalverteilungsgesetz folgt. Wenn wir zu höheren Zeitrahmen übergehen, erhalten wir natürlich alle die gleichen Kerzen, deren Größe proportional zur Quadratwurzel der Anzahl der Schritte ist. Kommen wir nun zurück zu Abbildung 2: Wenn eine Reihe falsch diskretisiert wird, wird als Ergebnis eine Zufallsfolge ausgegeben. Tatsächlich wandeln wir mit Hilfe der Zeitdiskretisierung eine Preisreihe in eine Zufallsfolge um. Nun, eine zeitdiskretisierte Sequenz kann immer noch Muster aufweisen, da der Markt keine Zufallssequenz ist und indirekte Abhängigkeiten von der Zeit aufweist, aber die Analyse einer solchen Serie und die Identifizierung von Mustern wird viel schwieriger. Dies ist die zeitliche Diskretisierung, die zu dem sogenannten "Rauschen" und der Nicht-Stationarität in der Preisreihe führt - sie werden oft diskutiert, aber niemand erklärt, woher dieses Rauschen kommen. Nun ist das Rauschen nicht nur ein Rauschen der Diskretisierung, die bei der Diskretisierung eines Signals auftreten, sondern es enthält auch eine Zufallskomponente, die aufgrund falscher Diskretisierungsparameter einer Preisreihe auftritt, die selbst diskret ist.

Um sicherzustellen, dass die Ergebnisse, die wir mit 1-Stunden-Kerzen erhalten haben, kein Zufall waren, wiederholen wir den gleichen Vorgang für Tageskerzen. Es gibt 24 Stunden pro Tag. Da Währungspaare rund um die Uhr gehandelt werden, nehmen wir an, dass die tägliche Kerze 1440 1-Minuten-Kerzen enthält. Nehmen wir dasselbe Intervall von 1-Minuten-Daten, das wir für H1 verwendet haben. Diesmal werden die relevanten Daten der Einfachheit halber in tabellarischer Form dargestellt.

Durchschnittliche Größe der Kerze M1	Durchschnittliche Größe der H1-Kerze	Theoretische Größe der H1-Kerze berechnet als 0,000117*(60^0,5)	Durchschnittliche reale Größe der D1-Kerze	Theoretische Größe der Kerze D1 berechnet als 0.00017*(1440^0.5)
0.000170	0.001117	0.001315	0.006547	0.006442

Wie Sie sehen, würde sich die reale Durchschnittsgröße einer Tageskerze nicht wesentlich von der theoretisch vorhergesagten Größe unterscheiden, wenn es sich nicht um einen realen Markt, sondern um einen Random Walk handeln würde. Die Excel-Datei mit historischen Daten und Berechnungen ist unten angehängt.

Um die durchschnittliche Größe einer Kerze mit einem höheren Zeitrahmen zu berechnen, haben wir 1-Minuten-Zeitrahmen-Daten verwendet. Aber was ist, wenn wir 'absteigen' zu den Tick-Daten - würde dies zu einem anderen Ergebnis führen? Was wir tun werden:

1. Wir nehmen die Tickdaten der 1-Minuten-Kerzen (aus einem realen Konto) für den gleichen Zeitraum und berechnen die durchschnittliche Anzahl von Ticks in einer 1-Minuten-Kerze - die durchschnittliche Anzahl beträgt 59,99 Ticks pro Minute. 
2. Wir laden die Tickdaten und ermitteln die durchschnittliche Tickgröße, sie beträgt 0,000014378. 
3. Wir berechnen die theoretische Größe einer 1-Minuten-Kerze als (59,99^0,5)*0,00014378=0,000111363
4. Wir berechnen die theoretische Größe einer 1-Stunden-Kerze als ((59.99*60)^0.5)* 0.000014378= 0.00086

Durchschnittliche Tickgröße	Durchschnittliche reale M1-Kerzengröße	Theoretische Größe der Kerze M1 berechnet als (59,99^0,5)*0,000014378	Durchschnittliche Größe der H1-Kerze	Theoretische Größe der H1-Kerze berechnet ((59.99*60)^0.5)*0.000014378
0.000014378	0.00017	0.000111363	0.001117	0.00086

Wie man sehen kann, unterscheidet sich die durchschnittliche Größe der M1- und H1-Kerzen nicht wesentlich von der theoretischen Größe, die die Preisreihe hätte, wenn es sich um einen Random Walk handeln würde. Daraus können wir schließen, dass sich die Preisreihe aus irgendeinem Grund wie ein Random Walk verhält, was wahrscheinlich auf eine falsche Diskretisierung der Zeitintervalle zurückzuführen sein kann.

Dichte der Verteilung der Inkremente der Preisreihen

Die quantitative Bewertung erlaubte es, grob abzuschätzen, wie die Preisreihen-Kerzengröße der Random-Walk-Kerzengröße entspricht. Interessanter ist es, die Verteilungsdichte der Preisserieninkremente darzustellen, was es uns erlaubt, die Ähnlichkeiten oder Unterschiede mit der Verteilungsdichte der Random-Walk-Inkremente visuell zu beurteilen.

Ein wichtiger Teil der Analyse ist die Datenaufbereitung. Die Dichte der Inkremente wird für die Anzahl der Punkte berechnet, die sich der Preis in 60 Minuten (in 1 Stunde), d.h. in 60 Schritten, bewegen kann. Hier müssen wir die durchschnittliche Größe einer 1-Minuten-Kerze und die Anzahl der Schritte kennen (die Anzahl der 1-Minuten-Kerzen in einer 1-Minuten-Kerze). Die durchschnittliche Größe einer 1-Minuten-Kerze haben wir bereits berechnet - sie entspricht 0,000170. Die Anzahl der 1-Minuten-Kerzen in einer 1-Stunden-Kerze beträgt 60. Das bedeutet, dass der Preis 60 Schritte pro Stunde machen kann, wobei jeder Schritt 0,000170 beträgt. Der Extremfall ist also, wenn sich der Preis vom Ausgangspunkt kontinuierlich um 60 Punkte nach oben oder 60 Punkte nach unten bewegt. Die Verteilungsdichte wird also im Bereich zwischen -0,00017*60=-0,0102 und 0,00017*60=0,0102 geschätzt. Mit anderen Worten, wir wissen, dass, wenn sich der Preis nur in Schritten von 0,00017 nach oben bewegt, er in 60 Schritten (in einer Stunde) ein Maximum von 0,0102 erreichen wird. Darüber hinaus kann der Preis bei 60 Schritten nur die diskreten Stufen 0, 0,00034, 0,00068, 0,00102 ... 0,0102 und ähnliche, negative Werte annehmen. Abbildung 6 zeigt, warum der Preis genau diese Stufen annehmen wird.

Bild 6.

Wenn irgendeine diskrete Funktion bei einem Nullpunkt beginnt, ihr Schritt gleich 1 ist und sie 6 Schritte macht, dann kann sie sich letztendlich vertikal 6, 4, 2 oder 0 Segmente bewegen und kann nur diskrete Werte mit einer doppelten Schrittweite annehmen. Unser Fall ist ähnlich: Wenn die durchschnittliche Größe einer 1-Minuten-Kerze 0,00017 beträgt, dann kann der Preis diskrete Werte mit einem Intervall annehmen, das der doppelten Größe der Kerze entspricht. In Wirklichkeit können Kerzen verschiedene Größen haben, nicht nur 0,00017, deshalb kann der Preis Zwischenwerte annehmen. Daher werden wir für die Analyse zählen, wie viele Ereignisse in die Intervalle mit einer doppelten durchschnittlichen Kerzengröße fallen. Um die Differenz der resultierenden Verteilung für die Preisreihe zu ermitteln, vergleichen Sie sie mit der Verteilung für einen Random Walk. Charakteristisch für einen Random Walk ist, dass die Richtungsänderungswahrscheinlichkeit bei jedem nächsten Schritt 50 % beträgt und dass kein Gedächtnis vorhanden ist. Abbildung 7 zeigt Wahrscheinlichkeitsdichteverteilungen in Schwarz für eine Preisreihe und in Rot für einen Random Walk.

Bild 7.

Aus Abbildung 7 ist ersichtlich, dass die Dichte der Preisreihen-Wahrscheinlichkeitsverteilung fast der Dichte der Random-Walk-Wahrscheinlichkeitsverteilung entspricht. Die Dichte der Preisreihen-Wahrscheinlichkeitsverteilung hat eine etwas höhere Spitze, ist etwas schmaler und im Vergleich zur Dichte der Random-Walk-Verteilung leicht nach rechts verschoben. Dies deutet darauf hin, dass die Wahrscheinlichkeit einer Umkehrung bei jedem nächsten Schritt in der Preisreihe etwas höher als 50% ist, und es gibt einen kleinen Aufwärtstrend, aber diese Unterschiede sind nicht groß. Es mag den Anschein haben, dass es nicht so schwierig ist, von dieser Abweichung zu profitieren, aber wir werden dies im nächsten Artikel berücksichtigen. Hier haben wir es mit einer idealen Zufallsvariablen zu tun, die bei einer ausreichend großen Stichprobe zu einem Benchmark tendiert. Das Diagramm der Wahrscheinlichkeitsdichteverteilung für einen Random Walk wird anhand einer Tabelle dargestellt, von der ein Teil in Abbildung 8 dargestellt ist.

Bild 8.

Dieses Diagramm der Wahrscheinlichkeitsdichteverteilung bestätigt unsere frühere Schlussfolgerung, dass die Kerzengröße (in diesem Fall H1-Kerze) zur Kerzengröße tendiert, was der Fall wäre, wenn die Preisreihe ein Random Walk wäre. Es ermöglicht auch eine visuelle und genauere Beurteilung dieser Tatsache.

Alle in diesem Artikel erwähnten Daten und Berechnungen sind in der xlsx-Datei unten angehängt.

Bereiche mit hoher und niedriger Volatilität

Aufmerksame Händler können feststellen, dass die Kerzen im Markt konventionell in Gruppen von "großen" und "kleinen" Kerzen (Bereiche mit hoher und niedriger Volatilität) eingeteilt sind, was bedeutet, dass das Chart kein Random Walk ist und es Muster gibt. Wenn die Zeitdiskretisierung starke Verzerrungen einführen würde, dann würde dieser Effekt nicht beobachtet werden. Dieses Merkmal lässt sich jedoch dadurch erklären, dass die Größe der Kerze von der Anzahl der innerhalb dieser Kerze ausgeführten Handelsgeschäfte abhängt. Wie lässt sich dies überprüfen? Sie können sich einfach den Chart mit den Tick-Volumina ansehen - "kleine Kerzen"-Perioden gehen mit niedrigen Tick-Volumina einher, und "große Kerzen"-Perioden korrespondieren mit Perioden mit hohen Tick-Volumina. Wenn wir davon ausgehen, dass ein Tick ein Schritt ist, dann macht der Preis während "großer Kerzen"-Perioden mehr Schritte, aber die Kerzengröße bleibt proportional zur Quadratwurzel aus der Anzahl der Schritte multipliziert mit der durchschnittlichen Schrittgröße (Beispiel in Abbildung 9). Die Tick-Volumina wiederum sind direkt mit dem Handelsgeschäft korreliert: Je höher die Handelsaktivität, desto mehr Ticks gibt es pro Zeiteinheit. Börsenmärkte liefern die Historie der realen Volumina, wobei Sie sehen können, dass die Tick-Volumina stark mit den realen Volumina korrelieren, was auch das Verhältnis zwischen der Anzahl der Ticks und der Intensität der Handelsgeschäfte anzeigt.

Bild 9.

Dies beweist auch, dass die Zeitdiskretisierung starke Verzerrungen in die resultierende Preisreihenform einführt und damit die Preisanalyse erschwert. Diese Verzerrung hat zur Entstehung einer eigenen Kategorie von Handelsgeschäften geführt, den sogenannten "night scalpers". Ich sage nicht, dass sie keine Gewinne erwirtschaften können, aber es ist notwendig, diese Besonderheit einer Preisreihendarstellung bei der Entwicklung solcher Systeme zu berücksichtigen und zusätzliche Untersuchungen durchzuführen, um die folgende Frage zu beantworten: "Ist die Wahrscheinlichkeit einer Umkehr in diesen Bereichen wirklich höher als die Wahrscheinlichkeit einer Trendfortsetzung?" und "Erlauben die statistischen Merkmale dieser Bereiche die Erzielung eines Gewinns?", denn solche Systeme basieren auf diesem Muster. 

Alternative Preisreihen-Diskretisierung

Die einfache Schlussfolgerung aus der obigen Analyse legt nahe, dass Tick-Daten für die Verarbeitung und Analyse besser geeignet sind, da sie Diskretisierungsfehler in einer Preisreihe vermeiden. Wenn wir einen größeren Maßstab benötigen, werden wir Blöcke von 10 oder 100 Ticks verwenden. Das Problem ist jedoch, dass Ticks selbst auch eine Methode zur Diskretisierung sind. Diese Methode ist weit verbreitet, aber sie kann dennoch Verzerrungen in den Prozess einbringen, da der Preis nicht von den empfangenen Ticks abhängt. Der Preis ist zumindest eine Funktion der ausgeführten Handelsgeschäfte, während ein Handelsgeschäft nicht immer einen Tick generiert. Ticks an einer Börse sind irgendwie mit dem realen Handelsgeschäft verbunden. Aber auf dem Forex-Markt kann jedes Unternehmen eine beliebige Anzahl von Ticks anbieten, und es ist schwer zu verstehen, welcher davon richtig ist. Selbst wenn wir also einfach davon ausgehen, dass der Preis eine Funktion von Handelsgeschäften ist, wird klar, dass Ticks die Preisreihe verzerren und eine Zufallskomponente einführen, die zu Fehlern führen kann.

Das Problem einer korrekten Diskretisierung ist ein wichtiger Teil der Datenanalyse. Abbildung 10 zeigt zum Beispiel zwei Charts des Bitcoin-Preises gegenüber dem Dollar. Das obere Chart ist ein regelmäßiges wöchentliches Kerzen-Chart, und das untere Chart ist in Blöcken von N Punkten diskretisiert. Es ist der gleiche Zeitraum, die gleiche Anzahl von Blöcken/Kerzen, aber unterschiedliche Diskretisierungsmethoden. Sie können sehen, dass die Charts desselben Instruments unterschiedlich sind. Es stellt sich eine natürliche Frage: "Welche dieser beiden Darstellungen ist richtig?"

Bild 10.

Ich kam zu dem Schluss, dass die korrekte Anzeige diejenige ist, die die Art der Diskrepanz der Preisreihen berücksichtigt. Da die Art der Diskrepanz jedoch unbekannt bleibt, wird es "korrekter" sein, eine solche Diskretisierungsmethode zu verwenden, die die Erzeugung von Gewinn/Verlust sowohl durch mich als auch durch andere Marktteilnehmer widerspiegeln kann. Es ist also besser, die Daten zu analysieren, auf deren Grundlage unsere Gewinne gebildet werden. Das heißt, wir sollten nicht die Kursbewegung in der Zeit betrachten, sondern nur berücksichtigen, um wie viel sich der Kurs bewegt hat.

Eine Alternative zur zeitlichen Diskretisierung kann die Diskretisierung mit fester Amplitude sein, bei der davon ausgegangen wird, dass der Preis eine Funktion seiner selbst ist. Dies sind die Blöcke, die wir vorhin diskutiert haben. Ein Block von N Punkten gilt als geschlossen, nachdem sich der Preis um N Punkte vertikal bewegt hat. Vielleicht ist dies nicht der beste Ansatz, aber wir sind daran interessiert, wie viele Punkte der Preis genau überschritten hat, da sich dies auf den von uns erwirtschafteten Gewinn oder Verlust auswirkt. Darüber hinaus ändert sich der Nutzen jedes Teilnehmers unmittelbar nachdem der Kurs N Punkte vertikal überschritten hat. Das bedeutet, dass das Modell, in dem der Preis eine Funktion von sich selbst ist, dem realen Handelsgeschäft am nächsten kommt. Abbildung 11 zeigt eine Sinuskurve, die in Blöcke fester Größe diskretisiert ist. Die Form geht verloren, aber die Hauptmerkmale bleiben erhalten, einschließlich Periode und Amplitude.

Bild 11.

Selbst wenn falsche Diskretisierungsparameter eingestellt werden, bleiben die Werte von Amplitude und Periode erhalten. Abbildung 12 zeigt ein Beispiel dafür, was passiert, wenn die Blockgröße zu groß ist. Ein Teil der Information, die sich innerhalb des Blocks befindet, geht verloren und damit ist die Genauigkeit schlechter (was bei der Datenkomprimierung unvermeidlich ist), aber die Information über die Amplitude und die Periode bleibt erhalten. Wenn die Blockgröße größer als die Preisreihenamplitude ist, werden die Blöcke nicht angezeigt. Wenn also im Gegensatz zu Abbildung 2 ein falscher Diskretisierungsparameter gewählt wird, verwandelt sich das ursprüngliche deterministische Signal nicht in ein Zufallssignal.

Abb. 12

Dies ermöglicht die Eliminierung der Zufallskomponente, die durch eine zeitdiskretisierte Preisreihe eingeführt wird, und in Situationen, in denen nicht bekannt ist, welche Funktion der Parameter der Ausgangsreihe hat. Diese Methode funktioniert besser als die zeitliche Diskretisierung und ermöglicht eine bequeme Skalierung eines Charts mit einer Genauigkeit der Skalierungsänderung bis zu 1 Punkt.

Schlussfolgerung

• Die Art der Preisreihen ist diskret, was sich aus der Preisstruktur ergibt.
• Ein Marktpreis ist keine Funktion der Zeit, sondern eine Funktion eng miteinander verbundener wirtschaftlicher Prozesse, und derzeit ist es nicht möglich, sie alle zu berücksichtigen.
• Die Diskretisierung einer Preisreihe in Zeitintervalle führt eine signifikante Zufallskomponente ein; dies verzerrt die reale Form des Preischarts, fügt Rauschen und Nicht-Stabilität zu diesem komplexen Prozess mit unbekannten Parametern hinzu.
  
• Bei der Entwicklung von Preisreihendiskretisierungsmethoden ist es notwendig, die Funktion, welcher Parameter der Preis ist, zu berücksichtigen.
• Die Nicht-Stationarität einer Preisreihe entsteht u.a. durch falsche Diskretisierungsparameter.
• Zeitdiskretisierte Preisdiagramme können analysiert werden, um Muster zu finden, aber es ist notwendig, die oben genannten Aspekte zu berücksichtigen, um die Natur eines bestimmten gefundenen Musters besser zu verstehen.
• Die Idee besteht darin, andere Preisreihen-Diskretisierungsmethoden zu entwickeln, die viel weniger Verzerrung in die Originaldaten einbringen. Eine dieser Methoden wird in diesem Artikel beschrieben.
• Handelsgeschäfte und statistische Marktstudien sollten unter Berücksichtigung der spezifischen Merkmale der verwendeten Preisreihendiskretisierung entwickelt werden.