Cálculo de expressões matemáticas (Parte 1). Analisadores descendentes recursivos

Ao automatizar tarefas de negociação, às vezes é necessário adicionar flexibilidade à execução de algoritmos computacionais. Assim, por exemplo, para configurar programas vindos numa forma fechada (compilada), podemos selecionar o tipo de função objetivo a partir de uma ampla gama de possíveis combinações. Em particular, isso ocorre ao otimizar um EA ou avaliar rapidamente um protótipo de indicador. Quando é assim, na caixa de diálogo de propriedades, o usuário pode alterar não apenas os parâmetros, mas também a fórmula de cálculo. Nesses casos, é necessário calcular a expressão aritmética com base na sua representação textual sem alterar o código MQL do programa.

Para resolver este problema, são utilizados distintos tipos de analisadores que permitem interpretar fórmulas em tempo real, compilando-as numa árvore sintática, gerando o chamado bytecode (sequências de instruções computacionais) e executando-o para calcular o resultado. Neste artigo, veremos alguns tipos de analisadores e como avaliar expressões.

Formulação do problema

Por expressão aritmética entenderemos uma sequência unilinear de itens de dados e de operadores que descrevem ações. Nossos itens de dados serão números e variáveis nomeadas. Os valores das variáveis poderão ser atribuídos e alterados externamente, ou seja, não dentro de uma expressão, mas, sim, usando atributos especiais do analisador. Em outras palavras, não há operador de atribuição ('=') para armazenar resultados intermediários. Eis a lista de operadores suportados com ordem de precedência de cálculos:

• !, - , + — negação lógica unária, menos e mais
• () — agrupamento usando colchetes
• *, /, % — multiplicação, divisão e módulo de divisão
• +, - — adição e subtração
• >, <, >=, <= — comparação mais-menos
• ==, != — comparação é igual ou diferente
• &&, || — E e OU lógicos (atenção, a prioridade é a mesma, são necessários colchetes)
• ?: — operador condicional ternário que permite desviar cálculos de acordo com condições

Além disso, permitimos que nas expressões sejam usadas funções matemáticas MQL padrão, que no total são 25. Dentre eles, em particular, existe uma função pow para exponenciação. Por esse motivo, na lista de operadores não existe um operador de exponenciação ('^'). Ademais, o operador '^' permite elevar apenas a uma potência inteira, já a função não está sujeita a essa restrição. Existe mais uma nuance que distingue o operador '^' dos outros considerados.

Acontece que entre as propriedades dos operadores existe uma que é chamada de associatividade que diz respeito à direção de execução de uma sequência de operadores com a mesma prioridade (em particular, do mesmo tipo), partindo da esquerda ou da direita. Em princípio, existem outros tipos de associatividade, mas eles estão fora do contexto da nossa tarefa atual.

Eis um exemplo de como a associatividade pode afetar o resultado de um cálculo.

1 - 2 - 3

Esta expressão não indica explicitamente a ordem em que as duas subtrações são realizadas usando parênteses. Como o operador '-' tem associatividade à esquerda, primeiro subtraímos 2 de 1 e, em seguida, 3 do intermediário -1 para obter -4, o que é equivalente a:

((1 - 2) - 3)

Se, hipoteticamente, o operador '-' tivesse associatividade à direita, as operações seriam realizadas na ordem inversa:

(1 - (2 - 3))

e obteríamos 2. Felizmente, o operador '-', contudo, possui associatividade à esquerda.

Consequentemente, a associatividade à esquerda ou à direita afeta as regras de análise de expressões e, portanto, complica o algoritmo. Entre os operadores binários listados, todos têm associatividade à esquerda e apenas '^', à direita.

Por exemplo, na expressão

3 ^ 2 ^ 5

primeiro 2 é elevado à potência de 5 e, em seguida, o 3 é elevado à potência de 32.

Para simplificar, faz sentido se livrar do operador de exponenciação (substituindo por pow) e implementar apenas algoritmos com a associatividade à esquerda. Os operadores unários são sempre associativos à direita e, portanto, são tratados de maneira uniforme.

Todos os números em nossas expressões (escritos como constantes e variáveis) serão do tipo real. Para saber se são iguais, definimos um valor de tolerância. Em expressões lógicas, os números são usados de acordo com um princípio simples: zero — false, diferente de zero — true.

Operadores bit a bit não são considerados. Não são suportadas matrizes.

Eis alguns exemplos de expressões:

• "1 + 2 * 3" — cálculos baseados na precedência das operações
• "(1 + 2) * 3" — agrupamento usando colchetes
• "(a + b) * c" — uso de variáveis
• "(a + b) * sqrt(1 / c)" — uso de função
• "a > 0 && a != b ? a : c" — cálculos com base em condições lógicas

As variáveis são identificadas por um nome dado segundo as regras usuais dos identificadores MQL: elas podem consistir em letras, números ou sublinhados e não podem começar com um número. Os nomes das variáveis não devem ser iguais aos nomes das funções integradas.

Analisaremos a string de entrada caractere por caractere. Verificações gerais de pertença de caracteres a um conjunto de letras ou números, tratamento de erros, configuração de variáveis e tabelas de funções embutidas (expansíveis conforme necessário) serão definidas na classe base da qual herdaremos todos os tipos de analisadores.

Vamos considerar todas as classes do analisador em sequência. Nos artigos elas são apresentadas com algumas simplificações. Os códigos-fonte completos estão anexados.

Classe base dos analisadores (modelo AbstractExpressionProcessor)

Esta classe é um modelo, pois o resultado da análise de uma expressão pode ser não apenas um valor escalar, mas também uma árvore de nós (objetos de uma classe especial) que descreve a sintaxe da expressão. Um pouco mais tarde, aprenderemos mais sobre como isso é feito e por que é necessário.

O objeto de classe armazena, em primeiro lugar, a expressão em si (_expression), seu comprimento (_length), a posição atual do cursor durante a leitura da linha (_index) e o caractere atual (_token). As variáveis também são reservadas como critério de erro na expressão (_failed) e de precisão ao comparar valores (_precision)

  template<typename T>
  class AbstractExpressionProcessor
  {
    protected:
      string _expression;
      int _index;
      int _length;
      ushort _token;
  
      bool _failed;
      double _precision;

Para armazenar variáveis e referências a funções, foram criadas as tabelas correspondentes, no entanto, iremos nos familiarizar com suas classes VariableTable e FunctionTable posteriormente.

      VariableTable *_variableTable;
      FunctionTable _functionTable;

Agora basta saber que as tabelas são mapas com pares "chave=valor", onde chave é uma string com o nome de uma variável ou função, e o valor é um valor double no caso de uma variável ou um objeto functor no caso de uma função.

A tabela de variáveis é descrita com uma referência, pois a expressão pode não conter variáveis. Já o conjunto mínimo de funções integradas no analisador está sempre presente (e pode ser estendido pelo usuário) e, portanto, a tabela de funções é representada por um objeto pronto.

O preenchimento da tabela de funções integradas é realizado no método:

      virtual void registerFunctions();

As seções a seguir descrevem funções que executam subtarefas comuns a vários analisadores, como ir para o próximo caractere, verificar se o caractere corresponde ao que era esperado (imprimindo um erro se não corresponder), ler sequencialmente dígitos que satisfaçam o formato de notação de números e vários métodos auxiliares estáticos para classificar caracteres.

      bool _nextToken();
      void _match(ushort c, string message, string context = NULL);
      bool _readNumber(string &number);
      virtual void error(string message, string context = NULL, const bool warning = false);
      
      static bool isspace(ushort c);
      static bool isalpha(ushort c);
      static bool isalnum(ushort c);
      static bool isdigit(ushort c);

Todas essas funções são definidas nesta classe base, em particular:

  template<typename T>
  bool AbstractExpressionProcessor::_nextToken()
  {
    _index++;
    while(_index < _length && isspace(_expression[_index])) _index++;
    if(_index < _length)
    {
      _token = _expression[_index];
      return true;
    }
    else
    {
      _token = 0;
    }
    return false;
  }
  
  template<typename T>
  void AbstractExpressionProcessor::_match(ushort c, string message, string context = NULL)
  {
    if(_token == c)
    {
      _nextToken();
    }
    else if(!_failed) // prevent chained errors
    {
      error(message, context);
    }
  }
  
  template<typename T>
  bool AbstractExpressionProcessor::_readNumber(string &number)
  {
    bool point = false;
    while(isdigit(_token) || _token == '.')
    {
      if(_token == '.' && point)
      {
        error("Too many floating points", __FUNCTION__);
        return false;
      }
      number += ShortToString(_token);
      if(_token == '.') point = true;
      _nextToken();
    }
    return StringLen(number) > 0;
  }

Ao analisar um número, a notação científica com expoente não é suportada.

Além deles, na classe é declarado o método principal evaluate que será sobrescrito nos descendentes. Aqui, ele apenas inicializa variáveis.

    public:
      virtual T evaluate(const string expression)
      {
        _expression = expression;
        _length = StringLen(_expression);
        _index = -1;
        _failed = false;
        return NULL;
      }

Este é o método principal da classe que recebe uma string com uma expressão como entrada e dá seu resultado de processamento: um valor específico se for realizado um cálculo, ou uma árvore de sintaxe se for realizada uma análise.

A interface pública da classe também contém construtores, nos quais, se necessário, podemos passar variáveis junto com seus valores (como uma string do tipo "name1=value1;name2=value2;..." ou como um objeto VariableTable pronto), métodos para definir tolerância ao comparar números, sinal de sucesso na análise (sem erros de sintaxe) e acesso às tabelas de variáveis e funções.

    public:
      AbstractExpressionProcessor(const string vars = NULL);
      AbstractExpressionProcessor(VariableTable &vt);
  
      bool success() { return !_failed; };
      void setPrecision(const double p) { _precision = p; };
      double getPrecision(void) const { return _precision; };
      virtual VariableTable *variableTable();
      virtual FunctionTable *functionTable();
  };

Observe que, mesmo se não houver erros de sintaxe, a avaliação da expressão pode terminar em erro (por exemplo, divisão por 0, raiz de um número negativo, etc.). Para controlar esse tipo de situações, deve-se verificar se o resultado é realmente um número com ajuda da função MathIsValidNumber. Nossos analisadores devem ser capazes de gerar os valores correspondentes para diferentes tipos de NaN (Not A Number) em vez de "falhar" no tempo de execução.

O mais fácil de aprender é o analisador descendente recursivo. Vamos começar com ele.

Analisador descendente recursivo (modelo ExpressionProcessor)

O analisador descendente recursivo é um conjunto de funções que são chamadas recursivamente umas das outras de acordo com as regras para cada operação individualmente. Se reduzirmos a sintaxe de várias das operações mais comuns numa gramática com notação BNF estendida (Extended Backus–Naur Form), a expressão poderá ser representada da seguinte forma (cada linha é uma regra separada):

  Expr    -> Sum
  Sum     -> Product { ('+' | '-') Product }
  Product -> Value { ('*' | '/') Value }
  Value   -> [0-9]+ | '(' Expr ')'

Na linguagem natural, essas regras são equivalentes a algo como o seguinte. A expressão começa a ser analisada com a operação de precedência mais baixa, neste exemplo, é adição/subtração. Soma (Sum) — dois operandos Product, separados por '+' ou '-', mas a operação em si e o segundo operando são opcionais. Produto (Product) — dois operandos Value, separados por '*' ou '/', mas novamente a operação e o segundo operando podem não estar presentes. Valor (Value) — número que consiste em dígitos ou uma expressão aninhada entre um par parênteses.

Por exemplo, a expressão "10" (apenas um número) será expandida na seguinte sequência de regras:

  Expr -> Sum -> Product -> Value -> 10

E a expressão "1 + 2 * 3" levará a uma construção mais complexa:

  Expr -> Sum -> Product -> Value -> 1
              |  '+'
              -> Product -> Value -> 2
                         |  '*'
                         -> Value -> 3

Como é fácil de ver, o algoritmo assume a varredura da gramática com correspondência entre o fluxo de entrada de caracteres e as regras de operações, com a particularidade de a varredura ser realizada a partir da regra principal (a expressão inteira) para componentes menores (até números individuais). O analisador descendente recursivo pertence à classe dos decrescentes (top-down).

No nosso analisador serão suportadas mais operações (consulte a lista na primeira seção), e cada uma delas tem um método reservado na classe derivada ExpressionProcessor.

  template<typename T>
  class ExpressionProcessor: public AbstractExpressionProcessor<T>
  {
    public:
      ExpressionProcessor(const string vars = NULL);
      ExpressionProcessor(VariableTable &vt);
      T evaluate(const string expression) override
      {
        AbstractExpressionProcessor<T>::evaluate(expression);
        if(_length > 0)
        {
          _nextToken();
          return _parse();
        }
        return NULL;
      }
      
    protected:
      T _parse();
      T _if();        // ?:
      T _logic();     // && ||
      T _eq();        // == !=
      T _compare();   // ><>=<=
      T _expr();      // +-
      T _term();      // */%
      T _unary();     // !-+
      T _factor();    // ()
      T _identifier();
      T _number();
      T _function(const string &name);
  };

Um exemplo de gramática EBNF de expressões serve como um guia para escrever o código dos métodos.

  expression -> if
  if         -> logic { '?' if ':' if }
  logic      -> eq { ('&&' | '||' ) eq }
  eq         -> compare { ('==' | '!=' ) compare }
  compare    -> expr { ('>' | '<' | '>=' | '<=') expr }
  expr       -> term  { ('+' | '-') term }
  term       -> unary { ('*' | '/' | '%') unary }
  unary      -> { ('!' | '-' | '+') } unary | factor
  factor     -> '(' if ')' | number | identifier
  identifier -> function | variable
  variable   -> name
  function   -> name '(' { arglist } ')'
  name       -> char { char | digit }*
  arglist    -> if { ',' if } 

O ponto descendente é o método _parse. Ele é chamado a partir do método público evaluate. Dada a precedência do operador, o método _parse transfere o controle para o "mais novo", _if. Depois de analisar toda a expressão, o caractere atual deve ser zero (critério de final de linha).

  template<typename T>
  T ExpressionProcessor::_parse(void)
  {
    T result = _if();
    if(_token != '\0')
    {
      error("Tokens after end of expression.", __FUNCTION__);
    }
    return result;
  }

O operador condicional ternário consiste em três subexpressões: uma condição booleana e duas variações de cálculo, para uma condição verdadeira e uma falsa. A condição booleana é o próximo nível da gramática: método _logic. Como as variações de cálculo podem, por sua vez, ser operadores ternários condicionais, chamamos recursivamente _if. Deve haver um '?' entre a condição e a variação verdadeira. Caso contrário, não é um operador ternário, e o algoritmo retornará o valor desde _logic tal como está. Se o sinal for '?', verificamos adicionalmente se o caractere ':' está entre as variações verdadeira e falsa. Quando todos os componentes estão presentes, verificamos a condição e retornamos o primeiro ou o segundo valor, dependendo da verdade.

  template<typename T>
  T ExpressionProcessor::_if()
  {
    T result = _logic();
    if(_token == '?')
    {
      _nextToken();
      T truly = _if();
      if(_token == ':')
      {
        _nextToken();
        T falsy = _if();
        return result ? truly : falsy; // NB: to be refined
      }
      else
      {
        error("Incomplete ternary if-condition", __FUNCTION__);
      }
    }
    return result;
  }

As operações lógicas E ou OU são apresentadas pelo método _logic. Nele, esperamos o aparecimento dos caracteres consecutivos "&&" ou "||" entre operandos que representam a comparação (método _eq). Se não houver operação booleana, o resultado será retornado diretamente desde o método _eq. Se ela existir, nós a calculamos. Graças ao ciclo while, o analisador pode realizar várias adições ou multiplicações lógicas numa linha, por exemplo "a > 0 && b > 0 && c > 0".

  template<typename T>
  T ExpressionProcessor::_logic()
  {
    T result = _eq();
    while(_token == '&' || _token == '|')
    {
      ushort previous = _token;
      _nextToken();
      if(previous == '&' && _token == '&')
      {
        _nextToken();
        result = _eq() && result;
      }
      else
      if(previous == '|' && _token == '|')
      {
        _nextToken();
        result = _eq() || result;
      }
      else
      {
        error("Unexpected tokens " + ShortToString(previous) + " and " + ShortToString(_token), __FUNCTION__);
      }
    }
    return result;
  }

Repare que "&&" e "||" nesta implementação são iguais e, portanto, ao gravar sequencialmente operações diferentes, é necessário indicar a ordem desejada usando parênteses.

As operações de comparação ('==', '!=') são tratadas de forma semelhante no método _eq.

  template<typename T>
  T ExpressionProcessor::_eq() 
  {
    T result = _compare();
    if(_token == '!' || _token == '=')
    {
      const bool equality = _token == '=';
      _nextToken();
      if(_token == '=')
      {
        _nextToken();
        const bool equal = fabs(result - _compare()) <= _precision; // NB: to be refined
        return equality ? equal : !equal;
      }
      else
      {
        error("Unexpected token " + ShortToString(_token), __FUNCTION__);
      }
    }
    return result;
  }

Para abreviar, pularemos alguns dos métodos do artigo, já aqueles que desejarem, podem se familiarizar com eles nos códigos-fonte anexados.

No método _factor, realmente chegamos aos operandos. Isso pode ser uma subexpressão entre parênteses, para ele é recursivamente chamado _if, um identificador ou um número (constante, literal).

  template<typename T>
  T ExpressionProcessor::_factor()
  {
    T result;
    
    if(_token == '(')
    {
      _nextToken();
      result = _if();
      _match(')', ") expected!", __FUNCTION__);
    }
    else if(isalpha(_token))
    {
      result = _identifier();
    }
    else
    {
      result = _number();
    }
    
    return result;
  }

Um identificador pode significar o nome de uma variável ou função se o nome for seguido por um parêntese aberto. Essa análise é tratada pelo método _identifier. No caso de uma função, o método especial _function encontra o objeto correspondente na tabela de funções _functionTable, analisa a lista de parâmetros (e cada um deles pode ser uma expressão independente e é obtido chamando recursivamente _if) e, em seguida, passa o controle para o objeto functor.

  template<typename T>
  T ExpressionProcessor::_identifier()
  {
    string variable;
  
    while(isalnum(_token))
    {
      variable += ShortToString(_token);
      _nextToken();
    }
    
    if(_token == '(')
    {
      _nextToken();
      return _function(variable);
    }
    
    return _variableTable.get(variable); // NB: to be refined
  }

O método _number simplesmente converte a sequência de dígitos lidos num número usando StringToDouble (a função auxiliar _readNumber foi apresentada acima).

  template<typename T>
  T ExpressionProcessor::_number()
  {
    string number;
    
    if(!_readNumber(number))
    {
      error("Number expected", __FUNCTION__);
    }
    return StringToDouble(number); // NB: to be refined
  }

Eis todo o analisador descendente recursivo. Está quase pronto para ser usado, porque a classe é um modelo e requer especialização com um tipo em particular. Para avaliar uma expressão a partir de variáveis de tipo numérico, basta especializar para double, algo assim:

  class ExpressionEvaluator: public ExpressionProcessor<double>
  {
    public:
      ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { }
      ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { }
  };

Mas, na prática, as coisas são um pouco mais complicadas. O algoritmo considerado avalia a expressão durante a análise. Ele é o modo intérprete, o mais simples, mas também o mais lento. Vamos imaginar que seja necessário calcular a mesma fórmula a cada tick para alterar os valores das variáveis (por exemplo, preços ou volumes). Para acelerar os cálculos, é bom separar os estágios de análise e execução de operações. Então, podemos analisar apenas uma vez, armazenar a estrutura da expressão em alguma representação intermediária otimizada para cálculos, e depois realizar um recálculo rápido com base nessa representação.

Para fazer isso, todos os resultados intermediários obtidos nos métodos considerados e passados ao longo da cadeia de chamadas recursivas até o retorno do valor final do método de avaliação público devem ser substituídos por objetos que armazenam a descrição dos operadores e operandos de um determinado fragmento da expressão (junto com todas as suas interligações) Com base nesta descrição, podemos calcular a expressão de forma diferida. Esses objetos são chamados de Promise (promessas).

Cálculos diferidos (Promise)

A classe Promise descreve uma entidade separada da composição de uma expressão: um operando ou uma operação junto com referências a operandos. Por exemplo, se um nome de variável for encontrado numa expressão, a linha será processada no método _identifier:

    return _variableTable.get(variable); // NB: to be refined

Ela retorna o valor atual de uma variável desde a tabela segundo seu nome. Ele é um valor double, que é adequado para o caso em que o analisador é especializado para o tipo double e executa cálculos em tempo real. No entanto, se quisermos adiar os cálculos, em vez do valor da variável, criamos um objeto Promise e armazenamos o nome da variável nele. No futuro, quando o valor de uma variável provavelmente mudar na tabela, devemos ser capazes de solicitar seu novo valor ao objeto Promise, e ele encontrará seu valor da mesma forma pelo nome. Assim, fica claro que a linha de código atual, marcada com o comentário "NB: to be refined", não é adequada para o caso geral do modelo ExpressionProcessor e deve ser substituída por algo. Na verdade, existem várias dessas linhas no ExpressionProcessor e em breve encontraremos uma solução uniforme para elas, mas primeiro veremos a classe Promise.

Existem vários campos na classe Promise para descrever um operando ou operação arbitrária.

  class Promise
  {
    protected:
      uchar code;
      double value;
      string name;
      int index;
      Promise *left;
      Promise *right;
      Promise *last;
      
    public:
      Promise(const uchar token, Promise *l = NULL, Promise *r = NULL, Promise *v = NULL):
        code(token), left(l), right(r), last(v), value(0), name(NULL), index(-1)
      {
      }
      Promise(const double v): // value (const)
        code('n'), left(NULL), right(NULL), last(NULL), value(v), name(NULL), index(-1)
      {
      }
      Promise(const string n, const int idx = -1): // name of variable
        code('v'), left(NULL), right(NULL), last(NULL), value(0), name(n), index(idx)
      {
      }
      Promise(const int f, Promise *&params[]): // index of function
        code('f'), left(NULL), right(NULL), last(NULL), value(0), name(NULL)
      {
        index = f;
        if(ArraySize(params) > 0) left = params[0];
        if(ArraySize(params) > 1) right = params[1];
        if(ArraySize(params) > 2) last = params[2];
        // more params not supported
      }

O campo de código armazena o atributo do tipo de elemento: 'n' é um número, 'v' é uma variável, 'f' é uma função e todos os outros caracteres são considerados como operações entre as permitidas (por exemplo, '+', '-', '*', '/', '%', etc.). No caso de um número, seu valor é armazenado no campo value. No caso de uma variável, seu nome é armazenado no campo name. Para acesso múltiplo rápido às variáveis, o Promise tentará após a primeira chamada armazenar em cache o número da variável no campo index e, em seguida, recuperá-lo desde a tabela por índice, não por nome. As funções são sempre identificadas por seu número no campo index, uma vez que ao contrário das variáveis, a tabela de funções é inicialmente preenchida com funções integradas e a tabela de variáveis ainda pode estar vazia no momento da análise da expressão.

As referências left, right e last são opcionais e podem conter operandos. Por exemplo, para números ou variáveis, todas as três referências são NULL. Para operações unárias, é usada apenas a referência left, para operações binárias, as referências left e right, e todas as três referências estão envolvidas apenas no operador condicional ternário: left contém a condição, rght é a expressão para a condição verdadeira e last é para a condição falsa. Além disso, as referências armazenam objetos-parâmetros de funções (a implementação atual do analisador limita o número de parâmetros de funções a três).

Como os objetos Promise estão envolvidos computacionalmente, substituiremos todos seus operadores básicos. Por exemplo, é assim que as operações de adição e subtração com "promessas" são tratadas.

      Promise *operator+(Promise *r)
      {
        return new Promise('+', &this, r);
      }
      Promise *operator-(Promise *r)
      {
        return new Promise('-', &this, r);
      }

O objeto atual (&this), ou seja, aquele à esquerda da operação na expressão e o objeto adjacente (r) à direita da operação são passados para o construtor de um novo objeto Promise criado com o código da operação correspondente.

Outras operações são tratadas da mesma maneira. Como resultado, a expressão inteira é mapeada para uma árvore de objetos da classe Promise, com a particularidade de o elemento raiz representar a expressão inteira. Para obter o valor real de qualquer objeto de "promessa", incluindo a expressão inteira, é fornecido o método resolve.

      double resolve()
      {
        switch(code)
        {
          case 'n': return value;        // number constant
          case 'v': value = _variable(); // variable name
                    return value;
          case 'f': value = _execute();  // function index
                    return value;
          default:  value = _calc();
                    return value;
        }
        return 0;
      };

Aqui se pode ver como o valor de uma constante numérica é retornado do campo value e os métodos auxiliares são implementados para variáveis, funções e operações.

      static void environment(AbstractExpressionProcessor<Promise *> *e)
      {
        variableTable = e.variableTable();
        functionTable = e.functionTable();
      }
      
    protected:
      static VariableTable *variableTable;
      static FunctionTable *functionTable;
  
      double _variable()
      {
        double result = 0;
        if(index == -1)
        {
          index = variableTable.index(name);
          if(index == -1)
          {
            return nan; // error: Variable undefined
          }
          result = variableTable[index];
        }
        else
        {
          result = variableTable[index];
        }
        return result;
      }
      
      double _execute()
      {
        double params[];
        if(left)
        {
          ArrayResize(params, 1);
          params[0] = left.resolve();
          if(right)
          {
            ArrayResize(params, 2);
            params[1] = right.resolve();
            if(last)
            {
              ArrayResize(params, 3);
              params[2] = last.resolve();
            }
          }
        }
        IFunctor *ptr = functionTable[index]; // TBD: functors
        if(ptr == NULL)
        {
          return nan; // error: Function index out of bound 
        }
        return ptr.execute(params);
      }
      
      double _calc()
      {
        double first = 0, second = 0, third = 0;
        if(left)
        {
          first = left.resolve();
          if(right)
          {
            second = right.resolve();
            if(last)
            {
              third = last.resolve();
            }
          }
        }
        
        switch(code)
        {
          case '+': return first + second;
          case '-': return first - second;
          case '*': return first * second;
          case '/': return safeDivide(first, second);
          case '%': return fmod(first, second);
          case '!': return !first;
          case '~': return -first;
          case '<': return first < second;
          case '>': return first > second;
          case '{': return first <= second;
          case '}': return first >= second;
          case '&': return first && second;
          case '|': return first || second;
          case '`': return _precision < fabs(first - second); // first != second;
          case '=': return _precision > fabs(first - second); // first == second;
          case '?': return first ? second : third;
        }
        return nan; // error: Unknown operator
      }

Aqui o tratamento de erros é omitido; se ocorrerem, será retornado um valor nan especial ("não é um número", a geração é movida para um arquivo de cabeçalho separado NaNs.mqh, ele pode ser estudado individualmente). Observe que a execução das operações é precedida por uma chamada recursiva para resolve em todos os objetos abaixo na hierarquia por referências. Assim, a chamada de resolve na expressão inicia o cálculo sequencial de todas as "promessas" associadas e à posterior transferência "para cima" dos resultados dos cálculos, já na forma de números double. No final, eles desabam no valor final da expressão.

Com a classe Promise podemos especializar o analisador descendente recursivo que retorna, como resultado do processamento, uma árvore de objetos semelhantes, ou seja, na verdade, uma árvore sintática de uma expressão.

Em todos os métodos da classe de modelo ExpressionProcessor, onde é retornado um certo T, ele deve ser igual a (Promise *). Em particular, no método _identifier, onde prestamos atenção à linha

    return _variableTable.get(variable); // NB: to be refined

deve-se de alguma forma garantir que, em vez de um double, possa ser criado e retornado um novo objeto Promise apontando para uma variável chamada variable.

Para resolver esse problema, seria necessário "envolver" a ação de retorno de um valor do tipo T para uma variável num método virtual separado que nas classes derivadas de ExpressionProcessor<double> e ExpressionProcessor<Promise *> realizaria as diferentes manipulações necessárias. Mas há um pequeno problema aqui.

Classe ExpressionHelper

Planejamos implementar várias classes de analisadores, todas herdadas de AbstractExpressionProcessor. Mas os métodos específicos para descida recursiva não são necessários em todas elas e em diferentes ramos da hierarquia de herança. Seria possível substituí-los por vazios onde eles não são necessários, mas isso não é muito bom do ponto de vista OOP. Se a MQL suportasse herança múltipla, poderíamos usar uma característica especial (trait), um conjunto adicional de métodos que podem ser incluídos na classe do analisador, se necessário. Como isso não é possível, projetaremos todos os métodos relevantes como uma classe de modelo separada e criaremos uma instância dela apenas nos analisadores em que for necessário.

  template<typename T>
  class ExpressionHelper
  {
    protected:
      VariableTable *_variableTable;
      FunctionTable *_functionTable;
  
    public:
      ExpressionHelper(AbstractExpressionProcessor<T> *owner): _variableTable(owner.variableTable()), _functionTable(owner.functionTable()) { }
  
      virtual T _variable(const string &name) = 0;
      virtual T _literal(const string &number) = 0;
      virtual T _negate(T result) = 0;
      virtual T _call(const int index, T &args[]) = 0;
      virtual T _ternary(T condition, T truly, T falsy) = 0;
      virtual T _isEqual(T result, T next, const bool equality) = 0;
  };

Aqui são coletadas todas as ações que são processadas de forma diferente em cálculos imediatos e diferidos. Em particular, o método _variable é responsável pelo acessa à variáveis nas quais nos concentramos anteriormente. _literal obtém o valor de uma constante, _negate faz a negação lógica, _call é uma chamada de função, _ternary é um operador condicional e _isEqual é usado para comparar magnitudes. Todos os outros casos de cálculos são tratados para double e Promise com a mesma sintaxe, substituindo os operadores na classe Promise.

Alguém pode se perguntar por que o operador lógico de negação '!' não foi substituído no Promise e, em vez disso, foi exigido o método _negate. A questão é que o operador '!' se aplica apenas a objetos, não a ponteiros. Em outras palavras, se tivermos uma variável do tipo Promise *p, não podemos escrever habitualmente !p na esperança de que o operador substituído funcione. Em vez disso, é preciso primeiro desreferenciar o ponteiro: !*p. E tal notação se torna inválida para outros tipos, em particular para T=double.

É assim que os métodos ExpressionHelper podem ser implementados para números double.

  class ExpressionHelperDouble: public ExpressionHelper<double>
  {
    public:
      ExpressionHelperDouble(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { }
  
      virtual double _variable(const string &name) override
      {
        if(!_variableTable.exists(name))
        {
          return nan;
        }
        return _variableTable.get(name);
      }
      virtual double _literal(const string &number) override
      {
        return StringToDouble(number);
      }
      virtual double _call(const int index, double &params[]) override
      {
        return _functionTable[index].execute(params);
      }
      virtual double _isEqual(double result, double next, const bool equality) override
      {
        const bool equal = fabs(result - next) <= _precision;
        return equality ? equal : !equal;
      }
      virtual double _negate(double result) override
      {
        return !result;
      }
      virtual double _ternary(double condition, double truly, double falsy) override
      {
        return condition ? truly : falsy;
      }
  };

Eis como são implementados para Promise.

  class ExpressionHelperPromise: public ExpressionHelper<Promise *>
  {
    public:
      ExpressionHelperPromise(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { }
  
      virtual Promise *_negate(Promise *result) override
      {
        return new Promise('!', result);
      }
      virtual Promise *_call(const int index, Promise *&params[]) override
      {
        return new Promise(index, params);
      }
      virtual Promise *_ternary(Promise *condition, Promise *truly, Promise *falsy) override
      {
        return new Promise('?', condition, truly, falsy);
      }
      virtual Promise *_variable(const string &name) override
      {
        if(CheckPointer(_variableTable) != POINTER_INVALID)
        {
          int index = _variableTable.index(name);
          if(index == -1)
          {
            return new Promise(nan); // error: Variable is undefined
          }
          return new Promise(name, index);
        }
        return new Promise(name);
      }
      virtual Promise *_literal(const string &number) override
      {
        return new Promise(StringToDouble(number));
      }
      virtual Promise *_isEqual(Promise *result, Promise *next, const bool equality) override
      {
        return new Promise((uchar)(equality ? '=' : '`'), result, next);
      }
  };

Agora podemos adicionar um campo helper a AbstractExpressionProcessor:

    protected:
      ExpressionHelper<T> *helper;
      
    public:  
      ~AbstractExpressionProcessor()
      {
        if(CheckPointer(helper) == POINTER_DYNAMIC) delete helper;
      }

e revisitar a implementação dos métodos ExpressionProcessor, que tinham strings marcadas com "NB" — eles deveriam delegar operações ao objeto helper. Por exemplo, assim:

  template<typename T>
  T ExpressionProcessor::_eq()
  {
    T result = _compare();
    if(_token == '!' || _token == '=')
    {
      const bool equality = _token == '=';
      _nextToken();
      if(_token == '=')
      {
        _nextToken();
        return helper._isEqual(result, _compare(), equality); // OK
      }
    }
    return result;
  }
  
  template<typename T>
  T ExpressionProcessor::_identifier()
  {
    string variable;
    while(isalnum(_token))
    {
      variable += ShortToString(_token);
      _nextToken();
    }
    ...
    return helper._variable(variable); // OK
  }
  
  template<typename T>
  T ExpressionProcessor::_number()
  {
    string number;
    if(!_readNumber(number))
    {
      error("Number expected", __FUNCTION__);
    }
    return helper._literal(number); // OK
  }

Com a ajuda das classes apresentadas, podemos finalmente montar o primeiro analisador que realiza cálculos no processo de análise de expressões, ExpressionEvaluator.

  class ExpressionEvaluator: public ExpressionProcessor<double>
  {
    public:
      ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperDouble(&this); }
      ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperDouble(&this); }
  };

E aqui temos um segundo analisador para cálculos diferidos, ExpressionCompiler.

  class ExpressionCompiler: public ExpressionProcessor<Promise *>
  {
    public:
      ExpressionCompiler(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperPromise(&this); }
      ExpressionCompiler(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperPromise(&this); }
      
      virtual Promise *evaluate(const string expression) override
      {
        Promise::environment(&this);
        return ExpressionProcessor<Promise *>::evaluate(expression);
      }
  };

As principais diferenças estão apenas nos objetos do campo helper e na chamada preliminar de Promise::environment para transferir tabelas de variáveis e funções dentro de Promise.

Para obter um analisador totalmente funcional, resta só tratar das tabelas de variáveis e funções.

Tabelas de variáveis e funções

Ambas as tabelas são classes de modelo de mapas que consistem em pares "chave=valor", onde a chave é um identificador de string e o valor é algum valor do tipo T. Sua implementação pode ser encontrada no arquivo VariableTable.mqh. A classe base descreve todas as operações com mapas exigidas: adição de elementos, alteração de valores e recuperação por nome ou índice.

  template<typename T>
  class Table
  {
    public:
      virtual T operator[](const int index) const;
      virtual int index(const string variableName);
      virtual T get(const string variableName) const;
      virtual int add(const string variableName, T value);
      virtual void update(const int index, T value);
      ...
  };

No caso de variáveis, o tipo T é double.

  class VariableTable: public Table<double>
  {
    public:
      VariableTable(const string pairs = NULL)
      {
        if(pairs != NULL) assign(pairs);
      }
      
      void assign(const string pairs);
  };

Por meio do método de atribuição, as variáveis podem ser adicionadas à tabela não apenas uma de cada vez, mas também logo como uma lista, como uma string como "nome1=valor1;nome2=valor2;...".

Para funções, precisamos criar uma interface functor especial contendo o código para calcular as funções.

  interface IFunctor
  {
    string name(void) const;
    int arity(void) const;
    double execute(const double &params[]);
  };

Cada função possui um nome e uma propriedade que descreve o número de argumentos (aridade). A função é avaliada pelo método execute que recebe argumentos. Todas as funções matemáticas MQL integradas precisarão ser agrupadas nesta interface e, em seguida, adicionar os objetos correspondentes à tabela (um por um ou numa matriz):

  class FunctionTable: public Table<IFunctor *>
  {
    public:
      void add(IFunctor *f)
      {
        Table<IFunctor *>::add(f.name(), f);
      }
      void add(IFunctor *&f[])
      {
        for(int i = 0; i < ArraySize(f); i++)
        {
          add(f[i]);
        }
      }
  };

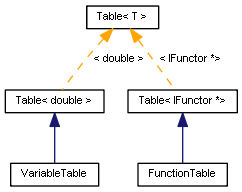
Diagrama de classes de tabelas de variáveis e funções

Para armazenar todos os functores é definida uma classe repositório.

  class AbstractFuncStorage
  {
    protected:
      IFunctor *funcs[];
      int total;
      
    public:
      ~AbstractFuncStorage()
      {
        for(int i = 0; i < total; i++)
        {
          CLEAR(funcs[i]);
        }
      }
      void add(IFunctor *f)
      {
        ArrayResize(funcs, total + 1);
        funcs[total++] = f;
      }
      void fill(FunctionTable &table)
      {
        table.add(funcs);
      }
  };

O método fill permite preencher a tabela passada para ela com funções integradas do repositório (matriz funcs). Para que todos os functores criados entrem automaticamente no armazenamento, nós os tornamos uma instância estática dentro da classe base das funções AbstractFunc e a preenchemos com referências a this desde o construtor.

  class AbstractFunc: public IFunctor
  {
    private:
      const string _name;
      const int _arity;
      static AbstractFuncStorage storage;
  
    public:
      AbstractFunc(const string n, const int a): _name(n), _arity(a)
      {
        storage.add(&this);
      }
      string name(void) const override
      {
        return _name;
      }
      int arity(void) const override
      {
        return _arity;
      }
      static void fill(FunctionTable &table)
      {
        storage.fill(table);
      }
  };
  
  static AbstractFuncStorage AbstractFunc::storage;

Obviamente, o construtor usa parâmetros de entrada para definir o nome e a aridade da função.

Para a declaração de funções de aridade específica, foi introduzida uma classe de modelo intermediária FuncN, na qual a aridade é definida pelo tamanho do tipo passado (uma vez que a aridade das funções não excede 3 para nós ainda, e não há tipos com tamanho zero, a notação sizeof(T) % 4 é usada, portanto, o tamanho 4 dará aridade 0).

  template<typename T>
  class FuncN: public AbstractFunc
  {
    public:
      FuncN(const string n): AbstractFunc(n, sizeof(T) % 4) {}
  };

Os próprios tipos com tamanhos de 0 a 3 são gerados usando macros.

  struct arity0 { char x[4]; };
  
  #define _ARITY(N)   struct arity##N { char x[N]; };
  
  _ARITY(1);
  _ARITY(2);
  _ARITY(3);

Também precisamos de listas de argumentos para automatizar a geração de descrições de funções.

  #define PARAMS0 
  #define PARAMS1 params[0]
  #define PARAMS2 params[0],params[1]
  #define PARAMS3 params[0],params[1],params[2]

Agora podemos definir uma macro para um functor baseado na classe FuncN<T>.

  #define FUNCTOR(CLAZZ,NAME,ARITY) \
  class Func_##CLAZZ: public FuncN<arity##ARITY> \
  { \
    public: \
      Func_##CLAZZ(): FuncN(NAME) {} \
      double execute(const double &params[]) override \
      { \
        return CLAZZ(PARAMS##ARITY); \
      } \
  }; \
  Func_##CLAZZ __##CLAZZ;

E, finalmente, uma lista de funções suportados com nomes e número de argumentos.

  FUNCTOR(fabs, "abs", 1);
  FUNCTOR(acos, "acos", 1);
  FUNCTOR(acosh, "acosh", 1);
  FUNCTOR(asin, "asin", 1);
  FUNCTOR(asinh, "asinh", 1);
  FUNCTOR(atan, "atan", 1);
  FUNCTOR(atanh, "atanh", 1);
  FUNCTOR(ceil, "ceil", 1);
  FUNCTOR(cos, "cos", 1);
  FUNCTOR(cosh, "cosh", 1);
  FUNCTOR(exp, "exp", 1);
  FUNCTOR(floor, "floor", 1);
  FUNCTOR(log, "log", 1);
  FUNCTOR(log10, "log10", 1);
  FUNCTOR(fmax, "max", 2);
  FUNCTOR(fmin, "min", 2);
  FUNCTOR(fmod, "mod", 2);
  FUNCTOR(pow, "pow", 2);
  FUNCTOR(rand, "rand", 0);
  FUNCTOR(round, "round", 1);
  FUNCTOR(sin, "sin", 1);
  FUNCTOR(sinh, "sinh", 1);
  FUNCTOR(sqrt, "sqrt", 1);
  FUNCTOR(tan, "tan", 1);
  FUNCTOR(tanh, "tanh", 1);

O diagrama de classes dos functores numa forma generalizada fica assim.

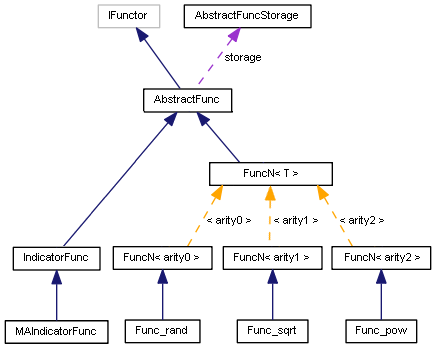
Diagrama de classe de functores

Aqui não são mostradas todas as funções, mas, sim, apenas uma de cada aridade. Existem também algumas classes que veremos mais tarde.

Com as funções em mente, tudo está pronto para usar os dois analisadores descendentes recursivos. Um é capaz de avaliar expressões no modo de interpretação, enquanto o outro, a partir de sua árvore de sintaxe.

Avaliação de expressões em tempo real (ExpressionEvaluator)

A maneira como o interpretador avalia uma expressão é realizada da seguinte maneira: criamos uma instância ExpressionEvaluator, passamos variáveis para ela se necessário e chamamos o método de avaliação com uma string contendo a expressão necessária.

  ExpressionEvaluator ee("a=-10");
  double result = ee.evaluate("1 + sqrt(a)"); // -nan(ind)
  bool success = ee.success();                // true

O método de success pode ser usado para verificar se sintaxe da expressão está certa, mas não garante que nenhum erro ocorrerá durante o cálculo. No exemplo acima, extrair a raiz de uma variável negativa retornará um resultado NaN. Portanto, é recomendável sempre verificar o resultado usando a função MathIsValidNumber.

Depois de desenvolver outros tipos de analisadores, escreveremos testes que demonstrarão as técnicas com mais detalhes.

"Compilação" de expressões numa árvore de sintaxe e computação com base na árvore (ExpressionCompiler)

A avaliação de uma expressão através da construção de uma árvore de sintaxe é realizada da seguinte maneira: criamos uma instância de ExpressionCompiler, passamos variáveis iniciais se necessário e chamamos o método de avaliação com uma string contendo a expressão necessária. Como resultado, obtemos uma referência ao objeto Promise, para o qual precisamos chamar resolve a fim de avaliar a expressão e obter um número. Parece mais complicado, mas funciona muito mais rápido quando é preciso realizar vários cálculos para diferentes valores de variáveis.

  double a[10] = {...}, b[10] = {...}, c[10] = {...};
  
  VariableTable vt;
  ExpressionCompiler с(vt);
  vt.adhocAllocation(true);
  const string expr = "(a + b) * sqrt(c)";
  Promise *p = c.evaluate(expr);
  
  for(int i = 0; i < 10; i++)
  {
    vt.set("a", a[i]);
    vt.set("b", b[i]);
    vt.set("c", c[i]);
    Print(p.resolve());
  }

Neste exemplo, é inicialmente criada uma tabela de variáveis vazia, na qual os valores alterados para as variáveis a, b, c são escritos dentro de um ciclo. O método adhocAllocation usado aqui, que omitimos ao estudar as classes da tabela, define um sinalizador instruindo o analisador a aceitar e reservar qualquer nome de variável na tabela no estágio de análise e geração de árvore. Qualquer variável implícita é definida como nan, portanto, o código que chama deve ter o cuidado de defini-la com valores reais antes de calcular a "promessa".

Se no exemplo mostrado não chamarmos vt.adhocAllocation(true) antes de c.evaluate, todas as variáveis encontradas na expressão irão gerar erros, uma vez que por padrão, assume-se que as variáveis devem ser descritas com antecedência e a tabela está vazia. Você pode verificar se há erros em seu código chamando c.success() após c.evaluate(). Erros também são registrados no log.

Como com o interpretador, o método de avaliação retornará algum resultado de qualquer maneira. Portanto, se as variáveis não forem conhecidas no estágio de análise, na árvore serão criados nós com o valor nan. Computação nessa árvore não faz sentido, já que também dará nan. Mas a presença de uma árvore nos permite entender qual é o problema. A classe Promise tem um método auxiliar para imprimir a árvore, print.

Fim do artigo

Neste artigo, vimos os fundamentos da análise de expressões matemáticas e criamos dois analisadores MQL prontos para serem utilizados. A esta primeira parte está anexado um pequeno script de teste que permite usar esta abordagem de forma independente em programas próprios. Continuaremos a explorar outros tipos de analisadores na segunda parte, compararemos seus desempenhos e exemplificaremos como aplicá-los para resolver as tarefas do trader.