
Discretización de series temporales con generación aleatoria de "ruidos"
Introducción
El método clásico de representación de los movimientos de precio en forma de segmentos temporales surgió en los albores de los mercados financieros, cuando aún no existían las computadoras y todo el comercio tenía lugar en mercados reales y con mercancías reales. Guardar cada cambio de precio durante el día resultaba complicado, y además no tenía sentido, ya que los precios no cambiaban tan rápido. Por eso, resultaba obvio que había que registrar el valor del precio en ciertos intervalos temporales. Es lógico: "hoy el trigo cuesta 50 rublos, y ayer costaba 49". Todo está muy claro: hoy la demanda ha crecido, y la mercancía ha aumentado de precio. Según las medidas actuales, se hacían pocas transacciones, y eso significa que, por consiguiente, el precio se redefinía con relativa poca frecuencia.
Conforme se ha ido desarrollando el análisis de datos, en un intento de mejorar el pronóstico del comportamiento de los precios, y con el aumento del número de las transacciones comerciales, la gente ha empezado a considerar importante comprender qué precio ha sido el máximo y el mínimo en un intervalo temporal determinado. Es decir, ahora ya no basta con conocer el precio de ayer, 49 rublos, y el de hoy, 50 rublos: necesitamos saber qué valores máximos y mínimos ha tenido el precio en un intervalo temporal establecido. Es decir, en su día, surgió una cierta necesidad, que tuvo como respuesta la invención de las velas y barras que usamos hasta día de hoy.
A medida que ha ido aumentando el número de operaciones comerciales, la discretización de la serie de precios se ha ido haciendo más precisa: ahora se usa ya la discretización por minutos, y algunos utilizan escalas aún menores, como los marcos de segundos o decenas de segundos, todo depende de las necesidades.
Las principales ventajas de la discretización temporal de la serie de precios son:
- Su comodidad. Sabemos exactamente que dentro de un minuto se formará la barra siguiente, y obtendremos los nuevos valores de los precios de apertura, cierre, mínimo y máximo.
- Ahorro de recursos. Los datos presentados en forma de veas, permiten guardar en un intervalo temporal solo 4 dígitos, si no requerimos de una gran precisión. Si guardamos cada cambio del precio bid, ask, last, la historia acumulada de un año tendrá un volumen considerable, de varios gigabytes, y en algunos casos, de decenas de gigabytes. Y si tenemos que guardar (descargar) la historia de varios años, digamos 10-20, y de varios instrumentos, digamos 200-500, esto se convertirá en un problema. Además, el procesamiento de gigabytes de historia para el análisis requiere de recursos computacionales significativos. Por eso, el análisis y el procesamiento de las velas resulta más atractivo.
- Escalado sencillo y análisis visual. Si deseamos obtener una panorámica general, podemos aumentar la escala de discretización hasta varias semanas o incluso meses, y tendremos acceso en el monitor a los cambios de precio de todos los años que necesitemos. Pero si necesitamos precisión, reduciremos la escala de discretización y veremos qué ha sucedido dentro de un minuto.
- Linealidad temporal. Posiblemente, lo más cómodo en esta representación sea que, de manera visual, la historia de cada año ocupe aproximadamente el mismo espacio en la pantalla. Así, resultará más cómodo e intuitivo encontrar en el gráfico el año pasado, la hora anterior, etcétera. A un nivel intuitivo, la linealidad temporal nos parece un parámetro muy importante, pero hay casos en los que las decisiones "correctas" son contrarias a la intuición.
- La sencillez de comparación de los precios de diferentes instrumentos en un momento temporal.
Peculiaridades de la discretización de las señales
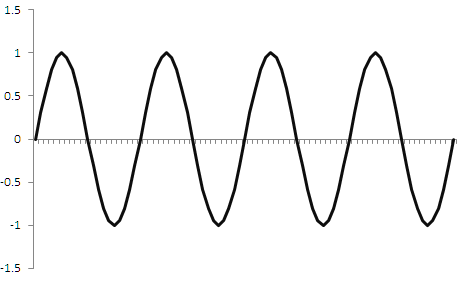
La necesidad de discretizar los datos existe no solo en el trading, sino también en otras muchas esferas del procesamiento de señales. Por ejemplo, cuando usted escucha música, la melodía ha sido inicialmente digitalizada a partir de una señal continua. La señal se digitaliza con la ayuda de la discretización temporal. Es decir, el valor de amplitud de la señal se toma cada cierto intervalo temporal y se registra en la memoria. A continuación, esta señal se puede transformar en señal continua con la ayuda ciertas manipulaciones. La esfera de la discretización de señales continuas ha sido investigada a fondo durante mucho tiempo. En concreto, existe una regla que se infiere del teorema de Kotélnikov (Nyquist-Shannon): Una señal se puede restaurar por completo si la frecuencia de discretización es 2 o más veces superior a la frecuencia de la señal. Esto significa que si tenemos una frecuencia de señal de 1 hercio, el valor de su amplitud se deberá comprobar como mínimo 2 veces por segundo (es decir, con una frecuencia de 2 hercios), solo entonces, después de la discretización, podremos obtener su forma original. En la figura 1, más abajo, mostramos qué sucederá si discretizamos una sinusoide con una frecuencia de 1 hercio, con una frecuencia de muestreo de 2 hercios. En color verde, se muestra la propia señal, mientras que en rojo se muestra qué resulta tras la discretización.
Figura 1.
Después de la discretización, obtendremos una señal de forma triangular a partir de la sinusoide. Claro que existe un cierto nivel de error, pero, con la ayuda de varios filtros de baja frecuencia, podemos transformar de forma inversa esta señal triangular en un seno. Es decir, resulta posible restaurar la señal original, y además conservar el sentido original, el periodo y la amplitud, con cierto margen de error. Si bien para la música estas divergencias se consideran críticas, en el trading no pasa nada. Pero, ¿qué sucederá si la frecuencia de discretización es inferior a la frecuencia de la señal original? Mostramos un ejemplo en la figura 2, más abajo.
 ---->>
---->> 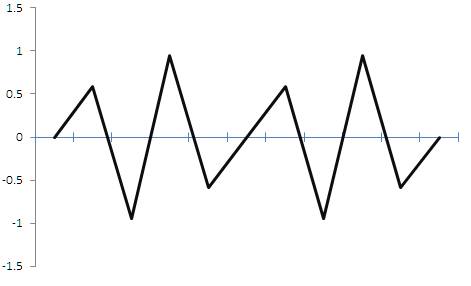
Figura 2.
En la figura podemos ver que si la frecuencia de discretización es inferior al doble de la frecuencia de la frecuencia de la señal, esta se distorsionará significativamente, obteniendo como resultado en la salida, en esencia, una señal aleatoria que no tiene nada que ver con la señal original. Si aplicamos lo dicho al trading, en el primer caso, podríamos vender cuando encontremos un máximo, y comprar cuando veamos un mínimo. Además, hemos averiguado la periodicidad, pero, después de realizar la discretización de forma "incorrecta", hemos perdido información tanto sobre la amplitud, como sobre la peridodicidad de la señal. Así, a partir de una señal periódica determinada con características conocidas hemos obtenido una señal no periódica aleatoria con características desconocidas, con solo cometer un error de selección de la frecuencia de discretización.
Sabiendo todo esto, lo lógico es que nos surjan 2 preguntas: "¿no habremos cometido un error al realizar la discretización de la serie de precios?" y "¿la serie de precios es una señal discreta o continua, y cuáles serían sus parámetros?"
La respuesta no es tan simple como puede parecer a primera vista, pero es muy importante.
¿Una serie de precios es discreta o continua?
Solo es posible responder a esta pregunta conociendo el mecanismo de formación de los precios de mercado. No vamos a describirlo, es de suponer que el lector estará al tanto, si no, le recomendamos el artículo: "Principios de formación de precios en el mercado bursátil tomando de ejemplo la Sección de Derivados de la Bolsa de Moscú". En la profundidad de mercado, algunos participantes colocan sus solicitudes, y después otros compran el volumen necesario al precio necesario, así se forma el gráfico de precios. Los propios niveles resultan discretos, es decir, podemos colocar una solicitud al precio 1, 2, 3, etcétera, con cierta precisión. El volumen colocado en las solicitudes y adquirido por los compradores también es discreto, porque podemos comprar 1,2,3 unidades de la mercancía, etcétera. En la figura 3, se muestra como ejemplo una profundidad de mercado: podemos ver que los precios y los volúmenes tienen valores discretos.
Figura 3.
De aquí, podemos sacar la siguiente conclusión: en sí, el gráfico de la serie de precios tiene un carácter discreto. El precio se desplaza por niveles discretos después de que los participantes compren valores de volumen discretos.
De qué supone una función el precio
Hemos aclarado que la serie de precios es discreta en sí, pero, ¿de qué parámetro es función el cambio de precio?
Discretizar una señal sonora a intervalos temporales iguales resulta una solución aceptable, porque una función sonora supone una función que cambia con el tiempo. En sí misma, una señal es una amplitud que depende del tiempo, y esta propiedad en ella es fundamental. Precisamente por eso, aquí no hay ningún problema.
La naturaleza de la serie de precios es otra; aquí, si bien la amplitud (el precio) cambia con el tiempo, no es este la causa que propicia dicho cambio. Si nos paramos a pensar cuál es el motivo del cambio de precio, la cuestión ya no parece tan sencilla. Solo podemos hacer varias suposiciones:
- El precio como función de las operaciones comerciales. Aquí, el precio cambia a causa de las operaciones comerciales realizadas, ya que son precisamente estas las que mueven el precio. Pero las operciones comerciales también pueden no provocar ningún cambio de precio. Por ejemplo, tenemos 10 acciones disponibles a un precio de 5 rublos por acción, un participante compra 4 acciones, y quedan 6 acciones disponibles al precio mencionado, por consiguiente, se ha realizado una operación comercial, pero el precio no ha cambiado. En este caso, además, dicha operación ha reducido el volumen disponible a ese precio, y podría provocar un cambio posterior en los precios, cuando el siguiente participante compre todo el volumen a este precio. Los precios solo cambian cuando el volumen de acciones disponibles a 5 rublos no ha sido suficiente para satisfacer la demanda y se ha comprado todo el volumen a un precio de 5 rublos. En este caso, el precio de ASK se desplazará 6 rublos, pero aun así, los demás participantes tendrán la posibilidad de colocar otra solicitud a 5 rublos y devolver el precio de ASK a su anterior lugar.
- El precio como función de todas las operaciones realizadas en el mercado. El precio puede cambiar no solo porque los participantes compren todo el volumen a un nivel determinado, sino también porque quiten sus solicitudes y las recoloquen en otros niveles. Así, no habrá operaciones comerciales, y los precios de BID y ASK se desplazarán.
- El precio como función del "beneficio". El precio también puede cambiar porque los participantes redefinan para sí mismos el precio del activo. No obstante, los motivos de la redefinición del precio de un activo pueden ser muy distintos. En cualquier caso, la redefinición del precio de un activo está estrechamente relacionada con el provecho de los participantes. En teoría, el precio establecido será provechoso al máximo para todo el conjunto de los participantes, tanto los compradores, como los vendedores (incluso si dicho beneficio es negativo). En sus inicios, el mercado se creó precisamente para maximizar el provecho y definir un precio óptimo y equilibrado que conviniera tanto a los compradores, como a los vendedores. Este provecho, además, puede incluso no estar relacionado con un activo en concreto. Por ejemplo, algún fondo de inversión necesita urgentemente salir de un activo, y está listo para hacerlo, incluso sufriendo pérdidas con este, por eso, considera que, realizando esta operación, obtendrá algún otro provecho, posiblemente comprando otro activo o incluso pagando beneficios a sus clientes. La naturaleza del provecho puede ser extraordinariamente variada. En este caso, el precio es precisamente la función de cada redefinición del provecho de cada participante.
- El precio como función de sí mismo. Obviamente, cada cambio de precio modifica el provecho que saca de él cada participante de las transacciones. El provecho también puede cambiar sin que lo haga el precio, pero cuando el precio cambia, el provecho de los participantes cambia. Puede que no sea el método más exacto para describir los cambios de precio, pero permite acercarse a grandes rasgos a un modelo ideal, y también hacer varios supuestos que, en lo sucesivo, no influirán significativamente en el resultado. Nosotros comerciamos principalmente con los cambios de precio, e incluso si seleccionamos las estrategias de dividendos (sin prestar ninguna atención al precio), al final, el pago de dividendos redundará en un cambio de los precios. Aquí, el cambio del precio será precisamente la señal para desplazar el gráfico hacia la izquierda. Registramos el cambio de precio solo en el momento en el que este se desplaza un punto. El salto puede ser cualquiera, dependerá de la escala preferida; podemos registrar el valor del precio cada vez que este se desplace n puntos en vertical.
Nosotros considereamos más probable una tercera opción: que el precio sea una función de redefinición del provecho. Pero resulta imposible calcular el provecho de cada participante para la discretización de la serie de precios. En los dos primeros casos, existe una posibilidad real de calcular las operaciones comerciales y no comerciales en los mercados bursátiles, pero también pueden surgir complicaciones. Por ejemplo, un activo puede comerciarse en dos o más bolsas distintas, o puede resultar que en un activo básico existen instrumentos derivados, tales como futuros u opciones: en dichos casos, decidir si calcular o no todas las operaciones relacionadas indirectamente con un activo es una cuestión importante, y requiere de una ingente investigación. En cualquier caso, los cuatro casos están indirectamente interrelacionados, y la cuarta opción, en la que el precio es una función de sí mismo, nos permite seguir investigando apoyándonos en la suposición de que este será un modelo menos preciso.
La velocidad de cambio del precio de un activo depende exactamente del número de operaciones comerciales. Cuantas más operaciones comerciales haya, con mayor frecuencia cambiará el precio: es decir, aquí existe una correlación directa. Por consiguiente, cuantos más participantes haya en el mercado, más operaciones realizarán y con mayor frecuencia se redefinirá el provecho para cada participante, y, por ende, cada participante tratará de redefinir con más frecuencia el precio, lo cual redundará en un mayor número de operaciones y una mayor frecuencia en el cambio de precio de los activos.
Peculiaridades de la discretización de la serie de precios según los segmentos temporales y el componente aleatorio
Tomaremos como modelo de baja precisión el precio como función de sí mismo, es decir, discretizaremos el precio solo cuando este cambie en un número determinado de puntos. Incluso de no ser así, esta suposición nos permitirá descubrir posteriormente el sentido del tema, sin influir significativamente en el resultado final. Asimismo, para ganar dinero, nos interesa precisamente el hecho de que el precio haya cambiado, y, a la hora de buscar patrones, resulta importante saber cómo ha cambiado.
Cada cambio de precio en 1 punto (entendemos por un punto el cambio de precio mínimo posible) representará un salto; vamos a analizar qué sucede cuando discretizamos dicha serie en el tiempo. Claro está que el número de puntos que se desplazará el precio por unidad de tiempo depende de la actividad comercial. Cuanto mayor sea la actividad comercial (número de transacciones realizadas), más saltos superará finalmente el precio. La actividad comercial no se relaciona directamente con el movimiento de los precios, pero, de una u otra forma, el movimiento del precio depende de la actividad comercial, y cuanto mayor sea esta, más movimiento habrá. La relación es indirecta, si bien la correlación resulta positiva. Por ejemplo, supongamos que un 1 salto sea igual a 10 puntos, y tomemos las velas de una hora. Las dos figuras siguientes muestran una representación de los precios en forma de bloques. Los bloques son similares al Renko, pero se construyen de una manera ligeramente distinta. Los valores de high y low se han tomado de las velas clásicas, que muestran qué valores máximos y mínimos adquirió el precio mientras se formaba el bloque. Al igual que las velas, los bloques tienen 4 características: Open High Low Close. La diferencia respecto a las velas es que la distancia entre Open y Close siempre es fija, y se representa en puntos. El bloque se cierra cuando el precio se desplaza N puntos en vertical. Por ejemplo, el tamaño de un bloque es de 10 puntos, y, en cuanto el precio se desplaza 10 puntos verticalmente, el bloque se cierra y comienza a formarse otro nuevo.
Figura 4.
Admitiendo que el tamaño de un bloque es igual a un salto de N puntos, vamos a analizar qué sucede dentro de la vela de una hora. En las dos figuras con el número 4, se muestran los movimientos que han sucedido durante la formación de la vela de una hora. Podemos ver que en la figura superior, el precio se ha desplazado 10 bloques verticalmente en una hora. Si los bloques tienen cada uno 10 puntos, el tamaño de la vela será de 100 puntos. Asimismo, en total, durante la formación de la vela, se han formado 25 bloques, es decir, 25 saltos. La figura inferior muestra otro ejemplo. En este, durante la formación de la vela, el precio se ha desplazado 0 bloques verticalmente, y, por consiguiente, 0 puntos. En este caso, además, el precio se ha desplazado 40 bloques o 40 saltos durante la formación del precio. Ahora, vamos a ver un gráfico con este tipo de velas, representado a continuación en la Figura 5. La vela se cierra una vez cada hora, y la serie de precios no es a todas luces una función del tiempo; en un caso simplificado, se trataría de una función de operaciones comerciales, que, como mencionamos anteriormente, tienen una correlación positiva con el número de puntos superados. Como estamos convirtiendo los puntos en bloques, el número de bloques posee una correlación positiva con el número de operaciones. Dentro de cada vela (cada hora, supongamos), se encuentra, de hecho, un número aleatorio de bloques o saltos por N puntos, y esto será más importante. Y todo porque que las velas se cierran según el tiempo transcurrido, sin atender a los procesos que ocurren en el mercado. El tiempo aquí se calcula según un parámetro externo que tiene poca relación con los procesos ocurridos con el precio. Dicho de otra forma: el precio cambia, no porque haya pasado una hora, sino según sus propios motivos, entre los que puede figurar el hecho de que haya transcurrido una hora.
Figura 5.
La actividad comercial puede variar sustancialmente dependiendo del tiempo, y es individual para cada instrumento. Además, con el desarrollo del comercio algorítmico, cada año aumenta la rotación comercial y el número de intercambios por unidad de tiempo, lo cual indica que sería incorrecto comparar directamente las velas de una hora de 2010 y las de hoy en día, porque dentro de cada vela, de hecho, hay un número diferente de operaciones.
A continuación, realizaremos una simplificación más, tomando el mercado como una deriva aleatoria. Como es natural, el mercado no supone un simple vagabundeo aleatorio, pero resultará más fácil de entender: luego regresaremos a los mercados reales.
El teorema del límite central afirma que la suma de un número lo suficientemente grande de variables aleatorias con una dependencia débil que poseen aproximadamente la misma escala (ninguno de los términos domina, ni hace una contribución determinante a la suma), tiene una distribución próxima a la normal. En lo que respecta a nuestro caso, partiendo del teorema del límite central, podemos inferir que, de media, nuestro proceso aleatorio superará en N saltos una distancia proporcional a la vertical, aproximadamente la raíz cuadrada del número de saltos. Si tenemos que 1 bloque es igual a 1 salto, en 100 bloques, el precio superará 100^0.5 = 10 bloques en vertical. Unas veces más, otras menos, pero de media, nuestra serie de precios aleatorios se someterá a la ley de distribución normal. Debemos advertir de inmediato que el número de saltos para una serie aleatoria determinada dependerá débilmente del tiempo, porque los saltos son generados por la actividad comercial, y esta cambia mucho con el tiempo.
Así, resultará que el tamaño de la vela de una hora para una serie de precios tan aleatoria será, de media, proporcional al número N ^ 0.5, donde N será el número de saltos dentro de la vela. Es decir, el tamaño de la vela de una hora se someterá a la ley de distribución normal. Además, considerando el hecho de que, en la práctica, dentro de la vela habrá un número aleatorio de saltos, podemos inferir que el tamaño de la vela en sí se someterá a la ley de distribución normal. Dicho de otra forma: el tamaño de la vela será igual a la raíz del número de saltos incluidos en esta vela. Vamos a comprobar esta afirmación. Para ello, utilizaremos 50 000 barras de minuto de GBPUSD en el intervalo desde 2020.05.18 hasta 2020.07.03.
- Así, hallaremos el tamaño promedio de una vela de un minuto en el módulo: este será el tamaño del salto. Para hacer esto, restaremos del precio de cierre de cada vela siguiente el precio de cierre de cada vela anterior, y tomaremos el valor del módulo. Así, obtenemos el tamaño promedio de una vela de un minuto GBPUSD = 0.000170
- Vamos a encontrar el tamaño promedio de la vela de una hora para el mismo periodo (en la vela de una hora hay 60 minutos). Para hacer esto, restaremos del precio de cierre de cada vela de hora siguiente el precio de cierre de cada vela de hora anterior, y tomaremos el valor del módulo. Hemos obtenido un tamaño medio de la vela de horas GBPUSD = 0,001117
- Vamos a encontrar cuánto debería desplazarse el precio de media por hora, si asumimos que la serie de precios es una deriva aleatoria. Para lograrlo, multiplicaremos el tamaño promedio de una vela de un minuto por la raíz del número de saltos y lo multiplicaremos por el tamaño promedio del salto. Nuestro número de saltos es 60 => 0,000170*(60^0.5) = 0.001315. El tamaño de la vela de una hora tendería a este tamaño promedio si la serie original se sometiera a la ley de distribución normal.
- Vamos a comparar el tamaño medio de una vela real y una vela de deriva aleatoria (real 0,001117) ≈ (0.001315 teórico). La diferencia es de solo 0,0002. Podemos deducir que el supuesto de que el tamaño de la vela se somete a la ley de distribución normal no solo es correcto, sino que también es confirmado por los datos de mercado de un instrumento real. Una diferencia de 0,0002 no es considerable.
Además, usando las velas de horas obtenidas, en esencia, estamos combinando y analizando una secuencia de ciertos segmentos de la serie de precios cuya amplitud se somete a la ley de distribución normal. Y no resulta sorprendente que más adelante, al tratar con periodos temporales más grandes, consigamos las mismas velas, cuyo tamaño es proporcional a la raíz del número de saltos. Así, vamos a volver a lo mostrado en la figura 2, es decir, si una serie se discretiza incorrectamente, obtendremos una secuencia aleatoria en la salida. De hecho, usando la discretización temporal, estamos transformando una serie de precios en una secuencia aleatoria. Sí, los patrones aún pueden seguir como secuencias con muestreo temporal, debido al hecho de que el mercado no es una secuencia aleatoria y aquí se perciben las dependencias indirectas del tiempo, pero se torna mucho más complicado analizar dicha serie e identificar los patrones. Debido precisamente al muestreo temporal, surgen en las series de precios los llamados "ruidos" y la no estacionariedad de los que habla mucha gente, pero sin decir qué tipo de ruido ni de dónde procede. Ahora, podemos entender que el ruido no solo supone el propio ruido de discretización producido durante la discretización de la señal, sino también un componente aleatorio que surge debido a parámetros de discrtización incorrectos en la serie de precios, que ya es discreta de por sí.
Para asegurarnos de que los resultados obtenidos con las velas de horas no supongan una coincidencia casual, llevaremos a cabo una operación similar para las velas de días. En un día hay 24 horas, y como las parejas de divisas se comercian las 24 horas del día, podemos decir que una vela diaria contiene las velas de 1440 minutos. Vamos a cortar el mismo intervalo de datos de minutos que hemos utilizado para construir H1. Sin embargo, en esta ocasión, mostraremos todos los datos en forma de recuadro para mayor conveniencia.
| Tamaño medio de la vela m1 | Tamaño medio real de la vela H1 | Tamaño teórico de la vela H1, calculado como 0.000117*(60^0.5) | Tamaño medio real de la vela D1 | Tamaño teórico de la vela D1, calculado como 0.00017*(1440^0.5) |
|---|---|---|---|---|
| 0.000170 | 0.001117 | 0.001315 | 0.006547 | 0.006442 |
Como podemos ver, el tamaño promedio real de una vela de días no se distingue mucho del tamaño teóricamente predicho si no fuera un mercado real, en lugar de una deriva aleatoria. Adjuntamos al artículo un archivo con los datos históricos y los cálculos en formato Excel.
Antes de ello, para poder calcular el tamaño promedio de la vela del periodo temporal más alto, usaremos los datos del periodo de un minuto. Pero, ¿qué ocurrirá si desciende y usa los datos de los ticks, tal vez estos sean diferentes? Para ello:
- Vamos a tomar los datos sobre el volumen de ticks de las velas de minuto (de una cuenta real) para el mismo periodo y buscar el número promedio de ticks en una vela de minuto; el valor promedio es de 59,99 ticks por minuto.
- Ahora, cargamos los datos de ticks y averiguamos el tamaño de un tick, que resulta igual a 0,000014378.
- Calculamos el tamaño teórico de la vela de minutos como (59,99^0.5)*0.00014378=0.000111363
- Calculamos el tamaño teórico de la vela de horas como ((59,99*60)^0.5)* 0.000014378= 0.00086
| Tamaño medio del tick | Tamaño medio real de la vela m1 | Tamaño teórico de la vela m1, calculado como (59,99^0.5)*0.000014378 | Tamaño medio real de la vela H1 | Tamaño teórico de la vela H1, calculado como ((59,99*60)^0.5)* 0.000014378 |
|---|---|---|---|---|
| 0.000014378 | 0.00017 | 0.000111363 | 0.001117 | 0.00086 |
Como podemos ver, el tamaño promedio de las velas m1 y H1 no es muy distinto del teórico que tendría la serie de precios si fuera una deriva aleatoria: de ahí, podemos inferir que, por alguna razón, la serie de precios se comporta como una deriva aleatoria, y quizás esto esté relacionado con una discretización incorrecta de los intervalos temporales.
Densidad de distribución de los incrementos de la serie de precios
La valoración cuantitativa ha permitido evaluar de forma aproximada cómo el tamaño de las velas en la serie de precios se corresponde con el tamaño de las velas de la deriva aleatoria, pero resulta más interesante construir la densidad de las distribuciones de los incrementos de la serie de precios para poder valorar visualmente las similitudes o diferencias con la densidad de la distribución de los incrementos para la deriva aleatoria.
La preparación de los datos a analizar es una parte de vital importancia. Vamos a construir la densidad de la distribución para el número de puntos que el precio puede superar en 60 minutos (una hora), es decir, en 60 saltos. Para lograrlo, necesitamos conocer el tamaño promedio de una vela de un minuto y el número de saltos (cuántas velas de un minuto hay en una vela de una hora). Así calculamos antes el tamaño promedio de una vela de un minuto, que resulta igual a 0.000170, el número de velas de un minuto en una hora es de 60. Esto significa que el precio puede desplazarse 60 saltos de 0,000170. Por consiguiente, veremos casos extremos cuando el precio se desplace desde el punto inicial 60 saltos hacia arriba o hacia abajo ininterrumpidamente. Por eso, valoraremos la densidad de la distribución en el intervalo de -0,00017*60=-0,0102 a 0,00017*60=0,0102. En otras palabras, sabemos que si el precio se desplaza solo hacia arriba a saltos de 0,00017, en 60 saltos (una hora), llegará como máximo hasta 0,0102. Además, para 60 saltos, el precio solo puede ocupar los niveles discretos 0; 0.00034; 0,00068; 0,00102...0,0102 y sus valores negativos análogos. Vamos a ilustrar por qué el precio ocupará precisamente estos niveles con la ayuda de la figura 6.
Figura 6.
La figura 6 muestra que si alguna función discreta parte desde el punto cero, su salto es de 1 y da 6 saltos en total, entonces podrá desplazarse verticalmente por las divisiones 6; 4; 2; 0, pudiendo solo tomar los valores discretos con un intervalo de doble salto. De manera semejante, en nuestro caso, si el tamaño promedio de una vela de un minuto es 0.00017, el precio podrá ocupar los niveles discretos con un intervalo igual al doble del tamaño de la vela. En realidad, como las velas son de diferentes tamaños, no solo de 0.00017, el precio podrá tomar valores intermedios, así que, para el análisis, calcularemos cuántos eventos entran en los intervalos con un tamaño del doble de la vela promedio. Para comparar cuánto se distingue la distribución resultante para la serie de precios, la compararemos con la distribución para una deriva aleatoria. Para esta, resulta característico que la probabilidad de cambio de dirección de cada salto siguiente sea del 50%, y no haya memoria. En la figura 7, las distribuciones de densidad de la probabilidad se muestran en negro para una serie de precios, y en rojo para una deriva aleatoria.
Figura 7.
En la figura 7, podemos ver que la densidad de distribución de la probabilidad de la serie de precios prácticamente coincide con la densidad de distribución de la probabilidad para una deriva aleatoria. La densidad de distribución de la probabilidad de la serie de precios tiene un pico ligeramente superior, algo más estrecho y ligeramente desplazado a la derecha, en relación con la densidad de distribución para una deriva aleatoria. Esto invita a pensar que la probabilidad de un viraje en cada próximo movimiento en la serie de precios se encuentra ligeramente por encima del 50%, y hay una pequeña tendencia alcista, pero estas diferencias no son significativas. Así, surge de inmediato la tentación de ganar dinero con esta desviación, pues no parece difícil conseguirlo, pero en el próximo artículo analizaremos más de cerca este patrón y la posibilidad de ganar dinero con él. Aquí, el lector debe entender que hablamos de una variable aleatoria ideal, que, con una muestra lo suficientemente grande, tenderá al estándar. El gráfico de distribución de la densidad de la probabilidad para una deriva aleatoria se construye usando el recuadro mostrado parcialmente en la figura 8.
Figura 8.
El gráfico construido sobre la distribución de la densidad de la probabilidad confirma las conclusiones anteriormente mencionadas, en las que el tamaño de las velas (en este caso, de horas) se acerca al tamaño de las velas que tendríamos si la serie de precios fuera una deriva aleatoria, pero permite valorar este hecho visualmente y con mayor precisión.
Todos los datos y cálculos con los que hemos operado en el artículo se adjuntan al artículo en formato xlsx: en dicho archivo, el lector podrá encontrar todos los cálculos.
Sectores de alta y baja volatilidad
Un tráder atento podrá argumentar que, en los gráficos, a menudo puede notar incluso de forma visual cómo las velas en el mercado se dividen condicionalmente en grupos de tamaños "grandes" y "pequeños" (áreas con alta y baja volatilidad), lo que indica que el gráfico no supone una deriva aleatoria, y por lo tanto, contiene patrones. Si la discretización temporal introdujese distorsiones tan fuertes, este efecto no se percibiría. Pero esta característica se explica precisamente por el hecho de que el tamaño de las velas depende del número de transacciones comerciales realizadas dentro de esta vela. ¿Cómo podemos comprobar esto? Basta con mirar el gráfico de los volúmenes de ticks para entender que los periodos con "velas pequeñas" se ven acompañados por periodos con volúmenes de ticks bajos, y los periodos con velas grandes están acompañados por periodos de volúmenes de ticks grandes. Si imaginamos un tick como un salto, entonces, durante los periodos de velas "grandes", el precio dará más saltos y, por consiguiente, tendrá un tamaño mayor, pero el tamaño de la vela en sí seguirá siendo proporcional a la raíz cuadrada del número de saltos multiplicada por el tamaño medio del salto (ejemplo en la figura 9). Los volúmenes de ticks, a su vez, poseen una correlación directa con la actividad comercial: cuanto mayor sea esta, más ticks pasarán por unidad de tiempo. La historia de los volúmenes reales está disponible en los mercados bursátiles: allí podemos observar que el tamaño de los volúmenes de ticks está fuertemente correlacionado con los volúmenes reales, lo que también indica una relación entre el número de ticks y la intensidad del comercio.
Figura 9.
Una vez más, este hecho demuestra que la discretización por intervalos temporales causa fuertes distorsiones en la forma final de la serie de precios, complicando significativamente el análisis. Esta distorsión ha provocado el surgimiento de toda una clase de sistemas comerciales, los llamados "scalpers nocturnos". No estamos afirmando que sean incapaces de obtener ganancias, pero durante el desarrollo de tales sistemas, resulta necesario considerar esta particularidad en la presentación de la serie de precios e investigar de manera adicional para responder a la pregunta: "¿es la probabilidad de un viraje en estas áreas realmente mayor que la probabilidad de la continuación de la tendencia?"; y "si las características estadísticas de estos sectores permiten obtener ganancias", es porque precisamente este patrón es utilizado por los sistemas de este tipo.
Opción alternativa de discretización de la serie de precios
Después de realizar el análisis, se nos antoja la siguiente conclusión, bastante simple: resulta mejor usar los datos de tick para el procesamiento y el análisis, para no introducir sus errores de discretización en la serie de precios original, porque el precio es de todos modos discreto. Si necesitamos aumentar la escala, solo tendremos que hacer bloques de 10 o 100 ticks. Pero el problema es que los ticks en sí mismos también suponen una forma de discretización. Sí, este método está bien establecido y es ampliamente utilizado, pero puede distorsionar el proceso, porque el precio no supone una función de los ticks entrantes. El precio supone, como mínimo, una función de las operaciones ejecutadas, y es posible que la operación no genere un tick. En la bolsa, los ticks están de alguna manera relacionados con el comercio real, y en FÓREX, cada compañía puede transmitir tantos ticks como desee, y no resultará posible averiguar cuáles son los "correctos". Por consiguiente, incluso suponiendo que el precio sea una función de las transacciones comerciales, queda claro que los ticks ya están distorsionando la forma de la serie de precios e introduciendo en ella un componente aleatorio que, tras un análisis más detallado, puede conducir a errores.
La cuestión del muestreo "correcto" constituye una parte importante del análisis de datos. Por ejemplo, la figura 10, más abajo, muestra 2 gráficos con el precio de Bitcoin frente al dólar. El gráfico superior es un gráfico regular, construido a partir de velas semanales, y el gráfico inferior, se representa en bloques de N puntos. Se trata del mismo periodo y el mismo número de bloques/velas, pero diferentes métodos de muestreo. Podemos ver cómo se diferencian los gráficos para el mismo activo. Por consiguiente, surge una pregunta natural: "¿cuál de las dos representaciones es correcta?"
Figura 10.
Hemos llegado a la conclusión de que la representación correcta es aquella que tenga en cuenta la naturaleza de la discreción de la serie de precios. Pero como desconocemos la naturaleza de la discretización, sería "más correcto" usar un método de discretización que sea capaz de reflejar la obtención de ganancias/pérdidas tanto por mi parte, como por la de los otros participantes del mercado. Por consiguiente, resulta preferible analizar los datos a partir de los que se forman nuestras ganancias. En otras palabras, no debemos considerar el movimiento del precio en el tiempo, sino cuánto se ha movido este, nada más.
Una alternativa a la discretización temporal sería una discretización de amplitud fija, donde se supone que el precio es una función de sí mismo. Es decir, esos bloques sobre los que hablamos anteriormente. Estamos considerando que un bloque de N pips se cierra cada vez que el precio se desplaza verticalmente en N pips. Puede que este no sea el mejor enfoque, pero durante el comercio, a nosotros, como a muchos otros participantes, nos interesa el número exacto de puntos que se ha desplazado el precio, porque de ello depende la cantidad de ganancias o pérdidas que obtendremos. Además, solo después de que el precio se haya desplazado los N puntos verticalmente, cambiará el beneficio de cada participante. Es decir, el modelo en el que el precio es una función de sí mismo es el más cercano al comercio real. La figura 11 refleja cómo se ha discretizado una sinusoide en bloques de tamaño fijo. Asimismo, se ha perdido la forma, pero se han conservado las principales características importantes para nosotros, como el periodo y la amplitud.
Figura 11.
Incluso si nos equivocamos con los parámetros de discretización, no pasará nada terrible, pues se guardarán los valores de la amplitud y el periodo. La figura 12, más abajo, muestra un ejemplo de lo que ocurre cuando el tamaño del bloque es demasiado grande: se pierde parte de la información que se encuentra dentro del bloque, es decir, la precisión se ve perjudicada y se pierde parte de la información (lo cual resulta inevitable al comprimir datos), pero se mantiene la información sobre la amplitud y periodo. Si el tamaño del bloque es mayor que la amplitud de la serie de precios, los bloques no se mostrarán. Como podemos ver, a diferencia del ejemplo mostrado en la figura 2, si el parámetro de discretización se elige incorrectamente, la señal determinada original no se convertirá en una señal aleatoria.
Figura 12
De esta manera, resulta posible gestionar el componente aleatorio introducido por la discretización de la serie de precios en el tiempo, y también en las situaciones en las que se desconoce de qué parámetro es función la serie original. Este método funciona mejor que la discretización temporal y permite escalar convenientemente el gráfico con una precisión de escala de hasta 1 punto.
Conclusión
- La naturaleza de la serie de precios es discreta, lo cual deriva de la propia estructura de los precios.
- El precio de mercado no es una función temporal, sino una función de procesos económicos estrechamente relacionados, que no pueden ser todos considerados en estos momentos.
- La discretización de la serie de precios por intervalos temporales introduce un componente aleatorio significativo, distorsionando la forma real del gráfico de precios, y añadiendo además "ruido" y no estacionariedad a un proceso ya complejo de por sí y con parámetros desconocidos.
- A la hora de desarrollar métodos para discretizar una serie de precios, es necesario considerar de qué parámetro es función el precio.
- La no estacionariedad de la serie de precios se forma, entre otros motivos, debido a los parámetros de discretización incorrectos.
- Resulta posible analizar los gráficos de precio usando la discretización temporal para detectar la presencia de patrones, pero se deben considerar los aspectos ya mencionados para comprender mejor la naturaleza de uno u otro patrón encontrado.
- Es necesario desarrollar formas para discretizar las series de precios que introduzcan mucha menos distorsión en los datos originales, y una de ellas se presenta en este artículo.
- A la hora de desarrollar algoritmos de negociación e investigación estadística del mercado, es necesario considerar las particularidades de la discretización usada en la serie de precios.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/8136
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Aplicación práctica de las redes neuronales en el trading
Aplicación práctica de las redes neuronales en el trading
 Cliente Nativo de Twitter: Parte 2
Cliente Nativo de Twitter: Parte 2
 Cómo escribir un cliente nativo de Twitter para MetaTrader 4 y MetaTrader 5 sin usar DLL
Cómo escribir un cliente nativo de Twitter para MetaTrader 4 y MetaTrader 5 sin usar DLL
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
¿En qué unidades sería más interesante hacerlo?
Es más lógico buscar en valores relativos. Por lo tanto, es aconsejable logaritmizar el CEVR antes de realizar estudios estadísticos con rendimientos.
Es más lógico fijarse en los valores relativos. Por lo tanto, es aconsejable logaritmizar el CEVR antes de realizar estudios estadísticos con rendimientos.
Usted no tenía esta pregunta cuando se tomó la diferencia de precios. Es lo mismo aquí.
¿Por qué los ladrillos tienen sombra superior e inferior? En la figura 4 hay muchos ladrillos, algunos con sombra superior e inferior. Si el precio de cierre es superior al de apertura, entonces este ladrillo está subiendo. En el momento en que se produce un precio alcista que cumple el tamaño del escalón, este ladrillo debe cerrarse inmediatamente y no habrá ningún precio superior a este precio de cierre, no habrá sombra superior.
Para los ladrillos alcistas, la sombra inferior es fácil de entender. Aparece un precio por debajo del precio de apertura, pero luego aparece un precio de cierre por encima del precio de apertura. La longitud de la sombra inferior no debe ser mayor que la longitud del escalón. De lo contrario, se convierte en un ladrillo bajista.
¿Por qué los ladrillos tienen sombra superior e inferior? En la figura 4 hay muchos ladrillos, algunos con sombra superior e inferior. Si el precio de cierre es superior al de apertura, entonces este ladrillo está subiendo. En el momento en que se produce un precio alcista que cumple el tamaño del escalón, este ladrillo debe cerrarse inmediatamente y no habrá ningún precio superior a este precio de cierre sin una sombra superior.
Para los ladrillos alcistas, la sombra inferior es fácil de entender. Aparece un precio por debajo del precio de apertura, pero luego aparece un precio de cierre por encima del precio de apertura. La longitud de la sombra inferior no debe ser mayor que la longitud del escalón. De lo contrario, se convierte en un ladrillo descendente.
Porque los ladrillos se construyen con el precio de cierre y las velas no tienen en cuenta el valor máximo.