
Otimização paralela pelo método de enxame de partículas (Particle Swarm Optimization)
Como sabemos, o MetaTrader 5 permite otimizar as estratégias de negociação usando um testador integrado com base em dois algoritmos, nomeadamente o de iteração direta de parâmetros de entrada e o genético, AG) A otimização genética é um tipo de algoritmo evolutivo que provê uma aceleração significativa do processo. Os resultados do AG podem depender significativamente da tarefa em questão e das nuances da implementação fornecida pelo testador. Por esse motivo, existem muitos traders que, por uma razão ou outra, não se encaixam na funcionalidade padrão e que, portanto, tentam criar seus próprios otimizadores para MetaTrader. Além disso, as possíveis formas de otimização rápida não se limitam à genética. Além do AG, métodos como o de "recozimento simulado" e o de "enxame de partículas" também são amplamente conhecidos.
Neste artigo, implementaremos o algoritmo de enxame de partículas (Particle Swarm Optimization, PSO) e tentaremos integrá-lo ao testador MetaTrader para ser executado em paralelo nos agentes locais disponíveis. A função de otimização de destino será o indicador de negociação do EA selecionado pelo usuário.
Método de enxame de partículas
A nível algorítmico, o método PSO é relativamente simples. A ideia principal é gerar um conjunto de partículas virtuais no espaço dos parâmetros de entrada do Expert Advisor. Em seguida, as partículas se movem e mudam sua velocidade dependendo dos indicadores de negociação do EA nos pontos correspondentes no espaço. O processo é repetido várias vezes até que o desempenho pare de melhorar. O pseudocódigo do algoritmo é mostrado abaixo:

Particle Swarm Optimization Pseudo-Code
Segundo esta abordagem, cada partícula tem uma posição atual, velocidade e memória do seu "melhor" ponto no passado. Por "melhor" queremos dizer o ponto (conjunto de parâmetros de entrada do EA) onde é alcançado o maior valor da função objetivo para dada partícula. Vamos descrever isso numa classe.
class Particle { public: double position[]; // current point double best[]; // best point known to the particle double velocity[]; // current speed double positionValue; // EA performance in current point double bestValue; // EA performance in the best point int group; Particle(const int params) { ArrayResize(position, params); ArrayResize(best, params); ArrayResize(velocity, params); bestValue = -DBL_MAX; group = -1; } };
O tamanho total das matrizes é igual à dimensão do espaço de otimização, ou seja, ao número de parâmetros do Expert Advisor a serem otimizados (passados para o construtor). Visto que a otimização padrão assume que quanto maior o valor da função objetivo, melhor será, inicializamos o campo bestValue com o número mínimo possível, DBL_MAX. Geralmente como critério de avaliação do EA é usado um dos indicadores de trading: lucro, rentabilidade, índice de Sharpe, etc. Se for necessária uma otimização da magnitude que fica melhor quando ocorre a diminuição, por exemplo, do rebaixamento, é fácil dar conversões equivalentes para maximizar as magnitudes inversas.
Matrizes e variáveis são tornadas públicas para facilitar o acesso e seu código de recálculo. A adesão estrita aos princípios da POO exigiria ocultá-los usando o modificador private e descrevendo métodos de leitura e modificação.
Além de partículas individuais, o algoritmo opera com as chamadas "topologias" ou subconjuntos de partículas. Eles podem ser construídos de acordo com diferentes princípios. Em nosso caso, escolhemos a "topologia de grupo social". Esse grupo armazena informações sobre a melhor posição entre todas as suas partículas.
class Group { private: double result; // best EA performance in the group public: double optimum[]; // best known position in the group Group(const int params) { ArrayResize(optimum, params); ArrayInitialize(optimum, 0); result = -DBL_MAX; } void assign(const double x) { result = x; } double getResult() const { return result; } bool isAssigned() { return result != -DBL_MAX; } };
O fato de uma partícula pertencer a um grupo é especificado pelo número do grupo no campo group na classe Particle (veja acima).
Agora vamos começar a codificar o próprio algoritmo de enxame de partículas, como uma classe separada. Vamos começar com matrizes de partículas e grupos.
class Swarm { private: Particle *particles[]; Group *groups[]; int _size; // number of particles int _globals; // number of groups int _params; // number of parameters to optimize
Para cada parâmetro, é necessário especificar a faixa de valores em que a otimização será realizada, bem como o incremento (passo).
double highs[]; double lows[]; double steps[];
Além disso, o conjunto ideal de parâmetros deve ser armazenado em algum lugar.
double solution[];
Como a classe terá diferentes construtores, descreveremos o método de inicialização unificado.
void init(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { _size = size; _globals = globals; _params = params; ArrayCopy(highs, max); ArrayCopy(lows, min); ArrayCopy(steps, inc); ArrayResize(solution, _params); ArrayResize(particles, _size); for(int i = 0; i < _size; i++) // loop through particles { particles[i] = new Particle(_params); ///do ///{ for(int p = 0; p < _params; p++) // loop through all dimesions { // random placement particles[i].position[p] = (MathRand() * 1.0 / 32767) * (highs[p] - lows[p]) + lows[p]; // adjust it according to step granularity if(steps[p] != 0) { particles[i].position[p] = ((int)MathRound((particles[i].position[p] - lows[p]) / steps[p])) * steps[p] + lows[p]; } // the only position is the best so far particles[i].best[p] = particles[i].position[p]; // random speed particles[i].velocity[p] = (MathRand() * 1.0 / 32767) * 2 * (highs[p] - lows[p]) - (highs[p] - lows[p]); } ///} ///while(index.add(crc64(particles[i].position)) && !IsStopped()); } ArrayResize(groups, _globals); for(int i = 0; i < _globals; i++) { groups[i] = new Group(_params); } for(int i = 0; i < _size; i++) { // random group membership particles[i].group = (_globals > 1) ? (int)MathMin(MathRand() * 1.0 / 32767 * _globals, _globals - 1) : 0; } }
Todas as matrizes são distribuídas de acordo com a dimensão dada e preenchidas com os dados transferidos. A posição inicial das partículas, sua velocidade e associação ao grupo são determinadas aleatoriamente. Algo importante está comentado por enquanto, já um pouco mais tarde revelaremos por que é necessário.
Deve-se notar que a versão clássica do "enxame de partículas" tem como objetivo otimizar funções definidas em coordenadas contínuas. No entanto, os parâmetros do Expert Advisor geralmente são testados com algum incremento. Por exemplo, em particular, uma média móvel padrão não pode ter um período de 11,5. Devido a isso, além da faixa de valores aceitáveis para todas as dimensões, também é definido o incremento, que serve para arredondar as posições das partículas. Veremos que isso será feito não apenas durante a fase de inicialização, mas também nos cálculos durante a otimização.
Agora podemos implementar alguns construtores usando o init.
#define AUTO_SIZE_FACTOR 5 public: Swarm(const int params, const double &max[], const double &min[], const double &step[]) { init(params * AUTO_SIZE_FACTOR, (int)MathSqrt(params * AUTO_SIZE_FACTOR), params, max, min, step); } Swarm(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { init(size, globals, params, max, min, step); }
O primeiro usa uma conhecida regra empírica para calcular o tamanho do enxame e o número de grupos com base no número de parâmetros. A constante AUTO_SIZE_FACTOR, que é 5 por padrão, pode ser alterada conforme desejado. O segundo permite especificar todos os valores explicitamente.
O destruidor libera a memória alocada.
~Swarm()
{
for(int i = 0; i < _size; i++)
{
delete particles[i];
}
for(int i = 0; i < _globals; i++)
{
delete groups[i];
}
}
Agora chegou a hora de escrever o método principal da classe que realiza diretamente a otimização.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4)
O primeiro parâmetro Functor &f é de particular interesse. Obviamente, durante o processo de otimização, chamaremos o Expert Advisor para vários parâmetros de entrada e em resposta receberemos um número estimado (lucro, rentabilidade ou outra característica). O enxame não sabe nada e não deveria saber sobre o EA. Sua única tarefa é encontrar o ótimo de uma função objetivo desconhecida com um conjunto arbitrário de argumentos numéricos. Por isso, entra em jogo uma interface abstrata, em nosso caso a classe Functor.
class Functor { public: virtual double calculate(const double &vector[]) = 0; };
O único método aceita uma matriz de parâmetros como entrada e retorna um número (todos os tipos são double). No futuro, o EA terá que implementar de alguma forma uma classe derivada de Functor e calcular o indicador necessário dentro do método calculate. Assim, o primeiro parâmetro do método optimize receberá um objeto com uma função de retorno de chamada fornecida pelo robô de negociação.
O segundo parâmetro do método optimize é o número máximo de loops para executar o algoritmo. Os 3 parâmetros a seguir definem os coeficientes PSO: inertia - conservação da velocidade da partícula (graças a valores menores que 1, a velocidade geralmente diminui), selfBoost e groupBoost determinam quão responsiva é a partícula para ajustar sua direção de movimento para as posições mais conhecidas, respectivamente, no histórico da própria partícula e de seu grupo.
Agora que todos os parâmetros foram considerados, podemos prosseguir com o algoritmo em si. Numa forma um tanto simplificada, os loops de otimização reproduzem quase completamente o pseudo-código.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4) { double result = -DBL_MAX; ArrayInitialize(solution, 0); for(int c = 0; c < cycles && !IsStopped(); c++) // predefined number of cycles { for(int i = 0; i < _size && !IsStopped(); i++) // loop through all particles { for(int p = 0; p < _params; p++) // update particle position and speed { double r1 = MathRand() * 1.0 / 32767; double rg = MathRand() * 1.0 / 32767; particles[i].velocity[p] = inertia * particles[i].velocity[p] + selfBoost * r1 * (particles[i].best[p] - particles[i].position[p]) + groupBoost * rg * (groups[particles[i].group].optimum[p] - particles[i].position[p]); particles[i].position[p] = particles[i].position[p] + particles[i].velocity[p]; // make sure to keep the particle inside the boundaries of parameter space if(particles[i].position[p] < lows[p]) particles[i].position[p] = lows[p]; else if(particles[i].position[p] > highs[p]) particles[i].position[p] = highs[p]; // respect step size if(steps[p] != 0) { particles[i].position[p] = ((int)MathRound((particles[i].position[p] - lows[p]) / steps[p])) * steps[p] + lows[p]; } } // get the function value for the particle i particles[i].positionValue = f.calculate(particles[i].position); // update the particle's best value and position (if improvement is found) if(particles[i].positionValue > particles[i].bestValue) { particles[i].bestValue = particles[i].positionValue; ArrayCopy(particles[i].best, particles[i].position); } // update the group's best value and position (if improvement is found) if(particles[i].positionValue > groups[particles[i].group].getResult()) { groups[particles[i].group].assign(particles[i].positionValue); ArrayCopy(groups[particles[i].group].optimum, particles[i].position); // update the global maximum value and solution (if improvement is found) if(particles[i].positionValue > result) { result = particles[i].positionValue; ArrayCopy(solution, particles[i].position); } } } } return result; }
O método retorna o valor máximo encontrado da função objetivo. Para a leitura de coordenadas (conjunto de parâmetros) é reservado outro método.
bool getSolution(double &result[]) { ArrayCopy(result, solution); return !IsStopped(); }
Esse é praticamente todo o algoritmo. Mas anteriormente não foi dito acidentalmente que existem algumas simplificações no código. Em primeiro lugar, consideraremos a seguinte nuance.
Um mundo discreto sem gêmeos
Embora o functor seja chamado várias vezes para recalcular dinamicamente os conjuntos de parâmetros, não há garantia de que o algoritmo não irá atingir o mesmo ponto várias vezes, especialmente considerando a discrição ao longo dos eixos. Para evitar isso, é necessário distinguir de alguma forma os pontos já calculados e deixar passá-los.
Os parâmetros são apenas números, uma sequência de bytes. A maneira mais famosa para verificar a exclusividade dos dados é através do hash. E forma mais popular de obter um hash pode ser por meio do CRC. CRC é um único número (geralmente, um inteiro, com vários dígitos) gerado a partir de dados de tal forma que se dois desses números característicos vindos de dois conjuntos de dados coincidirem, significa que os conjuntos são idênticos com alta probabilidade. Quanto mais dígitos (bits) no CRC, maior a probabilidade de coincidência (até quase 100%). Um CRC de 64 bits é provavelmente suficiente para nossa tarefa, mas, se necessário, ele pode ser estendido e alterado para outra função de hash. A implementação do cálculo CRC é fácil de portar para MQL a partir da linguagem C. Uma das variações está anexada a este artigo no arquivo crc64.mqh. A principal função de trabalho possui o seguinte protótipo.
ulong crc64(ulong crc, const uchar &s[], int l);
Ele aceita o CRC do bloco de dados anterior (se houver vários, para um bloco devemos especificar 0), uma matriz de bytes e o número de elementos a ser processado. A função retorna um CRC de 64 bits.
Precisamos fornecer um conjunto de parâmetros para a entrada desta função, mas isso não pode ser feito diretamente, pois cada parâmetro é do tipo double. Para convertê-lo numa matriz de bytes, usaremos a biblioteca TypeToBytes.mqh (o arquivo está anexado ao artigo, mas é melhor usar a versão mais recente do codebase).
Depois de habilitar essa biblioteca, podemos criar uma função wrapper para calcular CRC64 a partir de uma série de parâmetros:
#include <TypeToBytes.mqh> #include <crc64.mqh> template<typename T> ulong crc64(const T &array[]) { ulong crc = 0; int len = ArraySize(array); for(int i = 0; i < len; i++) { crc = crc64(crc, _R(array[i]).Bytes, sizeof(T)); } return crc; }
Mas surgem as seguintes questões: onde armazenar hashes e como verificá-los a nível de exclusividade. Aqui o melhor é usar uma árvore binária. Ela é uma estrutura de dados que dá operações rápidas para adicionar novos valores e verificar a existência dos já adicionados. A velocidade é fornecida por uma propriedade especial da árvore chamada B. Em outras palavras, ela deve ser uma árvore B (constantemente mantida num estado balanceado) para garantir a velocidade máxima das operações. Felizmente, o fato de os hashes serem armazenados na árvore joga nas nossas mãos. Vamos lembrar a definição de hash.
A função hash (algoritmo de geração de hash) gera, para qualquer dado de entrada, um valor de saída uniformemente distribuído, tanto quanto possível. Como resultado, adicionar um hash a uma árvore binária fornece estatisticamente um estado quase balanceado e, como consequência, alta eficiência.
Uma árvore binária é um conjunto de nós, cada um dos quais contém algum valor e duas referências opcionais para os chamados nós direito e esquerdo. O valor no nó esquerdo é sempre menor do que o valor no nó pai e o valor no nó direito é sempre maior do que no nó pai. A árvore começa a ser preenchida a partir da raiz, comparando o novo valor com os valores do nó. Se o valor adicionado for igual ao valor da raiz (ou de outro nó), basta retornar o sinal da existência do valor na árvore. Se o novo valor for menor que o valor no nó, movemo-nos pela referência para o nó esquerdo e processamos sua subárvore de maneira semelhante. Se o novo valor for maior, vamos ao longo da subárvore direita. Se alguma das referências for nula (não houver mais ramificações), a pesquisa será concluída sem resultados e, portanto, deverá ser criado um novo nó com um novo valor em vez de uma referência nula.
Para implementar essa lógica, foram criadas algumas classes-modelos: o nó TreeNode e a árvore BinaryTree. Todos os códigos-fonte podem ser encontrados no arquivo de cabeçalho anexo.
template<typename T> class TreeNode { private: TreeNode *left; TreeNode *right; T value; public: TreeNode(T t): value(t) {} // adds new value into subtrees and returns false or // returns true if t exists as value of this node or in subtrees bool add(T t); ~TreeNode(); TreeNode *getLeft(void) const; TreeNode *getRight(void) const; T getValue(void) const; }; template<typename T> class BinaryTree { private: TreeNode<T> *root; public: bool add(T t); ~BinaryTree(); };
Se o valor já estiver na árvore, o método add retornará true, já se ele for recém-adicionado, false. Excluir uma raiz no destruidor da árvore automaticamente excluirá todos os nós filhos.
A classe de árvore implementada é uma das variações mais simples, existem árvores mais avançadas, quem quiser pode embuti-las de forma independente.
Vamos adicionar BinaryTree à classe Swarm.
class Swarm { private: BinaryTree<ulong> index;
No método optimize, precisamos refinar os locais onde movemos as partículas para novas posições.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4) { // ... double next[]; ArrayResize(next, _params); for(int c = 0; c < cycles && !IsStopped(); c++) { int skipped = 0; for(int i = 0; i < _size && !IsStopped(); i++) { // new placement of particles using temporary array next for(int p = 0; p < _params; p++) { double r1 = MathRand() * 1.0 / 32767; double rg = MathRand() * 1.0 / 32767; particles[i].velocity[p] = inertia * particles[i].velocity[p] + selfBoost * r1 * (particles[i].best[p] - particles[i].position[p]) + groupBoost * rg * (groups[particles[i].group].optimum[p] - particles[i].position[p]); next[p] = particles[i].position[p] + particles[i].velocity[p]; if(next[p] < lows[p]) next[p] = lows[p]; else if(next[p] > highs[p]) next[p] = highs[p]; if(steps[p] != 0) { next[p] = ((int)MathRound(next[p] / steps[p])) * steps[p]; } } // check if the tree contains this parameter set and add it if not if(index.Add(crc64(next))) { skipped++; continue; } // apply new position to the particle ArrayCopy(particles[i].position, next); particles[i].positionValue = f.calculate(particles[i].position); // ... } Print("Cycle ", c, " done, skipped ", skipped, " of ", _size, " / ", result); if(skipped == _size) break; // full coverage }
Adicionamos uma matriz auxiliar next, onde as novas coordenadas geradas vão primeiro. Para eles é calculado o CRC e este valor é verificado a nível de exclusividade. Se ainda não for encontrada uma nova posição, ela será adicionada à árvore, copiada para a partícula correspondente e todos os seus cálculos necessários serão realizados. Se a posição já existir na árvore (ou seja, o functor já for calculado para ela), esta iteração é ignorada.
Testando a funcionalidade básica
Tudo o que vimos até agora constitui a base mínima necessária para a realização dos primeiros testes. Para termos certeza de que a otimização realmente funciona, podemos usar o script testpso.mq5. O arquivo de cabeçalho ParticleSwarmParallel.mqh utilizado por ele e anexado ao artigo contém, na verdade, não apenas as classes já conhecidas, mas também muitas melhorias que serão descritas a seguir.
Os testes são projetados num estilo POO, o que permite estendê-los com nossas funções objetivo favoritas. A classe BaseFunctor fornece a base para os testes.
class BaseFunctor: public Functor { protected: const int params; double max[], min[], steps[]; public: BaseFunctor(const int p): params(p) // number of parameters { ArrayResize(max, params); ArrayResize(min, params); ArrayResize(steps, params); ArrayInitialize(steps, 0); PSOTests::register(&this); } virtual void test(const int loop) // worker method { Swarm swarm(params, max, min, steps); swarm.optimize(this, loop); double result[]; swarm.getSolution(result); for(int i = 0; i < params; i++) { Print(i, " ", result[i]); } } };
Todos os objetos das classes derivadas se registrarão automaticamente ao serem criados usando o método register na classe PSOTests.
class PSOTests { static BaseFunctor *testCases[]; public: static void register(BaseFunctor *f) { int n = ArraySize(testCases); ArrayResize(testCases, n + 1); testCases[n] = f; } static void run(const int loop = 100) { for(int i = 0; i < ArraySize(testCases); i++) { testCases[i].test(loop); } } };
Os próprios testes (otimização) são executados pelo método run, pois ele chama test em todos os objetos registrados.
Existem muitas funções objetivo de teste populares. Entre elas, em particular, estão "rosenbrock", "griewank", "sphere", que estão programados no script. Por exemplo, para "sphere", podemos definir um escopo de pesquisa e o método calculate como segue.
class Sphere: public BaseFunctor { public: Sphere(): BaseFunctor(3) // expected global minimum (0, 0, 0) { for(int i = 0; i < params; i++) { max[i] = 100; min[i] = -100; } } virtual void test(const int loop) { Print("Optimizing " + typename(this)); BaseFunctor::test(loop); } virtual double calculate(const double &vec[]) { int dim = ArraySize(vec); double sum = 0; for(int i = 0; i < dim; i++) sum += pow(vec[i], 2); return -sum; // negative for maximization } };
Vale a pena ressaltar que as funções objetivo padrão pressupõem uma minimização, embora tenhamos implementado o algoritmo com o objetivo de maximizar (visto que devemos buscar o máximo desempenho do EA). Por isso, é necessário considerar o resultado do cálculo com um sinal negativo. Além disso, aqui ainda não é usada uma etapa discreta, ou seja, as funções são contínuas.
void OnStart()
{
PSOTests::Sphere sphere;
PSOTests::Griewank griewank;
PSOTests::Rosenbrock rosenbrock;
PSOTests::run();
}
Ao executar o script, podemos ter certeza de que os valores das coordenadas próximos à solução exata (extremos) são exibidos no log. Como as partículas são inicializadas aleatoriamente, cada execução dará valores ligeiramente diferentes. A precisão da solução depende dos parâmetros de entrada do algoritmo.
Optimizing PSOTests::Sphere PSO[3] created: 15/3 PSO Processing... Cycle 0 done, skipped 0 of 15 / -1279.167775306995 Cycle 10 done, skipped 0 of 15 / -231.4807406906516 Cycle 20 done, skipped 0 of 15 / -4.269510657558273 Cycle 30 done, skipped 0 of 15 / -1.931949742316357 Cycle 40 done, skipped 0 of 15 / -0.06018744740061506 Cycle 50 done, skipped 0 of 15 / -0.009498109984732127 Cycle 60 done, skipped 0 of 15 / -0.002058433538555499 Cycle 70 done, skipped 0 of 15 / -0.0001494176502579518 Cycle 80 done, skipped 0 of 15 / -4.141817579039349e-05 Cycle 90 done, skipped 0 of 15 / -1.90930142126799e-05 Cycle 99 done, skipped 0 of 15 / -8.161728746514931e-07 PSO Finished 1500 of 1500 planned calculations: true 0 -0.000594423827318461 1 -0.000484001094843528 2 0.000478096358862763 Optimizing PSOTests::Griewank PSO[2] created: 10/3 PSO Processing... Cycle 0 done, skipped 0 of 10 / -26.96927938978973 Cycle 10 done, skipped 0 of 10 / -0.939220906325796 Cycle 20 done, skipped 0 of 10 / -0.3074442362962919 Cycle 30 done, skipped 0 of 10 / -0.121905607345751 Cycle 40 done, skipped 0 of 10 / -0.03294107382891465 Cycle 50 done, skipped 0 of 10 / -0.02138355984774098 Cycle 60 done, skipped 0 of 10 / -0.01060479828529859 Cycle 70 done, skipped 0 of 10 / -0.009728742850384609 Cycle 80 done, skipped 0 of 10 / -0.008640623678293768 Cycle 90 done, skipped 0 of 10 / -0.008578769833161193 Cycle 99 done, skipped 0 of 10 / -0.008578769833161193 PSO Finished 996 of 1000 planned calculations: true 0 3.188612982502877 1 -4.435728146291838 Optimizing PSOTests::Rosenbrock PSO[2] created: 10/3 PSO Processing... Cycle 0 done, skipped 0 of 10 / -19.05855349617553 Cycle 10 done, skipped 1 of 10 / -0.4255148824156119 Cycle 20 done, skipped 0 of 10 / -0.1935391314277153 Cycle 30 done, skipped 0 of 10 / -0.006468452482022688 Cycle 40 done, skipped 0 of 10 / -0.001031992354315317 Cycle 50 done, skipped 0 of 10 / -0.00101322411502283 Cycle 60 done, skipped 0 of 10 / -0.0008800704421316765 Cycle 70 done, skipped 0 of 10 / -0.0005593151578155307 Cycle 80 done, skipped 0 of 10 / -0.0005516786893301249 Cycle 90 done, skipped 0 of 10 / -0.0005473814163781119 Cycle 99 done, skipped 0 of 10 / -7.255520122486163e-06 PSO Finished 982 of 1000 planned calculations: true 0 1.001858172119364 1 1.003524791491219
Observe que o tamanho do enxame e o número de grupos (escritos no log em linhas como PSO[N] created: X/G, onde N é a dimensão do espaço, X é o número de partículas, G é o número de grupos) são selecionados automaticamente de acordo com as regras práticas programadas com base em dados de entrada.
Prosseguimos com o mundo paralelo
Nosso primeiro teste é bom para todos, com exceção de uma nuance, o ciclo de contagem de partículas é executado numa única thread, embora o terminal permita carregar todos os núcleos do processador. Lembremo-nos de que o objetivo final é escrever um mecanismo de otimização usando o método PSO, que pode ser construído num Expert Advisors para otimização multi-thread no testador MetaTrader e, portanto, fornece uma alternativa ao algoritmo genético padrão.
Obviamente, a transferência mecânica do código do algoritmo dentro de um Expert Advisor em vez de um script não permitirá paralelizar cálculos. Para isso, o próprio algoritmo precisa ser modificado.
Se olharmos para o código no contexto da tarefa em questão, isso sugere que selecionamos grupos de partículas em cálculos paralelos. Cada grupo pode ser processado independentemente dos outros. Dentro de cada grupo, um ciclo completo é executado o número especificado de vezes.
Para não alterar o núcleo da classe Swarm, usaremos uma técnica simples: em vez de vários grupos dentro de uma classe, vamos criar várias instâncias de dada classe, em cada uma das quais o número de grupos será degenerado, ou seja, igual a um. Mas essa construção precisará ser complementada com algum código que permita às instâncias trocar informações entre si, pois, afinal, cada instância será executada em seu próprio agente de teste.
Primeiro, vamos adicionar uma nova maneira de inicializar objetos.
Swarm(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { if(MQLInfoInteger(MQL_OPTIMIZATION)) { init(size == 0 ? params * AUTO_SIZE_FACTOR : size, 1, params, max, min, step); } ...
Com base no sinal de operação do programa no modo de otimização, definimos o número de grupos para 1. O tamanho do enxame padrão é determinado por uma regra empírica (a menos que explicitamente definido um valor diferente de 0 no parâmetro size).
No manipulador de eventos OnTester, o Expert Advisor pode obter o resultado do mini-enxame (consistindo num único grupo) usando a função getSolution e enviá-lo como quadro para o terminal. Este último pode analisar as execuções e escolher a melhor. Faz sentido que o número de enxames/grupos paralelos seja igual, pelo menos, ao número de núcleos, mas pode ser maior (é desejável manter a multiplicidade do número de núcleos). Obviamente, quanto maior a dimensão do espaço de busca ideal, mais grupos podem ser necessários, mas para testes simples basta limitar o número de núcleos.
A troca de dados entre as instâncias é necessária para calcular o espaço sem pontos duplicados. Como lembramos, em cada objeto a lista de pontos processados é armazenada na árvore binária index. Poderíamos enviá-lo para o terminal dentro de um quadro, por analogia com os resultados, mas o problema é que o registro combinado hipotético dessas listas não pode ser enviado de volta aos agentes. Infelizmente, a arquitetura do testador oferece suporte à transferência de dados controlada durante a otimização apenas de agentes para o terminal, mas não vice-versa. A partir do terminal, as tarefas são distribuídas aos agentes num formato fechado.
Por isso, decidimos nos restringir aos agentes locais e salvar os index de cada grupo em arquivos de uma pasta compartilhada (FILE_COMMON). Com essa abordagem, cada agente grava seu próprio index e tem a capacidade de ler os index de todas as outras execuções a qualquer momento e adicioná-los ao seu próprio index. Em particular, faz sentido fazer isso ao inicializar uma execução.
Em MQL, as alterações num arquivo escrito podem ser lidas por outros processos somente após o arquivo ser fechado. Os sinalizadores FILE_SHARE_READ, FILE_SHARE_WRITE e a função FileFlush não ajudam aqui.
O suporte para escrever índices é implementado usando o conhecido padrão "visitante".
template<typename T> class Visitor { public: virtual void visit(TreeNode<T> *node) = 0; };
Sua interface minimalista declara que vamos realizar alguma operação arbitrária no nó da árvore passado. Para trabalhar com arquivos, foi criada uma implementação sucessora específica, Exporter. O valor interno de cada nó é armazenado numa linha separada do arquivo, na ordem em que é percorrida a árvore inteira com base nas referência.
template<typename T> class Exporter: public Visitor<T> { private: int file; uint level; public: Exporter(const string name): level(0) { file = FileOpen(name, FILE_READ | FILE_WRITE | FILE_CSV | FILE_ANSI | FILE_SHARE_READ| FILE_SHARE_WRITE | FILE_COMMON, ','); } ~Exporter() { FileClose(file); } virtual void visit(TreeNode<T> *node) override { #ifdef PSO_DEBUG_BINTREE if(node.getLeft()) visit(node.getLeft()); FileWrite(file, node.getValue()); if(node.getRight()) visit(node.getRight()); #else const T v = node.getValue(); FileWrite(file, v); level++; if((level | (uint)v) % 2 == 0) { if(node.getLeft()) visit(node.getLeft()); if(node.getRight()) visit(node.getRight()); } else { if(node.getRight()) visit(node.getRight()); if(node.getLeft()) visit(node.getLeft()); } level--; #endif } };
A passagem ordenada pela árvore, que parece ser a mais lógica, só pode ser usada para fins de depuração se quisermos obter strings classificadas dentro de arquivos para comparação contextual. Este método é cercado pela diretiva de compilação condicional PSO_DEBUG_BINTREE e é desabilitado por padrão. Na prática, conforme já mencionado, o equilíbrio estatístico da árvore é garantido pela adição de valores aleatórios e uniformemente distribuídos armazenados na árvore (hashes). Se salvarmos os elementos da árvore numa forma ordenada, seu carregamento subsequente desde o arquivo causará uma configuração mais lenta e abaixo do ideal (um segmento longo, na verdade, uma lista). Para evitar isso, na etapa de salvamento da árvore, um elemento de incerteza é introduzido na sequência em que os nós serão processados.
Usando a classe Explorer, é fácil adicionar um método especial à classe BinaryTree que salva a árvore para o "visitante" passado.
template<typename T> class BinaryTree { ... void visit(Visitor<T> *visitor) { visitor.visit(root); } };
Um novo método na classe Swarm também é necessário para iniciar a atividade.
void exportIndex(const int id) { const string name = sharedName(id); Exporter<ulong> exporter(name); index.visit(&exporter); }
O parâmetro id é um número de execução único (também conhecido como número do grupo); é esse parâmetro que usaremos para configurar a otimização no testador. Faz sentido chamar o método exportIndex logo após os dois métodos swarm terem sido trabalhados: optimize e getSolution. Isso é responsabilidade do código de chamada, porque nem sempre é necessário, pois nosso primeiro exemplo "paralelo" (veja mais adiante) não precisará dele. Por definição, se o número de grupos for igual ao número de núcleos, eles não terão tempo para trocar nenhuma informação, pois serão iniciados em paralelo, sendo ineficiente a leitura do arquivo dentro do loop.
A função auxiliar sharedName, mencionada em exportIndex, permite criar um nome exclusivo com base no número do grupo, no nome do EA e na pasta do terminal.
#define PPSO_FILE_PREFIX "PPSO-" string sharedName(const int id, const string prefix = PPSO_FILE_PREFIX, const string ext = ".csv") { ushort array[]; StringToShortArray(TerminalInfoString(TERMINAL_PATH), array); const string program = MQLInfoString(MQL_PROGRAM_NAME) + "-"; if(id != -1) { return prefix + program + StringFormat("%08I64X-%04d", crc64(array), id) + ext; } return prefix + program + StringFormat("%08I64X-*", crc64(array)) + ext; }
Se passarmos um identificador igual a -1 para a função, ela criará uma máscara para pesquisar todos os arquivos de dada instância do terminal. Isso é usado ao excluir arquivos temporários antigos (da otimização anterior do Expert Advisor em questão), bem como ao ler índices de fluxos paralelos. Vejamos como isso é feito em termos gerais.
bool restoreIndex() { string name; const string filter = sharedName(-1); // use wildcards to merge multiple indices for all cores long h = FileFindFirst(filter, name, FILE_COMMON); if(h != INVALID_HANDLE) { do { FileReader reader(name, FILE_COMMON); reader.read(this); } while(FileFindNext(h, name)); FileFindClose(h); } return true; }
Cada arquivo encontrado é transferido a uma nova classe FileReader para ser processado. Ela é responsável por abrir o arquivo em modo de leitura e carregar todas as linhas sequencialmente, com sua transferência imediata para a interface do Feed.
class Feed { public: virtual bool feed(const int dump) = 0; }; class FileReader { protected: int dump; public: FileReader(const string name, const int flags = 0) { dump = FileOpen(name, FILE_READ | FILE_CSV | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags, ','); } virtual bool isReady() const { return dump != INVALID_HANDLE; } virtual bool read(Feed &pass) { if(!isReady()) return false; while(!FileIsEnding(dump)) { if(!pass.feed(dump)) { return false; } } return true; } };
Como podemos imaginar, a interface do Feed deve ser implementada no próprio enxame, porque passamos this dentro do FileReader.
class Swarm: public Feed { private: ... int _read; int _unique; int _restored; BinaryTree<ulong> merge; public: ... virtual bool feed(const int dump) override { const ulong value = (ulong)FileReadString(dump); _read++; if(!index.add(value)) _restored++; // just added into the tree else if(!merge.add(value)) _unique++; // was already indexed, hitting _unique in total return true; } ...
Usando as variáveis _read, _unique e _restored, o método calcula, respectivamente, o número total de elementos lidos (de todos os arquivos), a quantidade que foi adicionada ao index e a quantidade de únicos entre aqueles que não foram adicionados (ou seja, que já estão no índice). Como os grupos operam de forma independente, pode haver duplicatas nos índices de grupos diferentes.
Essas estatísticas são importantes para determinar quando o espaço de pesquisa está totalmente explorado ou próximo a isso. Nesse caso, o número _unique se aproxima do número de combinações de parâmetros possíveis.
Conforme o número de passes concluídos aumenta, mais e mais pontos exclusivos do histórico compartilhado serão carregados nos índices locais. Após a próxima execução de calculate, o índice será preenchido com novos pontos verificados e os arquivos salvos aumentarão constantemente de tamanho. Gradualmente, a sobreposição de elementos nos arquivos começará a predominar. Isso significa alguma sobrecarga, mas em qualquer caso, será menor do que recalcular a atividade de negociação do EA. Isso será refletido na aceleração dos ciclos do PSO conforme cada um dos grupos subsequentes (tarefas do testador) é processado conforme se aproxima da cobertura total do espaço de otimização.
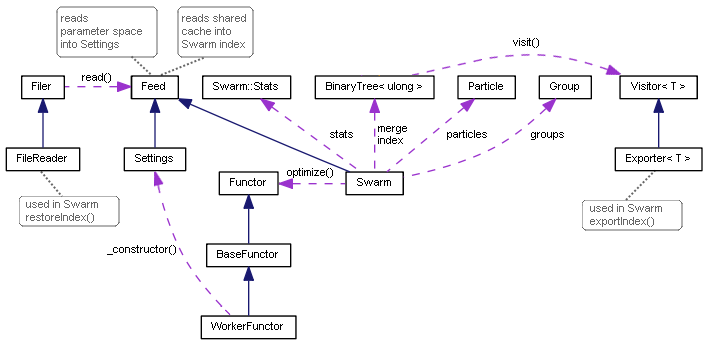
Diagrama de classes da Particle Swarm Optimization
Teste de computação paralela
Para testar o desempenho do algoritmo em várias threads, transformaremos o script antigo no Expert Advisor PPSO.mq5. Ele será executado no modo de cálculo matemático, já que o ambiente de negociação ainda não é necessário.
O conjunto de funções objetivo de teste permanecerá o mesmo, e as classes que os implementam ficarão praticamente inalteradas. A escolha de um determinado teste será feita nas variáveis de entrada.
enum TEST { Sphere, Griewank, Rosenbrock }; sinput int Cycles = 100; sinput TEST TestCase = Sphere; sinput int SwarmSize = 0; input int GroupCount = 0;
Aqui também podemos especificar o número de loops, o tamanho do enxame e o número de grupos. Tudo isso é usado na implementação do functor, em particular, no construtor Swarm. Valores padrão de zero significam, como antes, ajuste automático com base na dimensão do problema.
class BaseFunctor: public Functor { protected: const int params; double max[], min[], steps[]; double optimum; double result[]; public: ... virtual void test() { Swarm swarm(SwarmSize, GroupCount, params, max, min, steps); optimum = swarm.optimize(this, Cycles); swarm.getSolution(result); } double getSolution(double &output[]) const { ArrayCopy(output, result); return optimum; } };
Todos os cálculos são iniciados a partir do manipulador OnTester. O parâmetro GroupCount (pelo qual serão realizadas as iterações do testador) é usado como um randomizador para que as instâncias em diferentes threads contenham partículas diferentes. Dependendo do parâmetro TestCase, é criado determinado functor de teste. Em seguida, após o método functor.test() ser chamado, os resultados podem ser lidos usando functor.getSolution() e enviados num quadro para o terminal.
double OnTester() { MathSrand(GroupCount); // reproducable randomization BaseFunctor *functor = NULL; switch(TestCase) { case Sphere: functor = new PSOTests::Sphere(); break; case Griewank: functor = new PSOTests::Griewank(); break; case Rosenbrock: functor = new PSOTests::Rosenbrock(); break; } functor.test(); double output[]; double result = functor.getSolution(output); if(MQLInfoInteger(MQL_OPTIMIZATION)) { FrameAdd("PSO", 0xC0DE, result, output); } else { Print("Solution: ", result); for(int i = 0; i < ArraySize(output); i++) { Print(i, " ", output[i]); } } delete functor; return result; }
No próprio terminal funciona um conjunto de funções - OnTesterInit, OnTesterPass, OnTesterDeinit - que recolhe frames, determinando simultaneamente a melhor solução entre os enviados.
int passcount = 0; double best = -DBL_MAX; double location[]; void OnTesterPass() { ulong pass; string name; long id; double r; double data[]; while(FrameNext(pass, name, id, r, data)) { // compare r with all other passes results if(r > best) { best = r; ArrayCopy(location, data); } Print(passcount, " ", id); const int n = ArraySize(data); ArrayResize(data, n + 1); data[n] = r; ArrayPrint(data, 12); passcount++; } } void OnTesterDeinit() { Print("Solution: ", best); ArrayPrint(location); }
No log são registrados o contador de execuções, seu número de sequência (pode diferir em tarefas complexas, quando uma thread ultrapassa outra devido a diferenças nos dados), o valor da função objetivo e os parâmetros correspondentes. A decisão final é exibida em OnTesterDeinit.
Também faremos com que o Expert Advisor possa ser iniciado não apenas no testador, mas também num gráfico regular. Nesse caso, o algoritmo PSO funcionará no modo regular de thread única.
int OnInit() { if(!MQLInfoInteger(MQL_TESTER)) { EventSetTimer(1); } return INIT_SUCCEEDED; } void OnTimer() { EventKillTimer(); OnTester(); }
Vamos ver como isso funciona. Vamos escolher valores específicos dos parâmetros de entrada:
- Cycles — 100;
- TestCase — Griewank;
- SwarmSize — 100;
- GroupCount — 10;
Ao colocar um Expert Advisor no gráfico, teremos aproximadamente o seguinte log.
Successive PSO of Griewank PSO[2] created: 100/10 PSO Processing... Cycle 0 done, skipped 0 of 100 / -1.000317162069485 Cycle 10 done, skipped 0 of 100 / -0.2784790501384311 Cycle 20 done, skipped 0 of 100 / -0.1879188508394087 Cycle 30 done, skipped 0 of 100 / -0.06938172138150922 Cycle 40 done, skipped 0 of 100 / -0.04958694402304631 Cycle 50 done, skipped 0 of 100 / -0.0045818974357138 Cycle 60 done, skipped 0 of 100 / -0.0045818974357138 Cycle 70 done, skipped 0 of 100 / -0.002161613760466419 Cycle 80 done, skipped 0 of 100 / -0.0008991629607246754 Cycle 90 done, skipped 0 of 100 / -1.620636881582982e-05 Cycle 99 done, skipped 0 of 100 / -1.342285474092986e-05 PSO Finished 9948 of 10000 planned calculations: true Solution: -1.342285474092986e-05 0 0.004966759354110293 1 0.002079707592422949
Como os casos de teste são calculados muito rapidamente (em um ou dois segundos), não faz sentido medir o tempo. Para tarefas reais de negociação, faremos isso mais tarde.
Agora selecionamos o EA no testador, definimos “Cálculos matemáticos” na lista "Modelagem", deixamos os parâmetros do EA como os anteriores, exceto para GroupCount. A otimização será realizada para este parâmetro, portanto, os valores inicial e final serão definidos, por exemplo, como 0 e 3, respectivamente, com um passo de 1, para que 4 grupos sejam processados (com base no número de núcleos). Nesse caso, todos os grupos terão um tamanho de 100 (SwarmSize, o enxame inteiro). Quando o número de núcleos de processador é suficiente (se todos os grupos trabalharem em paralelo nos agentes), isso não deve afetar o desempenho e aumentará a precisão da solução devido a verificações adicionais do espaço de otimização. Obteremos aproximadamente o seguinte log.
Parallel PSO of Griewank -12.550070232909 -0.002332638407 -0.039510275469 -3.139749741924 4.438437934965 -0.007396077598 3.139620588383 4.438298282495 -0.007396126543 0.000374731767 -0.000072178955 -0.000000071551 Solution: -7.1550806279852e-08 (after 4 passes) 0.00037 -0.00007
Assim, garantimos que o algoritmo PSO ficasse disponível em sua modificação paralela no testador no modo de otimização. Mas até agora este foi apenas um teste usando "cálculos matemáticos". É hora de adaptar o PSO para otimizar os Expert Advisors num ambiente de negociação.
Virtualização e otimização do Expert Advisor (MQL4 API no MetaTrader 5)
Para otimizar Expert Advisors usando o motor PSO, é necessário implementar functores capazes de simular negociação com base no histórico e manter estatísticas de seus indicadores, tudo isso a partir de um conjunto de parâmetros de entrada.
Isso cria um dilema que muitos desenvolvedores de aplicativos enfrentam ao escrever seu próprio otimizador sobre e/ou em vez do padrão, ou seja, como fornecer um ambiente de negociação, antes de tudo, cotações, mas também o estado da conta, incluindo o arquivo de transações. Se usarmos o modo de cálculos matemáticos, precisaremos preparar de alguma forma e, em seguida, transferir os dados correspondentes para o EA (para os agentes). Além disso, será necessário desenvolver uma camada intermediária de API, que emula "transparentemente" muitas funções de negociação, para permitir que o Expert Advisor trabalhe por analogia com o modo online usual.
Para não fazer isso, decidimos usar uma solução existente para negociação virtual, criada inteiramente em MQL e utilizando estruturas de dados históricos padrão, em particular ticks e barras. Estamos falando sobre a biblioteca Virtual (autor fxsaber). Ela permite calcular a execução virtual de um Expert Advisor com base no histórico disponível tanto online (por exemplo, para auto-otimização periódica no gráfico) quanto no testador. É claro que, neste último caso, qualquer modo de tick usual ("Cada tick", "Cada tick baseado em ticks reais") ou mesmo "OHLC em M1" é usado para uma estimativa rápida, mas mais grosseira do sistema (o número de ticks é limitado a 4 em minuto).
Depois de incluir o arquivo de cabeçalho Virtual.mqh (baixado com as dependências necessárias) no código do EA, é fácil realizar um teste virtual usando as seguintes strings:
MqlTick _ticks[]; // global array ... // copy/collect ticks[] VIRTUAL::Tester(_ticks, OnTick /*, TesterStatistics(STAT_INITIAL_DEPOSIT)*/ ); Print(VIRTUAL::ToString(INT_MAX)); // output virtual trades in the log const double result = TesterStatistics(STAT_PROFIT); // get required performance meter VIRTUAL::ResetTickets(); // optional VIRTUAL::Delete(); // optional
O método estático VIRTUAL::Tester faz todo o trabalho. Será necessário transferir a ele uma matriz pré-preenchida de ticks com base no período histórico desejado, bem como o nível de detalhe, um ponteiro para a função OnTick (um manipulador padrão também vem a calhar se a lógica para alternar de negociação online para virtual estiver incorporada nele), bem como um depósito inicial (isso é opcional; se não for especificado, será usado o saldo atual da conta). Se colocarmos o fragmento - mostrado acima - no manipulador OnTester (como faremos), podemos transferir o depósito inicial do testador. Podemos saber o resultado da negociação virtual chamando a função TesterStatistics, que, após anexar a biblioteca, acaba sendo, de fato, "sobreposta", como muitas outras funções da API MQL (quem quiser pode olhar o código-fonte). Essa "sobreposição" é inteligente o suficiente para delegar chamadas à função do kernel original onde está acontecendo realmente o trading. Observe que nem todos os indicadores padrão de TesterStatistics são calculados na biblioteca durante a negociação virtual.
Uma característica da biblioteca é que ela é baseada na API de negociação MetaTrader 4. Em outras palavras, é aplicável apenas a EAs que usam funções "antigas" em seu código, embora sejam escritos em MQL5. Eles funcionam no ambiente MetaTrader 5 graças a outra biblioteca bem conhecida do mesmo autor, a MT4Orders.
Usaremos como cobaia uma modificação do Expert Advisor ExprBot.mq5, que foi originalmente apresentado no artigo Calculando Expressões Matemáticas (Parte 2). Ele é implementado apenas usando MT4Orders. Uma nova versão chamada ExprBotPSO.mq5 está anexada a este artigo.
O Expert Advisor usa um mecanismo de análise para calcular sinais de negociação com base em expressões. Como isso é útil para nós ficará claro um pouco mais tarde. Vamos deixar a estratégia de negociação igual, a interseção de duas médias móveis, levando em consideração o limite de divergência especificado. Vamos relembrar como eram as configurações junto com as expressões para sinais, elas não requerem muita explicação, uma vez que falam por si só:
input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold"; input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold"; input string Variables = "Threshold=0.001"; input int Fast = 10; input int Slow = 21;
Se você tiver alguma dúvida sobre como as variáveis de entrada são substituídas em expressões e como as funções EMA embutidas são integradas com o indicador correspondente, é recomendável ler o artigo mencionado. O novo robô funciona com os mesmos princípios e iremos melhorá-lo ligeiramente.
Observe que o mecanismo de análise foi atualizado para a versão v1.1 e também está incluído. Sua versão antiga, se tiver sido baixada antes, não funcionará.
Além dos parâmetros de entrada para sinais (sobre os quais ainda teremos que discutir uma nuance), ao EA foram adicionados parâmetros para gerenciar o teste virtual e o algoritmo PSO.
- VirtualTester — sinalizador para habilitar teste virtual e/ou otimização; por padrão false, o que significa operação normal;
- Estimator — indicador com base no qual é realizada a otimização, por padrão STAT_PROFIT;
- InternalOptimization — sinalizador para habilitar a otimização em nodo virtual, por padrão false, o que significa negociação virtual com uma única passagem; definir true iniciará a otimização interna pelo método PSO;
- PSO_Enable — habilitar/desabilitar PSO;
- PSO_Cycles — número de ciclos de recálculo do algoritmo PSO em cada execução; quanto maior for, melhor será a qualidade da pesquisa PSO, mas mais tempo levará uma única passagem sem feedback (registro no log);
- PSO_SwarmSize — tamanho do enxame; por padrão 0, o que significa seleção empírica automática com base no número de parâmetros;
- PSO_GroupCount — número de grupos; um parâmetro incremental para realizar várias execuções, começando de 0 até o número de kernels/agentes, para avaliar desempenho e qualidade; aumentar ainda mais;
- PSO_RandomSeed — randomizador; em cada grupo, o número do grupo é adicionado a ele, de modo que todos inicializam de forma diferente;
No modo VirtualTester, o EA coleta apenas tiques no OnTick numa matriz. Em seguida, no OnTester a biblioteca Virtual opera com base nesta matriz, chamando o mesmo manipulador OnTick, mas com um sinalizador pronto especial que permite a execução de código com operações virtuais.
Bem, para cada valor incrementado de PSO_GroupCount num agente separado, é executado um ciclo desde o PSO_Cycles de recálculos de enxame com o tamanho PSO_SwarmSize de partículas. Ao todo, obtemos uma verificação para PSO_GroupCount * PSO_Cycles * PSO_SwarmSize = N pontos no espaço de otimização. Cada ponto é uma execução virtual do sistema de negociação.
Os melhores resultados exigirão tentativa e erro para encontrar os parâmetros PSO corretos. Dado o número total de testes N, os componentes podem ser variados. Devido a acertos aleatórios nos mesmos pontos (lembre-se, eles são armazenados numa árvore binária dentro de um enxame), o número final de testes será menor que N.
A troca de dados entre os agentes ocorre apenas no momento do envio da próxima tarefa. As tarefas que são executadas em paralelo também não veem os resultados umas das outras e podem calcular várias coordenadas idênticas com alguma probabilidade.
Obviamente, ao ExprBotPSO foram adicionadas classes de functores, que geralmente são semelhantes às que vimos nos exemplos anteriores. Em particular, o método de teste, como esperado, instancia o enxame, executa a otimização e armazena os resultados em variáveis-membros (optimum, result[]).
class BaseFunctor: public Functor { ... public: virtual bool test(void) { Swarm swarm(PSO_SwarmSize, PSO_GroupCount, params, max, min, steps); if(MQLInfoInteger(MQL_OPTIMIZATION)) { if(!swarm.restoreIndex()) return false; } optimum = swarm.optimize(this, PSO_Cycles); swarm.getSolution(result); if(MQLInfoInteger(MQL_OPTIMIZATION)) { swarm.exportIndex(PSO_GroupCount); } return true; } };
No entanto, esta é a primeira vez que vemos como são usados os métodos restoreIndex e exportIndex descritos nas seções anteriores. As tarefas de otimização para um Expert Advisor geralmente requerem um grande número de cálculos (parâmetros e grupos, cada grupo precisa de uma execução do testador), por isso, os agentes precisarão trocar informações.
O teste virtual de um Expert Advisor é realizado no método de cálculo de acordo com o esquema declarado. Mas uma nova classe, Settings, está envolvida na inicialização do espaço de otimização.
class WorkerFunctor: public BaseFunctor { string names[]; public: WorkerFunctor(const Settings &s): BaseFunctor(s.size()) { s.getNames(names); for(int i = 0; i < params; i++) { max[i] = s.get<double>(i, SET_COLUMN_STOP); min[i] = s.get<double>(i, SET_COLUMN_START); steps[i] = s.get<double>(i, SET_COLUMN_STEP); } } virtual double calculate(const double &vec[]) { VIRTUAL::Tester(_ticks, OnTick, TesterStatistics(STAT_INITIAL_DEPOSIT)); VIRTUAL::ResetTickets(); const double r = TesterStatistics(Estimator); VIRTUAL::Delete(); return r; } };
O ponto é que, para iniciar a otimização, o usuário irá configurar os parâmetros de entrada do Expert Advisor da maneira usual. No entanto, o algoritmo de enxame usa o testador apenas como um meio de paralelizar tarefas (aumentando o número do grupo). Assim, nosso especialista deve ser capaz de ler as configurações dos parâmetros operacionais para otimização, salvá-los num arquivo auxiliar transmitido a cada agente, redefinir essas configurações no testador e atribuir a otimização por número de grupo. A classe Settings se destina apenas a ler as configurações de um arquivo auxiliar. Para nós ele será "expert_name.mq5.csv", que deve ser anexado usando a diretiva.
#define PPSO_SHARED_SETTINGS __FILE__ + ".csv" #property tester_file PPSO_SHARED_SETTINGS
Recomendamos que você se familiarize com a classe Settings. Ela lê o arquivo CSV linha por linha, assumindo as seguintes colunas:
#define MAX_COLUMN 4 #define SET_COLUMN_NAME 0 #define SET_COLUMN_START 1 #define SET_COLUMN_STEP 2 #define SET_COLUMN_STOP 3
Todas elas são lembradas em matrizes internas e estão disponíveis por meio de métodos get por nome ou número. O método isVoid() retorna uma indicação da ausência de configurações (o arquivo não pôde ser lido, está vazio ou no formato errado).
As configurações são gravadas num arquivo no manipulador OnTesterInit (veja
Recomenda-se criar imediatamente manualmente um arquivo vazio "expert_name.mq5.csv" na pasta MQL5/Files. Se isso não for feito, haverá problemas para executar a otimização pela primeira vez.
Infelizmente, na primeira inicialização, o testador, embora crie este arquivo automaticamente, não o envia aos agentes, razão pela qual a inicialização do Expert Advisor neles termina com o erro INIT_PARAMETERS_INCORRECT. Reiniciá-lo também não o enviará, pois o testador, aparentemente, armazena em cache informações sobre os recursos anexados e não leva em consideração o arquivo que aparece até que o usuário selecione o EA na lista suspensa das configurações do testador. Só depois esse arquivo começará a ser atualizado normalmente e enviado aos agentes. Portanto, é mais fácil criá-lo manualmente de antemão.
string header[]; void OnTesterInit() { int h = FileOpen(PPSO_SHARED_SETTINGS, FILE_ANSI|FILE_WRITE|FILE_CSV, ','); if(h == INVALID_HANDLE) { Print("FileSave error: ", GetLastError()); } MqlParam parameters[]; string names[]; EXPERT::Parameters(0, parameters, names); for(int i = 0; i < ArraySize(names); i++) { if(ResetOptimizableParam<double>(names[i], h)) { const int n = ArraySize(header); ArrayResize(header, n + 1); header[n] = names[i]; } } FileClose(h); // 5008 bool enabled; long value, start, step, stop; if(ParameterGetRange("PSO_GroupCount", enabled, value, start, step, stop)) { if(!enabled) { const int cores = TerminalInfoInteger(TERMINAL_CPU_CORES); Print("PSO_GroupCount is set to default (number of cores): ", cores); ParameterSetRange("PSO_GroupCount", true, 0, 1, 1, cores); } } // remove CRC indices from previous optimization runs Swarm::removeIndex(); }
A função adicional ResetOptimizableParam é responsável por encontrar os parâmetros para os quais o sinalizador de otimização está habilitado e redefinir esses sinalizadores. Também em OnTesterInit lembramos os nomes desses parâmetros usando a biblioteca Expert (autor fxsaber), para exibir os resultados com mais clareza posteriormente. Mas a biblioteca foi necessária principalmente porque para chamar as funções ParameterGetRange/ParameterSetRange padrão, precisamos saber os nomes com antecedência, e já a API MQL não permite que obtenhamos a lista de parâmetros. Ao mesmo tempo, eu queria tornar o código o mais versátil possível: adequado para inserção num Expert Advisor arbitrário sem quaisquer edições especiais.
template<typename T> bool ResetOptimizableParam(const string name, const int h) { bool enabled; T value, start, step, stop; if(ParameterGetRange(name, enabled, value, start, step, stop)) { // disable all native optimization except for PSO-related params // preserve original settings in the file h if((StringFind(name, "PSO_") != 0) && enabled) { ParameterSetRange(name, false, value, start, step, stop); FileWrite(h, name, start, step, stop); // 5007 return true; } } return false; }
No manipulador OnInit, que já é executado no agente, as configurações são lidas no objeto Settings globais da seguinte maneira.
Settings settings; int OnInit() { ... FileReader f(PPSO_SHARED_SETTINGS); if(f.isReady() && f.read(settings)) { const int n = settings.size(); Print("Got settings: ", n); } else { if(MQLInfoInteger(MQL_OPTIMIZATION)) { Print("FileLoad error: ", GetLastError()); return INIT_PARAMETERS_INCORRECT; } else { Print("WARNING! Virtual optimization inside single pass - slowest mode, debugging only"); } } ... }
Como veremos mais adiante, este objeto é passado para o objeto WorkerFunctor criado no manipulador OnTester, dentro do qual são realizados todos os cálculos e otimizações. Mas, para começar a calcular, devemos primeiro coletar os ticks. Isso acontece no manipulador OnTick.
bool OnTesterCalled = false; void OnTick() { if(VirtualTester && !OnTesterCalled) { MqlTick _tick; SymbolInfoTick(_Symbol, _tick); const int n = ArraySize(_ticks); ArrayResize(_ticks, n + 1, n / 2); _ticks[n] = _tick; return; // skip all time scope and collect ticks } ... // trading goes on here }
Por que isso é feito dessa maneira e não chamando a função CopyTicksRange diretamente no OnTester? Em primeiro lugar, esta função funciona apenas nos modos tick-by-tick, e é bom ter suporte para o modo rápido OHLC M1 (4 ticks por minuto). Em segundo lugar, no modo de geração de ticks, o tamanho da matriz retornada, por algum motivo, é limitado a 131 072 (não há tal restrição ao trabalhar com ticks reais).
A variável OnTesterCalled é inicialmente igual a false e, por isso, é coletado o histórico de ticks. OnTesterCalled é definido como true posteriormente, como seu nome indica, em OnTester, antes de iniciar o PSO. Então o objeto Swarm começa a calcular o functor num loop onde, como vimos acima, VIRTUAL::Tester é chamado com uma referência ao mesmo OnTick. Só agora OnTesterCalled será true e o controle será transferido não para o bloco de montagem de ticks, mas para o bloco de lógica de negociação. Vamos falar sobre isso a seguir. No futuro, à medida que a biblioteca PSO se desenvolve, os mecanismos podem parecer simplificar a integração em EAs existentes, substituindo o manipulador OnTick no arquivo de cabeçalho da própria biblioteca.
E agora o próprio OnTester (de forma simplificada).
double OnTester() { if(VirtualTester) { OnTesterCalled = true; // MQL API implies some limitations for CopyTicksRange function, so ticks are collected in OnTick const int size = ArraySize(_ticks); PrintFormat("Ticks size=%d error=%d", size, GetLastError()); if(size <= 0) return 0; if(settings.isVoid() || !InternalOptimization) // fallback to a single virtual test without PSO { VIRTUAL::Tester(_ticks, OnTick, TesterStatistics(STAT_INITIAL_DEPOSIT)); Print(VIRTUAL::ToString(INT_MAX)); Print("Trades: ", VIRTUAL::VirtualOrdersHistoryTotal()); return TesterStatistics(Estimator); } settings.print(); const int n = settings.size(); if(PSO_Enable) { MathSrand(PSO_GroupCount + PSO_RandomSeed); // reproducable randomization WorkerFunctor worker(settings); Swarm::Stats stats; if(worker.test(&stats)) { double output[]; double result = worker.getSolution(output); if(MQLInfoInteger(MQL_OPTIMIZATION)) { FrameAdd(StringFormat("PSO%d/%d", stats.done, stats.planned), PSO_GroupCount, result, output); } ArrayResize(output, n + 1); output[n] = result; ArrayPrint(output); return result; } } ... return 0; } return TesterStatistics(Estimator); }
Aqui vemos apenas a criação do functor WorkerFunctor com base num conjunto de parâmetros do objeto settings e a inicialização do enxame usando seu método test. Os resultados obtidos são enviados como um quadro para o terminal, de onde são enviados para o OnTesterPass.
O manipulador OnTesterPass é semelhante ao EA de teste PPSO, só que nele os dados recebidos nos quadros são enviados não para o log, mas para um arquivo CSV com um nome do tipo PPSO-name_expert-date_time.
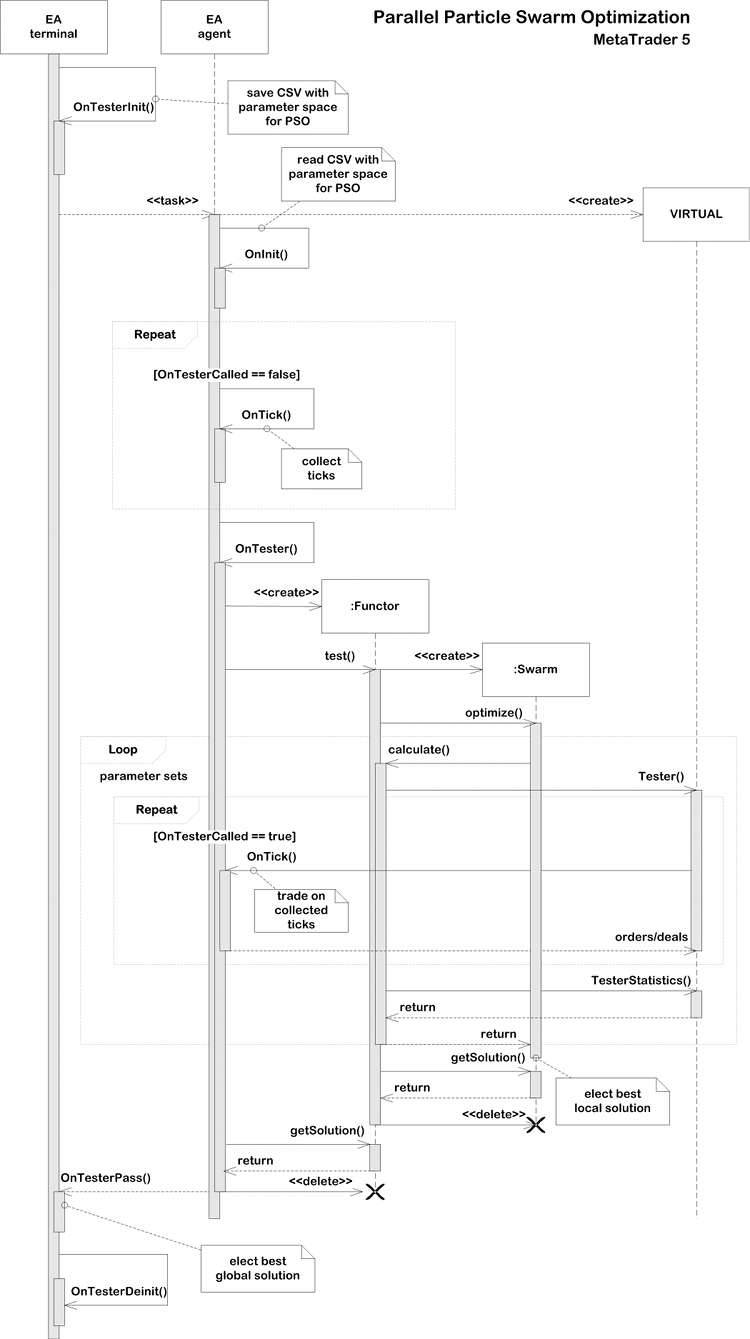
Diagrama de sequência da Parallel Particle Swarm Optimization
Vamos finalmente regressar à estratégia de negociação. Em essência, permanece a mesma que no artigo mencionado Cálculo de expressões matemáticas (Parte 2).. No entanto, para negociação virtual precisam ser feitos alguns ajustes. As fórmulas anteriores para sinais calculam os indicadores EMA com base nos preços de abertura numa barra zero:
input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold"; input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold";
Agora eles devem ser lidos a partir de barras históricas (afinal, os cálculos são feitos no final da passagem, a partir do OnTester). É muito fácil descobrir o número da barra "atual" no passado: a biblioteca virtual substitui a função do sistema TimeCurrent e, por isso, podemos escrever no OnTick:
const int bar = iBarShift(_Symbol, PERIOD_CURRENT, TimeCurrent());
O número da barra real deve ser adicionado com um nome adequado à tabela de variáveis para expressões, por exemplo, "Bar", e então as fórmulas de sinal podem ser reescritas da seguinte forma:
input string SignalBuy = "EMA_OPEN_{Fast}(Bar)/EMA_OPEN_{Slow}(Bar) > 1 + Threshold"; input string SignalSell = "EMA_OPEN_{Fast}(Bar)/EMA_OPEN_{Slow}(Bar) < 1 - Threshold";
Na versão atualizada dos analisadores, a alteração da variável (número da barra) e o cálculo da fórmula é feito com uma chamada intermediária do novo método with (também em OnTick):
const int bar = iBarShift(_Symbol, PERIOD_CURRENT, TimeCurrent()); // NEW bool buy = p1.with("Bar", bar).resolve(); // WAS: bool buy = p1.resolve(); bool sell = p2.with("Bar", bar).resolve(); // WAS: bool sell = p2.resolve();
Depois, todo o código de negociação OnTick permanece inalterado.
Mas as correções necessárias não param por aí.
As fórmulas atuais mostradas usam os períodos fixos do EMA especificados nas configurações e convertidos em variáveis dentro das expressões. No entanto, durante o processo de otimização, esses períodos precisam ser alterados, o que significa diferentes instâncias de indicadores. Mas, afinal, a otimização virtual com ajustes de parâmetros um enxame ocorre _dentro_ da execução do testador, bem no final, na função OnTester. É tarde demais para criar identificadores de indicadores.
Este problema é de natureza global para qualquer otimização virtual e suas 3 soluções mais óbvias são:
- não usar indicadores; os sistemas de negociação inicialmente sem indicadores têm uma vantagem aqui;
- considerar os indicadores de maneira especial e independente dentro do EA; muitos traders fazem exatamente isso, porque esta é a maneira mais rápida, mesmo em comparação com os indicadores padrão; mas também é o mais trabalhoso;
- criar um conjunto de indicadores com antecedência para todas as combinações de parâmetros das configurações; uso intensivo de recursos; pode exigir a limitação da faixa de parâmetros;
O último método deixa uma questão em aberto relacionada com sistemas que calculam sinais em modo tick-by-tick. Acontece que todas as barras do histórico virtual já estão fechadas e os indicadores já estão construídos. Em outras palavras, apenas estão disponíveis sinais de barras. Se com base em tal histórico executarmos o sistema sem controlar a abertura de barra, haverá muito menos transações e serão de qualidade inferior do que a não virtual com base em ticks.
Em nosso Expert Advisor, como a negociação é realizada por barras, isso não é um problema. Em alguns exemplos de Expert Advisors fornecidos com MetaTrader 5, este também é o caso, mas devemos prestar atenção em como é detectado o evento de uma nova abertura de barra. O método com um único controle de volume de tick não é adequado para histórico virtual, porque todas as barras já estão preenchidas com ticks. Portanto, recomenda-se definir uma nova barra comparando seu tempo com o anterior.
Para resolver esse problema, o motor de expressão foi estendido de uma terceira forma. Além das funções de indicadores MA individuais (MAIndicatorFunc), são criadas funções leques MA (MultiMAIndicatorFunc, veja Indicators.mqh). Seu nome deve começar com o prefixo "M_" e conter o período mínimo, passo do período e período máximo, por exemplo:
input string SignalBuy = "M_EMA_OPEN_9_6_27(Fast,Bar)/M_EMA_OPEN_9_6_27(Slow,Bar) > 1 + T"; input string SignalSell = "M_EMA_OPEN_9_6_27(Fast,Bar)/M_EMA_OPEN_9_6_27(Slow,Bar) < 1 - T";
O método de cálculo e o tipo de preço são indicados no nome como antes. Aqui nos sinais é prescrito criar um leque EMA com base no preço OPEN com períodos de 9 a 27 (inclusive), com um incremento de 6.
Outra inovação na biblioteca de expressões é um conjunto de variáveis que fornecem acesso às estatísticas de negociação desde TesterStatistics (veja TesterStats.mqh). Com base nela, agora é possível adicionar a variável de entrada Formula ao Expert Advisor para definir o indicador de destino na forma de uma expressão arbitrária. Quando esta variável é preenchida, o Estimator é ignorado. Em particular, em vez de STAT_PROFIT_FACTOR (que é indefinido para perdas zero) no Estimator, podemos definir um indicador mais suave com uma fórmula semelhante: "(GROSSPROFIT-(1/(TRADES+1)))/-(GROSSLOSS-1/(TRADES+1))".
Bem, tudo está pronto para iniciar a otimização da negociação virtual usando o método PSO.
Testando na prática
Vamos preparar um testador. Deve usar uma otimização lenta, ou seja, busca exaustiva completa de parâmetros. No nosso caso, não será lenta, porque em cada execução apenas o número do grupo muda, e a enumeração seletiva dos parâmetros de trabalho do EA é realizada por um enxame dentro de seu ciclo. Não podemos usar a genética por três motivos. Em primeiro lugar, não garante que todas as combinações de parâmetros serão calculadas (no nosso caso, um determinado número de grupos). Em segundo lugar, devido à sua especificidade, ele irá "se deslocar" gradualmente em direção aos parâmetros que deram um resultado mais atraente, não levando em consideração o fato de que não há dependência entre o número do grupo e seu sucesso - o número do grupo apenas atua como um randomizador da estrutura de dados PSO. Em terceiro lugar, o número de grupos geralmente não é tão grande, a genética é incluída.
A otimização é realizada de acordo com o critério personalizado máximo.
Primeiro, otimizamos o Expert Advisor da maneira padrão, com a biblioteca virtual desabilitada (arquivo com configurações ExprBotPSO-standard-optimization.set). O número de combinações de parâmetros para otimização é escolhido pequeno para fins de demonstração. Os parâmetros Fast e Slow mudam de 9 a 45 com incremento de 6, o parâmetro T muda de 0 a 0,01 com incremento de 0,0025.
EURUSD, H1, desde o início de 2020, com base em ticks reais. Obtemos aproximadamente os seguintes resultados:
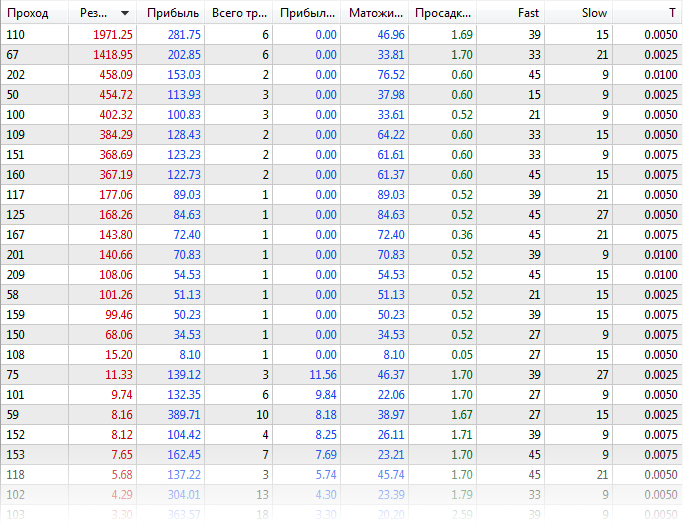
Tabela de resultados da otimização padrão
No log, vamos ver quanto tempo levou nos dois agentes - quase 21 minutos.
Experts optimization frame expert ExprBotPSO (EURUSD,H1) processing started Tester Experts\ExprBotPSO.ex5 on EURUSD,H1 from 2020.01.01 00:00 to 2020.08.01 00:00 Tester complete optimization started ... Core 2 connected Core 1 connected Core 2 authorized (agent build 2572) Core 1 authorized (agent build 2572) ... Tester optimization finished, total passes 245 Statistics optimization done in 20 minutes 55 seconds Statistics shortest pass 0:00:05.691, longest pass 0:00:23.114, average pass 0:00:10.206
Agora vamos otimizar o Expert Advisor com negociação virtual e PSO habilitado (ExprBotPSO-virtual-pso-optimization.set). O número de grupos igual a 4 é determinado pela iteração do parâmetro PSO_GroupCount de 0 a 3. Outros parâmetros operacionais para os quais a otimização está habilitada serão desabilitados à força na otimização geral, mas transferidos para os agentes em arquivos CSV para otimização virtual interna usando o algoritmo PSO.
Na simulação, sairemos do modo de ticks reais, mas também foi possível usar a geração ou OHLC M1 para cálculos rápidos. Cálculos matemáticos não serão adequados, uma vez que coletamos ticks no testador para negociação virtual.
No log do testador, obtemos algo assim:
Tester input parameter 'Fast' set to: enable=false, value=9, start=9, step=6, stop=45 Tester input parameter 'Slow' set to: enable=false, value=21, start=9, step=6, stop=45 Tester input parameter 'T' set to: enable=false, value=0, start=0, step=0.0025, stop=0.01 Experts optimization frame expert ExprBotPSO (EURUSD,H1) processing started Tester Experts\ExprBotPSO.ex5 on EURUSD,H1 from 2020.01.01 00:00 to 2020.08.01 00:00 Tester complete optimization started ... Core 1 connected Core 2 connected Core 2 authorized (agent build 2572) Core 1 authorized (agent build 2572) ... Tester optimization finished, total passes 4 Statistics optimization done in 4 minutes 00 seconds Statistics shortest pass 0:01:27.723, longest pass 0:02:24.841, average pass 0:01:56.597 Statistics 4 frames (784 bytes total, 196 bytes per frame) received
Cada passagem é agora um pacote de otimizações virtuais, por isso agora é mais longo, mas em geral há menos e o tempo total foi reduzido significativamente para 4 minutos.
No log do terminal, receberemos mensagens desde quadros (os melhores indicadores de cada grupo). É verdade que os indicadores de negociação real e virtual são ligeiramente diferentes.
22:22:52.261 ExprBotPSO (EURUSD,H1) 2 tmp-files deleted 22:25:07.981 ExprBotPSO (EURUSD,H1) 0 PSO75/1500 0 1974.400000000025 22:25:23.348 ExprBotPSO (EURUSD,H1) 2 PSO84/1500 2 402.6000000000062 22:26:51.165 ExprBotPSO (EURUSD,H1) 3 PSO70/1500 3 455.000000000003 22:26:52.451 ExprBotPSO (EURUSD,H1) 1 PSO79/1500 1 458.3000000000047 22:26:52.466 ExprBotPSO (EURUSD,H1) Solution: 1974.400000000025 22:26:52.466 ExprBotPSO (EURUSD,H1) 39.00000 15.00000 0.00500
É necessário ressaltar que os resultados não coincidirão exatamente (mesmo se tivéssemos uma estratégia sem indicadores sem ticks), porque há nuances a nível do trabalho do testador que não podem ser repetidas na biblioteca MQL. Aqui estão apenas alguns delas:
- ordens limitadas perto do preço de mercado podem ser acionadas de maneiras diferentes;
- a margem não é calculada ou não é calculada com precisão;
- a comissão não é considerada automaticamente (restrição API MQL), mas pode ser programada através de parâmetros de entrada adicionais;
- o registro de ordens e transações, quando é usada compensação, pode ser diferente;
- apenas é suportado o símbolo atual;
Mais informações sobre a biblioteca virtual podem ser encontradas em sua documentação e discussões.
Para fins de depuração e para compreender o processo de trabalho do enxame, o EA de teste suporta o modo de otimização virtual num kernel dentro de uma execução normal do testador. Um exemplo de configurações está anexado no arquivo ExprBotPSO-virtual-internal-optimization-single-pass.set. Não se esqueça de desabilitar a otimização no testador.
Nesse caso, os resultados intermediários são gravados em detalhes no log do testador. Em cada ciclo, a posição e o valor da função objetivo de cada partícula são derivados dos PSO_Cycles fornecidos. Se a partícula atingir as coordenadas já verificadas, o cálculo será ignorado.
Ticks size=15060113 error=0
[,0] [,1] [,2] [,3]
[0,] "Fast" "9" "6" "45"
[1,] "Slow" "9" "6" "45"
[2,] "T" "0" "0.0025" "0.01"
PSO[3] created: 15/3
PSO Processing...
Fast:9.0, Slow:33.0, T:0.0025, 1.31285
Fast:21.0, Slow:21.0, T:0.0025, -1.0
Fast:15.0, Slow:33.0, T:0.0075, -1.0
Fast:27.0, Slow:39.0, T:0.0025, 0.07673
Fast:9.0, Slow:9.0, T:0.005, -1.0
Fast:33.0, Slow:21.0, T:0.01, -1.0
Fast:39.0, Slow:45.0, T:0.0025, -1.0
Fast:15.0, Slow:15.0, T:0.0025, -1.0
Fast:33.0, Slow:21.0, T:0.0, 0.32895
Fast:33.0, Slow:39.0, T:0.0075, -1.0
Fast:33.0, Slow:15.0, T:0.005, 384.5
Fast:15.0, Slow:27.0, T:0.0, 2.44486
Fast:39.0, Slow:27.0, T:0.0025, 11.41199
Fast:9.0, Slow:15.0, T:0.0, 1.08838
Fast:33.0, Slow:27.0, T:0.0075, -1.0
Cycle 0 done, skipped 0 of 15 / 384.5000000000009
...
Fast:45.0, Slow:9.0, T:0.0025, 0.86209
Fast:21.0, Slow:15.0, T:0.005, -1.0
Cycle 15 done, skipped 13 of 15 / 402.6000000000062
Fast:21.0, Slow:15.0, T:0.0025, 101.4
Cycle 16 done, skipped 14 of 15 / 402.6000000000062
Fast:27.0, Slow:15.0, T:0.0025, 8.18754
Fast:39.0, Slow:15.0, T:0.005, 1974.40002
Cycle 17 done, skipped 13 of 15 / 1974.400000000025
Fast:45.0, Slow:9.0, T:0.005, 1.00344
Cycle 18 done, skipped 14 of 15 / 1974.400000000025
Cycle 19 done, skipped 15 of 15 / 1974.400000000025
PSO Finished 89 of 1500 planned calculations: true
39.00000 15.00000 0.00500 1974.40000
final balance 10000.00 USD
OnTester result 1974.400000000025
Como o espaço de otimização é pequeno, ele foi completamente coberto no ciclo 19. Claro, isso não acontecerá para problemas reais com milhões de combinações. Para eles, é muito importante escolher a combinação certa de PSO_Cycles, PSO_SwarmSize, PSO_GroupCount por tentativa e erro.
Não se esqueça de que, com o PSO, uma passagem do testador para cada PSO_GroupCount é executada internamente até PSO_Cycles*PSO_SwarmSize passagens únicas virtuais, de modo que a indicação de progresso será significativamente mais lenta do que o normal.
Muitos traders tentam obter os melhores resultados da otimização genética incorporada, executando-a várias vezes seguidas - isso coleta vários testes devido à inicialização aleatória e, após várias execuções, há uma chance de encontrar progresso. No caso do PSO, PSO_GroupCount atua como um análogo do lançamento de genética múltipla. O número de execuções únicas, que em genética pode chegar a 10 000, deve ser distribuído na PSO entre os dois componentes do produto PSO_Cycles*PSO_SwarmSize, por exemplo, 100*100. PSO_Cycles é análogo a gerações em genética e PSO_SwarmSize é o tamanho da população.
Virtualização de EAs da API MQL5
Até agora, estudamos um exemplo de Expert Advisor escrito usando a API de negociação MQL4. Isso se deve às peculiaridades de implementação de Virtual. Ao mesmo tempo, gostaria de aplicar PSO para EAs com as "novas" funções da API MQL5. Para este propósito, foi desenvolvida uma camada intermediária experimental para redirecionar chamadas de API MQL5 para API MQL4. Ela é projetada como um arquivo MT5Bridge.mqh, que requer a biblioteca Virtual e/ou MT4Orders para seu funcionamento.
#include <fxsaber/Virtual/Virtual.mqh> #include <MT5Bridge.mqh> #include <Expert\Expert.mqh> #include <Expert\Signal\SignalMA.mqh> #include <Expert\Trailing\TrailingParabolicSAR.mqh> #include <Expert\Money\MoneySizeOptimized.mqh> ...
Após adicionar Virtual e MT5Bridge no início do código, antes de outros #include, a chamada para as funções da API MQL5 passa pelas funções "ponte" redefinidas, a partir das quais as funções da API MQL4 "virtuais" são chamadas. Como resultado, é possível testar e otimizar virtualmente o Expert Advisor. Em particular, é possível realizar a otimização PSO da mesma forma que foi feito no ExprBotPSO. Precisaremos escrever (copiar parcialmente) um functor e manipuladores para o testador. Mas pode ser a adaptação mais demorada de geração de sinal de indicadores para parâmetros variáveis.
O status experimental de MT5Bridge.mqh indica que sua funcionalidade não foi amplamente testada. Esta é uma pesquisa de tipo "Proof Of the Concept". Use o código-fonte para depuração e correção de bugs.
Fim do artigo
Analisamos o algoritmo de otimização por meio do método de enxame de partículas e o implementamos em MQL com suporte para multithreading nos agentes do testador. A presença de configurações PSO abertas permite que o processo seja regulado com mais flexibilidade do que usar a otimização genética integrada. Além das configurações que agora estão nos parâmetros de entrada, faz sentido brincar com outros coeficientes adaptáveis, que até agora foram usados como argumentos para o método de otimização com valores padrão: inertia (0,8), selfBoost (0,4), groupBoost (0,4). Isso sem dúvida adicionará flexibilidade ao algoritmo, mas também tornará difícil selecionar configurações para uma tarefa específica. A biblioteca PSO fornecida pode ser usada tanto no modo de cálculos matemáticos (se você desenvolver seu próprio mecanismo para cotações, indicadores e trades virtuais), quanto nos modos de barra-tick usando classes de emulação de negociação prontas de terceiros, como Virtual.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8321
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Negociação Forex e sua matemática básica
Negociação Forex e sua matemática básica
 Símbolos personalizados: Fundamentos práticos
Símbolos personalizados: Fundamentos práticos
 Uma abordagem científica para o desenvolvimento de algoritmos de negociação
Uma abordagem científica para o desenvolvimento de algoritmos de negociação
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Com a diretiva tester_file, esse arquivo será encaminhado ao Agente durante uma alteração no pacote de trabalho?
Se sim, é possível alterar o conteúdo desse arquivo durante a otimização.
Você pode alterar o conteúdo, mas isso não terá efeito - parece que as informações são armazenadas em cache/armazenadas em algum lugar durante o início da otimização. Pelo menos era assim antes.
Qual é a maneira mais rápida de carregar grandes quantidades de dados em cada passagem?
Para agentes locais, provavelmente é a mais rápida por meio de um diretório compartilhado. Para agentes distribuídos, não há muitas opções.
Há poucas opções para os distribuídos.
Incorporar na fonte ZIP(MqlTick[]).
Incorporar na fonte ZIP(MqlTick[]).
Qual será a diferença em relação ao tester_file ou, mais precisamente, ao resource? Muito provavelmente, o tempo de acesso será diferente, mas de forma insignificante.
Qual será a diferença entre ele e o arquivo tester_file ou, mais precisamente, o recurso? Provavelmente, o tempo de acesso será diferente, mas de forma insignificante.
Ele não ficará em uma área restrita e dependerá da velocidade do FileLoad. Você deve medi-lo, em geral.