Rede neural na prática: Gradiente Descendente Estocástico

Introdução

No artigo anterior Rede neural na prática: Gradiente Descendente, mostrei algo que talvez tenha ficado um tanto quanto confuso. Então vou começar exatamente naquele ponto. Isto por que, é necessário que você meu caro leitor, não fique confuso com relação ao que estou falando dentro deste tema. O detalhe é visto logo abaixo:

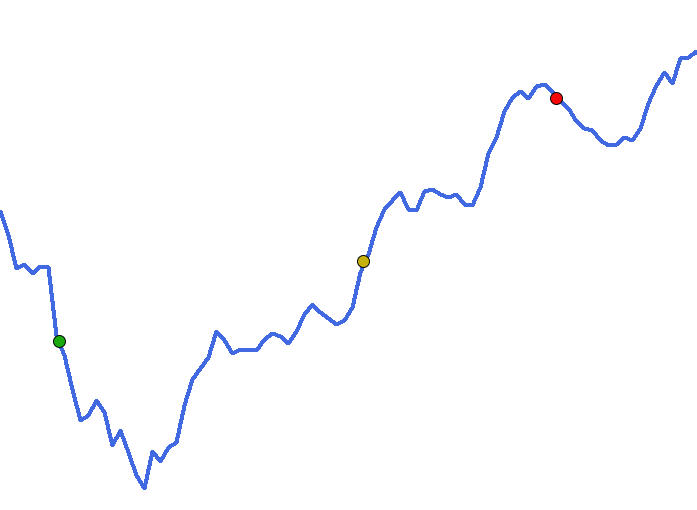
A questão aqui é a seguinte: No artigo anterior, menciono que você pode em algum momento, ter um banco de dados que poderá ser representado pela linha em azul. Ou seja, temos um polinômio bastante complexo. Este é dado a rede neural, para que ela tente encontrar, uma equação que consiga representar as informações presentes no banco de dados. Até este ponto acredito, não ser algo confuso de entender. Mas durante a explicação, menciono que os pontos visto na imagem, representam a medida de erro gerado durante a inicialização da rede neural. E esta é a parte que talvez tenha fico um tanto quanto confusa. E gostaria de esclarecer melhor esta questão.

O detalhe aqui, é de que, quando vamos representar algo em um gráfico, como muitos podem ver, nas explicações sobre erro. O gráfico normalmente é uma superfície. Porém o problema, é que para desenhar um gráfico de superfície, você precisa de duas variáveis, uma para o eixo X e outra para o eixo Y. Os valores que representam a combinação destas variáveis, são plotados usando o eixo Z. Algo parecido com o que pode ser visto na animação abaixo.

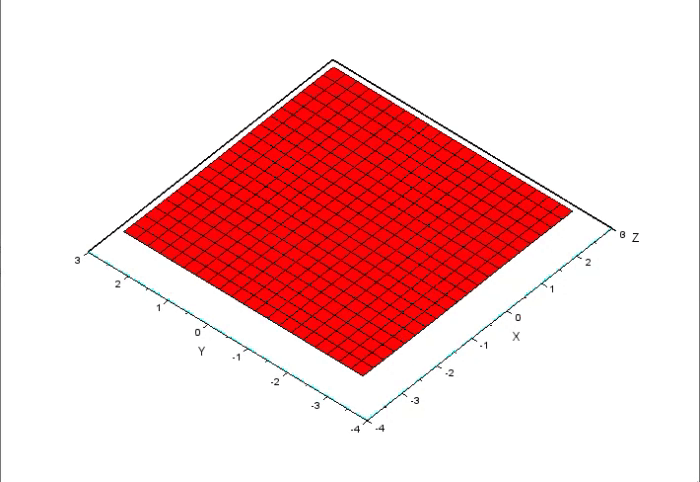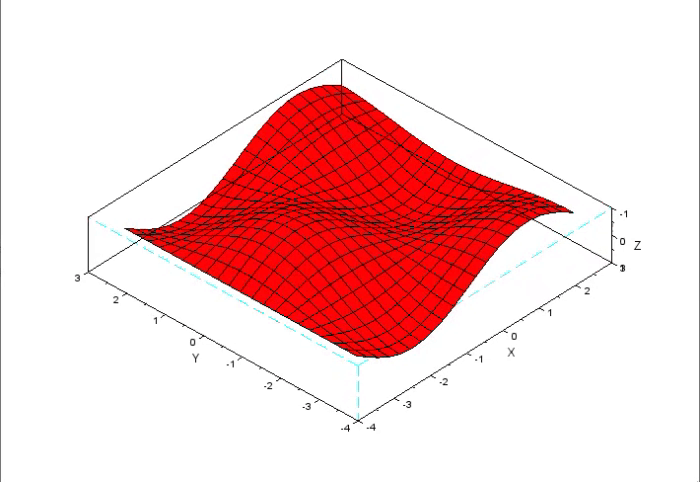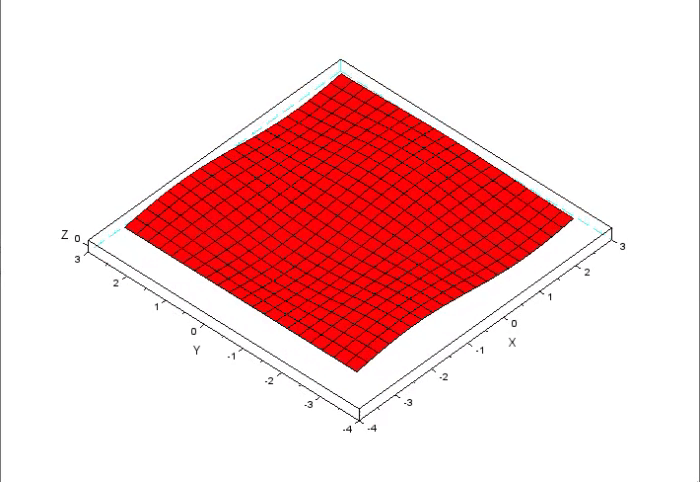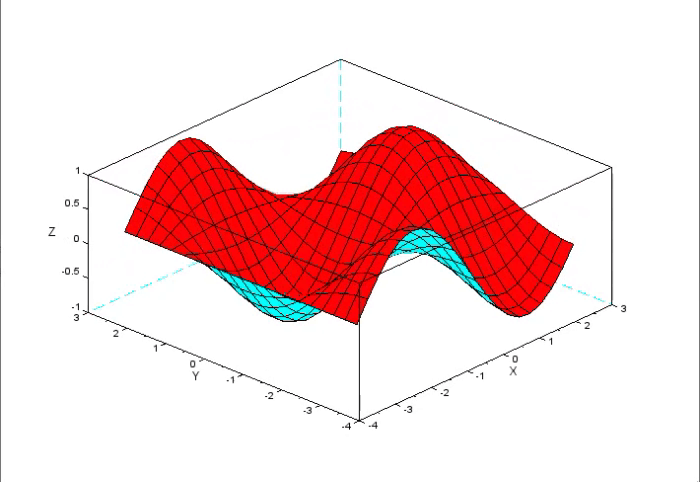
Nesta animação, podemos ver que se os valores do eixo Z mudam. Temos assim, uma combinação que representa o valor que estaria na variável em X, e outro para a variável que estaria no eixo Y. No entanto, na curva mostrada na imagem que pode ser vista, no começo do artigo, não tem como a plotarmos em um gráfico de superfície, ou se que imaginar como seria tal gráfico. Isto por que, nitidamente ela precisaria de muito mais do que apenas duas variáveis para ser desenhada.

Por conta disto, talvez tenha ficado um tanto quanto confuso, entender a questão sobre o erro ao observar a curva. Isto por que muitos podem vir a imaginar que o gráfico da representação de um banco de dados, contém internamente onde seria o ponto de erro mínimo. O que não é verdade. Peço desculpas se foi isto que ficou subentendido. Pois não é assim que as coisas de fato ocorrem. Apenas utilizei um gráfico 2D para representar a ideia de vales e picos. Onde nossa intenção muitas das vezes é tentar visualizar o que seria um vale ideal. Mas que dependendo de onde iniciamos, podemos nunca conseguir alcançar o ponto de menor valor de erro.

Sei que isto parece extremamente complicado. E de fato é complicado de explicar. Ainda mais pelo fato, de que desconheço, o quanto cada um tem de intimidade sobre a matemática usa em uma rede neural. Estou tentando deixar o material o mais simples e didático, quanto é possível ser feito. Mas seria bem mais simples se fosse feito de outra maneira. Mas tudo bem, espero ter elucidado esta questão, que ao meu ver ficou um tanto quanto confusa. Podendo levar a um entendimento equivocado sobre o assunto.

O código usado para criar a animação acima, pode ser visto logo abaixo. Trata-se de um código usado no SCILAB. Isto para quem tiver curiosidade em visualizar os dados, com mais calma.

 t=-%pi:0.3:%pi;
 plot3d(t,t,sin(t)'*cos(t),80,50,'X@Y@Z',[5,2,4]);

Se você tiver interesse em observar a coisa com mais calma. Pode experimentar o código acima, para entender melhor o conceito de vale e pico. Para movimentar o gráfico 3D, clique com o botão direito, segure e arraste ponteiro do mouse. Muito bem, uma vez que acredito ter esclarecido o ponto que me incomodava, podemos seguir para o que será visto neste artigo.

Adicionando o viés no gradiente descendente

Como tenho seguido uma certa metodologia, desde o começo, pretendo seguir a mesma em todos os artigos sobre rede neural. Mesmo que possa parecer que estamos andando em círculos. Quero lembrar a você, meu caro leitor, de que redes neurais, não é um estilo de material que temos um início e um objetivo final. Quando o assunto é redes neurais a coisa é bem mais extravagante. Sendo que as vezes você pensa que estamos no começo, quando na verdade estamos no final. E outras vezes você pensa que estamos no final, quando na verdade estamos no começo. É bem estranho e um tanto quanto confuso, ainda mais para quem deseja começar e finalizar as coisas em pontos bem definidos. Estas pessoas acabam por desistir de tentar estudar este tema.

O fato de isto acontecer, não temos um ponto de início e um ponto final. Tem um motivo, e este é o fato de que redes neurais, não tem apenas uma única solução. Cada classe de problema envolve, ou pode envolver, uma solução completamente diferente. Mas antes de entrar nestas questões, vamos ver o que ficou faltando para que o neurônio artificial, visto no artigo passado. De forma que o mesmo pudesse ser finalizado. O neurônio em questão é o que usava o gradiente descendente. Bem, no código original, que se encontra no artigo anterior, pode ser visto logo abaixo na íntegra.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define PrintEx(A) Print(#A, " => ", A)
05. #define macroRandom (rand() / (double)SHORT_MAX)
06. //+------------------------------------------------------------------+
07. double Train[][2] {
08.                     {0, 0},
09.                     {1, 3},
10.                     {2, 6},
11.                     {3, 9},
12.                     {4, 12},
13.                   };
14. //+------------------------------------------------------------------+
15. const uint nTrain = Train.Size() / 2;
16. const double epsilon = 1e-3;
17. //+------------------------------------------------------------------+
18. double Cost(const double w)
19. {
20.     double err, x, y;
21. 
22.     err = 0;
23.     for (uint c = 0; c < nTrain; c++)
24.     {
25.         x = Train[c][0];
26.         y = Train[c][1];
27.         err += 2 *(x * w - y) * x;
28.     }
29. 
30.     return err;
31. }
32. //+------------------------------------------------------------------+
33. void OnStart()
34. {
35.     double weight, err;
36.     ulong it0, it1, count;
37. 
38.     Print("************************************");
39.     Print("Linear gradient neuron...");
40.     MathSrand(512);
41.     weight = (double)macroRandom;
42. 
43.     it0 = GetTickCount();
44.     for(count = 0; (count < ULONG_MAX) && (MathAbs(err = Cost(weight)) > epsilon); count++)
45.         weight -= (err * epsilon);
46.     it1 = GetTickCount();
47.     Print("Time: ", (it1 - it0) / 1000.0, " seconds.");
48.     PrintEx(count);
49.     PrintEx(weight);
50.     PrintEx(err);
51. }
52. //+------------------------------------------------------------------+

Observe que na linha 18, onde definimos a função de custo, apenas o parâmetro de peso nos é fornecido. E na linha 27 onde o cálculo de fato está sendo executado, não estamos usando o viés, ou ponto de intersecção. Quero novamente lembrar ao leitor, de que o gradiente descendente nada mais é, do que apenas uma forma um tanto mais interessante de expressar a regressão linear. Nada mais do que isto. Para entender melhor isto, veja os artigos anteriores.

Porém apesar disto ele tem suas vantagens frente ao neurônio de regressão linear. No entanto, o simples fato de adicionarmos um parâmetro, para representar o viés na linha 18 e na linha 27, não torna o cálculo adequado. Isto por conta de que a forma como o erro é calculado, será ligeiramente diferente do cálculo para o erro de viés. Isto pode ser visto nas imagens abaixo.

A primeira imagem, mostra o cálculo para o erro no peso, já a segunda imagem, mostra o cálculo para o erro no viés. Note que são ligeiramente diferentes, devido a um valor usado em uma e não usado na outra. Mas temos um outro problema aqui. E este está ligado a questão do código que temos de criar. Observe que a função retorna um valor double, mas precisamos retornar dois valores double. Um para o viés e outro para o peso. Ok, se você já sabe como fazer as coisas em termos de programação MQL5. Não verá isto como um problema. Na verdade, existem diversas formas de solucionar este pequeno percalço. Algumas mais simples, enquanto outras são um tanto quanto mais elaboradas. Mas de qualquer forma, não me interessa como o problema será solucionado.

O que nos interessa, são os resultados obtidos. Você notará que durante o tempo, muito provavelmente, mudarei a forma de resolver esta questão. Mas quero deixar claro, novamente de que estamos interessados é no resultado, e não no modo de obter o mesmo. Assim uma primeira forma de resolver a questão pode ser observada no código abaixo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define PrintEx(A) Print(#A, " => ", A)
05. #define macroRandom (rand() / (double)SHORT_MAX)
06. //+------------------------------------------------------------------+
07. double Train[][2] {
08.                     {0, 0},
09.                     {1, 3},
10.                     {2, 6},
11.                     {3, 9},
12.                     {4, 12},
13.                   };
14. //+------------------------------------------------------------------+
15. const uint nTrain = Train.Size() / 2;
16. const double epsilon = 1e-3;
17. //+------------------------------------------------------------------+
18. struct stErr
19. {
20.     double  Weight,
21.             Bias;
22. };
23. //+------------------------------------------------------------------+
24. stErr Cost(const double w, const double b)
25. {
26.     double x, y, t;
27.     stErr err;
28. 
29.     ZeroMemory(err);
30.     for (uint c = 0; c < nTrain; c++)
31.     {
32.         x = Train[c][0];
33.         y = Train[c][1];
34.         t = 2 * ((x * w + b) - y);
35.         err.Weight += (t * x);
36.         err.Bias += t;
37.     }
38. 
39.     return err;
40. }
41. //+------------------------------------------------------------------+
42. void OnStart()
43. {
44.     double weight, bias;
45.     ulong it0, it1, count;
46.     stErr err;
47. 
48.     Print("************************************");
49.     Print("Gradient Descent Neuron...");
50.     MathSrand(512);
51.     weight = (double)macroRandom;
52.     bias = (double)macroRandom;
53. 
54.     it0 = GetTickCount();
55.     for(count = 0; count < ULONG_MAX; count++)
56.     {
57.         err = Cost(weight, bias);
58.         if ((MathAbs(err.Weight) <= epsilon) && (MathAbs(err.Bias) <= epsilon))
59.             break;
60.         weight -= (err.Weight * epsilon);
61.         bias -= (err.Bias * epsilon);
62.     }
63.     it1 = GetTickCount();
64.     Print("Time: ", (it1 - it0) / 1000.0, " seconds.");
65.     PrintEx(count);
66.     PrintEx(weight);
67.     PrintEx(bias);
68.     PrintEx(err.Weight);
69.     PrintEx(err.Bias);
70. }
71. //+------------------------------------------------------------------+

Olhando este código você pode estar pensando: Cara mais que coisa complicada. Não teria uma forma mais simples de fazer isto? Como eu disse a pouco. Não me interessa a forma de fazer. Estou interessado é nos resultados. Tanto que ao executar o mesmo no terminal do MetaTrader 5, você verá o seguinte resultado:

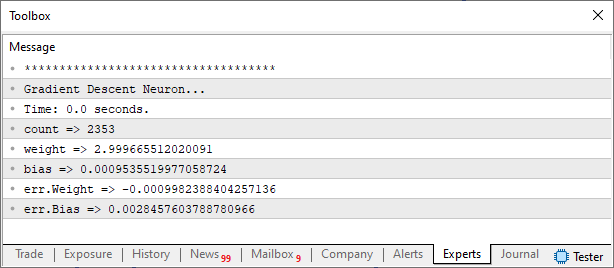
Bem, então vou dar uma rápida explicação. Isto para quem está chegando agora. Na linha 18 declaro uma estrutura. Esta será usada como forma de retornar o custo calculado. Observe na linha 24 como está a nova declaração da função de custo. Feito isto, na linha 27, declaramos uma variável interna para a função. Esta será usada para armazenar os valores a serem retornados. Efetuamos os cálculos na linha 34. Porém isto é apenas uma parte deles. Já que na linha 35 ajustamos, corrigimos o cálculo para incluir a parte faltante no cálculo sobre o erro no peso. No final temos o cálculo do erro no peso e no viés perfeitamente executados segundo o que consta na fórmula.

Mas ainda falta uma pequena questão, que é a função de ativação. Porém existem casos em que a função de ativação não é de fato necessária. Enquanto em outros casos ela é primordial. Vimos isto no artigo onde mostrei como treinar um neurônio para representar uma porta lógica. Mas aqui como estamos usando valores, cuja função claramente significa a equação abaixo:

A função de ativação não se torna necessária. Mas vamos em breve entender melhor esta questão da função de ativação. A única coisa que você neste momento precisa entende, meu caro leitor. É que não existe uma receita de bolo para se criar uma rede neural. Cada caso é um caso. E existem diversas situações em que uma rede neural mais atrapalha do que ajuda. Também iremos ver isto em breve. Mas vamos com calma, não há motivo para colocar o carro na frente dos bois. Uma coisa de cada vez.

Bem, mas vamos voltar a nossa questão principal. Que é o neurônio de gradiente descendente. Você pode compilar ele e executar o código no terminal. E notará que os resultados não mudarão frente ao que foi visto no artigo anterior. Tanto que um dos códigos presentes no anexo deste artigo, é justamente o código deste neurônio visto acima. Mas e se mudarmos a equação de modo a termos uma equação ligeiramente diferente. O que acontecerá com o neurônio? Visto que ele não tem uma função de ativação presente em seu código? Quero que você, meu caro leitor, faça esta experiência. E para lhe guiar, vamos experimentar usar valores para conseguir a seguinte equação, mostrada abaixo:

Para fazer isto precisamos mudar algumas coisas no código, tais mudanças podem ser vistas no fragmento abaixo:

. //+------------------------------------------------------------------+
07. double Train[][2] {
08.                     {0, -0.8},
09.                     {1, 0.85},
10.                     {2, 2.5},
11.                     {3, 4.15},
12.                     {4, 5.8},
13.                   };
14. //+------------------------------------------------------------------+
                                   .
                                   .
                                   .
41. //+------------------------------------------------------------------+
42. void OnStart()
43. {
                                   .
                                   .
                                   .
55.     for(count = 0; count < 10; count++)
56.     {
57.         err = Cost(weight, bias);
58.         if ((MathAbs(err.Weight) <= epsilon) && (MathAbs(err.Bias) <= epsilon))
59.             break;
60.         weight -= (err.Weight * epsilon);
61.         bias -= (err.Bias * epsilon);
62.         PrintFormat("%I64u > w0: %.4f %.4f || b: %.4f %.4f", count, weight, err.Weight, bias, err.Bias);
63.     }

Note os locais onde o código mudou. Primeiro foi nos dados a serem usados no treinamento. O próximo ponto foi no código do procedimento OnStart. Muito bem, antes de vermos o resultado, quero alerta a você meu caro leitor e entusiasta, de que estamos utilizando um neurônio que pode simplesmente dizer: NÃO VOU CONSEGUIR CONVERGIR. E se isto ocorrer, o laço na linha 55, pode fazer com que o programa demore um bom tempo para finalizar.

Como não temos esta certeza, precisamos limitar o tempo do laço a um número mínimo de interações. No caso estou definindo dez interações. A cada interação iremos imprimir o que está sendo feito pelo neurônio. Isto é de responsabilidade da linha 62. Assim poderemos visualizar se o neurônio está ou não conseguindo convergir. Muito bem, dado este alerta, podemos então compilar e executar o código modificado. Como resultado você verá a imagem abaixo no terminal do MetaTrader 5.

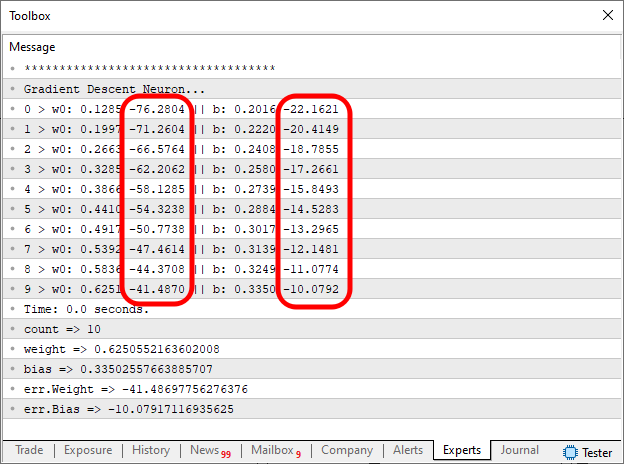
O que nos interessa é justamente as regiões marcadas na imagem. Queremos que elas tentem se tornar zero. Na verdade, elas jamais se tornarão de fato zero. Isto por conta do fato, que a linha 58 fará com que o laço de interação se encerre. Isto ocorrerá assim que o valor de erro ficar abaixo do valor definido de antemão. Isto precisará acontecer, tanto para o erro de peso, quanto para o erro de viés. Ao mesmo tempo. Caso contrário o laço ficará efetuando interações até que o limite de interações seja alcançado.

Muito bom, já sabemos que o neurônio está conseguindo convergir. Então vamos deixar ele tentar fazer isto, até que o limite definido na linha 58 seja alcançado. Ou até que o número de interações seja alcançado. Para isto mudamos o valor da linha 55, que está definido como dez e o deixamos como ULONG_MAX. Ou outro valor que você deseje. Como resultado temos o que é visto na imagem abaixo:

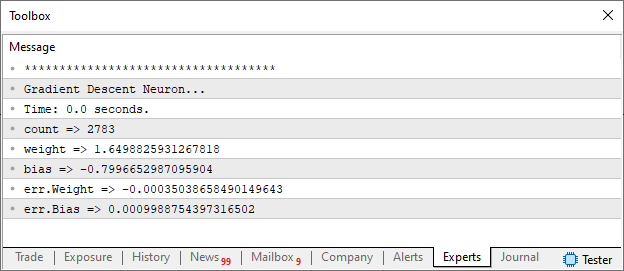
Veja que o resultado encontrado é bem próximo do esperado por nos. E nem mesmo foi preciso incluirmos uma função de ativação para que o neurônio conseguisse convergir. Ok, mas e se o neurônio não conseguisse convergir para um resultado. Isto para que os dados usados no treinamento viessem a ser representados por uma equação. Como deveríamos proceder? Bem, cada caso é um caso. Não existe uma regra na qual você precisa seguir. Ou melhor dizendo. Não existe uma receita de bolo para se conseguir a convergência dos dados em uma equação matemática. Isto para que o treinamento seja de fato conseguido. Tentar seguir uma regra para se conseguir o treinamento de um neurônio ou rede neural é um erro. Pois TAL REGRA NÃO EXISTE.

E este é um erro do qual muitos, dos que estão iniciando estudos de redes neurais acaba cometendo. Eles simplesmente querem, por que querem seguir regras rígidas. Sendo que na verdade devemos sim entender o que estamos criando. E não tentar seguir uma receita de bolo. Ou tentar usar algo já pronto. Por isto estou fazendo estes artigos sobre este tema. Estou tentando passar um pouco da minha experiência, sobre este assunto, para você meu caro leitor. Talvez um ou outro consiga absorver parte do que estou mostrando.

Ok, antes de passar para o próximo assunto, quero dar uma rápida pincelada, sobre algo que talvez você venha a ouvir falar. Talvez até já tenha ouvido, mas provavelmente não entendeu do que se tratava de fato. Estou falando do chamado gradiente descendente estocástico. Puxa vida, isto sim é que é um palavrão. Chega a dar arrepios de pavor só de ouvir falar em tal termo. Bem, muitos talvez pensem assim. Mas se este é o seu caso, ou se você nunca ouviu falar de tal coisa. Você não precisa ficar apavorado, correndo para procurar saber do que se trata. Este tal de gradiente descendente estocástico, nada mais é do que uma variação do gradiente descendente. Só que esta variação, visa justamente tentar, fazer com que o gradiente descendente, seja um pouco mais rápido, em usa execução.

Hum, e como podemos conseguir fazer isto? Talvez seja algo interessante de se utilizar. De fato, o gradiente descendente estocástico é algo interessante e ajuda a tornar o gradiente descendente mais rápido. Mas isto tem um custo. Não existe almoço de graça. Para tornar o gradiente descendente mais rápido. O estocástico, irei chamar assim para não ficar cansativo, faz o seguinte truque. Vamos ver o fragmento do código que criamos para entender. Este pode ser visto abaixo.

06. //+------------------------------------------------------------------+
07. double Train[][2] {
08.                     {0, -0.8},
09.                     {1, 0.85},
10.                     {2, 2.5},
11.                     {3, 4.15},
12.                     {4, 5.8},
13.                   };
14. //+------------------------------------------------------------------+
15. const uint nTrain = Train.Size() / 2;
16. const double epsilon = 1e-3;
17. //+------------------------------------------------------------------+
18. struct stErr
19. {
20.     double  Weight,
21.             Bias;
22. };
23. //+------------------------------------------------------------------+
24. stErr Cost(const double w, const double b)
25. {
26.     double x, y, t;
27.     stErr err;
28. 
29.     ZeroMemory(err);
30.     for (uint c = 0; c < nTrain; c++)
31.     {
32.         x = Train[c][0];
33.         y = Train[c][1];
34.         t = 2 * ((x * w + b) - y);
35.         err.Weight += (t * x);
36.         err.Bias += t;
37.     }
38. 
39.     return err;
40. }
41. //+------------------------------------------------------------------+

Nossa base de treinamento é bem curta, mas imagine que ela tivesse milhares ou milhões, quem sabe bilhões de dados. Se você fosse fazer uso deste fragmento acima, poderia vir a demorar horas ou mesmo dias para treinar um único neurônio. Isto se a base de dado permitisse treinar apenas um neurônio. Se fosse preciso usar uma rede neural, o tempo poderia escalar muito rapidamente. Muito bem, entendido isto, vamos ver como o estocástico resolve este problema de tempo.

A mágica acontece quando a linha 30 for se executada. No gradiente normal, toda a base de dados é usada a cada interação com a função de custo. Ou seja, cada vez que a linha 24 for chamada, teremos o laço da linha 30, varrendo toda a base de dados a fim de treinar a rede ou mesmo o neurônio. Porém, durante pesquisas, acabou se notando que tal coisa é um desperdício de tempo. Podemos conseguir o mesmo resultado, ou algo bem satisfatório, fazendo uma pequena mudança neste esquema. Em vez de usar toda a base de dados a cada interação, ou chamada da linha 24. Usaremos apenas uma parte da base de dados. Neste ponto, você deve estar imaginando: Mas isto não seria muito inteligente. Já que o treinamento ficaria incompleto. Mas este pensamento, se deve justamente por conta de você, meu caro leitor, não ter compreendido bem a ideia por trás da implementação. Vamos ver como o fragmento acima ficaria se usássemos o estocástico. Este pode ser visto logo abaixo.

23. //+------------------------------------------------------------------+
24. stErr Cost(const double w, const double b, const uint p1 = 0, const uint p2 = nTrain)
25. {
26.     double x, y, t;
27.     stErr err;
28. 
29.     ZeroMemory(err);
30.     for (uint c = p1; c < p2; c++)
31.     {
32.         x = Train[c][0];
33.         y = Train[c][1];
34.         t = 2 * ((x * w + b) - y);
35.         err.Weight += (t * x);
36.         err.Bias += t;
37.     }
38. 
39.     return err;
40. }
41. //+------------------------------------------------------------------+

Como apenas a parte responsável pela fatoração de custo, precisa ser modificado. Estou mostrando apenas o fragmento realmente necessário. Então agora, talvez fique mais claro como o estocástico funciona. Perceba que foram feitas mudanças apenas nas linhas 24 e 30. Todo o resto do código permanece idêntico. Os únicos cuidados a serem tomados são: Primeiro, que o valor de p1 deve ser diferente e menor que o de p2. Segundo o valor de p2 deve ser igual ou menor que o número de coisas no treinamento. Seguidas estas considerações vamos ver como isto poderia ser utilizado.

No chamador, você poderá executar um número de chamadas para treinar o sistema, X quantidade de dados. Quando a rede tiver sido treinada com estes X dados, você passa para a próxima leva de dados. Fazendo assim o treinamento de Y quantidade, que pode ser igual ou maior do que a quantidade anterior. Como a rede já estará em um estágio um pouco mais avançado com relação a redução de custo. Esta segunda onda de treinamento muitas das vezes será consideravelmente mais rápida de ser feita. E assim você vai fazendo.

Divide os dados a serem usados no treinamento em blocos menos, que são bem mais rápidos de passarem pela função de custo. Por exemplo: Supondo que nossa base tivesse um milhão de dados para ser usados no treinamento. Se precisássemos passar estes um milhão, cem mil vezes pela função de custo, levaríamos um tempo enorme. Porém, se passássemos dez mil, cem mil vezes. De forma a estabelecer um custo mais baixo para os pesos e viés. Daí a pouco a próxima leva de dez mil, não precisaria passar cem mil vezes. Talvez ela precisasse passar umas oitenta mil vezes até encerrar. E a próxima iria gastar ainda menos tentativas para reduzir ainda mais o custo. No final, você terá passado todos os dados de treinamento. Porém sem precisar gastar todo aquele tempo, que seria necessário para passar tudo de uma única vez.

Esta é a sacada do estocástico. Tentar reduzir o custo de maneira mais rápida possível. Como provavelmente você não terá a sorte de que o gerador pseudo aleatório, coloque valores próximos dos adequados nos pesos e viés. Fazer isto para uma grande base de dados é algo inteligente. Porém para pequenos bancos, ou mesmo o que estou usando para mostrar como funciona as coisas. Fazer uso de uma implementação de gradiente descendente estocástico, é algo completamente desnecessário e uma baita de uma perda de tempo. Então não faz muito sentido, quando métodos mais simples, e aparentemente mais lentos, podem conseguir bons resultados.

Ok. Considero este assunto sobre o gradiente descendente estocástico explicado. Já que não há muito para falar sobre ele. Mas como ainda temos um pouco de tempo. Posso começar a mostrar algo que será melhor entendido no próximo artigo. Então vamos dar uma pequena adiantada nas coisas. Mas para isto, vamos a um novo tópico.

Será que não existe outro caminho

Muito bem, meu caro leitor. Até o momento as coisas tem acontecido de forma gradual e sem muita turbulência. Sendo fácil de explicar grande parte das coisas. Mesmo por que ainda estamos bem no começo de tudo que podemos explicar. Porém como algumas das coisas, a serem vistas, são um tanto quanto complicadas de serem mostradas de forma simples. Tenho tentado ir o mais devagar e gradual quanto for possível ser feito. Isto para que o assunto possa ser apresentado de uma maneira didática. Para que todos consigam compreender. Apesar de estarmos tendo alguns altos e baixos. Mas acredito que você tem dado conta de acompanhar as explicações e compreendido o material.

Porém existe algo que eu gostaria de explicar, antes de entrar em outras questões um pouco mais profundas. Mas para fazer isto, será preciso mudar um pouco o código do neurônio, visto neste artigo. Não precisa ficar assustado, ou mesmo se perguntando o motivo. Como disse EN SABAH NUR: "Tudo será esclarecido no seu devido tempo, minha criança.". Ok, então compreendido este fato, vamos ver as mudanças que foram feitas no código, para que eu possa explicar uma coisa. Novamente não se preocupe em entender o motivo, apenas veja o código mostrado abaixo.

001. //+------------------------------------------------------------------+
002. #property copyright "Daniel Jose"
003. //+------------------------------------------------------------------+
004. #include <Canvas\Canvas.mqh>
005. //+------------------------------------------------------------------+
006. #define PrintEx(A)  Print(#A, " => ", A)
007. #define macroRandom (rand() / (double)SHORT_MAX)
008. #define _SizeLine   300
009. #define nColuns     2
010. //+------------------------------------------------------------------+
011. CCanvas canvas;
012. //+------------------------------------------------------------------+
013. double Train[][nColuns] {
014.                     {0, -0.8},
015.                     {1, 0.85},
016.                     {2, 2.5},
017.                     {3, 4.15},
018.                     {4, 5.8},
019.                   };
020. //+------------------------------------------------------------------+
021. const double epsilon = 1e-3;
022. //+------------------------------------------------------------------+
023. struct stErr
024. {
025.     double  Weight,
026.             Bias;
027. };
028. //+------------------------------------------------------------------+
029. stErr Cost(const double w, const double b, const uint p1 = 0, const uint p2 = Train.Size() / nColuns)
030. {
031.     double x, y, t;
032.     stErr err;
033. 
034.     ZeroMemory(err);
035.     for (uint c = p1; c < p2; c++)
036.     {
037.         x = Train[c][0];
038.         y = Train[c][1];
039.         t = 2 * ((x * w + b) - y);
040.         err.Weight += (t * x);
041.         err.Bias += t;
042.     }
043. 
044.     return err;
045. }
046. //+------------------------------------------------------------------+
047. void PlotText(const int x, const int y, const uchar line, const string sz0)
048. {
049.     uint w, h;
050. 
051.     TextGetSize(sz0, w, h);
052.     canvas.TextOut(x - (w / 2), y + _SizeLine + (line * h) + 5, sz0, ColorToARGB(clrBlack));   
053. }
054. //+------------------------------------------------------------------+
055. inline double CallZoom(void)
056. {
057.     double d1 = 0;
058. 
059.     for (uint c = 0; c < Train.Size() / nColuns; c++)
060.     {
061.         d1 = MathMax(d1, MathAbs(Train[c][0]));
062.         d1 = MathMax(d1, MathAbs(Train[c][1]));
063.     }
064. 
065.     return _SizeLine / d1;
066. }
067. //+------------------------------------------------------------------+
068. void Plot_Train2D(const int x, const int y, const double weight, double bias)
069. {
070.     int vx, vy;
071.     double zoom;
072.     uint n = Train.Size() / nColuns;
073. 
074.     zoom = CallZoom();
075.     canvas.LineVertical(x, y - _SizeLine, y + _SizeLine, ColorToARGB(clrRoyalBlue, 255));
076.     canvas.LineHorizontal(x - _SizeLine, x + _SizeLine, y, ColorToARGB(clrRoyalBlue, 255));
077.     for (uint c = 0; c < n; c++)
078.     {
079.         vx = (int)(Train[c][0] * zoom);
080.         vy = (int)(Train[c][1] * zoom);
081.        canvas.FillCircle(x + vx, y - vy, 5, ColorToARGB(clrRed, 255));
082.     }
083.     canvas.LineAA(
084.                 x + (int)(Train[0][0] * zoom), 
085.                 y - (int)((Train[0][0] * weight + bias) * zoom), 
086.                 x + (int)(Train[n - 1][0] * zoom), 
087.                 y - (int)((Train[n - 1][0] * weight + bias) * zoom), 
088.                 ColorToARGB(clrForestGreen));
089.     PlotText(x, y, 1, StringFormat("Zoom: %.2fx", zoom));
090.     PlotText(x, y, 2, StringFormat("f(x) = %.4fx %c %.4f", weight, (bias < 0 ? '-' : '+'), MathAbs(bias)));
091. }
092. //+------------------------------------------------------------------+
093. void OnStart()
094. {
095.     double weight, bias;
096.     int    x, y;
097.     ulong  it0, it1, count;
098.     stErr  err;
099. 
100.     Print("************************************");
101.     Print("Stochastic Gradient Descent Neuron...");
102.     Print("************************************");
103.     MathSrand(512);
104.     weight = (double)macroRandom;
105.     bias = (double)macroRandom;
106. 
107.     it0 = GetTickCount();
108.     for(count = 0; count < ULONG_MAX; count++)
109.     {
110.         err = Cost(weight, bias);
111.         if ((MathAbs(err.Weight) <= epsilon) && (MathAbs(err.Bias) <= epsilon))
112.             break;
113.         weight -= (err.Weight * epsilon);
114.         bias -= (err.Bias * epsilon);
115.     }
116.     it1 = GetTickCount();
117.     Print("Time: ", (it1 - it0) / 1000.0, " seconds.");
118.     PrintEx(count);
119.     PrintEx(weight);
120.     PrintEx(bias);
121.     PrintEx(err.Weight);
122.     PrintEx(err.Bias);
123.     Print("Press ESC to close....");
124.     Print("************************************");
125. 
126.    x = (int)ChartGetInteger(0, CHART_WIDTH_IN_PIXELS, 0);
127.    y = (int)ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS, 0);
128.    canvas.CreateBitmapLabel("BL", 0, 0, x, y, COLOR_FORMAT_ARGB_NORMALIZE);
129.    canvas.Erase(ColorToARGB(clrWhite, 255));
130.     x /= 2;
131.     y /= 2;
132.            
133.     Plot_Train2D(x, y, weight, bias);
134. 
135.    canvas.Update(true);
136. 
137.     while(!IsStopped())
138.         if (TerminalInfoInteger(TERMINAL_KEYSTATE_ESCAPE) !=0)
139.             break;
140. 
141.     canvas.Destroy();
142. }
143. //+------------------------------------------------------------------+

Este código estará disponível no anexo. Talvez até o próximo artigo, eu venha a fazer algumas mudanças para o tornar mais didático. Mas ainda vou pensar se isto será de fato necessário. De qualquer forma, o resultado ao executar o mesmo é visto na imagem abaixo.

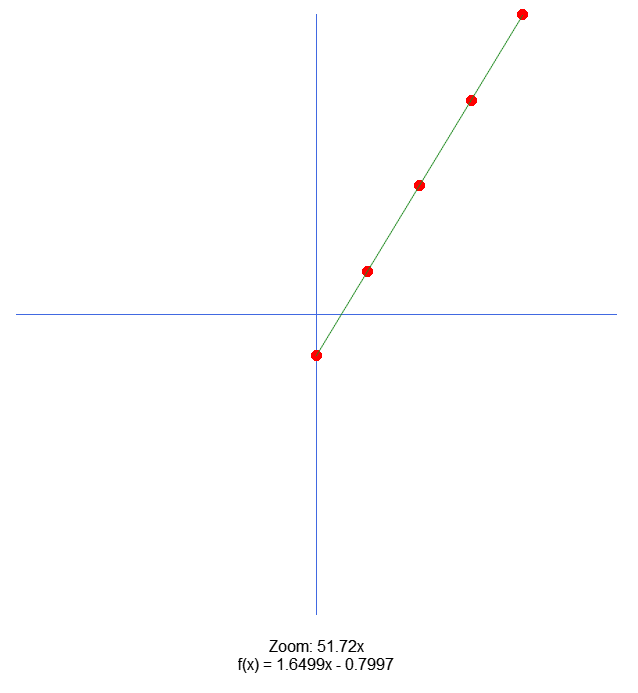
E no terminal, você poderá ver as seguintes informações:

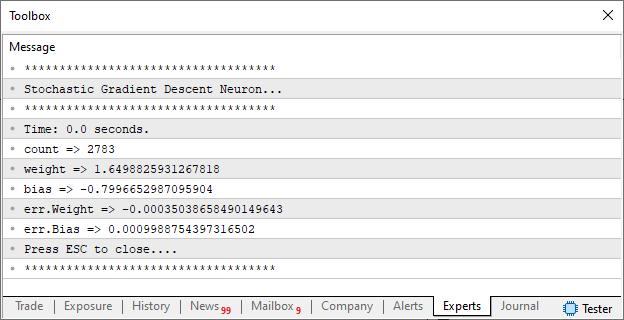
Bem, vamos entender o que está acontecendo aqui. Com base nos dados de treinamento, que estão declarados na linha 13. Temos durante o procedimento OnStart, a utilização do neurônio para gerar uma equação. Esta será uma reta. O neurônio criará a representação, com base no gradiente descendente estocástico. Mas como a base é muito pequena, iremos usar a forma mais simples, ou seja, via gradiente descendente. Uma vez que o neurônio reporte que seu trabalho está concluído. Iremos imprimir algumas informações no terminal. Isto é feito entre as linhas 117 e 124. Logo depois, faremos uso da biblioteca padrão CCanvas, para plotar um gráfico simples na tela do MetaTrader 5. Este gráfico será criado no momento em que a linha 133 for executada. Esta por sua vez irá mudar o fluxo para a linha 68.

Dentro do procedimento Plot_Train2D, iremos na linha 74 pedir para que a aplicação procure o melhor zoom para apresentar os dados. Visto que podemos estar mexendo com valores ou muito pequenos ou muito grandes. E queremos que todos sejam apresentados na região onde colocaremos um plano cartesiano. As linhas Y e X para representar o plano, são as linhas 75 e 76, respectivamente. Logo depois entramos em um laço for, isto na linha 77. O objetivo deste laço é nos apresentar todos os pontos usados no treinamento. Claro que eles estarão devidamente posicionados nos locais adequados. Isto seguindo o zoom que foi especificado, com base nos valores encontrados. Muito bem, feito isto, na linha 83, iremos desenhar uma linha, que se baseia na equação da reta encontrada pelo neurônio. Logo depois, nas linhas 89 e 90, informamos alguns dados sobre o que o gráfico representa e qual o zoom da imagem.

O objetivo aqui, é permitir que os dados sejam visualizados da melhor maneira possível. Assim você poderá começar a entender o que veremos no próximo artigo.

Considerações finais

Neste artigo, basicamente focamos em confeccionar um neurônio que pudesse usar o gradiente descendente. Vimos com seria uma atualização de tal modelo, que tem como denominação o nome de gradiente descendente estocástico. Mas nem tudo são flores. Existem alguns problemas aqui.

E neste ponto, quero que você meu caro leitor, procure pensar, e explorar este último código mostrado neste artigo. Mas faça isto com cautela, visto que o neurônio, não contém uma função de ativação. E isto, poderá fazer com que ele simplesmente encontre um ponto de estagnação. Isto já foi mostrado anteriormente. No entanto, ainda não vamos entrar nesta questão das funções de ativação e qual a importância real das mesmas. Mesmo por que, primeiro quero explicar algo. E para isto, é preciso que o neurônio esteja em seu modo mais simples e básico. Pois se você entender o que será visto no próximo artigo, verá que redes neurais nem sempre são a melhor escolha. Independentemente do que todos queiram lhe dizer.

Mas antes, procure modificar os valores de treinamento deste último neurônio, cujo código estará no anexo. Não mude outras coisas nele, apenas os valores de treinamento. Faça isto, procurando entender o que está acontecendo. Isto tornará mais simples entender o que será visto nos próximos artigos. Mas existem questões das quais não foram abordadas neste artigo. O que talvez torne o entendimento da matemática, um tanto quanto confusa. Mas não se preocupe iremos voltar nesta questão em um outro artigo.