Индикатор прогнозирования ARIMA на MQL5

Метеорологи не гадают на кофейной гуще, когда составляют прогноз погоды. Они анализируют то, что происходило в прошлом, чтобы понять, что случится завтра. Примерно так же работает модель ARIMA, только вместо облаков и давления, она изучает цены на финансовых рынках.

ARIMA расшифровывается как «Авторегрессионная Интегрированная Модель Скользящего Среднего». Звучит страшно, но на деле это довольно логичная система. Представьте, что вы пытаетесь предугадать, сколько будет стоить пара EUR/USD завтра, основываясь на том, как она вела себя последние несколько дней.

Три кита модели ARIMA

Авторегрессия (AR) — память о прошлом

Первая часть модели называется авторегрессией. Это красивое слово означает простую вещь: сегодняшняя цена зависит от вчерашней, позавчерашней и так далее. Как будто рынок помнит своё прошлое и строит будущее на его основе.

Если EUR/USD рос три дня подряд, есть вероятность, что завтра он тоже вырастет. Не обязательно, но тенденция может продолжиться. Авторегрессионная часть модели как раз и ловит эти закономерности, анализируя, насколько сильно прошлые значения влияют на настоящие.

Математика за простыми словами: представьте, что у вас есть курс EUR/USD за последние пять дней: 1.0800, 1.0825, 1.0850, 1.0875, 1.0900. Авторегрессия говорит: «Смотри, каждый день курс рос примерно на 25 пунктов (0.0025), значит, завтра он будет около 1.0925». Модель находит коэффициенты — числа, которые показывают, насколько сильно вчерашняя цена влияет на сегодняшнюю, позавчерашняя на сегодняшнюю, и так далее.

Формула выглядит примерно так: завтрашняя_цена = 0.7 × сегодняшняя_цена + 0.2 × вчерашняя_цена + 0.1 × позавчерашняя_цена. Эти коэффициенты 0.7, 0.2, 0.1 модель подбирает сама, анализируя историю. Чем больше коэффициент, тем сильнее влияние этого дня на прогноз.

Интегрирование (I) — укрощение хаоса

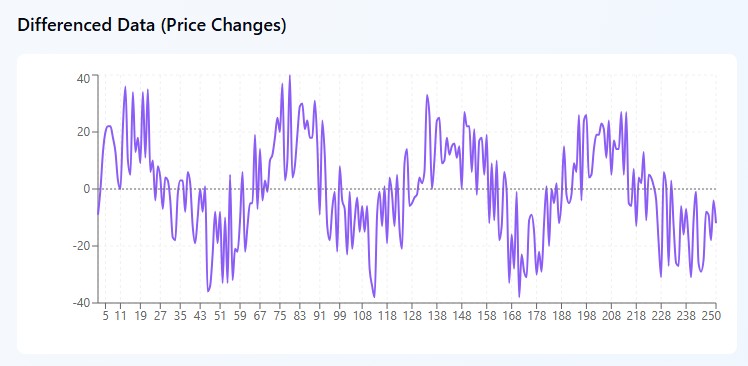
Представьте, что вы смотрите на график EUR/USD и видите полную кашу: 1.0800, 1.0850, 1.0820, 1.0880, 1.0860. Цена скачет туда-сюда, как пьяный моряк — никакой логики на первый взгляд. Именно такие данные математики называют нестационарными, а трейдеры — головной болью.

Но вот фокус: вместо того чтобы пытаться найти смысл в самих ценах, ARIMA делает хитрый ход. Она смотрит не на то, сколько стоит валютная пара, а на то, насколько она изменилась за день. Берём те же цифры и считаем разности: +50 пунктов, -30 пунктов, +60 пунктов, -20 пунктов. И вдруг хаос превращается в закономерность! Рынок качается между ростом на 50-60 пунктов и падением на 20-30 пунктов.

Это как если бы вы не следили за тем, где находится маятник, а только за тем, в какую сторону и с какой силой он качается. Математически всё просто: берём сегодняшнюю цену, вычитаем вчерашнюю — получаем изменение. Иногда нужно пойти дальше и взять "изменение изменений" — ну то есть, дифференцирование второго порядка. Звучит страшно, но принцип остаётся тем же: ищем закономерности там, где их на первый взгляд нет.

Скользящее среднее (MA) — учимся на ошибках

А теперь самое интересное — модель умеет учиться на собственных ошибках. Звучит как фантастика, но логика железная. Когда ARIMA вчера предсказала EUR/USD на уровне 1.0800, а он реально торговался на 1.0825, эта ошибка в 25 пунктов не просто досадная неточность. Это информация!

Представьте друга, который всегда опаздывает ровно на 10 минут. Когда он говорит "приду в шесть", вы уже знаете — реально будет в 6:10. Модель делает то же самое со своими промахами. Если она три дня подряд предсказывает цену ниже реальной на 10 пунктов, то запоминает эти ошибки и в следующий раз мысленно добавляет: "Обычно я занижаю на 10 пунктов, значит, к прогнозу нужна поправка".

Формула может выглядеть примерно так: "Поправка = 0.5 × вчерашняя ошибка + 0.3 × позавчерашняя ошибка". Модель не просто ошибается — она ошибается с умом, извлекая пользу из каждого промаха.

Как ARIMA использует психологию рынка

Инерция движения

Рынки обладают инерцией. Если EUR/USD растёт несколько дней подряд, все хотят его покупать — это толкает цену ещё выше. ARIMA ловит именно эту инерцию.

На практике: курс растёт пять дней с 1.0800 до 1.0900 (+20 пунктов ежедневно). Модель присваивает большой вес недавним дням и предсказывает продолжение тренда.

Возврат к среднему

Одновременно рынки стремятся к "справедливому" уровню. Если цена сильно отклонилась в одну сторону, рано или поздно она пытается вернуться обратно.

Пример: EUR/USD обычно торгуется в диапазоне 1.0800-1.0900. Если из-за новостей он подскочил до 1.1000, модель через компоненту скользящего среднего учтёт, что такие экстремальные движения обычно корректируются.

Циклические паттерны

Многие валютные пары показывают циклическое поведение — недельные, месячные или сезонные паттерны. ARIMA может их уловить при правильной настройке.

Минусы модели: когда ARIMA не работает

ARIMA не волшебный Грааль. Она работает с допущением, что будущее похоже на прошлое. Когда это допущение нарушается, модель даёт неточные прогнозы.

Модель плохо работает когда:

• Выходят неожиданные экономические новости
• Меняется денежная политика центробанков
• Происходят геополитические кризисы
• Рынок входит в новый режим (например, переходит от тренда к флету)

Лучше всего ARIMA работает в:

• Стабильных рыночных условиях
• Периодах без сильных фундаментальных изменений
• На инструментах с выраженными техническими закономерностями

Практическая реализация в MQL5

Создание рабочего индикатора ARIMA — это больше чем просто формулы. Нужна продуманная архитектура, которая справится с обработкой данных в реальном времени.

В сердце индикатора лежит модуль, который оценивает коэффициенты модели. Он использует метод максимального правдоподобия — звучит сложно, но это просто способ найти такие параметры, при которых модель лучше всего объясняет наблюдаемые данные.

Структура данных индикатора включает несколько взаимосвязанных буферов: основной буфер прогнозных значений ForecastBuffer, вспомогательный буфер исторических цен PriceBuffer и буфер ошибок ErrorBuffer для хранения остатков модели. Такая организация обеспечивает оптимальное использование памяти и высокую скорость вычислений.

Инициализация системы предполагает создание динамических массивов для хранения исходных ценовых данных, дифференцированного ряда, коэффициентов авторегрессии и скользящего среднего, а также массива остатков. Начальные значения коэффициентов устанавливаются на уровне 0.1, что обеспечивает устойчивость алгоритма оптимизации на начальном этапе.

int OnInit()
{
   // Настройка буферов индикатора для визуализации результатов
   SetIndexBuffer(0, ForecastBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PriceBuffer, INDICATOR_CALCULATIONS);
   SetIndexBuffer(2, ErrorBuffer, INDICATOR_CALCULATIONS);
   
   // Установка режима временных серий для корректной работы с историческими данными
   ArraySetAsSeries(ForecastBuffer, true);
   ArraySetAsSeries(PriceBuffer, true);
   ArraySetAsSeries(ErrorBuffer, true);
   
   // Конфигурация отображения прогноза с соответствующим сдвигом во времени
   PlotIndexSetString(0, PLOT_LABEL, "ARIMA Forecast");
   PlotIndexSetInteger(0, PLOT_SHIFT, forecast_bars);
   
   // Инициализация рабочих массивов с предварительно заданными размерами
   ArrayResize(prices, lookback);
   ArrayResize(differenced, lookback);
   ArrayResize(ar_coeffs, p);
   ArrayResize(ma_coeffs, q);
   ArrayResize(errors, lookback);
   
   // Установка начальных значений коэффициентов модели
   for(int i = 0; i < p; i++) ar_coeffs[i] = 0.1;
   for(int i = 0; i < q; i++) ma_coeffs[i] = 0.1;
   
   return(INIT_SUCCEEDED);
}

Входные параметры модели

Конфигурация индикатора осуществляется через систему входных параметров, каждый из которых играет критическую роль в определении поведения модели. Параметр lookback определяет объем исторических данных, используемых для обучения модели, параметр forecast_bars задает горизонт прогнозирования, а тройка параметров p, d, q определяет спецификацию модели ARIMA.

//--- Входные параметры конфигурации модели
input int lookback = 200;        // Период ретроспективного анализа для ARIMA
input int forecast_bars = 20;    // Количество прогнозируемых временных интервалов
input int p = 3;                 // Порядок авторегрессионной компоненты
input int d = 1;                 // Степень дифференцирования временного ряда
input int q = 2;                 // Порядок компоненты скользящего среднего
input double learning_rate = 0.01; // Коэффициент скорости обучения
input int max_iterations = 100;   // Максимальное количество итераций оптимизации

Методология оценки параметров модели

Центральным элементом алгоритма выступает функция вычисления логарифмической функции правдоподобия, которая служит критерием качества подгонки модели к наблюдаемым данным. Реализация данной функции основывается на предположении о нормальном распределении остатков модели, что позволяет использовать аналитическое выражение для плотности вероятности.

Функция правдоподобия и вычисление остатков

Алгоритм вычисления логарифмической функции правдоподобия представляет собой итерационный процесс, в котором для каждого временного момента вычисляются остатки модели как разность между наблюдаемым значением и модельным прогнозом. Авторегрессионная компонента формируется как линейная комбинация предшествующих значений дифференцированного ряда, в то время как компонента скользящего среднего использует предшествующие значения ошибок модели.

double ComputeLogLikelihood(double &data[], double &ar[], double &ma[])
{
   double ll = 0.0;
   double residuals[];
   ArrayResize(residuals, lookback);
   ArrayInitialize(residuals, 0.0);
   
   // Итерационное вычисление остатков модели
   for(int i = p; i < lookback; i++)
   {
      double ar_part = 0.0;
      double ma_part = 0.0;
      
      // Формирование авторегрессионной компоненты
      for(int j = 0; j < p && i - j - 1 >= 0; j++)
         ar_part += ar[j] * data[i - j - 1];
      
      // Формирование компоненты скользящего среднего
      for(int j = 0; j < q && i - j - 1 >= 0; j++)
         ma_part += ma[j] * errors[i - j - 1];
      
      // Вычисление остатка и обновление массива ошибок
      residuals[i] = data[i] - (ar_part + ma_part);
      errors[i] = residuals[i];
      
      // Накопление логарифмической функции правдоподобия
      ll -= 0.5 * MathLog(2 * M_PI) + 0.5 * residuals[i] * residuals[i];
   }
   
   return ll;
}

Процедура оптимизации коэффициентов

Процедура оптимизации коэффициентов реализована посредством метода градиентного спуска с адаптивным размером шага. Алгоритм итеративно обновляет значения коэффициентов в направлении, противоположном градиенту целевой функции, обеспечивая сходимость к локальному оптимуму функции правдоподобия.

void OptimizeCoefficients(double &data[])
{
   double temp_ar[], temp_ma[];
   ArrayCopy(temp_ar, ar_coeffs);
   ArrayCopy(temp_ma, ma_coeffs);
   
   double best_ll = -DBL_MAX;
   double grad_ar[], grad_ma[];
   ArrayResize(grad_ar, p);
   ArrayResize(grad_ma, q);
   
   // Итерационный процесс оптимизации
   for(int iter = 0; iter < max_iterations; iter++)
   {
      ArrayInitialize(grad_ar, 0.0);
      ArrayInitialize(grad_ma, 0.0);
      
      // Вычисление градиентов функции правдоподобия
      for(int i = p; i < lookback; i++)
      {
         double ar_part = 0.0, ma_part = 0.0;
         
         // Формирование компонент модели
         for(int j = 0; j < p && i - j - 1 >= 0; j++)
            ar_part += temp_ar[j] * data[i - j - 1];
         for(int j = 0; j < q && i - j - 1 >= 0; j++)
            ma_part += temp_ma[j] * errors[i - j - 1];
         
         double residual = data[i] - (ar_part + ma_part);
         
         // Накопление градиентов по AR коэффициентам
         for(int j = 0; j < p && i - j - 1 >= 0; j++)
            grad_ar[j] += -residual * data[i - j - 1];
            
         // Накопление градиентов по MA коэффициентам
         for(int j = 0; j < q && i - j - 1 >= 0; j++)
            grad_ma[j] += -residual * errors[i - j - 1];
      }
      
      // Обновление коэффициентов согласно правилу градиентного спуска
      for(int j = 0; j < p; j++)
         temp_ar[j] += learning_rate * grad_ar[j] / lookback;
      for(int j = 0; j < q; j++)
         temp_ma[j] += learning_rate * grad_ma[j] / lookback;
      
      // Оценка качества текущего приближения
      double current_ll = ComputeLogLikelihood(data, temp_ar, temp_ma);
      
      // Критерий остановки и обновление оптимального решения
      if(current_ll > best_ll)
      {
         best_ll = current_ll;
         ArrayCopy(ar_coeffs, temp_ar);
         ArrayCopy(ma_coeffs, temp_ma);
      }
      else
      {
         break; // Преждевременная остановка при отсутствии улучшения
      }
   }
}

Особое внимание уделяется вычислению частных производных функции правдоподобия по каждому из оптимизируемых параметров. Градиенты для коэффициентов авторегрессии вычисляются как сумма произведений остатков на соответствующие лаговые значения дифференцированного ряда, в то время как градиенты для коэффициентов скользящего среднего определяются через произведения остатков на предшествующие значения ошибок.

Алгоритм прогнозирования и обращения дифференцирования

Генерация прогнозных значений осуществляется рекурсивно, начиная с последнего наблюдаемого значения временного ряда. На каждом шаге прогнозирования вычисляется авторегрессионная компонента, как линейная комбинация предшествующих значений дифференцированного ряда с соответствующими коэффициентами. Компонента скользящего среднего формируется аналогично, через взвешенную сумму предшествующих остатков модели.

Основная процедура вычислений

Центральная функция OnCalculate представляет собой ядро вычислительного процесса, интегрирующее все компоненты алгоритма в единый поток обработки данных. Функция осуществляет последовательную обработку поступающих рыночных данных, применение процедуры дифференцирования, оптимизацию параметров модели и генерацию прогнозных значений.

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   ArraySetAsSeries(close, true);
   ArraySetAsSeries(time, true);
   
   // Проверка достаточности исторических данных
   if(rates_total < lookback + forecast_bars) return(0);
   
   // Формирование массива цен закрытия
   for(int i = 0; i < lookback; i++)
   {
      prices[i] = close[i];
      PriceBuffer[i] = close[i];
   }
   
   // Применение процедуры дифференцирования
   for(int i = 0; i < lookback - d; i++)
   {
      if(d == 1)
         differenced[i] = prices[i] - prices[i + 1];
      else if(d == 2)
         differenced[i] = (prices[i] - prices[i + 1]) - (prices[i + 1] - prices[i + 2]);
      else
         differenced[i] = prices[i];
   }
   
   // Оптимизация коэффициентов AR и MA
   ArrayInitialize(errors, 0.0);
   OptimizeCoefficients(differenced);
   
   // Генерация ARIMA прогноза
   double forecast[];
   ArrayResize(forecast, forecast_bars);
   double undiff[];
   ArrayResize(undiff, forecast_bars);
   
   // Инициализация прогнозного процесса
   forecast[0] = prices[0];
   undiff[0] = prices[0];
   
   // Итерационное формирование прогноза
   for(int i = 1; i < forecast_bars; i++)
   {
      double ar_part = 0.0;
      double ma_part = 0.0;
      
      // Вычисление авторегрессионной компоненты
      for(int j = 0; j < p && i - j - 1 >= 0; j++)
         ar_part += ar_coeffs[j] * (j < lookback ? differenced[j] : forecast[i - j - 1]);
      
      // Вычисление компоненты скользящего среднего
      for(int j = 0; j < q && i - j - 1 >= 0; j++)
         ma_part += ma_coeffs[j] * errors[j];
      
      // Формирование прогнозного значения
      forecast[i] = ar_part + ma_part;
      
      // Процедура обращения дифференцирования
      if(d == 1)
         undiff[i] = undiff[i - 1] + forecast[i];
      else if(d == 2)
         undiff[i] = undiff[i - 1] + (undiff[i - 1] - (i >= 2 ? undiff[i - 2] : prices[1])) + forecast[i];
      else
         undiff[i] = forecast[i];
      
      // Обновление массива ошибок для следующих итераций
      errors[i % lookback] = forecast[i] - (i < lookback ? differenced[i] : 0.0);
   }
   
   // Заполнение выходного буфера прогнозными значениями
   for(int i = 0; i < forecast_bars; i++)
   {
      ForecastBuffer[i] = undiff[i];
   }
   
   // Расширение исторических данных для непрерывности отображения
   for(int i = forecast_bars; i < lookback; i++)
   {
      ForecastBuffer[i] = prices[i - forecast_bars];
   }
   
   return(rates_total);
}

Процедура обращения дифференцирования представляет собой критически важный этап, обеспечивающий корректное восстановление исходного масштаба прогнозируемых значений. Для случая первого порядка дифференцирования, каждое прогнозное значение получается суммированием предыдущего недифференцированного значения с соответствующим прогнозом первой разности. При использовании дифференцирования второго порядка, применяется более сложная рекурсивная формула, учитывающая кривизну временного ряда.

Вычислительные аспекты и оптимизация производительности

Эффективность алгоритма во многом определяется правильной организацией вычислительного процесса и оптимальным использованием ресурсов процессора. Основная функция OnCalculate структурирована таким образом, чтобы минимизировать количество избыточных вычислений при поступлении новых рыночных данных.

Процедура дифференцирования реализована с учетом различных порядков преобразования. Для дифференцирования первого порядка вычисляется простая разность между соседними наблюдениями, в то время как для второго порядка применяется формула второй разности, позволяющая устранить не только тренд, но и изменения в скорости тренда.

Критическим аспектом реализации является управление памятью и корректная работа с массивами переменной длины. Использование функций ArrayResize и ArraySetAsSeries обеспечивает адаптацию структуры данных к изменяющимся параметрам модели и особенностям организации данных в MetaTrader 5.

Калибровка параметров и адаптация к рыночным условиям

Успешное применение модели ARIMA в реальных торговых условиях требует тщательной калибровки параметров с учетом специфики конкретного финансового инструмента и временного горизонта анализа. Параметр lookback определяет глубину исторического анализа и должен быть достаточным для обеспечения статистической значимости оценок, но не настолько большим, чтобы включать устаревшую информацию.

Выбор порядков p, d и q модели представляет собой компромисс между точностью описания данных и вычислительной сложностью. Увеличение порядка авторегрессии p позволяет учесть более сложные временные зависимости, однако, чрезмерное усложнение модели может привести к переобучению и снижению качества прогноза на новых данных.

Параметр скорости обучения learning_rate требует особенно тщательной настройки, поскольку слишком большое значение может привести к осцилляциям алгоритма оптимизации, в то время как слишком малое значение замедляет сходимость к оптимуму.

Статистическая валидация и оценка качества прогноза

Объективная оценка качества работы индикатора требует применения комплекса статистических критериев, позволяющих количественно охарактеризовать точность прогнозирования. Среди наиболее информативных метрик следует выделить среднюю абсолютную ошибку, корень среднеквадратичной ошибки и коэффициент детерминации.

Метрики качества прогнозирования

Реализация функций оценки качества прогноза позволяет осуществлять количественный анализ эффективности модели и сравнение различных спецификаций ARIMA. Средняя абсолютная ошибка предоставляет интуитивно понятную меру отклонения прогнозов от реальных значений, выраженную в единицах измерения исходного временного ряда.

// Функция вычисления средней абсолютной ошибки
double CalculateMAE(double &actual[], double &predicted[], int size)
{
   double mae = 0.0;
   for(int i = 0; i < size; i++)
   {
      mae += MathAbs(actual[i] - predicted[i]);
   }
   return mae / size;
}

// Функция вычисления корня среднеквадратичной ошибки
double CalculateRMSE(double &actual[], double &predicted[], int size)
{
   double mse = 0.0;
   for(int i = 0; i < size; i++)
   {
      double error = actual[i] - predicted[i];
      mse += error * error;
   }
   return MathSqrt(mse / size);
}

// Функция расчета коэффициента детерминации
double CalculateR2(double &actual[], double &predicted[], int size)
{
   double actual_mean = 0.0;
   for(int i = 0; i < size; i++)
      actual_mean += actual[i];
   actual_mean /= size;
   
   double ss_tot = 0.0, ss_res = 0.0;
   for(int i = 0; i < size; i++)
   {
      ss_tot += (actual[i] - actual_mean) * (actual[i] - actual_mean);
      ss_res += (actual[i] - predicted[i]) * (actual[i] - predicted[i]);
   }
   
   return 1.0 - (ss_res / ss_tot);
}

Диагностика остатков модели

Анализ остатков модели представляет критически важный аспект валидации, позволяющий выявить систематические отклонения от предположений модели. Тест Льюнга-Бокса на автокорреляцию остатков обеспечивает проверку адекватности спецификации модели, в то время как тест Жарка-Бера позволяет оценить нормальность распределения остатков.

// Функция вычисления автокорреляционной функции остатков
double CalculateAutocorrelation(double &residuals[], int lag, int size)
{
   double mean = 0.0;
   for(int i = 0; i < size; i++)
      mean += residuals[i];
   mean /= size;
   
   double numerator = 0.0, denominator = 0.0;
   
   for(int i = lag; i < size; i++)
   {
      numerator += (residuals[i] - mean) * (residuals[i - lag] - mean);
   }
   
   for(int i = 0; i < size; i++)
   {
      denominator += (residuals[i] - mean) * (residuals[i] - mean);
   }
   
   return numerator / denominator;
}

// Статистика Льюнга-Бокса для проверки автокорреляции
double LjungBoxTest(double &residuals[], int max_lag, int size)
{
   double lb_stat = 0.0;
   
   for(int k = 1; k <= max_lag; k++)
   {
      double rho_k = CalculateAutocorrelation(residuals, k, size);
      lb_stat += (rho_k * rho_k) / (size - k);
   }
   
   return size * (size + 2) * lb_stat;
}

Процедура кросс-валидации позволяет оценить устойчивость модели к изменениям в составе обучающей выборки. Методика скользящего окна обеспечивает более реалистичную оценку качества прогноза в условиях, приближенных к реальной торговле, когда модель последовательно применяется к новым данным без пересмотра параметров.

Анализ остатков модели предоставляет важную информацию о соответствии предположений модели характеристикам реальных данных. Тесты на автокорреляцию остатков позволяют выявить неучтенные временные зависимости, в то время как тесты на нормальность распределения остатков проверяют корректность использованной статистической модели.

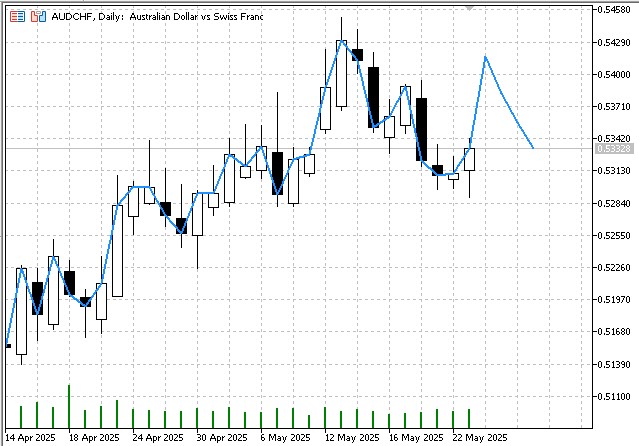
Итогом работы индикатора будет прогноз на указанный срок:

Перспективы развития и модификации алгоритма

Современные исследования в области анализа финансовых временных рядов открывают широкие возможности для развития базовой модели ARIMA. Включение сезонных компонент в рамках модели SARIMA позволяет учесть циклические паттерны, характерные для многих финансовых инструментов. Методы регуляризации, такие как L1 и L2 пенализация, способны повысить устойчивость модели к выбросам и предотвратить переобучение.

Адаптивные модификации алгоритма, предполагающие динамическое изменение параметров модели в зависимости от текущих рыночных условий, представляют особый интерес для высокочастотной торговли. Интеграция методов машинного обучения может обеспечить автоматический выбор оптимальной спецификации модели без участия аналитика.

Многомерные расширения модели ARIMA открывают возможности для одновременного моделирования нескольких взаимосвязанных финансовых инструментов, что особенно актуально для портфельного управления и арбитражных стратегий.

Заключительные соображения

Представленная реализация индикатора ARIMA в среде MQL5 демонстрирует возможность успешной адаптации классических эконометрических методов к задачам алгоритмического трейдинга. Строгое следование статистической методологии в сочетании с эффективной программной реализацией обеспечивает создание надежного инструмента для анализа финансовых временных рядов.

Практическое применение индикатора требует глубокого понимания как математических основ модели, так и специфики рынка, на котором она применяется. Модель работает явно хуже на системах с неустойчивыми трендами.