Rede neural na prática: Gradiente Descendente

Introdução

No artigo anterior Rede neural na prática: O caso da porta XOR, exploramos como poderíamos resolver o problema, ou melhor dizendo, o fato de um único neurônio não conseguir aprender como representar uma porta do tipo XOR ou sua inversa, a NXOR. Bem, apesar de que aquele único neurônio, venha a ser capaz de conseguir representar diversas situações. Acredito que tenha ficado bastante claro, de que existem situações em que um único neurônio, não consegue lidar. Mesmo que o caso possa estar se mostrando como sendo aparentemente bastante simples.

E que possa à primeira vista dar a entender que o neurônio conseguirá representar aqueles mesmos dados. Existem situações em que isto de fato não acontece. E este foi o intuito até o momento. Mostrar que diferente do que muitos dizem ou querem que você venha a acreditar. De que de fato, existem casos em que não temos como fazer as coisas funcionarem apenas por que funcionam em um caso simples e específico.

Assim sendo, um neurônio artificial, não é nem de longe algo tão extraordinário como muitos pensam. Ele por si só não passa de um mero e simples cálculo matemático. Nada além disto. Porém, acredito que você, deve ter notado que apesar de podermos forçar um neurônio artificial, a representar algo. Podemos em alguns casos ter alguns inconvenientes. Isto devido ao fato de que a cada mudança a ser feita, precisaremos a todo momento fazer algum tipo de manipulação no neurônio. Isto para que ele possa se comportar de forma a conseguir representar determinados tipos de dados. Este tipo de coisa, muitas das vezes inviabilizam totalmente um dado projeto.

Porém como você, que vem acompanhando estes meus artigos sobre rede neural deve ter notado. Não existe de fato uma solução definitiva. Temos sim, soluções que cobrem mais ou menos casos. Mas nunca uma que seja definitiva. Mas isto não nos impede nem um pouco, de tomar uma dada direção, ou tentar implementar algo, a fim de tornar viável o uso de neurônios artificiais.

Mas existem diversas coisas das quais, podem ser mais ou menos confusas quando o assunto é rede neurais. Ainda mais quando se está começando a estudar sobre o tema. Sei disto pois passei pelo mesmo processo no começo, quando comecei a aprender programação C/C++. Na época o tema não era tão divulgado e estava na boca de tanta gente. Para dizer a verdade, eram poucas as pessoas que diziam sobre o tema. E todos eram bem céticos quando iam falar sobre o mesmo.

Diferente do que acontece atualmente, em que a mídia no geral, parece estar forçando o tema. Dizendo que redes neurais são isto ou aquilo. E para piorar, muitos, mas principalmente investidores, tem dito coisas, que estão longe de serem realidade. Mas não estou aqui para julgar ou provocar polemica. Quero sim é passar um pouco do que sei. Da forma que seja o mais didática possível. Assim você, poderá pelo menos ter por onde começar para entender um pouco mais sobre o assunto.

Pois bem, neste artigo, vamos fazer algo um tanto quanto diferente. Sei que muitos acreditam que estes meus artigos sobre redes neurais, são uma sequência. Quando na verdade, não tem como criar uma sequência sobre o tema. Pode acreditar, e por mais estranho que possa parecer, criar uma sequência sobre redes neurais é algo praticamente impossível. Isto por que, vira e mexe, temos que voltar aos primórdios. E o motivo é simples: A HUMANIDADE NÃO TEM UMA IDEIA CLARA DE COMO DESENVOLVER TAL COISA.

Isto que acabei de dizer pode parecer completamente ilógico, já que aparentemente a cada dia que passa, surge alguma novidade sobre o tema. Mas na prática, as coisas não são bem assim. O que de fato acontece, é que vira e mexe, precisamos voltar e repensar o que já foi feito, a fim de tentar solucionar algum novo problema que surgiu.

Nos artigos anteriores, você deve ter visto que, apesar de tudo funcionar. Temos diversos problemas em mãos. Todos estes problemas, já foram, ou estão sendo solucionados neste exato momento. Seja de uma forma, seja de outra. Alguns dos problemas que posso citar aqui, e que já foram vistos nestes meus artigos são: Quando mais parâmetros, ou variáveis tivermos de tratar, mais lento o neurônio, ou rede neural se torna. E a taxa de crescimento do consumo de poder computacional cresce à medida que temos mais e mais variáveis para serem computadas. Outro problema, é que não temos muita flexibilidade para adicionar mais ou menos parâmetros ou variáveis ao neurônio.

Este problema, pode ser melhor entendido da seguinte forma: Nós começamos com uma única entrada no neurônio. Isto feito nos primeiros artigos, onde foi feito um esboço do neurônio. Mas logo foi preciso adicionar uma nova entrada. Então o código que antes era como mostrado no fragmento abaixo:

//+------------------------------------------------------------------+
double Cost(const double w)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((Train[c][0] * w) - Train[c][1], 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+

Logo passou a ser como mostrado no fragmento a seguir:

//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b, const double &Train[][])
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow(((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2], 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+

Observe que a coisa começou a crescer e a se tornar um tanto quando complica. Mas se você acha que não, quero que pense no seguinte fato: A cada nova variável ou parâmetro, que o neurônio passar a ter, teremos de mexer no código. Como cada novo parâmetro, representa uma nova entrada, se em um dado momento tivermos que usar mil entradas, teremos que colocar no código, as mesmas mil variáveis. E tudo isto de forma manual. Pense só na trabalheira que seria fazer isto.

Um outro problema, é relacionado a forma como efetuamos o cálculo para ajustar as variáveis. Ou seja, a forma como o neurônio ou rede neural, irá representar um dado banco de dados. Esta talvez seja a questão que mais vem a ter peso, nas tomadas de decisão a fim de construir um ou outro modelo de implementação para o neurônio. Para que você entenda isto, vamos tomar como base um código que foi visto em um artigo anterior. O código em questão pode ser visto no fragmento abaixo.

//+------------------------------------------------------------------+
double Cost(const double w0, const double w1, const double b)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
double Cost_2(double &w0, double &w1, double &b)
{
    double err, ew0, ew1, eb;

    err = ew0 = ew1 = eb = 0;
    for (uint c = 0; c < nTrain; c++)
    {
        err += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + b) - Train[c][2]), 2);
        ew0 += MathPow((macroSigmoid((Train[c][0] * (w0 + eps)) + (Train[c][1] * w1) + b) - Train[c][2]), 2);
        ew1 += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * (w1 + eps)) + b) - Train[c][2]), 2);
        eb += MathPow((macroSigmoid((Train[c][0] * w0) + (Train[c][1] * w1) + (b + eps)) - Train[c][2]), 2);
    }

    w0 -= (((ew0 - err)/ eps) * eps);
    w1 -= (((ew1 - err)/ eps) * eps);
    b  -= (((eb - err)/ eps) * eps);

    return err / nTrain;
}
//+------------------------------------------------------------------+

Nele fazemos uma adaptação do código a fim de tornar a execução mais rápida. Isto cai na questão do primeiro problema, que é onde o custo computacional cresce à medida que temos mais coisas a serem feitas. Ou como muitos dizem: Quanto mais coisas tivermos de analisar, mais poder computacional iremos precisar. Porém apesar de ambas funções vistas no fragmento acima, efetivamente usarem o mesmo cálculo. A velocidade de execução é imensamente diferente. E isto é devido justamente ao fato de que a primeira função precisa ser chamada diversas vezes ao longo do tempo. Já a segunda é chamada bem menos vezes, e isto faz toda a diferença.

Mas temos uma outra questão. Talvez você não tenha notado, mas desde o início, todos os códigos foram focados em uma única fórmula matemática. Esta fórmula é a da regressão linear. Ok, fizemos uso de diferentes metodologias para conseguir a regressão linear. Mas todas no final se resumiram em usar a regressão linear.

Mas se a regressão linear funciona, por que tentar outra metodologia? Bem, é aqui em que entramos em uma outra parte sobre redes neurais. Cada metodologia, tem como objetivo, criar uma representação matemática dos dados que estamos usando. Só que se você usar uma metodologia mais rápida, precisará de menos poder computacional para obter os mesmos resultados.

No pior dos casos, o uso da força bruta, que apesar de funcionar, será complemente inviável. Isto por que a força bruta, irá sempre precisar de muito mais poder computacional do que um método focado em algum tipo de formula matemática. A regressão linear funciona em diversos casos. Porém conforme o número de parâmetros cresce, ela também começa a cair no mesmo problema de usar a força bruta. Ou seja, começa a pedir cada vez mais poder computacional para ser executada em tempo hábil.

No entanto, se você observar a formulação da regressão linear que está sendo usada, irá notar algo curiosos e interessante. E é aqui em que começaremos a focar neste artigo. Vamos então começar um novo tópico para entender o que começaremos a fazer a partir de agora.

E novamente, derivadas, mas com um novo nome

Para simplificar ao máximo, vamos voltar aos primórdios, para que você consiga acompanhar a matemática que será usada. Não gosto muito de colocar fórmulas e coisas do tipo, pois isto muita das vezes dará a impressão de que as coisas venham a ser muito mais complicadas do que realmente são. Mas não tem jeito. Para explicar de forma adequada, precisamos ver um pouco de matemática. Na maior parte das vezes, a regressão linear é conseguida usando a redução de mínimo quadrado. Ou seja, você pega o erro gerado no cálculo e o eleva ao quadrado. Soma todos dos quadrados obtidos e terá um erro total. Isto é o que a equação abaixo representa.

Aqui estou reduzindo a coisa ao seu nível mais básico. Então não existe a questão do viés. Apenas e somente o peso é usado. Bem, o valor de < k > representa o total de dados que estamos usando. Ou melhor dizendo, ele representa quanta informação temos para encontra a regressão linear. O valor de < x > são os dados usados no treinamento, assim como o valor de < y >. Só que x são os dados de entrada e y o resultado esperado. A única coisa que precisamos mexer é no peso, que é o valor de < w >. Ok, está é a parte básica.

Porém esta equação nos diz o seguinte, se usarmos um valor arbitrário para < w >, que é a única coisa da qual podemos manipular. Iremos gerar um erro igualmente arbitrário. Daí se mudarmos o valor de < w > também de forma arbitrária, teremos um novo erro. Se compararmos ambos erros, poderemos saber se estamos indo na direção certa ou errada. Se estivermos indo na direção correta, podemos continuar, mas se estamos na direção errada devemos parar e mudar de direção. Simples assim. Porém esta mesma equação mostrada acima, tem um detalhe que nos chama a atenção. E este é justamente o fato de que estamos elevando o valor ao quadrado. E o simples fato de isto acontecer, nos permite criar uma derivada da mesma. E é aqui que a coisa começa realmente a ficar interessante.

Quando é feita a derivação desta equação, ela passa a receber um novo nome. Isto devido a um fato bem curioso a respeito dela. O novo nome é: GRADIENTE DESCENDENTE. Você muito provavelmente já deve ter ouvido falar sobre este tal gradiente descendente. Mas você tem noção de onde ele surgiu? Bem, se a resposta foi não, agora você sabe. O gradiente descendente é uma equação derivada da regressão linear. A forma de tornar a regressão linear em um gradiente descendente é algo que não vou mostrar aqui, pois foge completamente do meu objetivo neste artigo.

Porém para quem tiver curiosidade em entender como isto acontece, irei deixar no final deste artigo, nos campos de referências, um local para você estudar o tema. Mas prepare-se para ver bastante matemática envolvida. Mas a explicação ficou muito melhor do que se eu fosse fazer aqui, já que o objetivo aqui é a programação em si. Porém ao transformar ao derivar a equação acima, você acabará caindo na equação abaixo.

Mas isto é apenas quando usamos só e somente o peso. Mas e se desejarmos usar também o viés? Bem, neste caso, teremos duas funções distintas e não somente uma, como você poderia estar esperando. Estas duas funções são vistas abaixo.

Nesta estamos procurando o valor de custo baseado apenas no fato peso. Ou seja, mudamos o peso e mantemos o viés parado buscando assim o menor custo para o parâmetro peso. Já na imagem abaixo procuramos reduzir o custo, nos baseando no fator viés. Ou seja, ficamos com o peso parado, e manipulamos apenas o fator do viés.

Epá, mas espere um pouco aí. A única diferença é o fato de que em uma e outra é o final da equação? Sim, meu caro leitor, para que você entenda isto e por que desta diferença existir, sugiro que você leia o conteúdo que estou deixando como referência. Ou procure saber sobre como uma derivada é feita neste caso. Assim você de fato irá conseguir entender um pouco mais afundo as questões matemáticas envolvidas neste tal gradiente descendente.

Apesar do gradiente descendente ser apenas mais um, entre tantos outros métodos de redução de custo, a fim de construir a reta, ou equação que represente os dados. Devo admitir que ele é um dos atualmente mais usados. Mas existem métodos que em alguns casos são melhores do que ele. Enquanto em outros casos, mesmo este gradiente descendente, pode vir a sofrer novas manipulações matemáticas, cujo objetivo é o de tentar criar uma metodologia ainda melhor.

Por isto surge tantos e tantos termos matemáticos quando você estiver estudado sobre redes neurais. Não é por que uma metodologia é melhor ou pior. O fato é que, como programadores estamos sempre à procura de novas formas de cálculo. Mas sempre com um mesmo objetivo em comum, que é reduzir o custo computacional. Ou seja, fazer a mesma coisa, só que de forma mais rápida. Este é o objetivo de tanta pesquisa na área de matemática, quando o assunto é redes neurais.

Muito bem, mas como tudo isto fica em termos de código? Pois é isto que realmente nos interessa e também é o motivo para a escrita deste artigo. Bem, para ver isto, vamos a um novo tópico.

Codificando um neurônio usando gradiente descendente

Aqui vamos voltar novamente para o código mais simples de todos. Ou seja, não vamos nos preocupar com funções de ativação. Com viés. Com múltiplas entradas ou coisa do tipo. Vamos aqui começar novamente pelo sistema inicial. Ou seja, uma entrada e uma saída. Como se nada que foi feito anteriormente, tivesse de fato sido feito. Isto para que você realmente consiga entender como a coisa deve ser implementada. Se partirmos para algo já um tanto quanto mais elaborado, você ficaria muito tempo, tentando entender por que funciona. Ou por que não está funcionando como você esperava ver funcionar. Então vamos começar novamente tudo do zero.

Para fazer isto, vamos ver como era o primeiro neurônio, que vimos nestes artigos sobre redes neurais. O código pode ser visto logo abaixo, na íntegra.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define PrintEx(A) Print(#A, " => ", A)
05. #define macroRandom (rand() / (double)SHORT_MAX)
06. //+------------------------------------------------------------------+
07. double Train[][2] {
08.                     {0, 0},
09.                     {1, 3},
10.                     {2, 6},
11.                     {3, 9},
12.                     {4, 12},
13.                   };
14. //+------------------------------------------------------------------+
15. const uint nTrain = Train.Size() / 2;
16. const double epsilon = 1e-3;
17. //+------------------------------------------------------------------+
18. double Cost(const double w)
19. {
20.     double err, factor;
21. 
22.     err = 0;
23.     for (uint c = 0; c < nTrain; c++)
24.     {
25.         factor = Train[c][0] * w;
26.         err += MathPow(factor - Train[c][1], 2);
27.     }
28. 
29.     return err;
30. }
31. //+------------------------------------------------------------------+
32. void OnStart()
33. {
34.     double weight, err, e1;
35.     ulong it0, it1, count;
36. 
37.     Print("************************************");
38.     Print("Linear regression neuron...");
39.     MathSrand(512);
40.     weight = (double)macroRandom;
41. 
42.     it0 = GetTickCount();
43.     for(count = 0; (count < ULONG_MAX) && ((err = Cost(weight)) > epsilon); count++)
44.     {
45.         e1 = (Cost(weight + epsilon) - err) / epsilon;
46.         weight -= (e1 * epsilon);
47.     }
48.     it1 = GetTickCount();
49.     Print("Time: ", (it1 - it0) / 1000.0, " seconds.");
50.     PrintEx(count);
51.     PrintEx(weight);
52.     PrintEx(err);
53. }
54. //+------------------------------------------------------------------+

Claro que mudei algumas coisas no código, para deixá-lo ainda mais simples e didático, a fim de poder ser lido com facilidade. Mesmo por parte de pessoas que não entendem tanto de matemática, mas que tem um mínimo de conhecimento em programação. Coisa pouca, não precisa ser um mestre JEDI em programação para entender o que está acontecendo. Mesmo por que este código, mas não exatamente este, foi explicado antes. Porém a ideia e o funcionamento permanecem iguais. Note que na linha 38 estou dizendo qual foi a modelagem usada para a função de custo. Então ao executar este código, você verá a seguinte imagem no terminal do MetaTrader 5:

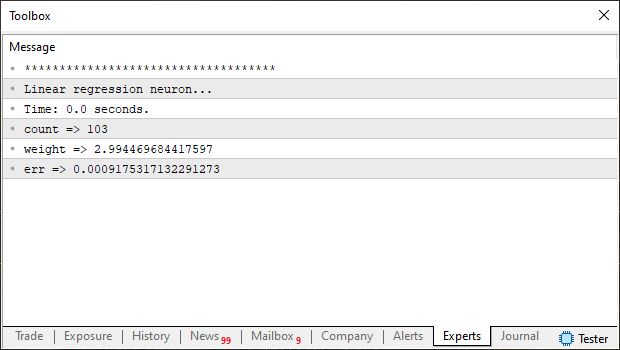
Preste atenção as informações desta imagem. Pois quero que você as compare com o que será visto próximo código. Ok, já temos um parâmetro para comparação, agora vamos ver este mesmo neurônio. Ou melhor dizendo, este mesmo treinamento sendo feito, porém com uma função de custo baseada em gradiente descendente. O código para isto, pode ser visto abaixo na íntegra.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define PrintEx(A) Print(#A, " => ", A)
05. #define macroRandom (rand() / (double)SHORT_MAX)
06. //+------------------------------------------------------------------+
07. double Train[][2] {
08.                     {0, 0},
09.                     {1, 3},
10.                     {2, 6},
11.                     {3, 9},
12.                     {4, 12},
13.                   };
14. //+------------------------------------------------------------------+
15. const uint nTrain = Train.Size() / 2;
16. const double epsilon = 1e-3;
17. //+------------------------------------------------------------------+
18. double Cost(const double w)
19. {
20.     double err, x, y;
21. 
22.     err = 0;
23.     for (uint c = 0; c < nTrain; c++)
24.     {
25.         x = Train[c][0];
26.         y = Train[c][1];
27.         err += 2 *(x * w - y) * x;
28.     }
29. 
30.     return err;
31. }
32. //+------------------------------------------------------------------+
33. void OnStart()
34. {
35.     double weight, err;
36.     ulong it0, it1, count;
37. 
38.     Print("************************************");
39.     Print("Linear gradient neuron...");
40.     MathSrand(512);
41.     weight = (double)macroRandom;
42. 
43.     it0 = GetTickCount();
44.     for(count = 0; (count < ULONG_MAX) && (MathAbs(err = Cost(weight)) > epsilon); count++)
45.         weight -= (err * epsilon);
46.     it1 = GetTickCount();
47.     Print("Time: ", (it1 - it0) / 1000.0, " seconds.");
48.     PrintEx(count);
49.     PrintEx(weight);
50.     PrintEx(err);
51. }
52. //+------------------------------------------------------------------+

Ao executar este código, você verá no terminal do MetaTrader 5, a seguinte imagem mostrada abaixo:

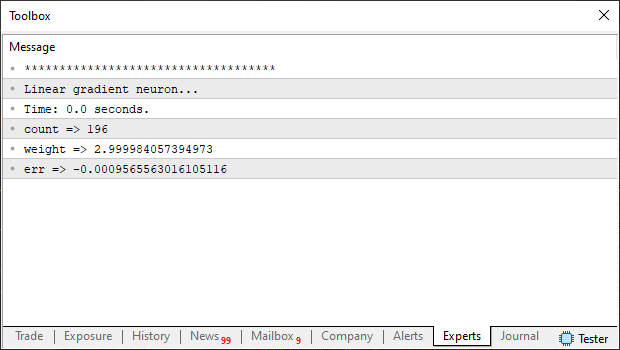
Agora compare ambas imagens, que foi gerada pelo gradiente descendente, com a gerada pela regressão linear. Você consegue notar alguma diferença? Sim, não, talvez ou quem sabe. Bem para evitar de você ficar se esforçando para tentar ver. Na imagem abaixo, temos ambos resultados postos juntos, assim será mais simples de notar alguma diferença.

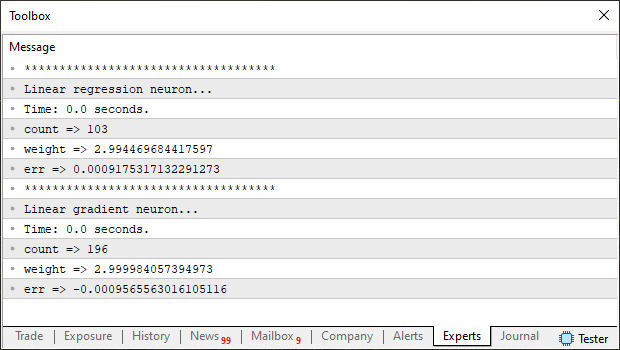
Cara, eu não estou conseguindo notar nenhuma diferença, a não ser no contador. Bem meu caro leitor, se este foi seu caso, observe novamente com mais calma. Note que a regressão linear foi aparentemente mais rápida. Porém o valor de peso encontrada por ela é ligeiramente menos preciso que o valor encontrado pelo gradiente descendente. Neste momento você pode estar imaginando: Bem, mas precisamos que a função de custo execute o mais rápido possível, não é mesmo? Sim, meu caro leitor, e concordo plenamente com esta sua observação. Por isto que estou mostrando esta comparação.

Quero que você não caia na falácia de muitos, que dizem, ou insistem em dizer, de que o gradiente descendente é melhor que a regressão linear. Tudo depende. E depende principalmente do tipo de coisa que estamos usando, para treinar o neurônio. Ou seja, do tipo de dados que estamos usando, a fim de gerar os valores da equação. Sendo que estes têm como objetivo, representar da melhor forma possível, o conteúdo que se encontra presente no nosso banco de dados. Nem sempre uma função dita ser melhor, de fato será melhor. Cada caso é um caso.

Agora observem também o fato de que o valor de erro é diferente. No caso da regressão linear ele sempre será positivo. Já no caso do gradiente descendente, ele hora poderá ser positivo. Hora poderá ser negativo. Isto por que a própria função está tentando alcançar o melhor posicionamento para reduzir o custo da função gerada. Mas espere um pouco. Como assim? Não estou entendendo. O resultado conseguido não seria sempre o mesmo? Independentemente do tipo de função que estamos usando para procurar a melhor representação dos dados? Não meu caro leitor, e este é outro dos erros ou falácias do qual muitos ficam falando quando o assunto é rede neurais. Ou melhor dizendo, quando o assunto é treinamento de uma rede neural. Seja usando um ou mais neurônios. Para explicar isto, vamos para um novo tópico, assim conseguirei separar melhor as coisas.

O que representa o tão falado custo da função

O valor que todos chamam de custo, representa o erro que uma função. Ou melhor, que a representação gerada por uma função tem frente as verdadeiras informações contidas no banco de dados, usados para gerar a tal função. Ok, mas onde está o problema nesta questão? Não consigo entender por que, mesmo um banco de dados com as mesmas informações pode vir a gerar uma função tão diferente. Elas não deveriam ser iguais, independentemente do tipo de modelagem usada para gerar a representação das informações no banco de dados? Definitivamente esta não é uma resposta tão simples de se dar. Mas de qualquer maneira, irá depender de cada caso específico.

Todos os exemplos que tenho mostrado, tem como objetivo serem o mais simples possível. Então em todos os casos a função geral para as informações de treinamento, podem ser facilmente representadas em uma parábola. Ou seja, temos um ponto único de convergência para o sistema. Desta forma, independentemente do ponto de origem, sempre e sempre, os modelos irão convergir para este ponto único. Mas em casos REAIS, nem sempre é assim. a curva que melhor represente as informações dentro do banco de dados, poderá ser um polinômio bastante complexo. Podendo ser de grau três ou mais, e quanto maior for este grau, mais o ponto de partida irá influenciar no quesito de encontrar a melhor representação para os dados. Ou seja, mesmo que a modelagem usada, não consiga convergir para um ponto onde o custo será menor. Ainda assim teremos a impressão de que conseguimos encontrar o melhor ponto possível.

Mostrar este tipo de coisa é muito mais difícil do que possa parecer. Mas mesmo assim, são mais comuns de acontecer do que você, meu caro leitor, possa estar imaginando. Para ilustrar um pouco melhor isto que acabei de dizer. Vamos pensar o seguinte: Suponhamos que você tenha um banco de dados. Cujo todo o conteúdo presente nele, possa ser representado por uma função matemática. E ao criar o gráfico de tal função, você obtenha o seguinte gráfico mostrado na imagem abaixo:

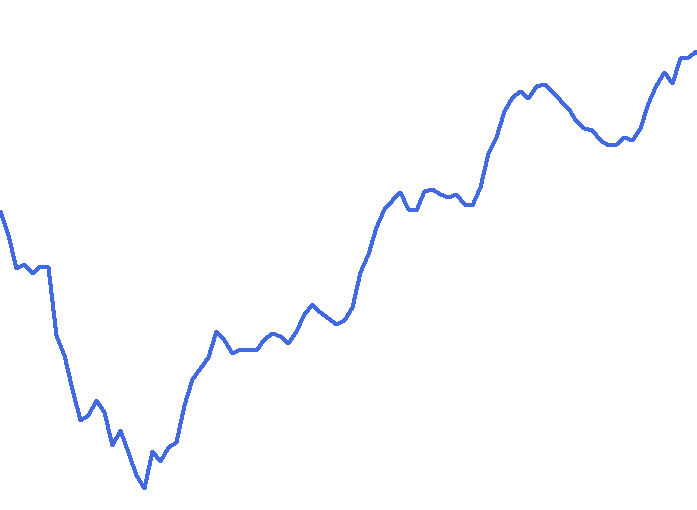
Minha pergunta é: Qual o melhor sistema de rede neural, que será capaz de criar uma representação matemática para este banco de dados? Isto para que nenhuma informação seja perdida por conta que o gráfico da representação gerada pela rede neural seja diferente do mostrado acima. Hum, agora realmente temos um problema não é mesmo?!!? E é exatamente neste ponto em que mora todas as pesquisas sobre redes neurais. Tudo absolutamente tudo se resume a isto.

Você pode pensar o seguinte: Podemos usar a regressão linear. Ou quem sabe o gradiente descendente. Ou o gradiente estocástico. Ou podemos usar a força bruta para isto. Sim, meu caro leitor. Na pior das hipóteses, tudo poderia ser resumido a força bruta. Mas pense só no poder computacional necessário para criar uma equação para representar estes dados. É algo quase impensável em tempos atuais. Quem sabe, se em algum momento surgir de fato um computador quântico. Mas até lá. Esqueçamos a força bruta. Precisamos usar um outro método. E é aqui que mora o problema.

Claramente você pode notar, que nesta curva, reside um ponto mínimo. Este ponto é onde a função terá o menor custo possível. Pelo menos no que está sendo mostrado no gráfico. Porém muitos dizem que ao tentar encontrar este ponto, estaremos na verdade fazendo um overfitting. Mas isto é pura bobagem. A ideia aqui é criar uma função que represente idealmente todas as informações dentro do banco de dados. Então de onde vem está de overfitting? Bem, esta ideia deriva do fato de que todos querem a melhor função, mas ao encontrar ela, podemos simplesmente não conseguir identificar coisas fora do banco de dados.

Mas tem um outro motivo para isto. O custo computacional. Pense no seguinte. Qualquer modelagem que visa representar um banco de dados, precisa de uma, ou mais informações iniciais. Quando todas as informações iniciais são computadas é gerado um custo inicial para a função. Agora vem o pulo do gato. Onde está este ponto inicial? Bem, vamos voltar a nossa figura, e desta vez com alguns pontos representados na reta.

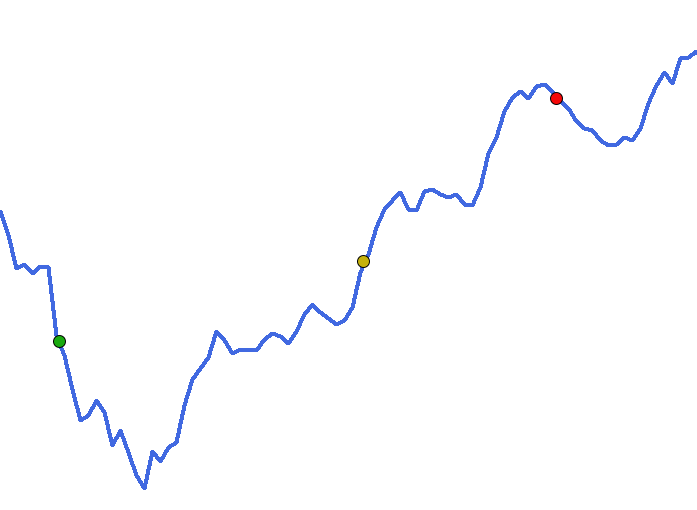
Cada um destes pontos, foram criados de forma totalmente aleatória. Da mesma forma que sempre iniciamos o neurônio, ou rede neural. Porém eles representam o custo inicial, gerado justamente por estes dados aleatórios. Agora vem a parte engraçada. Qual destes pontos atingirá de fato o ponto de menor custo nesta curva vista em azul? Bem, isto irá depende de como cada ponto irá procurar este local de menor custo. Dependendo da forma como cada um procurar, nenhum jamais atingirá o tal ponto de convergência máxima. Ou seja, o ponto de menor custo. Isto por que existem vales e picos no caminho deles. E nenhum deles sabe ao certo como superar tais picos, eles sempre procuram o vale mais profundo partindo do pico de onde surgirão. Por isto está coisa de overfitting, na verdade, não é o real problema. O real problema é: Quanto custo computacional será desperdiçado a procura do vale mais profundo. Ou ponto de menor custo?

Considerações finais

Neste artigo, tentei apresentar, de forma o mais simplificada e didática, quanto foi possível fazer, uma das questões mais controvérsias quando o assunto é rede neural. Que é justamente como procurar o melhor ponto possível, ou menor custo de uma função. Mostrei a diferença que existe entre uma regressão linear e um gradiente descendente. Ambos casos bastante simples e voltados para mostrar que nem sempre o que parece obvio, realmente é o melhor caminho.

Este campo de pesquisa chamado rede neural, ainda tem muito a progredir. Então se você tem interesse nele, procure estudar as coisas com calma. E sempre buscando material de qualidade. Pois existem diversas pessoas mal informadas, que apenas repetem falácias que eles simplesmente não compreendem. Deixo no anexo, os códigos usados neste artigo.

Mas apesar de tudo que foi dito aqui, neste artigo. Iremos voltar a falar novamente sobre este tema. Pois aqui apenas arranhei o que de fato rege este assunto.

Referência

Regressão Linear e Gradiente Descendente: Do zero à Bruxaria