
Deep neural network with Stacked RBM. Self-training, self-control
Contents
- 1. Structure of DBN
- 2. Preparation and selection of data
- 2.1. Input variables
- 2.2. Output variables
- 2.3. Initial data frame
- 2.3.1. Deleting highly correlated variables
- 2.4. Selection of the most important variables
- 3. Experimental part.
- 3.1. Building models
- 3.1.1. Brief description of the "darch" package
- 3.1.2. Building the DBN model. Parameters.
- 3.2. Formation of training and testing samples.
- 3.2.1. Balancing classes and pre-processing.
- 3.2.2. Coding the target variable
- 3.3. Training the model
- 3.3.1. Pre-training
- 3.3.2. Fine-tuning
- 3.4. Testing the model. Мetrics.
- 3.4.1. Decoding predictions.
- 3.4.2. Improving the prediction results
- Calibration
- Smoothing with a Markov chain model
- Correcting predicted signals on the theoretical balance curve
- 3.4.3. Metrics
- 4. Structure of the Expert Advisor
- 4.1. Description of the Expert Advisor's operation
- 4.2. Self-control. Self-training
- Installation and launching
- Ways and methods of improving qualitative indicators.
- Conclusion
Introduction
In preparation of data for conducting experiments, we will use variables from the previous article about evaluating and selecting predictors. We will form the initial sample, clean it and select the important variables.
We will consider ways of dividing the initial sample into training, testing and validation samples.
Using the "darch" package we will build a model of the DBN network, and train it on our sets of data. After testing the model, we will obtain metrics that will enable us to evaluate quality of the model. We will consider many opportunities that the package offers to configure settings of a neural network.
Also, we will see how hidden Markov models can help us improve neural network predictions.
We will develop an Expert Advisor where a model will be trained periodically on the fly without interruption in trade, based on results of continuous monitoring. The DBN model from the "darch" package will be used in the Expert Advisor. We will also incorporate the Expert Advisor built using SAE DBN from the previous article.
Furthermore, we will indicate ways and methods of improving qualitative indicators of the model.
1. Structure of a deep neural network initialized by Stacked RBM (DN_SRBM)
I recall that DN_SRBM consists of n-number of RBM that equals the number of hidden layers of neural network and, basically, the neural network itself. Training comprises two stages.
The first stage involves PRE-TRAINING. Every RBM is systematically trained without a supervisor on the input set (without target). After this weight of hidden layers, RBM are transferred to relevant hidden layers of neural network.
The second stage involves FINE-TUNING, where neural network is trained with a supervisor. Detailed information about it was provided in the previous article, so we don't have to repeat ourselves here. I will simply mention that unlike the "deepnet" package that we have used in the previous article, the "darch" package helps us to implement wider opportunities in building and tuning the model. More details will be provided when creating the model. Fig. 1 shows the structure and the training process of DN_SRBM
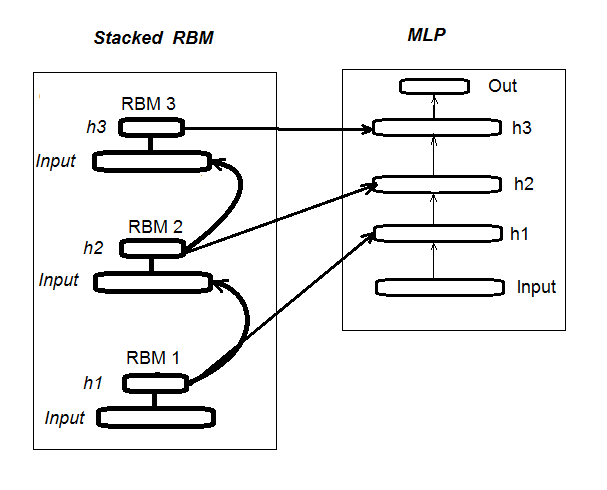
Fig. 1. Structure of DN SRBM
2. Preparation and selection of data
2.1. Input variables (signs, predictors)
In the previous article, we have already considered the evaluation and selection of predictors, so there is no need to provide additional information now. I will only mention that we used 11 indicators (all oscillators: ADX, aroon, ATR, CCI, chaikinVolatility, CMO, MACD, RSI, stoch, SMI, volatility). Several variables were selected from some indicators. This way we have formed the input set of 17 variables. Let's take quotes from the last 6000 bars on EURUSD, М30 as at 14.02.16, and calculate indicator values using the In() function.
#---2--------------------------------------------- In <- function(p = 16){ require(TTR) require(dplyr) require(magrittr) adx <- ADX(price, n = p) %>% as.data.frame %>% mutate(.,oscDX = DIp - DIn) %>% transmute(.,DX, ADX, oscDX) %>% as.matrix() ar <- aroon(price[ ,c('High', 'Low')], n = p) %>% extract(,3) atr <- ATR(price, n = p, maType = "EMA") %>% extract(,1:2) cci <- CCI(price[ ,2:4], n = p) chv <- chaikinVolatility(price[ ,2:4], n = p) cmo <- CMO(price[ ,'Med'], n = p) macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% as.data.frame() %>% mutate(., vsig = signal %>% diff %>% c(NA,.) %>% multiply_by(10)) %>% transmute(., sign = signal, vsig) %>% as.matrix() rsi <- RSI(price[ ,'Med'], n = p) stoh <- stoch(price[ ,2:4], nFastK = p, nFastD =3, nSlowD = 3, maType = "EMA") %>% as.data.frame() %>% mutate(., oscK = fastK - fastD) %>% transmute(.,slowD, oscK) %>% as.matrix() smi <- SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9) kst <- KST(price[ ,4])%>% as.data.frame() %>% mutate(., oscKST = kst - signal) %>% select(.,oscKST) %>% as.matrix() In <- cbind(adx, ar, atr, cci, chv, cmo, macd, rsi, stoh, smi, kst) return(In) }
We will get the input data matrix on the output.
2.2 Output data (target variable)
As a target variable we take signals obtained with ZZ. The function calculating a zigzag and a signal:
#----3------------------------------------------------ ZZ <- function(pr = price, ch = ch , mode="m") { require(TTR) require(magrittr) if (ch > 1) ch <- ch/(10 ^ (Dig - 1)) if (mode == "m") {pr <- pr[ ,'Med']} if (mode == "hl") {pr <- pr[ ,c("High", "Low")]} if (mode == "cl") {pr <- pr[ ,c("Close")]} zz <- ZigZag(pr, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) dz <- zz %>% diff %>% c(., NA) sig <- sign(dz) for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]} return(cbind(zz, sig)) }
Function parameters:
pr = price – matrix of OHLCMed quotes;
ch – minimum length of the zigzag bend in the points (4 signs) or in real terms (for example, ch = 0.0035);
mode – applied price ("m" - medium, "hl" - High and Low, "cl" - Close), medium used by default.
The function returns the matrix with two variables — in fact, the zigzag and the signal, obtained on the base of the zigzag angle in the range of [-1;1]. We shift the signal by one bar to the left (towards future). This specific signal will be used to train the neural network.
We calculate signals for ZZ with a bend length of at least 37 points (4 signs).
> out <- ZZ(ch = 37, mode = "m") Loading required package: TTR Loading required package: magrittr > table(out[ ,2]) -1 1 2828 3162
As we can see, the classes are slightly unbalanced. When forming samples for training the model, we will take necessary measures to level them off.
2.3. Initial data frame
Let's write a function that will create the initial data frame, clean it from uncertain data (NA) and convert the target variable to the factor with two classes "-1" and "+1". This function combines previously written functions In() and ZZ(). We will instantly crop the last 500 bars that will be used to evaluate the quality of the model's prediction.
#-----4--------------------------------- form.data <- function(n = 16, z = 37, len = 500){ require(magrittr) x <- In(p = n) out <- ZZ(ch = z, mode = "m") data <- cbind(x, y = out[ ,2]) %>% as.data.frame %>% head(., (nrow(x)-len))%>% na.omit data$y <- as.factor(data$y) return(data) }
2.3.1. Deleting highly correlated variables
We will delete variables with a correlation coefficient above 0.9 from our initial set. We will write a function that will form the initial data frame, remove highly correlated variables and return clean data.
We can check in advance which variables have a correlation above 0.9.
> data <- form.data(n = 16, z = 37) # prepare data frame > descCor <- cor(data[ ,-ncol(data)])# remove a target variable > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.1887 0.0532 0.2077 0.3040 0.5716 0.9588 > highCor <- caret::findCorrelation(descCor, cutoff = 0.9) > highCor [1] 12 9 15 > colnames(data[ ,highCor]) [1] "rsi" "cmo" "SMI"
Thus, the above listed variables are subject to removal. We will delete them from the data frame.
> data.f <- data[ ,-highCor] > colnames(data.f) [1] "DX" "ADX" "oscDX" "ar" "tr" [6] "atr" "cci" "chv" "sign" "vsig" [11] "slowD" "oscK" "signal" "vol" "Class"
We will write it compactly in one function:
#---5----------------------------------------------- cleaning <- function(n = 16, z = 37, cut = 0.9){ data <- form.data(n, z) descCor <- cor(data[ ,-ncol(data)]) highCor <- caret::findCorrelation(descCor, cutoff = cut) data.f <- data[ ,-highCor] return(data.f) } > data.f <- cleaning()
Not all authors of packages and researchers agree that highly correlated data should be removed from the sets. However, results using both options should be compared here. In our case, we will select the option with deleting.
2.4. Selection of the most important variables
Important variables will be selected based on three indicators: global importance, local importance (in conjunction) and partial importance by class. We will seize the opportunities of the "randomUniformForest" package as detailed in the previous article. All previous and following actions will be gathered in one function for compactness. Once executed, we will obtain three sets as a result:
- with best variables in contribution and interaction;
- with best variables for the class "-1";
- with best variables for the class "+1".
#-----6------------------------------------------------ prepareBest <- function(n, z, cut, method){ require(randomUniformForest) require(magrittr) data.f <<- cleaning(n = n, z = z, cut = cut) idx <- rminer::holdout(y = data.f$Class) prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)], method = method) x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)]) x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)]) y.train <- data.f[idx$tr, ncol(data.f)] y.test <- data.f[idx$ts, ncol(data.f)] #--------- ruf <- randomUniformForest( X = x.train, Y = y.train, xtest = x.test, ytest = y.test, mtry = 1, ntree = 300, threads = 2, nodesize = 1 ) imp.ruf <- importance(ruf, Xtest = x.test) best <- imp.ruf$localVariableImportance$classVariableImportance %>% head(., 10) %>% rownames() #-----partImport best.sell <- partialImportance(X = x.test, imp.ruf, whichClass = "-1", nLocalFeatures = 7) %>% row.names() %>% as.numeric() %>% colnames(x.test)[.] best.buy <- partialImportance(X = x.test, imp.ruf, whichClass = "1", nLocalFeatures = 7) %>% row.names() %>% as.numeric() %>% colnames(x.test)[.] dt <- list(best = best, buy = best.buy, sell = best.sell) return(dt) }
We will clarify the order of the function calculations. Official parameters:
n – input data parameter;
z – output data parameter;
cut – correlation threshold of variables;
method – input data pre-processing method.
Order of calculations:
- create the initial set of data.f, which has highly correlated variables removed, and save it for further use;
- identify indexes of the training and testing samples of idx;
- determine pre-processing parameters of prep;
- divide the initial sample into training and testing samples, input data normalized;
- obtain and test the ruf model on the obtained sets;
- calculate the importance of the imp.ruf variables;
- select 10 most important variables in terms of contribution and interaction — best;
- select 7 most important variables for each class "-1" and "+1" — best.buy, best.sell;
- Create a list with three sets of predictors — best, best.buy, best.sell.
We will calculate these samples and evaluate values of global, local and partial importance of the selected variables.
> dt <- prepareBest(16, 37, 0.9, c("center", "scale","spatialSign")) Loading required package: randomUniformForest Labels -1 1 have been converted to 1 2 for ease of computation and will be used internally as a replacement. 1 - Global Variable Importance (14 most important based on information gain) : Note: most predictive features are ordered by 'score' and plotted. Most discriminant ones should also be taken into account by looking 'class' and 'class.frequency'. variables score class class.frequency percent 1 cci 4406 -1 0.51 100.00 2 signal 4344 -1 0.51 98.59 3 ADX 4337 -1 0.51 98.43 4 sign 4327 -1 0.51 98.21 5 slowD 4326 -1 0.51 98.18 6 chv 4296 -1 0.52 97.51 7 oscK 4294 -1 0.52 97.46 8 vol 4282 -1 0.51 97.19 9 ar 4271 -1 0.52 96.95 10 atr 4237 -1 0.51 96.16 11 oscDX 4200 -1 0.52 95.34 12 DX 4174 -1 0.51 94.73 13 vsig 4170 -1 0.52 94.65 14 tr 4075 -1 0.50 92.49 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 7 14 7 2 - Local Variable importance Variables interactions (10 most important variables at first (columns) and second (rows) order) : For each variable (at each order), its interaction with others is computed. cci slowD atr tr DX atr 0.1804 0.1546 0.1523 0.1147 0.1127 cci 0.1779 0.1521 0.1498 0.1122 0.1102 slowD 0.1633 0.1375 0.1352 0.0976 0.0956 DX 0.1578 0.1319 0.1297 0.0921 0.0901 vsig 0.1467 0.1209 0.1186 0.0810 0.0790 oscDX 0.1452 0.1194 0.1171 0.0795 0.0775 tr 0.1427 0.1168 0.1146 0.0770 0.0750 oscK 0.1381 0.1123 0.1101 0.0725 0.0705 sign 0.1361 0.1103 0.1081 0.0704 0.0685 signal 0.1326 0.1068 0.1045 0.0669 0.0650 avg1rstOrder 0.1452 0.1194 0.1171 0.0795 0.0775 vsig oscDX oscK signal ar atr 0.1111 0.1040 0.1015 0.0951 0.0897 cci 0.1085 0.1015 0.0990 0.0925 0.0872 slowD 0.0940 0.0869 0.0844 0.0780 0.0726 DX 0.0884 0.0814 0.0789 0.0724 0.0671 vsig 0.0774 0.0703 0.0678 0.0614 0.0560 oscDX 0.0759 0.0688 0.0663 0.0599 0.0545 tr 0.0733 0.0663 0.0638 0.0573 0.0520 oscK 0.0688 0.0618 0.0593 0.0528 0.0475 sign 0.0668 0.0598 0.0573 0.0508 0.0455 signal 0.0633 0.0563 0.0537 0.0473 0.0419 avg1rstOrder 0.0759 0.0688 0.0663 0.0599 0.0545 chv vol sign ADX avg2ndOrder atr 0.0850 0.0850 0.0847 0.0802 0.1108 cci 0.0824 0.0824 0.0822 0.0777 0.1083 slowD 0.0679 0.0679 0.0676 0.0631 0.0937 DX 0.0623 0.0623 0.0620 0.0576 0.0881 vsig 0.0513 0.0513 0.0510 0.0465 0.0771 oscDX 0.0497 0.0497 0.0495 0.0450 0.0756 tr 0.0472 0.0472 0.0470 0.0425 0.0731 oscK 0.0427 0.0427 0.0424 0.0379 0.0685 sign 0.0407 0.0407 0.0404 0.0359 0.0665 signal 0.0372 0.0372 0.0369 0.0324 0.0630 avg1rstOrder 0.0497 0.0497 0.0495 0.0450 0.0000 Variable Importance based on interactions (10 most important) : cci atr slowD DX tr vsig oscDX 0.1384 0.1284 0.1182 0.0796 0.0735 0.0727 0.0677 oscK signal sign 0.0599 0.0509 0.0464 Variable importance over labels (10 most important variables conditionally to each label) : Class -1 Class 1 cci 0.17 0.23 slowD 0.20 0.09 atr 0.14 0.15 tr 0.04 0.12 oscK 0.08 0.03 vsig 0.06 0.08 oscDX 0.04 0.08 DX 0.07 0.08 signal 0.05 0.04 ar 0.04 0.02
Results
- In terms of global importance all 14 input variables are equal.
- The best 10 are defined by the overall contribution (global importance) and interaction (local importance).
- Seven best variables in partial importance for each class are shown on the charts below.
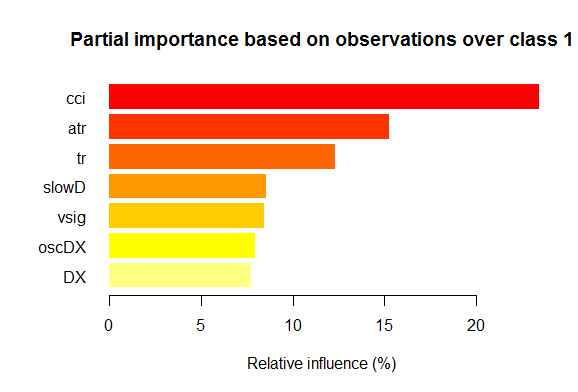
Fig. 2. Partial importance of variables for the "1" class
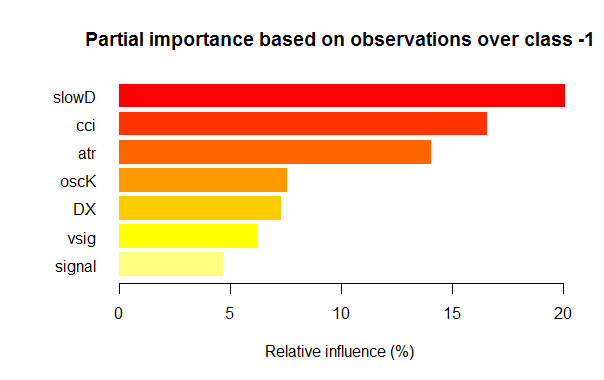
Fig. 3. Partial importance of variables for the "-1" class
As we can see, the most important variables for different classes are different in both structure and rankings. Thus, if for the "-1" class the slowD variable is the most important, then for the "+1" class it is only on the 4th place.
So, we have sets of data ready. Now we can proceed with the experiments.
3. Experimental part.
Experiments will be conducted in the R language — Revolution R Open, version 3.2.2, distribution of the Revolution Analytics company, to be specific. http://www.revolutionanalytics.com/revolution-r-open
This distribution has a number of advantages over regular R 3.2.2:
- quick and more qualitative calculations through applying the multi-threaded processing with Intel® Math Kernel Library ;
- advanced features of Reproducible R Toolkit. One slight clarification: the R language is actively developing by constantly improving the existing packages and adding the new ones. The flip side of such progress involves the loss of reproducibility. That is, your products that were written few months back and were functioning well, suddenly stop working after the next update of packages. Much time is wasted to identify and liquidate the error caused by the change in one of the packages. For example, the Expert Advisor attached to the first article on deep neural networks was functioning well at the point of creation. However, a few months after the publication a number of users have complained about its non-operability. The analysis showed that updating the "svSocket" package has led to the Expert Advisor's malfunction, and I was unable to find the reason behind it. The finalized Expert Advisor will be attached to this article. This problem has become a pressing issue, and it was easily solved in Revolution Analytics. Now, when a new distribution is released, the condition of all packages in the CRAN repositary is fixed at the release date by copying them on their mirror. No changes in the CRAN depositary after this date can affect the packages "frozen" on the Revolution mirror. Furthermore, starting from October 2014, the company makes daily snapshots of the CRAN depositary, fixing the relevant state and versions of packages. With their own "checkpoint" package we can now download necessary packages that are relevant at the date we need. In other words, we operate a some kind of time machine.
And another news. Nine months ago, when Microsoft purchased Revolution Analytics, it promised to support their developments and kept the Revolution R Open (RRO) distribution available free of charge. It was followed by numerous messages about novelties in RRO and Revolution R Enterpise (not to mention the integration of R with SQL Server, PowerBI, Azure and Cortana Analitics). Now we have information that the next RRO update will be called Microsoft R Open, and Revolution R Enterprise — Microsoft R Server. And not so long ago Microsoft has announced that R will be available in Visual Studio. R Tools for Visual Studio (RTVS) follows the Python Tools for Visual Studio model. It will be a free addition to Visual Studio that will provide a complete IDE for R with the possibility to edit and debug the scripts interactively.
By the time the article was finished, Microsoft R Open (R 3.2.3) was already released, therefore, further in the article we will refer to packages for this version.
3.1. Building models
3.1.1. Brief description of the "darch" package
The "darch" ver. 0.10.0 package offers a wide range of functions that don't just allow to create and train the model, but, literally, build it brick by brick and adjust it according to your preferences. As previously indicated, deep neural network consists of n-number of RBM (n = layers -1) and MLP neural network with a number of layers. Layer-wise pre-training of RBM is executed on unformatted data without a supervisor. Fine-tuning of neural network is performed with a supervisor on formatted data. Dividing the training stages gives us an opportunity to use data various in volume (but not structure!) or to obtain several various fine-tuned models on the basis of pre-training alone. Furthermore, if data for pre-training and fine-tuning are the same, it is possible to train in one go, instead of dividing in two stages. Or you can skip pre-training and use only multilayer neural network, or, on the other hand, use only RBM without the neural network. At the same time we have access to all internal parameters. The package is intended for advanced users. Further, we will analyze divided processes: pre-training and fine-tuning.
3.1.2. Building the DBN model. Parameters.
We will describe the process of building, training and testing the DBN model.
newDArch(layers, batchSize, ff=FALSE, logLevel=INFO, genWeightFunc=generateWeights),
where:
- layers: array indicating the number of layers and neurons in each layer. For example: layers = c(5,10,10,2) – an input layer with 5 neurons (visible), two hidden layers with 10 neurons each, and one output layer with 2 outputs.
- BatchSize: size of the mini-sample during training.
- ff: indicates whether the ff format should be used for weights, deviations and exits. The ff format is applied for saving large volumes of data with compression.
- LogLevel: level of logging and output when performing this function.
- GenWeightFunction: function for generating the matrix of RBM weights. There is an opportunity to use the user's activation function.
The created darch-object contains (layers - 1) RBM combined into the accumulating network that will be used for pre-training the neural network. Two attributes fineTuneFunction and executeFunction contain functions for fine-tuning (backpropagation by default) and for execution (runDarch by default). Training the neural network is performed with two training functions: preTrainDArch() and fineTuneDArch(). The first function trains the RBM network without a supervisor using a contrastive divergence method. The second function uses a function indicated in the fineTuneFunction attribute for a fine-tuning of neural network. After neural network performance, outputs of every layer can be found in the executeOutputs attribute or only output layer in the executeOutput attribute.
2. Function of pre-training the darch-object
preTrainDArch(darch, dataSet, numEpoch = 1, numCD = 1, ..., trainOutputLayer = F),where:
- darch: instance of the 'Darch' class;
- dataSet: data set for training;
- numEpoch: number of training epochs;
- numCD : number of sampling iterations. Normally, one is sufficient;
- ... : additional parameters that can be transferred to the trainRBM function;
- trainOutputLayer: logical value that shows whether the output layer of RBM should be trained.
The function performs the trainRBM() training function for every RBM, by copying after training weights and biases to the relevant neural network layers of the darch-object.
3. Fine-tune function of the darch-objectfineTuneDArch(darch, dataSet, dataSetValid = NULL, numEpochs = 1, bootstrap = T,
isBin = FALSE, isClass = TRUE, stopErr = -Inf, stopClassErr = 101,
stopValidErr = -Inf, stopValidClassErr = 101, ...),
where:
- darch: sample of the 'Darch' class;
- dataSet: set of data for training (can be used for validation) and testing;
- dataSetValid : set of data used for validation;
- numxEpoch: number of training epochs;
- bootstrap: logical, is it needed to apply bootstrap when creating validation data;
- isBin:indicates if output data should be interpreted as logical values. By default — FALSE. If TRUE, every value above 0.5 is interpreted as 1, and below — as 0.
- isClass : indicates if the network is trained for classification. If TRUE, then statistics for classifications will be determined. TRUE by default.
- stopErr : criterion for stopping the training of neural network due to error occurred during training. -Inf by default;
- stopClassErr : criterion for stopping the training of neural network due to classification error occurred during training. 101 by default;
- stopValidErr : criterion for stopping the neural network due to error in validation data. -Inf by default;
- stopValidClassErr : criterion for stopping the neural network due to classification error occurred during validation. 101 by default;
- ... : additional parameters that can be passed to the training function.
The function trains the network with a function saved in the fineTuneFunction attribute of the darch-object. Input data (trainData, validData, testData) and classes that belong to them (targetData, validTargets, testTargets) can be transferred as dataSet or ff-matrix. Data and classes for validation and testing are not obligatory. If they are provided, then neural network will be performed with these sets of data, and statistics will be calculated. The isBin attribute indicates if output data should be interpreted as binary. If isBin = TRUE, every output value above 0.5 is interpreted as 1, otherwise — as 0. Also, we can set a stopping criterion for the training based on error (stopErr, stopValidErr) or correct classification (stopClassErr, stopValidClassErr) on training or validation sets.
All function parameters have default values. However, other values are also available. So, for example:
Function of activating neurons — sigmoidUnitDerivative, linearUnitDerivative, softmaxUnitDerivative, tanSigmoidUnitDerivative are available. sigmoidUnitDerivative is used by default.
Functions of the neural network's fine-tune — backpropagation by default, resilient-propagation rpropagation is also available in four variations ("Rprop+", "Rprop-", "iRprop+", "iRprop-") and minimizeClassifier (this function is trained by the Darch network classifier using the nonlinear conjugate gradient method). For the last two algorithms and for those who have a deep knowledge of the subject, a separate implementation of the neural network's fine-tune with a configuration of their multiple parameters is provided. For example:
rpropagation(darch, trainData, targetData, method="iRprop+",
decFact=0.5, incFact=1.2, weightDecay=0, initDelta=0.0125,
minDelta=0.000001, maxDelta=50, ...),
where:
- darch – darch-object for training;
- trainData – input data set for training;
- targetData – expected output for the training set;
- method – training method. "iRprop+" by default. "Rprop+", "Rprop-", "iRprop-" are possible;
- decFact – decreasing factor for training. 0.5 by default;
- incFact - increasing factor for training. 1.2 by default;
- weightDecay – decreasing weight at the training. 0 by default;
- initDelta – initialization value at the update. 0.0125 by default;
- minDelta – minimum border for the step size. 0.000001 by default;
- maxDelta – upper border for the step size. 50 by default.
The function returns the darch-object with the trained neural network.
3.2. Formation of training and testing samples.
We have already formed the initial sample of data. Now, we need to divide it into training, validating and testing samples. The ratio by default is 2/3. Various packages have many functions that are used to divide samples. I use rminer::holdout() that calculates indexes for breaking down the initial sample into training and testing samples.
holdout(y, ratio = 2/3, internalsplit = FALSE, mode = "stratified", iter = 1,
seed = NULL, window=10, increment=1),
where:
- y – desired target variable, numeric vector or factor, in this case, the stratified separation is applied (i.e. proportions between the classes are the same for all parts);
- ratio – ratio of separation (in percentage — the size of the training sample is established; or in the total number of samples — the size of the testing sample is established);
- internalsplit – if TRUE, then training data is once again separated into training and validation samples. The same ratio is applied for the internal separation;
- mode – sampling mode. Options available:
- stratified – stratified random division (if у factor; otherwise standard random division);
- random – standard random division;
- order – static mode, when first examples are used for training, and the remaining ones — for testing (widely applied for time series);
- rolling – rolling window more commonly known as a sliding window (widely applied at the prediction of stock and financial markets), similarly order, except that window refers to window size, iter — rolling iteration and increment — number of samples the window slides forward at every iteration. The size of the training sample for every iteration is fixed with window, while the testing sample is equivalent to ratio, except for the last iteration (where it could be less).
- incremental – incremental mode of re-training, also known as an increasing window, same as order, except that window is an initial window size, iter — incremental iterations and increment — number of examples added at every iteration. The size of the training sample grows (+increment) at every iteration, whereas the size of the testing set is equivalent to ratio, except for the last iteration, where it can be smaller.
- iter – number of iterations of the incremental mode of re-training (used only when mode = "rolling" or "incremental", iter is usually set in a loop).
- seed – if NULL, then random seed is used, otherwise seed is fixed (further calculations will always have the same result returned);
- window – size of training window (if mode = "rolling") or the initial size of training window (if mode = "incremental");
- increment – number of examples added to the training window at every iteration (if mode="incremental" or mode="rolling").
3.2.1. Balancing classes and pre-processing.
We will write a function that will align (if required) the number of classes in the sample towards the higher number, divide the sample into training and testing samples, perform pre-processing (normalization, if necessary) and return the list with relevant samples — train, test. To achieve balancing, we are going to use the caret::upSample() function that adds samples randomly taken with replacement, making the class distribution equal. I must say that not all researchers find it necessary to balance classes. But, as already known, practice is a criterion of truth, and the results of my multiple experiments show that balanced samples always show better results in training. Although, it doesn't stop us to experiment on our own.
For pre-processing we will use the caret::preProcess() function. Parameters of preprocessing will be saved in the prepr variable. Since we have already considered and applied them in previous articles, I will not provide any further description here.
#---7---------------------------------------------------- prepareTrain <- function(x , y, rati, mod = "stratified", balance = F, norm, meth) { require(magrittr) require(dplyr) t <- rminer::holdout(y = y, ratio = rati, mode = mod) train <- cbind(x[t$tr, ], y = y[t$tr]) if(balance){ train <- caret::upSample(x = train[ ,best], y = train$y, list = F)%>% tbl_df train <- cbind(train[ ,best], select(train, y = Class)) } test <- cbind(x[t$ts, ], y = y[t$ts]) if (norm) { prepr <<- caret::preProcess(train[ ,best], method = meth) train = predict(prepr, train[ ,best])%>% cbind(., y = train$y) test = predict(prepr, test[ ,best] %>% cbind(., y = test$y)) } DT <- list(train = train, test = test) return(DT) }
One comment regarding pre-processing: input variables will be normalized into the range of (-1, 1).
3.2.2. Coding the target variable
When solving classification tasks, the target variable is a factor with several levels (classes). In a model it is set as a vector (column), that consists of the subsequent target states. For example, y = с("1", "1", "2", "3", "1"). In order to train the neural network, the target variable must be coded (transformed) into the matrix with the number of columns equal to the number of classes. In every row of this matrix, only one column may contain 1. Such transformation along with using the softmax() activation function in the output layer, allows to obtain probabilities of states of the predicted target variable in every class. The classvec2classmat() function will be used for coding. This in not the only or the best method for coding the target variable, but we will use it because it is simple. Inverse transformation (decoding) of predicted values of the target variable is achieved through different methods that we are going to cover soon.
3.3. Training the model
3.3.1. Pre-training
As mentioned above, first, we create the deep architecture object named DArch, that includes the required number of RBM with parameters of preliminary training by default, and the neural network initiated with random weights and neuron activation function set by default. At the object creation stage, the pre-training parameters can be changed, if necessary. Afterwards, the RBM network will be pre-trained without a supervisor by sending the training sample (without target variable) to the output. After it is complete, we get DАrch where weights and biases obtained during RBM training are transferred to the neural network. We should set in advance the distribution of hidden neurons in layers in a form of vector (for example):
L<- c( 14, 50, 50, 2)
Number of neurons in the input layer equals the number of input variables. Two hidden layers will contain 50 neurons each, the output layer will have two. Let me explain the last bit. If a target variable (factor) has two levels (classes), then, in fact, one output is sufficient. But converting vector into the matrix with two columns, each of them corresponding to one class, allows us to apply the softmaxactivation function, that operates well in the classification tasks, in the output layer. Furthermore, outputs in the form of the class probabilities give us additional opportunities in the subsequent analysis of results. This subject will be covered shortly.
The number of epochs when training is set experimentally, normally within range of 10-50.
The number of sampling iteration will stay by default, but this parameter can be increased if you wish to experiment. It will be defined in a separate function:
#----8-------------------------------------------------------------- pretrainDBN <- function(L, Bs, dS, nE, nCD, InM = 0.5, FinM = 0.9) { require(darch) # create object DArch dbn <- newDArch(layers = L, batchSize = Bs, logLevel = 5) # set initial moment setInitialMomentum(dbn) <- InM # set final moment setFinalMomentum(dbn) <- FinM # set time of switching moments from initial to final setMomentumSwitch(dbn) <- round(0.8 * nE) dbn <- preTrainDArch(dbn, dataSet = dS, numEpoch = nE, numCD = nCD, trainOutputLayer = T) return(dbn) }
3.3.2. Fine-tuning
As discussed previously, the package offers backpropagation(), rpropagation(), minimizeClassifier(), minimizeAutoencoder() for fine-tuning. The last two won't be considered, since they are not sufficiently documented in the package, and there are no examples of how to apply them. These functions in my experiments didn't show good results.
I would also like to add something about package updates. When I started writing this article, the current version was 0.9, and by the moment it was finished, a new 0.10 version containing multiple changes was released. All calculations had to be redone. Based on the results of short tests, I can tell that the operation speed has considerably increased, unlike the results' quality (which is more a fault of a user, then the package).
Let's consider two first functions. The first (backpropagation) is set by default in the DАrch object and uses the training neural network parameters provided here. The second function (rpropagation) also has default parameters and four training methods (described above) that are "iRprop+" by default. You can certainly change both parameters and the training method. It is easy to apply these functions: change the fine-tune function in FineTuneDarch()
setFineTuneFunction(dbn) <- rpropagation
In addition to fine-tuning settings, we must set (if necessary) the function of activating neurons in every layer. We know that sigmoidUnit is set in all layers by default. It is available in the package sigmoidUnitDerivative, linearUnitDerivative, tanSigmoidUnitDerivative, softmaxUnitDerivative . The fine-tune will be defined with a separate function with the ability to choose the fine-tune function. We will collect possible functions of activation in a separate list:
actFun <- list(sig = sigmoidUnitDerivative, tnh = tanSigmoidUnitDerivative, lin = linearUnitDerivative, soft = softmaxUnitDerivative)
We will write a fine-tune function that will train and generate two neural networks: first — trained using the backpropagation function, second — with rpropagation:
#-----9----------------------------------------- fineMod <- function(variant=1, dbnin, dS, hd = 0.5, id = 0.2, act = c(2,1), nE = 10) { setDropoutOneMaskPerEpoch(dbnin) <- FALSE setDropoutHiddenLayers(dbnin) <- hd setDropoutInputLayer(dbnin) <- id layers <<- getLayers(dbnin) stopifnot(length(layers)==length(act)) if(variant < 0 || variant >2) {variant = 1} for(i in 1:length(layers)){ fun <- actFun %>% extract2(act[i]) layers[[i]][[2]] <- fun } setLayers(dbnin) <- layers if(variant == 1 || variant == 2){ # backpropagation if(variant == 2){# rpropagation #setDropoutHiddenLayers(dbnin) <- 0.0 setFineTuneFunction(dbnin) <- rpropagation } mod = fineTuneDArch(darch = dbnin, dataSet = dS, numEpochs = nE, bootstrap = T) return(mod) } }
Some clarifications about formal parameters of the function.
- variant - selection of fine-tune function (1- backpropagation, 2- rpropagation).
- dbnin - model of receipt resulted from pre-training.
- dS - data set for fine-tune (dataSet).
- hd - coefficient of sampling (hiddenDropout) in hidden layers of neural network.
- id - coefficient of sampling (inputDropout) in input layer of neural network.
- act - vector with indication of function of neuron activation in every layer of neural network. The length of vector is one unit shorter than the number of layers.
- nE - number of training epochs.
dataSet — a new variable that appeared in this version. I don't really understand the reason behind its appearance. Normally, the language has two ways of transferring variables to a model — using a pair (x, y) or a formula (y~., data). The introduction of this variable doesn't improve the quality, but confuses the users instead. However, the author may have his reasons that are unknown to me.
3.4. Testing the model. Мetrics.
Testing the trained model is performed on testing samples. It must be considered that we will calculate two metrics: formal Accuracy and qualitative K. The relevant information will be provided below. For this purpose, we will need two different samples of data, and I will explain to you why. To calculate Accuracy we need values of the target variable, and the ZigZag, as we remember from before, most frequently is not defined on the last bars. Therefore, the testing sample for calculating Accuracy we will determine with the prepareTrain() function, and for qualitative indicators we will use the following function
#---10------------------------------------------- prepareTest <- function(n, z, norm, len = 501) { x <- In(p = n ) %>% na.omit %>% extract( ,best) %>% tail(., len) CO <- price[ ,"CO"] %>% tail(., len) if (norm) { x <- predict(prepr,x) } dt <- cbind(x = x, CO = CO) %>% as.data.frame() return(dt) }
The models will be tested on the last 500 bars of the history.
For actual testing, testAcc() and testBal() will be applied.
#---11----- testAcc <- function(obj, typ = "bin"){ x.ts <- DT$test[ ,best] %>% as.matrix() y.ts <- DT$test$y %>% as.integer() %>% subtract(1) out <- predict(obj, newdata = x.ts, type = typ) if (soft){out <- max.col(out)-1} else {out %<>% as.vector()} acc <- length(y.ts[y.ts == out])/length(y.ts) %>% round(., digits = 4) return(list(Acc = acc, y.ts = y.ts, y = out)) } #---12----- testBal <- function(obj, typ = "bin") { require(fTrading) x <- DT.test[ ,best] CO <- DT.test$CO out <- predict(obj, newdata = x, type = typ) if(soft){out <- max.col(out)-1} else {out %<>% as.vector()} sig <- ifelse(out == 0, -1, 1) sig1 <- Hmisc::Lag(sig) %>% na.omit bal <- cumsum(sig1 * tail(CO, length(sig1))) K <- tail(bal, 1)/length(bal) * 10 ^ Dig Kmax <- max(bal)/which.max(bal) * 10 ^ Dig dd <- maxDrawDown(bal) return(list(sig = sig, bal = bal, K = K, Kmax = Kmax, dd = dd)) }
The first function returns Acc and the target variable values (real or predicted) for a possible further analysis. The second function returns the predicted signals sig for the EA, the balance obtained based on these signals (bal), quality coefficient (К), maximum value of this coefficient on the tested area (Kmax) and the maximum drawdown (dd) in the same area.
When calculating the balance, it is important to remember that the last predicted signal refers to the future bar that hasn't been formed yet, therefore, it should be deleted at calculations. We have done it by moving the sig vector by one bar to the right.
3.4.1. Decoding predictions.
The obtained result can be decoded (converted from matrix to vector) using the "WTA" method. The class equals the column number with a maximum value of probability, and the value threshold of this probability can be set, below which the class is not determined.
out <- classmat2classvec(out, threshold = 0.5) or out <- max.col(out)-1
If the threshold is set as 0.5, and the biggest probability in the columns is below this threshold, we will obtain an additional class ("not defined"). It should be taken into consideration when calculating metrics like Accuracy.
3.4.2. Improving the prediction results
Is it possible to improve the prediction result after it is received? There are three possible ways that can be applied.
- Calibration
CORElearn::calibrate(correctClass, predictedProb, class1 = 1, method = c("isoReg", "binIsoReg", "binning", "mdlMerge"), weight=NULL, noBins=10, assumeProbabilities=FALSE)
where:
- correctClass — vector with correct labels of classes for problem classification;
- predictedProb — vector with the predicted class 1 (probability) of the same length as correctClass;
- method — one out of the following ("isoReg", "binIsoReg", "binning", "mdlMerge"). For further information please read the package description;
- weight — vector (if indicated) must be the same length as correctClass, and provide weights for each observation, otherwise weights of all observations equal 1 by default;
- noBins — parameter value depends on method and determines the desired or initial number of channels;
- assumeProbabilities — logical, if TRUE, then value in predictedProb is expected in the range [0, 1], i. e. as a possibility evaluation, otherwise the algorithm can be used as a simple isotonic regression.
This method is applied for a target variable with two levels set by a vector.
- Smoothing prediction results with the Markov chain model
This is a vast and complex subject that deserves a separate article, therefore I won't go deep into theory, and provide the most basic information.
Markov's process — is a random process with a following feature: for any point in time t0, probability of any state of the system in the future depends only on its state in the present and doesn't depend on when and how the system reaches this state.
Classification of random Markov's processes:
- with discrete states and discrete time (Markov chain);
- with continuous states and discrete time (Markov consistency);
- with discrete states and continuous time (continuous Markov chain);
- with continuous state and continuous time.
Only Markov processes with discrete states S1, S2, ..., Sn. are considered here further.
Markov chain — random Markov process with discrete states and discrete time.
Moments t1, t2, ... when the S system can change its state are considered as subsequent steps of the process. It is not the t time, but the step number 1,2,...,k,...that is used as an argument that the process depends on.
Random process is characterized by a sequence of states S(0), S(1), S(2), ..., S(k), ..., where S(0) is the initial state (before the first step); S(1) — state after the first step; S(k) — state of the system after the k-number step.
Probabilities of the Markov chain states are Pi(k) probabilities that after the k-number step (and before (k + 1)-step) the S system will be in the Si(i = 1 , 2 , ..., n) state.
Initial distribution of the Markov chain probabilities — distribution of the probabilities of states in the beginning of the process.
Probability of transition (transition probability) on the k-number step from the Si state to the Sj state — conditional probability that the S system after the k-number step will appear in the Sj state, on condition that it was in the Si state before that (after k—1 step).
Transitional probabilities of a uniform Markov chain Рij form a square matrix sized n х n. It has the following features:
- Each row describes the selected state of the system, and its elements — probabilities of all possible transitions in one step from the selected (from i-number) state.
- Elements of columns — probabilities of all possible transitions in one step to the set (j) state.
- The total of probabilities of each row equals one.
- On the main diagonal — Рij probabilities that the system won't exit from the Si state, and will remain there.
Markov process can be observed and hidden. Hidden Markov Model (HMM) consists of the pair of discrete stochastic processes {St} and {Xt}. The observed process {Xt} is linked with an unobserved (hidden) Markov process of states {St} through so-called conditional distributions.
Strictly speaking, the observed Markov process of states (classes) of our target time series is not uniform. Clearly, the probability of transition from one state to another depends on the time spent in the current state. It means that during the first steps after changing the state, the probability that it will change is low and grows with the increase of time spent in this state. These models are called semi-Markov's (HSMM). We won't go deep into analyzing them.
But the idea is the following: based on the discrete order of ideal signals (target) obtained from the ZigZag, we will find the parameters of НММ. Then, having the signals predicted by the neural network, we will smooth them using НММ.
What does it give us? Normally, in the neural network prediction there are so-called "emissions", areas of changing the state that is 1-2 bars long. We know that a target variable doesn't have such small lengths. By applying the model obtained on the target variable to the predicted order, we can bring it to more probable transitions.
We will use the "mhsmm" package designed for calculating hidden Markov and semi-Markov models for these calculations. We will use the smooth.discrete() function, that simply smooths the time series of discrete values.
obj <- smooth.discrete(y)
Smooth order of states obtained in the end by default — as a more likely order of states obtained using the Viterbi algorithm (so called global decoding). There is also an option to use other method — smoothed, where individual most probable states will be identified (so-called local decoding).
A standard method is applied to smooth new time series
sm.y <- predict(obj, x = new.y)
- Correcting predicted signals on the theoretical balance curve
The concept is the following. Having the balance line, we can calculate its deviation from the average one. Using these deviations we will calculate correction signals. In moments when deviations go minus, they either disable the performance of predicted signals, or make them inverse. The idea is generally good, but there is one disadvantage. The zero bar has a predicted signal, but it doesn't have a balance value and, therefore, a correction signal. There are two ways to solve this issue: through classification — to predict correction signal based on existing correction signals and deviations; through regression — using the existing deviations on the formed bars to predict deviations on the new bar and to identify the correction signal based on it. There is an easier solution, where you can take the correction signal for a new bar on the basis of the one that is already formed.
Since the above mentioned methods are already known to us and have been tested, we will try to implement opportunities of the Markov chains.The "markovchain" package that appeared recently has a range of functions that allow to determine the parameters of the hidden Markov model and to project future states by several future bars through the observed discrete process. The idea was taken from this article.
3.4.3. Metrics
To evaluate the quality of model prediction, the whole range of metrics (Accuracy, AUC, ROC and other) is applied. In the previous article I have mentioned that formal metrics can't define quality in our case. The Expert Advisor's goal is to get the maximum profit with an acceptable drawdown. For this purpose, K quality indicator was introduced, and it shows average profit in points for one bar on the fixed history segment with N length. It is calculated through dividing the cumulative Return(sig, N) by the length of the N segment. Accuracy will be calculated only indicatively.
Finally, we will perform calculations and obtain testing results:
- Output data. We already have the price[] matrix, obtained as a result of performing the price.OHLC() function. It contains quotes, average price and body of the bars. All output data can be obtained by downloading the "icon" that appears in the attachment to Rstudio.
# Find constanta n = 34; z = 37; cut = 0.9; soft = TRUE. # Find preprocessing method method = c("center", "scale","spatialSign") # form the initial set of data data.f <- form.data(n = n, z = z) # find the set of important predictors best <- prepareBest(n = n, z = z, cut = cut, norm = T, method) # Calculations take about 3 minutes on the 2-core processor. You can skip this stage if you like, # and use the whole set of predictors in the future. Therefore, comment the previous line and # uncomment two lowest lines. # data.f <- form.data(n = n, z = z) # best <- colnames(data.f) %>% head(., ncol(data.f) - 1) # Prepare the set for training neural network DT <- prepareTrain(x = data.f[ , best], y = data.f$y, balance = TRUE, rati = 501, mod = "stratified", norm = TRUE, meth = method) # Download required libraries require(darch) require(foreach) # Identify available functions for activation actFun <- list(sig = sigmoidUnitDerivative, tnh = tanSigmoidUnitDerivative, lin = linearUnitDerivative, soft = softmaxUnitDerivative) # Convert the target variable if (soft) { y <- DT$train$y %>% classvec2classmat()} # into matrix if (!soft) {y = DT$train$y %>% as.integer() %>% subtract(1)} # to vector with values [0, 1] # create dataSet for training dataSet <- createDataSet( data = DT$train[ ,best] %>% as.matrix(), targets = y , scale = F ) # Identify constants for neural network # Number of neurones in the input layer (equals the amount of predictors) nIn <- ncol(dataSet@data) # Number of neurones in the output layer nOut <- ncol(dataSet@targets) # Vector with a number of neurones in every layer of neural network # If you use another structure of neural network, this vector should be rewritten Layers = c(nIn, 2 * nIn , nOut) # Other data related to training Bath = 50 nEp = 100 ncd = 1 # Pre-training of neural network preMod <- pretrainDBN(Layers, Bath, dataSet, nEp, ncd) # Additional parameters for fine-tune Hid = 0.5; Ind = 0.2; nEp = 10 # Train two models, one with backpropagation, other with rpropagation # We only do this to compare results model <- foreach(i = 1:2, .packages = "darch") %do% { dbn <- preMod if (!soft) {act = c(2, 1)} if (soft) {act = c(2, 4)} fineMod(variant = i, dbnin = dbn, hd = Hid, id = Ind, dS = dataSet, act = act, nE = nEp) } # Test to get Accuracy resAcc <- foreach(i = 1:2, .packages = "darch") %do% { testAcc(model[[i]]) } # Prepare sample of data to test on quality coefficient DT.test <- prepareTest(n = n, z = z, T) # Test resBal <- foreach(i = 1:2, .packages = "darch") %do% { testBal(model[[i]]) }
Let's see the result:
> resAcc[[1]]$Acc [1] 0.5728543 > resAcc[[2]]$Acc [1] 0.5728543
It is equally bad for both models.
As for the quality coefficient:
> resBal[[1]]$K [1] 5.8 > resBal[[1]]$Kmax [1] 20.33673 > resBal[[2]]$Kmax [1] 20.33673 > resBal[[2]]$K [1] 5.8
It shows the same good performance. However, a large drawdown is somehow alarming:
> resBal[[1]]$dd$maxdrawdown [1] 0.02767
We will try to correct the drawdown with a correction signal obtained from the below calculation:
bal <- resBal[[1]]$bal # signal on the last 500 bars sig <- resBal[[1]]$sig[1:500] # average from the balance line ma <- pracma::movavg(bal,16, "t") # momentum from the average roc <- TTR::momentum(ma, 3)%>% na.omit # balance line deviation from the average dbal <- (bal - ma) %>% tail(., length(roc)) # summarize two vectors dbr <- (roc + dbal) %>% as.matrix() # calculate correction signal sig.cor <- ifelse(dbr > 0, 1, -1) # sign(dbr) gives the same result # resulting signal S <- sig.cor * tail(sig, length(sig.cor)) # balance on resulting signal Bal <- cumsum(S * (price[ ,"CO"]%>% tail(.,length(S)))) # quality coefficient on the corrected signal Kk <- tail(Bal, 1)/length(Bal) * 10 ^ Dig > Kk [1] 28.30382
The shown quality result on the corrected signal is very good. Let's see how the lines dbal, roc and dbr used for calculating the correction signal appear on the line chart.
matplot(cbind(dbr, dbal, roc), t="l", col=c(1,2,4), lwd=c(2,1,1)) abline(h=0, col=2) grid()
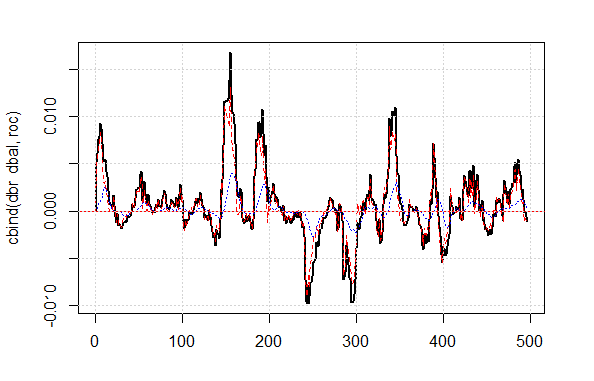
Fig.4 Balance line deviation from the average
Balance line before and after the signal correction is shown in fig. 5.
plot(c(NA,NA,NA,Bal), t="l") lines(bal, col= 2) lines(ma, col= 4)
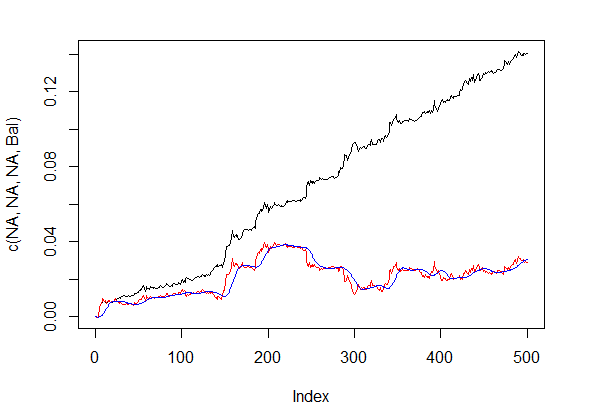
Fig.5 Balance line before and after the signal correction
So, we have the signal's value predicted by the neural network on the zero bar, but don't have a correction value. We want to use the hidden Markov model for predicting this signal. Based on the observed states of the correction signal we will identify the model's parameters using values of few last states, predict the state at one bar ahead. First, we will write the correct() function, that will calculate the correction signal based on the predicted one, resulting signal and its quality indicators. In other words, we will compactly write down calculations performed previously.
I wish to clarify: the "signal" in the article is a sequence of integer -1 and 1. The "state" is a sequence of integers 1 and 2 corresponding to these signals. For mutual conversions we will use the functions:
#---13---------------------------------- sig2stat <- function(x) {x %>% as.factor %>% as.numeric} stat2sig <- function(x) ifelse(x==1, -1, 1) #----14--correct----------------------------------- correct <- function(sig){ sig <- Hmisc::Lag(sig) %>% na.omit bal <- cumsum(sig * (price[ ,6] %>% tail(.,length(sig)))) ma <- pracma::movavg(bal, 16, "t") roc <- TTR::momentum(ma, 3)%>% na.omit dbal <- (bal - ma) %>% tail(., length(roc)) dbr <- (roc + dbal) %>% as.matrix() sig.cor <- sign(dbr) S <- sig.cor * tail(sig, length(sig.cor)) bal <- cumsum(S * (price[ ,6]%>% tail(.,length(S)))) K <- tail(bal, 1)/length(bal) * 10 ^ Dig Kmax <- max(bal)/which.max(bal) * 10 ^ Dig dd <- fTrading::maxDrawDown(bal) corr <<- list(sig.c = sig.cor, sig.res = S, bal = bal, Kmax = Kmax, K = K, dd = dd) return(corr) }
In order to obtain the signal vector with prediction of 1 bar ahead, we will use the "markovchain" package and the pred.sig() function.
#---15---markovchain---------------------------------- pred.sig <- function(sig, prev.bar = 10, nahead = 1){ require(markovchain) # Transform the observed correction signals into states stat <- sig2stat(sig) # Calculate model parameters # if there is no model in the environment if(!exists('MCbsp')){ MCbsp <<- markovchainFit(data = stat, method = "bootstrap", nboot = 10L, name="Bootstrap MС") } # Set necessary constants newData <- tail(stat, prev.bar) pr <- predict(object = MCbsp$estimate, newdata = newData, n.ahead = nahead) # attach the predicted signal to input signal sig.pr <- c(sig, stat2sig(pr)) return(sig.pr = sig.pr) }
Now, we will write down the resulting signal calculation for the Expert Advisor to perform compactly:
sig <- resBal[[1]]$sig sig.cor <- correct(sig) sig.c <- sig.cor$sig.c pr.sig.cor <- pred.sig(sig.c) sig.pr <- pr.sig.cor$sig.pr # Resulting vector of signals for Expert Advisor S <- sig.pr * tail(sig, length(sig.pr))
- Smoothing the predicted signal.
#---16---smooth------------------------------------
smoooth <- function(sig){
# smooth predicted signal
# define parameters of hidden Markov model
# if there is no model in the environment yet
require(mhsmm)
if(!exists('obj.sm')){
obj.sm <<- sig2stat(sig)%>% smooth.discrete()
}
# smooth the signal with the obtained model
sig.s <- predict(obj.sm, x = sig2stat(sig))%>%
extract2(1)%>% stat2sig()
# calculate balance with smoothed signal
sig.s1 <- Hmisc::Lag(sig.s) %>% na.omit
bal <- cumsum(sig.s1 * (price[ ,6]%>% tail(.,length(sig.s1))))
K <- tail(bal, 1)/length(bal) * 10 ^ Dig
Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
dd <- fTrading::maxDrawDown(bal)
return(list(sig = sig.s, bal = bal, Kmax = Kmax, K = K, dd = dd))
}
We will calculate and compare the balance based on predicted and smoothed signals.
sig <- resBal[[1]]$sig sig.sm <- smoooth(sig) plot(sig.sm$bal, t="l") lines(resBal[[1]]$bal, col=2)
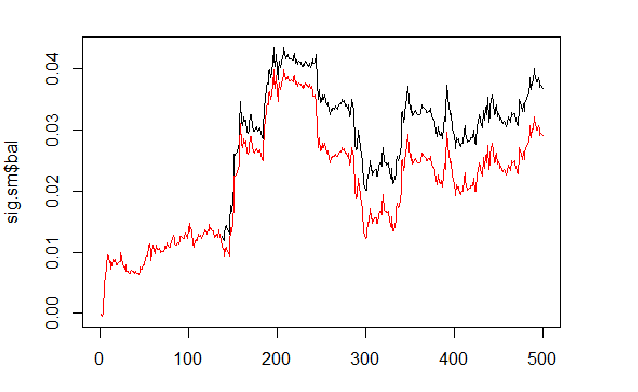
Fig.6 Balance based on smoothed and predicted signals
As we can see, the quality has slightly improved, but the drawdown still remains. We won't use this method in our Expert Advisor.
sig.sm$dd $maxdrawdown [1] 0.02335 $from [1] 208 $to [1] 300
4. Structure of the EA algorithm
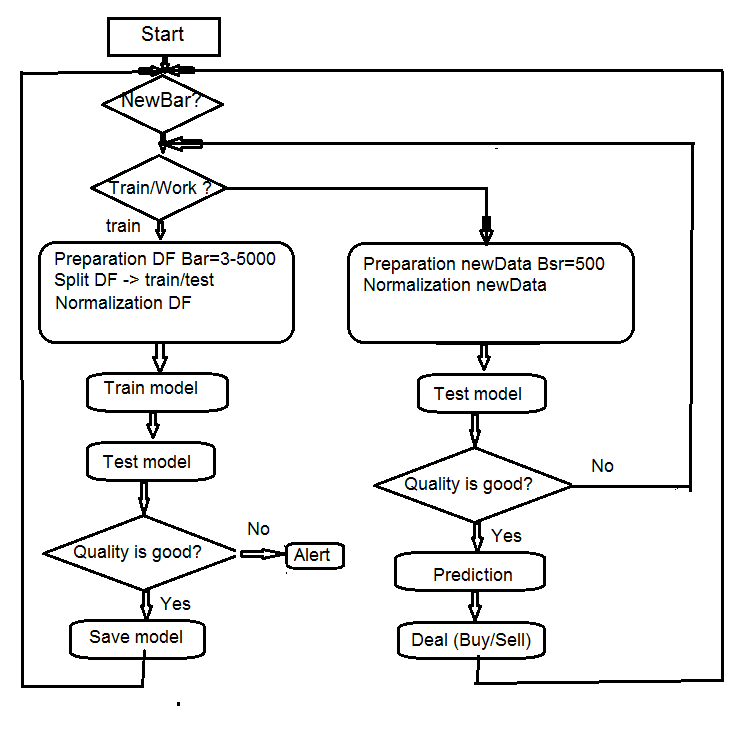
Fig.7 Structure of the EA algorithm
4.1. Description of the Expert Advisor's operation
Since the Expert Advisor operates in two streams (mql and Rterm), we will describe the process of their interaction. We will discuss the operations performed in each stream separately.
4.1.1 MQL
After placing the Expert Advisor on the chart:
in the init() function
- we check the terminal's settings (DLL availability, permission to trade);
- set the timer;
- launch Rterm;
- calculate and transfer constants required for work to the R-process environment;
- check if Rterm works, if not - alert;
- exit from init().
In the deinit() function
- we stop the timer;
- delete graphic objects;
- stop the Rterm.
In the onTimer()function
- check if Rterm is working;
- if Rterm is not occupied and the new bar is (LastTime != Time[0]):
- set the depth of history depending on if this is a first launch of the Expert Advisor;
- form four vectors of quotes (Open, High, Low, Close) and transfer them to Rterm;
- launch the script and leave without receiving the results of its performance;
- set the get_sig = true flag;
- set LastTime= Time[0].
- Otherwise, if Rterm works, is not occupied and the flag is get_sig = true:
- identify length of the sig vector that we should receive from Rterm;
- adjust the size of the receiving vector to the size of the source. When failing to comply, Rprocess will drop;
- obtain signals' order (vector);
- determine which operation has to be performed (BUY, SELL, Nothing) using the last signal;
- if we obtain the real signal, not ERR, we reset the flag get_sig=false.
- the rest is standard:
- CheckForClose()
- CheckForOpen()
Our expert in this part is a "Performer" that carries out orders obtained from its part that can "think", it sends orders, tracks the state of open positions and possible errors when opening them, and performs many other functions of a standard Expert Advisor.
4.1.2 Rterm
The operating script consists of two parts. One part is executed at the first entry, second — at the following ones.
- if first:
- upload (if required) necessary libraries from the depositary on the Internet, and install them to the environment of Rterm;
- define necessary functions;
- create the quote matrix;
- prepare the sample of data for training and testing the model;
- create and train the model;
- test the model;
- calculate signals for performance;
- check the quality of prediction. If it is above or equals the set minimum — proceed. Otherwise — send alert.
- if !first:
- prepare the sample of data for testing and prediction;
- test the model on new data;
- calculate signals for performance;
- check the quality of prediction. If it exceeds or equals the set minimum — we proceed. Otherwise — we set first = TRUE, i.e. we request to re-train the model.
4.2. Self-control and Self-training
The quality control of predicting signals with a model is performed using the К coefficient. There are two ways to identify limits of the acceptable quality. First — to set the maximum fall of the coefficient in relation to its maximum value. If К < Kmax * 0.8, then we should re-train or stop the Expert Advisor from performing signals. Second — to set the minimum value of К, that after being reached requires the same actions. We will use the second method in the Expert Advisor.
5. Installation and launching
There are two Expert Advisors attached to this article: e_DNSAE.mq4 and e_DNRBM.mq4. Both of them use the same samples of data and almost the same set of functions. The difference lies in the deep network model used. The first EA uses DN, initiated SAE and the "deepnet" package. The package description can be found in the previous article on deep neural networks. The second EA uses DN, initiated RBM and the "darch" package.
Standard distribution applies:
- *.mq4 in the ~/MQL4/Expert folder
- *.mqh in the ~/MQL4/Include folder
- *.dll in the ~/MQL4/Libraries folder
- *.r in the C:/RData folder
We correct the path to the set R language and scripts (in both mq4: #define and *.r: source() ).
When the Expert Advisor is launched for the first time, it will download necessary libraries from the repository and set them in the Rterm environment. You can also install them in advance according to the list attached.
Normally, the R process "drops" specifically due to the absence of necessary libraries, wrongly indicated paths to scripts, and only lastly, because of the script syntax errors.
The session's screenshot with the initial data is attached separately, and you can open it with Rstudio to check that all functions are working, as well as conduct the experiments.
6. Ways and methods of improving qualitative indicators.
There are few ways to improve qualitative indicators.
- evaluation and selection of predictors — apply genetic algorithm of optimization (GA).
- determine optimal parameters of predictors and target variable — GA.
- determine optimal parameters of a neural network — GA.
Conclusion
Experiments with the "darch" package have shown the following results.
- The deep neural network, initiated RBM are trained worse than with SAE. This is hardly news for us.
- The network is trained quickly.
- The package has a big potential in improving the quality of prediction, by providing access to almost all internal parameters of the model.
- The package allows to use only a neural network or RBM with a very wide set of parameters in relation to other, standard ones.
- The package is constantly evolving, and the developer promises to introduce additional features in the next release.
- R language integration with the МТ4/МТ5 terminals, as promised by the developers, will give traders an opportunity to use the newest algorithms without any additional DLL.
Attachements
- R session of the Sess_DNRBM_GBPUSD_30 process
- Zip file with the "e_DNRBM" Expert Advisor
- Zip file with the "e_DNSAE" Expert Advisor
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/1628
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Applying fuzzy logic in trading by means of MQL4
Applying fuzzy logic in trading by means of MQL4
 Calculator of signals
Calculator of signals
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Thanks for the response. It's interesting with the tester.
I will check the last remark about the signal. I did not experience such a mistake in the experiments.
Good luck and see my latest articles on deep networks. It will be interesting.
I'm thinking of starting a new branch of RuserGroup, regardless of the language of the participants. Would this be an intersex?
I will continue to read the series of article.
Please PM me if you have the said group. its good to experiment together.
I will continue to read the series of article.
Please PM me if you have the said group. its good to experiment together.
Hi isaacctk:
could you please elaborate a little, how you synch'd the tester and R-Term??
I also had the idea to use the synchronous execution, but that doesn't help me.
#ifdef STRATEGY
RExecute(hR, RUN);
#else
RExecuteAsync(hR, RUN);
#endif
What happens is that the tester continues to pump 1 min candles as "ticks", which are ignored in the expert "on Tick", because the thread is still in R-Term. Hence all 1 min candles are blown into nowhere and when the NN comes back into the expert, having learned, everything is already over. The only way to overcome this I currently have is starting the tester in visual mode and setting the speed slider to minimum. Then when the NN has finished learning, I move the slider to fast. However I am not sure, how many candles are skipped, nevertheless.
2nd, If I put more than 1000 candles into limit, the tester! (not R-term) crashs; how comes that you can put 5000?
MT4 and SAE
Thanks
hk
@ Vladimir,
would be interested in an R-group for NN as well!
Please PM, when established!
Rgds
hk
@Vladimir,
usage of rminer::holdout parameter.
You use mode="stratified" or "random" in your code/explanations. In these cases, the input values (remind you candles) are randomly chosen.
mode
sampling mode. Options are:
stratified – stratified randomized holdout if y is a factor; else it behaves as standard randomized holdout;
random – standard randomized holdout;
order – static mode, where the first examples are used for training and the later ones for testing (useful for time series data);
H=rminer::holdout(1:10,ratio=2,internal=TRUE,mode="stratified")
> print(H)
$tr
[1] 1 7 2 4 10 8 6 9
$ts
[1] 3 5
However, candles are time series (sequential). Isn't therefore the choice of random disrupting the price flow and confusing the NN??!!
Shouldn't "order" be used!!
H=rminer::holdout(1:10,ratio=2,internal=TRUE,mode="order")
> print(H)
$tr
[1] 1 2 3 4 5 6 7 8
$ts
[1] 9 10
Rgds
hk
To whom it may concern
Strategy Tester:
As the code (SAE) is constructed today, the NN goes into training upon the 1st occurrence of the OnTick() Event. Depending on complexity and PC-Power this can take several decades of seconds. During this time, the tester keeps on sending OnTick() Events, which are not processed, because RTERM is still busy, learning. Like this, several thousands ticks are not processed. In case that the code is modified to synchronous execution of RTERM, the problem remains. Now upon the 1st OnTick() Event, the network goes learning and execution is NOT returned to the EA, however the tester still keeps running and accumulating ticks, like in real life, where ticks are processed by MT4, regardless if the EA OnTick() handler returns, or not. If not, ticks are accumulated and processed, when the EA is ready to execute the OnTick() Handler for the next time. I summarize: In case of async execution of RTERM, thousands of ticks (hundreds of complete candles) are not processed. In case of sync'd execution, between the 1st Tick and the 2nd tick, the tester has accumulated thousands of ticks and candles.
The solution of the problem is to move the learning phase into the OnInit() handler. During OnInit(), the tester has already created a new chart with a history of 1002 candles. The 1002 cannot be changed. Hence, during OnInit(), all history information is available and the NN can start learning. Other than during the OnTick() event, the tester WAITS until the EA has finished his OnInit() handler. Using sync'd execution of RTERM forces the OnInit() handler and subsequently the tester to wait, until learning is finished and RTERM has returned. Herafter, the 1st Tick can then be processed normally.
In my setup, the PC takes ~20 sec for learning. In an 1H Chart, in average 800-900 ticks are created for one 1H candle. I observe a gap of several days between the 1st and 2nd tick, if learning happens within the OnTick() Handler.
Rgds
hk