Самооптимизирующийся советник на языках MQL5 и Python (Часть VI): Использование преимуществ глубокого двойного спуска
592
0
Переобучение в машинном обучении может принимать разные формы. Чаще всего это происходит, когда модель ИИ усваивает слишком много шума в данных и не может сделать никаких полезных обобщений. Это приводит к удручающим результатам, когда мы оцениваем модель на данных, с которыми она ранее не сталкивалась. Существует множество методов, разработанных для уменьшения эффекта переобучения, но такие методы часто могут оказаться сложными в реализации, особенно если вы только начинаете свой путь. Однако недавняя статья, опубликованная группой выпускников Гарварда, предполагает, что при решении некоторых задач переобучение уже не является проблемой. В этой статье вы ознакомитесь с исследованием и увидите, как можно создавать модели ИИ мирового класса в соответствии с ведущими мировыми исследованиями.
Обзор методологии
Существует множество методов обнаружения переобучения при разработке моделей ИИ. Самый надежный метод — это изучение графиков ошибок тестирования и обучения модели. Поначалу оба графика могут совпасть, что является хорошим знаком. По мере продолжения обучения нашей модели мы достигнем оптимального уровня ошибки, и как только мы его преодолеем, ошибка обучения продолжит снижаться, но ошибка тестирования только увеличится. Для решения этой проблемы было разработано много методов, например, ранняя остановка. Ранняя остановка прекращает процедуру обучения, если ошибка проверки модели существенно не меняется или постоянно ухудшается. После этого восстанавливаются лучшие веса, и предполагается, что найдена лучшая модель, как показано на рисунке 1 ниже.
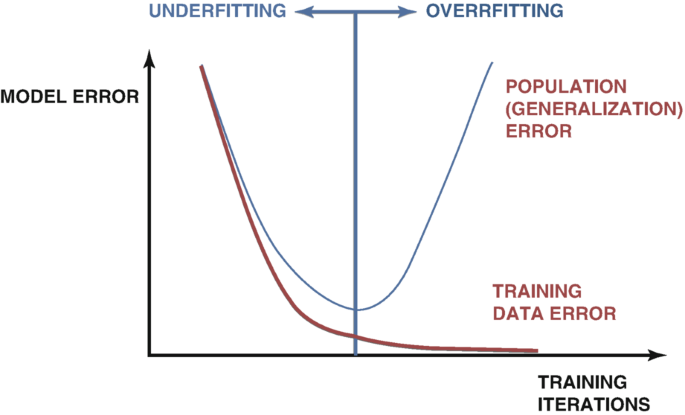
Рис. 1. Обобщенный график, демонстрирующий переобучение на практике
Эти идеи были подвергнуты сомнению в научной статье 2019 года "Deep Double Descent" (глубокий двойной спуск). Ознакомиться с ней можно здесь. Статья не пытается объяснить феномен, который она демонстрирует, она лишь описывает характеристики феномена, которые наблюдались на момент написания. По сути, статья показывает, что при решении определенных задач ошибка теста модели сначала упадет, прежде чем начнет расти, а затем резко упадет во второй раз, достигнув новых минимумов, прежде чем модель окончательно сойдется, как показано на рисунке 2 ниже.
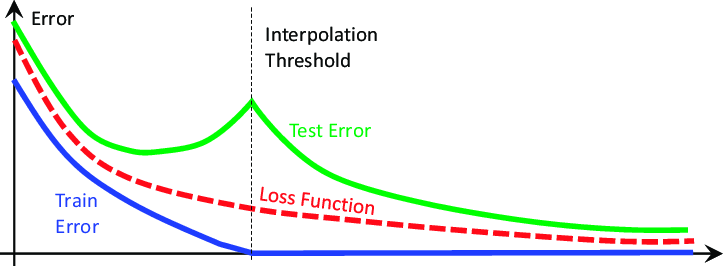
Рис. 2. Визуализация феномена глубокого двойного спуска
В статье показано, что это явление можно концептуализировать как функцию:
- Параметров модели.
- Максимального количества итераций обучения.
Другими словами, если вы постоянно обучаете все более крупные модели на одном и том же наборе данных, то увидите, что тестовая ошибка сначала упадет, а затем начнет расти, а если вы продолжите обучать более крупные модели, то увидите, что тестовая ошибка упадет во второй раз, до новых минимумов, создавая график ошибок, аналогичный рисунку 2 выше. Однако постепенное обучение все более крупных моделей не всегда возможно из-за вычислительных затрат. В нашем обсуждении мы рассмотрим явление глубокого двойного спуска как функцию максимального числа разрешенных нами итераций.
Идея заключается в том, что по мере того, как мы позволяем нашей модели выполнять больше итераций обучения, ее ошибка проверки будет всегда увеличиваться, прежде чем упадет до новых минимумов. Время, необходимое модели для достижения пикового уровня ошибок и начала их снижения, варьируется в зависимости от различных факторов, таких как уровень шума в наборе данных и тип обучаемой модели.
Общепринятых объяснений этого явления не существует, но на данный момент самый простой способ понять его — представить двойной спуск как функцию параметров модели.
Представьте, что мы начинаем с простой нейронной сети. Модель, скорее всего, будет не соответствовать нашим данным. Это означает, что его производительность может улучшиться за счет повышения сложности модели. По мере того, как мы увеличиваем сложность нашей нейронной сети, мы медленно приближаемся к точке, в которой наша модель точно соответствует нашим данным. В традиционном машинном обучении нас учат, что ошибка обучения модели всегда будет уменьшаться, если мы сделаем нашу модель более сложной. Это верно. Однако это не еще не всё.
Как только наша модель станет достаточно сложной, чтобы идеально соответствовать нашим данным, ошибка обучения обычно будет величиной, очень близкой к 0, и она перестанет уменьшаться по мере того, как мы усложняем нашу модель. Это первый удар по традиционным идеологиям машинного обучения. Эту точку обычно называют порогом интерполяции (interpolation threshold). Если мы продолжим увеличивать сложность модели сверх этого порога, мы увидим существенное падение точности тестирования. И в большинстве случаев показатели ошибок модели упадут до новых минимумов и стабилизируются там.
Алгоритмы, призванные смягчить переобучение, такие как ранняя остановка, по-видимому, непреднамеренно сдерживают нас. Эти алгоритмы всегда завершают процедуру обучения до того, как мы увидим второй спуск. Давайте воссоздадим явление двойного спуска, чтобы самостоятельно наблюдать его.
Начало работы
Сначала нам необходимо извлечь данные из MetaTrader 5 с помощью скрипта, который мы создали на языке MQL5.
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //+------------------------------------------------------------------+ //| Script Inputs | //+------------------------------------------------------------------+ input int size = 100000; //How much data should we fetch? //+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ //+------------------------------------------------------------------+ //| On start function | //+------------------------------------------------------------------+ void OnStart() { //--- File name string file_name = "Market Data " + Symbol()+ ".csv"; //--- Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= size;i>=0;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
Для начала давайте импортируем необходимые нам библиотеки.
#Standard libraries import pandas as pd import numpy as np import seaborn as sns import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from sklearn.linear_model import LinearRegression from sklearn.neural_network import MLPRegressor from sklearn.metrics import mean_squared_error from sklearn.model_selection import cross_val_score,TimeSeriesSplit
Теперь считаем данные.
#Read in the data
data = pd.read_csv('GBPUSD_Daily_20160103_20240131.csv',sep='\t') Очистим наши данные.
#Clean up the data
data.rename(columns={'<OPEN>':'Open','<HIGH>':'High','<LOW>':'Low','<CLOSE>':'Close'},inplace=True) Удалим ненужные столбцы.
#Drop columns we don't need data = data.drop(['<DATE>','<VOL>','<SPREAD>','<TICKVOL>'],axis=1) data
Визуализируем данные.
#Plot the close price plt.plot(data["Close"]) plt.xlabel("Time") plt.ylabel("Close Price") plt.title("GBPUSD Daily Close")
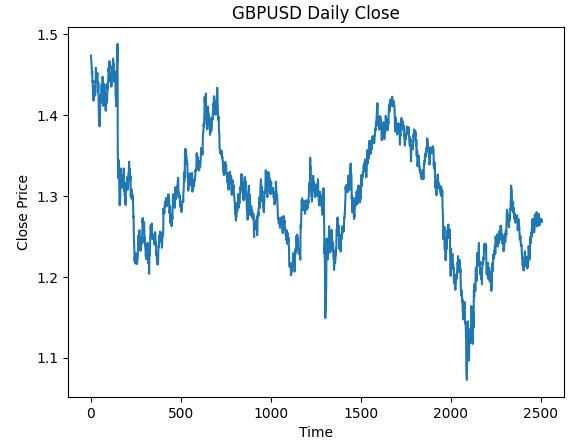
Рис. 3. Дневные данные OHLC GBPUSD, с которыми мы будем работать
Мы хотим обучить модель, которая прогнозирует дневную доходность GBPUSD. Однако нам предстоит выбрать две переменные:
- С какой периодичностью следует рассчитывать доходность?
- Насколько далеко в будущее следует делать прогнозы?
Обычно мы прогнозируем на один шаг вперед и рассчитываем доходность как разницу между двумя последовательными днями. Однако действительно ли это оптимальный вариант? Действительно ли это лучшее, что мы можем сделать в любой ситуации? Мы не будем отвечать на этот вопрос, сами данные ответят на него за нас.
Давайте выполним поиск по сетке параметров нашей доходности и нашего горизонта прогнозирования. Во-первых, нам необходимо определить единую ось для обоих параметров.
#Define the input range x_min , x_max = 2,100 #Look ahead y_min , y_max = 2,100 #Period
Теперь определим оси X и Y.
#Sample input range uniformly x_axis = np.arange(x_min,x_max,4) #Look ahead y_axis = np.arange(y_min,y_max,4) #Period
Нам нужно создать ячеистую сетку (mesh-grid). Она представляет собой два отдельных двумерных массива, которые можно использовать вместе для отображения всех возможных комбинаций входных данных, которые мы хотим оценить.
#Create a meshgrid
x , y = np.meshgrid(x_axis,y_axis) Функция будет использоваться для очистки набора данных перед проверкой точности нашей модели с новыми настройками, которые мы хотели бы оценить.
#This function will create and return a clean dataframe according to our specifications
def clean_data(look_ahead,period):
#Create a copy of the data
temp = pd.read_csv('GBPUSD_Daily_20160103_20240131.csv',sep='\t')
#Clean up the data
temp.rename(columns={'<OPEN>':'Open','<HIGH>':'High','<LOW>':'Low','<CLOSE>':'Close'},inplace=True)
temp = temp.drop(['<DATE>','<VOL>','<SPREAD>','<TICKVOL>'],axis=1)
#Define our target
temp["Target"] = temp["Close"].shift(-look_ahead)
#Apply the differencing
temp["Close"] = temp["Close"].diff(period)
temp["Open"] = temp["Open"].diff(period)
temp["High"] = temp["High"].diff(period)
temp["Low"] = temp["Low"].diff(period)
temp = temp.dropna()
temp = temp.reset_index(drop=True)
return(temp) Наша следующая функция выполнит перекрестную проверку нашей модели в соответствии с переданными нами настройками и вернет ошибку перекрестной проверки.
#Evaluate the objective function def evaluate(look_ahead,period): #Define the model model = LinearRegression() #Define our time series split tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead) temp = clean_data(look_ahead,period) score = np.mean(cross_val_score(model,temp.loc[:,["Open","High","Low","Close"]],temp["Target"],cv=tscv)) return(score)
Наконец, нам нужна функция, которая будет записывать наши результаты в массив, имеющий ту же форму, что и любая из наших сеток.
#Define the objective def objective(x,y): #Define the output matrix results = np.zeros([x.shape[0],y.shape[0]]) #Fill in the output matrix for i in np.arange(0,x.shape[0]): #Select the rows look_ahead = x[i] period = y[i] for j in np.arange(0,y.shape[0]): results[i,j] = evaluate(look_ahead[j],period[j]) return(results)
На данный момент мы реализовали функции, необходимые для того, чтобы увидеть, как изменяются уровни ошибок нашей модели при изменении интервала расчета доходности и того, насколько далеко в будущее мы хотим строить прогнозы. Давайте сначала посмотрим, как ведет себя простая модель при изменении этих параметров, прежде чем мы начнем работать с более сложными, глубокими нейронными сетями.
linear_reg_res = objective(x,y) linear_reg_res = np.abs(linear_reg_res)
Контурная диаграмма обычно используется в географии для отображения изменений высот на местности. Мы можем использовать такую диаграмму, чтобы определить, какая пара параметров дает наименьший уровень ошибок в нашей простой линейной регрессионной модели. Синие области — это комбинации, дающие низкую погрешность, а красные области — неудовлетворительные комбинации. Белая точка в самой темно-синей области нашей контурной диаграммы представляет собой наилучшие настройки прогнозирования для нашей модели линейной регрессии.
Как видно из графика ниже, наша простая линейная модель ИИ легко превзошла бы любого трейдера на рынке, который использовал бы классический период доходности 1 и прогнозировал бы 1 шаг в будущее.
plt.contourf(x,y,linear_reg_res,100,cmap="jet")
plt.plot(x_axis[linear_reg_res.min(axis=0).argmin()],y_axis[linear_reg_res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Linear Regression Accuracy Forecasting GBPUSD Daily Close")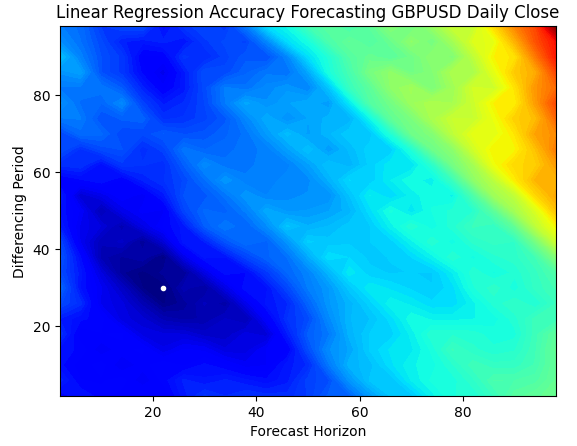 
Рис. 4. Контурная диаграмма точности нашей линейной регрессии, прогнозирующей GBPUSD Daily
Визуализация результатов в 3D создает поверхность, которая позволяет нам обнаружить связь нашей модели с рынком GBPUSD. Диаграмма показывает, что по мере того, как мы прогнозируем все дальше в будущее, наши показатели ошибок снижаются до оптимального уровня и начинают расти по мере того, как мы продолжаем смотреть в будущее все дальше. Однако наиболее важным выводом является то, что для нашей линейной модели, согласно рисунку 5 ниже, наилучшие входные данные находятся в диапазоне от 20 до 40 как для нашего горизонта прогнозирования, так и для периода доходности.
#Create a surface plot fig , ax = plt.subplots(subplot_kw={"projection":"3d"}) fig.set_size_inches(8,8) ax.plot_surface(x,y,linear_reg_res,cmap="jet")
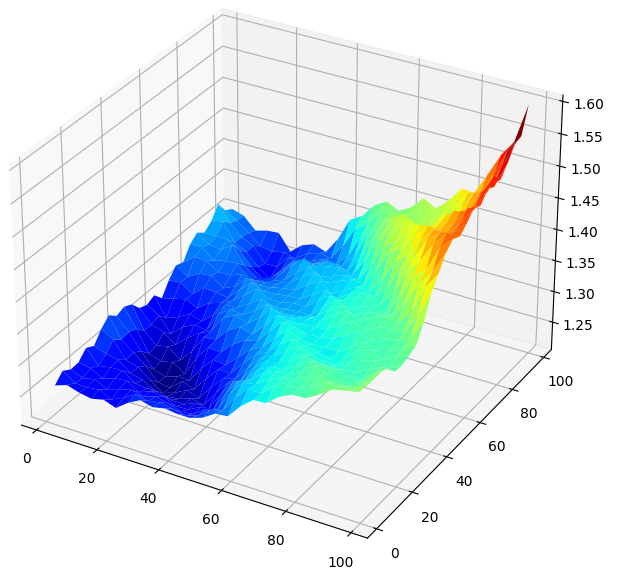
Рис. 5. Визуализация ошибки нашей линейной модели, прогнозирующей дневную доходность GBPUSD
Теперь, когда мы знакомы с контурными и поверхностными диаграммами, давайте посмотрим, как работает наша глубокая нейронная сеть, когда мы используем ее для поиска в том же пространстве параметров.
res = objective(x,y) res = np.abs(res)
График поверхности наших нейронных сетей экспоненциально сложнее визуализировать. Синие зоны предпочтительны, поскольку они представляют комбинации, дающие низкий уровень ошибок. Однако обратите внимание, что мы наблюдаем красные зоны, внезапно появляющиеся в середине оптимальных комбинаций. Довольно интересно, не так ли?
Как две комбинации могут быть настолько близки друг к другу и при этом иметь совершенно разные уровни ошибок? Отчасти это связано с природой алгоритмов оптимизации, используемых для обучения нейронных сетей. Если бы мы обучили эту модель второй раз, мы получили бы совершенно другую диаграмму с другой оптимальной точкой.
plt.contourf(x,y,res,100,cmap="jet")
plt.plot(x_axis[res.min(axis=0).argmin()],y_axis[res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")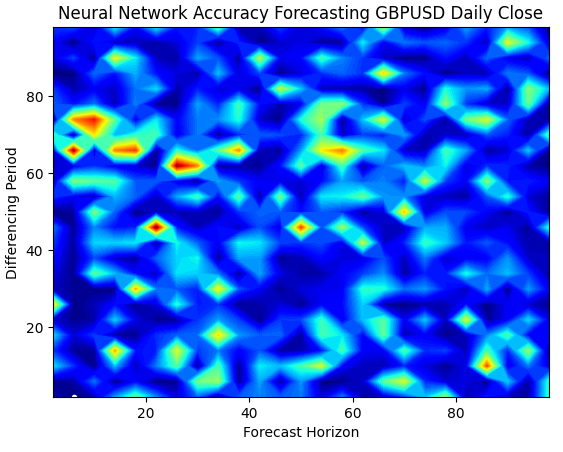 
Рис. 6. Нейронные сети очень чувствительны к имеющимся у нас входным данным
Когда мы визуализируем работу модели в 3D, мы видим, насколько нестабильными могут быть нейронные сети. Можем ли мы с уверенностью сказать, что нейронная сеть эффективно усвоила какие-либо полезные взаимосвязи? Какая модель на данный момент работает лучше? Если подойти к проблеме с традиционной точки зрения, мы выберем простую линейную модель, поскольку она создает более гладкие графики ошибок, что может быть признаком ее большей компетентности, а нестабильные показатели ошибок нейронной сети можно рассматривать как признак ее переобучения.
Однако это классический подход к машинному обучению. Согласно современным представлениям, мы рассматриваем графики ошибок нейронной сети как показатель того, что модель еще не сошлась по-настоящему, а не как показатель ее переобучения. Другими словами, согласно статье о двойном спуске, нам еще слишком рано сравнивать нейронные сети. Давайте не будем слепо доверять научной работе, а попробуем проверить это самостоятельно.
#Create a surface plot fig , ax = plt.subplots(subplot_kw={"projection":"3d"}) fig.set_size_inches(8,8) ax.plot_surface(x,y,res,cmap="jet")
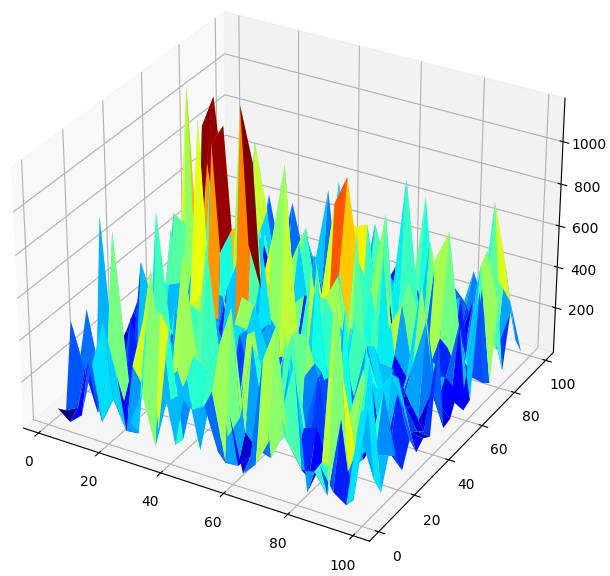
Рис. 7. Уровни ошибок наших нейронных сетей, прогнозирующих дневную доходность GBPUSD
Проверка на двойной спуск
Сначала мы применим наилучшие найденные нами параметры для расчета доходности и того, на какое будущее следует делать прогнозы.
#The best settings we have found so far look_ahead = x_axis[res.min(axis=0).argmin()] difference_period = y_axis[res.min(axis=1).argmin()] data["Target"] = data["Close"].shift(-look_ahead) #Apply the differencing data["Close"] = data["Close"].diff(difference_period) data["Open"] = data["Open"].diff(difference_period) data["High"] = data["High"].diff(difference_period) data["Low"] = data["Low"].diff(difference_period) data.dropna(inplace=True) data.reset_index(drop=True,inplace=True) data
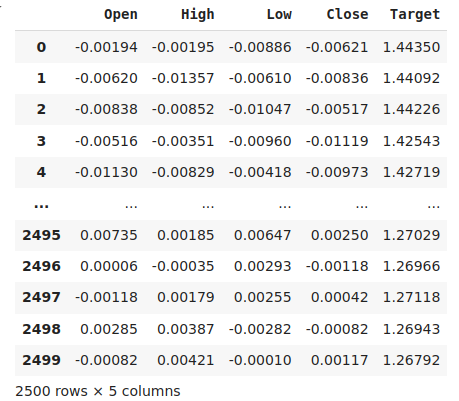
Рис. 8. Наши данные в их текущем виде
Импортируем необходимые нам библиотеки.
from sklearn.model_selection import train_test_split,TimeSeriesSplit from sklearn.metrics import mean_squared_error
Определим максимальное количество эпох. Напомним, что двойной спуск является функцией сложности модели или максимального числа итераций обучения. Мы проверим это с помощью простой нейронной сети и изменим максимальное количество итераций. Наше максимальное количество итераций обучения будет монотонно возрастать в степени числа 2.
max_epoch = 50 Создадим фрейм данных для хранения наших уровней ошибок.
err_rates = pd.DataFrame(columns = np.arange(0,max_epoch),index=["Train","Validation","Test"])
Нам необходимо задать объект разделения временного ряда.
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead) Теперь выполните разделение на обучающие и тестовые данные.
train , test = train_test_split(data,shuffle=False,test_size=0.5) Перекрестная проверка нашей модели по мере увеличения максимального числа итераций как равномерных степеней числа 2.
for j in np.arange(0,max_epoch): #Define our model and measure its error current_train_err = [] current_val_err = [] model = MLPRegressor(hidden_layer_sizes=(6,5),max_iter=(2 ** j)) for i,(train_index,test_index) in enumerate(tscv.split(train)): #Assess the model model.fit(train.loc[train_index,["Open","High","Low","Close"]],train.loc[train_index,'Target']) current_train_err.append(mean_squared_error(train.loc[train_index,'Target'],model.predict(train.loc[train_index,["Open","High","Low","Close"]]))) current_val_err.append(mean_squared_error(train.loc[test_index,'Target'],model.predict(train.loc[test_index,["Open","High","Low","Close"]]))) #Record our observations err_rates.loc["Train",j] = np.mean(current_train_err) err_rates.loc["Validation",j] = np.mean(current_val_err) err_rates.loc["Test",j] = mean_squared_error(test['Target'],model.predict(test.loc[:,["Open","High","Low","Close"]]))
Наши первые 6 итераций показывают, как изменились показатели ошибок наших моделей по мере перехода от 1 к 32 итерациям обучения. Как видно из графика ниже, наша тестовая ошибка сначала падала, затем начала расти, прежде чем достичь более высокого минимума. Наши показатели ошибок обучения и проверки сначала росли, затем немного снизились до минимума, а затем снова начали расти. Однако 32 итерации представляют собой лишь небольшой интервал процедуры обучения, давайте посмотрим, как разворачивается остальная часть процедуры обучения.
plt.plot(err_rates.iloc[0,0:5]) plt.plot(err_rates.iloc[1,0:5]) plt.plot(err_rates.iloc[2,0:5]) plt.legend(["Train Error","Validation Error","Test Error"]) plt.ylabel("RMSE") plt.xlabel("Epochs: Our Epochs Are Indices of 2") plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")
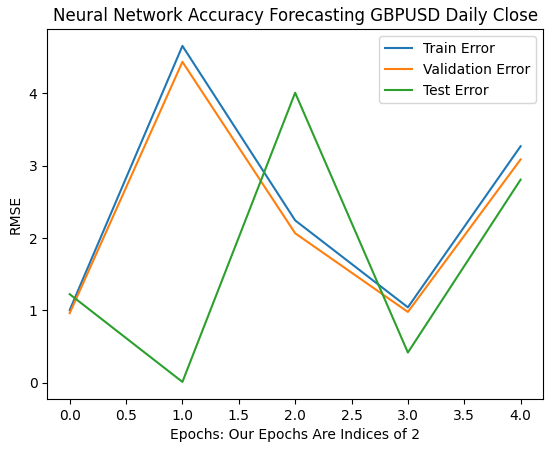
Рис. 9. Точность нашей проверки при переходе от 1 к 32 итерациям
Двигаясь дальше, мы видим, как изменяются показатели ошибок нашей модели в интервале от 64 до 256. Похоже, что после некоторого расхождения наши показатели ошибок наконец-то сходятся к минимуму. Однако, как утверждается в статье, нам предстоит пройти долгий путь.
Обратите внимание, что по умолчанию scikit-learn создает нейронные сети, которые выполняют только 200 итераций. Это число немного меньше 2 в восьмой степени. А с такими алгоритмами, как ранняя остановка, мы бы оказались в ловушке обманчивых локальных оптимумов, где-то среди холмов и впадин неровной поверхности, которую мы наблюдали на рисунке 7 выше.
plt.plot(err_rates.iloc[0,0:9]) plt.plot(err_rates.iloc[1,0:9]) plt.plot(err_rates.iloc[2,0:9]) plt.legend(["Train Error","Validation Error","Test Error"]) plt.ylabel("RMSE") plt.xlabel("Epochs: Our Epochs Are Indices of 2") plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")
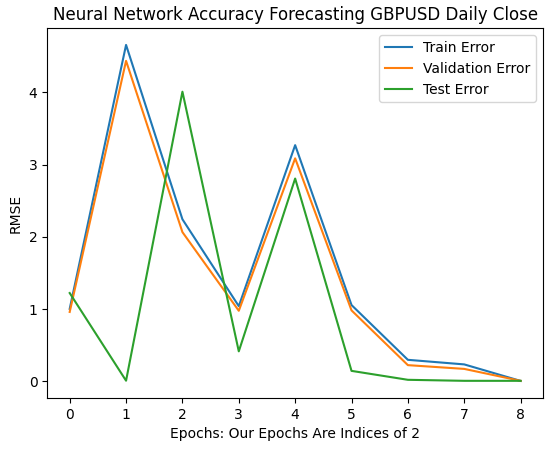
Рис. 10. Показатели ошибок нашей модели начинают сходиться
Оптимальный уровень ошибок был достигнут, когда нашей модели было разрешено выполнить более 1 миллиарда итераций! Точное число — 2 в 30-й степени. Эта точка отмечена красной вертикальной линией на рисунке 11 ниже. Обычно мы выполняем лишь часть оптимального числа итераций, чтобы избежать переобучение данных, что оставляет нас в ловушке неоптимальных уровней ошибок слева от красной линии.
plt.plot(err_rates.iloc[0,:])
plt.plot(err_rates.iloc[1,:])
plt.plot(err_rates.iloc[2,:])
plt.axvline(err_rates.loc["Test",:].argmin(),color='red')
plt.legend(["Train Error","Validation Error","Test Error","Double Descent Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")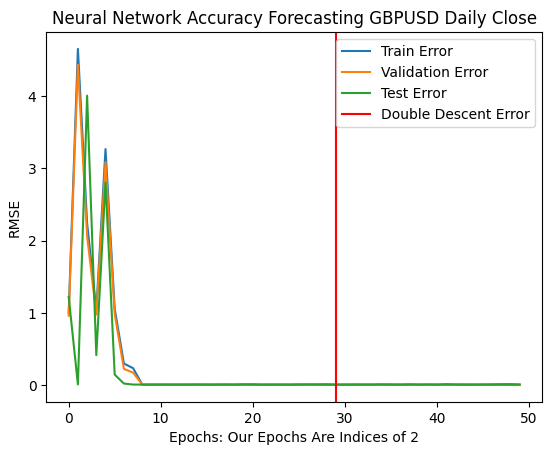 
Рис. 11. Уровни ошибок двойного спуска отмечены красной вертикальной линией, а слева мы можем наблюдать классическую область традиционного машинного обучения
Оптимизируем нашу нейросеть
Безусловно, идея статьи здравая. В обычных обстоятельствах мы бы даже не рассматривали возможность многочисленных итераций из-за страха переобучения. Теперь мы можем уверенно оптимизировать нашу модель, не опасаясь переобучения по отношению к обучающим данным.
from sklearn.model_selection import RandomizedSearchCV
Инициализируем модель.
#Reinitialize the model model = MLPRegressor(max_iter=(err_rates.loc["Test",:].argmin()))
Давайте определим параметры, по которым мы хотим производить поиск.
#Define the tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"learning_rate":['constant','adaptive','invscaling'],
"learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"hidden_layer_sizes":[(1,4),(5,8,10),(5,10,20),(10,50,10),(20,5),(1,5),(20,10)],
"early_stopping":[True,False],
"warm_start":[True,False],
"shuffle": [True,False]
},
n_iter=2**9,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
) Наконец, установим объект тюнера.
tuner.fit(train.loc[:,["Open","High","Low","Close"]],train.loc[:,"Target"])
Лучшие параметры, которые мы нашли.
tuner.best_params_
'tol': 0.1,
'solver': 'lbfgs',
'shuffle': False,
'learning_rate_init': 1e-06,
'learning_rate': 'adaptive',
'hidden_layer_sizes': (5, 8, 10),
'early_stopping': False,
'alpha': 1e-05,
'activation': 'relu'}
Конвертация в ONNX
Теперь, когда мы создали нашу модель, мы можем преобразовать ее в формат ONNX. ONNX означает Open Neural Network Exchange (открытый обмен нейронными сетями) и представляет собой протокол с открытым исходным кодом, который позволяет нам создавать и развертывать модели ИИ на любом языке программирования, который поддерживает спецификацию API ONNX. MQL5 позволяет нам импортировать наши модели ИИ и развертывать их непосредственно в нашем терминале. Сначала импортируем необходимые библиотеки.
import onnx from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
Затем давайте подгоним нашу модель под все имеющиеся у нас данные.
model = tuner.best_estimator_.fit(train.loc[:,["Open","High","Low","Close"]],train.loc[:,"Target"])
Укажем входную форму нашей модели.
#Define the input shape of 1,4
initial_type = [('float_input', FloatTensorType([1, 4]))]
#Specify the input shape
onnx_model = convert_sklearn(model, initial_types=initial_type) Сохраним модель ONNX.
#Save the onnx model onnx.save(onnx_model,"GBPUSD DAILY.onnx")
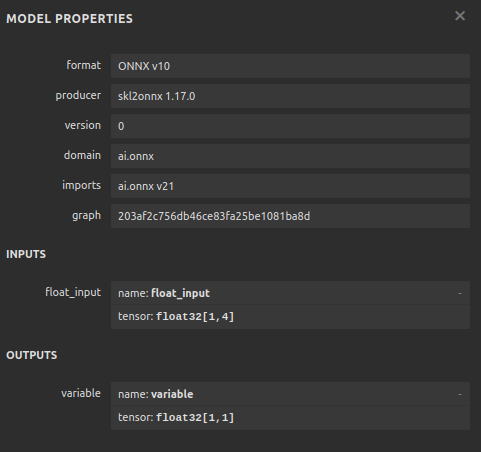
Рис. 12. Входные и выходные параметры нашей модели ONNX
Реализация средствами MQL5
Теперь мы можем приступить к реализации нашей торговой стратегии на MQL5. Наша стратегия будет основана на дневном таймфрейме. Мы будем использовать комбинацию полос Боллинджера и скользящих средних для определения преобладающего рыночного тренда.
Полосы Боллинджера обычно используются для определения перекупленных или перепроданных ценных бумаг. Обычно, когда уровни цен достигают верхней границы, рассматриваемая ценная бумага считается перекупленной. Обычно, когда уровни цен перекуплены, трейдеры ожидают, что будущие уровни цен упадут, вернувшись к среднему уровню. Вместо этого мы будем использовать полосы Боллинджера для следования за трендом.
Когда уровни цен пересекают среднюю линию полос вверх, мы будем считать это сильным бычьим сигналом, и наоборот, когда уровни цен опускаются ниже средней полосы, мы будем считать это сильным сигналом к продаже. Такие простые правила торговли неизбежно генерируют слишком много сигналов. Мы будем сортировать колебания цен, рассматривая значения скользящих средних, а не само ценовое движение.
Мы применим две скользящие средние: одну на максимальной цене, а другую - на минимальной, чтобы создать канал скользящей средней. Наши сигналы входа будут сформированы, когда обе скользящие средние пересекают среднюю линию полосы Боллинджера, и наш сигнал ИИ прогнозирует, что цена действительно будет двигаться в этом направлении.
Наконец, наши позиции будут закрываться всякий раз, когда каналы скользящей средней пересекают среднюю линию полос Боллинджера или если канал скользящей средней возвращается в пределы полос Боллинджера после прорыва за пределы полос, в зависимости от того, что произойдет раньше.
Давайте начнем с загрузки нашей ONNX-модели.
//+------------------------------------------------------------------+ //| GBPUSD AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Load our ONNX file | //+------------------------------------------------------------------+ #resource "\\Files\\GBPUSD DAILY.onnx" as const uchar onnx_buffer[];
Далее нам необходимо загрузить библиотеку Trade для помощи в управлении нашими позициями.
//+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> CTrade Trade;
Нам также понадобится несколько глобальных переменных для данных, которыми мы будем делиться в разных частях нашего приложения.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ bool patience = true; long onnx_model; int bb_handler,ma_h_handler,ma_l_handler; double ma_h_buffer[],ma_l_buffer[]; double bb_h_buffer[],bb_m_buffer[],bb_l_buffer[]; int state; double bid,ask; vectorf model_forecast = vectorf::Zeros(1);
Наши технические индикаторы имеют параметры периода, которые наш конечный пользователь мог бы корректировать по мере изменения рыночных условий.
//+------------------------------------------------------------------+ //| User Inputs | //+------------------------------------------------------------------+ input group "Technical Indicators" input int bb_period = 60; input int ma_period = 14;
При первой загрузке нашего приложения мы сначала загрузим наши технические индикаторы, а затем - нашу ONNX-модель. Используем буфер ONNX, который мы определили в начале нашей программы, для создания ONNX-модели. После этого мы проверим, что наша ONNX-модель надежна и что наши входные и выходные параметры соответствуют спецификациям.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Setup technical indicators bb_handler = iBands(Symbol(),PERIOD_D1,bb_period,0,1,PRICE_CLOSE); ma_h_handler = iMA(Symbol(),PERIOD_D1,ma_period,0,MODE_SMA,PRICE_HIGH); ma_l_handler = iMA(Symbol(),PERIOD_D1,ma_period,0,MODE_SMA,PRICE_LOW); //--- Define our ONNX model ulong input_shape [] = {1,4}; ulong output_shape [] = {1,1}; //--- Create the model onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); if(onnx_model == INVALID_HANDLE) { Comment("[ERROR] Failed to load AI module correctly"); return(INIT_FAILED); } //--- Validate I/O if(!OnnxSetInputShape(onnx_model,0,input_shape)) { Comment("[ERROR] Failed to set input shape correctly: ",GetLastError()," Actual shape: ",OnnxGetInputCount(onnx_model)); return(INIT_FAILED); } if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { Comment("[ERROR] Failed to load AI module correctly: ",GetLastError()," Actual shape: ",OnnxGetOutputCount(onnx_model)); return(INIT_FAILED); } //--- Everything was okay return(INIT_SUCCEEDED); }
Если наше торговое приложение больше не используется, мы освободим ресурсы, которые больше не используем.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- OnnxRelease(onnx_model); IndicatorRelease(bb_handler); IndicatorRelease(ma_h_handler); IndicatorRelease(ma_l_handler); }
Наконец, всякий раз, когда мы получаем новые котировки, мы обновляем наши глобальные переменные. Дальнейшие наши действия будут зависеть от количества открытых позиций. Если таковых нет, будем искать сигнал на вход. В противном случае мы будем проверять наличие сигналов выхода.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update technical data update(); if(PositionsTotal() == 0) { patience = true; check_setup(); } if(PositionsTotal() > 0) { string direction = model_forecast[0] > iClose(Symbol(),PERIOD_D1,0) ? "UP" : "DOWN"; Comment("Model Forecast: ",model_forecast[0]," ",direction); close_setup(); } }
Следующая функция будет получать прогноз от нашей модели.
//+------------------------------------------------------------------+ //| Get a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { double o,h,l,c; vector op,hi,lo,cl; op.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_OPEN,0,3); hi.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_HIGH,0,3); lo.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_LOW,0,3); cl.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_CLOSE,0,3); o = op[2] - op[0]; h = hi[2] - hi[0]; l = lo[2] - lo[0]; c = cl[2] - cl[0]; vectorf model_inputs = vectorf::Zeros(4); model_inputs[0] = o; model_inputs[1] = h; model_inputs[2] = l; model_inputs[3] = c; OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast); }
Теперь определим, как наше приложение должно закрывать свои позиции. Логическое значение patience используется для управления тем, когда приложение должно закрывать наши позиции. Если канал скользящей средней не вышел за пределы полос Боллинджера при первоначальном открытии позиций, переменная patience будет установлена в значение true. Это значение будет сохраняться, пока канал скользящей средней не выйдет за пределы полос. В этот момент флаг терпения устанавливается на false, и если канал вернется в пределы полос, наши позиции будут закрыты.
//+------------------------------------------------------------------+ //| Close our open positions | //+------------------------------------------------------------------+ void close_setup(void) { if(patience) { if(state == 1) { if(ma_l_buffer[0] > bb_h_buffer[0]) { patience = false; } if((ma_h_buffer[0] < bb_m_buffer[0]) && (ma_l_buffer[0] < bb_m_buffer[0])) { Trade.PositionClose(Symbol()); } } else if(state == -1) { if(ma_h_buffer[0] < bb_l_buffer[0]) { patience = false; } if((ma_h_buffer[0] > bb_m_buffer[0]) && (ma_l_buffer[0] > bb_m_buffer[0])) { Trade.PositionClose(Symbol()); } } } else { if((state == -1) && (ma_l_buffer[0] > bb_l_buffer[0])) { Trade.PositionClose(Symbol()); } if((state == 1) && (ma_h_buffer[0] < bb_h_buffer[0])) { Trade.PositionClose(Symbol()); } } }
Чтобы считать настройку действительной, мы хотим, чтобы канал скользящей средней находился полностью по одну сторону от средней полосы, а прогноз ИИ совпадал с поведением цены. В противном случае мы просто подождем, вместо того чтобы гоняться за мимолетными колебаниями цен.
//+------------------------------------------------------------------+ //| Check for valid trade setups | //+------------------------------------------------------------------+ void check_setup(void) { if((ma_h_buffer[0] < bb_m_buffer[0]) && (ma_l_buffer[0] < bb_m_buffer[0])) { model_predict(); if((model_forecast[0] < iClose(Symbol(),PERIOD_CURRENT,0))) { if(ma_h_buffer[0] < bb_l_buffer[0]) patience = false; Trade.Sell(0.3,Symbol(),bid,0,0,"GBPUSD AI"); state = -1; } } if((ma_h_buffer[0] > bb_m_buffer[0]) && (ma_l_buffer[0] > bb_m_buffer[0])) { model_predict(); if(model_forecast[0] > iClose(Symbol(),PERIOD_CURRENT,0)) { if(ma_l_buffer[0] > bb_h_buffer[0]) patience = false; Trade.Buy(0.3,Symbol(),ask,0,0,"GBPUSD AI"); state = 1; } } }
Наконец, нам нужна функция, отвечающая за обновление наших глобальных переменных.
//+------------------------------------------------------------------+ //| Update our market data | //+------------------------------------------------------------------+ void update(void) { CopyBuffer(bb_handler,0,0,1,bb_m_buffer); CopyBuffer(bb_handler,1,0,1,bb_h_buffer); CopyBuffer(bb_handler,2,0,1,bb_l_buffer); CopyBuffer(ma_h_handler,0,0,1,ma_h_buffer); CopyBuffer(ma_l_handler,0,0,1,ma_l_buffer); } //+------------------------------------------------------------------+
Теперь мы можем провести обратное тестирование нашей торговой стратегии. Мы использовали тестер стратегий для оценки нашего приложения на основе ежедневных рыночных данных GBPUSD примерно за 3 года. Обратите внимание, что при построении нашей модели ИИ мы использовали ежедневные рыночные данные за период с 2016 по 2024 год. Таким образом, представленное ниже тестирование на истории фактически тестирует нашу стратегию ИИ на данных, которые модель уже видела. Обратите внимание, что, несмотря на то, что наша модель была подвергнута воздействию данных и хорошо обучена, баланс нашего счета был очень нестабильным.
Это показывает, что, хотя мы хорошо обучили нашу модель, модели ИИ не "помнят" то, чему они "научились", в том смысле, в каком это делает человек. Они пытаются создать формулу, которая хорошо обобщает данные. Это значит, что они все равно могут допускать ошибки на данных, на которых уже были обучены.
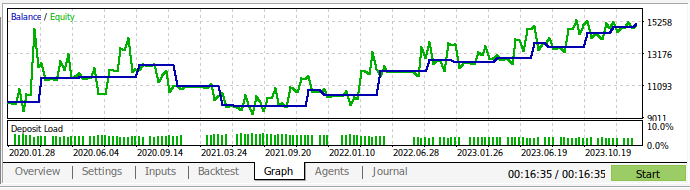
Рис. 13. Мы провели обратное тестирование нашего приложения на основе ежедневных рыночных данных GBPUSD примерно за 3 года
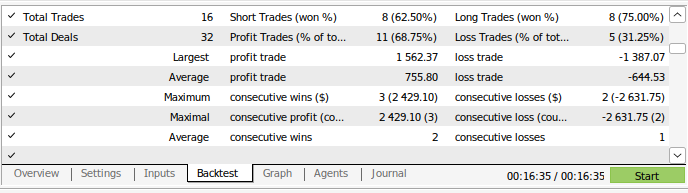
Рис. 14. Результаты нашей модели
Заключение
Мы продемонстрировали, что "переобучение" в некоторых обстоятельствах может быть лишь призывом к большим усилиям. Классическая идеология переобучения моделей ИИ в определенной степени удерживает нас на неоптимальном уровне ошибок. Однако мы уверены, что теперь вы сможете эффективнее использовать свои модели. У нас также была возможность просто увеличить количество скрытых слоев в модели или просто обучить модель с одним слоем и увеличить ширину слоя модели. Однако обучение таких огромных моделей потребует совершенно иного подхода, требующего навыков параллельных вычислений.
В этой статье представлен недорогой с точки зрения вычислений подход к обучению базовой модели фиксированного размера и использованию ежедневных данных ввиду небольшого количества строк, которые нам придется обрабатывать за такой промежуток времени. Однако для того, чтобы наши результаты были окончательными и надежными, нам, возможно, придется сократить обучающий набор вдвое, чтобы наша модель обучалась с 2016 по 2020 год, а все данные с 2020 по 2024 год не подвергались воздействию нашей модели во время обучения.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15971
Нейросети в трейдинге: Интеллектуальный конвейер прогнозов (Time-MoE)
Разработка системы репликации (Часть 76): Новый Chart Trade (III)
Гауссовcкие процессы в машинном обучении: регрессионная модель в MQL5
От начального до среднего уровня: Плавающая точка
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования