基于MQL5和Python的自优化EA（第六部分）：利用深度双重下降算法

机器学习中的过拟合可以有多种形式。最常见的情况是，当人工智能模型学习了数据中过多的噪声，而无法做出任何有用的泛化时，就会出现过拟合。这会导致我们在用模型评估之前未见过的数据时，表现不佳。为了缓解过拟合，已经开发出了许多技术，但这些方法对于刚接触AI的你来说往往很难实施。然而，最近由一群勤奋的哈佛校友发表的一篇论文表明，在某些任务中，过拟合可能已经成为过去式。本文将带你了解研究论文，并展示如何按照世界领先的研究成果，构建世界级的人工智能模型。

方法论概述

在开发人工智能模型时，有许多技术用于检测过拟合。最可信的方法是检查模型的测试误差和训练误差的图表。最初，这两个图表可能会一起下降，这是一个好迹象。随着我们继续训练模型，会达到一个最优误差水平，一旦超过这个水平，我们的训练误差会继续下降，但测试误差只会变得更糟。为了补救这个问题，已经开发出了许多技术，例如提前停止。提前停止会在模型的验证误差没有显著变化或持续恶化时终止训练过程。之后，恢复最佳权重，并假设已经找到了最佳模型，如图1所示。

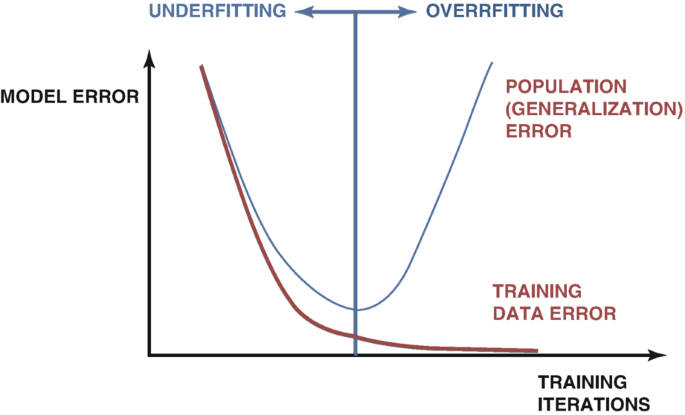
图1：一个展示过拟合的常规图表

这些观点的基础被2019年发表的一篇名为“深度双重下降”的研究论文撼动了。该论文并未试图解释它所展示的现象，只是描述了在撰写时观察到的现象的特征。本质上，论文展示了在某些问题上，模型的测试误差最初会下降，然后开始上升，之后又会第二次急剧下降，达到新的低点，直到模型最终收敛，如下面的图2所示。

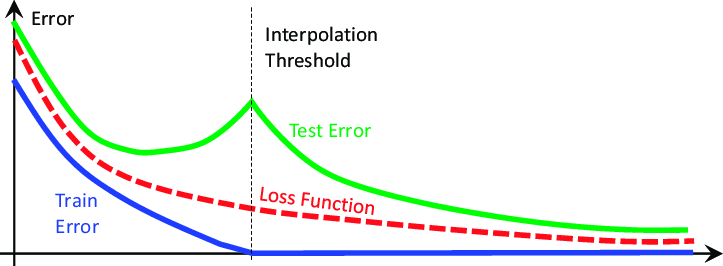
图2：深度双重下降现象的可视化

论文表明，这种现象可以被概念化为以下因素的函数：

1. 模型中的参数。
2. 最大训练迭代次数。

也就是说，如果我们持续在相同的数据集上训练越来越大的模型，我们会观察到测试误差最初会下降，然后开始上升，如果我们继续训练更大的模型，我们会观察到我们的测试误差第二次下降，达到新的低点，形成类似于上面图2的误差图。然而，由于计算成本的原因，持续训练越来越大的模型并不总是可行的。对于今天的讨论，我们将探索深度双重下降现象作为我们允许的最大迭代次数的函数。

这个观点是，随着我们允许模型执行更多的训练迭代，其验证误差总是会先增加，然后才会下降到新的低点。模型达到峰值误差水平并开始下降所需的时间各不相同，这取决于各种因素，例如数据集中的噪声量和正在训练的模型类型。

目前还没有被广泛接受的对这一现象的解释，但到目前为止，最容易理解这一现象的方式是将双重下降想象成模型参数的函数。

想象我们从一个简单的神经网络开始，模型很可能会对我们的数据欠拟合。也就是说，通过增加模型的复杂性，其性能可以得到改善。随着我们增加神经网络的复杂性，逐渐接近一个点，即模型完全拟合我们的数据。在传统的机器学习中，我们被告知，如果使模型更复杂，模型的训练误差总是会下降。这是真的。然而，这并非全部事实。

一旦我们的模型足够复杂，能够完美拟合我们的数据，此时训练误差通常是一个非常接近0的量，并且随着我们使模型更复杂，它不再下降。这是对传统机器学习理念的第一次冲击。这个点通常被称为插值阈值。如果我们继续增加模型的复杂性，超过这个阈值，我们会观察到测试精度显著下降。在大多数情况下，模型的误差率会下降到新的低点并稳定在那里。

旨在缓解过拟合的算法，如提前停止，似乎无意中阻碍了我们。这些算法总是在我们观察到第二次下降之前终止训练过程。让我们重现双重下降现象，独立地观察它。

让我们开始

首先需要使用我们在MQL5中构建的脚本，从MetaTrader 5平台中提取数据。

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| Script Inputs                                                    |
//+------------------------------------------------------------------+
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//| On start function                                                |
//+------------------------------------------------------------------+
void OnStart()
  {

//--- File name
   string file_name = "Market Data " + Symbol()+  ".csv";

//--- Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i)
                  );
        }
     }
//--- Close the file
   FileClose(file_handle);
  }
//+------------------------------------------------------------------+

开始前，让我们先加载所需的库函数。

#Standard libraries
import pandas                  as     pd
import numpy                   as     np
import seaborn                 as     sns
import matplotlib.pyplot       as     plt
from   mpl_toolkits.mplot3d    import Axes3D
from   sklearn.linear_model    import LinearRegression
from   sklearn.neural_network  import MLPRegressor
from   sklearn.metrics         import mean_squared_error
from   sklearn.model_selection import cross_val_score,TimeSeriesSplit

现在，读取数据。

#Read in the data
data = pd.read_csv('GBPUSD_Daily_20160103_20240131.csv',sep='\t')

清洗数据。

#Clean up the data
data.rename(columns={'<OPEN>':'Open','<HIGH>':'High','<LOW>':'Low','<CLOSE>':'Close'},inplace=True)

去掉不必要的数据列。

#Drop columns we don't need
data = data.drop(['<DATE>','<VOL>','<SPREAD>','<TICKVOL>'],axis=1)
data

可视化数据。

#Plot the close price
plt.plot(data["Close"])
plt.xlabel("Time")
plt.ylabel("Close Price")
plt.title("GBPUSD Daily Close")

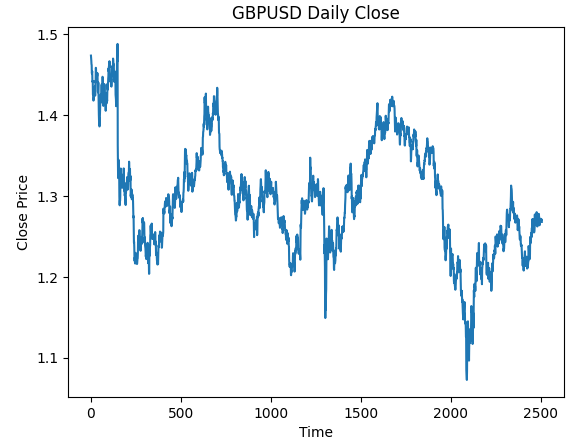
图3 ：我们将要处理的GBPUSD日线OHLC数据

我们想要训练一个模型来预测GBPUSD的每日行情。然而，我们有两个变量需要选择：

1. 我们应该以什么频率计算？
2. 我们应该预测多远的未来？

通常情况下，我们预测未来一步，并将返回值计算为连续两天之间的差值。然而，这真的是最优的吗？这真的是我们能做到的最好结果吗？我们不会回答这个问题，数据本身会为我们回答这个问题。

让我们对返回值的参数和预测范围进行网格搜索。首先，我们需要为两个参数定义一个统一的坐标轴。

#Define the input range
x_min , x_max = 2,100 #Look ahead
y_min , y_max = 2,100 #Period

现在，定义x轴和y轴。

#Sample input range uniformly
x_axis = np.arange(x_min,x_max,4) #Look ahead
y_axis = np.arange(y_min,y_max,4) #Period

我们需要创建一个网格。网格是两个独立的二维数组，可以一起使用，以映射我们想要评估的所有可能的输入组合。

#Create a meshgrid
x , y = np.meshgrid(x_axis,y_axis)

这个函数将用于在我们用新设置测试模型的准确性之前清理数据集。

#This function will create and return a clean dataframe according to our specifications
def clean_data(look_ahead,period):
    #Create a copy of the data
    temp = pd.read_csv('GBPUSD_Daily_20160103_20240131.csv',sep='\t')
    #Clean up the data
    temp.rename(columns={'<OPEN>':'Open','<HIGH>':'High','<LOW>':'Low','<CLOSE>':'Close'},inplace=True)
    temp = temp.drop(['<DATE>','<VOL>','<SPREAD>','<TICKVOL>'],axis=1)
    #Define our target
    temp["Target"] = temp["Close"].shift(-look_ahead)
    #Apply the differencing
    temp["Close"] = temp["Close"].diff(period)
    temp["Open"] = temp["Open"].diff(period)
    temp["High"] = temp["High"].diff(period)
    temp["Low"] = temp["Low"].diff(period)
    temp = temp.dropna()
    temp = temp.reset_index(drop=True)
    return(temp)

下一个函数，用我们传入的参数来交叉验证我们的模型，并返回交叉验证误差。

#Evaluate the objective function
def evaluate(look_ahead,period):
    #Define the model
    model = LinearRegression()
    #Define our time series split
    tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
    temp = clean_data(look_ahead,period)
    score = np.mean(cross_val_score(model,temp.loc[:,["Open","High","Low","Close"]],temp["Target"],cv=tscv))
    return(score)

最后，我们需要一个函数，将我们的结果记录在一个与我们的网格形状相同的数组中。

#Define the objective
def objective(x,y):
    #Define the output matrix
    results = np.zeros([x.shape[0],y.shape[0]])
    #Fill in the output matrix
    for i in np.arange(0,x.shape[0]):
        #Select the rows
        look_ahead = x[i]
        period     = y[i]
        for j in np.arange(0,y.shape[0]):
            results[i,j] = evaluate(look_ahead[j],period[j])
    return(results)

到目前为止，我们已经实现了所需的函数，以观察当我们在计算返回值时改变时间间隔以及改变希望预测未来的长度时，模型的误差水平如何变化。让我们先观察一个简单模型在改变这些参数时的行为，然后再开始处理更复杂、更深的神经网络。

linear_reg_res = objective(x,y)
linear_reg_res = np.abs(linear_reg_res)

等高线图通常用于地理学中，以显示地形上的海拔变化。我们可以使用这些曲面图，来找出哪一对参数能从我们的简单线性回归模型中产生最低的误差水平。蓝色区域是产生低误差的组合，而红色区域是不令人满意的组合。在等高线图中最深蓝色区域中的白点，代表线性回归模型的最佳预测设置。

正如下面的图表所示，我们的简单线性人工智能模型本可以轻松超越市场上任何使用周期为1，并预测未来1步的经典价格模型的交易者。

plt.contourf(x,y,linear_reg_res,100,cmap="jet")
plt.plot(x_axis[linear_reg_res.min(axis=0).argmin()],y_axis[linear_reg_res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Linear Regression Accuracy Forecasting GBPUSD Daily Close")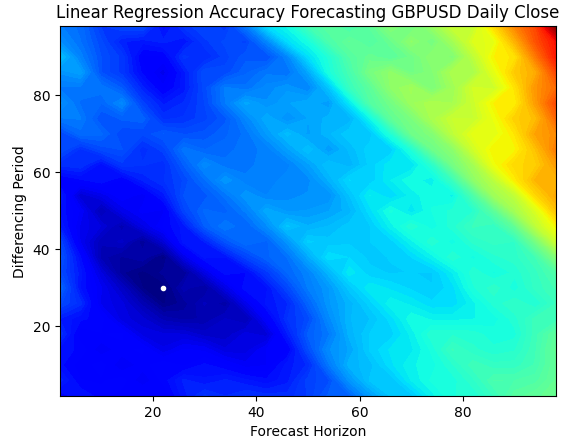

图4 ：我们线性回归预测GBPUSD日收盘价准确性的等高线图

将结果以3D形式可视化会生成一个曲面，这让我们能够直观地看到模型与GBPUSD市场的关联。图表显示，随着预测的时间范围越来越远，误差率会下降到一个最优水平，然后随着我们继续向更远的未来预测，误差率又开始上升。然而，最重要的一点是，对于我们的线性模型，下面的图5 明确地显示，我们最佳模型输入的预测范围和日线周期都在20到40之间。

#Create a surface plot
fig , ax = plt.subplots(subplot_kw={"projection":"3d"})
fig.set_size_inches(8,8)
ax.plot_surface(x,y,linear_reg_res,cmap="jet")

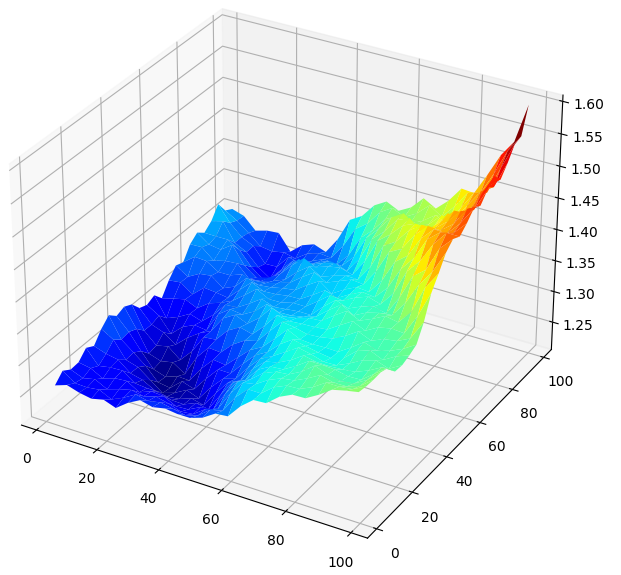
图5 ：可视化我们线性模型预测GBPUSD日收盘价的误差

现在我们已经熟悉了等高线图和曲面图，让我们来看看当我们使用深度神经网络在相同的参数空间中进行搜索时，它的表现如何。

res = objective(x,y)
res = np.abs(res)

神经网络的曲面图要复杂得多，难以可视化。蓝色区域是理想的，因为它们代表产生低误差水平的组合。然而，注意我们观察到红色区域突然出现在最佳组合的中间。这很有趣，不是吗？

两个组合如此接近，却有着截然不同的误差水平，这是如何发生的？这部分是由于用于训练神经网络的优化算法的性质。如果我们再次训练这个模型，我们将得到一个完全不同的图表，以及一个不同的最佳点。

plt.contourf(x,y,res,100,cmap="jet")
plt.plot(x_axis[res.min(axis=0).argmin()],y_axis[res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")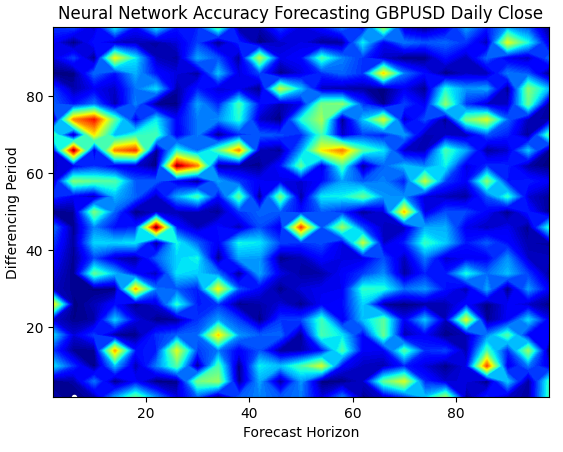

图6 ：神经网络对我们的输入非常敏感

当我们以3D形式可视化模型的表现时，我们可以看到神经网络是多么不稳定。我们能有信心地说神经网络已经有效地学习了任何有用的关系吗？到目前为止，哪个模型表现得更好？如果我们从传统的角度来处理这个问题，我们会选择简单的线性模型，因为它产生了更平滑的误差图，这可能是它更有技能的迹象，而神经网络的波动误差率可能被视为过拟合数据的迹象。

然而，这是机器学习的经典方法，从当代的角度来看，我们把神经网络的误差图看作是模型还没有真正收敛的迹象，而不是过拟合的迹象。换句话说，根据双重下降论文，现在比较神经网络还为时过早。让我们自己独立地证明这一点，而不是盲目地因为作者的资历而信任研究论文。

#Create a surface plot
fig , ax = plt.subplots(subplot_kw={"projection":"3d"})
fig.set_size_inches(8,8)
ax.plot_surface(x,y,res,cmap="jet")

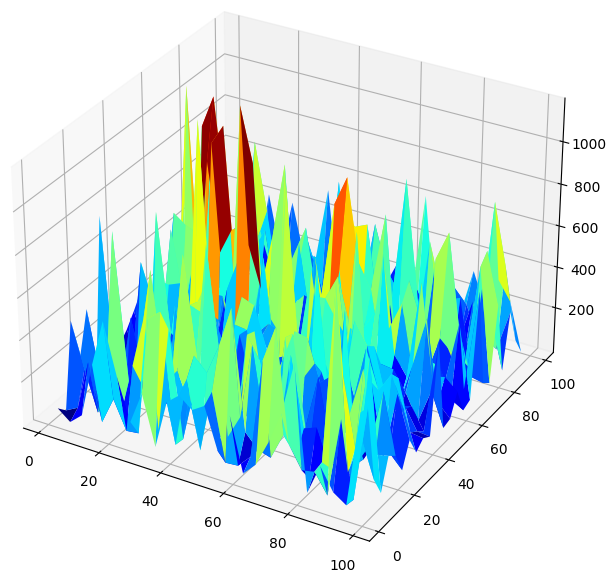
图7 ：我们神经网络预测GBPUSD日收盘价的误差水平

检查双重下降

我们将首先应用发现的最佳参数，这些参数用于计算价格和预测深度。

#The best settings we have found so far
look_ahead = x_axis[res.min(axis=0).argmin()]
difference_period = y_axis[res.min(axis=1).argmin()]
data["Target"] = data["Close"].shift(-look_ahead)
#Apply the differencing
data["Close"] = data["Close"].diff(difference_period)
data["Open"] = data["Open"].diff(difference_period)
data["High"] = data["High"].diff(difference_period)
data["Low"] = data["Low"].diff(difference_period)
data.dropna(inplace=True)
data.reset_index(drop=True,inplace=True)
data

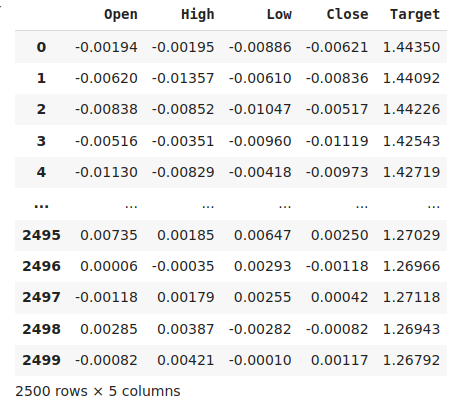
图8：当前的数据形式

导入所需的库。

from sklearn.model_selection import train_test_split,TimeSeriesSplit
from sklearn.metrics         import mean_squared_error

定义最大间隔数量。回想一下，双重下降是模型复杂度或最大训练迭代次数的函数。我们将通过一个简单的神经网络来测试这一点，并改变最大迭代次数。我们的最大训练迭代次数将是2的连续幂。

max_epoch = 50

创建一个数据结构来存储我们的误差水平。

err_rates = pd.DataFrame(columns = np.arange(0,max_epoch),index=["Train","Validation","Test"])

我们需要设置时间序列分割对象。

tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

现在进行训练测试分割。

train , test = train_test_split(data,shuffle=False,test_size=0.5)

随着我们增加最大迭代次数为2的均匀幂，对我们的模型进行交叉验证。

for j in np.arange(0,max_epoch):
  #Define our model and measure its error
  current_train_err = []
  current_val_err = []
  model = MLPRegressor(hidden_layer_sizes=(6,5),max_iter=(2 ** j))

  for i,(train_index,test_index) in enumerate(tscv.split(train)):
    #Assess the model
    model.fit(train.loc[train_index,["Open","High","Low","Close"]],train.loc[train_index,'Target'])
    current_train_err.append(mean_squared_error(train.loc[train_index,'Target'],model.predict(train.loc[train_index,["Open","High","Low","Close"]])))
    current_val_err.append(mean_squared_error(train.loc[test_index,'Target'],model.predict(train.loc[test_index,["Open","High","Low","Close"]])))

  #Record our observations
  err_rates.loc["Train",j]      = np.mean(current_train_err)
  err_rates.loc["Validation",j] = np.mean(current_val_err)
  err_rates.loc["Test",j]       = mean_squared_error(test['Target'],model.predict(test.loc[:,["Open","High","Low","Close"]]))

我们的前6次迭代展示了模型误差率从1到32次迭代过程的变化。正如下面的图表所示，测试误差最初下降，然后开始上升，然后又出现了更高的低点。我们的训练和验证误差率最初上升，然后下降到一个略高的低点，然后再次上升。然而，32次迭代只代表了训练过程的一个小间隔，让我们看看接下来的训练过程是如何展开的。

plt.plot(err_rates.iloc[0,0:5])
plt.plot(err_rates.iloc[1,0:5])
plt.plot(err_rates.iloc[2,0:5])
plt.legend(["Train Error","Validation Error","Test Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")

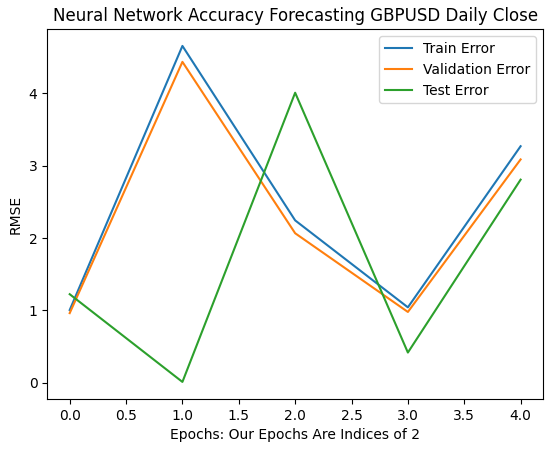
图9 ：从1到32次迭代验证的准确性

随着验证的继续进行，现在我们看到了模型的误差率如何在64到256次迭代间隔内的演变。看起来在一些发散之后，误差率终于开始收敛到一个最小值。然而，根据论文，我们还有很长的路要走。

请注意，scikit-learn默认初始化的神经网络只执行200次迭代。这个数字略小于2的8次方。有了像提前停止这样的算法，我们可能会被困在上面图7中观察到的不均匀表面上的欺骗性局部最优解中。 

plt.plot(err_rates.iloc[0,0:9])
plt.plot(err_rates.iloc[1,0:9])
plt.plot(err_rates.iloc[2,0:9])
plt.legend(["Train Error","Validation Error","Test Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")

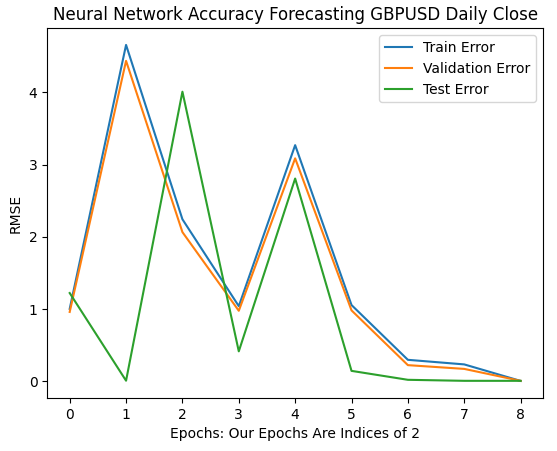
图10 ：我们模型的误差率开始收敛

最佳误差率是在我们的模型被执行超过10亿次迭代时产生的！确切的数字是2的30次方。这个点在下面的图11中用红色垂直线标记。我们通常执行的迭代次数只是最佳迭代次数的一小部分，因为我们害怕过拟合数据，这让我们被困在红色线左侧的次优误差水平上。

plt.plot(err_rates.iloc[0,:])
plt.plot(err_rates.iloc[1,:])
plt.plot(err_rates.iloc[2,:])
plt.axvline(err_rates.loc["Test",:].argmin(),color='red')
plt.legend(["Train Error","Validation Error","Test Error","Double Descent Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")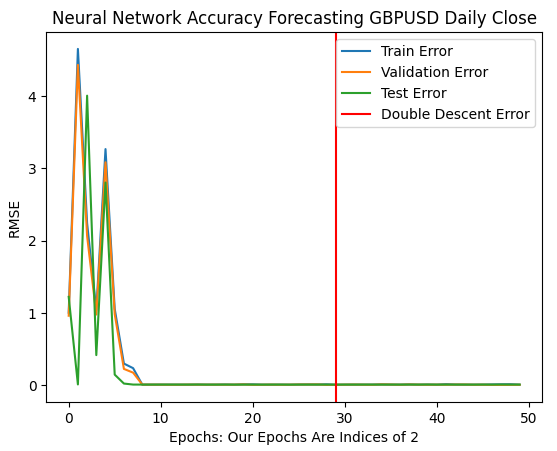

图11 ：双重下降误差水平由红色垂直线标记，在左侧我们可以观察到传统机器学习的经典领域

优化我们的神经网络

显然，这篇论文是有一定道理的。在正常情况下，我们根本不会考虑允许大量的迭代，因为我们害怕过度拟合。我们现在可以自信地优化我们的模型，而不用担心过度拟合训练数据。

from sklearn.model_selection import RandomizedSearchCV

初始化模型。

#Reinitialize the model
model = MLPRegressor(max_iter=(err_rates.loc["Test",:].argmin()))

让我们定义想要搜索的参数。

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "activation" : ["relu","logistic","tanh","identity"],
        "solver":["adam","sgd","lbfgs"],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "learning_rate":['constant','adaptive','invscaling'],
        "learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "hidden_layer_sizes":[(1,4),(5,8,10),(5,10,20),(10,50,10),(20,5),(1,5),(20,10)],
        "early_stopping":[True,False],
        "warm_start":[True,False],
        "shuffle": [True,False]
        },
        n_iter=2**9,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

最后，拟合调优器对象。

tuner.fit(train.loc[:,["Open","High","Low","Close"]],train.loc[:,"Target"])

这些是我们找到的最佳参数。

tuner.best_params_

{'warm_start': True,
 'tol': 0.1,
 'solver': 'lbfgs',
 'shuffle': False,
 'learning_rate_init': 1e-06,
 'learning_rate': 'adaptive',
 'hidden_layer_sizes': (5, 8, 10),
 'early_stopping': False,
 'alpha': 1e-05,
 'activation': 'relu'}

转换为 ONNX

现在我们已经创建了模型，可以将其转换为ONNX格式。ONNX代表开放神经网络交换协议，这是一个开源协议，允许我们在任何支持ONNX API规范的编程语言中创建和部署人工智能模型。MQL5允许我们导入人工智能模型，并将其直接部署到我们的终端中。首先，我们导入所需的库。

import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

然后，在所有的数据上拟合我们的模型。

model = tuner.best_estimator_.fit(train.loc[:,["Open","High","Low","Close"]],train.loc[:,"Target"])

指定模型的输入参数格式。

#Define the input shape of 1,4
initial_type = [('float_input', FloatTensorType([1, 4]))]
#Specify the input shape
onnx_model = convert_sklearn(model, initial_types=initial_type)

保存ONNX模型。

#Save the onnx model
onnx.save(onnx_model,"GBPUSD DAILY.onnx")

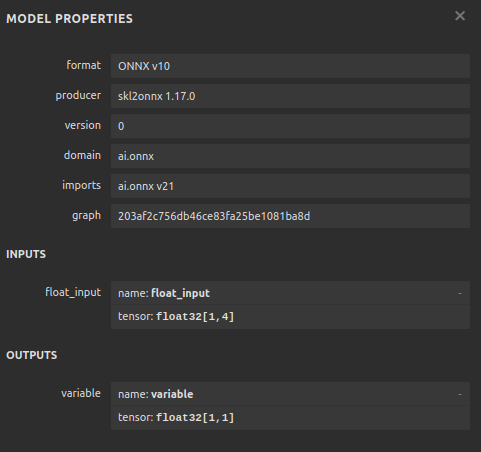
图12 ：ONNX模型的输入和输出参数

 

在MQL5中的实现

现在可以开始在MQL5中实现我们的交易策略。我们的策略将基于日线时间框架。我们将使用布林带和移动平均线的组合来确定当前的市场趋势。

布林带通常用于识别超买或超卖。通常情况下，当价格水平达到上轨时，被观察的交易品种被认为是超买的。一般来说，当价格水平超买时，交易者预期未来价格水平会下跌并回归到平均价格水平。我们将以趋势跟踪的方式使用布林带。

当价格水平穿过布林带中线时，我们将认为这是一个强烈的看涨信号，反之，当价格水平跌破中线时，我们将认为这是一个强烈的卖出信号。如此简单的交易规则肯定会产生过多的信号，这并不总是理想的。我们将通过考虑移动平均值而不是价格行为本身来过滤价格波动。

我们将在最高价和最低价上分别应用两个移动平均线，以创建一个移动平均通道。当两个移动平均线都穿过布林带中线，并且我们的人工智能信号预测价格确实会朝那个方向移动时，我们将生成入场信号。 

最后，当移动平均通道穿过布林带中线，或者移动平均通道在突破布林带后又回到布林带内时，我们将平仓，以先发生的情况为准。

让我们先加载我们的ONNX模型，开始着手进行下一步。

//+------------------------------------------------------------------+
//|                                                    GBPUSD AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Load our ONNX file                                               |
//+------------------------------------------------------------------+
#resource  "\\Files\\GBPUSD DAILY.onnx" as const uchar onnx_buffer[];

接着，需要加载Trade库来帮助我们管理头寸。

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
CTrade Trade;

我们还需要一些全局变量，以便在程序的不同地方共享它们的值。

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
bool   patience = true;
long   onnx_model;
int    bb_handler,ma_h_handler,ma_l_handler;
double ma_h_buffer[],ma_l_buffer[];
double bb_h_buffer[],bb_m_buffer[],bb_l_buffer[];
int    state;
double bid,ask;
vectorf model_forecast = vectorf::Zeros(1);

我们的技术指标具有周期参数，我们希望终端用户能够根据市场条件的变化进行调整。

//+------------------------------------------------------------------+
//| User Inputs                                                      |
//+------------------------------------------------------------------+
input group "Technical Indicators"
input int bb_period = 60;
input int ma_period = 14;

当我们的应用程序首次加载时，将首先加载技术指标，然后才加载我们的ONNX模型。我们将使用在程序开头定义的ONNX缓冲区，从该缓冲区创建一个ONNX模型。从那里，我们将验证我们的ONNX模型是否健全，以及输入和输出参数是否符合我们的规范。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Setup technical indicators
   bb_handler   = iBands(Symbol(),PERIOD_D1,bb_period,0,1,PRICE_CLOSE);
   ma_h_handler = iMA(Symbol(),PERIOD_D1,ma_period,0,MODE_SMA,PRICE_HIGH);
   ma_l_handler = iMA(Symbol(),PERIOD_D1,ma_period,0,MODE_SMA,PRICE_LOW);
//--- Define our ONNX model
   ulong input_shape [] = {1,4};
   ulong output_shape [] = {1,1};
//--- Create the model
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

   if(onnx_model == INVALID_HANDLE)
     {
      Comment("[ERROR] Failed to load AI module correctly");
      return(INIT_FAILED);
     }

//--- Validate I/O
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      Comment("[ERROR] Failed to set input shape correctly: ",GetLastError()," Actual shape: ",OnnxGetInputCount(onnx_model));
      return(INIT_FAILED);
     }

   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      Comment("[ERROR] Failed to load AI module correctly: ",GetLastError()," Actual shape: ",OnnxGetOutputCount(onnx_model));
      return(INIT_FAILED);
     }


//--- Everything was okay
   return(INIT_SUCCEEDED);
  }

如果交易程序不再使用，我们需要释放相关资源。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   OnnxRelease(onnx_model);
   IndicatorRelease(bb_handler);
   IndicatorRelease(ma_h_handler);
   IndicatorRelease(ma_l_handler);
  }

最后，每当收到新的报价时，我们将更新全局变量。接下来要采取的步骤，取决于持有的头寸数量。如果没有，我们将寻找入场信号。否则，我们将检查平仓信号。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update technical data
   update();

   if(PositionsTotal() == 0)
     {
      patience = true;
      check_setup();
     }

   if(PositionsTotal() > 0)
     {
      string direction = model_forecast[0] > iClose(Symbol(),PERIOD_D1,0) ? "UP" : "DOWN";
      Comment("Model Forecast: ",model_forecast[0]," ",direction);
      close_setup();
     }
  }

下面的函数将从我们的模型中获取一个预测信号。

//+------------------------------------------------------------------+
//| Get a prediction from our model                                  |
//+------------------------------------------------------------------+
void model_predict(void)
  {
   double o,h,l,c;
   vector op,hi,lo,cl;
   op.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_OPEN,0,3);
   hi.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_HIGH,0,3);
   lo.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_LOW,0,3);
   cl.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_CLOSE,0,3);

   o =  op[2]  - op[0];
   h =  hi[2]  - hi[0];
   l =  lo[2]  - lo[0];
   c =  cl[2]  - cl[0];

   vectorf model_inputs = vectorf::Zeros(4);
   model_inputs[0] = o;
   model_inputs[1] = h;
   model_inputs[2] = l;
   model_inputs[3] = c;

   OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast);
  }

现在我们将定义应用程序应该如何平仓。布尔变量patience用于控制应用程序何时应该平仓。如果在我们最初开仓时，移动平均通道没有突破布林带，patience变量将被设置为true。该值将保持为true，直到移动平均通道突破布林带。在那时，patience被设置为false，如果通道重新回到布林带内，我们的头寸将被平仓。

//+------------------------------------------------------------------+
//| Close our open positions                                         |
//+------------------------------------------------------------------+
void close_setup(void)
  {
   if(patience)
     {
      if(state == 1)
        {
         if(ma_l_buffer[0] > bb_h_buffer[0])
           {
            patience = false;
           }


         if((ma_h_buffer[0] < bb_m_buffer[0]) && (ma_l_buffer[0] < bb_m_buffer[0]))
           {
            Trade.PositionClose(Symbol());
           }
        }

      else
         if(state == -1)
           {
            if(ma_h_buffer[0] < bb_l_buffer[0])
              {
               patience = false;
              }

            if((ma_h_buffer[0] > bb_m_buffer[0]) && (ma_l_buffer[0] > bb_m_buffer[0]))
              {
               Trade.PositionClose(Symbol());
              }
           }
     }

   else
     {
      if((state == -1) && (ma_l_buffer[0] > bb_l_buffer[0]))
        {
         Trade.PositionClose(Symbol());
        }

      if((state == 1) && (ma_h_buffer[0] < bb_h_buffer[0]))
        {
         Trade.PositionClose(Symbol());
        }
     }

  }

为了使设置有效，我们希望移动平均通道完全位于中带的一侧，并且我们的人工智能预测与价格走势一致。否则，我们将仅仅是等待，而不是追逐价格的短暂波动。

//+------------------------------------------------------------------+
//| Check for valid trade setups                                     |
//+------------------------------------------------------------------+
void check_setup(void)
  {

   if((ma_h_buffer[0] < bb_m_buffer[0]) && (ma_l_buffer[0] < bb_m_buffer[0]))
     {
      model_predict();
      if((model_forecast[0] < iClose(Symbol(),PERIOD_CURRENT,0)))
        {
         if(ma_h_buffer[0] < bb_l_buffer[0])
            patience = false;

         Trade.Sell(0.3,Symbol(),bid,0,0,"GBPUSD AI");
         state = -1;
        }
     }

   if((ma_h_buffer[0] > bb_m_buffer[0]) && (ma_l_buffer[0] > bb_m_buffer[0]))
     {
      model_predict();
      if(model_forecast[0] > iClose(Symbol(),PERIOD_CURRENT,0))
        {
         if(ma_l_buffer[0] > bb_h_buffer[0])
            patience = false;

         Trade.Buy(0.3,Symbol(),ask,0,0,"GBPUSD AI");
         state = 1;
        }
     }
  }

最后，我们需要一个函数来更新全局变量。

//+------------------------------------------------------------------+
//| Update our market data                                           |
//+------------------------------------------------------------------+
void update(void)
  {
   CopyBuffer(bb_handler,0,0,1,bb_m_buffer);
   CopyBuffer(bb_handler,1,0,1,bb_h_buffer);
   CopyBuffer(bb_handler,2,0,1,bb_l_buffer);
   CopyBuffer(ma_h_handler,0,0,1,ma_h_buffer);
   CopyBuffer(ma_l_handler,0,0,1,ma_l_buffer);
  }
//+------------------------------------------------------------------+

现在我们对交易策略进行回测。使用策略测试器来评估策略程序在大约3年的GBPUSD日线市场数据上的表现。请注意，当我们构建人工智能模型时，我们使用了2016年到2024年的日线市场数据。因此，在下面展示的回测，实际上是在测试我们的人工智能策略在模型已经见过的数据上的表现。请注意，尽管我们的模型已经接触过这些数据并且训练得很好，但我们的账户余额随时间波动很大。

这表明，尽管我们已经很好地训练了模型，但人工智能模型并不会像人类那样“记住”它们“学到”的东西。它试图创建一个对数据有良好泛化的公式。这意味着它可能仍然会在已经训练过的数据上犯错误。

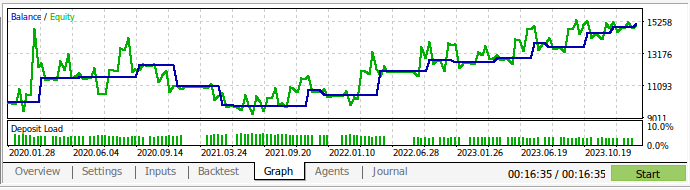
图13：在大约3年的GBPUSD日线市场数据上进行回测

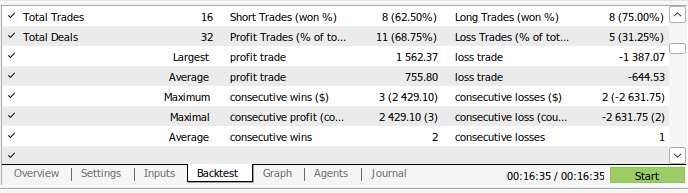
图14：模型的交易表现细节

结论

总结一下，我们已经证明，在某些情况下，“过拟合”的出现可能只是需要更大努力的信号。在一定程度上，关于过拟合人工智能模型的经典观念使我们停留在次优的误差水平上。然而，我们相信，在阅读了这篇文章之后，你将能够更好地利用你的模型。请读者回想一下，我们还可以选择简单地增加模型中的隐藏层数量，或者简单地训练一个只有一层的模型，并增加模型层的宽度。然而，训练如此庞大的模型将需要一种完全不同的方法，需要掌握并行计算的技能。

本文为你提供了一种计算成本较低的方法，即训练一个固定大小的基本模型，并使用日线数据，因为在这种时间框架下，我们只需要处理少量的行。然而，为了使我们的结果具有结论性和稳健性，可能需要将我们的训练集减少到其大小的一半，以便我们的模型从2016年训练到2020年，而2020年到2024年的所有数据在训练过程中不暴露给我们的模型。