MQL5とPythonで自己最適化エキスパートアドバイザーを構築する（第6回）： Deep Double Descentの活用

機械学習における過剰適合は、さまざまな形で現れる可能性があります。最も一般的なのは、AIモデルがデータのノイズを過剰に学習し、有用な一般化ができなくなる場合です。その結果、未見のデータでモデルを評価すると、期待外れの結果が得られることがあります。過剰適合を軽減するために数多くのテクニックが開発されていますが、特に初心者にとってはこれらのテクニックを実装するのが難しい場合もあります。しかし、最近ハーバード大学の卒業生たちによって発表された論文では、特定のタスクにおいては過剰適合がもはや問題ではなくなる可能性があることが示されています。本記事では、この研究論文を詳しく紹介し、世界最先端の研究に基づいて世界クラスのAIモデルを構築する方法を解説します。

方法論の概要

AIモデルを開発する際、過剰適合を検出するためのさまざまなテクニックがあります。最も信頼できる方法の一つは、モデルのテスト誤差と訓練誤差のプロットを調べることです。初期段階では、2つのプロットが同時に減少し、良好な傾向を示します。しかし、モデルの訓練を続けると、最適な誤差レベルに達し、それを超えると、訓練誤差は引き続き減少する一方で、テスト誤差は悪化していきます。この問題を改善するために、早期停止など多くのテクニックが開発されてきました。早期停止では、モデルの検証誤差が大きく変化しなくなったり、悪化し続けたりした場合に訓練プロセスを終了します。その後、以下の図1のように、最適な重みが復元され、最適なモデルが見つかったとみなされます。

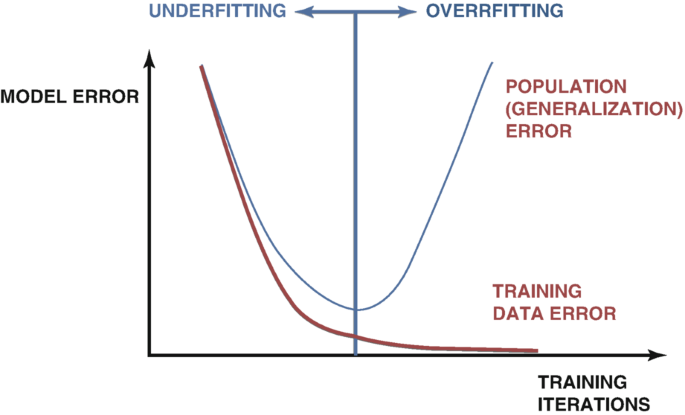
図1：実際の過剰適合を示す一般化されたプロット

このような考え方は、2019年に発表された『Deep Double Descent』という研究論文によって根本から揺るがされました（リンクはこちらです）。この論文は、観察された現象を説明しようとするものではなく、執筆時点で観測された現象の特徴を記述しているに過ぎません。  要するに、この論文では、特定の問題において、モデルのテスト誤差が最初は下降した後、上昇し始め、そして劇的に2度目の下降を経て新たな低水準に達し、最終的にモデルが収束することを実証しています。この現象は、以下の図2に示されている通りです。

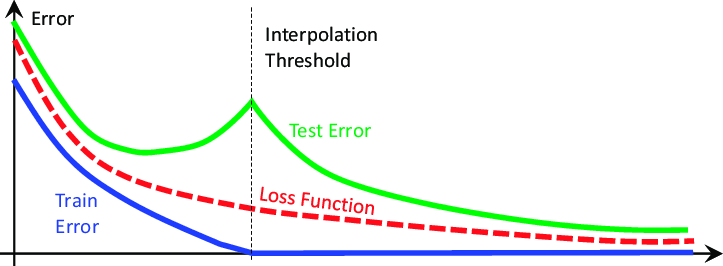
図2： Deep Double Descent現象の視覚化

本稿では、この現象が以下の2つの要因の関数として概念化できることを示します。

1. モデルのパラメータ
2. 訓練の最大反復回数

つまり、同じデータセットでより大きなモデルを継続的に訓練した場合、テスト誤差は最初に低下し、その後上昇し始めます。そしてさらに大きなモデルを訓練し続けると、テスト誤差は2度目の低下を迎え、新たな低水準に達します。この現象によって、上記の図2のような誤差プロットが作成されます。しかし、計算コストの問題から、より大きなモデルを段階的に訓練し続けることは必ずしも現実的ではありません。本稿では、Deep Double Descent現象を、訓練の最大反復回数の関数として探求します。

この考え方は、モデルにより多くの訓練反復を許容すると、検証誤差が一旦増加した後、新たな最低値に低下するというものです。モデルが誤差レベルのピークに達し、その後低下し始めるまでにかかる時間は、データセットのノイズ量や訓練されるモデルの種類など、さまざまな要因によって異なります。

現時点では、この現象に関する広く受け入れられた説明はありませんが、最も理解しやすい説明方法は、二重降下(double descent)をモデルのパラメータの関数として想像することです。

単純なニューラルネットワークを例に取ると、そのモデルはデータに適合しない（過少適合する）可能性が高いです。つまり、モデルにより複雑さを加えることで、パフォーマンスが向上する可能性があるということです。ニューラルネットワークの複雑さを増していくと、モデルは次第にデータに完全に適合する状態に近づきます。  従来の機械学習では、モデルの複雑さを増すと、訓練誤差が常に低下すると教えられてきました。これは事実ですが、完全な真実ではありません。

モデルがデータに完全に適合するほど複雑になると、この時点で訓練誤差は通常0に非常に近い値となり、それ以上複雑さを増しても低下しなくなります。これが機械学習の伝統的な考え方に対する最初の打撃です。この点は一般に「補間閾値」と呼ばれます。この補間閾値を超えてモデルの複雑さをさらに増やすと、テストの精度が一時的に著しく低下します。しかし、多くの場合、モデルの誤差率は新たな最低値まで下がり、最終的には安定します。

過剰適合を緩和するために設計されたアルゴリズム、例えば早期停止（early stopping）は、意図せず私たちの進歩を阻害している可能性があります。これらのアルゴリズムは、2回目の誤差の低下が観察される前に、訓練プロセスを終了してしまうのです。では、この二重降下現象を再現し、自分自身で独立に観察してみましょう。

はじめに

まず、MQL5で作成したスクリプトを使用して、MetaTrader 5プラットフォームからデータを抽出する必要があります。

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| Script Inputs                                                    |
//+------------------------------------------------------------------+
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+

//+------------------------------------------------------------------+
//| On start function                                                |
//+------------------------------------------------------------------+
void OnStart()
  {

//--- File name
   string file_name = "Market Data " + Symbol()+  ".csv";

//--- Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i)
                  );
        }
     }
//--- Close the file
   FileClose(file_handle);
  }
//+------------------------------------------------------------------+

はじめに、必要なライブラリをインポートしましょう。

#Standard libraries
import pandas                  as     pd
import numpy                   as     np
import seaborn                 as     sns
import matplotlib.pyplot       as     plt
from   mpl_toolkits.mplot3d    import Axes3D
from   sklearn.linear_model    import LinearRegression
from   sklearn.neural_network  import MLPRegressor
from   sklearn.metrics         import mean_squared_error
from   sklearn.model_selection import cross_val_score,TimeSeriesSplit

次に、データを読み込みます。

#Read in the data
data = pd.read_csv('GBPUSD_Daily_20160103_20240131.csv',sep='\t')

データをクリーンアップします。

#Clean up the data
data.rename(columns={'<OPEN>':'Open','<HIGH>':'High','<LOW>':'Low','<CLOSE>':'Close'},inplace=True)

不要な列は削除します。

#Drop columns we don't need
data = data.drop(['<DATE>','<VOL>','<SPREAD>','<TICKVOL>'],axis=1)
data

データを視覚化します。

#Plot the close price
plt.plot(data["Close"])
plt.xlabel("Time")
plt.ylabel("Close Price")
plt.title("GBPUSD Daily Close")

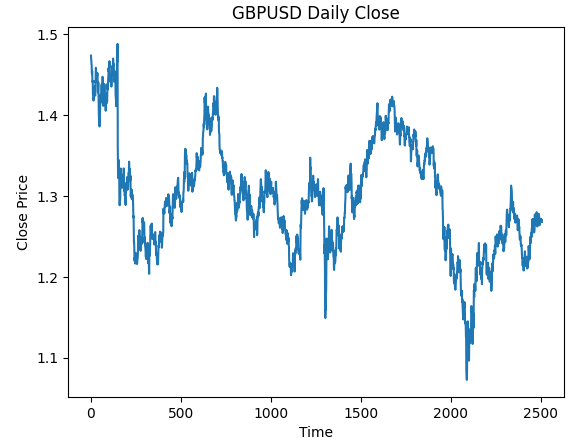
図3：使用するGBPUSD日足OHLCデータ

GBPUSDの日次リターンを予測するモデルを訓練したいのですが、選択しなければならない変数が2つあります。

1. リターンをどの頻度で計算すべきか
2. どこまで将来を予測すべきか

通常、1ステップ先の未来を予測し、リターンは連続する2日間の差として計算します。しかし、これが本当に最適な方法でしょうか。常にこれがベストな選択と言えるでしょうか。この問いに答えるのは私たちではなく、データそのものに委ねます。

リターンの頻度と予測水平線（予測する未来の範囲）のパラメータをグリッドサーチで探してみましょう。まず、両方のパラメータに対して一様な軸を定義する必要があります。

#Define the input range
x_min , x_max = 2,100 #Look ahead
y_min , y_max = 2,100 #Period

次に、x軸とy軸を定義します。

#Sample input range uniformly
x_axis = np.arange(x_min,x_max,4) #Look ahead
y_axis = np.arange(y_min,y_max,4) #Period

メッシュグリッドを作成する必要があります。メッシュグリッドは2つの独立した2次元配列で構成されており、評価したいすべての入力の組み合わせをマッピングするために使用できます。

#Create a meshgrid
x , y = np.meshgrid(x_axis,y_axis)

次の関数は、評価したい新しい設定でモデルの精度をテストする前に、データセットをクリーンアップするために使用されます。

#This function will create and return a clean dataframe according to our specifications
def clean_data(look_ahead,period):
    #Create a copy of the data
    temp = pd.read_csv('GBPUSD_Daily_20160103_20240131.csv',sep='\t')
    #Clean up the data
    temp.rename(columns={'<OPEN>':'Open','<HIGH>':'High','<LOW>':'Low','<CLOSE>':'Close'},inplace=True)
    temp = temp.drop(['<DATE>','<VOL>','<SPREAD>','<TICKVOL>'],axis=1)
    #Define our target
    temp["Target"] = temp["Close"].shift(-look_ahead)
    #Apply the differencing
    temp["Close"] = temp["Close"].diff(period)
    temp["Open"] = temp["Open"].diff(period)
    temp["High"] = temp["High"].diff(period)
    temp["Low"] = temp["Low"].diff(period)
    temp = temp.dropna()
    temp = temp.reset_index(drop=True)
    return(temp)

次の関数は、渡した設定のもとでモデルを交差検証し、その交差検証の誤差を返します。

#Evaluate the objective function
def evaluate(look_ahead,period):
    #Define the model
    model = LinearRegression()
    #Define our time series split
    tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)
    temp = clean_data(look_ahead,period)
    score = np.mean(cross_val_score(model,temp.loc[:,["Open","High","Low","Close"]],temp["Target"],cv=tscv))
    return(score)

最後に、メッシュグリッドと同じ形状の配列に結果を記録する関数が必要です。

#Define the objective
def objective(x,y):
    #Define the output matrix
    results = np.zeros([x.shape[0],y.shape[0]])
    #Fill in the output matrix
    for i in np.arange(0,x.shape[0]):
        #Select the rows
        look_ahead = x[i]
        period     = y[i]
        for j in np.arange(0,y.shape[0]):
            results[i,j] = evaluate(look_ahead[j],period[j])
    return(results)

ここまでで、リターンを計算する間隔や、予測したい未来の距離を変更することで、モデルの誤差レベルがどのように変化するかを確認するために必要な関数を実装しました。より複雑なディープニューラルネットワークを扱う前に、まず単純なモデルがこれらのパラメータを変更した際にどのような挙動を示すかを観察してみましょう。

linear_reg_res = objective(x,y)
linear_reg_res = np.abs(linear_reg_res)

等高線プロットは、地形上の高度の変化を示すために地理学でよく使用されます。このようなサーフェスプロットを利用すると、単純な線形回帰モデルにおいて誤差が最も少ないパラメータの組み合わせを特定できます。青い領域は誤差が少ない良好な組み合わせを示し、赤い領域は不満足な組み合わせを表しています。等高線プロット内の最も濃い青色の領域にある白い点は、線形回帰モデルにおける最適な予測設定を示しています。

以下のプロットから明らかなように、私たちの単純な線形AIモデルは、リターン期間を1とし、1ステップ先の未来を予測する古典的な方法を用いていた市場のトレーダーを簡単に上回る成果を挙げたことでしょう。

plt.contourf(x,y,linear_reg_res,100,cmap="jet")
plt.plot(x_axis[linear_reg_res.min(axis=0).argmin()],y_axis[linear_reg_res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Linear Regression Accuracy Forecasting GBPUSD Daily Close")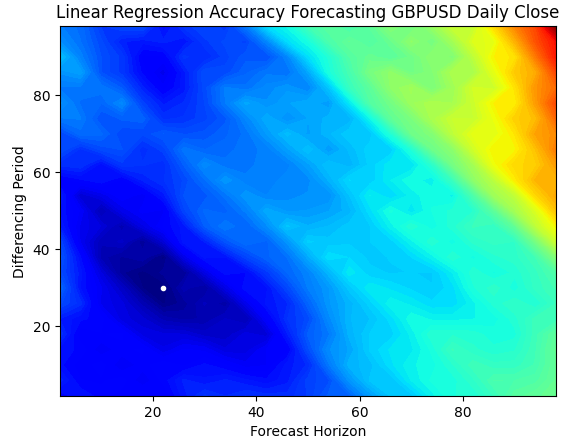

図4：GBPUSD日足の線形回帰の予測精度の等高線プロット

結果を3Dで視覚化すると、サーフェスが生成され、GBPUSD市場とモデルの関係を視覚化することができます。このプロットは、将来の予測範囲を拡大するにつれて誤差率が低下し、最適なレベルに達した後、さらに先を予測しようとすると誤差率が再び上昇し始めることを示しています。しかし、最も重要な点は、私たちの線形モデルにおいて、以下の図5が明確に示しているように、予測水平線とリターン期間の両方において最適なモデル入力が20から40の範囲内にあるということです。

#Create a surface plot
fig , ax = plt.subplots(subplot_kw={"projection":"3d"})
fig.set_size_inches(8,8)
ax.plot_surface(x,y,linear_reg_res,cmap="jet")

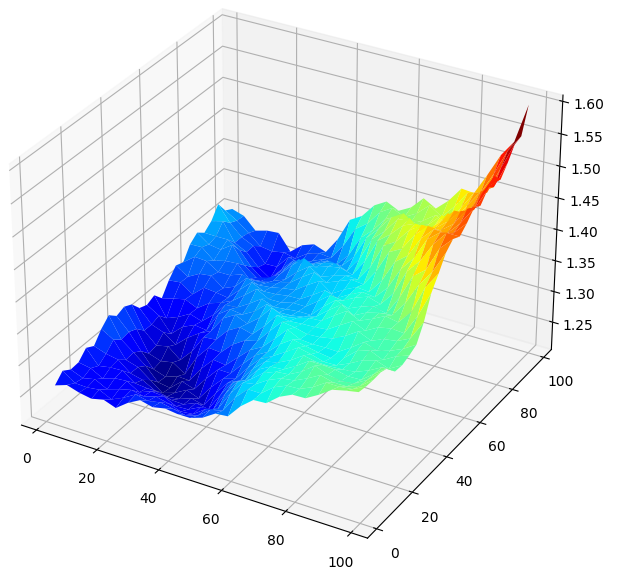
図5：線形モデルによるGBPUSD日次リターンの予測誤差の可視化

等高線プロットと曲面プロットに慣れたところで、同じパラメータ空間を探索するためにディープニューラルネットワークを使用した場合のパフォーマンスを観察してみましょう。

res = objective(x,y)
res = np.abs(res)

ニューラルネットワークのサーフェスプロットは、視覚化が非常に複雑で、直感的に理解するのが難しくなります。青い領域は誤差レベルが低い組み合わせを示しており、望ましい領域です。しかし、興味深いことに、最適な組み合わせが並ぶ途中に、突然赤い領域が現れる様子が見られます。これは非常に興味深い現象です。

なぜこれほど近い2つの組み合わせが、誤差レベルにおいてこれほど大きな違いを生じるのでしょうか。この理由の一端は、ニューラルネットワークの学習に使用される最適化アルゴリズムの性質にあります。もしこのモデルを再度訓練すれば、最適点が異なるだけでなく、まったく異なる形状のプロットが得られる可能性があります。

plt.contourf(x,y,res,100,cmap="jet")
plt.plot(x_axis[res.min(axis=0).argmin()],y_axis[res.min(axis=1).argmin()],'.',color='white')
plt.ylabel("Differencing Period")
plt.xlabel("Forecast Horizon")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")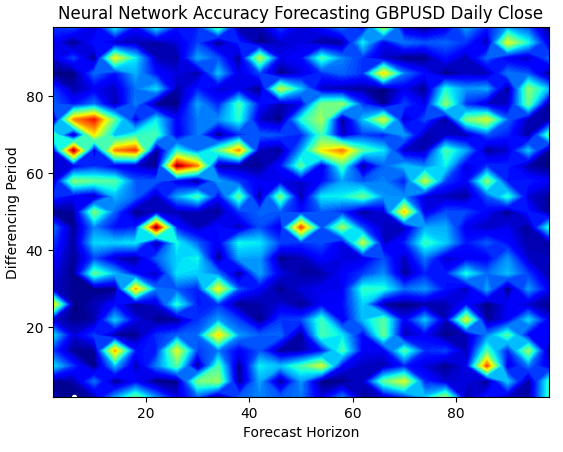

図6：ニューラルネットワークは、私たちが持っている入力に非常に敏感である

モデルのパフォーマンスを3Dで視覚化すると、ニューラルネットワークの不安定性が浮き彫りになります。ニューラルネットワークが本当に有用な関係を効果的に学習していると言い切れるでしょうか。現在の段階では、どちらのモデルが優れているのかを判断する必要があります。伝統的な視点でこの問題に取り組むと、単純な線形モデルを選ぶことになりそうです。なぜなら、線形モデルはより滑らかな誤差プロットを生成し、それがモデルの熟練度を示している可能性があるからです。一方、ニューラルネットワークの変動する誤差率は、データへの過剰適合を示唆していると解釈されるかもしれません。

しかし、これは古典的な機械学習アプローチに基づく見解です。一方で、現代的な視点では、ニューラルネットワークの誤差プロットは、モデルがまだ真に収束していないことを示していると考えます。過剰適合ではなく、学習が進行中である可能性が高いという解釈です。つまり、Double Descentの論文が示唆するように、ニューラルネットワークを現段階で他のモデルと比較するのは時期尚早であると言えます。とはいえ、著名な研究論文の信頼性に盲目的に依存するのではなく、自分たちでこの理論を独自に検証してみることが重要です。

#Create a surface plot
fig , ax = plt.subplots(subplot_kw={"projection":"3d"})
fig.set_size_inches(8,8)
ax.plot_surface(x,y,res,cmap="jet")

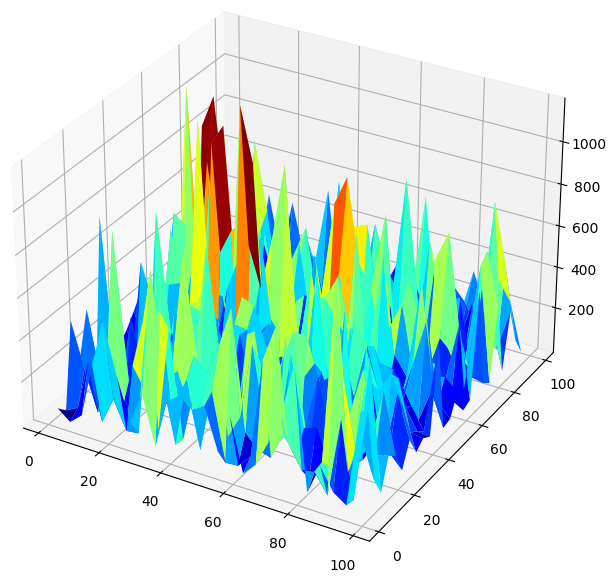
図7：GBPUSDの日次リターンを予測したニューラルネットワークの誤差レベル

二重降下の確認

まず、リターンを計算するために見つけた最適なパラメータを適用し、どのくらい先の未来を予測すべきかを考えます。

#The best settings we have found so far
look_ahead = x_axis[res.min(axis=0).argmin()]
difference_period = y_axis[res.min(axis=1).argmin()]
data["Target"] = data["Close"].shift(-look_ahead)
#Apply the differencing
data["Close"] = data["Close"].diff(difference_period)
data["Open"] = data["Open"].diff(difference_period)
data["High"] = data["High"].diff(difference_period)
data["Low"] = data["Low"].diff(difference_period)
data.dropna(inplace=True)
data.reset_index(drop=True,inplace=True)
data

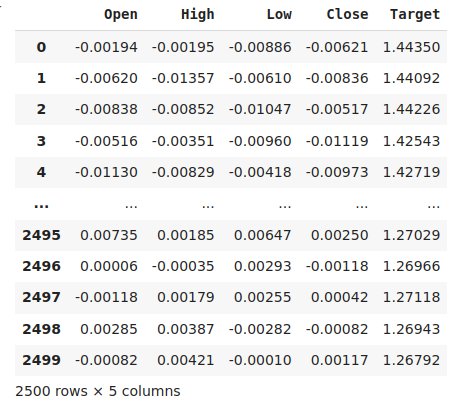
図8：現在のデータ

必要なライブラリをインポートします。

from sklearn.model_selection import train_test_split,TimeSeriesSplit
from sklearn.metrics         import mean_squared_error

最大エポック数を定義します。二重降下はモデルの複雑さ、または最大学習反復回数の関数であることを思い出してください。単純なニューラルネットワークでこれをテストし、最大反復回数を変えてみます。訓練の最大反復回数は2の累乗です。

max_epoch = 50

誤差レベルを保存するためのデータフレームを作成します。

err_rates = pd.DataFrame(columns = np.arange(0,max_epoch),index=["Train","Validation","Test"])

時系列分割オブジェクトを設定する必要があります。

tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

次に、訓練とテストを分割します。

train , test = train_test_split(data,shuffle=False,test_size=0.5)

反復回数の最大値を2の冪乗として増加させながら、モデルを相互検証します。

for j in np.arange(0,max_epoch):
  #Define our model and measure its error
  current_train_err = []
  current_val_err = []
  model = MLPRegressor(hidden_layer_sizes=(6,5),max_iter=(2 ** j))

  for i,(train_index,test_index) in enumerate(tscv.split(train)):
    #Assess the model
    model.fit(train.loc[train_index,["Open","High","Low","Close"]],train.loc[train_index,'Target'])
    current_train_err.append(mean_squared_error(train.loc[train_index,'Target'],model.predict(train.loc[train_index,["Open","High","Low","Close"]])))
    current_val_err.append(mean_squared_error(train.loc[test_index,'Target'],model.predict(train.loc[test_index,["Open","High","Low","Close"]])))

  #Record our observations
  err_rates.loc["Train",j]      = np.mean(current_train_err)
  err_rates.loc["Validation",j] = np.mean(current_val_err)
  err_rates.loc["Test",j]       = mean_squared_error(test['Target'],model.predict(test.loc[:,["Open","High","Low","Close"]]))

最初の6回の反復は、1回から32回の訓練において、モデルの誤差率がどのように変化したかを示しています。以下のプロットからわかるように、テスト誤差は最初に低下した後、上昇に転じ、その後、より低い値（高値圏の中では低い値）を示しました。一方、訓練誤差率と検証誤差率は、最初に上昇してからわずかに低下し、その後再び上昇しました。しかし、32回の反復は訓練プロセス全体のごく一部に過ぎません。続きを観察してみましょう。

plt.plot(err_rates.iloc[0,0:5])
plt.plot(err_rates.iloc[1,0:5])
plt.plot(err_rates.iloc[2,0:5])
plt.legend(["Train Error","Validation Error","Test Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")

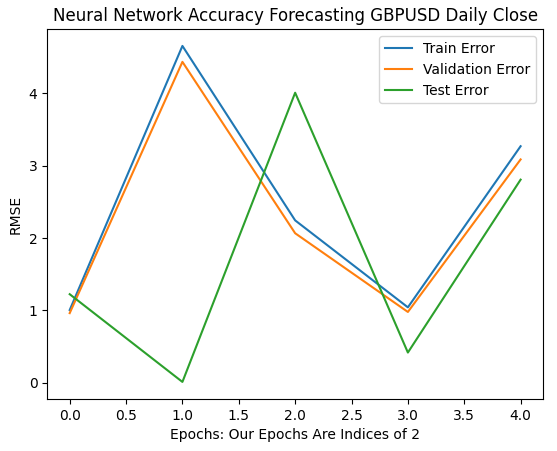
図9：1回から32回まで繰り返したときの検証精度

次に、モデルの誤差率が64回から256回の反復にかけてどのように進化するかを見てみましょう。初期段階では誤差率が一時的に発散しているように見えるものの、最終的には最小値に向かって収束し始めているようです。しかし、参考としている論文によれば、これで訓練が完了したわけではありません。

ここで注目すべき点として、scikit-learnではデフォルト設定でニューラルネットワークが200回の反復しか行わないようにインスタンス化されます。この200回という数字は2の8乗(256)よりやや小さい値です。そのため、早期停止のようなアルゴリズムを使用していた場合、図7で観察した凹凸のある不均一な表面のどこか、局所的な丘や谷に存在する欺瞞的な局所最適に捕らわれてしまう可能性が高かったと言えるでしょう。 

plt.plot(err_rates.iloc[0,0:9])
plt.plot(err_rates.iloc[1,0:9])
plt.plot(err_rates.iloc[2,0:9])
plt.legend(["Train Error","Validation Error","Test Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")

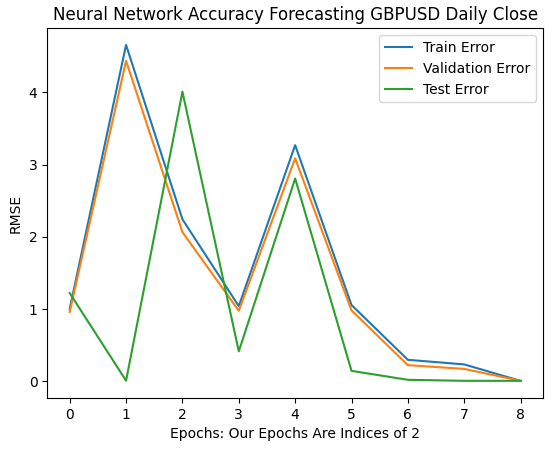
図10：モデルの誤差率は収束し始めている

最適な誤差率は、モデルに10億回以上の反復を行わせた場合に達成されました。正確には2の30乗です。この点は、下の図11において赤い縦線で示されています。通常、私たちはデータのかじょうｔ駅号を懸念して、最適な反復回数のごく一部しか実行しません。その結果、赤い線の左側、すなわち最適に達していない誤差レベルで訓練を終了してしまうことがあります。

plt.plot(err_rates.iloc[0,:])
plt.plot(err_rates.iloc[1,:])
plt.plot(err_rates.iloc[2,:])
plt.axvline(err_rates.loc["Test",:].argmin(),color='red')
plt.legend(["Train Error","Validation Error","Test Error","Double Descent Error"])
plt.ylabel("RMSE")
plt.xlabel("Epochs: Our Epochs Are Indices of 2")
plt.title("Neural Network Accuracy Forecasting GBPUSD Daily Close")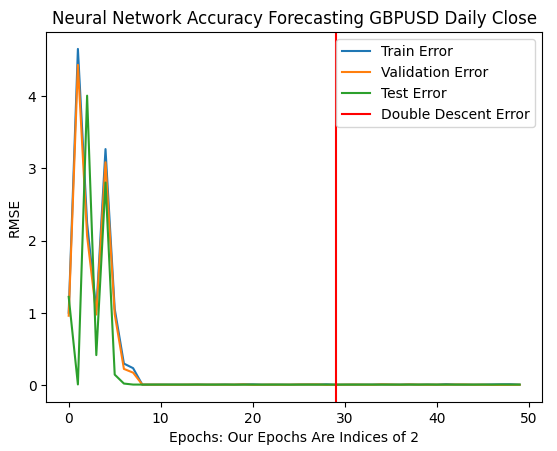

図11：二重降下誤差レベルは赤い縦線で示されており、左側には従来の機械学習の古典的な領域を見ることができる

ニューラルネットワークの最適化

この論文には確かに価値があります。通常であれば、過剰適合のリスクを懸念して、何度も反復を繰り返すことを選択肢に入れることすらしないでしょう。この論文によって、学習データへの過剰適合を恐れることなく、自信を持ってモデルを最適化できます。

from sklearn.model_selection import RandomizedSearchCV

モデルを初期化します。

#Reinitialize the model
model = MLPRegressor(max_iter=(err_rates.loc["Test",:].argmin()))

検索したいパラメータを定義してみましょう。

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "activation" : ["relu","logistic","tanh","identity"],
        "solver":["adam","sgd","lbfgs"],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "learning_rate":['constant','adaptive','invscaling'],
        "learning_rate_init":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "hidden_layer_sizes":[(1,4),(5,8,10),(5,10,20),(10,50,10),(20,5),(1,5),(20,10)],
        "early_stopping":[True,False],
        "warm_start":[True,False],
        "shuffle": [True,False]
        },
        n_iter=2**9,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

最後に、チューナーオブジェクトを適合します。

tuner.fit(train.loc[:,["Open","High","Low","Close"]],train.loc[:,"Target"])

以下が、見つかった最高のパラメータです。

tuner.best_params_

{'warm_start':True,
 'tol':0.1,
 'solver': 'lbfgs',
 'shuffle':False,
 'learning_rate_init':1e-06,
 'learning_rate': 'adaptive',
 'hidden_layer_sizes':(5, 8, 10),
 'early_stopping':False,
 'alpha':1e-05,
 'activation': 'relu'}

ONNXへの変換

モデルを作成したので、次にそれをONNX形式に変換します。ONNX（Open Neural Network Exchange）は、オープンソースのプロトコルであり、ONNX API仕様をサポートする任意のプログラミング言語でAIモデルを作成および展開することを可能にします。また、MQL5を使用すれば、ONNX形式のAIモデルをインポートし、直接取引端末に導入することが可能です。まず、必要なライブラリをインポートします。

import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

次に、今あるすべてのデータに対してモデルを適合させましょう。

model = tuner.best_estimator_.fit(train.loc[:,["Open","High","Low","Close"]],train.loc[:,"Target"])

モデルの入力形状を指定します。

#Define the input shape of 1,4
initial_type = [('float_input', FloatTensorType([1, 4]))]
#Specify the input shape
onnx_model = convert_sklearn(model, initial_types=initial_type)

ONNXモデルを保存します。

#Save the onnx model
onnx.save(onnx_model,"GBPUSD DAILY.onnx")

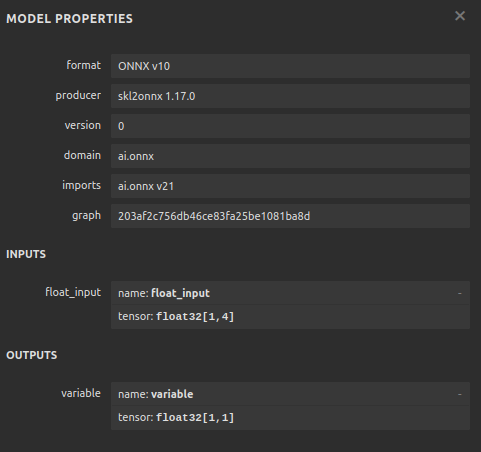
図12：ONNXモデルの入出力パラメータ

 

MQL5での実装

これでMQL5を使った取引戦略の実装を始めることができます。私たちの戦略は日足チャートに基づき、ボリンジャーバンドと移動平均線を組み合わせて、市場のトレンドを判断します。

ボリンジャーバンドは、証券が買われ過ぎや売られ過ぎの状態にあるかを特定するために広く使用されます。一般的に、価格が上限バンドに達すると、その証券は買われ過ぎと見なされます。通常、価格が買われ過ぎると、トレーダーは価格が下落し、平均価格に戻ると予測しますが、私たちはボリンジャーバンドをトレンドフォロー型に利用します。

価格がバンドの中間線を越えると、強い買いシグナルとし、逆に価格が中間線を下回ると、強い売りシグナルと見なします。このようなシンプルな売買ルールではシグナルが多すぎるため、常に理想的な結果が得られるわけではありません。そこで、価格の動きだけでなく、移動平均を使って価格の変動をフィルタリングします。

具体的には、高値と安値のそれぞれに移動平均を適用し、移動平均チャネルを作成します。エントリーシグナルは、両方の移動平均がボリンジャーバンドの中間線を越え、かつAIモデルがその方向に価格が動くと予測した場合に発生します。 

ポジションは、移動平均チャネルがボリンジャーバンドの中間線を越えるか、移動平均チャネルがボリンジャーバンドを抜けた後に再度バンド内に戻るタイミングでクローズされます。

まずは、ONNXモデルをロードすることから始めましょう。

//+------------------------------------------------------------------+
//|                                                    GBPUSD AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/ja/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Load our ONNX file                                               |
//+------------------------------------------------------------------+
#resource  "\\Files\\GBPUSD DAILY.onnx" as const uchar onnx_buffer[];

次に、ポジション管理に役立つTradeライブラリをロードする必要があります。

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include <Trade\Trade.mqh>
CTrade Trade;

また、アプリケーションのさまざまな部分で共有するデータのために、いくつかのグローバル変数も必要です。

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
bool   patience = true;
long   onnx_model;
int    bb_handler,ma_h_handler,ma_l_handler;
double ma_h_buffer[],ma_l_buffer[];
double bb_h_buffer[],bb_m_buffer[],bb_l_buffer[];
int    state;
double bid,ask;
vectorf model_forecast = vectorf::Zeros(1);

私たちのテクニカル指標には、エンドユーザーが市場環境の変化に応じて調整できるようにするための期間パラメータがあります。

//+------------------------------------------------------------------+
//| User Inputs                                                      |
//+------------------------------------------------------------------+
input group "Technical Indicators"
input int bb_period = 60;
input int ma_period = 14;

アプリケーションを最初にロードする際、まずテクニカル指標をロードし、その後にONNXモデルをロードします。プログラムの冒頭で定義したONNXバッファを使用して、そのバッファからONNXモデルを作成します。次に、ONNXモデルが正常であり、入力および出力パラメータが仕様に沿っていることを確認します。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Setup technical indicators
   bb_handler   = iBands(Symbol(),PERIOD_D1,bb_period,0,1,PRICE_CLOSE);
   ma_h_handler = iMA(Symbol(),PERIOD_D1,ma_period,0,MODE_SMA,PRICE_HIGH);
   ma_l_handler = iMA(Symbol(),PERIOD_D1,ma_period,0,MODE_SMA,PRICE_LOW);
//--- Define our ONNX model
   ulong input_shape [] = {1,4};
   ulong output_shape [] = {1,1};
//--- Create the model
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

   if(onnx_model == INVALID_HANDLE)
     {
      Comment("[ERROR] Failed to load AI module correctly");
      return(INIT_FAILED);
     }

//--- Validate I/O
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      Comment("[ERROR] Failed to set input shape correctly: ",GetLastError()," Actual shape: ",OnnxGetInputCount(onnx_model));
      return(INIT_FAILED);
     }

   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      Comment("[ERROR] Failed to load AI module correctly: ",GetLastError()," Actual shape: ",OnnxGetOutputCount(onnx_model));
      return(INIT_FAILED);
     }


//--- Everything was okay
   return(INIT_SUCCEEDED);
  }

取引アプリケーションが使用されなくなった場合、使用しなくなったリソースを解放します。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
   OnnxRelease(onnx_model);
   IndicatorRelease(bb_handler);
   IndicatorRelease(ma_h_handler);
   IndicatorRelease(ma_l_handler);
  }

最後に、新しい価格提示を受けるたびに、グローバル変数を更新します。そこから次のステップに進むかどうかは、ポジションの数によります。ポジションがなければ、エントリーシグナルを探します。ポジションがある場合は、エグジットシグナルを確認します。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update technical data
   update();

   if(PositionsTotal() == 0)
     {
      patience = true;
      check_setup();
     }

   if(PositionsTotal() > 0)
     {
      string direction = model_forecast[0] > iClose(Symbol(),PERIOD_D1,0) ? "UP" : "DOWN";
      Comment("Model Forecast: ",model_forecast[0]," ",direction);
      close_setup();
     }
  }

次の関数は、モデルから予測を取得します。

//+------------------------------------------------------------------+
//| Get a prediction from our model                                  |
//+------------------------------------------------------------------+
void model_predict(void)
  {
   double o,h,l,c;
   vector op,hi,lo,cl;
   op.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_OPEN,0,3);
   hi.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_HIGH,0,3);
   lo.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_LOW,0,3);
   cl.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_CLOSE,0,3);

   o =  op[2]  - op[0];
   h =  hi[2]  - hi[0];
   l =  lo[2]  - lo[0];
   c =  cl[2]  - cl[0];

   vectorf model_inputs = vectorf::Zeros(4);
   model_inputs[0] = o;
   model_inputs[1] = h;
   model_inputs[2] = l;
   model_inputs[3] = c;

   OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_forecast);
  }

ここでは、アプリケーションがどのようにポジションをクローズするかを定義します。patienceというブール値は、ポジションをクローズするタイミングを制御するために使用されます。ポジションが最初に建てられた時点で、移動平均チャネルがボリンジャーバンドをブレイクアウトしていなければ、patienceはtrueに設定されます。この状態は、移動平均チャネルがバンドをブレイクするまで維持されます。その後、patienceフラグがfalseに設定され、チャネルが再びバンド内に戻ると、ポジションがクローズされます。

//+------------------------------------------------------------------+
//| Close our open positions                                         |
//+------------------------------------------------------------------+
void close_setup(void)
  {
   if(patience)
     {
      if(state == 1)
        {
         if(ma_l_buffer[0] > bb_h_buffer[0])
           {
            patience = false;
           }


         if((ma_h_buffer[0] < bb_m_buffer[0]) && (ma_l_buffer[0] < bb_m_buffer[0]))
           {
            Trade.PositionClose(Symbol());
           }
        }

      else
         if(state == -1)
           {
            if(ma_h_buffer[0] < bb_l_buffer[0])
              {
               patience = false;
              }

            if((ma_h_buffer[0] > bb_m_buffer[0]) && (ma_l_buffer[0] > bb_m_buffer[0]))
              {
               Trade.PositionClose(Symbol());
              }
           }
     }

   else
     {
      if((state == -1) && (ma_l_buffer[0] > bb_l_buffer[0]))
        {
         Trade.PositionClose(Symbol());
        }

      if((state == 1) && (ma_h_buffer[0] < bb_h_buffer[0]))
        {
         Trade.PositionClose(Symbol());
        }
     }

  }

このセットアップを有効と見なすためには、移動平均チャネルがミドルバンドの片側に完全に位置し、かつAI予測が価格の動きと一致している必要があります。それ以外の場合は、価格の一時的な変動を追うのではなく、静観することにします。

//+------------------------------------------------------------------+
//| Check for valid trade setups                                     |
//+------------------------------------------------------------------+
void check_setup(void)
  {

   if((ma_h_buffer[0] < bb_m_buffer[0]) && (ma_l_buffer[0] < bb_m_buffer[0]))
     {
      model_predict();
      if((model_forecast[0] < iClose(Symbol(),PERIOD_CURRENT,0)))
        {
         if(ma_h_buffer[0] < bb_l_buffer[0])
            patience = false;

         Trade.Sell(0.3,Symbol(),bid,0,0,"GBPUSD AI");
         state = -1;
        }
     }

   if((ma_h_buffer[0] > bb_m_buffer[0]) && (ma_l_buffer[0] > bb_m_buffer[0]))
     {
      model_predict();
      if(model_forecast[0] > iClose(Symbol(),PERIOD_CURRENT,0))
        {
         if(ma_l_buffer[0] > bb_h_buffer[0])
            patience = false;

         Trade.Buy(0.3,Symbol(),ask,0,0,"GBPUSD AI");
         state = 1;
        }
     }
  }

最後に、グローバル変数の更新を担当する関数が必要です。

//+------------------------------------------------------------------+
//| Update our market data                                           |
//+------------------------------------------------------------------+
void update(void)
  {
   CopyBuffer(bb_handler,0,0,1,bb_m_buffer);
   CopyBuffer(bb_handler,1,0,1,bb_h_buffer);
   CopyBuffer(bb_handler,2,0,1,bb_l_buffer);
   CopyBuffer(ma_h_handler,0,0,1,ma_h_buffer);
   CopyBuffer(ma_l_handler,0,0,1,ma_l_buffer);
  }
//+------------------------------------------------------------------+

これで取引戦略をバックテストできます。ストラテジーテスターを使用し、およそ3年間のGBPUSD日足市場データを基にアプリケーションを評価しました。なお、AIモデルを構築する際には、2016年から2024年までのデイリー市場データを使用しています。したがって、以下に示すバックテストは、実際にはモデルがすでに見たデータでAI戦略をテストしていることになります。モデルがデータにさらされ、十分に訓練されているにもかかわらず、口座残高は時間の経過とともに非常に不安定であったことに注意してください。

これは、私たちがモデルをうまく訓練したにもかかわらず、AIモデルが人間のように「学んだことを記憶」していないことを示しています。AIモデルは、データに対してうまく一般化できる公式を作ろうとしますが、すでに訓練されたデータに対してもミスを犯す可能性があるのです。

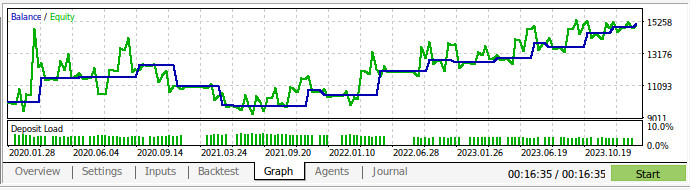
図13：およそ3年間のGBPUSDの日次市場データでアプリケーションをバックテストした

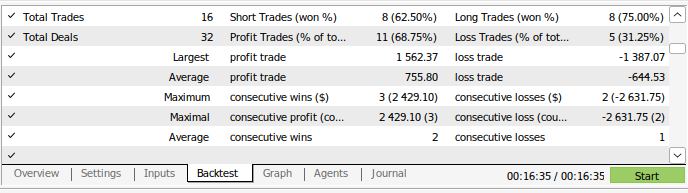
図14：モデルの取引実績詳細

結論

要約すると、「過剰適合」のように見える現象は、状況によっては、より大きな努力を要するというサインに過ぎない可能性があることを示しました。AIモデルを過剰適合させるという古典的な考え方は、一定の範囲で私たちを最適とは言えない誤差レベルに閉じ込めてきました。しかし、この記事を読んでいただければ、モデルをより有効に活用できるようになると確信しています。さらに、モデルの隠れ層を増やしたり、単層でモデルを訓練し、層の幅を広げるという選択肢もあったことを思い出してください。しかし、その場合、巨大なモデルを訓練するためにはまったく異なるアプローチが必要であり、並列コンピューティングのスキルが求められます。

この記事では、計算コストが低いアプローチとして、一定サイズの基本的なモデルを訓練し、日次データを活用する方法を提案しました。しかし、結果がより決定的で堅牢であるためには、訓練セットを半分のサイズに縮小し、モデルを2016年から2020年までのデータで訓練し、2020年から2024年までのデータには訓練中に触れさせないようにする方が良いかもしれません。しかし、結果がより決定的で堅牢であるためには、訓練セットを半分のサイズに縮小し、モデルを2016年から2020年までのデータで訓練し、2020年から2024年までのデータには訓練中に触れさせないようにする方が良いかもしれません。