Expert Advisor Auto-otimizável com MQL5 e Python (Parte IV): Empilhamento de Modelos

Nesta série de artigos, vamos discutir diferentes maneiras de construir aplicações de trading capazes de se ajustar dinamicamente às condições de mercado em evolução. Existem potencialmente infinitas maneiras de abordar este problema, mas é improvável que todas as soluções possíveis sejam válidas. Portanto, nosso objetivo hoje é demonstrar e analisar empiricamente os méritos e limitações de diferentes soluções possíveis, para ajudá-lo a melhorar suas estratégias de trading.

Visão Geral da Estratégia de Trading

Vamos direcionar nossa atenção para a previsão do par de moedas NZDJPY. Queremos aprender, de forma algorítmica, uma estratégia de trading a partir dos dados que coletaremos sobre o símbolo em nosso Terminal MetaTrader 5. Como seres humanos, podemos ser naturalmente tendenciosos em relação a estratégias de trading alinhadas com nossas próprias crenças e interesses. Modelos de machine learning também são tendenciosos. O viés de um modelo de machine learning é o grau em que as suposições feitas pelo modelo são violadas. Nossa estratégia de trading irá se basear em um conjunto de 2 modelos de IA. O primeiro modelo será treinado para prever o preço de fechamento futuro do par NZDJPY, 20 minutos adiante. O segundo modelo será treinado para prever o erro da previsão feita pelo primeiro modelo. Esta técnica é conhecida como stacking (empilhamento). Nossa esperança é que, ao empilhar 2 modelos, possamos superar nosso viés humano e, quem sabe, isso seja suficiente para alcançar níveis mais altos de desempenho.

Visão Geral da Metodologia

Buscamos aproximadamente 9.000 linhas de dados de mercado M1 do par NZDJPY a partir do nosso Terminal MetaTrader 5, usando um script MQL5 personalizado. Criamos gráficos de dispersão 2D e 3D dos dados de mercado. No entanto, não conseguimos identificar nenhum relacionamento perceptível nos dados. Também realizamos uma decomposição de séries temporais no conjunto de dados, e conseguimos identificar uma clara tendência de baixa e a presença de fortes efeitos sazonais nos dados.

Nossos dados foram então divididos em conjuntos de treinamento e teste. Um conjunto de 15 modelos diferentes foi ajustado e avaliado no conjunto de treinamento. O Regressor Stochastic Gradient Descent (SGD) foi o modelo de melhor desempenho do grupo

Posteriormente, ao analisarmos nossas métricas de importância das variáveis, descobrimos que o preço máximo (High) parecia ser o preditor mais informativo que tínhamos para prever o preço de fechamento futuro do par NZDJPY. O preço máximo obteve a melhor pontuação de Informação Mútua (MI). Além disso, também empregamos a implementação do scikit-learn do algoritmo Recursive Feature Elimination (RFE). Todos os preditores que possuímos foram considerados importantes pelo algoritmo RFE. No entanto, como veremos na discussão, só porque existe uma relação, não garante que conseguiremos capturá-la e modelá-la com sucesso.

Após identificar nosso melhor modelo, procedemos para ajustar os parâmetros do modelo. Normalmente, em nossas discussões, após o ajuste de parâmetros, seguimos para testar o overfitting, comparando o desempenho do nosso modelo customizado com o desempenho do modelo padrão. No entanto, existem muitas maneiras diferentes de testar o overfitting. Hoje, escolhemos testar o overfitting analisando os resíduos do nosso modelo. Observamos altos níveis de correlação entre os resíduos do modelo e seus atrasos (lags). Normalmente, os resíduos de um modelo que aprendeu suficientemente não devem apresentar correlação. Portanto, isso sugeriu para nós que o modelo de melhor desempenho pode não ter aprendido de forma eficaz, ou que existem outros dados que podem nos ajudar a explicar nosso alvo, e não incluímos esses dados.

Depois, registramos os resíduos do nosso modelo nos conjuntos de treinamento e teste. Não ajustamos o modelo no conjunto de teste neste ponto. Em seguida, fizemos validação cruzada dos nossos 15 modelos nos resíduos de treinamento do nosso Regressor SGD. Nosso melhor modelo foi a Regressão Lasso, porém selecionamos o terceiro melhor modelo, uma Rede Neural Profunda (DNN), como nossa solução candidata. Nossa justificativa foi que a flexibilidade da rede neural profunda nos daria uma oportunidade de ajustá-la melhor aos dados, mais do que poderíamos ajustar a Lasso devido ao número limitado de parâmetros de ajuste.

Ajustamos nosso Regressor DNN para prever os resíduos do Regressor SGD em um processo de 2 etapas que resultou em 2 modelos únicos. Primeiro, realizamos 100 iterações de uma busca aleatória sobre os parâmetros do nosso Regressor DNN, criando assim o primeiro modelo. Os melhores parâmetros contínuos identificados foram usados como ponto de partida para uma tentativa de otimização global irrestrita usando o algoritmo L-BFGS-B de memória limitada, e assim obtivemos o segundo modelo. Ambos os modelos superaram o Regressor DNN padrão em dados de validação não vistos. Além disso, nosso último modelo foi o de melhor desempenho, ou seja, não perdemos tempo ao dar esses passos extras de forma dupla.

Por fim, exportamos ambos os modelos para o formato ONNX e passamos a construir um Expert Advisor com IA que aprendeu a corrigir seus próprios erros.

Buscando os Dados que Precisamos

Vamos começar buscando os dados que precisamos do nosso Terminal MetaTrader 5. O script abaixo irá buscar tantas barras de dados históricos de preço quanto especificarmos no Terminal, antes de gravar esses dados em formato CSV e armazená-los para nós na pasta “Files”.

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| Script Inputs                                                    |
//+------------------------------------------------------------------+
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int rsi_handler;
double rsi_buffer[];

//+------------------------------------------------------------------+
//| On start function                                                |
//+------------------------------------------------------------------+
void OnStart()
  {

//--- Load indicator
   rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,20,PRICE_CLOSE);
   CopyBuffer(rsi_handler,0,0,size,rsi_buffer);
   ArraySetAsSeries(rsi_buffer,true);

//--- File name
   string file_name = "Market Data " + Symbol() + ".csv";

//--- Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i)
                  );
        }
     }
//--- Close the file
   FileClose(file_handle);

  }
//+------------------------------------------------------------------+

Limpando os Dados

Vamos começar formatando nossos dados. Primeiro, carregue as bibliotecas necessárias.

#Import the libraries we need
import pandas as pd
import numpy as np

Agora, leia os dados de mercado.

#Read in the market data
nzd_jpy = pd.read_csv('Market Data NZDJPY.csv')

Os dados estão na ordem errada, vamos reorganizá-los para que fiquem do mais antigo para o mais recente, sendo a data mais próxima do presente por último.

#Format the data
nzd_jpy = nzd_jpy[::-1]
nzd_jpy.reset_index(inplace=True, drop=True)

Defina o alvo.

#Labelling the data
nzd_jpy['Target'] = nzd_jpy['Close'].shift(-20)
nzd_jpy.dropna(inplace=True)

Também vamos adicionar alvos binários para fins de plotagem.

#Add binary target for plotting
nzd_jpy['Binary Target'] = np.nan
nzd_jpy.loc[nzd_jpy['Close'] > nzd_jpy['Target'],'Binary Target'] = 1
nzd_jpy.loc[nzd_jpy['Close'] <= nzd_jpy['Target'],'Binary Target'] = 0

Vamos inspecionar os dados.

#Current state of our dataframe
nzd_jpy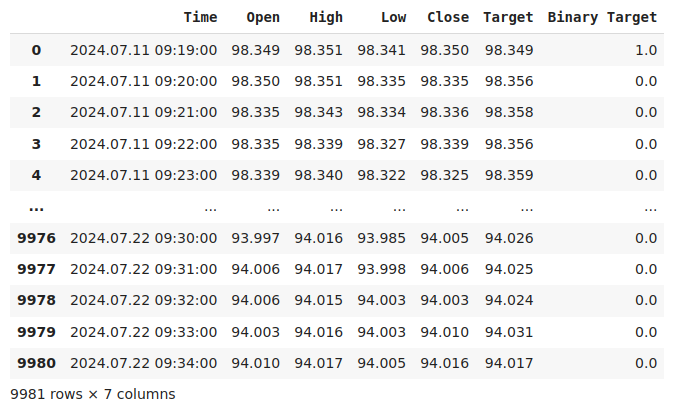

Fig 1: Nosso DataFrame atual

Análise Exploratória dos Dados

Vamos criar gráficos de dispersão para verificar se conseguimos observar algum relacionamento. Infelizmente, nossos dados parecem distribuídos aleatoriamente, sem separações claras entre movimentos de alta e baixa do mercado.

#Lets perform scatter plots
sns.scatterplot(data=nzd_jpy,x=nzd_jpy['Open'], y=nzd_jpy['Close'],hue='Binary Target')

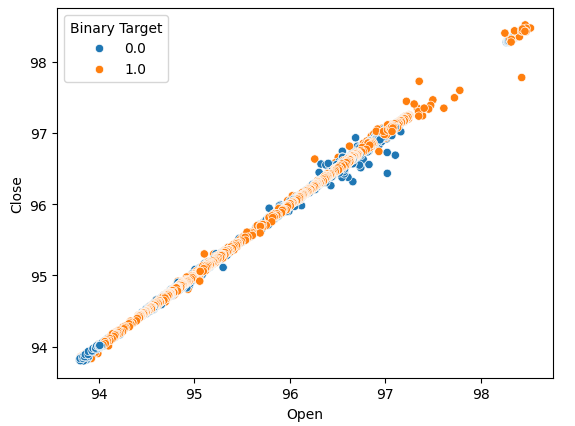
Fig 2: Um gráfico de dispersão do preço de Abertura e Fechamento

Pensamos em criar box plots para resumir todas as situações em que o preço subiu ou caiu. Acreditávamos que poderiam existir diferenças entre a distribuição dos dados nesses dois possíveis alvos. Lamentavelmente, nossos box-plots mostram que dificilmente há diferença entre a distribuição dos dados nos dois possíveis desfechos.

#Let's create categorical box plots
sns.catplot(data=nzd_jpy,x='Binary Target',y='Close',kind='box')

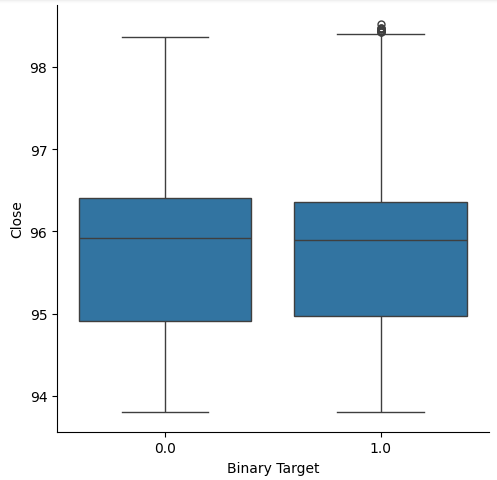
Fig 3: Um box-plot resumindo todos os casos em que o preço caiu (0) ou subiu (1)

Também podemos decompor a série temporal em 3 componentes:

1. Tendências
2. Sazonalidade
   
3. Resíduo
   

 A componente de tendência representa o movimento médio de longo prazo dos preços. A componente sazonal contabiliza padrões cíclicos que se repetem nos dados, enquanto os resíduos são o que não pôde ser explicado pelas duas componentes anteriores. Como estamos usando dados M1 do par NZDJPY, definimos nosso período como 1440, ou seja, o desempenho médio dos preços em um dia completo. É possível observar uma tendência de baixa clara e forte nos dados mesmo antes da decomposição. Porém, ao subtrair a tendência dos dados originais, podemos observar claramente os efeitos sazonais nos dados.

#Time series decomposition
import statsmodels.api as sm
nzd_jpy_decomposition = sm.tsa.seasonal_decompose(nzd_jpy['Close'],period=1440,model='additive')
fig = nzd_jpy_decomposition.plot()

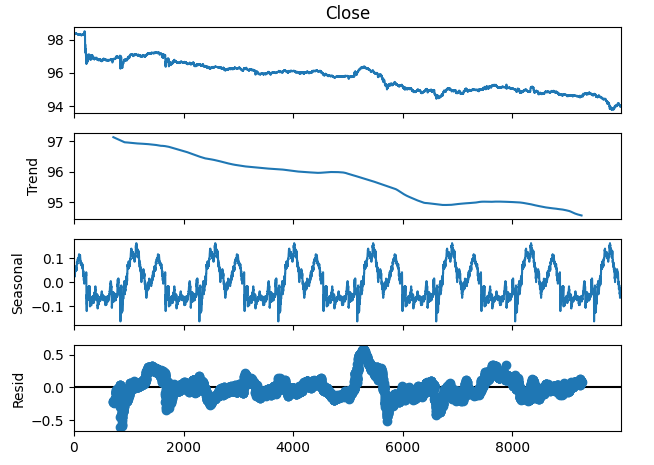
Fig 4: Decomposição de série temporal dos nossos dados

Alguns efeitos podem estar ocultos em dimensões mais altas. Criar gráficos de dispersão 3D pode nos permitir revelar efeitos escondidos além do que conseguimos ver em gráficos 2D. Infelizmente, esse não foi o caso deste conjunto de dados. Nossos dados ainda são bastante difíceis de separar e não apresentam relações perceptíveis.

#Let's also perform 3D plots
#Visualizing our data in 3D

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111,projection='3d')
colors = ['blue' if movement == 0 else 'red' for movement in nzd_jpy.loc[:,"Binary Target"]]
ax.scatter(nzd_jpy.loc[:,"Low"],nzd_jpy.loc[:,"High"],nzd_jpy.loc[:,"Close"],c=colors)

ax.set_xlabel('NZDJPY Low')
ax.set_ylabel('NZDJPY High')
ax.set_zlabel('NZDJPY Close')

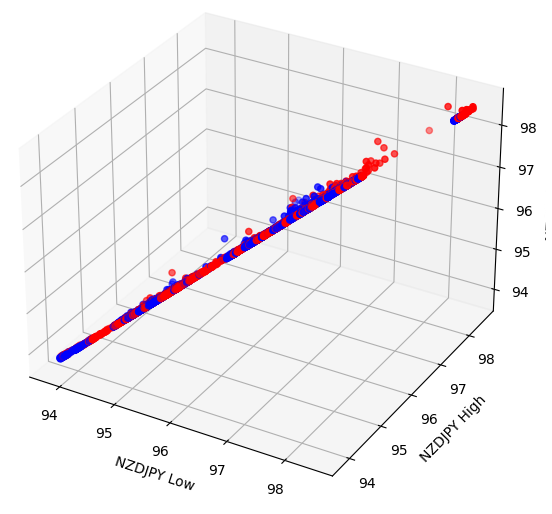
Fig 5: Visualização do nosso gráfico de dispersão 3D

Preparando os Dados para Modelagem

Antes de modelar nossos dados, precisamos primeiro padronizá-los e escalá-los. Carregue as bibliotecas necessárias.

#Let's prepare the data for modelling
from sklearn.preprocessing import RobustScaler

Escalar os dados.

#Scale the data
X = pd.DataFrame(RobustScaler().fit_transform(nzd_jpy.loc[:,['Close']]),columns=['Close'])
residuals_X = pd.DataFrame(RobustScaler().fit_transform(nzd_jpy.loc[:,['Open','High','Low']]),columns=['Open','High','Low'])
y = nzd_jpy.loc[:,'Target']

Seleção de Modelos

Vamos carregar as bibliotecas necessárias para modelar os dados.

#Cross validating the models
from sklearn.model_selection import cross_val_score,train_test_split
from sklearn.linear_model import Lasso,LinearRegression,Ridge,ElasticNet,SGDRegressor,HuberRegressor
from sklearn.ensemble import RandomForestRegressor,GradientBoostingRegressor,AdaBoostRegressor,ExtraTreesRegressor,BaggingRegressor
from sklearn.svm import LinearSVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.neural_network import MLPRegressor

Agora, particione os dados em 2 metades.

#Create train-test splits
train_X,test_X,train_y,test_y = train_test_split(nzd_jpy.loc[:,['Close']],y,test_size=0.5,shuffle=False)
residuals_train_X,residuals_test_X,residuals_train_y,residuals_test_y = train_test_split(nzd_jpy.loc[:,['Open','High','Low']],y,test_size=0.5,shuffle=False)

Armazene os modelos em uma lista e crie um DataFrame para registrar nossos níveis de erro de validação.

#Store the models
models = [
    Lasso(),
    LinearRegression(),
    Ridge(),
    ElasticNet(),
    SGDRegressor(),
    HuberRegressor(),
    RandomForestRegressor(),
    GradientBoostingRegressor(),
    AdaBoostRegressor(),
    ExtraTreesRegressor(),
    BaggingRegressor(),
    LinearSVR(),
    KNeighborsRegressor(),
    DecisionTreeRegressor(),
    MLPRegressor(),
]

#Store the names of the models
model_names = [
    'Lasso',
    'Linear Regression',
    'Ridge',
    'Elastic Net',
    'SGD Regressor',
    'Huber Regressor',
    'Random Forest Regressor',
    'Gradient Boosting Regressor',
    'Ada Boost Regressor',
    'Extra Trees Regressor',
    'Bagging Regressor',
    'Linear SVR',
    'K Neighbors Regressor',
    'Decision Tree Regressor',
    'MLP Regressor',
]

#Create a dataframe to store our cv error
cv_error = pd.DataFrame(columns=model_names,index=np.arange(0,5))

Valide cruzadamente cada modelo.

#Cross validate each model
for model in models:
  cv_score = cross_val_score(model,X,y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
  for i in np.arange(0,5):
    index = models.index(model)
    cv_error.iloc[i,index] = cv_score[i]

Visualizando os resultados.

cv_error

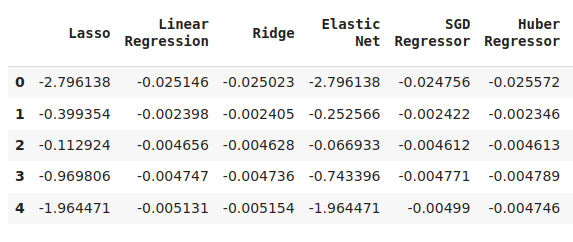
Fig 6: Alguns dos nossos níveis de erro ao prever o preço de fechamento futuro do NZDJPY

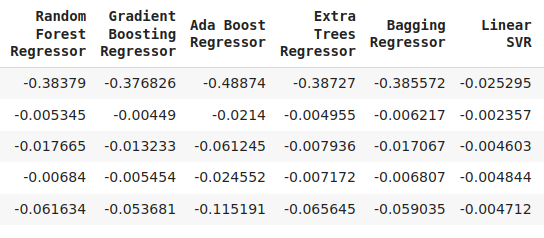
Fig 7: Continuação dos nossos níveis de erro

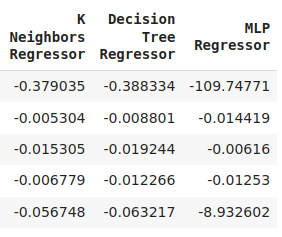
Fig 8: Níveis finais de erro do nosso modelo

Podemos plotar nossos níveis de desempenho em todas as 5 divisões (folds). O baixo desempenho da nossa rede neural foi alarmante ao visualizarmos os dados nesse formato. Provavelmente ela se beneficiaria bastante de um ajuste fino de parâmetros.

cv_error.plot()

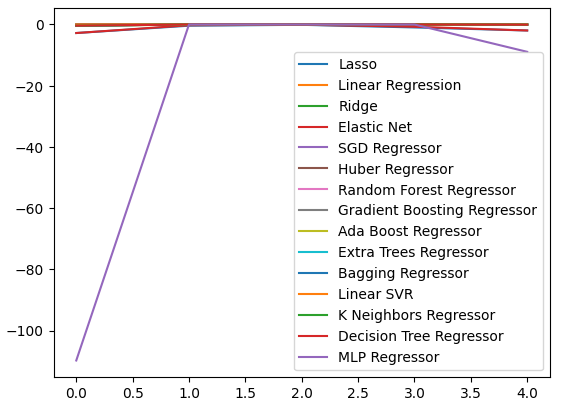
Fig 9: Visualizando nossos níveis de erro

Box-plots nos ajudam a resumir muita informação em um único gráfico. Por exemplo, nos gráficos abaixo, podemos ver claramente o quão mal a DNN se saiu nesta tarefa. É o último modelo à direita, e mostra muito mais variância em seu desempenho do que os outros modelos.

sns.boxplot(cv_error)

Fig 10: Visualizando nossos erros em box-plots

Podemos identificar o melhor modelo como aquele com o menor nível médio de erro.

#Our mean validation error
cv_error.mean()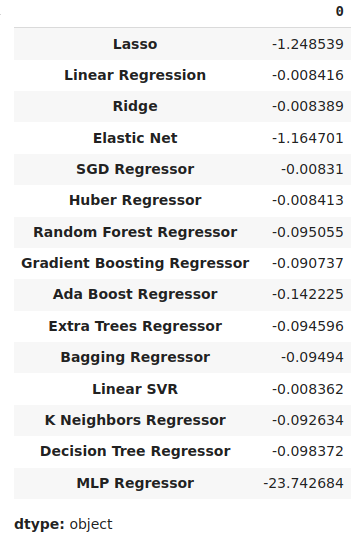

Fig 11: Visualizando nossos níveis médios de erro

Importância das Variáveis

Os algoritmos de importância de variáveis nos ajudam a entender se nosso modelo aprendeu associações significativas, ou se identificou relações que talvez nem conhecêssemos. Primeiro, vamos importar as bibliotecas necessárias.

#Feature importance
from sklearn.feature_selection import mutual_info_regression,RFE

Vamos começar calculando as pontuações de Informação Mútua (MI). MI nos informa sobre o potencial de cada preditor para ajudar a prever o alvo. Por fim, MI é medida em escala logarítmica. Portanto, valores de MI acima de 3 raramente são vistos na prática.

mi_score = pd.DataFrame(mutual_info_regression(X,y),columns=['MI Score'],index=X.columns)

Plotar nossas pontuações de MI mostra claramente que o preço máximo (High) parece ter o maior potencial para prever o preço de fechamento futuro do NZDJPY.

mi_score.plot()

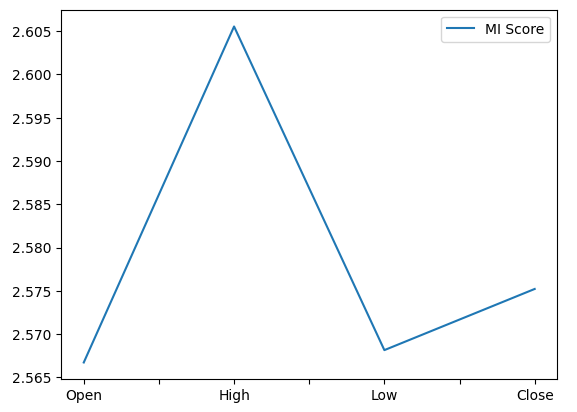
Fig 12: Plotando nossas pontuações de MI

O algoritmo RFE é igualmente simples de usar como qualquer objeto da biblioteca scikit-learn. Basta criar uma instância da classe, ajustar nos dados, e então podemos avaliar os níveis de importância atribuídos a cada preditor. Nosso algoritmo RFE considerou que todos os preditores eram igualmente importantes para prever o preço de fechamento do NZDJPY.

#Select the best features
rfe = RFE(model, n_features_to_select=5, step=1)
rfe = rfe.fit(X, y)
rfe.ranking_

array([1, 1, 1, 1])

Ajuste de Parâmetros

Agora vamos extrair o máximo desempenho do nosso modelo SGD Regressor. Faremos uma busca aleatória por uma amostra do espaço de parâmetros do modelo. Vamos primeiro importar as bibliotecas de que precisamos.

#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV

Crie uma instância do modelo padrão.

#Initialize the model
model = SGDRegressor()

Crie um objeto tuner e especifique os possíveis valores de parâmetros que gostaríamos de amostrar.

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "loss" : ['squared_error', 'huber', 'epsilon_insensitive','squared_epsilon_insensitive'],
        "penalty":['l2','l1', 'elasticnet', None],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001,10,100,1000,10000,100000],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "fit_intercept": [True,False],
        "early_stopping": [True,False],
        "learning_rate":['constant','optimal','adaptive','invscaling'],
        "shuffle": [True,False]
        },
        n_iter=100,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Ajustar (fit) o objeto tuner.

#Fit the tuner
tuner.fit(train_X,train_y)

Os melhores parâmetros que encontramos.

#Our best parameters
tuner.best_params_

{'tol': 0.001,
 'shuffle': False,
 'penalty': 'elasticnet',
 'loss': 'huber',
 'learning_rate': 'adaptive',
 'fit_intercept': True,
 'early_stopping': True,
 'alpha': 1e-05}

Testando Overfitting

Podemos detectar overfitting se observarmos correlação nos resíduos do modelo. Se um modelo aprendeu efetivamente, seus resíduos devem ser ruído branco aleatório, indicando que não há padrão previsível nos erros cometidos. Por outro lado, um modelo que apresenta autocorrelação nos resíduos pode ser motivo de preocupação. Isso pode indicar que a regressão realizada é espúria, ou que escolhemos um modelo inadequado para nossa tarefa. Para começar, precisamos capturar os resíduos do nosso modelo customizado.

#Model validation
model = SGDRegressor(
    tol             = tuner.best_params_['tol'],
    shuffle         = tuner.best_params_['shuffle'],
    penalty         = tuner.best_params_['penalty'],
    loss            = tuner.best_params_['loss'],
    learning_rate   = tuner.best_params_['learning_rate'],
    alpha           = tuner.best_params_['alpha'],
    fit_intercept   = tuner.best_params_['fit_intercept'],
    early_stopping  = tuner.best_params_['early_stopping']
)
model.fit(train_X,train_y)
residuals = test_y - model.predict(test_X)

Podemos visualizar os resíduos do nosso modelo em um gráfico. Infelizmente, podemos ver claramente que existe autocorrelação nos resíduos do modelo. Ou seja, sempre que os resíduos caem, tendem a continuar caindo, e quando sobem, tendem a continuar subindo. Isso significa que os valores futuros dos resíduos podem ter relação com seus valores anteriores, um sinal clássico de que nosso modelo pode não ter aprendido de forma eficaz, mesmo após o ajuste de parâmetros!

#Plot the residuals
residuals.plot()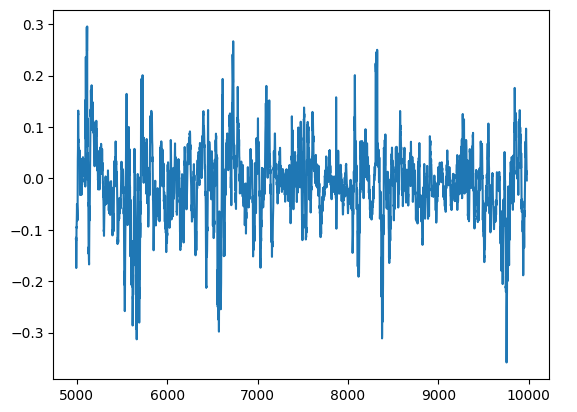

Fig 13: Resíduos do nosso modelo

Existem testes mais robustos para autocorrelação; por exemplo, podemos criar um gráfico de autocorrelação (ACF). O gráfico ACF terá picos em cada valor de lag possível. A altura de cada pico representa os níveis de correlação dos dados da série temporal com seu valor defasado. Há também uma estrutura semelhante a um cone azul ao fundo do gráfico; esse cone azul representa nossos intervalos de confiança. Qualquer nível de correlação além do intervalo de confiança é considerado estatisticamente significativo.

#The residuals appear to have autocorrelation
from statsmodels.graphics.tsaplots import plot_acf
fig = plot_acf(residuals)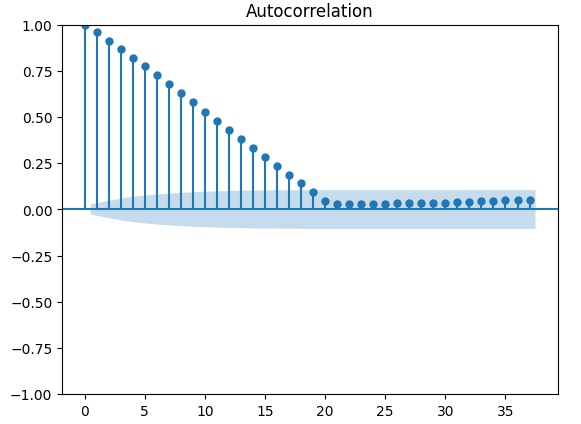

Fig 14: A autocorrelação dos resíduos do nosso modelo

Isso não é um bom sinal. Esperamos conseguir amenizar isso treinando nossa DNN para corrigir nosso primeiro modelo. Vamos registrar os erros do nosso Regressor SGD nos dados de treino e depois nos dados de teste. Note que não ajustaremos o modelo nos dados de teste neste ponto, apenas iremos medir seus níveis de erro.

#Prepare the residuals for our second model
model = SGDRegressor(tol= 0.001,
 shuffle=False,
 penalty= 'elasticnet',
 loss= 'huber',
 learning_rate='adaptive',
 fit_intercept= True,
 early_stopping= True,
 alpha= 1e-05)

#Store the model residuals
model.fit(train_X,train_y)
residuals_train_y = train_y - model.predict(train_X)
residuals_test_y = test_y - model.predict(test_X)

Agora vamos validar cruzadamente nossos modelos na previsão dos níveis de erro do Regressor SGD.

#Cross validate each model
for model in models:
  cv_score = cross_val_score(model,residuals_train_X,residuals_train_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
  for i in np.arange(0,5):
    index = models.index(model)
    cv_error.iloc[i,index] = cv_score[i]

Vamos visualizar o erro de validação.

#Cross validaton error levels
cv_error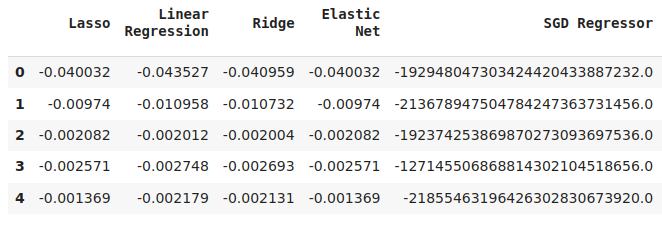

Fig 15: Alguns níveis de erro de validação dos modelos ao prever os níveis de erro do nosso primeiro modelo

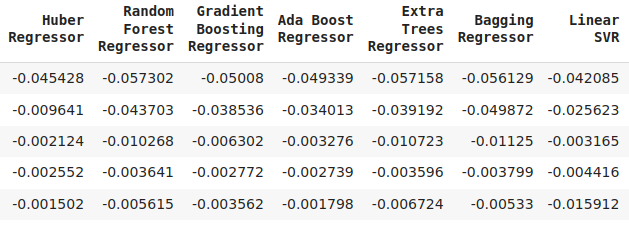
Fig 16: Continuação dos nossos níveis de erro de validação

Podemos visualizar nossos níveis médios de erro em ordem decrescente para rapidamente identificar nosso modelo de melhor desempenho.

#Store the model's performance
cv_error.mean().sort_values(ascending=False)

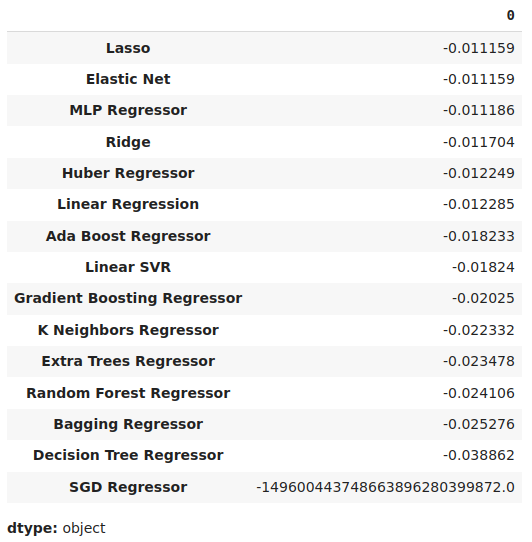
Fig 17: Nossos níveis médios de erro de validação mostram claramente que a Lasso é o melhor modelo que temos

Nossos box-plots mostram o quão mal o Regressor SGD se saiu ao tentar prever seus próprios níveis de erro.

sns.boxplot(cv_error)

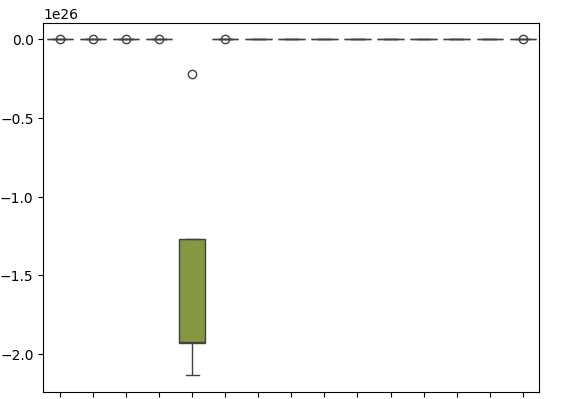
Fig 18: Box-plots do erro de validação ao prever os resíduos do nosso modelo

Também podemos criar gráficos de linha para visualizar nossos dados.

cv_error.plot()

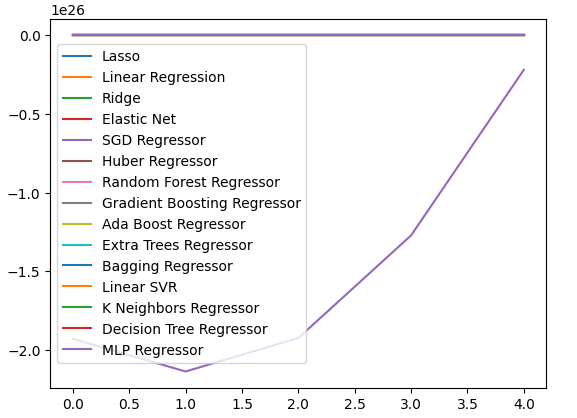
Fig 19: Visualizando nossos níveis de erro em gráficos de linha

Ajuste de Parâmetros da Nossa Rede Neural Profunda

Agora vamos preparar o ajuste dos parâmetros do nosso Regressor DNN. Primeiro, definiremos o objeto tuner e uma amostra do espaço de parâmetros que desejamos explorar.

#Let's tune the model
#Reinitialize the model

model = MLPRegressor()

#Define the tuner

tuner = RandomizedSearchCV(
        model,
        {
                "activation":["relu","tanh","logistic","identity"],
                "solver":["adam","sgd","lbfgs"],
                "alpha":[0.1,0.01,0.001,0.00001,0.000001],
                "learning_rate": ["constant","invscaling","adaptive"],
                "learning_rate_init":[0.1,0.01,0.001,0.0001,0.000001,0.0000001],
                "power_t":[0.1,0.5,0.9,0.01,0.001,0.0001],
                "shuffle":[True,False],
                "tol":[0.1,0.01,0.001,0.0001,0.00001],
                "hidden_layer_sizes":[(10,20),(100,200),(30,200,40),(5,20,6)],
                "max_iter":[10,50,100,200,300],
                "early_stopping":[True,False]
        },
        n_iter=100,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Agora vamos ajustar o objeto tuner.

#Fit the tuner
tuner.fit(residuals_train_X,residuals_train_y)

Por fim, podemos ver os melhores parâmetros que encontramos.

#The best parameters we found
tuner.best_params_

{'tol': 0.0001,
 'solver': 'lbfgs',
 'shuffle': False,
 'power_t': 0.5,
 'max_iter': 300,
 'learning_rate_init': 0.01,
 'learning_rate': 'constant',
 'hidden_layer_sizes': (30, 200, 40),
 'early_stopping': False,
 'alpha': 1e-05,
 'activation': 'identity'}

Ajuste de Parâmetros Mais Profundo

Agora vamos testar se conseguimos encontrar parâmetros ainda melhores. Como não sabemos necessariamente onde estão os melhores valores de entrada, vamos tentar realizar uma otimização global irrestrita usando o algoritmo L-BFGS-B da biblioteca SciPy. O algoritmo L-BFGS-B pode ser utilizado de forma eficaz em problemas de otimização global. O solucionador numérico é implementado em Fortran, e a biblioteca SciPy oferece um wrapper leve para interagir facilmente com a rotina. Vamos começar importando as bibliotecas necessárias.

Fig 20: Os desenvolvedores do algoritmo BFGS original, da esquerda para a direita: Broyden, Fletcher, Goldfarb e Shanno

#Deeper optimization
from scipy.optimize import minimize

Agora vamos definir a função objetivo a ser minimizada: queremos minimizar o erro de treinamento do nosso Regressor DNN. Fixaremos todos os outros parâmetros de entrada do modelo, pois os minimizadores do SciPy só lidam com problemas de otimização contínua.

#Define the objective function
def objective(x):
    #Create a dataframe to store our accuracy
    cv_error = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])
    #The parameter x represents a new value for our neural network's settings
    #In order to find optimal settings, we will perform 10 fold cross validation using the new setting
    #And return the average RMSE from all 10 tests
    #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization
    MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=x[0],tol=x[1])
    model = MLPRegressor(
    tol                 = x[0],
    solver              = tuner.best_params_['solver'],
    power_t             = x[1],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = x[2],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = x[3],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
    )
    #Cross validate the model
    cv_score = cross_val_score(model,residuals_train_X,residuals_train_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
    for i in np.arange(0,5):
      cv_error.iloc[i,0] = cv_score[i]
    #Return the Mean CV RMSE
    return(cv_error.iloc[:,0].mean())

Vamos definir o ponto inicial do nosso procedimento de otimização usando os melhores parâmetros que encontramos na busca aleatória. Também passaremos restrições para nosso procedimento de otimização: vamos forçar todos os valores a serem positivos e, além disso, permitiremos todos os valores no intervalo de 10 elevado a -100 até 10 elevado a 100. Esse é um domínio muito amplo e, esperamos, conterá os parâmetros ideais que estamos procurando.

#Define the starting point
pt = [tuner.best_params_['tol'],tuner.best_params_['power_t'],tuner.best_params_['learning_rate_init'],tuner.best_params_['alpha']]
bnds = ((10.0 ** -100,10.0 ** 100),
        (10.0 ** -100,10.0 ** 100),
        (10.0 ** -100,10.0 ** 100),
        (10.0 ** -100,10.0 ** 100))

Buscando os melhores parâmetros.

#Searching deeper for better parameters
result = minimize(objective,pt,method="L-BFGS-B",bounds=bnds)

Nossos resultados de otimização.

Resultados

message: CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
  success: True
   status: 0
      fun: -0.01143352283130129
        x: [ 1.000e-04  5.000e-01  1.000e-02  1.000e-05]
      nit: 2
      jac: [-1.388e+04 -4.657e+04  5.625e+04 -1.033e+04]
     nfev: 120
     njev: 24
 hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>

Testando Overfitting

Agora vamos testar o overfitting. Desta vez, vamos comparar nossos 2 modelos com o desempenho do DNN Regressor padrão. Vamos instanciar cada DNN Regressor que desejamos testar.

#Model validation
default_model = MLPRegressor()

customized_model = MLPRegressor(
    tol                 = tuner.best_params_['tol'],
    solver              = tuner.best_params_['solver'],
    power_t             = tuner.best_params_['power_t'],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = tuner.best_params_['learning_rate_init'],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = tuner.best_params_['alpha'],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
)

lbfgs_customized_model = MLPRegressor(
    tol                 = result.x[0],
    solver              = tuner.best_params_['solver'],
    power_t             = result.x[1],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = result.x[2],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = result.x[3],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
)

Agora vamos criar uma lista de modelos e também criar um DataFrame para armazenar nossos níveis de erro de validação.

models = [default_model,customized_model,lbfgs_customized_model]
cv_error = pd.DataFrame(index=np.arange(0,5),columns=['Default NN','Random Search NN','L-BFGS-B NN'])

Validando cruzadamente cada modelo.

#Cross validate the model
for model in models:
  model.fit(residuals_train_X,residuals_train_y)
  cv_score = cross_val_score(model,residuals_test_X,residuals_test_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
  for i in np.arange(0,5):
    index = models.index(model)
    cv_error.iloc[i,index] = cv_score[i]

Nosso erro de validação cruzada.

cv_error

NN padrão	Random Search NN	L-BFGS-B NN
-0.007735	-0.007708	-0.007692
-0.00635	-0.006344	-0.006329
-0.003307	-0.003265	-0.00328
0.005225	-0.004803	-0.004761
-0.004469	-0.004447	-0.004492

Agora vamos analisar nossos níveis médios de erro.

cv_error.mean().sort_values(ascending=False)

Modelo	Erro de Validação
L-BFGS-B NN	-0.005311
Random Search NN	-0.005313
NN padrão	-0.005417

Como podemos ver, todos os nossos modelos apresentaram desempenho dentro da mesma faixa. No entanto, nossos modelos customizados claramente apresentaram níveis médios de erro mais baixos. Infelizmente, a variância exibida pelos nossos modelos é praticamente a mesma em todos, como mostrado pelos box-plots. Os níveis de variância nos ajudam a determinar o nível de habilidade do modelo.

sns.boxplot(cv_error)

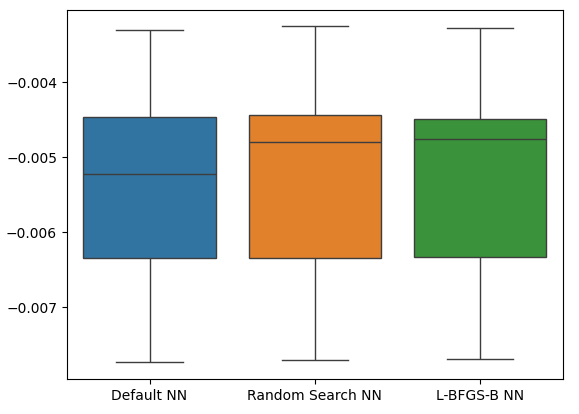
Fig 21: Níveis de erro de validação nos dados de validação

Agora vamos verificar se nossa abordagem de ensemble é melhor do que usar apenas um modelo para prever os preços. Primeiro, vamos preparar os modelos necessários.

#Now that we have come this far, let's see if our ensemble approach is worth the trouble
baseline = LinearRegression()
default_nn = MLPRegressor()

#The SGD Regressor will predict the future price
sgd_regressor = SGDRegressor(tol= 0.001,
 shuffle=False,
 penalty= 'elasticnet',
 loss= 'huber',
 learning_rate='adaptive',
 fit_intercept= True,
 early_stopping= True,
 alpha= 1e-05)

#The deep neural network will predict the error in the SGDRegressor's prediction
lbfgs_customized_model = MLPRegressor(
    tol                 = result.x[0],
    solver              = tuner.best_params_['solver'],
    power_t             = result.x[1],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = result.x[2],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = result.x[3],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
)

Ajustando os modelos no conjunto de treinamento.

#Fit the models on the train set
baseline.fit(train_X.loc[:,['Close']],train_y)
default_nn.fit(train_X.loc[:,['Close']],train_y)
sgd_regressor.fit(train_X.loc[:,['Close']],train_y)
lbfgs_customized_model.fit(residuals_train_X.loc[:,['Open','High','Low']],residuals_train_y)

Armazene os modelos em uma lista.

#Store the models in a list
models = [baseline,default_nn,sgd_regressor,lbfgs_customized_model]

Criando um DataFrame para armazenar nossos níveis de erro.

#Create a dataframe to store our error
ensemble_error = pd.DataFrame(index=np.arange(0,5),columns=['Baseline','Default NN','SGD','Customized NN'])

Importando as bibliotecas necessárias.

from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import mean_squared_error

Crie o objeto de divisão de séries temporais.

#Create the time-series object
tscv = TimeSeriesSplit(n_splits=5,gap=20)

Precisamos redefinir os índices dos nossos dados.

#Reset the indexes so we can perform cross validation
test_y = test_y.reset_index()
residuals_test_y = residuals_test_y.reset_index()

test_X = test_X.reset_index()
residuals_test_X = residuals_test_X.reset_index()

Agora vamos realizar a validação cruzada para séries temporais. Observe que o modelo que prevê os resíduos precisa ser treinado separadamente dos outros modelos que simplesmente prevêem o preço de fechamento futuro.

#Cross validate the models
for j in np.arange(0,4):
  model = models[j]
  for i,(train,test) in enumerate(tscv.split(test_X)):
    #The model predicting the residuals
    if(j == 3):
      model.fit(residuals_test_X.loc[train[0]:train[-1],['Open','High','Low']],residuals_test_y.loc[train[0]:train[-1],'Target'])
      #Measure the loss
      ensemble_error.iloc[i,j] = mean_squared_error(residuals_test_y.loc[test[0]:test[-1],'Target' ], model.predict(residuals_test_X.loc[test[0]:test[-1],['Open','High','Low']]))

    elif(j <= 2):
      #Fit the model
      model.fit(test_X.loc[train[0]:train[-1],['Close']],test_y.loc[train[0]:train[-1],'Target'])
      #Measure the loss
      ensemble_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],'Target' ],model.predict(test_X.loc[test[0]:test[-1],['Close']]))

Agora vamos analisar nossos níveis de erro de validação. Infelizmente, não conseguimos superar o desempenho de um simples modelo de regressão linear, indicando que nosso modelo pode ser sensível demais à variância dos dados. A boa notícia é que superamos nosso DNN Regressor padrão.

ensemble_error.mean().sort_values(ascending=True)

Modelos	Erro de Validação
Baseline	0.004784
NN L-BFGS-B Customizado	0.004891
SGD	0.005937
NN padrão	35.35851

Exportando para formato ONNX

Open Neural Network Exchange (ONNX) é um protocolo open-source para construir e implantar modelos de machine learning de forma independente de linguagem. O ONNX nos permite integrar facilmente nossos modelos do scikit-learn em nossos Expert Advisors, aproveitando o suporte da API MQL5 para ONNX. Primeiro, vamos importar as bibliotecas necessárias.

#Prepare to export to ONNX
import onnx
import netron
from   skl2onnx import convert_sklearn
from   skl2onnx.common.data_types import FloatTensorType

Agora vamos ajustar os modelos em todos os dados disponíveis.

#Fit the SGD model on all the data we have
close_model = SGDRegressor(tol= 0.001,
 shuffle=False,
 penalty= 'elasticnet',
 loss= 'huber',
 learning_rate='adaptive',
 fit_intercept= True,
 early_stopping= True,
 alpha= 1e-05)

close_model.fit(nzd_jpy.loc[:,['Close']],nzd_jpy.loc[:,'Target'])

Depois, ajustaremos nosso DNN Regressor.

#Fit the deep neural network on all the data we have
residuals_model = MLPRegressor(
 tol=0.0001,
 solver= 'lbfgs',
 shuffle=False,
 power_t= 0.5,
 max_iter= 300,
 learning_rate_init= 0.01,
 learning_rate='constant',
 hidden_layer_sizes=(30, 200, 40),
 early_stopping=False,
 alpha=1e-05,
 activation='identity')

#Fit the model on the residuals
residuals_model.fit(residuals_train_X,residuals_train_y)
residuals_model.fit(residuals_test_X,residuals_test_y)

Vamos definir os formatos de entrada dos nossos 2 modelos.

# Define the input type
close_initial_types = [("float_input",FloatTensorType([1,1]))]
residuals_initial_types = [("float_input",FloatTensorType([1,3]))]

Precisamos criar representações ONNX dos nossos modelos.

# Create the ONNX representation
close_onnx_model = convert_sklearn(close_model,initial_types=close_initial_types,target_opset=12)
residuals_onnx_model = convert_sklearn(residuals_model,initial_types=residuals_initial_types,target_opset=12)

Por fim, precisamos salvar nossos modelos no formato ONNX.

#Save the ONNX Models
onnx.save_model(close_onnx_model,'close_model.onnx')
onnx.save_model(residuals_onnx_model,'residuals_model.onnx')

Visualizando nossos Modelos ONNX

Vamos também visualizar nossos modelos para garantir que possuem os formatos de entrada e saída especificados. Começaremos visualizando nosso DNN Regressor. Primeiro, vamos importar a biblioteca necessária.

#Import netron
import netron 

Agora vamos visualizar nossa DNN.

#Visualizing the residuals model
netron.start("/ENTER/YOUR/PATH/residuals_model.onnx")

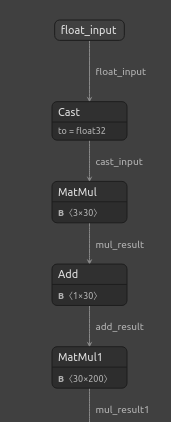
Fig 22: Visualizando o modelo DNN Regressor

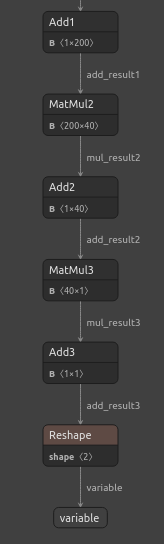
Fig 23: Visualizando o modelo DNN Regressor

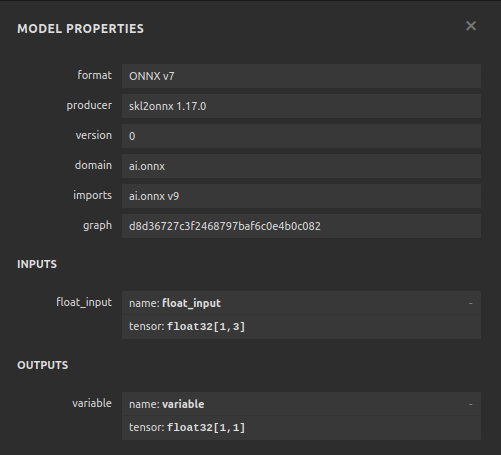
Fig 24: O formato de entrada e saída do nosso DNN Regressor está conforme o esperado

Vamos também visualizar o modelo SGD Regressor.

#Visualizing the close model
netron.start("/ENTER/YOUR/PATH/close_model.onnx")

Fig 25: Visualizando o modelo SGD Regressor

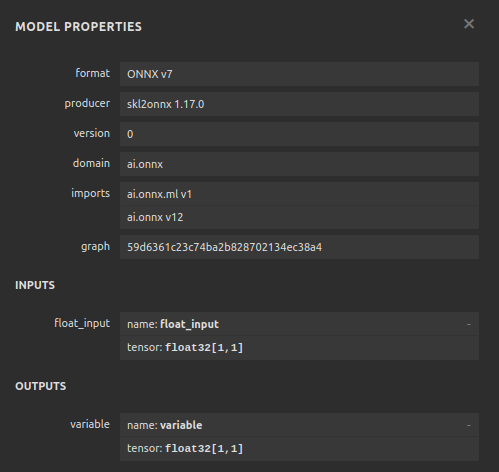
Fig 26: Visualizando o modelo SGD Regressor

Implementando em MQL5

Para começar a construir nosso Expert Advisor com IA, primeiro precisamos carregar os arquivos ONNX que acabamos de criar na aplicação.

//+------------------------------------------------------------------+
//|                                                   NZD JPY AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Load the ONNX models                                             |
//+------------------------------------------------------------------+
#resource "\\Files\\residuals_model.onnx" as const uchar residuals_onnx_buffer[];
#resource "\\Files\\close_model.onnx" as const uchar close_onnx_buffer[];

Agora, precisamos da biblioteca de trade para nos ajudar a abrir e fechar posições.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

Vamos também criar variáveis globais que serão usadas em todo o programa.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long residuals_model,close_model;
vectorf residuals_forecast   = vectorf::Zeros(1);
vectorf close_forecast       = vectorf::Zeros(1);
float forecast = 0;
int model_state,system_state;
int counter = 0;
double bid,ask;

No procedimento de inicialização do nosso modelo, primeiro carregamos nossos 2 modelos ONNX e, em seguida, validamos se os modelos estão funcionando.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the ONNX models
   if(!load_onnx_models())
     {
      return(INIT_FAILED);
     }

//--- Validate the model is working
   model_predict();
   if(forecast == 0)
     {
      Comment("The ONNX models are not working correctly!");
      return(INIT_FAILED);
     }

//--- We managed to load our ONNX models
   return(INIT_SUCCEEDED);
  }

Sempre que nosso modelo for removido do gráfico, liberamos todos os recursos que não estivermos mais usando.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we no longer need
   release_resorces();
  }

Se recebermos novos preços, primeiro atualizamos nossos preços de mercado. Depois, obtemos uma previsão do modelo. Quando tivermos uma previsão, verificamos se temos alguma posição aberta. Se não houver posições abertas, seguiremos a previsão do modelo, desde que as mudanças de preço em timeframes maiores permitam. Caso já haja uma posição aberta, aguardamos 20 candles antes de verificar se o modelo está prevendo uma reversão. Lembre-se: treinamos o modelo para prever 20 passos à frente, então devemos aguardar antes de checar por reversão.

//--- If we have no positions, follow the model's forecast
   if(PositionsTotal() == 0)
     {
      //--- Our model is suggesting we should buy
      if(model_state == 1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Buy(0.3,Symbol(),ask,0,0,"NZD JPY AI");
            system_state = 1;
           }
        }

      //--- Our model is suggesting we should sell
      if(model_state == -1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Sell(0.3,Symbol(),bid,0,0,"NZD JPY AI");
            system_state = -1;
           }
        }
     }

   else
     {
      //--- We want to wait 20 mins before forecating again.
      if(time_stamp != time)
        {
         time_stamp= time;
         counter += 1;
        }

      if((system_state!= model_state) && (counter >= 20))
        {
         Alert("Reversal detected by our AI system, closing all positions");
         Trade.PositionClose(Symbol());
         counter = 0;
        }
     }
  }

Vamos definir a função para buscar previsões dos nossos modelos; lembre-se que temos 2 modelos distintos que devem ser chamados em sequência.

//+------------------------------------------------------------------+
//| Fetch a prediction from our models                               |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- Define the inputs
   vectorf close_inputs = vectorf::Zeros(1);
   vectorf residuals_inputs = vectorf::Zeros(3);

   close_inputs[0]     = (float) iClose(Symbol(),PERIOD_M1,0);
   residuals_inputs[0] = (float) iOpen(Symbol(),PERIOD_M1,0);
   residuals_inputs[1] = (float) iHigh(Symbol(),PERIOD_M1,0);
   residuals_inputs[2] = (float) iLow(Symbol(),PERIOD_M1,0);

//--- Fetch predictions
   OnnxRun(residuals_model,ONNX_DEFAULT,residuals_inputs,residuals_forecast);
   OnnxRun(close_model,ONNX_DEFAULT,close_inputs,close_forecast);

//--- Our forecast
   forecast = residuals_forecast[0] + close_forecast[0];
   Comment("Model forecast: ",forecast);

//--- Remember the model's prediction
   if(forecast > close_inputs[0])
     {
      model_state = 1;
     }
   else
     {
      model_state = -1;
     }
  }

Também precisamos de uma função para atualizar nossos preços de mercado.

//+------------------------------------------------------------------+
//| Update the market data we have                                   |
//+------------------------------------------------------------------+
void update_market_data(void)
  {
   bid = SymbolInfoDouble(Symbol(),SYMBOL_BID);
   ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK);
  }

Esta função liberará os recursos que não estivermos mais usando.

//+------------------------------------------------------------------+
//| Rlease the resources we no longer need                           |
//+------------------------------------------------------------------+
void release_resorces(void)
  {
   OnnxRelease(residuals_model);
   OnnxRelease(close_model);
   ExpertRemove();
  }

Por fim, esta função irá preparar nossos modelos ONNX a partir dos buffers ONNX criados no início da aplicação.

//+------------------------------------------------------------------+
//| This function will load our ONNX models                          |
//+------------------------------------------------------------------+
bool load_onnx_models(void)
  {
//--- Load the ONNX models from the buffers we created
   residuals_model = OnnxCreateFromBuffer(residuals_onnx_buffer,ONNX_DEFAULT);
   close_model = OnnxCreateFromBuffer(close_onnx_buffer,ONNX_DEFAULT);

//--- Validate the models
   if((residuals_model == INVALID_HANDLE) || (close_model == INVALID_HANDLE))
     {
      //--- We failed to load the models
      Comment("Failed to create the ONNX models: ",GetLastError());
      return(false);
     }

//--- Set the I/O shapes of the models
   ulong residuals_inputs[] = {1,3};
   ulong close_inputs[]     = {1,1};
   ulong model_output[]     = {1,1};

//---- Validate the I/O shapes
   if((!OnnxSetInputShape(residuals_model,0,residuals_inputs)) || (!OnnxSetInputShape(close_model,0,close_inputs)))
     {
      //--- We failed to set the input shapes
      Comment("Failed to set model input shapes: ",GetLastError());
      return(false);
     }

   if((!OnnxSetOutputShape(residuals_model,0,model_output)) || (!OnnxSetOutputShape(close_model,0,model_output)))
     {
      //--- We failed to set the output shapes
      Comment("Failed to set model output shapes: ",GetLastError());
      return(false);
     }

//--- Everything went fine
   return(true);
  }
//+------------------------------------------------------------------+

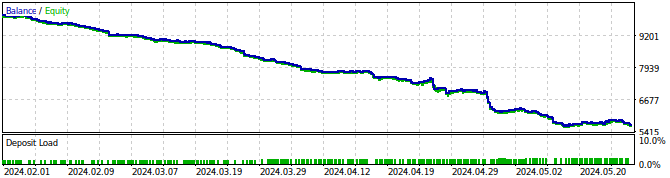
Fig 27: Backtestando nosso Expert Advisor

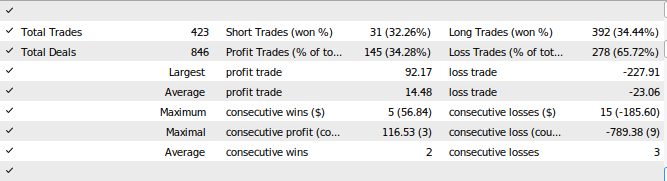
Fig 28: Resultados do teste do nosso Expert Advisor

Conclusão

Neste artigo, mostramos como construir aplicações de trading auto-corretivas. A conversa destacou como analisar os resíduos do seu modelo para detectar overfitting e viés em modelos de machine learning. Infelizmente, detectamos que os resíduos do nosso modelo de melhor desempenho estavam "desajustados". Poderíamos tentar corrigir isso diferenciando os dados de série temporal e o alvo até não observar mais autocorrelação nos resíduos, porém isso também pode tornar o modelo mais difícil de interpretar. Embora não possamos garantir que os pontos discutidos neste artigo irão gerar sucesso consistente, vale a pena considerar se você deseja aplicar IA em suas estratégias de trading. Junte-se a nós na próxima discussão, onde tentaremos remediar as armadilhas observadas hoje, equilibrando interpretabilidade do modelo.