MQL5とPythonで自己最適化エキスパートアドバイザーを構築する（第4回）：スタッキングモデル

本連載では、変化する市場環境に柔軟に対応可能な取引アプリケーションを設計・構築する方法を詳しく解説します。市場へのアプローチは無数に存在しますが、すべてのソリューションが効果を発揮するわけではありません。そのため、本記事では、さまざまなアプローチのメリットとデメリットを具体例を通じて示し、経験に基づいて分析することで、取引戦略の改善を支援することを目的としています。

取引戦略の概要

NZDJPY通貨ペアの予測に焦点を当て、MetaTrader 5端末から収集した銘柄データを元に、アルゴリズムによる取引戦略の学習を目指しています。人間は自身の信念や関心に基づいた取引戦略に偏りがちですが、機械学習モデルにも同様の偏りが存在します。機械学習モデルの偏りとは、モデルがおこなう仮定がどの程度現実と乖離しているかを示すものです。私たちの取引戦略は、2つのAIモデルのアンサンブルに基づいています。最初のモデルは、20分後のNZDJPYペアの終値を予測するように訓練されます。次に、2番目のモデルは、最初のモデルの予測誤差を予測するように訓練されます。この手法は「スタッキング」と呼ばれています。2つのモデルを組み合わせることで、人間による偏りを克服し、パフォーマンスをさらに向上させることが期待できます。

方法論の概要

カスタマイズされたMQL5スクリプトを使用して、MetaTrader 5端末からNZDJPYペアのM1市場データを約9000行収集しました。その後、市場データを基に2Dおよび3Dの散布図を作成しましたが、データに明確な関係性を見つけることはできませんでした。また、データセットの時系列分解を行い、データに明らかな下降トレンドと強い季節性の影響があることを確認しました。

次に、データは訓練セットとテストセットに分割されました。15種類のモデルセットが訓練セットに適合され、評価されました。最もパフォーマンスが良かったのは、確率的勾配降下法(SGD)回帰モデルでした。

その後、特徴量の重要度メトリックを分析した結果、NZDJPYペアの将来の終値を予測する上で「高値」が最も有益な予測変数であることが判明しました。高値は、最高の相互情報量(MI)スコアを獲得しました。さらに、scikit-learnの再帰的特徴除去(RFE)アルゴリズムを実装し、すべての予測変数が重要と判定されました。しかし、この後の説明でわかるように、関係が存在していても、それをうまく捉えてモデル化できるとは限りません。

最もパフォーマンスの高いモデルを特定した後、次にモデルのパラメータ調整に進みました。通常、パラメータ調整後はカスタマイズしたモデルのパフォーマンスをデフォルトモデルと比較し、過剰適合をテストします。ただし、過剰適合をテストする方法は多数存在し、今回はモデルの残差を分析して過剰適合をテストすることにしました。その結果、モデルの残差とそのラグの間に高い相関関係が見られました。通常、十分に学習したモデルの残差には相関関係がないはずです。このことから、最もパフォーマンスの高いモデルが効果的に学習していないか、ターゲットの予測に有用な他のデータがあり、そのデータがモデルに含まれていないことを示唆しています。

その後、訓練セットとテストセットでモデルの残差を記録しました。この段階では、モデルをテストセットに適合させることはしませんでした。次に、SGD回帰モデルの訓練残差を基に、15個のモデルセットを交差検証しました。最もパフォーマンスが高かったモデルはラッソ回帰でしたが、候補ソリューションとして3番目に優れたモデルであるディープニューラルネットワーク(DNN)を選択しました。この選択の理由は、ラッソ回帰のチューニングパラメータの数が限られているのに対して、DNNは、その柔軟性により、データにより適切にチューニングできるからです。

DNN回帰モデルを調整して、SGD回帰モデルの残差を予測する2段階のプロセスで、2つの独自モデルを作成しました。最初に、DNN回帰モデルのパラメータに対してランダムサーチを100回繰り返し、最良のパラメータを特定して最初のモデルを作成しました。特定した最良のパラメータは、メモリ制限のあるL-BFGS-Bアルゴリズムを使用した制約なしの大域的最適化試行の開始点として使用され、2番目のモデルが得られました。どちらのモデルも、未知の検証データに対してデフォルトのDNN回帰モデルよりも優れたパフォーマンスを発揮しました。さらに、最終モデルは最高のパフォーマンスを示しました。つまり、これらの追加手順を2段階で実行した結果、時間を無駄にすることなく最良の結果を得ることができました。

最後に、両方のモデルをONNX形式にエクスポートし、自己修正型のAI搭載エキスパートアドバイザー(EA)の構築に進みました。

必要なデータの取得

MetaTrader 5端末から必要なデータを取得することから始めます。まず、MetaTrader 5端末から必要なデータを取得します。以下に添付されているスクリプトは、端末から指定した数のバーの履歴価格データを取得し、そのデータをCSV形式で書き込んで「Files」フォルダーに保存します。

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| Script Inputs                                                    |
//+------------------------------------------------------------------+
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int rsi_handler;
double rsi_buffer[];

//+------------------------------------------------------------------+
//| On start function                                                |
//+------------------------------------------------------------------+
void OnStart()
  {

//--- Load indicator
   rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,20,PRICE_CLOSE);
   CopyBuffer(rsi_handler,0,0,size,rsi_buffer);
   ArraySetAsSeries(rsi_buffer,true);

//--- File name
   string file_name = "Market Data " + Symbol() + ".csv";

//--- Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i)
                  );
        }
     }
//--- Close the file
   FileClose(file_handle);

  }
//+------------------------------------------------------------------+

データのクリーニング

データの書式設定から始めます。まず、必要なライブラリをロードします。

#Import the libraries we need
import pandas as pd
import numpy as np

次に市場データを読み取ります。

#Read in the market data
nzd_jpy = pd.read_csv('Market Data NZDJPY.csv')

データの順序が間違っています。最も古い日付から順に実行され、現在に最も近い日付が最後になるようにリセットしましょう。

#Format the data
nzd_jpy = nzd_jpy[::-1]
nzd_jpy.reset_index(inplace=True, drop=True)

ターゲットを定義します。

#Labelling the data
nzd_jpy['Target'] = nzd_jpy['Close'].shift(-20)
nzd_jpy.dropna(inplace=True)

プロット目的でバイナリターゲットも追加します。

#Add binary target for plotting
nzd_jpy['Binary Target'] = np.nan
nzd_jpy.loc[nzd_jpy['Close'] > nzd_jpy['Target'],'Binary Target'] = 1
nzd_jpy.loc[nzd_jpy['Close'] <= nzd_jpy['Target'],'Binary Target'] = 0

データを検査してみましょう。

#Current state of our dataframe
nzd_jpy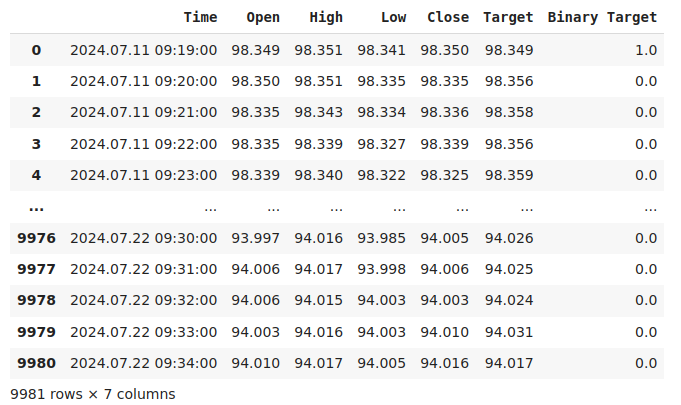

図1：現在のデータフレーム

探索的データ分析

観察できる関係性があるかどうかを判断するために散布図を作成しましょう。残念ながら、データはランダムに分布しており、市場の上昇と下降の動きが明確に区別されていません。

#Lets perform scatter plots
sns.scatterplot(data=nzd_jpy,x=nzd_jpy['Open'], y=nzd_jpy['Close'],hue='Binary Target')

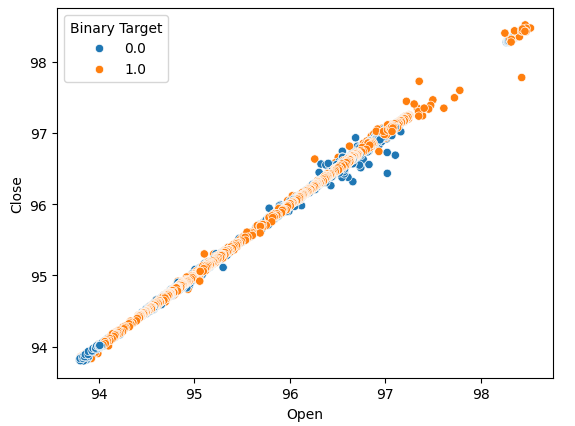
図2：始値と終値の散布図

価格が上昇または下落したすべての事例をまとめるために箱ひげ図を作成することを考えました。これら2つの可能性のあるターゲットにおけるデータの分布には、潜在的に違いがある可能性があると考えました。残念ながら、箱ひげ図では、2つの可能性のある結果におけるデータの分布にほとんど違いがないことが示されています。

#Let's create categorical box plots
sns.catplot(data=nzd_jpy,x='Binary Target',y='Close',kind='box')

図3：価格レベルが下落(0)または上昇(1)したすべての事例をまとめた箱ひげ図

時系列データを3つのコンポーネントに分解することもできます。

1. トレンド
2. 季節性
   
3. 残差
   

 トレンド要素は、価格レベルの平均的な長期的変動を表します。季節性コンポーネントは、データにおいて繰り返し現れる周期的なパターンを示し、残差コンポーネントは、前述の2つのコンポーネントでは説明できない部分を表します。NZDJPYペアのM1データを使用する場合、期間を1440（すなわち1日）の価格平均パフォーマンスに設定します。分解を実行する前から、データには非常に明確で強い下降トレンドが確認できます。しかし、元のデータからトレンドを差し引くと、季節的な影響がはっきりと観察されることがわかります。

#Time series decomposition
import statsmodels.api as sm
nzd_jpy_decomposition = sm.tsa.seasonal_decompose(nzd_jpy['Close'],period=1440,model='additive')
fig = nzd_jpy_decomposition.plot()

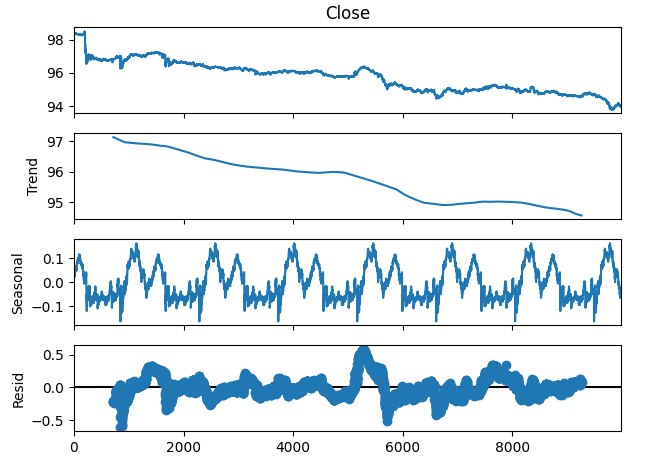
図4：データの時系列分解

いくつかの効果は、高次元に隠れている可能性があります。データの3D散布図を作成すると、2D散布図の範囲を超えて隠れている効果を明らかにすることができます。残念ながら、このデータセットはそのようなケースではありませんでした。私たちのデータは分離するのがまだ非常に難しく、識別可能な関係は示されていません。

#Let's also perform 3D plots
#Visualizing our data in 3D

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111,projection='3d')
colors = ['blue' if movement == 0 else 'red' for movement in nzd_jpy.loc[:,"Binary Target"]]
ax.scatter(nzd_jpy.loc[:,"Low"],nzd_jpy.loc[:,"High"],nzd_jpy.loc[:,"Close"],c=colors)

ax.set_xlabel('NZDJPY Low')
ax.set_ylabel('NZDJPY High')
ax.set_zlabel('NZDJPY Close')

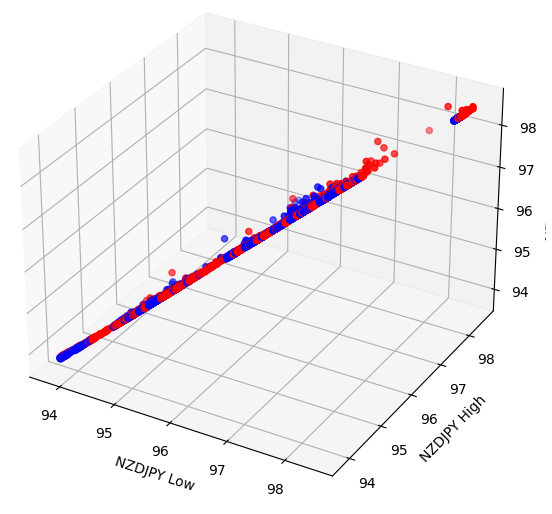
図5：3D散布図の可視化

データモデル化の準備

データのモデリングを開始する前に、まずデータを標準化してスケーリングする必要があります。必要なライブラリをロードします。

#Let's prepare the data for modelling
from sklearn.preprocessing import RobustScaler

データをスケーリングします。

#Scale the data
X = pd.DataFrame(RobustScaler().fit_transform(nzd_jpy.loc[:,['Close']]),columns=['Close'])
residuals_X = pd.DataFrame(RobustScaler().fit_transform(nzd_jpy.loc[:,['Open','High','Low']]),columns=['Open','High','Low'])
y = nzd_jpy.loc[:,'Target']

モデルの選択

データをモデル化するために必要なライブラリをロードしましょう。

#Cross validating the models
from sklearn.model_selection import cross_val_score,train_test_split
from sklearn.linear_model import Lasso,LinearRegression,Ridge,ElasticNet,SGDRegressor,HuberRegressor
from sklearn.ensemble import RandomForestRegressor,GradientBoostingRegressor,AdaBoostRegressor,ExtraTreesRegressor,BaggingRegressor
from sklearn.svm import LinearSVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.neural_network import MLPRegressor

次に、データを2つに分割します。

#Create train-test splits
train_X,test_X,train_y,test_y = train_test_split(nzd_jpy.loc[:,['Close']],y,test_size=0.5,shuffle=False)
residuals_train_X,residuals_test_X,residuals_train_y,residuals_test_y = train_test_split(nzd_jpy.loc[:,['Open','High','Low']],y,test_size=0.5,shuffle=False)

モデルをリストに保存し、検証の誤差レベルを保存するデータフレームを作成します。

#Store the models
models = [
    Lasso(),
    LinearRegression(),
    Ridge(),
    ElasticNet(),
    SGDRegressor(),
    HuberRegressor(),
    RandomForestRegressor(),
    GradientBoostingRegressor(),
    AdaBoostRegressor(),
    ExtraTreesRegressor(),
    BaggingRegressor(),
    LinearSVR(),
    KNeighborsRegressor(),
    DecisionTreeRegressor(),
    MLPRegressor(),
]

#Store the names of the models
model_names = [
    'Lasso',
    'Linear Regression',
    'Ridge',
    'Elastic Net',
    'SGD Regressor',
    'Huber Regressor',
    'Random Forest Regressor',
    'Gradient Boosting Regressor',
    'Ada Boost Regressor',
    'Extra Trees Regressor',
    'Bagging Regressor',
    'Linear SVR',
    'K Neighbors Regressor',
    'Decision Tree Regressor',
    'MLP Regressor',
]

#Create a dataframe to store our cv error
cv_error = pd.DataFrame(columns=model_names,index=np.arange(0,5))

各モデルを交差検証します。

#Cross validate each model
for model in models:
  cv_score = cross_val_score(model,X,y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
  for i in np.arange(0,5):
    index = models.index(model)
    cv_error.iloc[i,index] = cv_score[i]

結果を可視化します。

cv_error

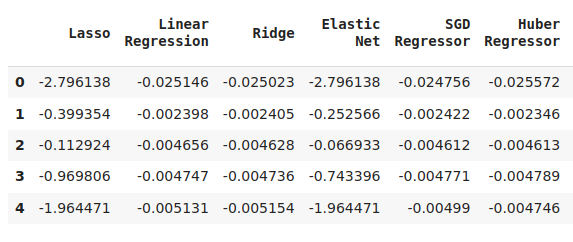
図6：NZDJPYの将来の終値を予測する際の誤差レベルの一部

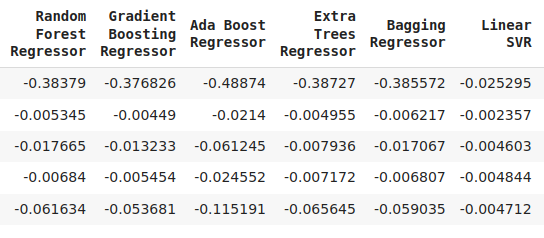
図7：誤差レベルの継続

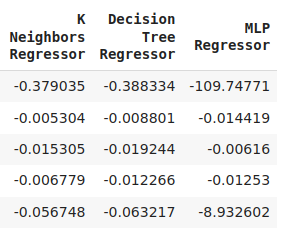
図8：最終的なモデルの誤差レベル

5つのフォールド全体にわたるパフォーマンスレベルをプロットすることで、ニューラルネットワークのパフォーマンスの低さが明らかになりました。パラメータの調整により、おそらく大きな改善が期待できるでしょう。

cv_error.plot()

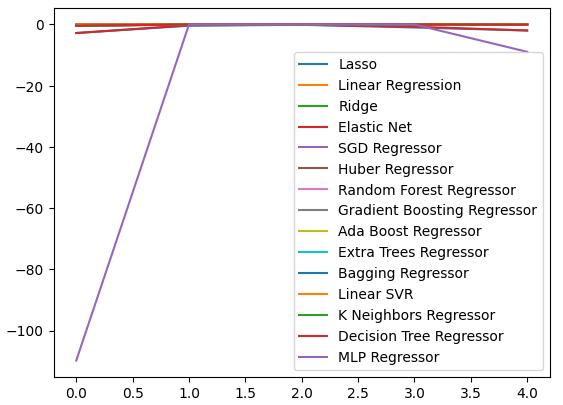
図9：誤差レベルの可視化

箱ひげ図を使用すると、多くの情報を1つのプロットにまとめることができます。たとえば、以下のグラフでは、このタスクにおけるDNNのパフォーマンスがいかに悪かったかがはっきりとわかります。これは右側の最後のモデルであり、他のモデルよりもパフォーマンスにかなりのばらつきが見られます。

sns.boxplot(cv_error)

図10：誤差を箱ひげ図として可視化する

平均誤差レベルが最も低いモデルが、最もパフォーマンスの高いモデルであると特定できます。

#Our mean validation error
cv_error.mean()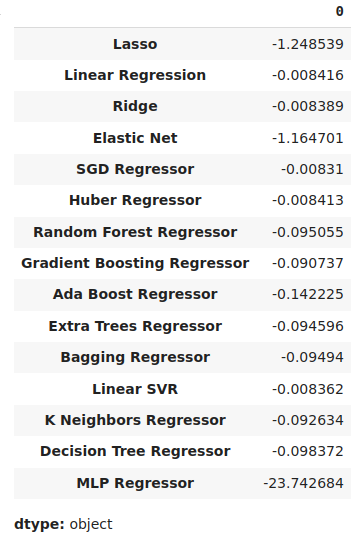

図11：平均誤差レベルの可視化

特徴量の重要性

特徴重要度アルゴリズムは、モデルが意味のある関連性を学習したかどうか、または私たちが知らなかった関係をモデルが学習したかどうかを理解するのに役立ちます。まず、必要なライブラリをインポートしましょう。

#Feature importance
from sklearn.feature_selection import mutual_info_regression,RFE

まず相互情報量(MI)スコアを計算します。MIは、各予測変数が持つ可能性について知らせ、ターゲットを予測するのに役立ちます。最後に、MIは対数スケールで測定されます。したがって、MIスコアが3を超えることは実際にはほとんど見られません。

mi_score = pd.DataFrame(mutual_info_regression(X,y),columns=['MI Score'],index=X.columns)

MIスコアをプロットすると、高値がNZDJPYの将来の終値を予測する上で最も可能性が高いことが明確にわかります。

mi_score.plot()

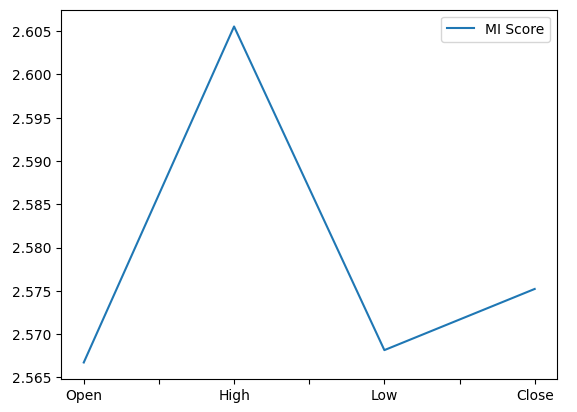
図12：MIスコアのプロット

RFEアルゴリズムは、scikit-learnライブラリのほぼすべてのオブジェクトと同様に簡単に使用できます。クラスのインスタンスを作成し、それをデータに適合させるだけで、各予測変数に割り当てられた特徴の重要度レベルを評価できます。RFEアルゴリズムでは、すべての予測変数がNZDJPYの終値を予測するのに同等に重要であると想定していました。

#Select the best features
rfe = RFE(model, n_features_to_select=5, step=1)
rfe = rfe.fit(X, y)
rfe.ranking_

array([1, 1, 1, 1])

パラメータチューニング

ここで、SGD回帰モデルから可能な限り多くのパフォーマンスを抽出してみましょう。モデルのパラメータ空間のサンプルに対してランダムサーチを実行します。まず必要なライブラリをインポートしましょう。

#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV

デフォルトモデルのインスタンスを作成します。

#Initialize the model
model = SGDRegressor()

チューナーオブジェクトを作成し、サンプリングする可能性のあるパラメータ値を指定します。

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "loss" : ['squared_error', 'huber', 'epsilon_insensitive','squared_epsilon_insensitive'],
        "penalty":['l2','l1', 'elasticnet', None],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001,10,100,1000,10000,100000],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "fit_intercept": [True,False],
        "early_stopping": [True,False],
        "learning_rate":['constant','optimal','adaptive','invscaling'],
        "shuffle": [True,False]
        },
        n_iter=100,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

チューナーオブジェクトを適合させます。

#Fit the tuner
tuner.fit(train_X,train_y)

以下が、見つかった最高のパラメータです。

#Our best parameters
tuner.best_params_

{'tol':0.001,
 'shuffle':False,
 'penalty': 'elasticnet',
 'loss': 'huber',
 'learning_rate': 'adaptive',
 'fit_intercept':True,
 'early_stopping':True,
 'alpha':1e-05}

過剰適合のテスト

モデルの残差に相関が見られる場合、過剰適合を検出できます。モデルが効果的に学習した場合、その残差はランダムなホワイトノイズになるはずです。これは、モデルによって発生する誤差に予測可能なパターンがないことを示しています。ただし、残差に自己相関が見られるモデルは、懸念すべき事態である可能性があります。これは、実行した回帰が誤っているか、タスクに不適切なモデルを選択したことを示す可能性があります。まず、カスタマイズしたモデルの残差を取得する必要があります。

#Model validation
model = SGDRegressor(
    tol             = tuner.best_params_['tol'],
    shuffle         = tuner.best_params_['shuffle'],
    penalty         = tuner.best_params_['penalty'],
    loss            = tuner.best_params_['loss'],
    learning_rate   = tuner.best_params_['learning_rate'],
    alpha           = tuner.best_params_['alpha'],
    fit_intercept   = tuner.best_params_['fit_intercept'],
    early_stopping  = tuner.best_params_['early_stopping']
)
model.fit(train_X,train_y)
residuals = test_y - model.predict(test_X)

モデルの残差をプロットで可視化できます。残念ながら、モデルの残差には自己相関があることがはっきりとわかります。言い換えれば、残差が下がると下がり続ける傾向があり、残差が上がると上がり続ける傾向があります。これは、残差の将来の値が以前の値と関係がある可能性があることを意味し、パラメータ調整を実行した後でもモデルが効果的に学習していない可能性があることを示す明らかな兆候です。

#Plot the residuals
residuals.plot()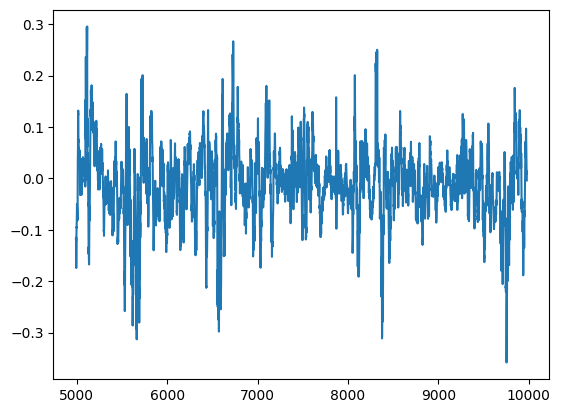

図13：モデルの残差

自己相関にはより堅牢なテストがあり、たとえば自己相関(ACF)プロットを作成できます。ACFプロットには、考えられる各遅延値でスパイクが表示されます。各スパイクの高さは、時系列データとその遅延値との相関レベルを表します。プロットの背景には青い円錐のような構造もあり、青い円錐は信頼区間を表しています。信頼区間を超える相関レベルは、統計的に有意であると見なされます。

#The residuals appear to have autocorrelation
from statsmodels.graphics.tsaplots import plot_acf
fig = plot_acf(residuals)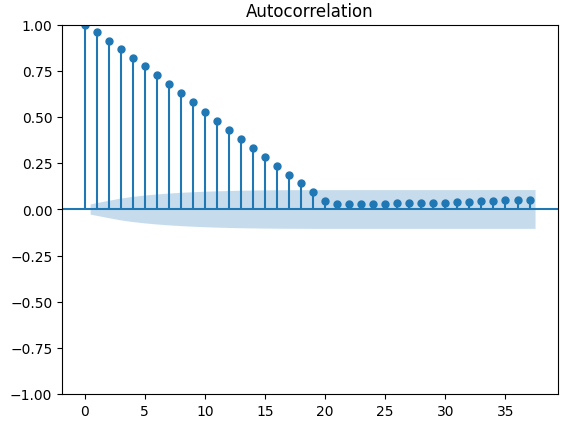

図14：モデル残差の自己相関

これは良い兆候ではありませんが、最初のモデルを修正するようにDNNを訓練することで、この問題を軽減できる可能性があります。SGD回帰モデルの誤差を、訓練データとテストデータで記録してみましょう。注意：この時点ではモデルをテストデータに適合させるのではなく、誤差レベルのみを測定します。

#Prepare the residuals for our second model
model = SGDRegressor(tol= 0.001,
 shuffle=False,
 penalty= 'elasticnet',
 loss= 'huber',
 learning_rate='adaptive',
 fit_intercept= True,
 early_stopping= True,
 alpha= 1e-05)

#Store the model residuals
model.fit(train_X,train_y)
residuals_train_y = train_y - model.predict(train_X)
residuals_test_y = test_y - model.predict(test_X)

ここで、SGD回帰モデルの誤差レベルを予測するモデルを交差検証します。

#Cross validate each model
for model in models:
  cv_score = cross_val_score(model,residuals_train_X,residuals_train_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
  for i in np.arange(0,5):
    index = models.index(model)
    cv_error.iloc[i,index] = cv_score[i]

検証誤差を可視化してみましょう。

#Cross validaton error levels
cv_error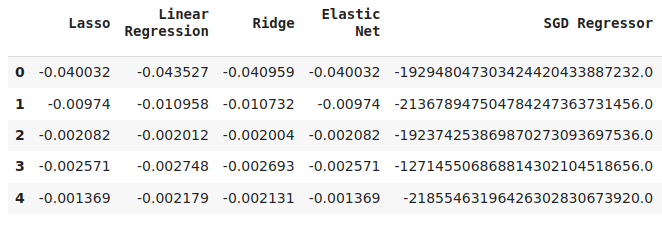

図15：最初のモデルの誤差レベルを予測する際のモデル検証誤差レベルの一部

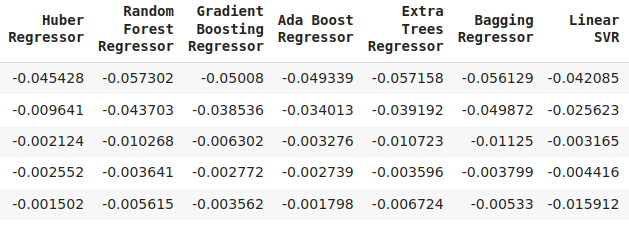
図16：検証誤差レベルの継続

平均誤差レベルを降順で表示して、パフォーマンスが最も優れたモデルをすばやく特定できます。

#Store the model's performance
cv_error.mean().sort_values(ascending=False)

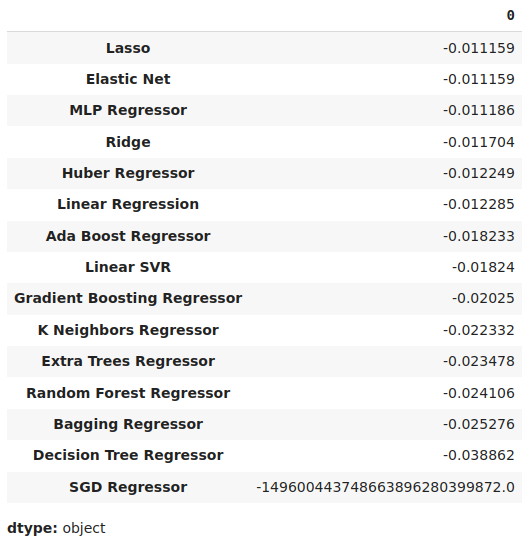
図17：検証誤差の平均レベルは、ラッソが最高のパフォーマンスを発揮するモデルであることを明確に示している

箱ひげ図は、SGD回帰関数が自身の誤差レベルを予測しようとしたときに、どれほどパフォーマンスが悪かったかを示しています。

sns.boxplot(cv_error)

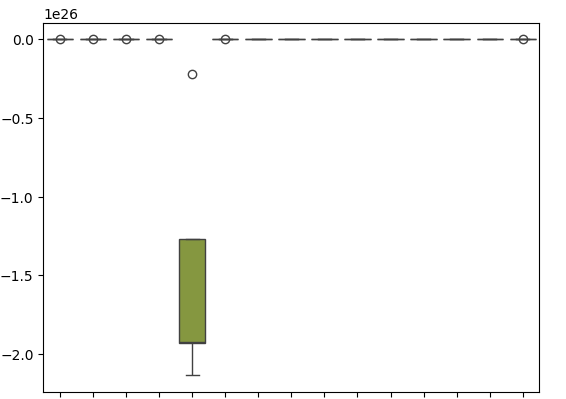
図18：モデルの残差を予測する際の検証誤差の箱ひげ図

データを可視化するために折れ線グラフを作成することもできます。

cv_error.plot()

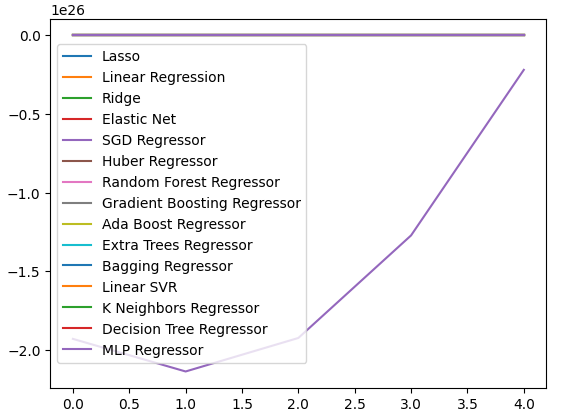
図19：誤差レベルを線グラフで可視化する

ディープニューラルネットワークのパラメータ調整

ここで、DNN回帰モデルのパラメータを調整する準備をしましょう。まず、チューナーオブジェクトと、検索するパラメータ空間のサンプルを定義します。

#Let's tune the model
#Reinitialize the model

model = MLPRegressor()

#Define the tuner

tuner = RandomizedSearchCV(
        model,
        {
                "activation":["relu","tanh","logistic","identity"],
                "solver":["adam","sgd","lbfgs"],
                "alpha":[0.1,0.01,0.001,0.00001,0.000001],
                "learning_rate": ["constant","invscaling","adaptive"],
                "learning_rate_init":[0.1,0.01,0.001,0.0001,0.000001,0.0000001],
                "power_t":[0.1,0.5,0.9,0.01,0.001,0.0001],
                "shuffle":[True,False],
                "tol":[0.1,0.01,0.001,0.0001,0.00001],
                "hidden_layer_sizes":[(10,20),(100,200),(30,200,40),(5,20,6)],
                "max_iter":[10,50,100,200,300],
                "early_stopping":[True,False]
        },
        n_iter=100,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

次に、チューナーオブジェクトを適合させます。

#Fit the tuner
tuner.fit(residuals_train_X,residuals_train_y)

最後に、私たちが見つけた最適なパラメータを確認できます。

#The best parameters we found
tuner.best_params_

{'tol':0.0001,
 'solver': 'lbfgs',
 'shuffle':False,
 'power_t':0.5,
 'max_iter':300,
 'learning_rate_init':0.01,
 'learning_rate': 'constant',
 'hidden_layer_sizes':(30, 200, 40),
 'early_stopping':False,
 'alpha':1e-05,
 'activation': 'identity'}

より詳細なパラメーターチューニング

ここで、さらに優れたパラメータが見つからないかテストしてみましょう。最適な入力値がどこにあるかは必ずしもわからないため、SciPyライブラリのメモリ制限付きL-BFGS-Bアルゴリズムを使用して、制約のない大域的最適化を実行してみます。L-BFGS-Bアルゴリズムは、大域的最適化問題に効果的に使用できます。数値ソルバー自体はFortranコードで実装されており、SciPyライブラリはルーチンと簡単にインターフェイスするための薄いラッパーを提供します。まず、必要なライブラリをインポートすることから始めます。

図20：オリジナルのBFGSアルゴリズムの開発者（左から右へ）Broyden、Fletcher、Goldfarb、Shanno

#Deeper optimization
from scipy.optimize import minimize

ここで、最小化する目的関数を定義します。DNN回帰モデルの訓練誤差を最小化したいと考えています。SciPy最小化ツールは連続最適化問題のみを処理できるため、モデルの他のすべての入力パラメータを修正します。

#Define the objective function
def objective(x):
    #Create a dataframe to store our accuracy
    cv_error = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])
    #The parameter x represents a new value for our neural network's settings
    #In order to find optimal settings, we will perform 10 fold cross validation using the new setting
    #And return the average RMSE from all 10 tests
    #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization
    MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=x[0],tol=x[1])
    model = MLPRegressor(
    tol                 = x[0],
    solver              = tuner.best_params_['solver'],
    power_t             = x[1],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = x[2],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = x[3],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
    )
    #Cross validate the model
    cv_score = cross_val_score(model,residuals_train_X,residuals_train_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
    for i in np.arange(0,5):
      cv_error.iloc[i,0] = cv_score[i]
    #Return the Mean CV RMSE
    return(cv_error.iloc[:,0].mean())

ランダム検索から見つかった最適なパラメータによって、最適化手順の開始点を定義します。最適化手順に制約を適用します。すべての値が正の値であることを強制し、さらに、値の範囲を10のマイナス100乗から10の100乗まで許可します。これは非常に大きなドメインであり、私たちが探している最適なパラメータが含まれていることを期待しています。

#Define the starting point
pt = [tuner.best_params_['tol'],tuner.best_params_['power_t'],tuner.best_params_['learning_rate_init'],tuner.best_params_['alpha']]
bnds = ((10.0 ** -100,10.0 ** 100),
        (10.0 ** -100,10.0 ** 100),
        (10.0 ** -100,10.0 ** 100),
        (10.0 ** -100,10.0 ** 100))

最適なパラメータを検索します。

#Searching deeper for better parameters
result = minimize(objective,pt,method="L-BFGS-B",bounds=bnds)

最適化の結果です。

result

message:CONVERGENCE:REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
  success:True
   status:0
      fun: -0.01143352283130129
        x: [ 1.000e-04  5.000e-01  1.000e-02  1.000e-05]
      nit:2
      jac: [-1.388e+04 -4.657e+04  5.625e+04 -1.033e+04]
     nfev:120
     njev:24
 hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>

過剰適合のテスト

ここで過剰適合をテストしてみましょう。今回は、2つのモデルをデフォルトのDNN回帰モデルのパフォーマンスと比較します。テストしたい各DNN回帰モデルのインスタンスをインスタンス化しましょう。

#Model validation
default_model = MLPRegressor()

customized_model = MLPRegressor(
    tol                 = tuner.best_params_['tol'],
    solver              = tuner.best_params_['solver'],
    power_t             = tuner.best_params_['power_t'],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = tuner.best_params_['learning_rate_init'],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = tuner.best_params_['alpha'],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
)

lbfgs_customized_model = MLPRegressor(
    tol                 = result.x[0],
    solver              = tuner.best_params_['solver'],
    power_t             = result.x[1],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = result.x[2],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = result.x[3],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
)

ここで、モデルのリストを作成し、検証誤差レベルを格納するためのデータフレームも作成します。

models = [default_model,customized_model,lbfgs_customized_model]
cv_error = pd.DataFrame(index=np.arange(0,5),columns=['Default NN','Random Search NN','L-BFGS-B NN'])

各モデルを交差検証します。

#Cross validate the model
for model in models:
  model.fit(residuals_train_X,residuals_train_y)
  cv_score = cross_val_score(model,residuals_test_X,residuals_test_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
  for i in np.arange(0,5):
    index = models.index(model)
    cv_error.iloc[i,index] = cv_score[i]

交差検証誤差です。

cv_error

デフォルトNN	ランダムサーチNN	L-BFGS-B NN
-0.007735	-0.007708	-0.007692
-0.00635	-0.006344	-0.006329
-0.003307	-0.003265	-0.00328
0.005225	-0.004803	-0.004761
-0.004469	-0.004447	-0.004492

それでは、平均誤差レベルを分析してみましょう。

cv_error.mean().sort_values(ascending=False)

モデル	検証誤差
L-BFGS-B NN	-0.005311
ランダムサーチNN	-0.005313
デフォルトNN	-0.005417

ご覧のとおり、モデルはすべて同じ範囲内で動作していました。しかし、カスタマイズされたモデルでは、平均的には明らかに誤差レベルが低くなっていました。残念ながら、モデルによって表示される分散は全体的にほぼ同じであり、これは箱ひげ図によって示されます。分散レベルはモデルのスキルレベルを判断するのに役立ちます。

sns.boxplot(cv_error)

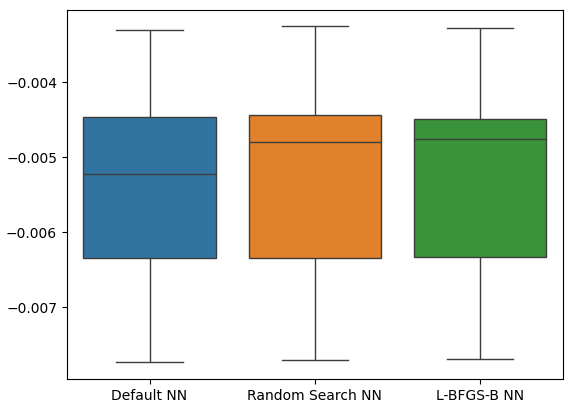
図21：保留データに対する検証誤差レベル

ここで、価格レベルを予測するために単一のモデルを使用するよりも、アンサンブルアプローチの方が優れているかどうかを確認してみましょう。まず必要なモデルを準備します。

#Now that we have come this far, let's see if our ensemble approach is worth the trouble
baseline = LinearRegression()
default_nn = MLPRegressor()

#The SGD Regressor will predict the future price
sgd_regressor = SGDRegressor(tol= 0.001,
 shuffle=False,
 penalty= 'elasticnet',
 loss= 'huber',
 learning_rate='adaptive',
 fit_intercept= True,
 early_stopping= True,
 alpha= 1e-05)

#The deep neural network will predict the error in the SGDRegressor's prediction
lbfgs_customized_model = MLPRegressor(
    tol                 = result.x[0],
    solver              = tuner.best_params_['solver'],
    power_t             = result.x[1],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = result.x[2],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = result.x[3],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
)

モデルを訓練セットに適合させます。

#Fit the models on the train set
baseline.fit(train_X.loc[:,['Close']],train_y)
default_nn.fit(train_X.loc[:,['Close']],train_y)
sgd_regressor.fit(train_X.loc[:,['Close']],train_y)
lbfgs_customized_model.fit(residuals_train_X.loc[:,['Open','High','Low']],residuals_train_y)

モデルをリストに保存します。

#Store the models in a list
models = [baseline,default_nn,sgd_regressor,lbfgs_customized_model]

誤差レベルを保存するためのデータフレームを作成します。

#Create a dataframe to store our error
ensemble_error = pd.DataFrame(index=np.arange(0,5),columns=['Baseline','Default NN','SGD','Customized NN'])

必要なライブラリをインポートします。

from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import mean_squared_error

時系列分割オブジェクトを作成します。

#Create the time-series object
tscv = TimeSeriesSplit(n_splits=5,gap=20)

データのインデックスをリセットする必要があります。

#Reset the indexes so we can perform cross validation
test_y = test_y.reset_index()
residuals_test_y = residuals_test_y.reset_index()

test_X = test_X.reset_index()
residuals_test_X = residuals_test_X.reset_index()

ここで、時系列交差検証を実行します。残差を予測するモデルは、将来の終値を単純に予測する他のモデルとは別に訓練する必要があることに注意してください。

#Cross validate the models
for j in np.arange(0,4):
  model = models[j]
  for i,(train,test) in enumerate(tscv.split(test_X)):
    #The model predicting the residuals
    if(j == 3):
      model.fit(residuals_test_X.loc[train[0]:train[-1],['Open','High','Low']],residuals_test_y.loc[train[0]:train[-1],'Target'])
      #Measure the loss
      ensemble_error.iloc[i,j] = mean_squared_error(residuals_test_y.loc[test[0]:test[-1],'Target' ], model.predict(residuals_test_X.loc[test[0]:test[-1],['Open','High','Low']]))

    elif(j <= 2):
      #Fit the model
      model.fit(test_X.loc[train[0]:train[-1],['Close']],test_y.loc[train[0]:train[-1],'Target'])
      #Measure the loss
      ensemble_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],'Target' ],model.predict(test_X.loc[test[0]:test[-1],['Close']]))

それでは、検証誤差レベルを分析してみましょう。残念ながら、単純な線形回帰モデルのパフォーマンスを上回ることはできず、モデルがデータの分散に対して敏感すぎる可能性があることが示されました。良いニュースは、デフォルトのDNN回帰モデルよりも優れたパフォーマンスを示したことです。

ensemble_error.mean().sort_values(ascending=True)

モデル	検証誤差
ベースライン	0.004784
カスタマイズされたL-BFGS-B NN	0.004891
SGD	0.005937
デフォルトNN	35.35851

ONNX形式へのエクスポート

Open Neural Network Exchange (ONNX)は、言語に依存しない方法で機械学習モデルを構築および展開するためのオープンソースプロトコルです。ONNXを使用すると、ONNXのMQL5 APIサポートを利用して、scikit-learnモデルをEAに簡単に統合できます。まず、必要なライブラリをインポートします。

#Prepare to export to ONNX
import onnx
import netron
from   skl2onnx import convert_sklearn
from   skl2onnx.common.data_types import FloatTensorType

次に、利用可能なすべてのデータにモデルを適合させてみましょう。

#Fit the SGD model on all the data we have
close_model = SGDRegressor(tol= 0.001,
 shuffle=False,
 penalty= 'elasticnet',
 loss= 'huber',
 learning_rate='adaptive',
 fit_intercept= True,
 early_stopping= True,
 alpha= 1e-05)

close_model.fit(nzd_jpy.loc[:,['Close']],nzd_jpy.loc[:,'Target'])

最後に、DNN回帰モデルを適合させます。

#Fit the deep neural network on all the data we have
residuals_model = MLPRegressor(
 tol=0.0001,
 solver= 'lbfgs',
 shuffle=False,
 power_t= 0.5,
 max_iter= 300,
 learning_rate_init= 0.01,
 learning_rate='constant',
 hidden_layer_sizes=(30, 200, 40),
 early_stopping=False,
 alpha=1e-05,
 activation='identity')

#Fit the model on the residuals
residuals_model.fit(residuals_train_X,residuals_train_y)
residuals_model.fit(residuals_test_X,residuals_test_y)

2つのモデルの入力形状を定義しましょう。

# Define the input type
close_initial_types = [("float_input",FloatTensorType([1,1]))]
residuals_initial_types = [("float_input",FloatTensorType([1,3]))]

モデルのONNX表現を作成する必要があります。

# Create the ONNX representation
close_onnx_model = convert_sklearn(close_model,initial_types=close_initial_types,target_opset=12)
residuals_onnx_model = convert_sklearn(residuals_model,initial_types=residuals_initial_types,target_opset=12)

最後に、モデルをONNX形式で保存します。

#Save the ONNX Models
onnx.save_model(close_onnx_model,'close_model.onnx')
onnx.save_model(residuals_onnx_model,'residuals_model.onnx')

ONNXモデルの可視化

また、モデルを可視化して、指定した入力と出力の形状になっていることを確認しましょう。まず、DNN回帰モデルを可視化します。まず、必要なライブラリをインポートします。

#Import netron
import netron 

ここで、DNNを可視化します。

#Visualizing the residuals model
netron.start("/ENTER/YOUR/PATH/residuals_model.onnx")

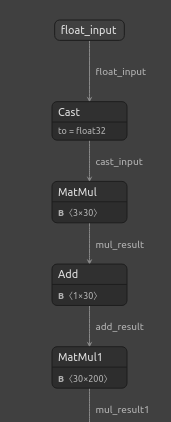
図22：DNN回帰モデルの可視化

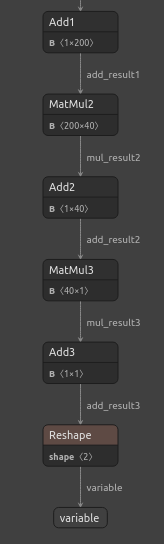
図23：DNN回帰モデルの可視化

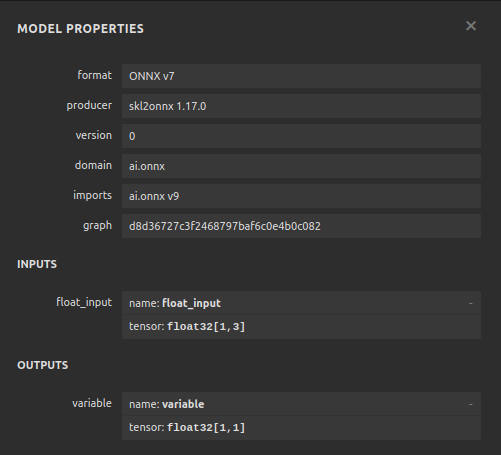
図24：DNN回帰モデルの入力と出力の形状は期待どおりである

SGD回帰モデルも可視化してみましょう。

#Visualizing the close model
netron.start("/ENTER/YOUR/PATH/close_model.onnx")

図25：SGD回帰モデルの可視化

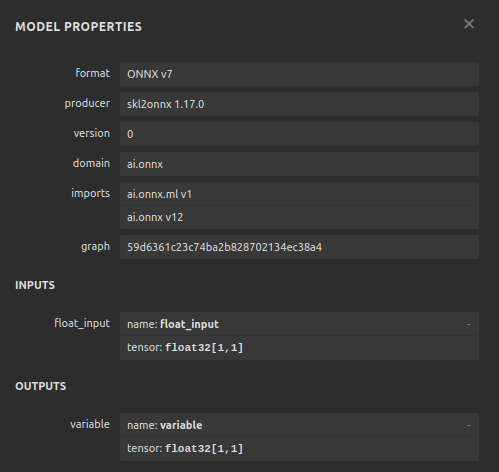
図26：SGD回帰モデルの可視化

MQL5での実装

AI搭載EAの構築を開始するには、まず、作成したONNXファイルをアプリケーションに読み込む必要があります。

//+------------------------------------------------------------------+
//|                                                   NZD JPY AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/ja/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Load the ONNX models                                             |
//+------------------------------------------------------------------+
#resource "\\Files\\residuals_model.onnx" as const uchar residuals_onnx_buffer[];
#resource "\\Files\\close_model.onnx" as const uchar close_onnx_buffer[];

ここで、ポジションのオープンとクローズを支援する取引ライブラリが必要です。

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

プログラム全体で使用するグローバル変数も作成しましょう。

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long residuals_model,close_model;
vectorf residuals_forecast   = vectorf::Zeros(1);
vectorf close_forecast       = vectorf::Zeros(1);
float forecast = 0;
int model_state,system_state;
int counter = 0;
double bid,ask;

モデルの初期化プロシージャでは、まず2つのONNXモデルをロードし、次にモデルが動作していることを検証します。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the ONNX models
   if(!load_onnx_models())
     {
      return(INIT_FAILED);
     }

//--- Validate the model is working
   model_predict();
   if(forecast == 0)
     {
      Comment("The ONNX models are not working correctly!");
      return(INIT_FAILED);
     }

//--- We managed to load our ONNX models
   return(INIT_SUCCEEDED);
  }

モデルがチャートから削除されるたびに、使用しなくなったリソースが解放されます。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we no longer need
   release_resorces();
  }

新しい価格が発表された場合は、まず市場価格を更新します。その後、モデルから予測を取得します。予測ができたら、ポジションがあるかどうかを確認します。ポジションがない場合、より長い時間枠での価格変動が許す限り、モデルの予測に従います。それ以外の場合、すでにポジションがある場合は、まず20本のローソク足が経過するまで待ってから、モデルが反転を予測しているかどうかを確認します。モデルを20ステップ先まで予測するように訓練したことを思い出してください。したがって、反転を確認する前に、ある程度の時間が経過するのを待つ必要があります。

//--- If we have no positions, follow the model's forecast
   if(PositionsTotal() == 0)
     {
      //--- Our model is suggesting we should buy
      if(model_state == 1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Buy(0.3,Symbol(),ask,0,0,"NZD JPY AI");
            system_state = 1;
           }
        }

      //--- Our model is suggesting we should sell
      if(model_state == -1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Sell(0.3,Symbol(),bid,0,0,"NZD JPY AI");
            system_state = -1;
           }
        }
     }

   else
     {
      //--- We want to wait 20 mins before forecating again.
      if(time_stamp != time)
        {
         time_stamp= time;
         counter += 1;
        }

      if((system_state!= model_state) && (counter >= 20))
        {
         Alert("Reversal detected by our AI system, closing all positions");
         Trade.PositionClose(Symbol());
         counter = 0;
        }
     }
  }

モデルから予測を取得する関数を定義しましょう。2つの別々のモデルがあり、それぞれを順番に呼び出す必要があることを思い出してください。

//+------------------------------------------------------------------+
//| Fetch a prediction from our models                               |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- Define the inputs
   vectorf close_inputs = vectorf::Zeros(1);
   vectorf residuals_inputs = vectorf::Zeros(3);

   close_inputs[0]     = (float) iClose(Symbol(),PERIOD_M1,0);
   residuals_inputs[0] = (float) iOpen(Symbol(),PERIOD_M1,0);
   residuals_inputs[1] = (float) iHigh(Symbol(),PERIOD_M1,0);
   residuals_inputs[2] = (float) iLow(Symbol(),PERIOD_M1,0);

//--- Fetch predictions
   OnnxRun(residuals_model,ONNX_DEFAULT,residuals_inputs,residuals_forecast);
   OnnxRun(close_model,ONNX_DEFAULT,close_inputs,close_forecast);

//--- Our forecast
   forecast = residuals_forecast[0] + close_forecast[0];
   Comment("Model forecast: ",forecast);

//--- Remember the model's prediction
   if(forecast > close_inputs[0])
     {
      model_state = 1;
     }
   else
     {
      model_state = -1;
     }
  }

市場価格を更新する関数も必要です。

//+------------------------------------------------------------------+
//| Update the market data we have                                   |
//+------------------------------------------------------------------+
void update_market_data(void)
  {
   bid = SymbolInfoDouble(Symbol(),SYMBOL_BID);
   ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK);
  }

この関数は、使用しなくなったリソースを解放します。

//+------------------------------------------------------------------+
//| Rlease the resources we no longer need                           |
//+------------------------------------------------------------------+
void release_resorces(void)
  {
   OnnxRelease(residuals_model);
   OnnxRelease(close_model);
   ExpertRemove();
  }

最後に、この関数は、アプリケーションの最初に作成したONNXバッファからONNXモデルを準備します。

//+------------------------------------------------------------------+
//| This function will load our ONNX models                          |
//+------------------------------------------------------------------+
bool load_onnx_models(void)
  {
//--- Load the ONNX models from the buffers we created
   residuals_model = OnnxCreateFromBuffer(residuals_onnx_buffer,ONNX_DEFAULT);
   close_model = OnnxCreateFromBuffer(close_onnx_buffer,ONNX_DEFAULT);

//--- Validate the models
   if((residuals_model == INVALID_HANDLE) || (close_model == INVALID_HANDLE))
     {
      //--- We failed to load the models
      Comment("Failed to create the ONNX models: ",GetLastError());
      return(false);
     }

//--- Set the I/O shapes of the models
   ulong residuals_inputs[] = {1,3};
   ulong close_inputs[]     = {1,1};
   ulong model_output[]     = {1,1};

//---- Validate the I/O shapes
   if((!OnnxSetInputShape(residuals_model,0,residuals_inputs)) || (!OnnxSetInputShape(close_model,0,close_inputs)))
     {
      //--- We failed to set the input shapes
      Comment("Failed to set model input shapes: ",GetLastError());
      return(false);
     }

   if((!OnnxSetOutputShape(residuals_model,0,model_output)) || (!OnnxSetOutputShape(close_model,0,model_output)))
     {
      //--- We failed to set the output shapes
      Comment("Failed to set model output shapes: ",GetLastError());
      return(false);
     }

//--- Everything went fine
   return(true);
  }
//+------------------------------------------------------------------+

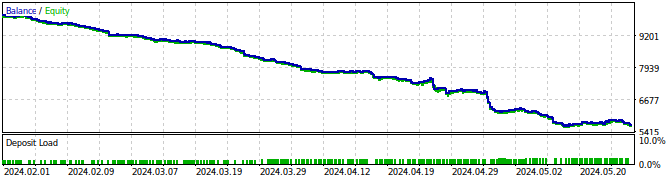
図27：EAのバックテスト

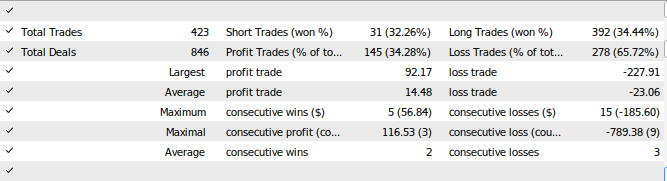
図28：EAのテスト結果

結論

この記事では、自己修正型取引アプリケーションの構築方法について紹介しました。特に、モデルの残差を分析し、機械学習モデルの過剰適合や偏りを検出する手法に焦点を当てました。しかし、最もパフォーマンスが高いと評価されたモデルの残差に問題があり、自己相関が見られることが判明しました。この問題は、時系列データとターゲットを差分処理することで解決可能ですが、同時にモデルの解釈性を損なうリスクも伴います。本記事で提示した方法がすべてのケースで成功を保証するわけではありませんが、取引戦略にAIを適用することに関心がある方にとって、十分に検討する価値のある内容です。次回の記事では、モデルの解釈性を維持しつつ、今回確認した課題を解決するアプローチを検討します。ぜひ次回もご覧ください。