Asesores Expertos Auto-Optimizables con MQL5 y Python (Parte IV): Apilamiento de modelos

En esta serie de artículos, analizaremos distintas formas de crear aplicaciones comerciales capaces de ajustarse dinámicamente a las condiciones cambiantes del mercado. Hay potencialmente infinitas formas de abordar este problema, pero es poco probable que todas las soluciones posibles sean válidas. Por lo tanto, nuestro objetivo hoy es demostrar y analizar empíricamente los méritos y las deficiencias de diferentes soluciones posibles, para ayudarle a mejorar sus estrategias comerciales.

Descripción general de la estrategia comercial

Dirigiremos nuestra atención a la previsión del par de divisas NZDJPY. Deseamos aprender algorítmicamente una estrategia comercial a partir de los datos que recopilaremos sobre el símbolo desde nuestro terminal MetaTrader 5. Como seres humanos, podemos tener una predisposición natural hacia estrategias comerciales que estén alineadas con nuestras propias creencias e intereses. Los modelos de aprendizaje automático también están sesgados. El sesgo de un modelo de aprendizaje automático es el grado en el que se violan las suposiciones hechas por el modelo. Nuestra estrategia comercial se basará en un conjunto de dos modelos de IA. El primer modelo se entrenará para predecir el precio de cierre futuro del par NZDJPY, 20 minutos en el futuro. El segundo modelo se entrenará para predecir la cantidad de error en la predicción realizada por el primer modelo. Esta técnica se conoce como apilamiento. Nuestra esperanza es que al combinar 2 modelos, podamos superar nuestro sesgo humano y, con suerte, esto será suficiente para llevarnos a niveles más altos de rendimiento.

Descripción general de la metodología

Obtuvimos aproximadamente 9000 filas de datos del mercado M1 en el par NZDJPY desde nuestro terminal MetaTrader 5 usando un script MQL5 personalizado. Creamos gráficos de dispersión 2D y 3D de los datos del mercado. Sin embargo, no pudimos identificar ninguna relación discernible en los datos. También realizamos una descomposición de series de tiempo en el conjunto de datos y pudimos identificar una clara tendencia descendente y la presencia de fuertes efectos estacionales en los datos.

Luego nuestros datos se dividieron en conjuntos de entrenamiento y de prueba. Se ajustó y evaluó un conjunto de 15 modelos diferentes en el conjunto de entrenamiento. El regresor de gradiente descendente estocástico (Stochastic Gradient Descent, SGD) fue el modelo con mejor rendimiento del grupo.

Posteriormente, cuando analizamos nuestras métricas de importancia de características, descubrimos que el precio alto parecía ser el predictor más informativo que teníamos para predecir el precio de cierre futuro del par NZDJPY. El precio Alto obtuvo el mejor puntaje de Información Mutua (Mutual Information, MI). Además, también empleamos la implementación de Scikit-learn del algoritmo de eliminación de características recursivas (Recursive Feature Elimination, RFE). Todos los predictores que tenemos fueron considerados importantes por el algoritmo RFE. Sin embargo, como veremos en nuestro debate, el mero hecho de que exista una relación no garantiza que podamos capturarla y modelarla con éxito.

Después de identificar nuestro modelo con mejor rendimiento, procedimos a ajustar los parámetros de nuestro modelo. Normalmente en nuestras discusiones, luego de ajustar los parámetros, procedemos a probar si hay sobreajuste comparando el rendimiento de nuestro modelo personalizado con el rendimiento del modelo predeterminado. Sin embargo, hay muchas formas diferentes de comprobar el sobreajuste. Hoy, decidimos probar el sobreajuste analizando los residuos de nuestro modelo. Observamos altos niveles de correlación entre los residuos de nuestro modelo y sus retardos. Normalmente, los residuos de un modelo que ha aprendido lo suficiente no deberían tener correlación. Por lo tanto, esto nos sugirió que nuestro modelo con mejor rendimiento podría no haber aprendido de manera efectiva, o que existen otros datos que podrían ayudarnos a explicar nuestro objetivo y no hemos incluido esos datos.

Luego, registramos los residuos de nuestro modelo en los conjuntos de entrenamiento y prueba. En este momento no pudimos adaptar el modelo al conjunto de pruebas. Luego, validamos de forma cruzada nuestro conjunto de 15 modelos en los residuos de entrenamiento de nuestro regresor SGD. Nuestro modelo con mejor rendimiento fue la regresión Lasso, sin embargo, seleccionamos el tercer mejor modelo, una red neuronal profunda (Deep Neural Network, DNN), como nuestra solución candidata. Nuestra razón para hacerlo fue la flexibilidad que nos ofrece la red neuronal profunda, que nos da la oportunidad de ajustarla mejor a los datos de lo que podríamos ajustar Lasso debido a su número limitado de parámetros de ajuste.

Ajustamos nuestro regresor DNN para predecir los residuos de nuestro regresor SGD en un proceso de 2 pasos que resultó en 2 modelos únicos. Primero realizamos 100 iteraciones de una búsqueda aleatoria sobre los parámetros de nuestro regresor DNN, y así creamos el primer modelo. Los mejores parámetros continuos que identificamos se utilizaron como punto de partida para un intento de optimización global sin restricciones utilizando el algoritmo de memoria limitada L-BFGS-B, y así es como obtuvimos nuestro segundo modelo. Ambos modelos superaron al regresor DNN predeterminado en datos de validación no vistos. Además, nuestro último modelo fue el que obtuvo mejores resultados, lo que significa que no perdimos el tiempo dando estos pasos adicionales por partida doble.

Finalmente, exportamos ambos modelos al formato ONNX y procedimos a construir un Asesor Experto impulsado por IA que ha aprendido a corregir sus propios errores.

Obteniendo los datos que necesitamos

Comenzaremos obteniendo los datos que necesitamos de nuestro terminal MetaTrader 5. El script adjunto a continuación obtendrá tantas barras de datos de precios históricos como especifiquemos desde nuestro terminal, antes de escribir esos datos en formato CSV y almacenarlos para nosotros en nuestra carpeta "Files".

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| Script Inputs                                                    |
//+------------------------------------------------------------------+
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int rsi_handler;
double rsi_buffer[];

//+------------------------------------------------------------------+
//| On start function                                                |
//+------------------------------------------------------------------+
void OnStart()
  {

//--- Load indicator
   rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,20,PRICE_CLOSE);
   CopyBuffer(rsi_handler,0,0,size,rsi_buffer);
   ArraySetAsSeries(rsi_buffer,true);

//--- File name
   string file_name = "Market Data " + Symbol() + ".csv";

//--- Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i)
                  );
        }
     }
//--- Close the file
   FileClose(file_handle);

  }
//+------------------------------------------------------------------+

Limpieza de datos

Comenzaremos formateando nuestros datos. Primero, cargamos las bibliotecas que necesitamos.

#Import the libraries we need
import pandas as pd
import numpy as np

Ahora lea los datos del mercado.

#Read in the market data
nzd_jpy = pd.read_csv('Market Data NZDJPY.csv')

Los datos están en el orden incorrecto, restablezámoslos para que comiencen desde la fecha más antigua y la fecha más cercana al momento actual sea la última.

#Format the data
nzd_jpy = nzd_jpy[::-1]
nzd_jpy.reset_index(inplace=True, drop=True)

Definir el objetivo.

#Labelling the data
nzd_jpy['Target'] = nzd_jpy['Close'].shift(-20)
nzd_jpy.dropna(inplace=True)

También agregaremos objetivos binarios para fines de trazado.

#Add binary target for plotting
nzd_jpy['Binary Target'] = np.nan
nzd_jpy.loc[nzd_jpy['Close'] > nzd_jpy['Target'],'Binary Target'] = 1
nzd_jpy.loc[nzd_jpy['Close'] <= nzd_jpy['Target'],'Binary Target'] = 0

Inspeccionemos los datos.

#Current state of our dataframe
nzd_jpy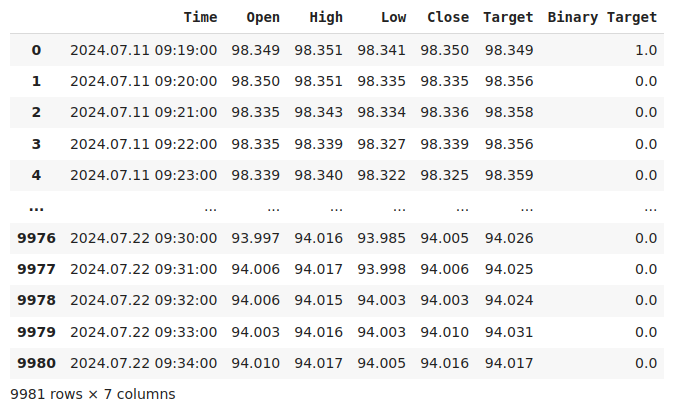

Figura 1: Nuestro marco de datos actual.

Análisis exploratorio de datos

Creemos diagramas de dispersión para determinar si hay alguna relación que podamos observar. Desafortunadamente, nuestros datos parecen estar distribuidos aleatoriamente sin separaciones claras entre los movimientos ascendentes y descendentes del mercado.

#Lets perform scatter plots
sns.scatterplot(data=nzd_jpy,x=nzd_jpy['Open'], y=nzd_jpy['Close'],hue='Binary Target')

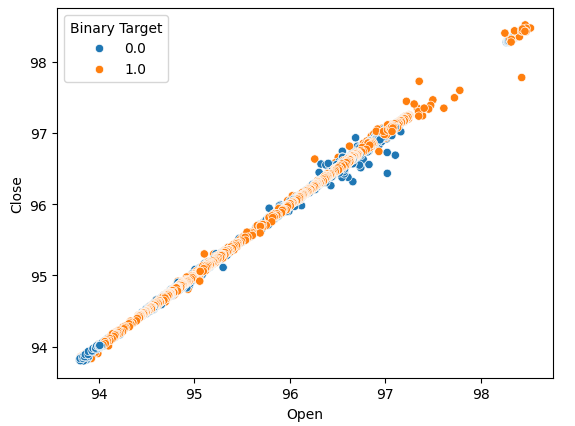
Figura 2: Un diagrama de dispersión del precio de apertura y cierre.

Pensamos en crear diagramas de caja para resumir todos los casos en los que el precio subió o bajó. Creíamos que potencialmente podría haber diferencias entre la distribución de datos en estos dos posibles objetivos. Lamentablemente, nuestros diagramas de caja muestran que prácticamente no hay diferencia entre la distribución de datos en los dos resultados posibles.

#Let's create categorical box plots
sns.catplot(data=nzd_jpy,x='Binary Target',y='Close',kind='box')

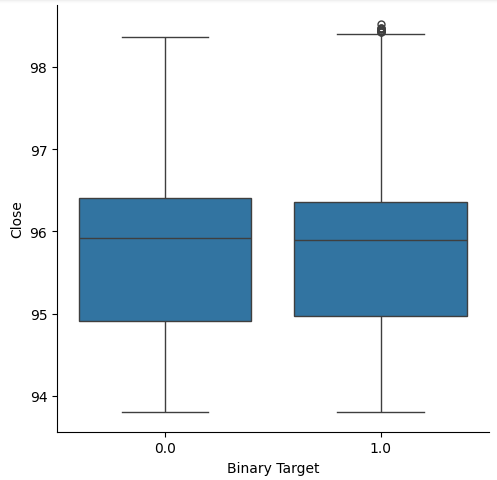
Figura 3: Diagrama de caja que resume todos los casos en los que los niveles de precios cayeron (0) o aumentaron (1).

También podemos descomponer los datos de series de tiempo en tres componentes:

1. Tendencia
2. Estacional
   
3. Residual
   

 El componente de tendencia representa el movimiento promedio a largo plazo de los niveles de precios. El componente estacional da cuenta de patrones cíclicos que se observan repetidamente en los datos, mientras que los componentes residuales son el resto de lo que no pudo explicarse con los dos componentes anteriores. Dado que utilizamos datos M1 en el par NZDJPY, establecemos nuestro período en 1440, o en otras palabras, el rendimiento promedio del precio durante 1 día completo. Podemos observar una tendencia bajista muy clara y fuerte en los datos incluso antes de realizar la descomposición. Sin embargo, al restar la tendencia de los datos originales, ahora podemos observar claramente los efectos estacionales en los datos.

#Time series decomposition
import statsmodels.api as sm
nzd_jpy_decomposition = sm.tsa.seasonal_decompose(nzd_jpy['Close'],period=1440,model='additive')
fig = nzd_jpy_decomposition.plot()

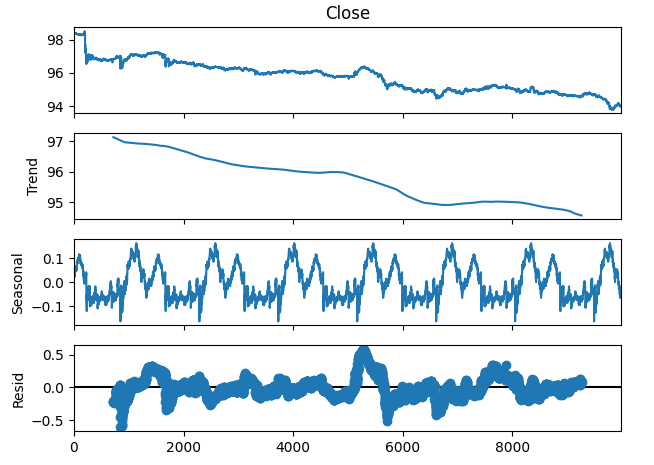
Figura 4: Descomposición de series temporales de nuestros datos.

Algunos efectos pueden estar ocultos en dimensiones superiores. La creación de diagramas de dispersión 3D de nuestros datos puede permitirnos revelar efectos ocultos más allá de nuestro alcance con un diagrama de dispersión 2D. Desafortunadamente, este conjunto de datos no fue uno de esos casos. Nuestros datos aún son bastante difíciles de separar y no muestran ninguna relación discernible.

#Let's also perform 3D plots
#Visualizing our data in 3D

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(7,7))
ax = fig.add_subplot(111,projection='3d')
colors = ['blue' if movement == 0 else 'red' for movement in nzd_jpy.loc[:,"Binary Target"]]
ax.scatter(nzd_jpy.loc[:,"Low"],nzd_jpy.loc[:,"High"],nzd_jpy.loc[:,"Close"],c=colors)

ax.set_xlabel('NZDJPY Low')
ax.set_ylabel('NZDJPY High')
ax.set_zlabel('NZDJPY Close')

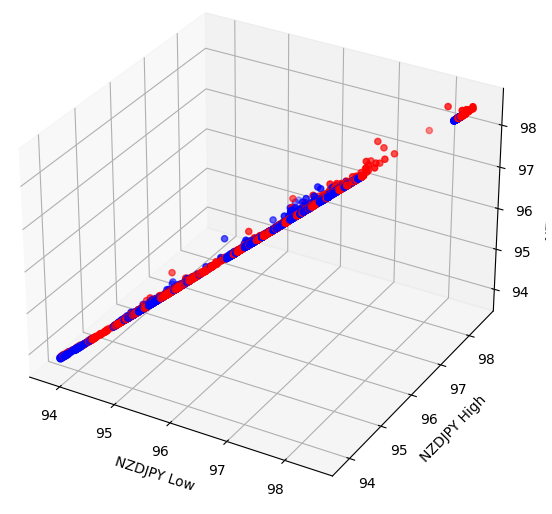
Figura 5: Visualización de nuestro diagrama de dispersión 3D.

Preparación para modelar los datos

Antes de que podamos comenzar a modelar nuestros datos, primero debemos estandarizarlos y escalarlos. Cargue las bibliotecas que necesitamos.

#Let's prepare the data for modelling
from sklearn.preprocessing import RobustScaler

Escalar los datos.

#Scale the data
X = pd.DataFrame(RobustScaler().fit_transform(nzd_jpy.loc[:,['Close']]),columns=['Close'])
residuals_X = pd.DataFrame(RobustScaler().fit_transform(nzd_jpy.loc[:,['Open','High','Low']]),columns=['Open','High','Low'])
y = nzd_jpy.loc[:,'Target']

Selección de modelos

Carguemos las bibliotecas que necesitamos para modelar los datos.

#Cross validating the models
from sklearn.model_selection import cross_val_score,train_test_split
from sklearn.linear_model import Lasso,LinearRegression,Ridge,ElasticNet,SGDRegressor,HuberRegressor
from sklearn.ensemble import RandomForestRegressor,GradientBoostingRegressor,AdaBoostRegressor,ExtraTreesRegressor,BaggingRegressor
from sklearn.svm import LinearSVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.neural_network import MLPRegressor

Ahora divide los datos en dos mitades.

#Create train-test splits
train_X,test_X,train_y,test_y = train_test_split(nzd_jpy.loc[:,['Close']],y,test_size=0.5,shuffle=False)
residuals_train_X,residuals_test_X,residuals_train_y,residuals_test_y = train_test_split(nzd_jpy.loc[:,['Open','High','Low']],y,test_size=0.5,shuffle=False)

Almacene los modelos en una lista y cree un marco de datos para almacenar nuestros niveles de error de validación.

#Store the models
models = [
    Lasso(),
    LinearRegression(),
    Ridge(),
    ElasticNet(),
    SGDRegressor(),
    HuberRegressor(),
    RandomForestRegressor(),
    GradientBoostingRegressor(),
    AdaBoostRegressor(),
    ExtraTreesRegressor(),
    BaggingRegressor(),
    LinearSVR(),
    KNeighborsRegressor(),
    DecisionTreeRegressor(),
    MLPRegressor(),
]

#Store the names of the models
model_names = [
    'Lasso',
    'Linear Regression',
    'Ridge',
    'Elastic Net',
    'SGD Regressor',
    'Huber Regressor',
    'Random Forest Regressor',
    'Gradient Boosting Regressor',
    'Ada Boost Regressor',
    'Extra Trees Regressor',
    'Bagging Regressor',
    'Linear SVR',
    'K Neighbors Regressor',
    'Decision Tree Regressor',
    'MLP Regressor',
]

#Create a dataframe to store our cv error
cv_error = pd.DataFrame(columns=model_names,index=np.arange(0,5))

Validar de forma cruzada cada modelo.

#Cross validate each model
for model in models:
  cv_score = cross_val_score(model,X,y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
  for i in np.arange(0,5):
    index = models.index(model)
    cv_error.iloc[i,index] = cv_score[i]

Visualizando los resultados.

cv_error

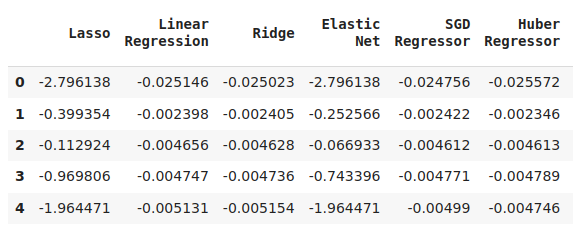
Figura 6: Algunos de nuestros niveles de error al pronosticar el precio de cierre futuro del NZDJPY.

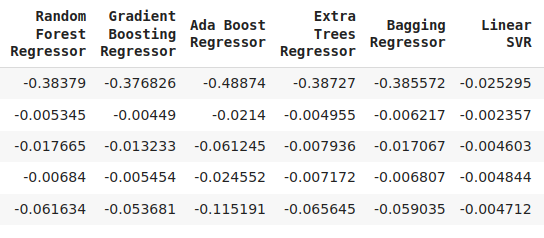
Figura 7: Una continuación de nuestros niveles de error.

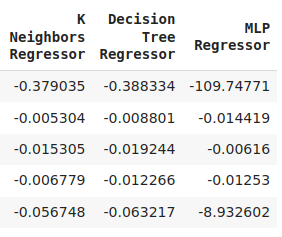
Figura 8: Nuestros niveles de error del modelo final.

Podemos representar gráficamente nuestros niveles de rendimiento en los cinco aspectos. El bajo rendimiento de nuestra red neuronal fue alarmante cuando visualizamos los datos en este formato. Probablemente sería mucho más beneficioso ajustar los parámetros.

cv_error.plot()

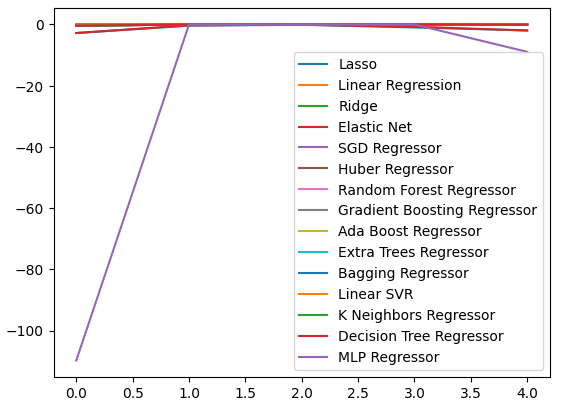
Figura 9: Visualizando nuestros niveles de error.

Los diagramas de caja nos ayudan a resumir mucha información en un solo gráfico. Por ejemplo, en nuestros gráficos a continuación, podemos ver claramente cuán mal se desempeñó la DNN en esta tarea. Es el último modelo a la derecha y muestra mucha más variación en su rendimiento que los otros modelos.

sns.boxplot(cv_error)

Figura 10: Visualizando nuestros errores como diagramas de caja.

Podemos identificar el modelo con mejor rendimiento como el modelo con los niveles de error medio más bajos.

#Our mean validation error
cv_error.mean()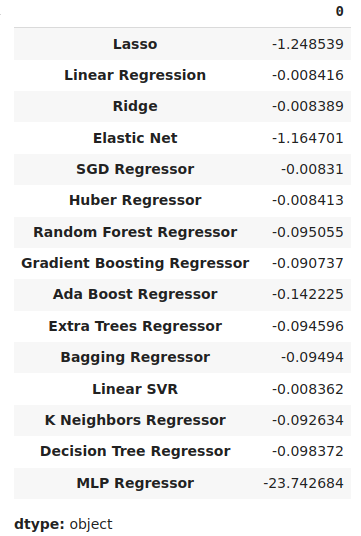

Figura 11: Visualización de nuestros niveles de error medio.

Importancia de las características

Los algoritmos de importancia de características nos ayudan a comprender si nuestro modelo ha aprendido asociaciones significativas o si ha aprendido relaciones que quizás no conocíamos. Primero, importemos las bibliotecas que necesitamos.

#Feature importance
from sklearn.feature_selection import mutual_info_regression,RFE

Comenzaremos calculando las puntuaciones de información mutua (Mutual Information, MI). MI nos informa sobre el potencial que posee cada predictor, para ayudarnos a predecir el objetivo. Por último, MI se mide en una escala logarítmica. Por lo tanto, en la práctica rara vez se observan puntuaciones MI superiores a 3.

mi_score = pd.DataFrame(mutual_info_regression(X,y),columns=['MI Score'],index=X.columns)

Al trazar nuestras puntuaciones MI, se muestra claramente que el precio alto parece tener el mayor potencial para predecir el precio de cierre futuro del NZDJPY.

mi_score.plot()

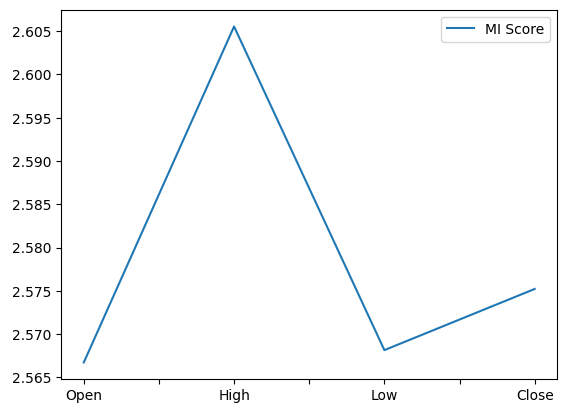
Figura 12: Representación gráfica de nuestras puntuaciones MI.

El algoritmo RFE es tan sencillo de utilizar como casi cualquier objeto de la biblioteca Scikit-learn. Simplemente creamos una instancia de la clase y la ajustamos a los datos, antes de poder evaluar los niveles de importancia de las características que atribuye a cada predictor. Nuestro algoritmo RFE consideró que todos los predictores eran igualmente importantes para predecir el precio de cierre del NZDJPY.

#Select the best features
rfe = RFE(model, n_features_to_select=5, step=1)
rfe = rfe.fit(X, y)
rfe.ranking_

array([1, 1, 1, 1])

Ajuste de parámetros

Extraigamos ahora el máximo rendimiento que podamos de nuestro modelo regresor SGD. Realizaremos una búsqueda aleatoria sobre una muestra del espacio de parámetros del modelo. Primero importemos las bibliotecas que necesitamos.

#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV

Crea una instancia del modelo predeterminado.

#Initialize the model
model = SGDRegressor()

Cree un objeto sintonizador y especifique los posibles valores de parámetros que nos gustaría muestrear.

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "loss" : ['squared_error', 'huber', 'epsilon_insensitive','squared_epsilon_insensitive'],
        "penalty":['l2','l1', 'elasticnet', None],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001,10,100,1000,10000,100000],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "fit_intercept": [True,False],
        "early_stopping": [True,False],
        "learning_rate":['constant','optimal','adaptive','invscaling'],
        "shuffle": [True,False]
        },
        n_iter=100,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Ajustar el objeto afinador.

#Fit the tuner
tuner.fit(train_X,train_y)

Los mejores parámetros que encontramos.

#Our best parameters
tuner.best_params_

{'tol': 0.001,
 'shuffle': False,
 'penalty': 'elasticnet',
 'loss': 'huber',
 'learning_rate': 'adaptive',
 'fit_intercept': True,
 'early_stopping': True,
 'alpha': 1e-05}

Prueba de sobreajuste

Podemos detectar sobreajuste si observamos correlación en los residuos del modelo. Si un modelo ha aprendido eficazmente, sus residuos deberían ser ruido blanco aleatorio, lo que indica que no hay un patrón predecible en los errores que comete nuestro modelo. Sin embargo, un modelo que demuestre autocorrelación en sus residuos puede ser motivo de preocupación. Puede indicar que la regresión que hemos realizado es espuria o que hemos seleccionado un modelo inadecuado para nuestra tarea. Para comenzar, necesitamos capturar los residuos de nuestro modelo personalizado.

#Model validation
model = SGDRegressor(
    tol             = tuner.best_params_['tol'],
    shuffle         = tuner.best_params_['shuffle'],
    penalty         = tuner.best_params_['penalty'],
    loss            = tuner.best_params_['loss'],
    learning_rate   = tuner.best_params_['learning_rate'],
    alpha           = tuner.best_params_['alpha'],
    fit_intercept   = tuner.best_params_['fit_intercept'],
    early_stopping  = tuner.best_params_['early_stopping']
)
model.fit(train_X,train_y)
residuals = test_y - model.predict(test_X)

Podemos visualizar los residuos de nuestro modelo en un gráfico. Desafortunadamente, podemos ver claramente que hay autocorrelación en los residuos del modelo. En otras palabras, cuando los residuos caen, tienden a seguir cayendo, y cuando los residuos aumentan, tienden a seguir aumentando. Esto significa que los valores futuros de los residuos pueden tener una relación con sus valores anteriores, una señal reveladora de que nuestro modelo puede no haber aprendido de manera efectiva, incluso después de realizar el ajuste de parámetros.

#Plot the residuals
residuals.plot()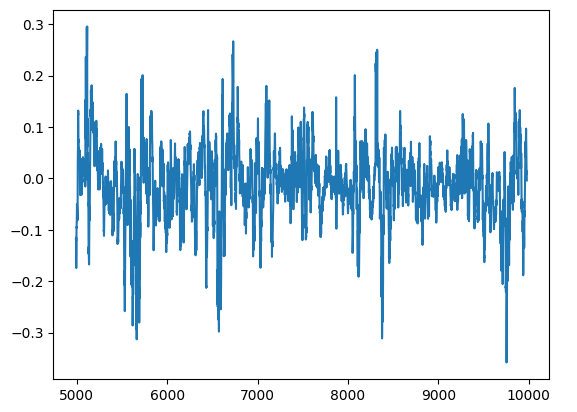

Figura 13: Residuos de nuestro modelo.

Existen pruebas más robustas para la autocorrelación, por ejemplo, podemos crear un gráfico de autocorrelación (Autocorrelation Function, ACF). El gráfico ACF tendrá picos en cada valor de rezago posible. La altura de cada pico representa los niveles de correlación que tienen los datos de la serie temporal con su valor retardado. También hay una estructura similar a un cono azul en el fondo de nuestro gráfico; el cono azul representa nuestros intervalos de confianza. Cualquier nivel de correlación más allá del intervalo de confianza se considera estadísticamente significativo.

#The residuals appear to have autocorrelation
from statsmodels.graphics.tsaplots import plot_acf
fig = plot_acf(residuals)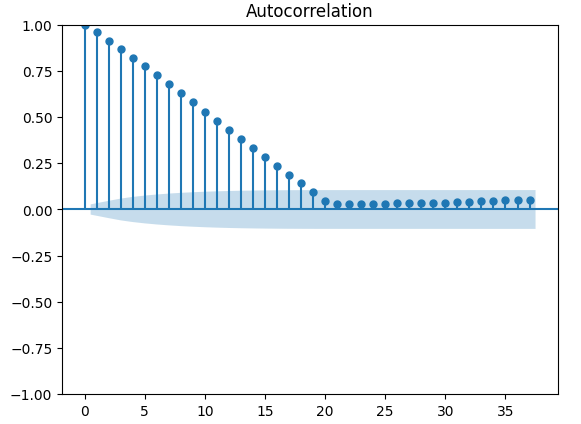

Figura 14: La autocorrelación de los residuos de nuestro modelo.

Esto no es una buena señal, esperamos que podamos aliviarlo entrenando nuestra DNN para corregir nuestro primer modelo. Registremos los errores de nuestro regresor SGD en los datos de entrenamiento y luego en los datos de prueba. Tenga en cuenta que en este punto no ajustaremos el modelo a los datos de prueba, solo mediremos sus niveles de error.

#Prepare the residuals for our second model
model = SGDRegressor(tol= 0.001,
 shuffle=False,
 penalty= 'elasticnet',
 loss= 'huber',
 learning_rate='adaptive',
 fit_intercept= True,
 early_stopping= True,
 alpha= 1e-05)

#Store the model residuals
model.fit(train_X,train_y)
residuals_train_y = train_y - model.predict(train_X)
residuals_test_y = test_y - model.predict(test_X)

Ahora validaremos nuestros modelos para predecir los niveles de error del regresor SGD.

#Cross validate each model
for model in models:
  cv_score = cross_val_score(model,residuals_train_X,residuals_train_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
  for i in np.arange(0,5):
    index = models.index(model)
    cv_error.iloc[i,index] = cv_score[i]

Visualicemos el error de validación.

#Cross validaton error levels
cv_error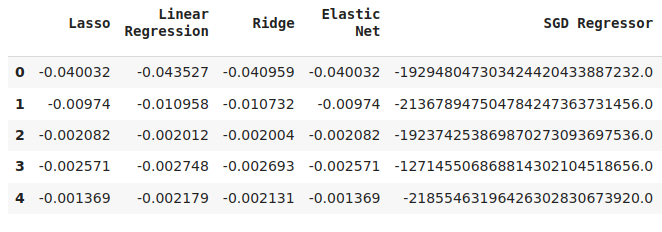

Figura 15: Algunos de los niveles de error de validación del modelo al pronosticar los niveles de error de nuestro primer modelo.

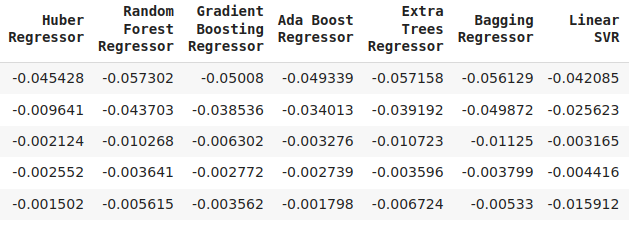
Figura 16: Una continuación de nuestros niveles de error de validación.

Podemos ver nuestros niveles de error promedio en orden descendente para identificar rápidamente nuestro modelo con mejor rendimiento.

#Store the model's performance
cv_error.mean().sort_values(ascending=False)

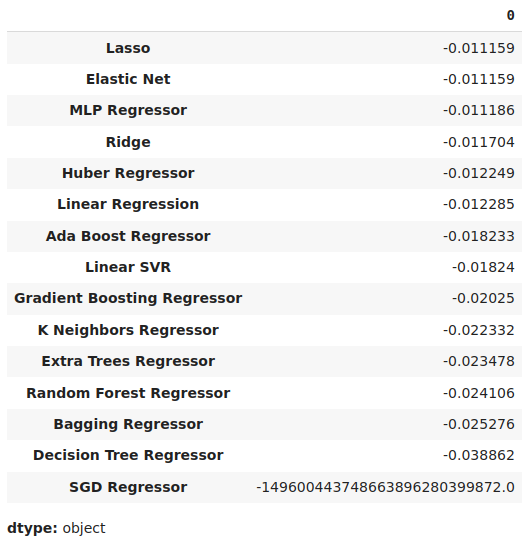
Figura 17: Nuestros niveles de error de validación promedio muestran claramente que Lasso es el modelo con mejor rendimiento que tenemos.

Nuestros diagramas de caja muestran cuán pobremente funcionó el regresor SGD al intentar predecir sus propios niveles de error.

sns.boxplot(cv_error)

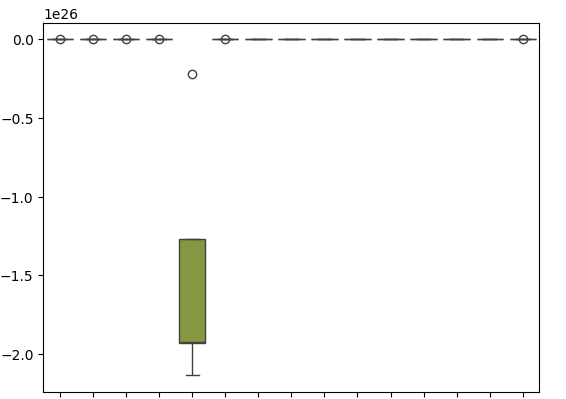
Figura 18: Diagramas de caja de nuestro error de validación al pronosticar los residuos de nuestro modelo.

También podemos crear gráficos lineales para visualizar nuestros datos.

cv_error.plot()

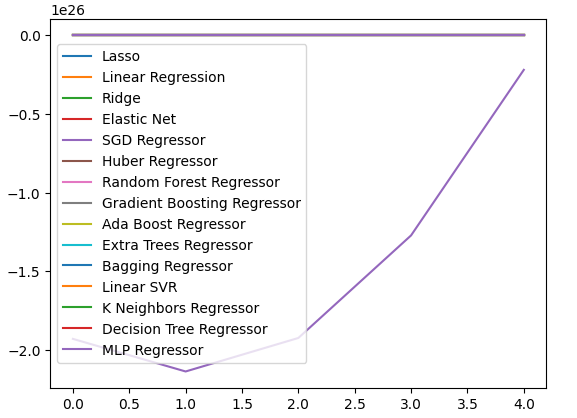
Figura 19: Visualización de nuestros niveles de error y gráficos de líneas.

Ajuste de parámetros de nuestra red neuronal profunda

Preparémonos ahora para ajustar los parámetros de nuestro regresor DNN, primero definiremos el objeto sintonizador y una muestra del espacio de parámetros que deseamos buscar.

#Let's tune the model
#Reinitialize the model

model = MLPRegressor()

#Define the tuner

tuner = RandomizedSearchCV(
        model,
        {
                "activation":["relu","tanh","logistic","identity"],
                "solver":["adam","sgd","lbfgs"],
                "alpha":[0.1,0.01,0.001,0.00001,0.000001],
                "learning_rate": ["constant","invscaling","adaptive"],
                "learning_rate_init":[0.1,0.01,0.001,0.0001,0.000001,0.0000001],
                "power_t":[0.1,0.5,0.9,0.01,0.001,0.0001],
                "shuffle":[True,False],
                "tol":[0.1,0.01,0.001,0.0001,0.00001],
                "hidden_layer_sizes":[(10,20),(100,200),(30,200,40),(5,20,6)],
                "max_iter":[10,50,100,200,300],
                "early_stopping":[True,False]
        },
        n_iter=100,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Ahora ajustaremos el objeto sintonizador.

#Fit the tuner
tuner.fit(residuals_train_X,residuals_train_y)

Finalmente podemos ver los mejores parámetros que encontramos.

#The best parameters we found
tuner.best_params_

{'tol': 0.0001,
 'solver': 'lbfgs',
 'shuffle': False,
 'power_t': 0.5,
 'max_iter': 300,
 'learning_rate_init': 0.01,
 'learning_rate': 'constant',
 'hidden_layer_sizes': (30, 200, 40),
 'early_stopping': False,
 'alpha': 1e-05,
 'activation': 'identity'}

Ajuste más profundo de parámetros

Ahora probemos para ver si no podemos encontrar parámetros aún mejores, ya que no sabemos necesariamente dónde pueden estar los mejores valores de entrada, intentaremos realizar una optimización global sin restricciones utilizando el algoritmo de memoria limitada L-BFGS-B en la biblioteca SciPy. El algoritmo L-BFGS-B se puede utilizar eficazmente para problemas de optimización global. El solucionador numérico en sí está implementado en código Fortran, y la biblioteca SciPy proporciona un envoltorio delgado para interactuar fácilmente con la rutina. Comenzaremos importando las librerías que necesitamos.

Figura 20: Los desarrolladores del algoritmo BFGS original, de izquierda a derecha: Broyden, Fletcher, Goldfarb y Shanno.

#Deeper optimization
from scipy.optimize import minimize

Ahora definiremos la función objetivo a minimizar, queremos minimizar el error de entrenamiento de nuestro regresor DNN. Arreglaremos todos los demás parámetros de entrada del modelo ya que nuestros minimizadores SciPy solo pueden manejar problemas de optimización continua.

#Define the objective function
def objective(x):
    #Create a dataframe to store our accuracy
    cv_error = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])
    #The parameter x represents a new value for our neural network's settings
    #In order to find optimal settings, we will perform 10 fold cross validation using the new setting
    #And return the average RMSE from all 10 tests
    #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization
    MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=x[0],tol=x[1])
    model = MLPRegressor(
    tol                 = x[0],
    solver              = tuner.best_params_['solver'],
    power_t             = x[1],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = x[2],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = x[3],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
    )
    #Cross validate the model
    cv_score = cross_val_score(model,residuals_train_X,residuals_train_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
    for i in np.arange(0,5):
      cv_error.iloc[i,0] = cv_score[i]
    #Return the Mean CV RMSE
    return(cv_error.iloc[:,0].mean())

Definiremos el punto de partida de nuestro procedimiento de optimización por los mejores parámetros que encontremos en nuestra búsqueda aleatoria. También pasaremos restricciones para nuestro procedimiento de optimización, forzaremos a que todos los valores sean positivos y además permitiremos todos los valores en el rango de 10 a la potencia -100 hasta 10 a la potencia 100. Este es un dominio muy grande y esperamos que contenga los parámetros óptimos que estamos buscando.

#Define the starting point
pt = [tuner.best_params_['tol'],tuner.best_params_['power_t'],tuner.best_params_['learning_rate_init'],tuner.best_params_['alpha']]
bnds = ((10.0 ** -100,10.0 ** 100),
        (10.0 ** -100,10.0 ** 100),
        (10.0 ** -100,10.0 ** 100),
        (10.0 ** -100,10.0 ** 100))

Buscando los mejores parámetros.

#Searching deeper for better parameters
result = minimize(objective,pt,method="L-BFGS-B",bounds=bnds)

Nuestros resultados de optimización.

result

message: CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
  success: True
   status: 0
      fun: -0.01143352283130129
        x: [ 1.000e-04  5.000e-01  1.000e-02  1.000e-05]
      nit: 2
      jac: [-1.388e+04 -4.657e+04  5.625e+04 -1.033e+04]
     nfev: 120
     njev: 24
 hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>

Prueba de sobreajuste

Ahora probemos si hay sobreajuste. Esta vez, compararemos nuestros dos modelos contra el rendimiento del regresor DNN predeterminado. Instanciemos instancias de cada regresor DNN que deseamos probar.

#Model validation
default_model = MLPRegressor()

customized_model = MLPRegressor(
    tol                 = tuner.best_params_['tol'],
    solver              = tuner.best_params_['solver'],
    power_t             = tuner.best_params_['power_t'],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = tuner.best_params_['learning_rate_init'],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = tuner.best_params_['alpha'],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
)

lbfgs_customized_model = MLPRegressor(
    tol                 = result.x[0],
    solver              = tuner.best_params_['solver'],
    power_t             = result.x[1],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = result.x[2],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = result.x[3],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
)

Ahora crearemos una lista de modelos y también crearemos un marco de datos para almacenar nuestros niveles de error de validación.

models = [default_model,customized_model,lbfgs_customized_model]
cv_error = pd.DataFrame(index=np.arange(0,5),columns=['Default NN','Random Search NN','L-BFGS-B NN'])

Validación cruzada de cada modelo.

#Cross validate the model
for model in models:
  model.fit(residuals_train_X,residuals_train_y)
  cv_score = cross_val_score(model,residuals_test_X,residuals_test_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error')
  for i in np.arange(0,5):
    index = models.index(model)
    cv_error.iloc[i,index] = cv_score[i]

Nuestro error de validación cruzada.

cv_error

NN predeterminado	Búsqueda aleatoria NN	L-BFGS-B NN
-0.007735	-0.007708	-0.007692
-0.00635	-0.006344	-0.006329
-0.003307	-0.003265	-0.00328
0.005225	-0.004803	-0.004761
-0.004469	-0.004447	-0.004492

Ahora analicemos nuestros niveles de error promedio.

cv_error.mean().sort_values(ascending=False)

Modelo	Error de validación
L-BFGS-B NN	-0.005311
Búsqueda aleatoria NN	-0.005313
NN predeterminado	-0.005417

Como podemos ver, todos nuestros modelos funcionaron dentro del mismo rango. Sin embargo, nuestros modelos personalizados claramente nos proporcionaban niveles de error más bajos en promedio. Desafortunadamente, la varianza que muestran nuestros modelos es casi la misma en todos los ámbitos, esto nos lo muestran nuestros diagramas de caja. Los niveles de varianza nos ayudan a determinar el nivel de habilidad del modelo.

sns.boxplot(cv_error)

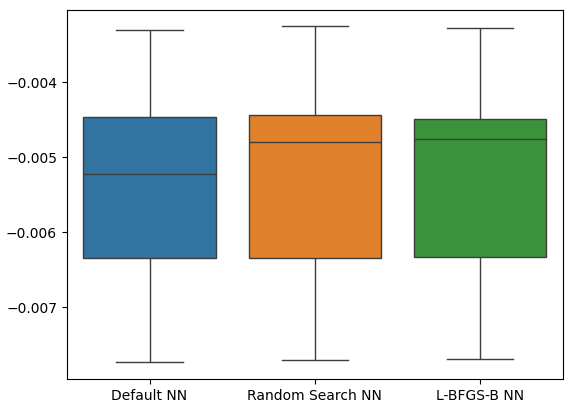
Figura 21: Nuestros niveles de error de validación en los datos retenidos.

Veamos ahora si nuestro enfoque de conjunto es mejor que utilizar simplemente un único modelo para pronosticar los niveles de precios. Primero prepararemos los modelos que necesitamos.

#Now that we have come this far, let's see if our ensemble approach is worth the trouble
baseline = LinearRegression()
default_nn = MLPRegressor()

#The SGD Regressor will predict the future price
sgd_regressor = SGDRegressor(tol= 0.001,
 shuffle=False,
 penalty= 'elasticnet',
 loss= 'huber',
 learning_rate='adaptive',
 fit_intercept= True,
 early_stopping= True,
 alpha= 1e-05)

#The deep neural network will predict the error in the SGDRegressor's prediction
lbfgs_customized_model = MLPRegressor(
    tol                 = result.x[0],
    solver              = tuner.best_params_['solver'],
    power_t             = result.x[1],
    max_iter            = tuner.best_params_['max_iter'],
    learning_rate       = tuner.best_params_['learning_rate'],
    learning_rate_init  = result.x[2],
    hidden_layer_sizes  = tuner.best_params_['hidden_layer_sizes'],
    alpha               = result.x[3],
    early_stopping      = tuner.best_params_['early_stopping'],
    activation          = tuner.best_params_['activation'],
)

Ajuste del modelo al conjunto de entrenamiento.

#Fit the models on the train set
baseline.fit(train_X.loc[:,['Close']],train_y)
default_nn.fit(train_X.loc[:,['Close']],train_y)
sgd_regressor.fit(train_X.loc[:,['Close']],train_y)
lbfgs_customized_model.fit(residuals_train_X.loc[:,['Open','High','Low']],residuals_train_y)

Almacene los modelos en una lista.

#Store the models in a list
models = [baseline,default_nn,sgd_regressor,lbfgs_customized_model]

Creando un marco de datos para almacenar nuestros niveles de error.

#Create a dataframe to store our error
ensemble_error = pd.DataFrame(index=np.arange(0,5),columns=['Baseline','Default NN','SGD','Customized NN'])

Importando las librerias que necesitamos.

from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import mean_squared_error

Cree el objeto de división de series de tiempo.

#Create the time-series object
tscv = TimeSeriesSplit(n_splits=5,gap=20)

Necesitamos restablecer los índices de nuestros datos.

#Reset the indexes so we can perform cross validation
test_y = test_y.reset_index()
residuals_test_y = residuals_test_y.reset_index()

test_X = test_X.reset_index()
residuals_test_X = residuals_test_X.reset_index()

Ahora realizaremos una validación cruzada de series de tiempo. Tenga en cuenta que el modelo que predice los residuos debe entrenarse por separado de los otros modelos que simplemente predicen el precio de cierre futuro.

#Cross validate the models
for j in np.arange(0,4):
  model = models[j]
  for i,(train,test) in enumerate(tscv.split(test_X)):
    #The model predicting the residuals
    if(j == 3):
      model.fit(residuals_test_X.loc[train[0]:train[-1],['Open','High','Low']],residuals_test_y.loc[train[0]:train[-1],'Target'])
      #Measure the loss
      ensemble_error.iloc[i,j] = mean_squared_error(residuals_test_y.loc[test[0]:test[-1],'Target' ], model.predict(residuals_test_X.loc[test[0]:test[-1],['Open','High','Low']]))

    elif(j <= 2):
      #Fit the model
      model.fit(test_X.loc[train[0]:train[-1],['Close']],test_y.loc[train[0]:train[-1],'Target'])
      #Measure the loss
      ensemble_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],'Target' ],model.predict(test_X.loc[test[0]:test[-1],['Close']]))

Ahora analicemos nuestros niveles de error de validación. Lamentablemente, no pudimos superar el desempeño de un modelo de regresión lineal simple, lo que indica que nuestro modelo puede ser demasiado sensible a la varianza de los datos. La buena noticia es que superamos a nuestro regresor DNN predeterminado.

ensemble_error.mean().sort_values(ascending=True)

Modelos	Error de validación
Base	0.004784
L-BFGS-B NN personalizado	0.004891
SGD	0.005937
NN predeterminado	35.35851

Exportación al formato ONNX

Open Neural Network Exchange (ONNX) es un protocolo de código abierto para crear e implementar modelos de aprendizaje automático de manera independiente del lenguaje. ONNX nos permite integrar fácilmente nuestros modelos scikit-learn en nuestros Asesores Expertos confiando en el soporte de la API MQL5 para ONNX. Primero, importaremos las bibliotecas que necesitamos.

#Prepare to export to ONNX
import onnx
import netron
from   skl2onnx import convert_sklearn
from   skl2onnx.common.data_types import FloatTensorType

Ahora ajustemos los modelos a todos los datos que tenemos disponibles.

#Fit the SGD model on all the data we have
close_model = SGDRegressor(tol= 0.001,
 shuffle=False,
 penalty= 'elasticnet',
 loss= 'huber',
 learning_rate='adaptive',
 fit_intercept= True,
 early_stopping= True,
 alpha= 1e-05)

close_model.fit(nzd_jpy.loc[:,['Close']],nzd_jpy.loc[:,'Target'])

Luego por último ajustaremos nuestro regresor DNN.

#Fit the deep neural network on all the data we have
residuals_model = MLPRegressor(
 tol=0.0001,
 solver= 'lbfgs',
 shuffle=False,
 power_t= 0.5,
 max_iter= 300,
 learning_rate_init= 0.01,
 learning_rate='constant',
 hidden_layer_sizes=(30, 200, 40),
 early_stopping=False,
 alpha=1e-05,
 activation='identity')

#Fit the model on the residuals
residuals_model.fit(residuals_train_X,residuals_train_y)
residuals_model.fit(residuals_test_X,residuals_test_y)

Definamos las formas de entrada de nuestros 2 modelos.

# Define the input type
close_initial_types = [("float_input",FloatTensorType([1,1]))]
residuals_initial_types = [("float_input",FloatTensorType([1,3]))]

Necesitamos crear representaciones ONNX de nuestros modelos.

# Create the ONNX representation
close_onnx_model = convert_sklearn(close_model,initial_types=close_initial_types,target_opset=12)
residuals_onnx_model = convert_sklearn(residuals_model,initial_types=residuals_initial_types,target_opset=12)

Por último, necesitamos almacenar nuestros modelos en formato ONNX.

#Save the ONNX Models
onnx.save_model(close_onnx_model,'close_model.onnx')
onnx.save_model(residuals_onnx_model,'residuals_model.onnx')

Visualizando nuestros modelos ONNX

Visualicemos también nuestros modelos para asegurarnos de que tengan las formas de entrada y salida que especificamos. Comenzaremos visualizando nuestro regresor DNN. Primero, importaremos la biblioteca que necesitamos.

#Import netron
import netron 

Ahora visualizaremos nuestro DNN.

#Visualizing the residuals model
netron.start("/ENTER/YOUR/PATH/residuals_model.onnx")

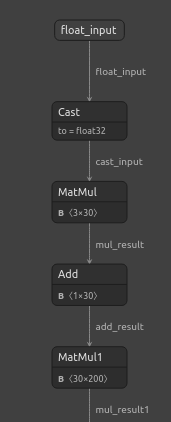
Figura 22: Visualización de nuestro modelo de regresor DNN.

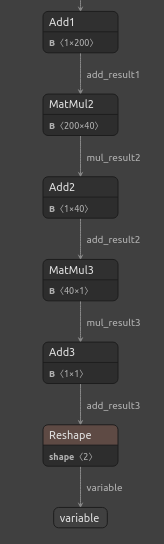
Figura 23: Visualización de nuestro modelo regresor DNN.

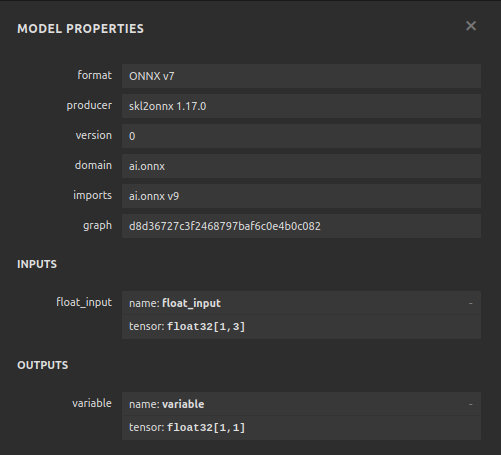
Figura 24: La forma de entrada y salida de nuestro regresor DNN cumple con nuestras expectativas.

Visualicemos también nuestro modelo regresor SGD.

#Visualizing the close model
netron.start("/ENTER/YOUR/PATH/close_model.onnx")

Figura 25: Visualización de nuestro modelo regresor SGD.

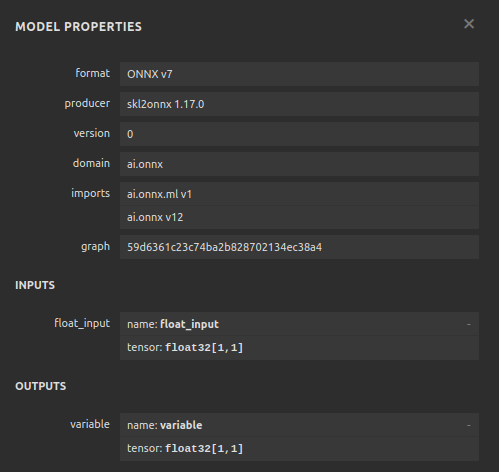
Figura 26: Visualización de nuestro modelo regresor SGD.

Implementación en MQL5

Para comenzar a construir nuestro Asesor Experto impulsado por IA, primero debemos cargar los archivos ONNX que acabamos de crear en la aplicación.

//+------------------------------------------------------------------+
//|                                                   NZD JPY AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Load the ONNX models                                             |
//+------------------------------------------------------------------+
#resource "\\Files\\residuals_model.onnx" as const uchar residuals_onnx_buffer[];
#resource "\\Files\\close_model.onnx" as const uchar close_onnx_buffer[];

Ahora necesitamos la biblioteca comercial para ayudarnos a abrir y cerrar nuestras posiciones.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

Creemos también variables globales que utilizaremos a lo largo de nuestro programa.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long residuals_model,close_model;
vectorf residuals_forecast   = vectorf::Zeros(1);
vectorf close_forecast       = vectorf::Zeros(1);
float forecast = 0;
int model_state,system_state;
int counter = 0;
double bid,ask;

En el procedimiento de inicialización de nuestro modelo, primero cargaremos nuestros 2 modelos ONNX, luego validaremos que nuestros modelos estén funcionando.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the ONNX models
   if(!load_onnx_models())
     {
      return(INIT_FAILED);
     }

//--- Validate the model is working
   model_predict();
   if(forecast == 0)
     {
      Comment("The ONNX models are not working correctly!");
      return(INIT_FAILED);
     }

//--- We managed to load our ONNX models
   return(INIT_SUCCEEDED);
  }

Cada vez que eliminemos nuestro modelo del gráfico, liberaremos cualquier recurso que ya no utilicemos.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we no longer need
   release_resorces();
  }

Si recibimos nuevos precios, primero actualizaremos nuestros precios de mercado. Luego obtendremos una predicción de nuestro modelo. Una vez que tengamos un pronóstico, verificaremos si tenemos posiciones abiertas. Si no tenemos posiciones abiertas, seguiremos la predicción de nuestro modelo siempre que los cambios de precios en marcos temporales superiores nos permitan hacerlo. De lo contrario, si ya tenemos una posición abierta, primero esperaremos a que transcurran 20 velas antes de verificar si nuestro modelo está prediciendo una reversión. Recordemos que entrenamos el modelo para pronosticar 20 pasos en el futuro, por lo tanto, debemos dejar pasar un tiempo antes de verificar si hay una reversión.

//--- If we have no positions, follow the model's forecast
   if(PositionsTotal() == 0)
     {
      //--- Our model is suggesting we should buy
      if(model_state == 1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Buy(0.3,Symbol(),ask,0,0,"NZD JPY AI");
            system_state = 1;
           }
        }

      //--- Our model is suggesting we should sell
      if(model_state == -1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Sell(0.3,Symbol(),bid,0,0,"NZD JPY AI");
            system_state = -1;
           }
        }
     }

   else
     {
      //--- We want to wait 20 mins before forecating again.
      if(time_stamp != time)
        {
         time_stamp= time;
         counter += 1;
        }

      if((system_state!= model_state) && (counter >= 20))
        {
         Alert("Reversal detected by our AI system, closing all positions");
         Trade.PositionClose(Symbol());
         counter = 0;
        }
     }
  }

Definamos la función para obtener la predicción de nuestros modelos, recordemos que tenemos dos modelos separados que deben llamarse a su vez.

//+------------------------------------------------------------------+
//| Fetch a prediction from our models                               |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- Define the inputs
   vectorf close_inputs = vectorf::Zeros(1);
   vectorf residuals_inputs = vectorf::Zeros(3);

   close_inputs[0]     = (float) iClose(Symbol(),PERIOD_M1,0);
   residuals_inputs[0] = (float) iOpen(Symbol(),PERIOD_M1,0);
   residuals_inputs[1] = (float) iHigh(Symbol(),PERIOD_M1,0);
   residuals_inputs[2] = (float) iLow(Symbol(),PERIOD_M1,0);

//--- Fetch predictions
   OnnxRun(residuals_model,ONNX_DEFAULT,residuals_inputs,residuals_forecast);
   OnnxRun(close_model,ONNX_DEFAULT,close_inputs,close_forecast);

//--- Our forecast
   forecast = residuals_forecast[0] + close_forecast[0];
   Comment("Model forecast: ",forecast);

//--- Remember the model's prediction
   if(forecast > close_inputs[0])
     {
      model_state = 1;
     }
   else
     {
      model_state = -1;
     }
  }

También necesitamos una función para actualizar nuestros precios de mercado.

//+------------------------------------------------------------------+
//| Update the market data we have                                   |
//+------------------------------------------------------------------+
void update_market_data(void)
  {
   bid = SymbolInfoDouble(Symbol(),SYMBOL_BID);
   ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK);
  }

Esta función liberará los recursos que ya no estamos utilizando.

//+------------------------------------------------------------------+
//| Rlease the resources we no longer need                           |
//+------------------------------------------------------------------+
void release_resorces(void)
  {
   OnnxRelease(residuals_model);
   OnnxRelease(close_model);
   ExpertRemove();
  }

Por último, esta función preparará nuestros modelos ONNX a partir de los buffers ONNX que creamos al comienzo de nuestra aplicación.

//+------------------------------------------------------------------+
//| This function will load our ONNX models                          |
//+------------------------------------------------------------------+
bool load_onnx_models(void)
  {
//--- Load the ONNX models from the buffers we created
   residuals_model = OnnxCreateFromBuffer(residuals_onnx_buffer,ONNX_DEFAULT);
   close_model = OnnxCreateFromBuffer(close_onnx_buffer,ONNX_DEFAULT);

//--- Validate the models
   if((residuals_model == INVALID_HANDLE) || (close_model == INVALID_HANDLE))
     {
      //--- We failed to load the models
      Comment("Failed to create the ONNX models: ",GetLastError());
      return(false);
     }

//--- Set the I/O shapes of the models
   ulong residuals_inputs[] = {1,3};
   ulong close_inputs[]     = {1,1};
   ulong model_output[]     = {1,1};

//---- Validate the I/O shapes
   if((!OnnxSetInputShape(residuals_model,0,residuals_inputs)) || (!OnnxSetInputShape(close_model,0,close_inputs)))
     {
      //--- We failed to set the input shapes
      Comment("Failed to set model input shapes: ",GetLastError());
      return(false);
     }

   if((!OnnxSetOutputShape(residuals_model,0,model_output)) || (!OnnxSetOutputShape(close_model,0,model_output)))
     {
      //--- We failed to set the output shapes
      Comment("Failed to set model output shapes: ",GetLastError());
      return(false);
     }

//--- Everything went fine
   return(true);
  }
//+------------------------------------------------------------------+

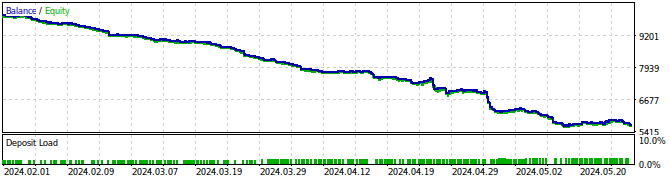
Figura 27: Prueba retrospectiva de nuestro Asesor Experto.

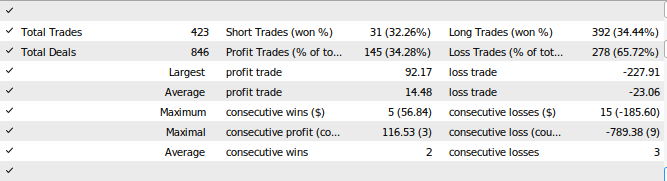
Figura 28: Los resultados de la prueba de nuestro Asesor Experto.

Conclusión

En este artículo, demostramos cómo podemos crear aplicaciones comerciales autocorrectivas. Nuestra conversación destacó cómo analizar los residuos de su modelo para detectar sobreajuste y sesgo en sus modelos de aprendizaje automático. Lamentablemente, detectamos que los residuos de nuestro modelo con mejor rendimiento tenían un comportamiento incorrecto. Podríamos intentar remediar esto diferenciando los datos de la serie temporal y el objetivo hasta que ya no observemos ninguna autocorrelación en los residuos, sin embargo esto también podría hacer que nuestro modelo sea más difícil de interpretar. Si bien no podemos garantizar que los puntos que hemos planteado en este artículo generen un éxito constante, definitivamente vale la pena considerarlo si está interesado en aplicar IA en sus estrategias comerciales. Únase a nosotros en nuestra próxima discusión, en la que intentaremos remediar los problemas que hemos observado hoy, al tiempo que equilibramos la interpretabilidad del modelo.