Ganhe Vantagem em Qualquer Mercado (Parte IV): Índices de Volatilidade do Euro e do Ouro da CBOE

Na era dos grandes volumes de dados, existem centenas de milhões de conjuntos de dados com potencial inexplorado de melhorar a precisão das previsões dos mercados financeiros. Infelizmente, é improvável que todos esses conjuntos de dados cumpram esse potencial. Nesta série de artigos, nosso objetivo é ajudar você a navegar pela vasta paisagem de conjuntos de dados possíveis e, ao final da discussão, você estará bem posicionado para decidir se os dados alternativos sugeridos devem ser incluídos na sua estratégia de negociação, ou se será melhor seguir sem eles.

Visão Geral da Estratégia de Negociação

Vamos analisar o mercado XAUEUR. Esse símbolo acompanha o preço do ouro em Euros. O ouro é minerado em todos os continentes da Terra, exceto na Antártida. Uma proporção significativa do ouro do mundo é negociada pela London Bullion Market Association (LBMA), que estabelece um referencial globalmente reconhecido para o preço do ouro. A Chicago Board of Options Exchange (CBOE) é uma empresa americana que fornece infraestrutura de mercado global. A CBOE usa suas redes para criar índices de volatilidade que acompanham os principais mercados ao redor do mundo. Vamos analisar 2 dos índices de volatilidade da CBOE que acompanham os mercados do Euro e do ouro, respectivamente.

Ao longo dos anos, os traders desenvolveram várias estratégias para negociar mercados voláteis com sucesso, minimizando o risco. De modo geral, quando os mercados estão voláteis, os traders podem alcançar metas de lucro em períodos relativamente curtos. Por outro lado, também é possível perder grandes somas de capital rapidamente, devido a grandes variações nos níveis de preço que podem não acionar ordens de stop loss em tempo hábil.

De forma geral, alguns traders preferem abrir menos posições, ou arriscar menos capital do que normalmente fariam em um maior número de posições, buscando lucrar com movimentos de preços favoráveis, enquanto minimizam sua exposição ao mercado. Em geral, traders experientes em mercados voláteis tendem a realizar seus lucros muito mais rapidamente do que fariam em mercados mais calmos. Outros traders esperam que os níveis de preço fiquem presos em uma faixa entre níveis de suporte e resistência. Quando os níveis de preço finalmente rompem essa faixa, os traders podem abrir posições antecipando movimentos mais fortes fora da zona identificável.

Sob condições normais de mercado, um rompimento de uma zona de suporte e resistência pode rapidamente perder força e começar a oscilar. No entanto, quando o mercado está volátil, os rompimentos podem ser seguidos por mudanças bruscas de preço na mesma direção, proporcionando retornos acima da média para os traders que seguem essas estratégias. Lamentavelmente, tais estratégias estão sujeitas a rompimentos falsos que podem se reverter violentamente, deixando alguns traders em posições desfavoráveis com perdas significativas.

Visão Geral da Metodologia

Utilizamos a API Python do Federal Reserve Economic Database (FRED), mantida pelo Federal Reserve de St. Louis, para recuperar as séries temporais econômicas dos índices de volatilidade do Euro e do ouro da CBOE. Os dados são fornecidos em formato diário e continham valores ausentes.

Infelizmente, nenhuma das descrições fornecidas com os conjuntos de dados explica os valores ausentes. Portanto, aplicamos imputação por média em todos os valores ausentes de ambos os conjuntos de dados.

No nosso Terminal MetaTrader 5, buscamos aproximadamente 4000 linhas de cotações diárias do mercado com os preços de abertura, máxima, mínima e fechamento (OHLC) do símbolo XAUEUR, usando um script personalizado que escrevemos em MQL5.

Ao analisarmos a correlação entre os dados alternativos da CBOE e os dados de mercado do MetaTrader 5, observamos níveis de correlação não significativamente diferentes de 0. Notavelmente, o nível de correlação entre os dois conjuntos de dados alternativos foi de 0,4. Esse nível positivo de correlação pode sugerir a presença de interações ou participantes comuns atuando nos dois mercados.

Ao traçarmos gráficos de dispersão dos dados, usando um dos conjuntos alternativos no eixo x e o preço de fechamento do XAUEUR no eixo y, parecia haver um limiar de altos níveis de volatilidade que consistentemente resultava em aumento dos preços. Lamentavelmente, nosso conjunto de dados pequeno — totalizando aproximadamente 3000 linhas após a junção com os dados alternativos — pode ser um motivo legítimo para cautela quanto a identificar padrões inexistentes.

Visualizar dados de alta dimensionalidade pode ser desafiador. Portanto, aplicamos um procedimento em duas etapas para visualizar nossos dados. Inicialmente, criamos gráficos de dispersão 3D, utilizando os dois conjuntos de dados da CBOE nos eixos x e y, respectivamente, e o fechamento do XAUEUR no eixo z. O agrupamento de candles de alta que observamos nos gráficos 2D ainda era claramente visível.

Por fim, podemos sempre aproveitar algoritmos projetados para reduzir dados de alta dimensão a um subespaço de menor dimensão. Um algoritmo bem conhecido de redução de dimensionalidade é a Análise de Componentes Principais (PCA). Escolhemos usar a implementação do algoritmo t-SNE (t-distributed stochastic neighbor embedding) da biblioteca scikit-learn para criar uma representação bidimensional de nosso conjunto de dados de seis dimensões. O gráfico resultante sugeriu a presença de quatro agrupamentos distintos em nosso conjunto. Além disso, observamos o que parece ser um efeito de dependência serial nos dados, sugerindo que há uma relação em desenvolvimento entre os conjuntos de dados da CBOE e do MetaTrader 5.

A última técnica de visualização utilizada foram os gráficos de autocorrelação. Todos os gráficos exibiram caudas longas, o que pode indicar a presença de efeitos persistentes de longo prazo nas séries temporais. Isso pode ser causado por tendências fortes ou efeitos sazonais. Nossos gráficos de autocorrelação parcial sugeriram que apenas alguns defasamentos explicavam a maior parte da autocorrelação observada. Isso sugere que os dados da série temporal podem ser modelados com sucesso como um modelo de média móvel (MA).

Após visualizar nossos dados, criamos três conjuntos de preditores:

1. Dados de mercado OHLC do MetaTrader 5
2. Conjuntos de dados alternativos da CBOE via FRED
3. Um superconjunto dos dois anteriores

Três redes neurais profundas idênticas foram utilizadas para comparar os três conjuntos de preditores, com validação cruzada em séries temporais com 5 divisões (5-fold), sem embaralhamento aleatório. O último conjunto de preditores gerou a menor taxa de erro ao prever o preço de fechamento futuro do símbolo XAUEUR. Isso pode sugerir que há relações entre os dois conjuntos de dados que estão ajudando nosso modelo.  

Confiantes com nosso primeiro teste, buscamos avaliar a importância global das variáveis no desempenho de nossa rede neural profunda. Selecionamos os métodos ALE (Efeitos Locais Acumulados) e SHAP (Explicações Aditivas de Shapley) para entender de quais variáveis nosso modelo mais depende. Nenhum dos métodos rejeitou os conjuntos de dados alternativos que selecionamos.

Ajustamos os hiperparâmetros do nosso modelo no conjunto de treino, em um processo de duas etapas que gerou dois modelos. Inicialmente, realizamos 500 iterações de busca aleatória sobre um conjunto selecionado de parâmetros do modelo. Na segunda etapa, otimizamos os melhores valores dos parâmetros contínuos do modelo, obtidos na busca aleatória, usando o algoritmo L-BFGS-B (Limited Memory Broyden Fletcher Goldfarb Shano). Todos os demais parâmetros, que não eram contínuos, foram fixados na segunda fase.

Ambos os modelos personalizados superaram a rede neural padrão nos dados de validação. Entretanto, o modelo obtido por busca aleatória teve o melhor desempenho no conjunto de teste. Isso indica que conseguimos otimizar nosso modelo com sucesso para os dados de treino, sem overfitting.

A partir daí, preparamos nosso melhor modelo para exportação no formato ONNX, para ser integrado a um programa personalizado no MetaTrader 5, e por fim, escrevemos um script em Python para compartilhar os dados mais recentes do FRED com nosso Terminal por meio de um arquivo CSV compartilhado.

Buscando os Dados

Incluí um script prático escrito em MQL5 para buscar nossos dados de mercado e salvá-los em formato CSV. O script possui 1 parâmetro de entrada, que especifica quantos candles (barras de dados) devem ser buscados. Basta arrastar e soltar o script sobre o seu gráfico, e você estará pronto para acompanhar.

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| Script Inputs                                                    |
//+------------------------------------------------------------------+
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int rsi_handler;
double rsi_buffer[];

//+------------------------------------------------------------------+
//| On start function                                                |
//+------------------------------------------------------------------+
void OnStart()
  {

//--- Load indicator
   rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,20,PRICE_CLOSE);
   CopyBuffer(rsi_handler,0,0,size,rsi_buffer);
   ArraySetAsSeries(rsi_buffer,true);

//--- File name
   string file_name = "Market Data " + Symbol() + ".csv";

//--- Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i)
                  );
        }
     }
//--- Close the file
   FileClose(file_handle);

  }
//+------------------------------------------------------------------+

Preparação dos Dados

Após coletarmos nossos dados de mercado OHLC do MetaTrader 5, iniciamos o processo de limpeza e formatação dos dados. Nosso primeiro passo foi importar bibliotecas padrão do Python para aprendizado de máquina.

#Import the libraries we need
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
from fredapi import Fred
from datetime import datetime
import time

Estas são as versões das bibliotecas que estamos utilizando.

#Display library versions
print(f"Pandas version {pd.__version__}")
print(f"Numpy version {np.__version__}")
print(f"Seaborn version {sns.__version__}")
print(f"Statsmodels version {statsmodels.__version__}")

Versão do Pandas: 2.1.4
Versão do Numpy: 1.26.4
Versão Seaborn 0.13.1
Versão Statsmodels 0.14.

Agora podemos ler o arquivo CSV que acabamos de criar e definir a coluna de tempo como nosso índice. Fazer isso nos permitirá mesclar os dados do MetaTrader 5 com os dados da CBOE de forma cronológica.

#Read in the data
xau_eur = pd.read_csv("Market Data XAUEUR.csv")
xau_eur = xau_eur.loc[96911:,:]
xau_eur.set_index("Time",inplace=True)
xau_eur.index = pd.to_datetime(xau_eur.index)

Vamos agora buscar os dados de mercado alternativos da CBOE via FRED. Observe que, antes de prosseguir, é necessário criar uma conta gratuita no site do FRED para obter uma chave de API privada. É um processo fácil de concluir, sem taxas escondidas.

#Fetch FRED data
fred = Fred(api_key='ENTER YOUR API KEY HERE')
fred_euro_data = pd.DataFrame(fred.get_series('EVZCLS'),columns=["EVZCLS"])
fred_gold_data = pd.DataFrame(fred.get_series('GVZCLS'),columns=["GVZCLS"])
#Fill in any missing values with the column mean
fred_euro_data = fred_euro_data.fillna(fred_euro_data.mean())
fred_gold_data = fred_gold_data.fillna(fred_gold_data.mean())

O Pandas possui comandos semelhantes ao SQL para mesclar dataframes. Mesclamos os dados apenas nas datas que são compartilhadas por ambas as séries temporais.

#Merge the data
merged_data = pd.merge(xau_eur,fred_euro_data,left_index=True,right_index=True)
merged_data = pd.merge(merged_data,fred_gold_data,left_index=True,right_index=True)
merged_data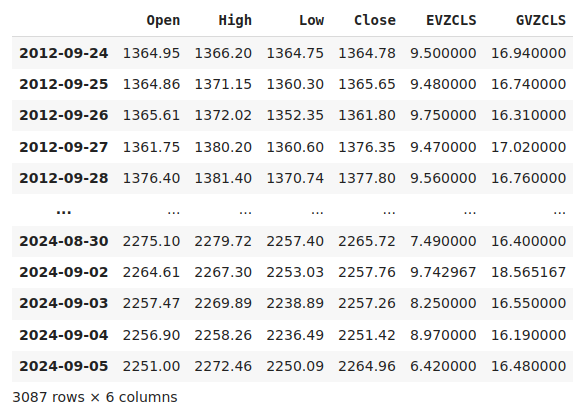

Fig 1: Nosso conjunto de dados mesclado

Rotular os dados é uma etapa importante em qualquer projeto de aprendizado de máquina supervisionado. Primeiramente, definimos nosso horizonte de previsão, que neste caso é de 20 dias no futuro. Em seguida, definimos o alvo como o preço de fechamento futuro do símbolo XAUEUR. Também criamos alvos binários para resumir se os níveis de preço se valorizaram ou desvalorizaram. Os alvos binários serão usados exclusivamente para fins de visualização.

#Let us label the data
look_ahead = 20

#Define the labels
merged_data["Target"] = merged_data["Close"].shift(-look_ahead)
merged_data["Binary Target"] = np.nan

merged_data.loc[merged_data["Target"] > merged_data["Close"],"Binary Target"] = 1
merged_data.loc[merged_data["Target"] <= merged_data["Close"],"Binary Target"] = 0

merged_data.dropna(inplace=True)
merged_data

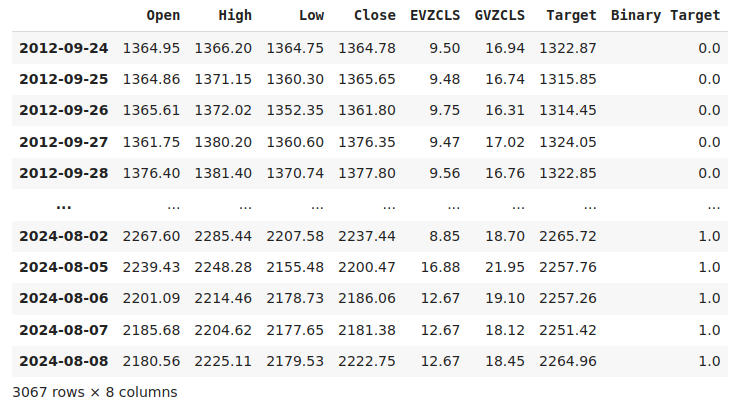
Fig 2: Nosso conjunto de dados com o alvo incluído

Por fim, definimos os 3 conjuntos de preditores que vamos comparar empiricamente.

#Let us define the predictors and target
ohlc_predictors = ["Open","High","Low","Close"]
fred_predictors = ["EVZCLS","GVZCLS"]
predictors = ohlc_predictors + fred_predictors
target = "Target"
binary_target = "Binary Target"

Análise Exploratória dos Dados

A presença ou ausência de fortes níveis de correlação não implica necessariamente na presença ou ausência de uma relação entre os dados analisados. Nossos dados alternativos parecem ter níveis de correlação intermitentes com o conjunto de dados do XAUEUR. No entanto, parecia haver fortes níveis de correlação diretamente entre os dois conjuntos de dados alternativos.

#Exploratory Data Analysis
#Analyzing correlation levels
sns.heatmap(merged_data[predictors].corr(),annot=True)

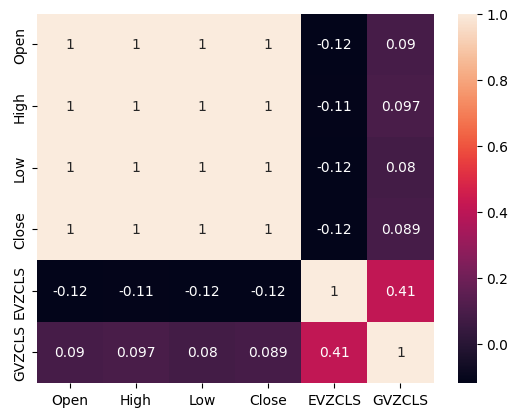
Fig 3: Nosso mapa de calor de correlação

Criamos 3 gráficos de dispersão com os dados que temos. Os dois primeiros usaram o índice de volatilidade do ouro e do euro no eixo x, e o preço de fechamento do XAUEUR no eixo y. No primeiro gráfico de dispersão, parece que quando os níveis de volatilidade do ouro sobem acima da faixa de 30-35, observamos consistentemente movimentos altistas.

#Let's create scatter plots
sns.scatterplot(data=merged_data,x="GVZCLS",y="Close",hue="Binary Target")

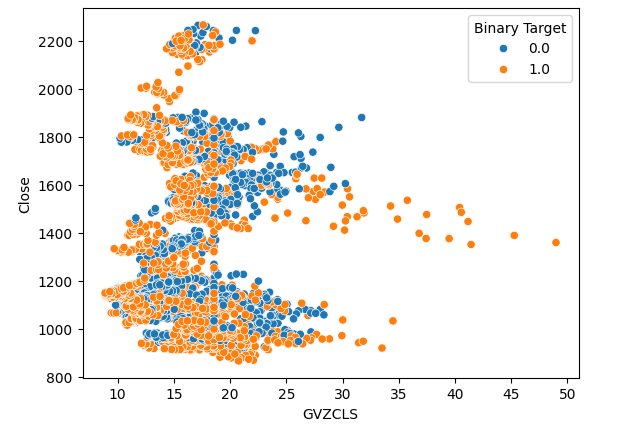
Fig 4: Nosso primeiro gráfico de dispersão

O mesmo fenômeno é observado no segundo gráfico. Parece que quando os níveis de volatilidade do Euro sobem além da faixa de 14-16, os preços tendem a se valorizar de forma consistente. No entanto, nosso conjunto de dados é limitado e pode não representar completamente a relação verdadeira entre os dois mercados.

#Let's create scatter plots
sns.scatterplot(data=merged_data,x="EVZCLS",y="Close",hue="Binary Target")

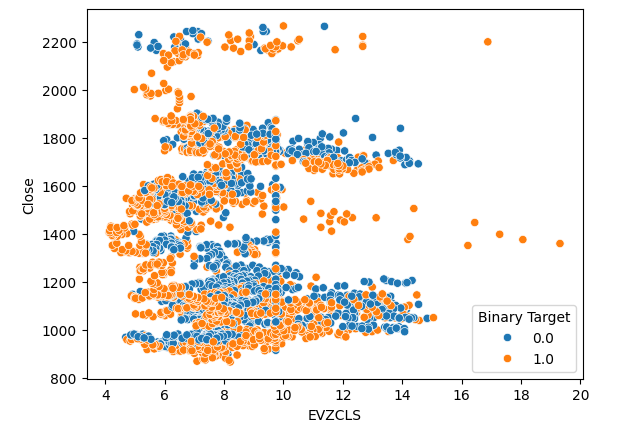
Fig 5: Nosso segundo gráfico de dispersão

Por fim, criamos um gráfico de dispersão utilizando os dois conjuntos de dados alternativos em ambos os eixos. Os dados formaram uma estrutura semelhante a um cone, com o agrupamento de candles altistas ainda claramente visível e bem separado.

#Let's create scatter plots
sns.scatterplot(data=merged_data,x="GVZCLS",y="EVZCLS",hue="Binary Target")

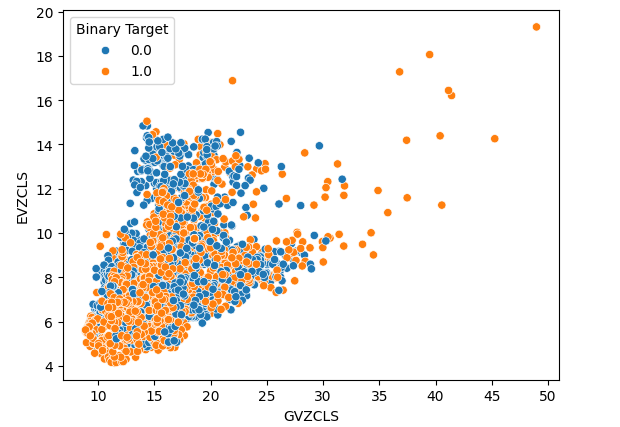
Fig 6: Nosso gráfico de dispersão final

Podem existir estruturas ocultas em nossos dados que não são visíveis em duas dimensões. Portanto, criamos um gráfico de dispersão 3D para visualizar o efeito de ambos os conjuntos de dados alternativos sobre o XAUEUR. O agrupamento de candles altistas ainda é claramente visível no gráfico 3D. Isso pode indicar que nossos dados alternativos estão separando bem os dados em determinados pontos.

#Define the 3D Plot
fig = plt.figure(figsize=(7,7))
ax = plt.axes(projection="3d")
ax.scatter(merged_data["GVZCLS"],merged_data["EVZCLS"],merged_data["Close"],c=merged_data["Binary Target"],cmap="plasma")
ax.set_xlabel("GVZCLS")
ax.set_ylabel("EVZCLS")
ax.set_zlabel("Close")

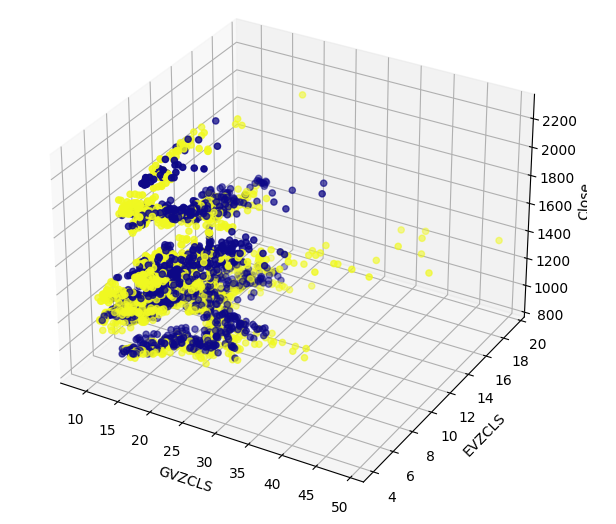
Fig 7: Um gráfico de dispersão 3D dos nossos dados de mercado

Também podemos empregar técnicas de redução de dimensionalidade para criar uma representação bidimensional de nossos dados de mercado com 6 dimensões. Vamos usar o algoritmo t-SNE para realizar essa tarefa. O algoritmo foi proposto pela primeira vez em um artigo de 2002 publicado por Geoffrey Hinton et al. O artigo original pode ser acessado por este link, aqui. Hinton é considerado um pioneiro na área de aprendizado de máquina, especialmente por seu artigo de 1986 que demonstrou como o algoritmo de retropropagação pode ser usado para treinar uma rede neural para prever a próxima palavra em uma representação vetorial de uma frase. Suas contribuições ajudaram a popularizar a adoção do algoritmo de retropropagação.

Fig 8: Dr Geoffrey Hinton

O algoritmo t-SNE foi projetado para criar uma representação compacta de dados de alta dimensão em que a proximidade entre todos os pontos de dados no espaço de alta dimensão é preservada na nova representação de menor dimensão. Para atingir esse objetivo, o algoritmo minimiza uma função de custo especializada que mede a diferença entre duas distribuições. Normalmente, esse processo de otimização é feito via gradiente descendente. Primeiramente, o algoritmo cria uma matriz de menor rank a partir dos dados originais de alta dimensão. Depois, ele move iterativamente os pontos de dados para minimizar o custo — lembrando que esse custo é a diferença entre a distribuição dos dados na matriz de rank reduzido e a distribuição original dos dados. O algoritmo t-SNE é útil para visualizar agrupamentos de dados que estão ocultos em espaços de maior dimensão.

Vamos importar as bibliotecas necessárias.

#Let's create a TSNE Plot
from sklearn.manifold import TS

Depois vamos instanciar o objeto t-SNE e instruí-lo a criar uma representação bidimensional de nossos dados.

#Create a TSNE object which will reduce the data to 2 dimensions
tsne = TSNE(n_components=2,perplexity=30)

Ajustar o objeto t-SNE aos dados que temos.

#Apply TSNE to the data
tsne_data = tsne.fit_transform(merged_data[predictors])

Plotar a nova representação dos dados.

#Create a scatter plot
plt.scatter(tsne_data[:,0],tsne_data[:,1])

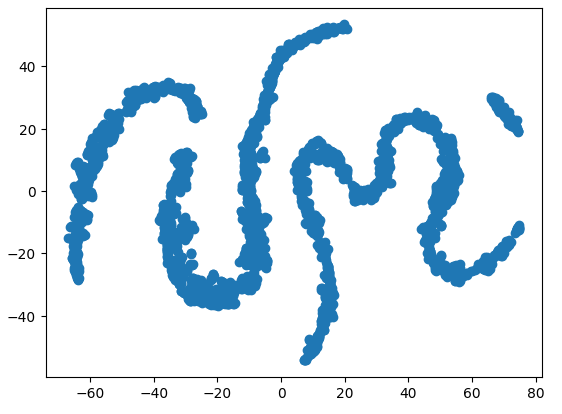
Fig 9: Nosso gráfico t-SNE dos dados de mercado

Devido à natureza estocástica do processo iterativo de otimização, pode ser difícil reproduzir exatamente o gráfico obtido nesta discussão. Além disso, se realizarmos o procedimento uma segunda vez, não será surpreendente se obtivermos um gráfico de dispersão diferente. Nosso principal interesse aqui é o número de agrupamentos que o algoritmo tenta preservar. Parece que nosso conjunto de dados possui 4 agrupamentos distintos, e a natureza curva dos gráficos pode sugerir uma dependência compartilhada ao longo do tempo dentro desses agrupamentos.

Gráficos de Autocorrelação (ACF) são amplamente utilizados na análise de séries temporais para inspecionar se os dados são estacionários, possuem flutuações sazonais, entre outros aspectos. Gráficos ACF nos mostram o nível de correlação entre o valor atual de uma série temporal e seus valores anteriores. Executamos 3 gráficos ACF para o fechamento do XAUEUR e os 2 conjuntos de dados alternativos da CBOE. Todos os 3 gráficos sugeriram que os dados têm componentes persistentes, o que também foi indicado pelo mapa de calor que visualizamos anteriormente. Quando gráficos ACF possuem caudas longas que decaem lentamente para zero, consideramos naturalmente a possibilidade de haver fortes tendências ou componentes sazonais nos dados.

#Let's look at an autocorrelation plot of the data
close_acf = plot_acf(merged_data["Close"])

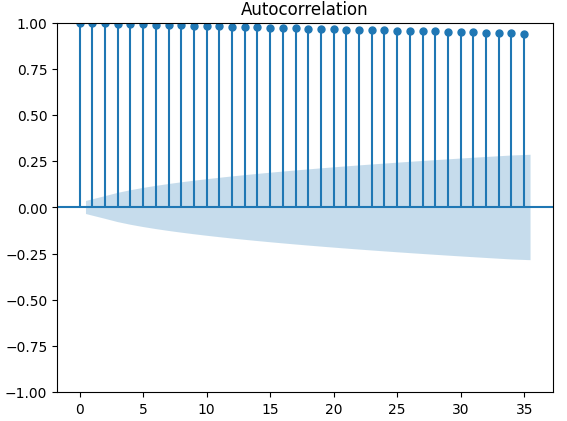
Fig 10: Gráfico ACF do preço de fechamento do XAUEUR

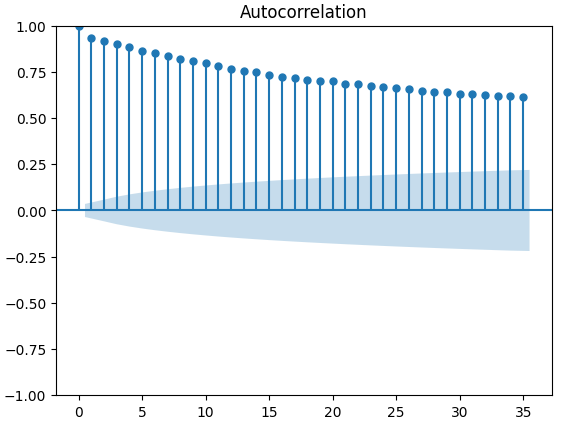
Fig 11: Gráfico ACF do índice de volatilidade do euro CBOE

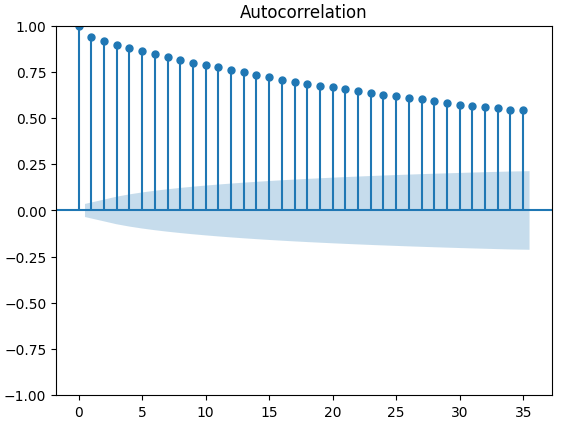
Fig 12: Gráfico ACF do índice de volatilidade do ouro CBOE

Os gráficos de autocorrelação parcial (PACF) nos informam até onde devemos olhar para trás no tempo para explicar a maior parte da correlação observada entre a série temporal e suas defasagens. Em outras palavras, quanto da correlação observada no lag 3 não foi transportada do lag 2? Todos os 3 gráficos PACF sugeriram que no máximo 4 defasagens explicam a maior parte da autocorrelação nos dados de série temporal.

#Let's look at an partial autocorrelation plot of the close data
close_pacf = plot_pacf(merged_data["Close"])

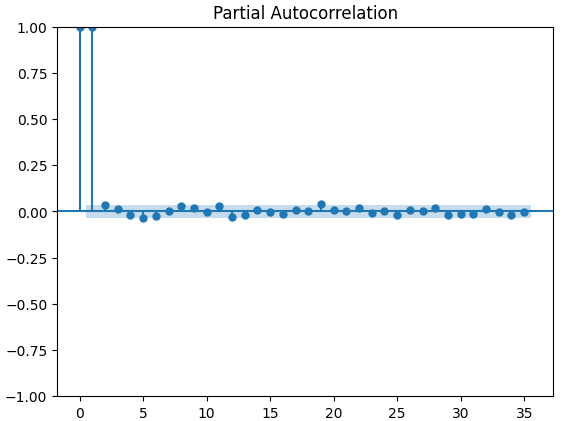
Fig 13: Gráficos PACF do fechamento do XAUEUR

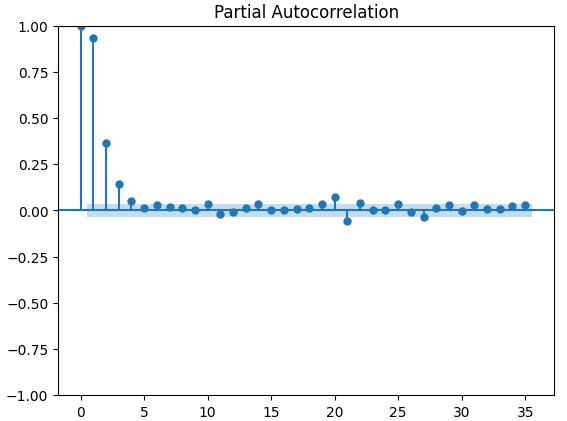
Fig 14: Gráficos PACF do índice de volatilidade do euro CBOE

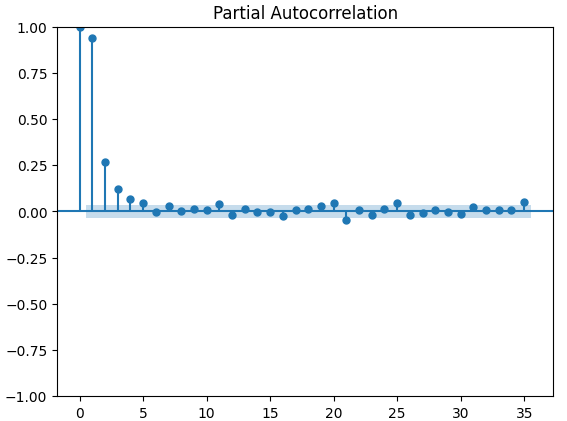
Fig 15: Gráficos PACF do índice de volatilidade do ouro CBOE

Preparando os Dados para Modelagem

Antes de podermos começar a modelar nossos dados com a nossa rede neural profunda, devemos primeiro fazer algumas preparações.

#Preparing to model the data
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import TimeSeriesSplit,train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.neural_network import MLPRegressor

O primeiro passo é padronizar e escalar os dados de entrada para que nosso modelo aprenda de forma eficaz.

#Reset the index of our data
merged_data.reset_index(inplace=True)

X = merged_data.loc[:,predictors]
y = merged_data.loc[:,target]

#Scale our data
scaler = RobustScaler()
X = pd.DataFrame(scaler.fit_transform(merged_data[predictors]),columns=predictors)

Agora precisamos criar divisões de treino e teste para os 3 conjuntos de preditores que temos. Tome cuidado para não embaralhar seus dados aleatoriamente nesta etapa. Caso contrário, comprometeríamos a integridade da nossa análise.

#Perform train test splits
ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,shuffle=False,train_size=0.5)
fred_train_X,fred_test_X,_,_ = train_test_split(X.loc[:,fred_predictors],y,shuffle=False,train_size=0.5)
train_X,test_X,_,_ = train_test_split(X.loc[:,predictors],y,shuffle=False,train_size=0.5)

Por fim, precisamos criar nosso objeto de série temporal e, posteriormente, criar um data frame para armazenar nossos níveis de erro de validação.

#Let's now cross-validate each of the predictors
#Create the time-series split object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

validation_error = pd.DataFrame(columns=["OHLC Predictors","FRED Predictors","All Predictors"],index=np.arange(0,5))

Modelagem dos Dados

Agora estamos prontos para começar a modelar nossos dados e validar nossos modelos cruzadamente.

#Performing cross validation
model = MLPRegressor(hidden_layer_sizes=(20,5))
for i,(train,test) in enumerate(tscv.split(train_X)):
  model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]])
  validation_error.iloc[i,2] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:]))

Nossos níveis de erro de validação.

#Our validation error
validation_error

Dados OHLC MetaTrader 5	Dados Alternativos FRED CBOE	Todos os Dados
875423.637167	881892.498319	857846.11554
794999.120981	831138.370726	946193.178747
1058884.292095	474744.732539	631259.842972
419566.842693	882615.372658	483408.373559
96693.318078	618647.934237	237935.04009

Pode não ser imediatamente óbvio para nós qual modelo está apresentando o melhor desempenho, porém, ao analisarmos as médias das colunas, podemos ver claramente que o último modelo está tendo desempenho excepcional. No gráfico abaixo, subtraímos o valor médio da primeira coluna das demais colunas. Ao fazer isso, o valor da primeira coluna é 0 e todos os modelos insatisfatórios terão valores de coluna maiores que 0. Portanto, podemos ver claramente que nosso último modelo está indo muito bem.

#Our mean error levels
val_err = validation_error.mean()
val_err = val_err.iloc[:] - val_err.iloc[0]
val_err.plot(kind="bar")

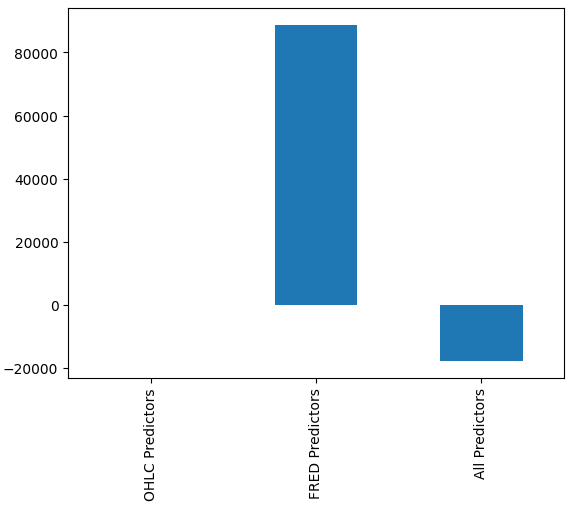
Fig 16: Desempenho do nosso modelo usando 3 conjuntos de dados diferentes

A realização de boxplots do desempenho do modelo mostra ainda mais que o último conjunto de preditores parece ser a escolha ideal para nós: a média do erro é a menor e a variância não é tão grande quanto ao usar apenas dados OHLC.

#Let's perform boxplots of our validation error
sns.boxplot(validation_error)

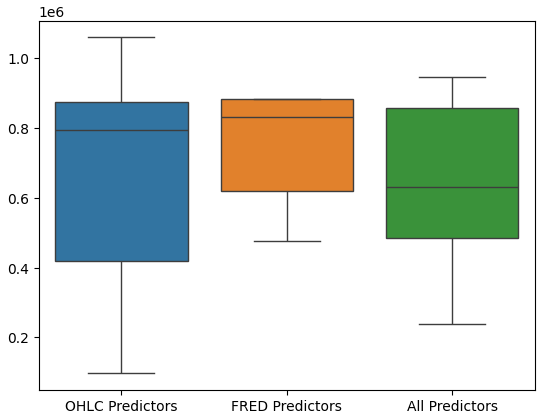
Fig 17: Desempenho do nosso modelo visualizado em boxplots

Importância das Variáveis

Nunca devemos confiar cegamente em qualquer modelo e implantá-lo em produção apenas porque produziu métricas de erro baixas. Vamos inspecionar os relacionamentos que o modelo aprendeu. Gostaríamos de entender a importância global das variáveis para o nosso modelo. Vamos começar criando gráficos de Efeito Local Acumulado (ALE). ALE é projetado para fornecer explicações robustas para modelos de machine learning treinados com dados com altos níveis de correlação. ALE tenta isolar o efeito que cada entrada tem sobre a saída do modelo.

#Feature importance
from alibi.explainers import ALE , plot_ale

Agora vamos instanciar nosso objeto ALE e buscar explicações sobre a importância global das variáveis para nossa rede neural profunda. Isso nos ajudará a entender o efeito que cada uma das entradas parece ter na predição do modelo.

#Explaining our deep neural network
model = MLPRegressor(hidden_layer_sizes=(20,5))
model.fit(train_X,train_y)
dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["XAUEUR Close"])

Vamos agora calcular e plotar nossos valores ALE para cada uma das entradas do modelo.

#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None)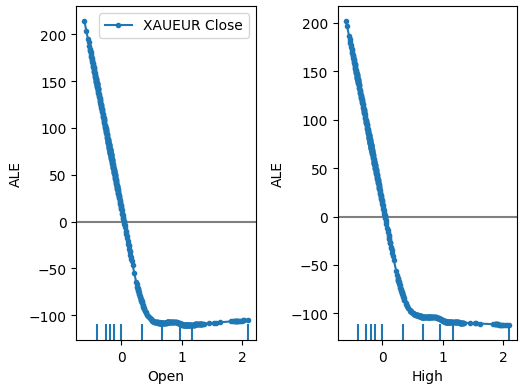

Fig 18: Nossos gráficos ALE para alguns dos preditores Open e High do XAUEUR

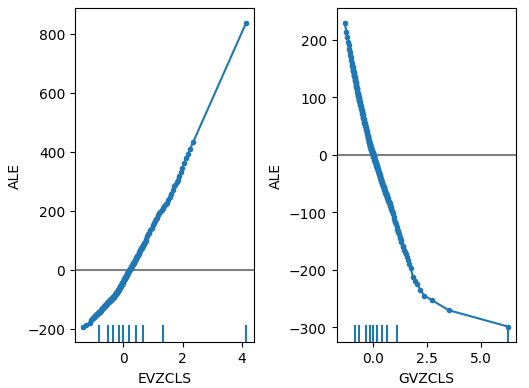
Fig 19: Nossos gráficos ALE para os índices de volatilidade FRED CBOE

Interpretar gráficos ALE é bastante intuitivo: o gráfico ilustra como a predição do modelo muda à medida que o valor de cada preditor muda. Como podemos ver, à medida que os preços Open e High aumentam, a predição do modelo inicialmente cai. No entanto, ela se torna menos sensível à medida que os níveis de preço continuam subindo. Embora não tenhamos incluído aqui, os gráficos ALE dos preços Low e Close são idênticos aos 2 gráficos que mostramos.

Ao olharmos para os gráficos ALE dos dados alternativos, observamos que o índice de volatilidade do euro criou um gráfico ALE que cobre parte do gráfico que as outras variáveis não conseguiram cobrir. Em outras palavras, o preditor parece explicar variância no alvo que não conseguimos explicar sem ele. Além disso, a inclinação ascendente do gráfico ALE sugere que, à medida que o valor do preditor aumenta, a previsão do modelo também aumenta.

A seguir, vamos buscar explicações SHAP para o desempenho do nosso modelo. Os valores SHAP nos ajudam a quantificar como cada entrada do modelo contribuiu para uma predição específica em comparação com a predição média do modelo. Os valores SHAP têm raízes no campo matemático da teoria dos jogos. O algoritmo considera cada possível conjunto de preditores e então calcula o efeito médio das entradas em todos os conjuntos possíveis.

Primeiro, vamos importar a biblioteca SHAP.

#SHAP Values
import shap

Calcule os valores SHAP.

#Calculating SHAP values
explainer = shap.Explainer(model.predict,train_X)
shap_values = explainer(test_X)#Calculating SHAP values

Plote os valores SHAP.

#Plot the beeswarm plot
shap.plots.beeswarm(shap_values)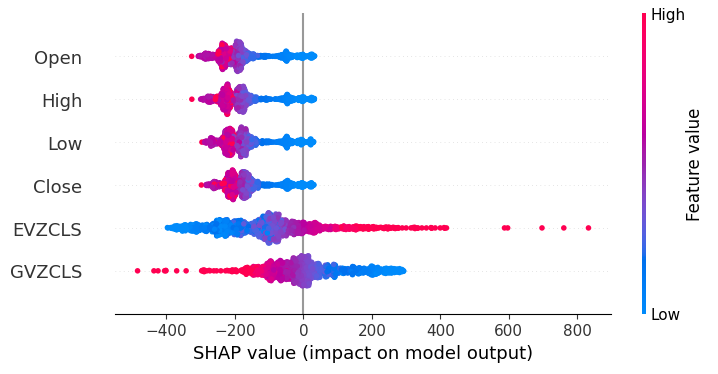

Fig 20: Nossas explicações SHAP

De acordo com nossas explicações SHAP, os dados de mercado obtidos diretamente do XAUEUR são os dados mais importantes que temos. Além disso, o gráfico SHAP também sugere que, à medida que o preço atual do mercado aumenta, o alvo tende a cair.

Ajuste de Parâmetros

Vamos tentar obter mais desempenho do nosso modelo. Começaremos importando as bibliotecas necessárias.

#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV

Inicializar o modelo.

#Reinitialize the model
model = MLPRegressor(hidden_layer_sizes=(20,5))

Definir o objeto de ajuste (tuner).

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "activation" : ["relu","logistic","tanh","identity"],
        "solver":["adam","sgd","lbfgs"],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "learning_rate":['constant','adaptive','invscaling'],
        "shuffle": [True,False]
        },
        n_iter=500,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Ajuste o tuner.

#Fit the tuner
tuner_results = tuner.fit(train_X,train_y)

Os melhores parâmetros que encontramos.

#The best parameters we found
tuner_results.best_params_

{'tol': 1e-07,
 'solver': 'lbfgs',
 'shuffle': True,
 'learning_rate': 'adaptive',
 'alpha': 0.1,
 'activation': 'identity'}

O Scipy inclui procedimentos de otimização em seu módulo minimize. Esses procedimentos exigem um ponto de partida para o processo de otimização. Usaremos os melhores valores de parâmetro encontrados pela busca aleatória como ponto de partida em nossa segunda fase de otimização.

#Deeper optimization
from scipy.optimize import minimize

Agora, vamos criar um objeto DataFrame para armazenar nossos níveis de erro na validação.

#Create a dataframe to store our accuracy
current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])

Todo algoritmo de otimização precisa de uma função objetivo para operar. No nosso caso, a função objetivo é o erro médio validado cruzado do modelo no conjunto de treinamento. Nosso procedimento de otimização irá buscar por parâmetros do modelo que minimizem nosso erro médio.

#Define the objective function
def objective(x):
    #The parameter x represents a new value for our neural network's settings
    #In order to find optimal settings, we will perform 10 fold cross validation using the new setting
    #And return the average RMSE from all 10 tests
    #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization
    model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=x[0],tol=x[1])
    #Now we will cross validate the model
    for i,(train,test) in enumerate(tscv.split(train_X)):
        #Train the model
        model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]])
        #Measure the RMSE
        current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:]))
    #Return the Mean CV RMSE
    return(current_error_rate.iloc[:,0].mean())

Vamos definir o ponto de partida para o procedimento de otimização, e também devemos definir os limites para os valores de entrada permitidos.

#Define the starting point
pt = [0.1,0.00000001]
bnds = ((0.0000000000000000001,10000000000),(0.0000000000000000001,10000000000))

Otimizando o modelo.

#Searchin deeper for parameters
result = minimize(objective,pt,method="L-BFGS-B",bounds=bnds)

Testando Overfitting

Overfitting é um problema em qualquer projeto de aprendizado de máquina. Ele ocorre quando nosso modelo falha em criar generalizações significativas dos dados, passando a aprender ruídos e outras associações sem sentido nos dados. Para testar overfitting, vamos comparar a acurácia dos nossos 2 modelos customizados com o modelo padrão.

#Testing for overfitting
default_model          = MLPRegressor(hidden_layer_sizes=(20,5))
customized_model       = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=0.1,tol=0.0000001)
customized_lbfgs_model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=result.x[0],tol=result.x[1])

Agora, vamos nos preparar para validar cada modelo por validação cruzada.

#Preparing to cross validate the models
models = [
    default_model,
    customized_model,
    customized_lbfgs_model
]

#We will store our validation error here
validation_error = pd.DataFrame(columns=["Default Model","Customized Model","L-BFGS Model"],index=np.arange(0,5))

#We will now reset the indexes
test_y = test_y.reset_index()
test_X = test_X.reset_index()

Devemos ajustar cada um dos modelos ao conjunto de treinamento.

#Fit each of the models
for m in models:
  m.fit(train_X,train_y)

Agora, vamos validar por validação cruzada a performance do nosso modelo em dados não vistos, ou seja, no conjunto de teste que separamos até agora.

#Cross validating each model
for j in np.arange(0,len(models)):
  model = models[j]
  for i,(train,test) in enumerate(tscv.split(test_X)):
    model.fit(test_X.loc[train[0]:train[-1],:],test_y.loc[train[0]:train[-1],"Target"])
    validation_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],"Target"],model.predict(test_X.loc[test[0]:test[-1],:]))

Nossos níveis de erro de validação.

#Our validation error
validation_error

Modelo Padrão	Modelo de Busca Aleatória	Modelo L-BFGS-B
22360.060721	5917.062055	3734.212826
17385.289026	36726.684574	35886.972729
13782.649037	5128.022626	20886.845316
3082484.290698	6950.786438	5789.948045
4076009.132941	27729.589769	22931.572161

O modelo com melhor desempenho é o modelo de busca aleatória.

#Plotting the difference in our performance levels
mean = validation_error.mean()
mean = mean.iloc[:] - mean.iloc[0]
mean.plot(kind="bar")

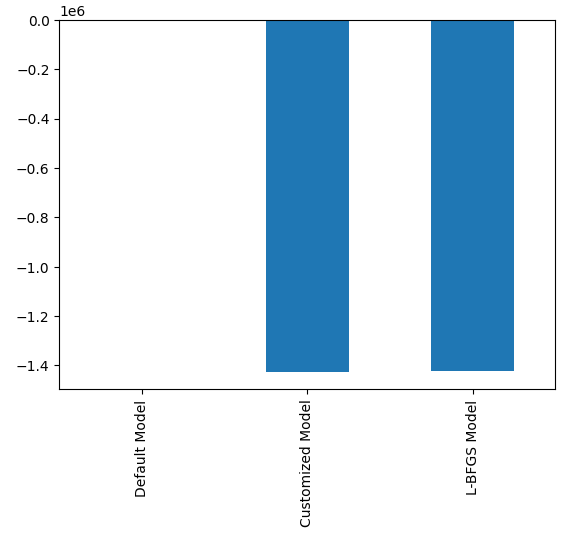
Fig 21: Nossos níveis de erro na validação

Visualizando a performance do nosso modelo fica claro o quão mal o modelo padrão lida com os dados.

#Visualizing the results
validation_error.plot()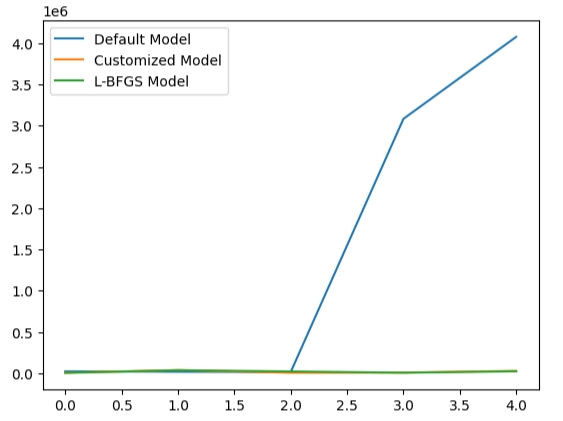

Fig 22: Testando para overfitting

Esse ponto é ainda mais evidenciado por nossos boxplots. Podemos perceber que superamos o modelo padrão com uma margem considerável.

#Visualizing our results
sns.boxplot(validation_error)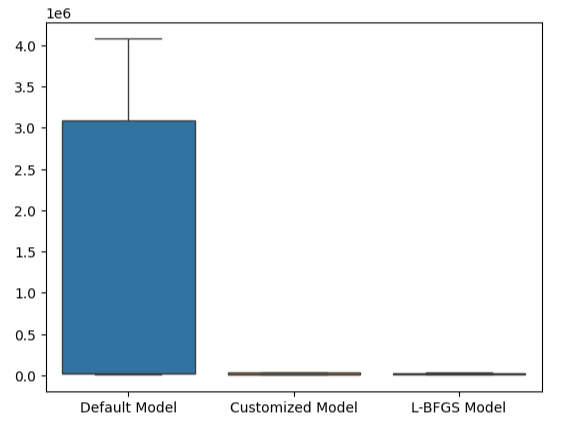

Fig 23: Estamos superando o modelo padrão por ampla margem

Preparando para exportar em formato ONNX

Antes de podermos exportar nosso modelo para o formato ONNX, devemos primeiro padronizar e escalar nossos dados de uma forma que possamos reproduzir no nosso terminal MetaTrader 5. Para isso, subtrairemos a média de cada coluna e depois dividiremos cada coluna pelo seu desvio padrão. Vamos salvar nossos fatores de escala em formato CSV para que possamos recuperá-los no nosso terminal MetaTrader 5 e escalar as entradas do nosso modelo.

#Let us now prepare to export our model to onnx format
scale_factors = pd.DataFrame(columns=predictors,index=["mean","standard deviation"])

for i in np.arange(0,len(predictors)):
  scale_factors.iloc[0,i] = merged_data.loc[:,predictors[i]].mean()
  scale_factors.iloc[1,i] =  merged_data.loc[:,predictors[i]].std()
  merged_data.loc[:,predictors[i]] = (merged_data.loc[:,predictors[i]] - merged_data.loc[:,predictors[i]].mean())/merged_data.loc[:,predictors[i]].std()

scale_factors

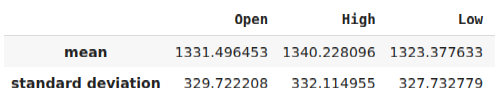
Fig 24: Alguns dos nossos fatores de escala

Agora vamos salvar os dados em formato CSV.

#Save the scale factors to CSV
scale_factors.to_csv("scale_factors.csv")

Exportando para formato ONNX

O Open Neural Network Exchange (ONNX) é um protocolo para construir e compartilhar modelos de aprendizado de máquina entre diferentes linguagens de programação. O protocolo ONNX permite incorporar nossa rede neural profunda ao nosso Expert Advisor usando a API ONNX do MQL5.

Vamos primeiro carregar as bibliotecas de que precisamos.

#Exporting to ONNX format
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

Treine o modelo com todos os dados que possuímos.

#Fit the model on all the data we have
customized_model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target])

Ao exportar modelos ONNX, o formato de entrada pode ser perdido. Portanto, vamos especificar explicitamente o formato de entrada.

# Define the input type
initial_types = [("float_input",FloatTensorType([1,6]))]

Crie a representação ONNX do modelo.

# Create the ONNX representation
onnx_model = convert_sklearn(customized_model,initial_types=initial_types,target_opset=12)

Salve a representação ONNX em um arquivo com extensão ".onnx".

# Save the ONNX model
onnx_name = "XAUEUR FRED D1.onnx"
onnx.save_model(onnx_model,onnx_name)

Obtendo dados FRED atualizados

Antes de começarmos a construir nosso Expert Advisor, precisamos criar um script Python que irá constantemente compartilhar dados FRED atualizados com nosso terminal. Vamos criar um script que irá buscar os dados mais recentes disponíveis uma vez ao dia e salvá-los em CSV na pasta "Files" para que possamos acessar os dados com nosso aplicativo de negociação.

#A function to write out our alternative data to CSV
def write_out_alternative_data():
        euro = fred.get_series("EVZCLS")
        euro = euro.iloc[-1]
        gold = fred.get_series("GVZCLS")
        gold = gold.iloc[-1]
        data = pd.DataFrame(np.array([euro,gold]),columns=["Data"],index=["Fred Euro","Fred Gold"])
        data.to_csv("C:\\ENTER\\YOUR\\PATH\\HERE\\MetaQuotes\\Terminal\\D0E8209F77C8CF37AD8BF550E51FF075\\MQL5\\Files\\fred_xau_eur.csv")

Agora, vamos escrever um loop infinito para gravar os dados e, em seguida, dormir por um dia.

while True:
        #Update the fred data for our MT5 EA
        write_out_alternative_data()
        #If we have finished all checks then we can wait for one day before checking for new data
        time.sleep(24 * 60 * 60)

Construindo Nosso Expert Advisor

Agora estamos preparados para começar a construir nosso Expert Advisor. Vamos começar exigindo primeiro o arquivo ONNX que acabamos de criar.

//+------------------------------------------------------------------+
//|                                               EURXAU Fred AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Volatility Doctor"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Require the ONNX file                                            |
//+------------------------------------------------------------------+
#resource "\\Files\\XAUEUR FRED D1.onnx" as const uchar onnx_buffer[];

Carregue a biblioteca de trades para nos ajudar a gerenciar nossas posições.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

Essas variáveis globais serão compartilhadas em diversas partes diferentes do nosso aplicativo.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long    onnx_model;
vector  mean_values  = vector::Zeros(6);
vector  std_values   = vector::Zeros(6);
vectorf model_inputs = vectorf::Zeros(6);
vectorf model_output = vectorf::Zeros(1);
double  bid,ask;
int     system_state,model_sate;

Agora, precisamos de uma função que crie nosso modelo ONNX, a partir do buffer ONNX que criamos no início do nosso aplicativo. Nossa função irá primeiro criar e validar o modelo ONNX, e por fim irá definir e validar os formatos de entrada e saída do modelo. Se falharmos em algum ponto, a função irá retornar falso, o que por sua vez irá interromper o procedimento de inicialização

//+------------------------------------------------------------------+
//| Load the ONNX file                                               |
//+------------------------------------------------------------------+
bool load_onnx_file(void)
  {
//--- Create the ONNX model from the buffer we loaded earlier
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

//--- Validate the model we just created
   if(onnx_model == INVALID_HANDLE)
     {
      //--- Give the user feedback on the error
      Comment("Failed to create the ONNX model: ",GetLastError());
      //--- Break initialization
      return(false);
     }

//--- Define the I/O shape
   ulong input_shape [] = {1,6};

//--- Validate the input shape
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      //--- Give the user feedback
      Comment("Failed to define the ONNX input shape: ",GetLastError());
      //--- Break initialization
      return(false);
     }

   ulong output_shape [] = {1,1};

//--- Validate the output shape
   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      //--- Give the user feedback
      Comment("Failed to define the ONNX output shape: ",GetLastError());
      //--- Break initialization
      return(false);
     }

//--- We've finished
   return(true);
  }
//+------------------------------------------------------------------+

A partir daqui, agora definiremos os fatores de escala que precisaremos para normalizar as entradas do nosso modelo.

//+------------------------------------------------------------------+
//| Load our scaling factors                                         |
//+------------------------------------------------------------------+
bool load_scaling_factors(void)
  {
//--- Load the scaling values
   mean_values[0] = 1331.4964525595044;
   mean_values[1] = 1340.2280958591457;
   mean_values[2] = 1323.3776328659928;
   mean_values[3] = 1331.706768829475;
   mean_values[4] = 8.258127607767035;
   mean_values[5] = 16.35582438284101;
   std_values[0] = 329.7222075527991;
   std_values[1] = 332.11495530642173;
   std_values[2] = 327.732778866831;
   std_values[3] = 330.1146052811378;
   std_values[4] = 2.199782202942867;
   std_values[5] = 4.241112965400358;

//--- Validate the values loaded correctly
   if((mean_values.Sum() > 0) && (std_values.Sum() > 0))
     {
      return(true);
     }

//--- We failed to load the scaling values
   return(false);
  }

Sempre que nosso aplicativo não estiver mais em uso, vamos liberar os recursos que não estivermos mais utilizando.

//+------------------------------------------------------------------+
//| Free up the resources we no longer need                          |
//+------------------------------------------------------------------+
void release_resources(void)
  {
//--- Free up all the resources we have used so far
   OnnxRelease(onnx_model);
   ExpertRemove();
   Print("Thank you for choosing Volatility Doctor");
  }

Esta função será responsável por atualizar nossas informações de preço de mercado.

//+------------------------------------------------------------------+
//| Fetch market data                                                |
//+------------------------------------------------------------------+
void fetch_market_data(void)
  {
//--- Update the market data
   bid = SymbolInfoDouble(Symbol(),SYMBOL_BID);
   ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK);
  }

A função a seguir é responsável por buscar uma previsão do nosso modelo. Primeiro, buscaremos os dados OHLC atuais do símbolo XAUEUR usando a função de matriz CopyRates() do MQL5. Após buscar os dados, vamos normalizá-los e armazená-los no vetor de entrada que definimos anteriormente. A partir daqui, chamaremos outra função para ler os dados FRED mais recentes que temos em arquivo.

//+------------------------------------------------------------------+
//| This function will fetch a prediction from our model             |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- Get the input data ready
   for(int i =0; i < 6; i++)
     {
      //--- The first 4 inputs will be fetched from the market
      matrix xau_eur_ohlc = matrix::Zeros(1,4);
      xau_eur_ohlc.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_OHLC,0,1);
      //--- Fill in the data
      if(i<4)
        {
         model_inputs[i] = (float)((xau_eur_ohlc[i,0] - mean_values[i])/ std_values[i]);
        }
      //--- We have to read in the fred alternative data
      else
        {
         read_fred_data();
        }
     }
  }

A função, definida abaixo, irá ler o arquivo CSV com os dados FRED mais recentes e normalizar os dados antes de armazená-los no vetor de entrada e buscar uma previsão do nosso modelo. Vamos representar a previsão do modelo usando um número inteiro. Isso nos ajudará a identificar rapidamente possíveis reversões e fechar nossas posições, de preferência do lado certo do mercado.

//+-------------------------------------------------------------------+
//| Read in the FRED data                                             |
//+-------------------------------------------------------------------+
void read_fred_data(void)
  {
//--- Read in the file
   string file_name = "fred_xau_eur.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols).

//--- Check the result
   if(result != INVALID_HANDLE)
     {
      Print("Opened the file");
      //--- Store the values of the file

      int counter = 0;
      string value = "";
      while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end
        {
         if(counter > 10)  //if you aim to read 10 values set a break point after 10 elements have been read
            break;          //stop the reading progress

         value = FileReadString(result);
         Print("Counter: ");
         Print(counter);
         Print("Trying to read string: ",value);

         if(counter == 3)
           {
            Print("Fred Euro data: ",value);
            model_inputs[4] = (float)((((float) value) - mean_values[4])/std_values[4]);
           }

         if(counter == 5)
           {
            Print("Fred Gold data: ",value);
            model_inputs[5] = (float)((((float) value) - mean_values[5])/std_values[5]);
           }

         if(FileIsLineEnding(result))
           {
            Print("row++");
           }

         counter++;
        }

      //--- Show the input and Fred data
      Print("Input Data: ");
      Print(model_inputs);

      //---Close the file
      FileClose(result);

      //--- Store the model prediction
      OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_output);
      Comment("Model Forecast",model_output[0]);
      if(model_output[0] > iClose(Symbol(),PERIOD_D1,0))
        {
         model_sate = 1;
        }

      else
        {
         model_sate = -1;
        }
     }

//--- We failed to find the file
   else
     {
      //--- Give the user feedback
      Print("We failed to find the file with the FRED data");
     }
  }

Agora, vamos definir como nossa aplicação deve iniciar. Nossa aplicação deve primeiro criar o modelo ONNX e, em seguida, carregar os fatores de escala necessários. Se algum desses passos falhar, vamos abortar completamente o procedimento de inicialização.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the ONNX model
   if(!load_onnx_file())
     {
      //--- We failed to load our ONNX model
      return(INIT_FAILED);
     }

//--- Load the scaling factors
   if(!load_scaling_factors())
     {
      //--- We failed to read in the scaling factors
      return(INIT_FAILED);
     }

//--- We mamnaged to load our model
   return(INIT_SUCCEEDED);
  }

Quando nossa aplicação for removida do gráfico, libere os recursos que não precisamos mais.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we no longer need
   release_resources();
  }

Por fim, sempre que recebermos cotações de mercado atualizadas, primeiro iremos armazenar os preços de mercado atualizados na memória. Subsequentemente, se não tivermos posições abertas, seguiremos a previsão do nosso modelo apenas se ela for confirmada pela ação do preço em timeframes superiores. Alternativamente, se já tivermos posições abertas, iremos fechá-las caso nosso modelo antecipe reversões nos níveis de preço.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update market data
   fetch_market_data();

//--- Fetch a prediction from our model
   model_predict();

//--- If we have no positions follow the model's lead
   if(PositionsTotal() == 0)
     {
      //--- Buy position
      if(model_sate == 1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Buy(0.3,Symbol(),ask,0,0,"XAUEUR Fred AI");
            system_state = 1;
           }
        };

      //--- Sell position
      if(model_sate == -1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Sell(0.3,Symbol(),bid,0,0,"XAUEUR Fred AI");
            system_state = -1;
           }
        };
     }

//--- If we allready have positions open, let's manage them
   if(model_sate != system_state)
     {
      Trade.PositionClose(Symbol());
     }

  }
//+------------------------------------------------------------------+

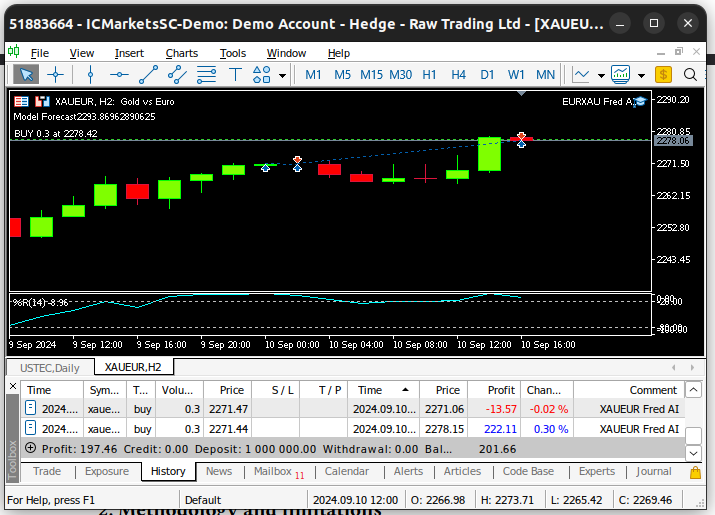
Fig 25: Nosso Consultor Especialista em ação

Conclusão

Neste artigo, demonstramos que pode ser vantajoso incluir os índices de volatilidade FRED CBOE para ajudar a melhorar a precisão dos seus modelos de aprendizado de máquina. Embora não possamos garantir que as informações fornecidas neste artigo gerarão sucesso de forma consistente, certamente vale a pena considerar se você está pronto para começar a empregar dados alternativos em suas estratégias de trading.