
Selbstoptimierender Expert Advisor mit MQL5 und Python (Teil IV): Stacking-Modelle
In dieser Artikelserie werden wir verschiedene Möglichkeiten zur Entwicklung von Handelsanwendungen erörtern, die in der Lage sind, sich dynamisch an sich verändernde Marktbedingungen anzupassen. Es gibt potenziell unendlich viele Möglichkeiten, dieses Problem anzugehen, aber es ist unwahrscheinlich, dass alle möglichen Lösungen gültig sind. Unser heutiges Ziel ist es daher, die Vor- und Nachteile verschiedener möglicher Lösungen aufzuzeigen und empirisch zu analysieren, um Sie bei der Verbesserung Ihrer Handelsstrategien zu unterstützen.
Überblick über die Handelsstrategie
Wenden wir uns nun der Prognose für das Währungspaar NZDJPY zu. Wir möchten aus den Daten, die wir über unser MetaTrader 5-Terminal für das Symbol sammeln, algorithmisch eine Handelsstrategie lernen. Als Menschen sind wir möglicherweise von Natur aus voreingenommen gegenüber Handelsstrategien, die mit unseren eigenen Überzeugungen und Interessen übereinstimmen. Auch Modelle des maschinellen Lernens sind voreingenommen. Die Voreingenommenheit (bias) eines maschinellen Lernmodells ist das Ausmaß, in dem die Annahmen des Modells verletzt werden. Unsere Handelsstrategie wird sich auf ein Ensemble von 2 KI-Modellen stützen. Das erste Modell wird trainiert, um den zukünftigen Schlusskurs des Paares NZDJPY 20 Minuten in der Zukunft vorherzusagen. Das zweite Modell wird so trainiert, dass es die Höhe des Fehlers in der Vorhersage des ersten Modells vorhersagt. Diese Technik wird als Stacking bezeichnet. Wir hoffen, dass wir durch das Stapeln von 2 Modellen in der Lage sein werden, unsere menschliche Voreingenommenheit zu überwinden, und dass dies hoffentlich ausreichen wird, um uns zu höheren Leistungen zu führen.
Überblick über die Methodik
Wir haben etwa 9000 Zeilen von M1-Marktdaten für das NZDJPY-Paar von unserem MetaTrader 5-Terminal mithilfe eines angepassten MQL5-Skripts abgerufen. Wir haben 2D- und 3D-Punktdiagramme der Marktdaten erstellt. Allerdings konnten wir in den Daten keine erkennbaren Zusammenhänge feststellen. Wir haben auch eine Zeitreihendekomposition des Datensatzes durchgeführt und konnten einen klaren Abwärtstrend und starke saisonale Effekte in den Daten feststellen.
Unsere Daten wurden dann in Trainings- und Testsätze aufgeteilt. Eine Reihe von 15 verschiedenen Modellen wurde angepasst und anhand des Trainingssatzes bewertet. Der Stochastic Gradient Descent (SGD)-Regressor war das leistungsstärkste Modell der Gruppe.
Bei der anschließenden Analyse unserer Metriken der Merkmalsbedeutungen stellten wir fest, dass der Höchstkurs der aussagekräftigste Prädiktor für die Vorhersage des zukünftigen Schlusskurses des NZDJPY-Paares zu sein schien. Das Hoch erzielte das beste Ergebnis bei der wechselseitigen (mutual) Information (MI). Darüber hinaus haben wir auch die Implementierung des Algorithmus der rekursiven Merkmalseliminierung (RFE) von scikit-learn verwendet. Alle Prädiktoren, die wir haben, wurden vom RFE-Algorithmus als wichtig eingestuft. Wie wir jedoch in unserer Diskussion sehen werden, ist die Tatsache, dass eine Beziehung existiert, keine Garantie dafür, dass wir sie erfolgreich erfassen und modellieren können.
Nachdem wir unser leistungsstärkstes Modell identifiziert hatten, fuhren wir fort, die Parameter unseres Modells zu optimieren. Normalerweise testen wir in unseren Diskussionen nach der Parameteranpassung auf Überanpassung, indem wir die Leistung unseres angepassten Modells mit der Leistung des Standardmodells vergleichen. Es gibt jedoch viele verschiedene Möglichkeiten, auf Überanpassung zu testen. Heute haben wir uns entschieden, die Residuen unseres Modells auf Überanpassung zu testen. Wir haben eine hohe Korrelation zwischen den Residuen unseres Modells und seinen Verzögerungen festgestellt. Normalerweise sollten die Residuen eines ausreichend gelernten Modells keine Korrelation aufweisen. Dies deutet darauf hin, dass unser leistungsstärkstes Modell möglicherweise nicht effektiv gelernt hat oder dass es andere Daten gibt, die uns helfen könnten, unser Ziel zu erklären, und wir haben diese Daten nicht berücksichtigt.
Anschließend haben wir die Residuen unseres Modells auf den Trainings- und Testmengen aufgezeichnet. Zu diesem Zeitpunkt haben wir das Modell noch nicht auf die Testmenge angewendet. Anschließend haben wir unsere 15 Modelle anhand der Trainingsresiduen unseres SGD-Regressors kreuzvalidiert. Unser bestes Modell war die Lasso-Regression, aber wir wählten das drittbeste Modell, ein Deep Neural Network (DNN), als unsere Kandidatenlösung. Der Grund dafür war, dass uns die Flexibilität des tiefen neuronalen Netzes die Möglichkeit gibt, es besser auf die Daten abzustimmen als die Lasso-Regression aufgrund seiner begrenzten Anzahl von Abstimmungsparametern.
Wir haben unseren DNN-Regressor so abgestimmt, dass er die Residuen unseres SGD-Regressors in einem zweistufigen Prozess vorhersagt, der zu zwei einzigartigen Modellen führte. Wir haben zunächst 100 Iterationen einer Zufallssuche über die Parameter unseres DNN-Regressors durchgeführt und so das erste Modell erstellt. Die von uns ermittelten besten kontinuierlichen Parameter dienten als Ausgangspunkt für einen Versuch der uneingeschränkten globalen Optimierung mit dem L-BFGS-B-Algorithmus mit begrenztem Speicher, und so erhielten wir unser zweites Modell. Beide Modelle übertrafen den Standard-DNN-Regressor bei ungesehenen Validierungsdaten. Außerdem war unser letztes Modell das leistungsstärkste, was bedeutet, dass wir unsere Zeit nicht damit verschwendet haben, diese zusätzlichen Schritte in zweifacher Hinsicht durchzuführen.
Schließlich haben wir unsere beiden Modelle in das ONNX-Format exportiert und einen KI-gesteuerten Expert Advisor erstellt, der gelernt hat, seine eigenen Fehler zu korrigieren.
Abrufen der benötigten Daten
Wir beginnen damit, die benötigten Daten von unserem MetaTrader 5 Terminal zu holen. Das unten angehängte Skript holt so viele Balken historischer Kursdaten, wie wir angeben, von unserem Terminal, bevor es diese Daten im CSV-Format schreibt und für uns in unserem Ordner „Files“ speichert.
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //+------------------------------------------------------------------+ //| Script Inputs | //+------------------------------------------------------------------+ input int size = 100000; //How much data should we fetch? //+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ int rsi_handler; double rsi_buffer[]; //+------------------------------------------------------------------+ //| On start function | //+------------------------------------------------------------------+ void OnStart() { //--- Load indicator rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,20,PRICE_CLOSE); CopyBuffer(rsi_handler,0,0,size,rsi_buffer); ArraySetAsSeries(rsi_buffer,true); //--- File name string file_name = "Market Data " + Symbol() + ".csv"; //--- Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= size;i>=0;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
Bereinigung der Daten
Wir beginnen mit der Formatierung unserer Daten. Laden wir zunächst die benötigten Bibliotheken
#Import the libraries we need import pandas as pd import numpy as np
und lesen nun die Marktdaten ein.
#Read in the market data
nzd_jpy = pd.read_csv('Market Data NZDJPY.csv') Die Daten allerdings sind in der falschen Reihenfolge, wir müssen die Daten so organisieren, dass das älteste Datum zuerst und das Datum, das dem jetzigen Zeitpunkt am nächsten liegt, zuletzt angezeigt wird.
#Format the data nzd_jpy = nzd_jpy[::-1] nzd_jpy.reset_index(inplace=True, drop=True)
Definieren wir das Ziel.
#Labelling the data nzd_jpy['Target'] = nzd_jpy['Close'].shift(-20) nzd_jpy.dropna(inplace=True)
Wir werden auch binäre Ziele für die Darstellung hinzufügen.
#Add binary target for plotting nzd_jpy['Binary Target'] = np.nan nzd_jpy.loc[nzd_jpy['Close'] > nzd_jpy['Target'],'Binary Target'] = 1 nzd_jpy.loc[nzd_jpy['Close'] <= nzd_jpy['Target'],'Binary Target'] = 0
Schauen wir uns die Daten an.
#Current state of our dataframe
nzd_jpy 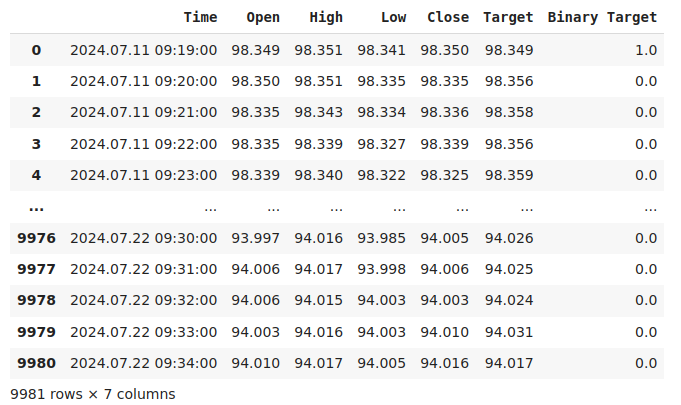
Abb. 1: Unser aktueller Datenrahmen
Explorative Datenanalyse
Wir erstellen Streudiagramme, um festzustellen, ob es Beziehungen gibt, die wir beobachten können. Leider scheinen unsere Daten willkürlich verteilt zu sein, ohne dass es eine klare Trennung zwischen Aufwärts- und Abwärtsbewegungen auf dem Markt gibt.
#Lets perform scatter plots sns.scatterplot(data=nzd_jpy,x=nzd_jpy['Open'], y=nzd_jpy['Close'],hue='Binary Target')
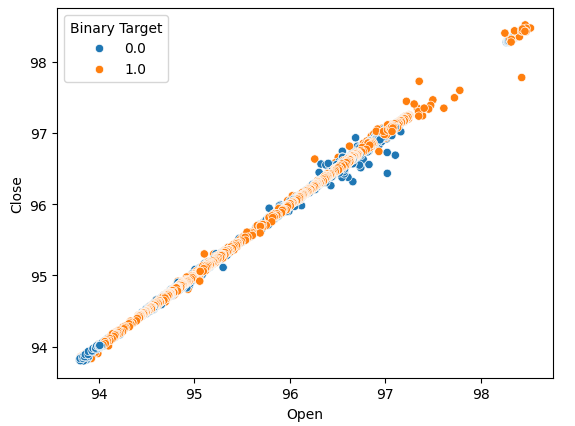
Abb. 2: Ein Streudiagramm des Eröffnungs- und Schlusskurses
Wir dachten daran, Boxplots zu erstellen, um alle Fälle zusammenzufassen, in denen der Preis entweder stieg oder fiel. Wir glaubten, dass es möglicherweise Unterschiede in der Verteilung der Daten für diese beiden möglichen Ziele geben könnte. Bedauerlicherweise zeigen unsere Box-Plots, dass es kaum einen Unterschied zwischen der Verteilung der Daten bei den beiden möglichen Ergebnissen gibt.
#Let's create categorical box plots sns.catplot(data=nzd_jpy,x='Binary Target',y='Close',kind='box')

Abb. 3: Ein Box-Plot, das alle Fälle zusammenfasst, in denen das Preisniveau fiel (0) oder stieg (1)
Wir können die Zeitreihendaten auch in 3 Komponenten zerlegen:
- Trend
- Saisonale
- Restbetrag
Die Trendkomponente stellt die durchschnittliche langfristige Bewegung der Preisniveaus dar. Die saisonale Komponente berücksichtigt zyklische Muster, die wiederholt in den Daten zu beobachten sind, während die Restkomponenten den Rest dessen darstellen, was nicht durch die beiden vorherigen Komponenten erklärt werden konnte. Da wir M1-Daten für das Paar NZDJPY verwenden, setzen wir unseren Zeitraum auf 1440, oder anders ausgedrückt, auf die durchschnittliche Kursentwicklung über einen ganzen Tag. Wir können einen sehr klaren und starken Abwärtstrend in den Daten beobachten, noch bevor wir die Zerlegung durchführen. Zieht man jedoch den Trend von den ursprünglichen Daten ab, können wir die saisonalen Effekte in den Daten deutlich erkennen.
#Time series decomposition import statsmodels.api as sm nzd_jpy_decomposition = sm.tsa.seasonal_decompose(nzd_jpy['Close'],period=1440,model='additive') fig = nzd_jpy_decomposition.plot()
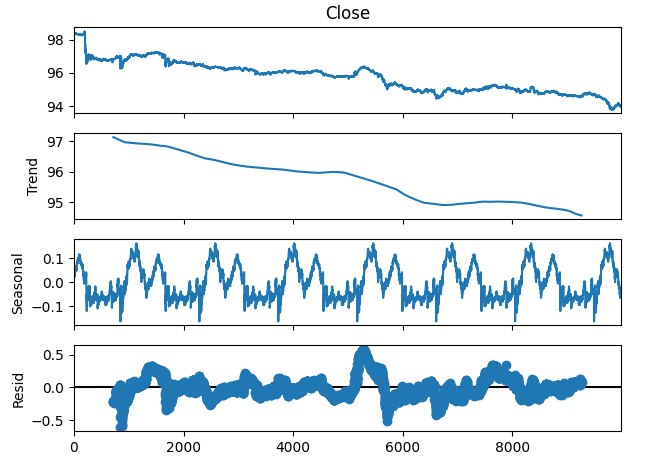
Abb. 4: Zeitserienzerlegung unserer Daten
Einige Effekte können in höheren Dimensionen verborgen sein. Durch die Erstellung von 3D-Streudiagrammen unserer Daten können wir möglicherweise Effekte aufdecken, die uns mit einem 2D-Streudiagramm verborgen bleiben. Leider gehörte dieser Datensatz nicht zu diesen Fällen. Unsere Daten sind nach wie vor schwer zu trennen und weisen keine erkennbaren Beziehungen auf.
#Let's also perform 3D plots #Visualizing our data in 3D import matplotlib.pyplot as plt fig = plt.figure(figsize=(7,7)) ax = fig.add_subplot(111,projection='3d') colors = ['blue' if movement == 0 else 'red' for movement in nzd_jpy.loc[:,"Binary Target"]] ax.scatter(nzd_jpy.loc[:,"Low"],nzd_jpy.loc[:,"High"],nzd_jpy.loc[:,"Close"],c=colors) ax.set_xlabel('NZDJPY Low') ax.set_ylabel('NZDJPY High') ax.set_zlabel('NZDJPY Close')
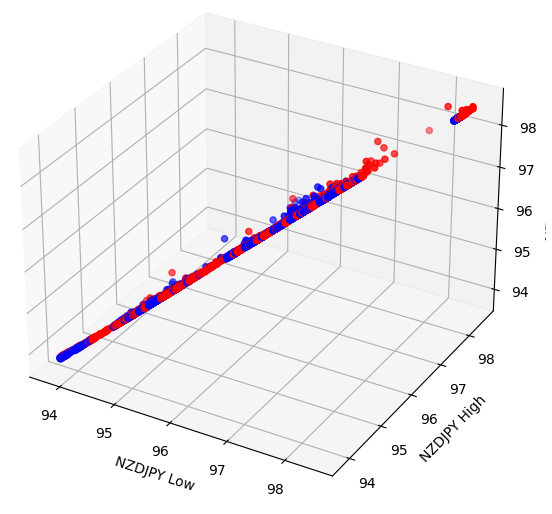
Abb. 5: Visualisierung unseres 3D-Streudiagramms
Vorbereiten der Datenmodellierung
Bevor wir mit der Modellierung unserer Daten beginnen können, müssen wir die Daten zunächst standardisieren und skalieren. Laden Sie die benötigten Bibliotheken.
#Let's prepare the data for modelling from sklearn.preprocessing import RobustScaler
Skalieren wir die Daten.
#Scale the data X = pd.DataFrame(RobustScaler().fit_transform(nzd_jpy.loc[:,['Close']]),columns=['Close']) residuals_X = pd.DataFrame(RobustScaler().fit_transform(nzd_jpy.loc[:,['Open','High','Low']]),columns=['Open','High','Low']) y = nzd_jpy.loc[:,'Target']
Auswahl des Modells
Laden wir die Bibliotheken, die wir zur Modellierung der Daten benötigen.
#Cross validating the models from sklearn.model_selection import cross_val_score,train_test_split from sklearn.linear_model import Lasso,LinearRegression,Ridge,ElasticNet,SGDRegressor,HuberRegressor from sklearn.ensemble import RandomForestRegressor,GradientBoostingRegressor,AdaBoostRegressor,ExtraTreesRegressor,BaggingRegressor from sklearn.svm import LinearSVR from sklearn.neighbors import KNeighborsRegressor from sklearn.tree import DecisionTreeRegressor from sklearn.neural_network import MLPRegressor
Teilen wir nun die Daten in 2 Hälften.
#Create train-test splits train_X,test_X,train_y,test_y = train_test_split(nzd_jpy.loc[:,['Close']],y,test_size=0.5,shuffle=False) residuals_train_X,residuals_test_X,residuals_train_y,residuals_test_y = train_test_split(nzd_jpy.loc[:,['Open','High','Low']],y,test_size=0.5,shuffle=False)
Wir speichern die Modelle in einer Liste und erstellen einen Datenrahmen, um unsere Validierungsfehlerstufen zu speichern.
#Store the models models = [ Lasso(), LinearRegression(), Ridge(), ElasticNet(), SGDRegressor(), HuberRegressor(), RandomForestRegressor(), GradientBoostingRegressor(), AdaBoostRegressor(), ExtraTreesRegressor(), BaggingRegressor(), LinearSVR(), KNeighborsRegressor(), DecisionTreeRegressor(), MLPRegressor(), ] #Store the names of the models model_names = [ 'Lasso', 'Linear Regression', 'Ridge', 'Elastic Net', 'SGD Regressor', 'Huber Regressor', 'Random Forest Regressor', 'Gradient Boosting Regressor', 'Ada Boost Regressor', 'Extra Trees Regressor', 'Bagging Regressor', 'Linear SVR', 'K Neighbors Regressor', 'Decision Tree Regressor', 'MLP Regressor', ] #Create a dataframe to store our cv error cv_error = pd.DataFrame(columns=model_names,index=np.arange(0,5))
Kreuzvalidierung jedes Modells.
#Cross validate each model for model in models: cv_score = cross_val_score(model,X,y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error') for i in np.arange(0,5): index = models.index(model) cv_error.iloc[i,index] = cv_score[i]
Visualisierung der Ergebnisse.
cv_error
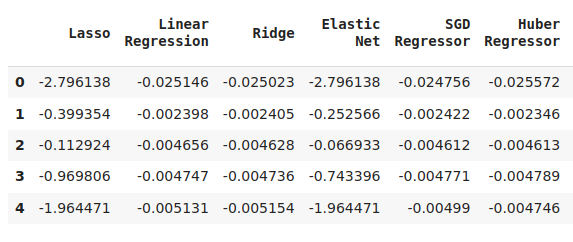
Abb. 6: Einige unserer Fehler bei der Vorhersage des zukünftigen Schlusskurses des NZDJPY
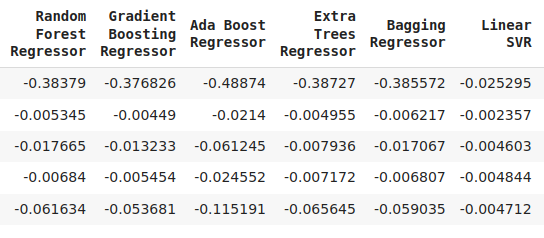
Abb. 7: Eine Fortsetzung unserer Fehlerwerte
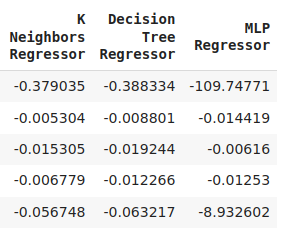
Abb. 8: Unsere endgültigen Fehlerwerte des Modells
Wir können unser Leistungsniveau über alle 5 Faltungen hinweg darstellen. Die schlechte Leistung unseres neuronalen Netzes war alarmierend, als wir die Daten in diesem Format visualisierten. Es würde wahrscheinlich sehr von einer Anpassung der Parameter profitieren.
cv_error.plot()
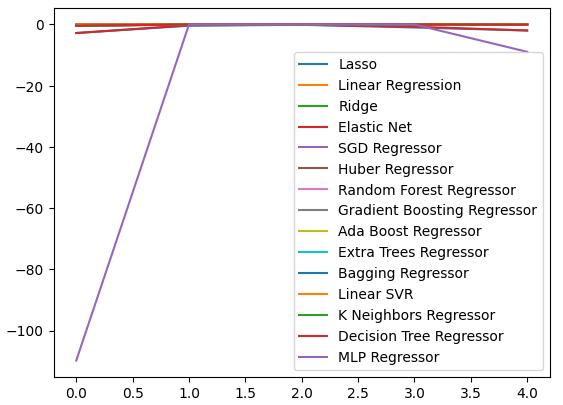
Abb. 9: Visualisierung unserer Fehlerquoten
Mit Hilfe von Box-Plots lassen sich viele Informationen in einem einzigen Diagramm zusammenfassen. In den folgenden Diagrammen ist beispielsweise deutlich zu sehen, wie schlecht das DNN bei dieser Aufgabe abgeschnitten hat. Es ist das letzte Modell auf der rechten Seite, und es zeigt eine viel größere Varianz in seiner Leistung als die anderen Modelle.
sns.boxplot(cv_error)

Abb. 10: Visualisierung unserer Fehler als Boxplots
Das Modell mit der besten Leistung ist das Modell mit den niedrigsten mittleren Fehlern.
#Our mean validation error
cv_error.mean() 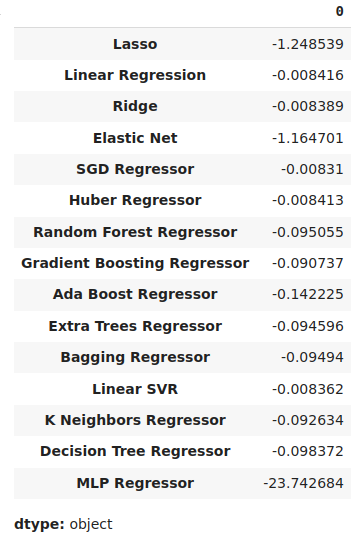
Abb. 11: Veranschaulichung unserer mittleren Fehlergrenzen
Die Bedeutung der Merkmale
Algorithmen zur Merkmalsbedeutung helfen uns zu verstehen, ob unser Modell sinnvolle Assoziationen gelernt hat oder ob das Modell Beziehungen gelernt hat, von denen wir möglicherweise nichts wussten. Lassen Sie uns zunächst die benötigten Bibliotheken importieren.
#Feature importance
from sklearn.feature_selection import mutual_info_regression,RFE Wir beginnen mit der Berechnung der wechselseitigen (mutual) Informationswerte (MI). MI informiert uns über das Potenzial, das jeder Prädiktor besitzt, um uns bei der Vorhersage des Ziels zu helfen. Und schließlich wird die MI auf einer logarithmischen Skala gemessen. Daher sind MI-Werte über 3 in der Praxis selten anzutreffen.
mi_score = pd.DataFrame(mutual_info_regression(X,y),columns=['MI Score'],index=X.columns)
Die Darstellung unserer MI-Scores zeigt deutlich, dass der Höchstkurs das größte Potenzial zur Vorhersage des zukünftigen Schlusskurses des NZDJPY zu haben scheint.
mi_score.plot()
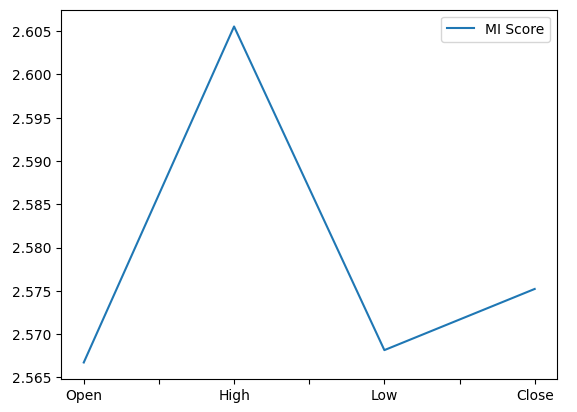
Abb. 12: Darstellung unserer MI-Werte
Der RFE-Algorithmus ist ähnlich einfach zu verwenden wie fast jedes Objekt aus der scikit-learn-Bibliothek. Wir erstellen einfach eine Instanz der Klasse und passen sie an die Daten an, bevor wir die Merkmalsbedeutung bewerten können, die sie jedem Prädiktor zuweist. Unser RFE-Algorithmus ging davon aus, dass alle Prädiktoren gleich wichtig für die Vorhersage des NZDJPY-Schlusskurses waren.
#Select the best features rfe = RFE(model, n_features_to_select=5, step=1) rfe = rfe.fit(X, y) rfe.ranking_
Einstellung der Parameter
Lassen Sie uns nun so viel Leistung wie möglich aus unserem SGD-Regressor-Modell herausholen. Wir werden eine randomisierte Suche über eine Stichprobe des Parameterraums des Modells durchführen. Importieren wir zunächst die benötigten Bibliotheken.
#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV Dann erstellen wir eine Instanz des Standardmodells.
#Initialize the model
model = SGDRegressor() Nun erstellen wir ein Tuner-Objekt, geben die möglichen Parameterwerte an, die wir abfragen möchten.
#Define the tuner
tuner = RandomizedSearchCV(
model,
{
"loss" : ['squared_error', 'huber', 'epsilon_insensitive','squared_epsilon_insensitive'],
"penalty":['l2','l1', 'elasticnet', None],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001,10,100,1000,10000,100000],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"fit_intercept": [True,False],
"early_stopping": [True,False],
"learning_rate":['constant','optimal','adaptive','invscaling'],
"shuffle": [True,False]
},
n_iter=100,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
) und passen das Tuner-Objekt an.
#Fit the tuner
tuner.fit(train_X,train_y) Die besten Parameter, die wir gefunden haben.
#Our best parameters
tuner.best_params_ 'shuffle': False,
'penalty': 'elasticnet',
'loss': 'huber',
'learning_rate': 'adaptive',
'fit_intercept': True,
'early_stopping': True,
'alpha': 1e-05}
Test auf Überanpassung
Wir können eine Überanpassung feststellen, wenn wir eine Korrelation in den Residuen des Modells beobachten. Wenn ein Modell effektiv gelernt hat, sollten seine Residuen zufälliges weißes Rauschen sein, was bedeutet, dass es kein vorhersehbares Muster in den Fehlern gibt, die unser Modell macht. Ein Modell, das eine Autokorrelation in seinen Residuen aufweist, kann jedoch Anlass zur Sorge geben. Dies kann darauf hindeuten, dass die von uns durchgeführte Regression fehlerhaft ist oder dass wir ein für unsere Aufgabe ungeeignetes Modell gewählt haben.1 Zunächst müssen wir die Residuen unseres angepassten Modells erfassen.
#Model validation model = SGDRegressor( tol = tuner.best_params_['tol'], shuffle = tuner.best_params_['shuffle'], penalty = tuner.best_params_['penalty'], loss = tuner.best_params_['loss'], learning_rate = tuner.best_params_['learning_rate'], alpha = tuner.best_params_['alpha'], fit_intercept = tuner.best_params_['fit_intercept'], early_stopping = tuner.best_params_['early_stopping'] ) model.fit(train_X,train_y) residuals = test_y - model.predict(test_X)
Wir können die Residuen unseres Modells in einem Diagramm visualisieren. Leider ist in den Residuen des Modells eindeutig eine Autokorrelation zu erkennen. Mit anderen Worten: Wenn die Residuen fallen, tendieren sie dazu, weiter zu fallen, und wenn die Residuen steigen, tendieren sie dazu, weiter zu steigen. Dies bedeutet, dass die zukünftigen Werte der Residuen eine Beziehung zu den vorherigen Werten haben können, ein verräterisches Zeichen dafür, dass unser Modell möglicherweise nicht effektiv gelernt hat, selbst nach der Durchführung der Parameteroptimierung!
#Plot the residuals
residuals.plot() 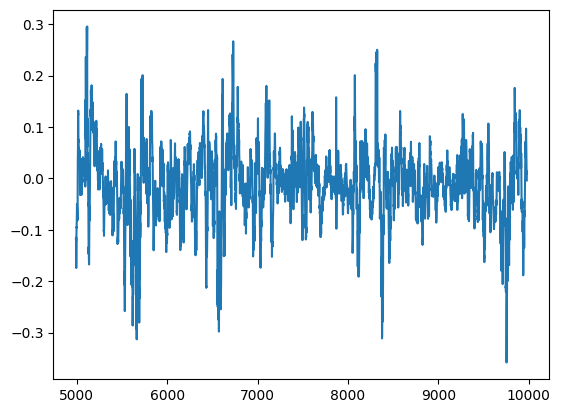
Abb. 13: Die Residuen unseres Modells
Es gibt robustere Tests für die Autokorrelation, z. B. können wir ein Autokorrelationsdiagramm (ACF) erstellen. Das ACF-Diagramm wird bei jedem möglichen Verzögerungswert Spitzen aufweisen. Die Höhe der einzelnen Spikes stellt den Grad der Korrelation der Zeitreihendaten mit ihrem verzögerten Wert dar. Im Hintergrund unseres Diagramms befindet sich außerdem eine blaue kegelförmige Struktur, die unsere Konfidenzintervalle darstellt. Alle Korrelationswerte, die über dem Konfidenzintervall liegen, werden als statistisch signifikant angesehen.
#The residuals appear to have autocorrelation
from statsmodels.graphics.tsaplots import plot_acf
fig = plot_acf(residuals) 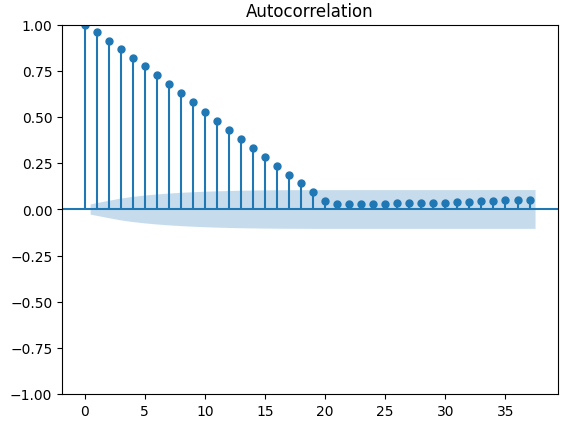
Abb. 14: Die Autokorrelation der Residuen unseres Modells
Dies ist kein gutes Zeichen, und wir hoffen, dass wir dies durch das Training unseres DNN zur Korrektur unseres ersten Modells abmildern können. Lassen Sie uns die Fehler unseres SGD Regresosr für die Trainingsdaten und dann für die Testdaten aufzeichnen. Beachten Sie, dass wir das Modell an dieser Stelle nicht an die Testdaten anpassen, sondern nur seine Fehlergrenzen messen.
#Prepare the residuals for our second model model = SGDRegressor(tol= 0.001, shuffle=False, penalty= 'elasticnet', loss= 'huber', learning_rate='adaptive', fit_intercept= True, early_stopping= True, alpha= 1e-05) #Store the model residuals model.fit(train_X,train_y) residuals_train_y = train_y - model.predict(train_X) residuals_test_y = test_y - model.predict(test_X)
Wir werden nun unsere Modelle bei der Vorhersage der Fehlerniveaus des SGD-Regressors kreuzvalidieren.
#Cross validate each model for model in models: cv_score = cross_val_score(model,residuals_train_X,residuals_train_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error') for i in np.arange(0,5): index = models.index(model) cv_error.iloc[i,index] = cv_score[i]
Lassen Sie uns den Validierungsfehler veranschaulichen.
#Cross validaton error levels
cv_error 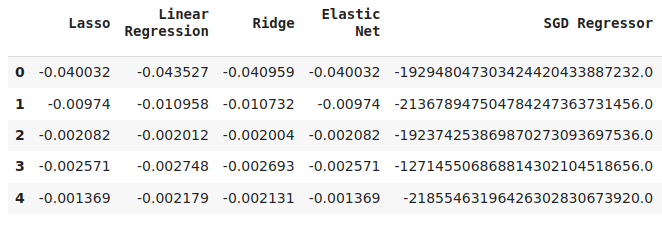
Abb. 15: Einige der Fehlerwerte der Modellvalidierung bei der Vorhersage der Fehlerwerte unseres ersten Modells
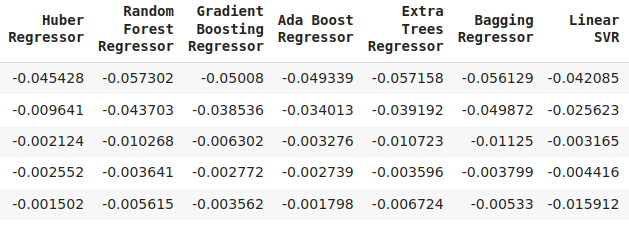
Abb. 16: Eine Fortsetzung unserer Validierungsfehlerstufen
Wir können unsere durchschnittlichen Fehlerniveaus in absteigender Reihenfolge anzeigen, um schnell unser leistungsstärkstes Modell zu ermitteln.
#Store the model's performance cv_error.mean().sort_values(ascending=False)
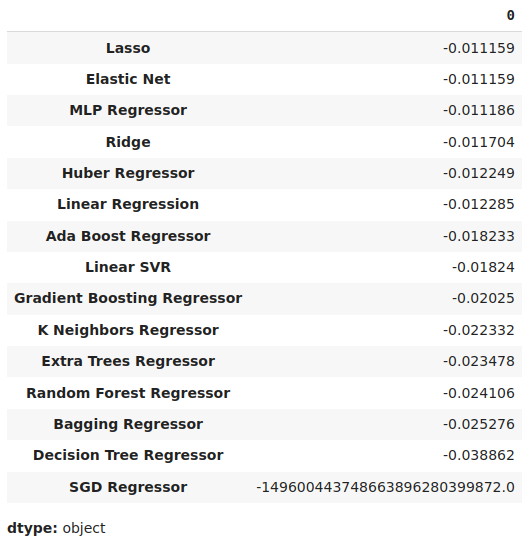
Abb. 17: Unsere mittleren Validierungsfehler zeigen deutlich, dass die Lasso-Regression das beste Modell ist, das wir haben.
Unsere Box-Plots zeigen, wie schlecht der SGD-Regressor bei der Vorhersage seiner eigenen Fehlerwerte abschneidet.
sns.boxplot(cv_error)
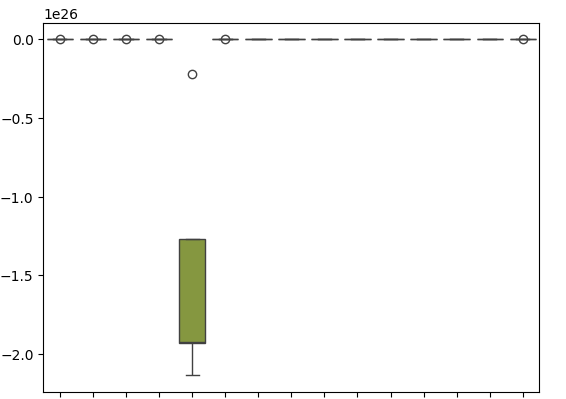
Abb. 18: Die Box-Plots unseres Validierungsfehlers bei der Vorhersage der Residuen unseres Modells
Wir können auch Liniendiagramme erstellen, um unsere Daten zu visualisieren.
cv_error.plot()
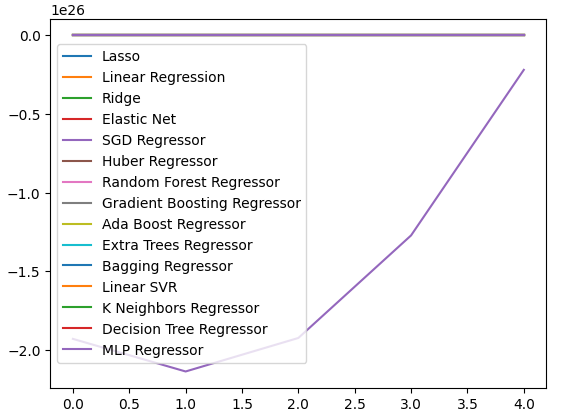
Abb. 19: Visualisierung der Fehlerniveaus durch Liniendiagramme
Parameterabstimmung unseres tiefen neuronalen Netzes
Bereiten wir uns nun darauf vor, die Parameter unseres DNN-Regressors abzustimmen. Dazu definieren wir zunächst das Tuner-Objekt und ein Beispiel für den Parameterraum, den wir durchsuchen wollen.
#Let's tune the model
#Reinitialize the model
model = MLPRegressor()
#Define the tuner
tuner = RandomizedSearchCV(
model,
{
"activation":["relu","tanh","logistic","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.00001,0.000001],
"learning_rate": ["constant","invscaling","adaptive"],
"learning_rate_init":[0.1,0.01,0.001,0.0001,0.000001,0.0000001],
"power_t":[0.1,0.5,0.9,0.01,0.001,0.0001],
"shuffle":[True,False],
"tol":[0.1,0.01,0.001,0.0001,0.00001],
"hidden_layer_sizes":[(10,20),(100,200),(30,200,40),(5,20,6)],
"max_iter":[10,50,100,200,300],
"early_stopping":[True,False]
},
n_iter=100,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
) Jetzt werden wir das Tuner-Objekt einbauen.
#Fit the tuner
tuner.fit(residuals_train_X,residuals_train_y) Schließlich können wir die besten Parameter sehen, die wir gefunden haben.\
#The best parameters we found
tuner.best_params_ 'solver': 'lbfgs',
'shuffle': False,
'power_t': 0.5,
'max_iter': 300,
'learning_rate_init': 0.01,
'learning_rate': 'constant',
'hidden_layer_sizes': (30, 200, 40),
'early_stopping': False,
'alpha': 1e-05,
'activation': 'identity'}
Tiefergehende Parameterabstimmung
Da wir nicht unbedingt wissen, wo die besten Eingabewerte liegen, werden wir versuchen, eine uneingeschränkte globale Optimierung mit dem L-BFGS-B-Algorithmus mit begrenztem Speicher in der SciPy-Bibliothek durchzuführen. Der L-BFGS-B-Algorithmus kann effektiv für globale Optimierungsprobleme eingesetzt werden. Der numerische Löser selbst ist in Fortran-Code implementiert, und die SciPy-Bibliothek bietet einen dünnen Wrapper für die einfache Anbindung an die Routine. Wir beginnen damit, die benötigten Bibliotheken zu importieren.

Abb. 20: Die Entwickler des ursprünglichen BFGS-Algorithmus, von links nach rechts: Broyden, Fletcher, Goldfarb und Shanno
#Deeper optimization
from scipy.optimize import minimize Nun definieren wir die zu minimierende Zielfunktion: Wir wollen den Trainingsfehler unseres DNN-Regressors minimieren. Wir werden alle anderen Eingabeparameter des Modells festlegen, da unsere SciPy-Minimierer nur kontinuierliche Optimierungsprobleme behandeln können.
#Define the objective function def objective(x): #Create a dataframe to store our accuracy cv_error = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"]) #The parameter x represents a new value for our neural network's settings #In order to find optimal settings, we will perform 10 fold cross validation using the new setting #And return the average RMSE from all 10 tests #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=x[0],tol=x[1]) model = MLPRegressor( tol = x[0], solver = tuner.best_params_['solver'], power_t = x[1], max_iter = tuner.best_params_['max_iter'], learning_rate = tuner.best_params_['learning_rate'], learning_rate_init = x[2], hidden_layer_sizes = tuner.best_params_['hidden_layer_sizes'], alpha = x[3], early_stopping = tuner.best_params_['early_stopping'], activation = tuner.best_params_['activation'], ) #Cross validate the model cv_score = cross_val_score(model,residuals_train_X,residuals_train_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error') for i in np.arange(0,5): cv_error.iloc[i,0] = cv_score[i] #Return the Mean CV RMSE return(cv_error.iloc[:,0].mean())
Wir werden den Ausgangspunkt unseres Optimierungsverfahrens durch die besten Parameter definieren, die wir bei unserer Zufallssuche gefunden haben. Wir werden auch Einschränkungen für unser Optimierungsverfahren machen, wir werden alle Werte zwingen, positiv zu sein, und außerdem werden wir alle Werte im Bereich von 10 hoch -100 bis 10 hoch 100 zulassen. Dies ist ein sehr großer Bereich, der hoffentlich die optimalen Parameter enthält, nach denen wir suchen.
#Define the starting point pt = [tuner.best_params_['tol'],tuner.best_params_['power_t'],tuner.best_params_['learning_rate_init'],tuner.best_params_['alpha']] bnds = ((10.0 ** -100,10.0 ** 100), (10.0 ** -100,10.0 ** 100), (10.0 ** -100,10.0 ** 100), (10.0 ** -100,10.0 ** 100))
Auf der Suche nach den besten Parametern.
#Searching deeper for better parameters result = minimize(objective,pt,method="L-BFGS-B",bounds=bnds)
Unsere Optimierungsergebnisse.
result
success: True
status: 0
fun: -0.01143352283130129
x: [ 1.000e-04 5.000e-01 1.000e-02 1.000e-05]
nit: 2
jac: [-1.388e+04 -4.657e+04 5.625e+04 -1.033e+04]
nfev: 120
njev: 24
hess_inv: <4x4 LbfgsInvHessProduct with dtype=float64>
Test auf Überanpassung
Testen wir nun auf Überanpassung. Dieses Mal werden wir unsere 2 Modelle mit der Leistung des Standard-DNN-Regressors vergleichen. Instanziieren wir die Instanzen jedes DNN-Regressors, den wir testen wollen.
#Model validation default_model = MLPRegressor() customized_model = MLPRegressor( tol = tuner.best_params_['tol'], solver = tuner.best_params_['solver'], power_t = tuner.best_params_['power_t'], max_iter = tuner.best_params_['max_iter'], learning_rate = tuner.best_params_['learning_rate'], learning_rate_init = tuner.best_params_['learning_rate_init'], hidden_layer_sizes = tuner.best_params_['hidden_layer_sizes'], alpha = tuner.best_params_['alpha'], early_stopping = tuner.best_params_['early_stopping'], activation = tuner.best_params_['activation'], ) lbfgs_customized_model = MLPRegressor( tol = result.x[0], solver = tuner.best_params_['solver'], power_t = result.x[1], max_iter = tuner.best_params_['max_iter'], learning_rate = tuner.best_params_['learning_rate'], learning_rate_init = result.x[2], hidden_layer_sizes = tuner.best_params_['hidden_layer_sizes'], alpha = result.x[3], early_stopping = tuner.best_params_['early_stopping'], activation = tuner.best_params_['activation'], )
Jetzt erstellen wir eine Liste von Modellen und einen Datenrahmen, um die Fehlerstufen der Validierung zu speichern.
models = [default_model,customized_model,lbfgs_customized_model] cv_error = pd.DataFrame(index=np.arange(0,5),columns=['Default NN','Random Search NN','L-BFGS-B NN'])
Kreuzvalidierung jedes Modells.
#Cross validate the model for model in models: model.fit(residuals_train_X,residuals_train_y) cv_score = cross_val_score(model,residuals_test_X,residuals_test_y,cv=5,n_jobs=-1,scoring='neg_mean_squared_error') for i in np.arange(0,5): index = models.index(model) cv_error.iloc[i,index] = cv_score[i]
Unser Kreuzvalidierungsfehler.
cv_error
| Standard NN | Zufällige Suche NN | L-BFGS-B NN |
|---|---|---|
| -0.007735 | -0.007708 | -0.007692 |
| -0.00635 | -0.006344 | -0.006329 |
| -0.003307 | -0.003265 | -0.00328 |
| 0.005225 | -0.004803 | -0.004761 |
| -0.004469 | -0.004447 | -0.004492 |
Analysieren wir nun unsere durchschnittlichen Fehlerquoten.
cv_error.mean().sort_values(ascending=False)
| Modell | Validierungsfehler |
|---|---|
| L-BFGS-B NN | -0.005311 |
| Zufällige Suche NN | -0.005313 |
| Standard NN | -0.005417 |
Wie wir sehen, lagen die Ergebnisse unserer Modelle alle im gleichen Bereich. Unsere maßgeschneiderten Modelle lieferten uns jedoch im Durchschnitt deutlich niedrigere Fehlerquoten. Leider ist die von unseren Modellen angezeigte Varianz in allen Bereichen fast gleich, wie unsere Box-Plots zeigen. Anhand der Varianzniveaus lässt sich der Kenntnisstand des Modells bestimmen,
sns.boxplot(cv_error)
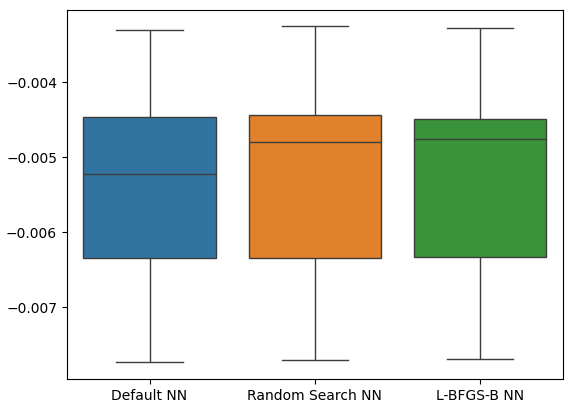
Abb. 21: Unsere Fehlerquote bei der Validierung der übermittelten Daten
Nun wollen wir sehen, ob unser Ensemble-Ansatz besser ist als die Verwendung eines einzelnen Modells zur Vorhersage des Preisniveaus. Wir werden zunächst die benötigten Modelle vorbereiten.
#Now that we have come this far, let's see if our ensemble approach is worth the trouble baseline = LinearRegression() default_nn = MLPRegressor() #The SGD Regressor will predict the future price sgd_regressor = SGDRegressor(tol= 0.001, shuffle=False, penalty= 'elasticnet', loss= 'huber', learning_rate='adaptive', fit_intercept= True, early_stopping= True, alpha= 1e-05) #The deep neural network will predict the error in the SGDRegressor's prediction lbfgs_customized_model = MLPRegressor( tol = result.x[0], solver = tuner.best_params_['solver'], power_t = result.x[1], max_iter = tuner.best_params_['max_iter'], learning_rate = tuner.best_params_['learning_rate'], learning_rate_init = result.x[2], hidden_layer_sizes = tuner.best_params_['hidden_layer_sizes'], alpha = result.x[3], early_stopping = tuner.best_params_['early_stopping'], activation = tuner.best_params_['activation'], )
Wir passen das Modell an die Trainingsmenge an
#Fit the models on the train set baseline.fit(train_X.loc[:,['Close']],train_y) default_nn.fit(train_X.loc[:,['Close']],train_y) sgd_regressor.fit(train_X.loc[:,['Close']],train_y) lbfgs_customized_model.fit(residuals_train_X.loc[:,['Open','High','Low']],residuals_train_y)
und speichern die Modelle in einer Liste.
#Store the models in a list
models = [baseline,default_nn,sgd_regressor,lbfgs_customized_model] Wir erstellen einen Datenrahmens zum Speichern unserer Fehlerstufen
#Create a dataframe to store our error ensemble_error = pd.DataFrame(index=np.arange(0,5),columns=['Baseline','Default NN','SGD','Customized NN'])
und importieren der benötigten Bibliotheken.
from sklearn.model_selection import TimeSeriesSplit from sklearn.metrics import mean_squared_error
Jetzt erstellen wir das geteilte Zeitreihenobjekt.
#Create the time-series object tscv = TimeSeriesSplit(n_splits=5,gap=20)
Wir müssen die Indizes unserer Daten zurücksetzen.
#Reset the indexes so we can perform cross validation
test_y = test_y.reset_index()
residuals_test_y = residuals_test_y.reset_index()
test_X = test_X.reset_index()
residuals_test_X = residuals_test_X.reset_index() Nun werden wir eine Zeitreihen-Kreuzvalidierung durchführen. Beachten Sie, dass das Modell, das die Residuen vorhersagt, getrennt von den anderen Modellen trainiert werden muss, die lediglich den zukünftigen Schlusskurs vorhersagen.
#Cross validate the models for j in np.arange(0,4): model = models[j] for i,(train,test) in enumerate(tscv.split(test_X)): #The model predicting the residuals if(j == 3): model.fit(residuals_test_X.loc[train[0]:train[-1],['Open','High','Low']],residuals_test_y.loc[train[0]:train[-1],'Target']) #Measure the loss ensemble_error.iloc[i,j] = mean_squared_error(residuals_test_y.loc[test[0]:test[-1],'Target' ], model.predict(residuals_test_X.loc[test[0]:test[-1],['Open','High','Low']])) elif(j <= 2): #Fit the model model.fit(test_X.loc[train[0]:train[-1],['Close']],test_y.loc[train[0]:train[-1],'Target']) #Measure the loss ensemble_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],'Target' ],model.predict(test_X.loc[test[0]:test[-1],['Close']]))
Lassen Sie uns nun unsere Validierungsfehler analysieren. Leider ist es uns nicht gelungen, die Leistung eines einfachen linearen Regressionsmodells zu übertreffen, was darauf hindeutet, dass unser Modell möglicherweise zu empfindlich auf die Varianz der Daten reagiert. Die gute Nachricht ist, dass wir unseren Standard-DNN-Regressor übertroffen haben.
ensemble_error.mean().sort_values(ascending=True)
| Modelle | Validierungsfehler |
|---|---|
| Basislinie | 0.004784 |
| Kundenspezifisch L-BFGS-B NN | 0.004891 |
| SGD | 0.005937 |
| Standard NN | 35.35851 |
Exportieren ins ONNX-Format
Open Neural Network Exchange (ONNX) ist ein Open-Source-Protokoll für die Erstellung und den Einsatz von Modellen für maschinelles Lernen in einer sprachunabhängigen Weise. ONNX ermöglicht uns die einfache Integration unserer Scikit-Learn-Modelle in unsere Expert Advisors, indem wir uns auf die MQL5-API-Unterstützung für ONNX verlassen. Zunächst werden wir die benötigten Bibliotheken importieren. #Prepare to export to ONNX import onnx import netron from skl2onnx import convert_sklearn from skl2onnx.common.data_types import FloatTensorType
Nun wollen wir die Modelle auf alle uns zur Verfügung stehenden Daten anwenden.
#Fit the SGD model on all the data we have close_model = SGDRegressor(tol= 0.001, shuffle=False, penalty= 'elasticnet', loss= 'huber', learning_rate='adaptive', fit_intercept= True, early_stopping= True, alpha= 1e-05) close_model.fit(nzd_jpy.loc[:,['Close']],nzd_jpy.loc[:,'Target'])
Als Letztes werden wir unseren DNN-Regressor anpassen.
#Fit the deep neural network on all the data we have residuals_model = MLPRegressor( tol=0.0001, solver= 'lbfgs', shuffle=False, power_t= 0.5, max_iter= 300, learning_rate_init= 0.01, learning_rate='constant', hidden_layer_sizes=(30, 200, 40), early_stopping=False, alpha=1e-05, activation='identity') #Fit the model on the residuals residuals_model.fit(residuals_train_X,residuals_train_y) residuals_model.fit(residuals_test_X,residuals_test_y)
Definieren wir die Eingangsformen unserer 2 Modelle.
# Define the input type close_initial_types = [("float_input",FloatTensorType([1,1]))] residuals_initial_types = [("float_input",FloatTensorType([1,3]))]
Wir müssen ONNX-Darstellungen unserer Modelle erstellen.
# Create the ONNX representation close_onnx_model = convert_sklearn(close_model,initial_types=close_initial_types,target_opset=12) residuals_onnx_model = convert_sklearn(residuals_model,initial_types=residuals_initial_types,target_opset=12)
Zu guter Letzt müssen wir unsere Modelle im ONNX-Format speichern.
#Save the ONNX Models onnx.save_model(close_onnx_model,'close_model.onnx') onnx.save_model(residuals_onnx_model,'residuals_model.onnx')
Visualisierung unserer ONNX-Modelle
Wir sollten unsere Modelle auch visualisieren, um sicherzustellen, dass sie die von uns spezifizierten Eingabe- und Ausgabeformen haben. Wir beginnen mit der Visualisierung unseres DNN-Regressors. Zunächst importieren wir die Bibliothek, die wir benötigen.
#Import netron
import netron Jetzt werden wir unser DNN visualisieren.
#Visualizing the residuals model netron.start("/ENTER/YOUR/PATH/residuals_model.onnx")
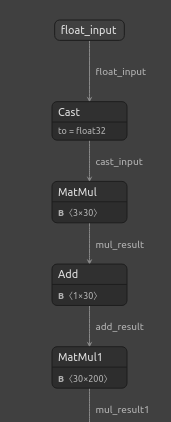
Abb. 22: Visualisierung unseres DNN-Regressor-Modells
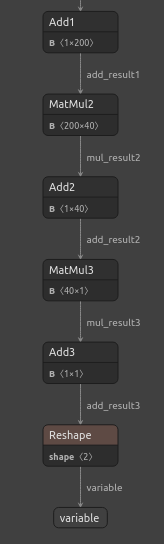
Abb. 23: Visualisierung unseres DNN-Regressor-Modells
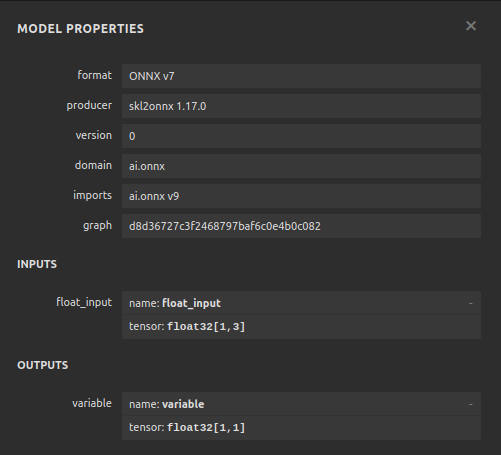
Abb. 24: Die Eingangs- und Ausgangsform unseres DNN-Regressors entspricht unseren Erwartungen
Lassen Sie uns auch unser SGD-Regressor-Modell visualisieren.
#Visualizing the close model netron.start("/ENTER/YOUR/PATH/close_model.onnx")

Abb. 25: Visualisierung unseres SGD-Regressor-Modells
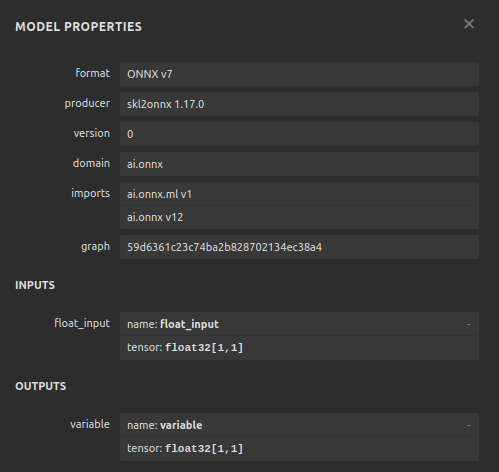
Abb. 26: Visualisierung unseres SGD-Regressor-Modells
Implementierung in MQL5
Um mit dem Aufbau unseres KI-gestützten Expert Advisors zu beginnen, müssen wir zunächst die soeben erstellten ONNX-Dateien in die Anwendung laden.
//+------------------------------------------------------------------+ //| NZD JPY AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Load the ONNX models | //+------------------------------------------------------------------+ #resource "\\Files\\residuals_model.onnx" as const uchar residuals_onnx_buffer[]; #resource "\\Files\\close_model.onnx" as const uchar close_onnx_buffer[];
Jetzt brauchen wir die Handelsbibliothek, um unsere Positionen zu öffnen und zu schließen.
//+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Lassen Sie uns auch globale Variablen erstellen, die wir in unserem Programm verwenden werden.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long residuals_model,close_model; vectorf residuals_forecast = vectorf::Zeros(1); vectorf close_forecast = vectorf::Zeros(1); float forecast = 0; int model_state,system_state; int counter = 0; double bid,ask;
In der Initialisierungsprozedur unseres Modells werden wir zunächst unsere 2 ONNX-Modelle laden und dann überprüfen, ob unsere Modelle funktionieren.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX models if(!load_onnx_models()) { return(INIT_FAILED); } //--- Validate the model is working model_predict(); if(forecast == 0) { Comment("The ONNX models are not working correctly!"); return(INIT_FAILED); } //--- We managed to load our ONNX models return(INIT_SUCCEEDED); }
Wenn unser Modell vom Chart entfernt wird, werden alle nicht mehr benötigten Ressourcen freigegeben.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Free up the resources we no longer need release_resorces(); }
Wenn wir neue Preise erhalten, werden wir zunächst unsere Marktpreise aktualisieren. Anschließend holen wir eine Vorhersage von unserem Modell ab. Sobald wir eine Prognose haben, werden wir prüfen, ob wir offene Stellen haben. Wenn wir keine offenen Positionen haben, folgen wir der Vorhersage unseres Modells so lange, wie die Preisänderungen auf höheren Zeitrahmen dies zulassen. Andernfalls, wenn wir bereits eine offene Position haben, warten wir zunächst 20 Kerzen ab, bevor wir prüfen, ob unser Modell eine Umkehrung vorhersagt. Es sei daran erinnert, dass wir das Modell so trainiert haben, dass es 20 Schritte in die Zukunft voraussagen kann, weshalb wir eine gewisse Zeit verstreichen lassen sollten, bevor wir auf eine Umkehrung prüfen.
//--- If we have no positions, follow the model's forecast if(PositionsTotal() == 0) { //--- Our model is suggesting we should buy if(model_state == 1) { if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,12)) { Trade.Buy(0.3,Symbol(),ask,0,0,"NZD JPY AI"); system_state = 1; } } //--- Our model is suggesting we should sell if(model_state == -1) { if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,12)) { Trade.Sell(0.3,Symbol(),bid,0,0,"NZD JPY AI"); system_state = -1; } } } else { //--- We want to wait 20 mins before forecating again. if(time_stamp != time) { time_stamp= time; counter += 1; } if((system_state!= model_state) && (counter >= 20)) { Alert("Reversal detected by our AI system, closing all positions"); Trade.PositionClose(Symbol()); counter = 0; } } }
Definieren wir die Funktion, mit der wir die Vorhersagen unserer Modelle abrufen. Denken Sie daran, dass wir 2 separate Modelle haben, die nacheinander aufgerufen werden müssen.
//+------------------------------------------------------------------+ //| Fetch a prediction from our models | //+------------------------------------------------------------------+ void model_predict(void) { //--- Define the inputs vectorf close_inputs = vectorf::Zeros(1); vectorf residuals_inputs = vectorf::Zeros(3); close_inputs[0] = (float) iClose(Symbol(),PERIOD_M1,0); residuals_inputs[0] = (float) iOpen(Symbol(),PERIOD_M1,0); residuals_inputs[1] = (float) iHigh(Symbol(),PERIOD_M1,0); residuals_inputs[2] = (float) iLow(Symbol(),PERIOD_M1,0); //--- Fetch predictions OnnxRun(residuals_model,ONNX_DEFAULT,residuals_inputs,residuals_forecast); OnnxRun(close_model,ONNX_DEFAULT,close_inputs,close_forecast); //--- Our forecast forecast = residuals_forecast[0] + close_forecast[0]; Comment("Model forecast: ",forecast); //--- Remember the model's prediction if(forecast > close_inputs[0]) { model_state = 1; } else { model_state = -1; } }
Wir brauchen auch eine Funktion zur Aktualisierung unserer Marktpreise.
//+------------------------------------------------------------------+ //| Update the market data we have | //+------------------------------------------------------------------+ void update_market_data(void) { bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); }
Diese Funktion gibt die Ressourcen frei, die wir nicht mehr benötigen.
//+------------------------------------------------------------------+ //| Rlease the resources we no longer need | //+------------------------------------------------------------------+ void release_resorces(void) { OnnxRelease(residuals_model); OnnxRelease(close_model); ExpertRemove(); }
Schließlich bereitet diese Funktion unsere ONNX-Modelle aus den ONNX-Puffern vor, die wir zu Beginn unserer Anwendung erstellt haben.
//+------------------------------------------------------------------+ //| This function will load our ONNX models | //+------------------------------------------------------------------+ bool load_onnx_models(void) { //--- Load the ONNX models from the buffers we created residuals_model = OnnxCreateFromBuffer(residuals_onnx_buffer,ONNX_DEFAULT); close_model = OnnxCreateFromBuffer(close_onnx_buffer,ONNX_DEFAULT); //--- Validate the models if((residuals_model == INVALID_HANDLE) || (close_model == INVALID_HANDLE)) { //--- We failed to load the models Comment("Failed to create the ONNX models: ",GetLastError()); return(false); } //--- Set the I/O shapes of the models ulong residuals_inputs[] = {1,3}; ulong close_inputs[] = {1,1}; ulong model_output[] = {1,1}; //---- Validate the I/O shapes if((!OnnxSetInputShape(residuals_model,0,residuals_inputs)) || (!OnnxSetInputShape(close_model,0,close_inputs))) { //--- We failed to set the input shapes Comment("Failed to set model input shapes: ",GetLastError()); return(false); } if((!OnnxSetOutputShape(residuals_model,0,model_output)) || (!OnnxSetOutputShape(close_model,0,model_output))) { //--- We failed to set the output shapes Comment("Failed to set model output shapes: ",GetLastError()); return(false); } //--- Everything went fine return(true); } //+------------------------------------------------------------------+
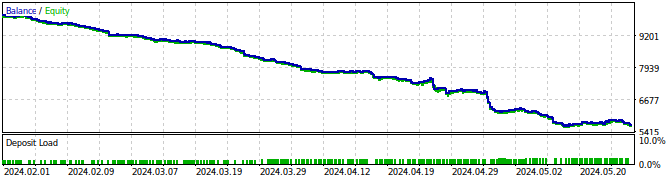
Abb. 27: Testen Sie unseren Expert Advisor
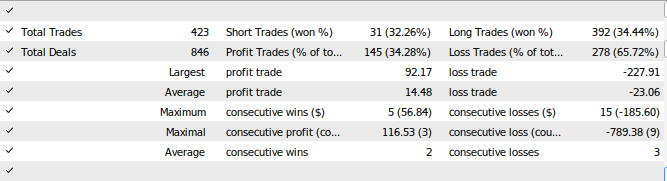
Abb. 28: Die Ergebnisse des Tests unseres Expert Advisors
Schlussfolgerung
In diesem Artikel haben wir gezeigt, wie wir selbstkorrigierende Handelsanwendungen erstellen können. In unserem Gespräch ging es darum, wie Sie die Residuen Ihres Modells analysieren können, um Überanpassungen und Verzerrungen in Ihren Machine-Learning-Modellen zu erkennen. Leider mussten wir feststellen, dass die Residuen des Modells mit der besten Leistung fehlerhaft waren. Wir könnten versuchen, dies zu beheben, indem wir die Zeitreihendaten und die Zielvorgabe so lange differenzieren, bis wir keine Autokorrelation mehr in den Residuen feststellen, doch könnte dies auch die Interpretation unseres Modells erschweren. Auch wenn wir nicht garantieren können, dass die in diesem Artikel angesprochenen Punkte zu dauerhaftem Erfolg führen, ist es auf jeden Fall eine Überlegung wert, wenn Sie KI in Ihren Handelsstrategien einsetzen möchten. Bei unserer nächsten Diskussion werden wir versuchen, die heute festgestellten Fallstricke zu beseitigen und gleichzeitig die Interpretierbarkeit der Modelle zu gewährleisten.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15886
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Verschaffen Sie sich einen Vorteil auf jedem Markt (Teil IV): CBOE: Volatilitätsindizes von Euro und Gold
Verschaffen Sie sich einen Vorteil auf jedem Markt (Teil IV): CBOE: Volatilitätsindizes von Euro und Gold
 MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 39): RSI (Relative Strength Index)
MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 39): RSI (Relative Strength Index)
 MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 40): Parabolic SAR
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 40): Parabolic SAR
 Analyse mehrerer Symbole mit Python und MQL5 (Teil I): NASDAQ für Hersteller von integrierten Schaltungen
Analyse mehrerer Symbole mit Python und MQL5 (Teil I): NASDAQ für Hersteller von integrierten Schaltungen
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Guter Artikel.
Vielen Dank, Kikkih, das bedeutet mir sehr viel.