Elementos da análise correlacional em MQL5: Critério de independência qui-quadrado de Pearson e relação de correlação

Introdução

Hoje gostaríamos de abordar uma área importante da estatística matemática, a análise correlacional, que visa detectar e avaliar as dependências entre variáveis aleatórias. A ferramenta mais popular no arsenal da análise correlacional é, sem dúvida, o coeficiente de correlação. No entanto, para avaliar dependências em dados, especialmente como os incrementos de preços de mercado, o cálculo de um único coeficiente de correlação é completamente insuficiente. Primeiro, ele avalia apenas a dependência linear. Em segundo lugar, valores nulos do coeficiente de correlação não indicam necessariamente a ausência de dependência, caso a amostra de dados utilizada tenha uma distribuição diferente da normal. Para responder à questão de se os dados são dependentes, observa-se os critérios de independência. Falaremos sobre o mais conhecido deles — o critério de independência qui-quadrado de Pearson. Também discutiremos uma característica numérica, o coeficiente de relação de correlação, que ajuda a determinar se a dependência estudada é não linear.

Hipótese de independência

Supõe-se que os dados representam observações de uma variável aleatória bidimensional (X, Y) com função de distribuição desconhecida F(X, Y), sobre a qual é necessário verificar a hipótese de independência H0: F(X, Y) = F(X)*F(Y), onde F(X) e F(Y) são funções de distribuição unidimensionais.

Por variáveis aleatórias X e Y, neste artigo, referir-me-ei a incrementos dos logaritmos dos preços de diferentes instrumentos financeiros ou a incrementos de preços de um único instrumento, mas tomados com um atraso de uma unidade.

Critério de independência qui-quadrado de Pearson

O critério de independência qui-quadrado é aplicado tanto para variáveis aleatórias discretas com número finito de resultados, quanto para variáveis contínuas, mas com a condição obrigatória de agrupamento prévio. Assim, o conjunto de todos os valores possíveis da variável aleatória X é dividido em i intervalos não sobrepostos A1,A2,Ai, e o conjunto de todos os valores de Y em j intervalos não sobrepostos B1,B2,Bj. Dessa forma, o conjunto de valores da variável bidimensional (X, Y) é dividido em i*j retângulos (células). Para visualização, esses dados são apresentados na chamada tabela de contingência (tabela de correlação, tabela de distribuição de probabilidade da variável aleatória bidimensional etc.).

                              

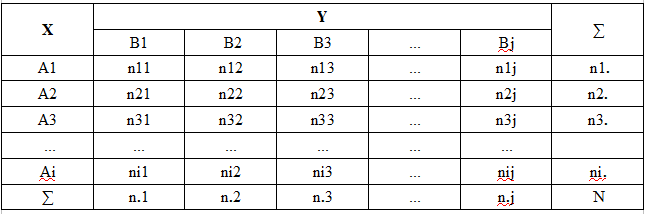
Nesta tabela:

• Ai = (Xi-1, Xi) - o i-ésimo intervalo de agrupamento da variável aleatória X

• Bj = (Yj-1,Yj) – o j-ésimo intervalo de agrupamento da variável aleatória Y

• nij - a frequência grupal real da célula (o número de pares de observações (X, Y) cujos valores caíram no intervalo Ai e Bj)

• ni. - número de observações na i-ésima linha

• n.j – número de observações na j-ésima coluna

• N – tamanho da amostra

Como critério de independência qui-quadrado, é utilizada a estatística:

CHI2 = (Actual – Expected) ^2 / Expected,

onde

• Actual - frequência grupal real da célula nij,

• Expected – frequência grupal esperada da célula nij

Essa estatística segue a distribuição qui-quadrado com v = (j-1)(i-1) graus de liberdade.

A hipótese nula de independência é rejeitada se a estatística calculada CHI2 exceder os valores críticos da distribuição qui-quadrado com v graus de liberdade em um nível de significância alfa.

As frequências reais são calculadas a partir dos dados da amostra, e o princípio para construir as frequências esperadas é o seguinte: se as variáveis aleatórias X e Y são independentes, então a fórmula a seguir é válida:

P {Ai, Bj} = P {Ai}*P{Bj},

ou seja, a probabilidade de ocorrência simultânea dos eventos Ai e Bj é igual ao produto da probabilidade de ocorrência de Ai pela probabilidade de ocorrência de Bj.

Para encontrar as expectativas matemáticas dos eventos {Ai, Bj}, {Ai} e {Bj}, multiplicamos ambos os lados da igualdade pelo quadrado do número de observações, ou seja, por N*N.

N*N * P {Ai, Bj} = N *P{Ai} * N* P{Bj}

Assim, obtemos:

• N *P{Ai} - expectativa matemática do número de observações na i-ésima linha

• N* P{Bj} - expectativa matemática do número de observações na j-ésima coluna

• N * P {Ai, Bj} = (N *P{Ai} * N* P{Bj})/N - expectativa matemática do número de ocorrências na célula na interseção da i-ésima linha e j-ésima coluna

Então, substituindo as expectativas N *P{Ai} e N* P{Bj} por suas estimativas ni. e n.j (ou seja, as frequências reais da tabela de contingência), obtemos a estimativa desejada das frequências esperadas:

Expected = (ni. * n.j) / N

Dessa forma, sob a hipótese de independência, a frequência esperada de ocorrência na célula na interseção da i-ésima linha e j-ésima coluna é igual ao produto das somas do número de observações na i-ésima linha e j-ésima coluna, dividido pelo tamanho da amostra.

Portanto, ao calcular o critério, é natural esperar que quanto maior a diferença entre as frequências reais e esperadas, maior a probabilidade de que os dados não sejam independentes.

Indicador Chi2Test

O cálculo do critério de independência qui-quadrado de Pearson é implementado no indicador Chi2Test. O indicador verifica a hipótese de independência em cada barra entre incrementos de preços consecutivos para um instrumento financeiro.

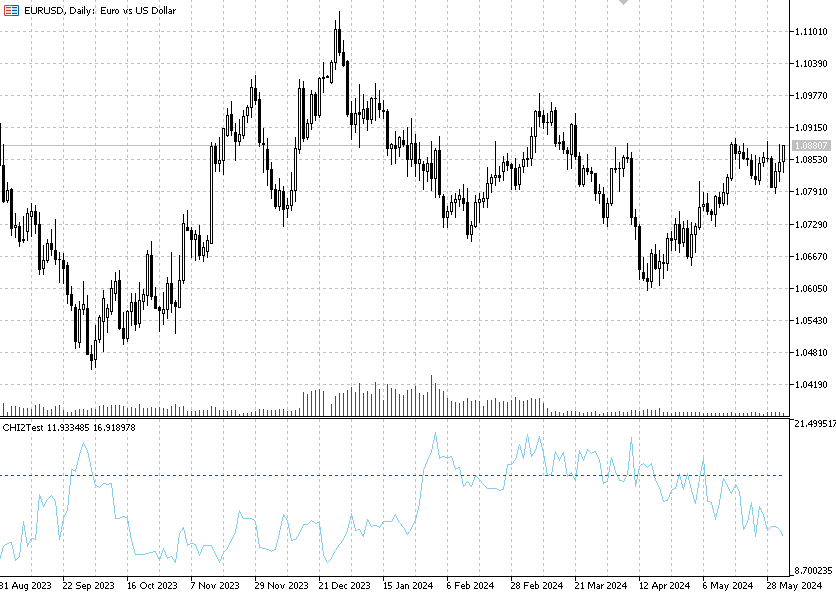
Este indicador possui quatro parâmetros de entrada:

• alpha – nível de significância

• Data – janela de dados para cálculo

• Tails – número de desvios padrão

• Contingency coefficient – coeficiente de contingência

Para calcular a estatística qui-quadrado, primeiro precisamos calcular as frequências reais na tabela de contingência das características. Para isso, utiliza-se a função crosstab.

//+------------------------------------------------------------------+
//|  Функция рассчитывает таблицу сопряженности двух СВ (X,Y)        |
//+------------------------------------------------------------------+
bool Crosstab(const double &dataX[],const double &dataY[],const double &bins[],matrix &freq)
  {

   int datasizeX=ArraySize(dataX);
   int datasizeY=ArraySize(dataY);
   int binssize=ArraySize(bins);
   if(datasizeX==0 || datasizeY==0 || binssize==0)
      return(false);
   if(datasizeX != datasizeY)
      return(false);

   for(int i=0; i<datasizeX; i++)
     {
      if(!MathIsValidNumber(dataX[i]) || !MathIsValidNumber(dataY[i]))
         return(false);
     }

   matrix m_freq=matrix::Zeros(binssize, binssize);
   
   for(int x=0; x<binssize; x++)
     {
      for(int i=0; i<datasizeX; i++)
        {
         for(int y=0; y<binssize; y++)
           {
            if(dataX[i]<=bins[x] && dataY[i]<=bins[y]) 
              {
               m_freq[x,y]=m_freq[x,y]+1;
               break;
              }
           }
        }
     }
     
   matrix Actual = m_freq;
   vector p1,p2,diffp;
   for (int j=1; j<binssize; j++)
   {
   p1 = m_freq.Row(j-1);
   p2 = m_freq.Row(j);
   diffp = p2-p1;
   Actual.Row(diffp,j);   
   }
   freq = Actual; 
   
   return(true);
  }

Como os dados com os quais estamos lidando são contínuos, devemos agrupá-los primeiro. Além disso, recomenda-se que, para um cálculo adequado do critério, o valor mínimo da frequência esperada nas células não seja inferior a um, e o número de células com frequência esperada inferior a cinco não deve ser grande (por exemplo, são permitidas duas dessas células se o número total de células for menor que 10). Como sabemos, as distribuições dos dados de mercado possuem caudas pesadas, o que traz certa dificuldade na construção de intervalos de agrupamento que atendam aos requisitos descritos acima.

Sugiro agrupar os dados após padronizá-los. Em seguida, podemos truncar as caudas pesadas da distribuição até 2-3-4 sigma, dependendo do volume de dados analisado. No indicador, o parâmetro Tails é responsável por essa função. Por exemplo, se o volume de dados for pequeno (200-300 valores), recomenda-se definir Tails como 2 sigma, resultando nos intervalos de agrupamento: (-2,-1),(-1,0),(0,1),(1,2) e, consequentemente, uma tabela de contingência de 4x4. Assim, para calcular corretamente a estatística qui-quadrado, agruparemos os intervalos de baixa frequência esperada adjacentes.

Coeficiente de contingência de Cramer

A estatística CHI2, infelizmente, não serve como uma medida quantitativa de dependência probabilística, portanto, o coeficiente de contingência de Cramer é utilizado para esse fim. Seus valores variam de zero a um. Zero indica ausência de dependência entre os dados, e um indica uma dependência funcional.

O coeficiente de contingência de Cramer é baseado na estatística qui-quadrado:

Contingency coefficient = sqrt (CHI2 / N*(Bins_count-1)),

onde Bins_count representa o número de linhas (ou colunas) na tabela de contingência.

Assim, um único indicador implementa duas estatísticas – a estatística qui-quadrado principal e, com base nela, o coeficiente de contingência (Contingency coefficient).

Para verificar a independência entre dois instrumentos financeiros diferentes, use o script Crosstab. Para isso, ative o parâmetro X vs Y (true). Caso contrário, o script calcula a estatística com os dados do símbolo atual. Os dados amostrais para o cálculo são contados a partir da penúltima barra no gráfico.

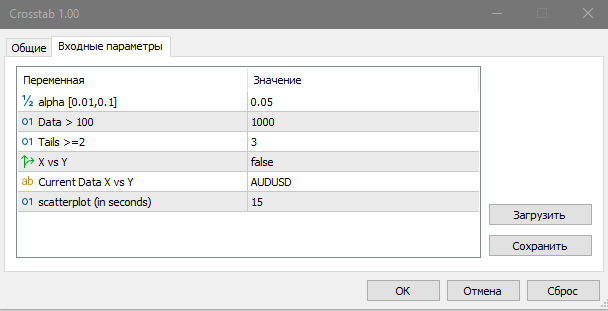
O script Crosstab calcula e registra as seguintes informações no log:

• matriz de frequências reais (Actual) e esperadas (Expected)

• coeficiente de correlação r, calculado com os dados agrupados

• coeficiente de correlação de Pearson, calculado com dados não agrupados (para comparar a precisão dos cálculos, já que a estatística calculada com dados agrupados é menos precisa)

• razão de correlação Nxy, Nyx (Correlation ratio)

• teste de hipótese de ausência de dependência correlacional (f statistic correl independence)

• teste de hipótese de linearidade da dependência correlacional (f statistic Linear/Nonlinear)

• estatística qui-quadrado CHI2

• coeficiente de contingência de Cramer (Contingency coefficient)

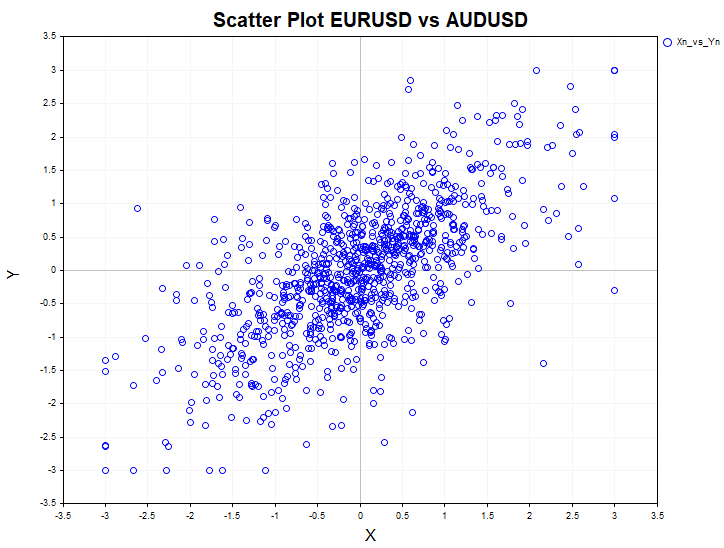
Também é exibido um diagrama de dispersão (campo de correlação) para avaliação visual da dependência par (scatterplot).

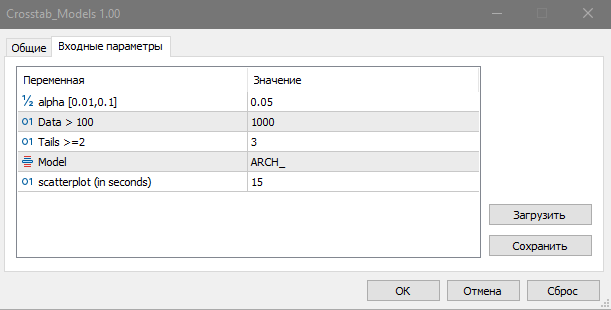
Para testar a independência de dados modelados, utilize o script Crosstab_Models. Como modelos, são utilizados a distribuição uniforme, a autoregressão de primeira ordem, a heterocedasticidade condicional autoregressiva ARCH e o mapeamento logístico.

Os dados modelados funcionam como um tipo de padrão com o qual podemos comparar os resultados obtidos em dados reais. Por exemplo, assim se apresenta a dependência não linear em um sistema dinâmico unidimensional não linear — mapeamento logístico:

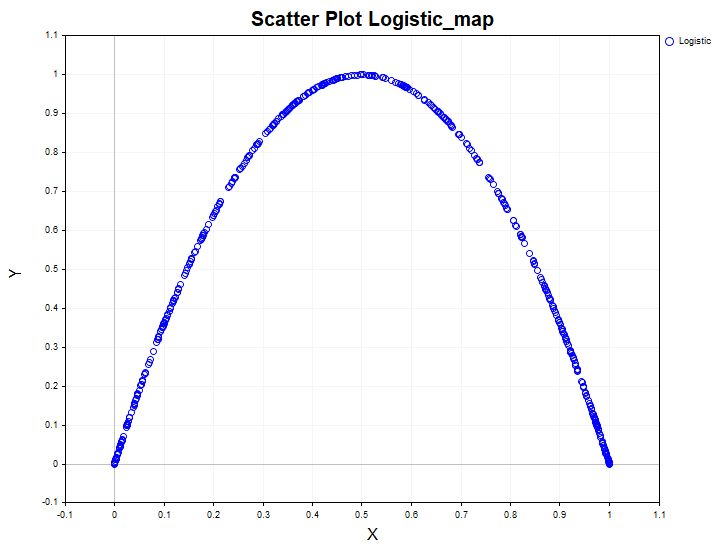
Analisando os dados desse sistema apenas pelo coeficiente de correlação linear, poderíamos chegar ao erro de concluir que o processo é um ruído branco. Contudo, o critério de independência qui-quadrado revela facilmente que os dados são dependentes, e a razão de correlação confirma que essa dependência é não linear.

Razão de correlação

Para avaliar a não linearidade da dependência correlacional, utiliza-se a razão de correlação (Correlation ratio):

Nyx = sqrt (D[E(Y|X)]/Sy)

Nxy = sqrt (D[E(X|Y)])/Sx)

onde:

• E(Y|X) — expectativa condicional da variável aleatória Y

• E(X|Y) — expectativa condicional da variável aleatória X

• D[E(Y|X)] – variância da expectativa condicional da variável aleatória Y

• D[E(X|Y)] – variância da expectativa condicional da variável aleatória X

• Sy, Sx – variâncias incondicionais das variáveis aleatórias Y e X

Lembremos que:

• a expectativa condicional E(Y|X) é uma variável aleatória.

• E[E(Y|X)] = E[Y] (a expectativa da expectativa condicional de Y é igual à expectativa incondicional de Y).

• a variância de Y é D[Y] = E[(Y – E(Y))^2], ou seja, a expectativa do quadrado da diferença entre Y e sua expectativa E[Y].

• Então, D[E(Y|X)] = E{[ E(Y|X) – E[Y] ] ^ 2}, o que significa que a variância da expectativa condicional E(Y|X) é a expectativa do quadrado da diferença entre E(Y|X) e a expectativa incondicional E[Y].

Em outras palavras, a razão de correlação — é a raiz quadrada da razão entre duas variâncias — a condicional e a incondicional. A razão de correlação só pode ser calculada a partir da tabela de correlação, ou seja, com dados agrupados. Listemos suas propriedades:

• a razão de correlação não é simétrica em relação a X e Y, ou seja, Nxy ≠ Nyx.

• 0 ≤ | r | ≤ Nxy ≤ 1, 0 ≤ | r | ≤ Nyx ≤ 1, com valores do índice no intervalo [0,1] e sempre maior ou igual ao coeficiente de correlação linear r em módulo.

• se os dados são independentes, então Nxy=Nyx=0. O inverso não é verdadeiro, ou seja, a ausência de correlação não implica independência.

• se | r | = Nyx = Nyx <1, a correlação entre X e Y é linear, ou seja, para a equação de regressão não há melhor ajuste do que uma linha reta.

• se a correlação entre X e Y é não linear, então | r | < min (Nxy, Nyx). Quanto menor a diferença entre o coeficiente de correlação e a razão de correlação, mais próxima é a relação linear entre X e Y.

Calculando a razão de correlação amostral, podemos testar a hipótese de ausência de dependência correlacional entre duas variáveis aleatórias (H0: Nyx = 0).

Para isso, calcula-se a estatística:

F = Nyx^2 * (N - Bins_count) / (1 - Nyx^2) * (Bins_count - 1)

Se a hipótese testada é verdadeira, então a estatística F segue uma distribuição de Fisher com v1 = Bins_count - 1 e v2 = N - Bins_count graus de liberdade.

A hipótese nula é rejeitada ao nível de significância alpha se o valor calculado da estatística F exceder o valor crítico dessa estatística (nesse caso, é aceita a alternativa H1: Nyx > 0).

Suponhamos que confirmamos a presença de dependência correlacional. A questão que surge então é: essa dependência é linear ou não linear? Esse questionamento é respondido pela hipótese de linearidade da dependência correlacional entre duas variáveis aleatórias.

Ao testar a hipótese de linearidade da dependência correlacional de Y em relação a X (H0: Nyx^2 = r^2) utiliza-se a estatística:

F = (Nyx^2 - r^2) * (N - Bins_count) / (1 - Nyx^2) * (Bins_count - 2)

Se a hipótese em teste for verdadeira, então a estatística F segue uma distribuição de Fisher com v1 = Bins_count - 2 e v2 = N - Bins_count graus de liberdade.

A hipótese nula de linearidade da correlação é rejeitada ao nível de significância alpha se o valor calculado da estatística F exceder o valor crítico dessa estatística (nesse caso, é aceita a alternativa H1: Nyx^2 ≠ r^2).

Considerações finais

Neste artigo, foram examinadas ferramentas importantes da análise correlacional, como o critério de independência qui-quadrado de Pearson e a razão de correlação. Com esses métodos, é possível avaliar com mais precisão a existência de interdependências ocultas nos dados. O indicador CHI2Test realiza a verificação da hipótese de independência, permitindo obter conclusões estatisticamente fundamentadas sobre a presença de relações nos dados.

Os scripts Crosstab e Crosstab_Models, além da estatística qui-quadrado, também calculam a razão de correlação e testam a hipótese de dependência correlacional e a linearidade dessa dependência, inclusive para dados modelados. Adicionalmente, é exibido na tela um gráfico de campo de correlação para a avaliação visual da dependência par. O usuário pode ajustar a precisão dos testes estatísticos, selecionando o nível de significância alpha desejado. Quanto menor o nível de significância, menor a probabilidade de obter um resultado falso.