Técnicas do MQL5 Wizard que você deve conhecer (Parte 26): Médias Móveis e o Exponente de Hurst

Introdução

Continuamos esta série de técnicas com o MQL5 Wizard que foca em métodos alternativos na análise de séries temporais financeiras para o benefício dos traders. Para este artigo, consideramos o Exponente de Hurst. Esta é uma métrica que nos diz se uma série temporal tem uma alta autocorrelação positiva ou uma autocorrelação negativa ao longo do tempo. As aplicações dessa medida podem ser muito extensas. Como a usaríamos? Bem, primeiramente, calcularíamos o Exponente de Hurst para determinar se o mercado está em tendência (o que tipicamente nos daria um valor maior que 0,5) ou se o mercado é de reversão à média/volátil (o que nos daria um valor menor que 0,5). Para este artigo, como estamos em uma "temporada de análise de médias móveis" devido aos últimos artigos, vamos combinar a informação do Exponente de Hurst com a posição relativa do preço atual em relação a uma média móvel. A posição relativa do preço em relação a uma média móvel pode ser indicativa da direção do preço, com uma grande ressalva.

Você precisaria saber se os mercados estão em tendência ou se estão em faixa (reversão à média). Como podemos usar o Exponente de Hurst para responder a essa questão, seguiríamos simplesmente a posição do preço em relação à média e então realizaríamos uma negociação. No entanto, até isso pode ser um pouco apressado, dado que mercados em faixa tendem a ser melhor estudados em períodos de tempo mais curtos, enquanto mercados em tendência são mais evidentes quando analisados em períodos muito mais longos. É por isso que precisaríamos de duas médias móveis separadas para ponderar a posição relativa do preço antes que uma condição definitiva possa ser avaliada. Essas médias serão uma média móvel rápida para mercados em faixa ou de reversão à média, e uma média móvel lenta para mercados em tendência, conforme determinado pelo Exponente de Hurst. Portanto, cada tipo de mercado, conforme definido pelo Exponente, terá sua própria média móvel. Este artigo, portanto, irá analisar a Análise de Faixa Redimensionada como uma forma de estimar o Exponente de Hurst. Vamos passar pelo processo de estimativa passo a passo e concluir com uma Classe de Sinal de Expert que implementa este Exponente.

Dividindo a Série Temporal

De acordo com Wikipedia, a fórmula para o Exponente de Hurst é apresentada como:

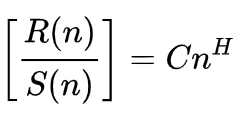
Onde

• n é o tamanho da amostra analisada
• R() é a faixa redimensionada da amostra
• S() é o desvio padrão da amostra
• C é uma constante
• H é o Exponente de Hurst

Esta fórmula apresenta intrinsecamente 2 incógnitas, e a solução para isso, para encontrar tanto a constante C quanto o exponente H, é realizar uma regressão em múltiplos segmentos do conjunto amostral. H é uma potência, o que nos leva a tomar logaritmos de ambos os lados da equação para resolver para H, e este é o nosso último passo, como veremos a seguir. Portanto, o primeiro passo é identificar ou definir segmentos dentro dos dados amostrais.

O número mínimo de segmentos que podemos obter de qualquer amostra é 2. O máximo que podemos obter depende do tamanho da amostra, e a fórmula rudimentar é o tamanho da amostra dividido por 2. Agora estamos procurando duas incógnitas, o que significa que precisamos de mais do que um par de pontos para ter pelo menos 2 equações, como é comum. O número de equações ou pares de pontos que podemos gerar de uma amostra é dado pela metade do tamanho da amostra menos 1. Portanto, uma amostra com 4 pontos de dados só geraria um par de pontos para regressão, o que claramente não seria suficiente para encontrar o Exponente de Hurst e a constante C.

Uma amostra com 6 pontos de dados pode gerar os 2 pares de pontos necessários para estimar o exponente e a constante. Na prática, queremos que o tamanho da amostra seja o maior possível, porque, como mencionado na definição, o Exponente de Hurst é uma propriedade de "longo prazo". Além disso, a fórmula da Wikipedia compartilhada acima se aplica para amostras quando n tende para o infinito. Portanto, é importante que o tamanho da amostra seja o maior possível para estimar um Exponente de Hurst mais representativo.

A divisão da amostra em segmentos, onde cada divisão/segmento gera um único par de pontos, é o "primeiro passo". Eu uso "primeiro passo" porque, no método que utilizamos para este artigo, como mostrado no código abaixo, não dividimos unilateralmente os dados e definimos todos os segmentos de uma vez, mas, sim, para cada divisão, calculamos o par de pontos mapeado daquela divisão. Parte do código fonte que realiza isso está mostrado abaixo:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   double _std = Data.Std();
   if(_std == 0.0)
   {  printf(__FUNCSIG__ + " uniform sample with no standard deviation! ");
      return;
   }
   int _t = Fraction(Data.Size(), 2);
   if(_t < 3)
   {  printf(__FUNCSIG__ + " too small sample size, cannot generate minimum 2 regression points! ");
      return;
   }
   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  matrix _segments;
      int _rows = Fraction(Data.Size(), t);
      _segments.Init(_rows, t);
      int _r = 0, _c = 0;
      for(int s = 0; s < int(Data.Size()); s++)
      {  _segments[_r][_c] = Data[s];
         _c++;
         if(_c >= t)
         {  _c = 0;
            _r++;
            if(_r >= _rows)
            {  break;
            }
         }
      }
      
      ...

   }
   ...
}

Assim, usamos uma matriz em cada passo para registrar os segmentos não sobrepostos da amostra de dados. Na iteração geral, começamos com o menor tamanho de segmento (2) e depois avançamos até metade do tamanho da amostra de dados. Por isso, temos um passo de validação para o tamanho da amostra de dados, onde verificamos se a metade do seu tamanho é pelo menos 3. Se for menor que três, não há sentido em calcular o Exponente de Hurst, pois não podemos obter pelo menos dois pares de pontos necessários para a regressão no último passo.

O outro passo de validação que realizamos na amostra de dados é garantir que haja variabilidade entre os dados, pois um desvio padrão zero leva a um número que não é válido ou a uma divisão por zero.

Ajuste da Média

Após termos um conjunto de segmentos em uma iteração dada (onde o número total de iterações é limitado pela metade do tamanho da amostra), precisamos encontrar a média de cada segmento. Como nossos segmentos estão em uma matriz, por linhas, cada linha pode ser recuperada como um vetor. Uma vez armados com o vetor de cada linha, podemos facilmente obter a média usando a função interna de média do vetor, o que economiza o trabalho de programar de forma desnecessária. A média de cada segmento é então subtraída de cada ponto de dados em seu respectivo segmento. Isso é o que chamamos de ajuste da média. É importante no processo de análise de faixa redimensionada por várias razões.

Primeiramente, ele normaliza todos os dados em cada segmento, o que garante que a análise se concentre na flutuação em torno da média, em vez de ser influenciada pelos valores absolutos de cada ponto de dados em um segmento. Em segundo lugar, essa normalização serve para reduzir o viés causado por distorções e outliers, que poderiam dificultar a obtenção de uma escala de faixa mais representativa.

Além disso, garante consistência entre os segmentos, tornando-os mais comparáveis do que se os valores absolutos fossem considerados sem essa normalização. Realizamos esse ajuste no MQL5 por meio do seguinte código fonte:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   
   ...

   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  
      ...

      vector _means;
      _means.Init(_rows);
      _means.Fill(0.0);
      for(int r = 0; r < _rows; r++)
      {  vector _row = _segments.Row(r);
         _means[r] = _row.Mean();
      }
      
      ...
   }
   ...
}

Os tipos de dados matriz e vetor são novamente indispensáveis, não apenas para encontrar as médias, mas também para agilizar a normalização.

Desvio Cumulativo

Após termos os segmentos ajustados pela média, precisamos somar esses desvios da média para cada segmento e obter os desvios cumulativos de cada segmento. Isso pode ser visto como uma forma de redução de dimensionalidade que serve como a base da análise de faixa redimensionada. Realizamos isso da seguinte maneira no nosso código fonte:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   
   ...

   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  matrix _segments;
      
      ...

      matrix _deviations;
      _deviations.Init(_rows, t);
      for(int r = 0; r < _rows; r++)
      {  for(int c = 0; c < t; c++)
         {  _deviations[r][c] = _segments[r][c] - _means[r];
         }
      }
      vector _cumulations;
      _cumulations.Init(_rows);
      _cumulations.Fill(0.0);
      for(int r = 0; r < _rows; r++)
      {  for(int c = 0; c < t; c++)
         {  _cumulations[r] += _deviations[r][c];
         }
      }

      ...

   }
   ...
}

Então, para recapitular brevemente, para cada valor ‘t’ obtemos um grupo de segmentos que particionam nossa amostra de dados. De cada amostra, obtemos sua média e subtraímos a média dos pontos de dados dentro de seu respectivo segmento. Essa subtração serve como uma forma de normalização, e, uma vez concluída, temos essencialmente uma matriz de pontos de dados, onde cada linha é um segmento da amostra original. Como método para reduzir as dimensões dos segmentos, somamos esses desvios de suas respectivas médias, de forma que um segmento multidimensional nos dê um único valor. Isso implica que, depois de realizarmos as somas dos desvios na matriz, restamos com um vetor de somas, e esse vetor é rotulado como ‘_cumulações’ em nosso código fonte acima.

Faixa Redimensionada e Gráfico Log-Log

Uma vez que temos as somas dos desvios através de todos os segmentos em um vetor, o próximo passo é simplesmente encontrar a faixa, que é a diferença entre o maior e o menor desvio total. Lembre-se que, ao registrar os desvios de cada ponto de dados nos segmentos acima, não registramos o valor absoluto. Simplesmente registramos o valor do segmento menos a média do segmento. Isso implica que é muito fácil que nossas somas de desvios somem para zero. Na verdade, isso deve passar por uma verificação de validação antes de prosseguir com os cálculos do Exponente de Hurst, pois pode facilmente levar a um resultado inválido. Essa validação não é realizada no código fonte anexado, e os leitores podem fazer esses ajustes à vontade. Realizamos esse penúltimo passo no seguinte código:

//+------------------------------------------------------------------+
// Function to Estimate Hurst Exponent & Constant C
//+------------------------------------------------------------------+
void CSignalHurst::Hurst(vector &Data, double &H, double &C)
{  matrix _points;
   
   ...

   _points.Init(_t - 1, 2);
   _points.Fill(0.0);
   for (int t = 2; t <= _t; t++)
   {  
       ...
       
       ...

      _points[t - 2][0] = log((_cumulations.Max() - _cumulations.Min()) / _std);
      _points[t - 2][1] = log(t);
   }
   LinearRegression(_points, H, C);
}

Como podemos ver na parte do código fonte acima, obtemos as faixas cumulativas e também seus logaritmos naturais, pois estamos buscando um expoente (potência) e logaritmos ajudam a resolver para expoentes. Da equação acima, o tamanho da amostra estava de um lado da equação, portanto também obtemos seu logaritmo natural, e isso serve como nosso gráfico y, com o gráfico x sendo o logaritmo natural da faixa redimensionada dividida pelo desvio padrão da amostra de dados. Esses pares de pontos, x e y, são únicos para cada tamanho de segmento. Um tamanho de segmento diferente, dentro da amostra de dados, representa outro par de pontos x-y, e quanto mais desses tivermos, mais representativo será o nosso Exponente de Hurst. E como mencionado acima, o número total de pares possíveis de pontos x-y que podemos ter é limitado pela metade do tamanho da amostra de dados.

Portanto, nossa matriz ‘_points’ representa o gráfico logaritmo sobre logaritmo encontrado na análise de faixa redimensionada. É este gráfico que serve como entrada para os cálculos de regressão linear.

Regressão Linear

A regressão linear é realizada por uma função separada do método ‘Hurst’. Seu código simples é compartilhado abaixo:

//+------------------------------------------------------------------+
// Function to perform linear regression
//+------------------------------------------------------------------+
void CSignalHurst::LinearRegression(matrix &Points, double &Slope, double &Intercept)
{  double _sum_x = 0.0, _sum_y = 0.0, _sum_xy = 0.0, _sum_xx = 0.0;
   for (int r = 0; r < int(Points.Rows()); r++)
   {  _sum_x += Points[r][0];
      _sum_y += Points[r][1];
      _sum_xy += (Points[r][0] * Points[r][1]);
      _sum_xx += (Points[r][0] * Points[r][0]);
   }
   Slope = ((Points.Rows() * _sum_xy) - (_sum_x * _sum_y)) / ((Points.Rows() * _sum_xx) - (_sum_x * _sum_x));
   Intercept = (_sum_y - (Slope * _sum_x)) / Points.Rows();
}

Regressão linear é o processo pelo qual chegamos aos coeficientes chave na equação y = mx + c de um conjunto dado de pontos. Os coeficientes fornecidos definem a equação da linha de melhor ajuste desses pontos x-y de entrada. Essa equação é importante para nós porque a inclinação dessa linha de melhor ajuste é o Exponente de Hurst, enquanto o intercepto com o eixo y serve como a constante C. Para esse fim, a função ‘LinearRegression’ recebe como entradas de referência dois valores do tipo double, que servem como o marcador do Exponente de Hurst e a constante C, e assim como a função ‘Hurst’, ela retorna void.

Para este artigo, nosso objetivo principal é calcular o Exponente de Hurst, no entanto, parte dos resultados que obtemos desse processo, como já mencionado, é a constante C. Qual então é a finalidade dessa constante C? Ela é uma métrica para a variabilidade de uma amostra de dados. Considere um cenário onde as séries de preços de 2 ações têm o mesmo Exponente de Hurst, mas diferentes constantes C, onde uma tem C igual a 7 e a outra tem C igual a 21.

O valor semelhante do Exponente indicaria que as duas ações têm características de "persistência" semelhantes, ou seja, se o Exponente de Hurst de ambas for abaixo de 0,5, então ambas as ações tendem a reverter à média frequentemente, enquanto se esse Exponente for maior que 0,5, então elas tendem a ter tendência no longo prazo. No entanto, suas constantes C diferentes, apesar de ações com movimentos de preço semelhantes, indicariam claramente perfis de risco diferentes. Isso ocorre porque a constante C poderia ser entendida como um proxy para volatilidade. As ações com uma constante C mais alta teriam oscilações de preço mais amplas em torno de suas médias, ao contrário da ação com uma constante C menor. Isso poderia implicar diferentes regimes de dimensionamento de posições nas duas ações, com todos os outros fatores constantes.

Compilação em uma Classe de Sinal

Usamos os valores do Exponente de Hurst gerados para determinar as condições de compra e venda do símbolo negociado dentro de uma classe de sinal personalizada. O Exponente de Hurst é destinado a capturar tendências de longo prazo, razão pela qual, por definição, tende a ser mais preciso à medida que o tamanho da amostra tende ao infinito. Para fins práticos, no entanto, precisamos medi-lo a partir de um tamanho definido de histórico de preços de segurança. Vamos considerar uma das duas médias móveis diferentes na avaliação das nossas condições de compra/venda, e assim o tamanho do histórico utilizado no cálculo do Exponente de Hurst é considerado como a soma dos dois períodos usados no cálculo dessas duas médias.

Isso pode não ser suficiente, porque como já mencionado, quanto maior o período da amostra de dados, mais confiável é o Exponente de Hurst por definição, portanto o leitor pode fazer ajustes conforme necessário para obter um tamanho de histórico mais representativo para sua perspectiva. Como sempre, o código-fonte completo está anexado. Portanto, para cada uma das funções de condição (compra e venda), começamos copiando os preços de fechamento em um vetor até o tamanho da nossa amostra de dados. O tamanho da nossa amostra de dados é a soma dos períodos de compra e venda.

Uma vez feito isso, calculamos o Exponente de Hurst chamando a função ‘Hurst’ e depois avaliamos o valor retornado para determinar como ele se compara com 0,5. Variações dessa implementação podem ser feitas onde um limiar é adicionado acima e abaixo do valor de 0,5, para estreitar os pontos de entrada ou decisão. Se o nosso Exponente de Hurst for acima de 0,5, então há persistência e, portanto, para a condição de compra, verificaríamos se estamos acima da média móvel de longo prazo. Se estivermos, isso poderia indicar uma posição de compra. Da mesma forma, para a condição de venda, verificaríamos se estamos abaixo da média móvel de longo prazo e, se estivermos, isso marcaria a abertura de uma posição de venda.

No caso de o Exponente de Hurst estar abaixo de 0,5, isso indicaria que estamos em um mercado em faixa ou de reversão à média. Neste caso, compararíamos o preço atual com a média móvel de período rápido. Na condição de compra, se o preço estiver abaixo da média móvel rápida, isso indicaria uma posição de compra. Por outro lado, na condição de venda, se o preço estiver acima da média móvel rápida, isso indicaria a abertura de uma posição de venda. A implementação dessas duas condições é compartilhada abaixo:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalHurst::LongCondition(void)
{  int result = 0;
   vector _data;
   if(_data.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period + m_slow_period))
   {  double _hurst = 0.0, _c = 0.0;
      Hurst(_data, _hurst, _c);
      vector _ma;
      if(_hurst > 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() > _ma.Mean())
            {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_hurst < 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
         {  if(m_symbol.Bid() < _ma.Mean())
            {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalHurst::ShortCondition(void)
{  int result = 0;
   vector _data;
   if(_data.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period + m_slow_period))
   {  double _hurst = 0.0, _c = 0.0;
      Hurst(_data, _hurst, _c);
      vector _ma;
      if(_hurst > 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() < _ma.Mean())
            {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_hurst < 0.5)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
         {  if(m_symbol.Bid() > _ma.Mean())
            {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
   }
   return(result);
}

Teste de Estratégia & Relatórios

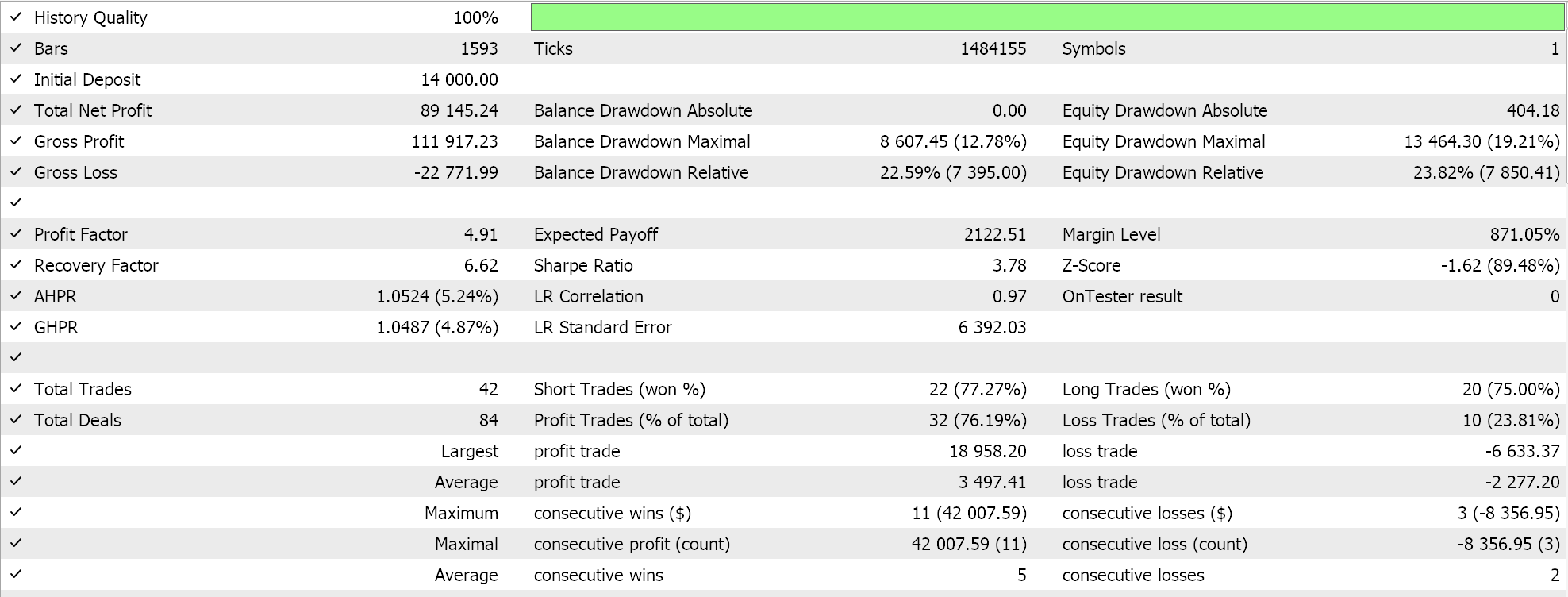
Realizamos testes no intervalo de 4 horas para o par GBPCHF para o ano de 2023 e obtemos os seguintes resultados:

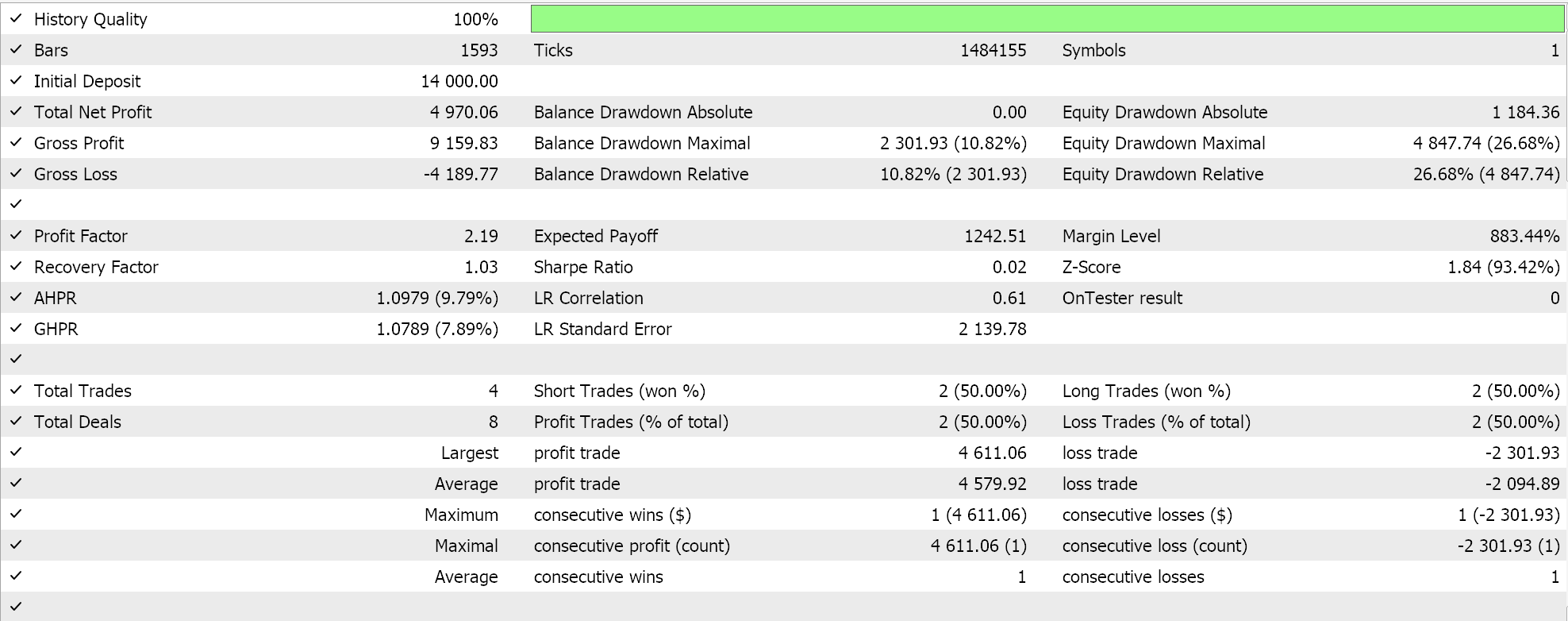
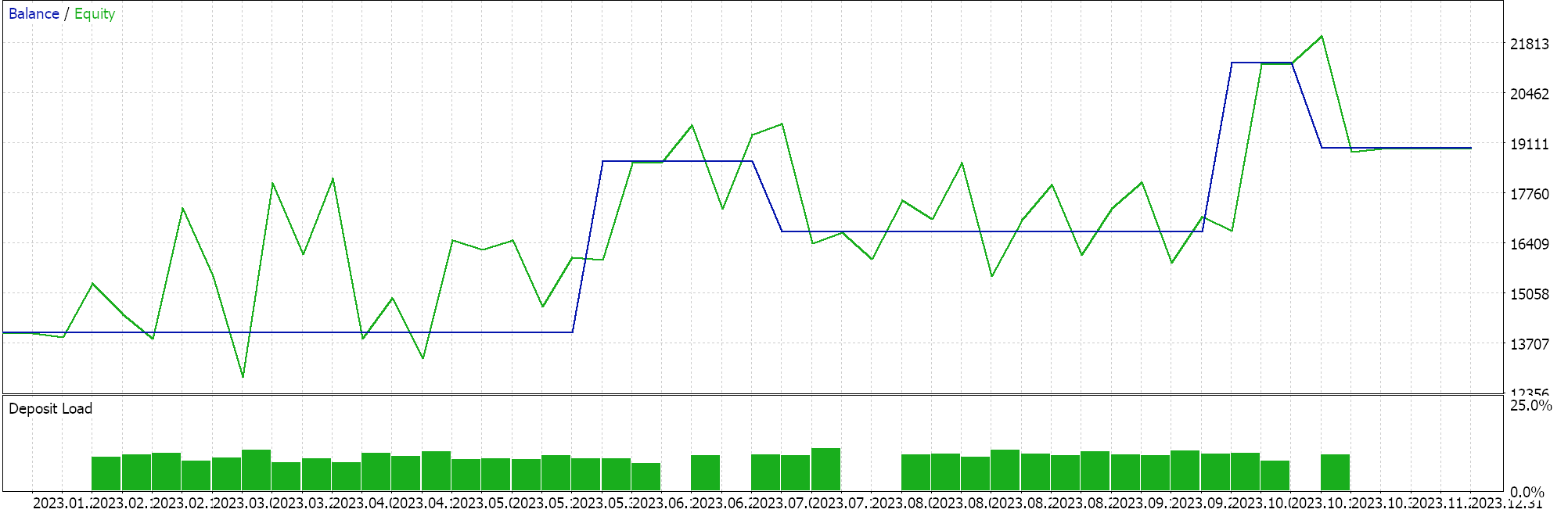
A partir do nosso teste acima, no intervalo de 4 horas, não estão sendo feitas muitas negociações, e isso pode ser um bom sinal, pois aponta para um Expert Advisor discriminante. No entanto, como sempre, testar durante períodos mais longos e especialmente com "forward walks" é sempre um requisito antes de tomar decisões sobre a eficácia do Expert.

Autocorrelação Bruta como Controle

O Exponente de Hurst afirma ser capaz de avaliar se uma série tem características persistentes (valores acima de 0,5) ou é anti-persistente (valores abaixo de 0,5) atuando como uma métrica de autocorrelação. Mas suponhamos que simplesmente medimos as correlações da série de dados sem nos preocupar em calcular esse Exponente e usamos os resultados de nossas medições reais de correlação para avaliar as condições do mercado, quão diferente seria o desempenho do nosso Expert Advisor?

Desenvolvemos tal classe de sinal personalizada que, como se espera, tem menos funções e simplesmente primeiro avalia qualquer correlação positiva sobre o período de média mais longo (mais lento). Se houver alguma correlação positiva, então a média móvel desse período mais lento é usada para avaliar configurações de seguimento de tendência, onde preços acima dessa média são altistas e preços abaixo são baixistas. Se, no entanto, não houver correlação positiva sobre os períodos mais longos, então procuramos uma correlação negativa no período de média mais curto (mais rápido). Neste caso, buscaríamos configurações de reversão à média, onde preço abaixo da média móvel rápida seria altista, enquanto preço acima seria baixista. O código para nossa condição de compra e venda é o seguinte:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAC::LongCondition(void)
{  int result = 0;
   vector _new,_old;
   if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_slow_period, m_slow_period))
   {  vector _ma;
      if(_new.CorrCoef(_old) >= m_threshold)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() > _ma.Mean())
            {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_fast_period, m_fast_period))
      {  if(_new.CorrCoef(_old) <= -m_threshold)
         {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
            {  if(m_symbol.Bid() < _ma.Mean())
               {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
               }
            }
         }
      }
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAC::ShortCondition(void)
{  int result = 0;
   vector _new,_old;
   if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_slow_period, m_slow_period))
   {  vector _ma;
      if(_new.CorrCoef(_old) >= m_threshold)
      {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period))
         {  if(m_symbol.Bid() < _ma.Mean())
            {  result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
            }
         }
      }
      else if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_fast_period, m_fast_period))
      {  if(_new.CorrCoef(_old) <= -m_threshold)
         {  if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period))
            {  if(m_symbol.Bid() > _ma.Mean())
               {  result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min())))));
               }
            }
         }
      }
   }
   return(result);
}

Realizamos testes semelhantes para o mesmo par GBPCHF no intervalo de 4 horas para o ano de 2023, e nossos resultados dos melhores testes são apresentados abaixo:

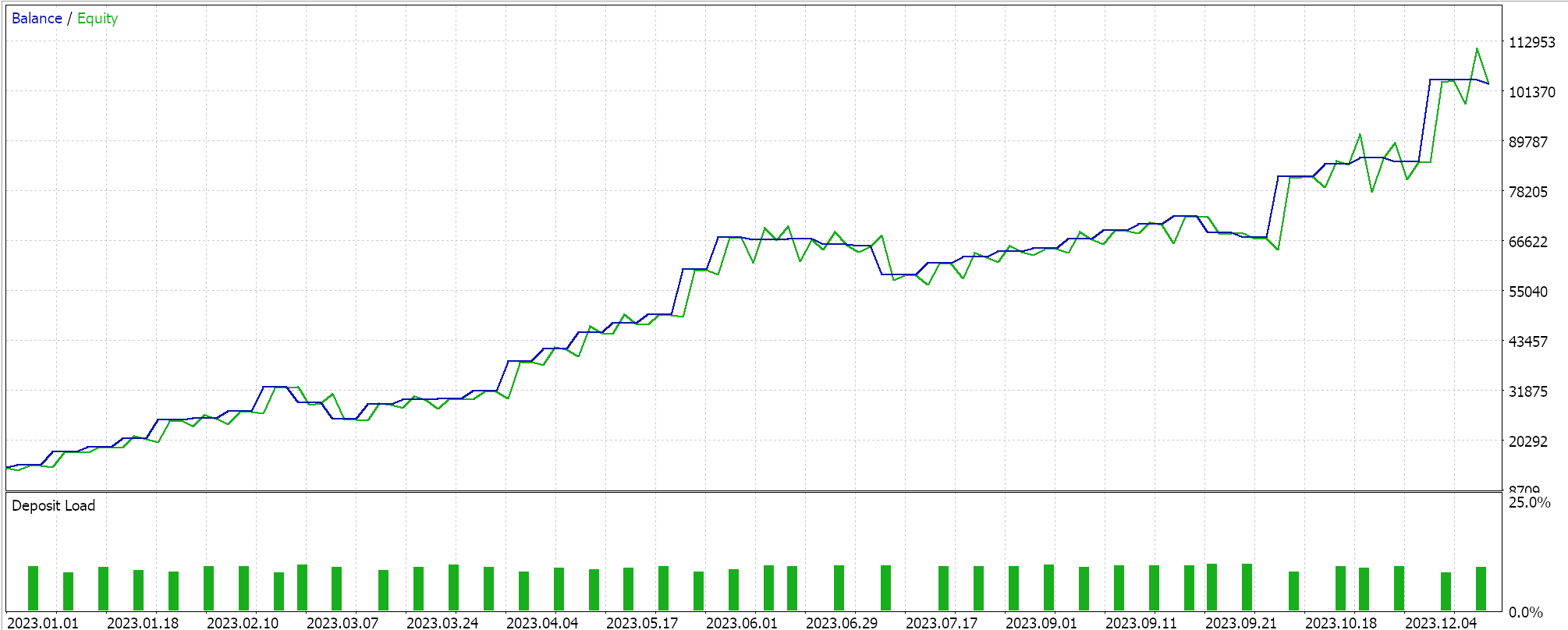
Claramente, há uma diferença no desempenho entre este e o sinal do Exponente de Hurst.

Conclusão

O Exponente de Hurst foi desenvolvido no início do século passado principalmente como uma ferramenta para potencialmente prever as flutuações do rio Nilo, uma vez munido de um conjunto considerável de pontos de marcas d'água. Desde então, foi adotado em uma gama mais ampla de aplicações, entre as quais se destaca a análise de séries temporais financeiras. Para este artigo, combinamos seu expoente de série temporal com médias móveis para distinguir melhor os mercados em tendência dos mercados de reversão à média na criação de uma classe de sinal personalizada.

Embora tenha claramente algum potencial nos primeiros testes que realizamos acima, ainda há um caso a ser feito para seu uso, dado seu desempenho relativo contra nosso sinal de autocorrelação bruta. É computacionalmente intenso, filtra excessivamente suas negociações e seus melhores testes apresentam muito drawdown, o que é uma preocupação dado a janela de teste relativamente pequena usada para esses testes. Como sempre, testes independentes podem gerar resultados diferentes e até mais promissores, e o leitor está convidado a testar essas abordagens. A montagem e compilação do código-fonte anexado em um Expert Advisor segue as diretrizes que estão aqui e aqui. Recomenda-se que esses novos testes sejam feitos com dados de tick real de um corretor e abranjam um número saudável de anos.