您应当知道的 MQL5 向导技术（第 26 部分）：移动平均和赫斯特（Hurst）指数
417
5
概述
我们继续本系列讲解 MQL5 向导技术的文章，重点放在金融时间序列分析中的可替代方法，从而造福交易者。至于本文，我们研究赫斯特（Hurst）指数。这是一个计量度，其会告诉我们，时间序列从长远来看，是具有较高正自相关、亦或负自相关。这种衡量的应用可能非常广泛。我们如何运用它？好的，首先，我们将计算赫斯特指数，以便判定行情是处于趋势（通常会给我们一个大于 0.5 的值），亦或行情是均值回归/反复拉扯（这将给我们一个小于 0.5 的值）。至于本文，鉴于我们处在前两篇文章给出的“观察移动均线的季节性”，故我们把赫斯特指数信息、与当前价格相对移动平均线的位置结伴。价格与移动平均线的相对位置可以指明价格接下来的方向，隐含一个主要警告。
您需要知道行情是否处于趋势，亦或范围振荡（均值回归）。鉴于我们可用赫斯特指数来回答这个问题，令我们只需查看价格相对于均值所处的位置，随之进行交易。然而，即便如此也许仍就有点草率，在短线区间内更倾向研究范围振荡行情更佳，而趋势行情在长线区间更多出现。正是出于这个原因，在评估确立条件之前，我们需要两条单独的移动平均线来权衡价格的相对位置。其一是针对范围振荡或均值回归行情的快速移动平均线，以及针对趋势行情的慢速移动平均线，由赫斯特指数判定。故此，按指数设置的每种行情类型，都有自己的移动平均线。因此，本文计划视察重伸缩范围分析法，作为评估赫斯特指数的一种手段。我们将一次一步遍历评估过程，并实现该指数的智能信号类。
拆分时间序列
根据维基百科，赫斯特指数的公式表示为：
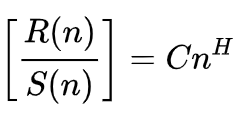
其中
- n 是所分析样品的大小
- R() 是样本的重伸缩范围
- S() 是样本的标准差
- C 是常数
- H 是赫斯特指数
这个公式内在为我们带来 2 个未知数，而找到常数 C、及我们所寻求的指数 H 的变通方法，则是回归样本集的多个分段。从算术中来看，H 是一个幂，这意味着我们在方程的两边都取对数来求解 H，这是我们的最后一步，我们将在下面看到。故此，第一步是在样本数据中识别、或定义分段。
我们可以从任何样本中获得的最小分段数量为 2。我们可以从样本中获得的最大值取决于样本规模，基本公式是样本规模除以 2。现在我们正在寻找两个未知数，这意味着我们需要不止一个配对点，如此即可按惯例获得最少 2 个方程。我们可从样本中生成的方程、或点配对的数量是样本规模的一半减 1 。故此，4 个数据点的样本规模仅生成一个配对回归点，这显然不足以找到赫斯特指数、及 C 常数。
一个具有 6 个数据点的样本可生成至少 2 个配对点，可用于估算指数和常数。在实践中，我们希望样本规模尽可能大，因为如定义中所述，赫斯特指数是一个“长期”属性。此外，上面分享的维基百科公式适用于样本，而 n 趋向于无穷大。故此，重点是样本规模必须尽可能大，以便估算更具代表性的赫斯特指数。
将样本切分为多个分段，其中每次切分/分段集生成的单一的配对点是“第一步”。我使用“第一步”是因为本文中我们所用的方式中，如下面的源代码所示，我们不会在转到下一步之前，单方面切分数据，并一次性定义所有分段，但我们会依据每次切分，计算该样本映射的点配对。下面给出执行该操作的源代码部分：
//+------------------------------------------------------------------+ // Function to Estimate Hurst Exponent & Constant C //+------------------------------------------------------------------+ void CSignalHurst::Hurst(vector &Data, double &H, double &C) { matrix _points; double _std = Data.Std(); if(_std == 0.0) { printf(__FUNCSIG__ + " uniform sample with no standard deviation! "); return; } int _t = Fraction(Data.Size(), 2); if(_t < 3) { printf(__FUNCSIG__ + " too small sample size, cannot generate minimum 2 regression points! "); return; } _points.Init(_t - 1, 2); _points.Fill(0.0); for (int t = 2; t <= _t; t++) { matrix _segments; int _rows = Fraction(Data.Size(), t); _segments.Init(_rows, t); int _r = 0, _c = 0; for(int s = 0; s < int(Data.Size()); s++) { _segments[_r][_c] = Data[s]; _c++; if(_c >= t) { _c = 0; _r++; if(_r >= _rows) { break; } } } ... } ... }
故此，我们在每个步骤都用一个矩阵来记录数据样本中非重叠的分段。在整个迭代中，我们按最小的分段大小 2 开始，然后逐步增加到数据样本大小的一半。这就是为什么我们要有一个步骤，验证数据样本大小，其中我们检查并查看其大小的一半是否至少为 3。如果它小于 3，那么计算赫斯特指数就没有意义，因为我们无法在最后一步中获得回归所需的至少两个点配对。
我们对数据样本执行的另一个验证步骤，是确保数据之间存在可变性，这是因为零标准差会导致数字无效、或除零。
均值调整
在给定迭代中我们得到一组分段（其中迭代总数的上限为样本规模的一半）之后，我们需要找到每个分段的均值。由于我们的分段都在矩阵当中，每行都能作为向量提取。一旦配备了每行的向量，我们就能轻松获得均值，这要归功于向量内置的均值函数，这节省了不必要的编码需求。然后，从其各自分段中的每个数据点中减去每个分段的均值。这就是所谓的均值调整。出于多种原因，它在范围-重伸缩分析过程中很重要。
首先，它对每个分段中的所有数据进行归一化，这确保分析会专注于有关其平均值的波动，而不会被分段中每个数据点的绝对值所左右。其次，这种归一化的意图在于降低朝向扭曲和异常值的乖离，而这可能会妨碍获得更具代表性的范围-重伸缩。
此外，还确保跨越所有分段的一致性，如此这般，参考无此归一化的绝对值，它们更具可比性。我们在 MQL5 中执行以下源代码进行调整：
//+------------------------------------------------------------------+ // Function to Estimate Hurst Exponent & Constant C //+------------------------------------------------------------------+ void CSignalHurst::Hurst(vector &Data, double &H, double &C) { matrix _points; ... _points.Init(_t - 1, 2); _points.Fill(0.0); for (int t = 2; t <= _t; t++) { ... vector _means; _means.Init(_rows); _means.Fill(0.0); for(int r = 0; r < _rows; r++) { vector _row = _segments.Row(r); _means[r] = _row.Mean(); } ... } ... }
矩阵和向量数据类型不仅在查找平均值时不可或缺，且能加速归一化。
累积偏差
一旦我们得到均值调整后的分段，我们就需要将这些偏差与来自每个分段的平均值相加，从而获得每个分段的累积偏差。这可当作一种降维的形式，作为范围-重伸缩分析的基础。在源代码中我们如下执行该操作：
//+------------------------------------------------------------------+ // Function to Estimate Hurst Exponent & Constant C //+------------------------------------------------------------------+ void CSignalHurst::Hurst(vector &Data, double &H, double &C) { matrix _points; ... _points.Init(_t - 1, 2); _points.Fill(0.0); for (int t = 2; t <= _t; t++) { matrix _segments; ... matrix _deviations; _deviations.Init(_rows, t); for(int r = 0; r < _rows; r++) { for(int c = 0; c < t; c++) { _deviations[r][c] = _segments[r][c] - _means[r]; } } vector _cumulations; _cumulations.Init(_rows); _cumulations.Fill(0.0); for(int r = 0; r < _rows; r++) { for(int c = 0; c < t; c++) { _cumulations[r] += _deviations[r][c]; } } ... } ... }
故此，简要回顾，对于每个 't' 值，我们得出一组分段，可对数据样本进行分区。从每个样本中，我们得到其均值，并分别从分段内的数据点中减去平均值。这种减法作为一种归一化的形式，一旦完成，我们实质上得到一个数据点矩阵，其中每行都是来自原始数据样本的一个分段。作为降低分段维度的一种方法，我们将这些偏差与各自平均值相加，如此这般一个多维分段就可为我们提供单个值。这意味着在我们在矩阵上执行偏差累积之后，我们只留下一个合计向量，该向量在上面的源代码中被标记为 '_cumulations'。
重新伸缩范围 & 对数-对数图
一旦我们得到向量中跨所有分段的偏差累积，下一步跟着就是简单地找到范围，即最大总偏差和最小总偏差之间的差值。记住，当我们记录上述分段中每个数据点的偏差时，我们没有记录绝对值。我们只是记录了分区值减去分段的均值。这意味着我们的累积值很容易为零。事实上，在以赫斯特指数进行处理之前，应该对其进行底层验证检查，因为它很容易导致无效结果。该验证未在随附的源代码中执行，读者可以随意进行调整。我们在以下代码中执行倒数第二步：
//+------------------------------------------------------------------+ // Function to Estimate Hurst Exponent & Constant C //+------------------------------------------------------------------+ void CSignalHurst::Hurst(vector &Data, double &H, double &C) { matrix _points; ... _points.Init(_t - 1, 2); _points.Fill(0.0); for (int t = 2; t <= _t; t++) { ... ... _points[t - 2][0] = log((_cumulations.Max() - _cumulations.Min()) / _std); _points[t - 2][1] = log(t); } LinearRegression(_points, H, C); }
正如我们从上面的源代码部分所见，我们得到了累积范围，以及它们的自然对数，因为我们正在搜寻指数（幂）、和对数来帮助求解指数。上面的方程式中，样本规模位于方程的一侧，因此我们也得到了它的自然对数，这当作我们的 y 图，其中 x 图是伸缩范围的自然对数除以数据样本的标准差。这些点配对，x & y，对于每个分段大小都是唯一的。数据样本中不同的分段大小，代表另一个 x-y 点对，我们拥有越多的 x-y 点对，我们的赫斯特指数就越具有代表性。如上所述，我们可得到的 x-y 点对的总数量，上限为数据样本大小的一半。
故此，我们的 '_points' 矩阵代表重新缩放范围分析中发现的对数-对数图。这张图，可当作线性回归计算的输入。
线性回归
线性回归从 'Hurst' 方法里由单独的函数执行。其简单代码分享如下：
//+------------------------------------------------------------------+ // Function to perform linear regression //+------------------------------------------------------------------+ void CSignalHurst::LinearRegression(matrix &Points, double &Slope, double &Intercept) { double _sum_x = 0.0, _sum_y = 0.0, _sum_xy = 0.0, _sum_xx = 0.0; for (int r = 0; r < int(Points.Rows()); r++) { _sum_x += Points[r][0]; _sum_y += Points[r][1]; _sum_xy += (Points[r][0] * Points[r][1]); _sum_xx += (Points[r][0] * Points[r][0]); } Slope = ((Points.Rows() * _sum_xy) - (_sum_x * _sum_y)) / ((Points.Rows() * _sum_xx) - (_sum_x * _sum_x)); Intercept = (_sum_y - (Slope * _sum_x)) / Points.Rows(); }
线性回归是我们求解一组给定点的 y = mx + c 方程中关键系数的过程。所提供系数定义的方程，是这些输入 x-y 点的最佳拟合线。这个方程对我们很重要，因为这条最佳拟合线的斜率是赫斯特指数，而 y-截距是常数 C。最后，'LinearRegression' 函数取两个双精度值作为参考输入，即当作赫斯特指数、及 C 常数的占位符，就像 'Hurst' 函数一样，它返回类型是 void。
至于本文，我们的主要目标是计算赫斯特指数，不过如上所述，我们从该过程中得到的输出部分是 C 常数。那么这个 C 常数做什么用途呢？它是数据样本可变性的计量值。参考一个场景：2 只股票的价格序列具有相同的赫斯特指数，但 C 常数不同，其中一只股票的 C 为 7，另一个 C 为 21。
相似的指数值表明两只股票具有相似的“持久”特征，即如果两者的赫斯特指数都低于 0.5，那么两只股票都更倾向于回归，而如果该指数大于 0.5，那么它们更倾向于在长期呈现趋势性。然而，尽管价格走势相似，但它们不同的 C 常数显然代表不同的风险配置。这是因为 C 常数可以理解为波动性的代理。股票的 C 常数较高，在跨平均线的价格摆动会更宽，这与较小的 C 常数不同。这可能意味着，若所有其它因素保持不变，2 只股票的持仓规模机制不同。
编译成信号类
我们用自己生成的赫斯特指数值，来判定自定义信号类中交易品种的做多和做空条件。赫斯特指数旨在捕捉非常长期的趋势，这就是为什么根据定义，当样本规模趋于无限时，它趋于更准确。不过，出于实际目的，我们需要依据历史证券价格的确切规模来衡量它。在评估我们的做多/做空条件时，我们将参考两条不同移动平均线之一，并在计算赫斯特指数时采用确切的历史规模，在计算这两个平均值时采用两个周期的合计。
这也许还不够，因为如前所述，数据采样周期越长，根据定义，赫斯特指数就越可靠，因此读者可以根据需要对此进行修改，以便获得更能代表其前景的历史规模。如常，完整的源代码附于文后。故此，对于每个条件函数（做多和做空），我们由复制收盘价到一个向量中开始，最大到我们的数据样本大小。我们的数据样本规模是长期和短期之和。
完成该操作之后，我们调用 'Hurst' 函数计算出赫斯特指数，然后我们估算返回值，来判定它与 0.5 的比较结果。该实现的变体，能把阈值添加到高于和低于 0.5 的值，以便收窄入场、或决策点。如果我们的赫斯特高于 0.5，那么存在持久性，因此对于做多条件，我们会查看我们是否高于慢速周期（长期）移动平均线。如果是，那么这可能示意一个看涨开仓。同样，对于做空条件，我们会查看我们是否低于慢速移动平均线，如果是，这标记着做空开仓。
如果赫斯特指数低于 0.5，则意味着我们处于范围振荡、或均值回归行情。在这种情况下，我们会将当前出价、与快速周期移动平均线进行比较。若是做多条件，如果价格低于快速移动平均线，则表明看涨开仓。相反，若是做空条件，如果价格高于快速周期移动平均线，则表明做空开仓。这两个条件的实现如下：
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalHurst::LongCondition(void) { int result = 0; vector _data; if(_data.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period + m_slow_period)) { double _hurst = 0.0, _c = 0.0; Hurst(_data, _hurst, _c); vector _ma; if(_hurst > 0.5) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period)) { if(m_symbol.Bid() > _ma.Mean()) { result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } else if(_hurst < 0.5) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period)) { if(m_symbol.Bid() < _ma.Mean()) { result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } } return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalHurst::ShortCondition(void) { int result = 0; vector _data; if(_data.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period + m_slow_period)) { double _hurst = 0.0, _c = 0.0; Hurst(_data, _hurst, _c); vector _ma; if(_hurst > 0.5) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period)) { if(m_symbol.Bid() < _ma.Mean()) { result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } else if(_hurst < 0.5) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period)) { if(m_symbol.Bid() > _ma.Mean()) { result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } } return(result); }
策略测试和报告
我们依据 GBPCHF 货币对，2023 年的 H4 时间帧数据进行了 测试，并得到以下结果：
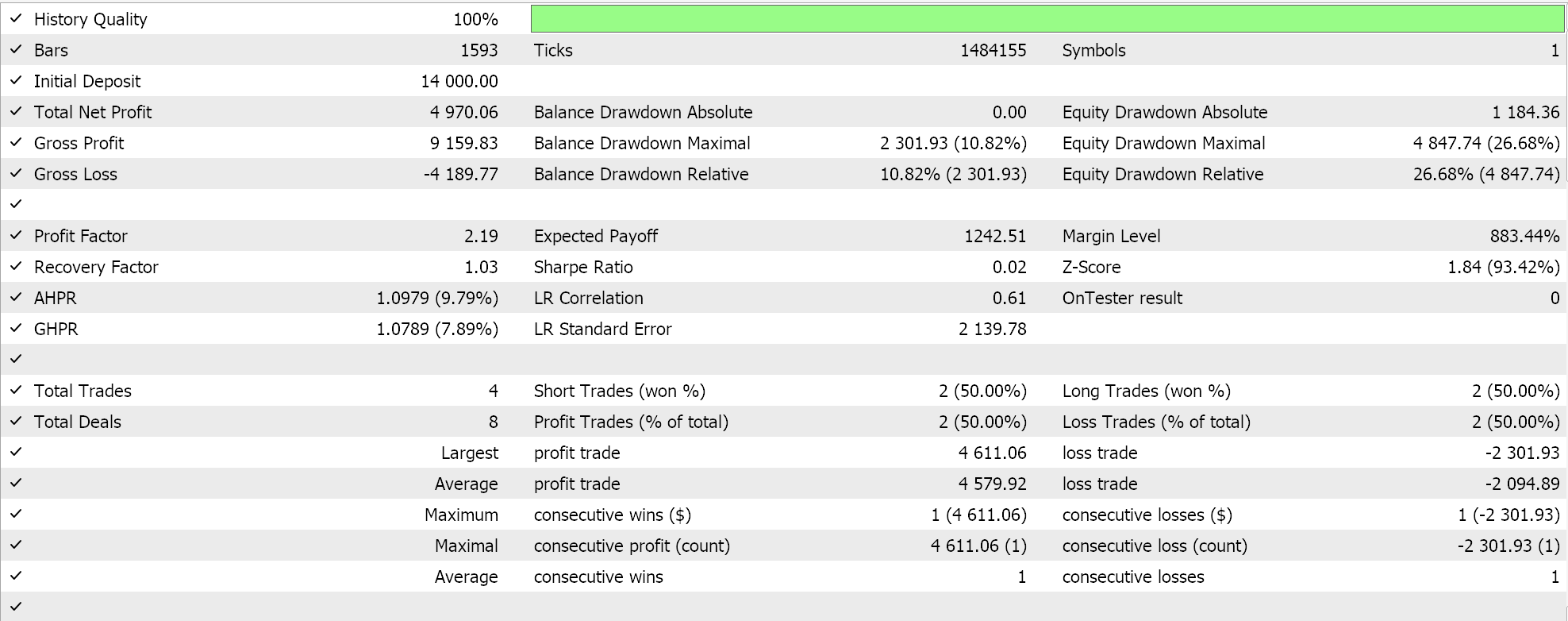
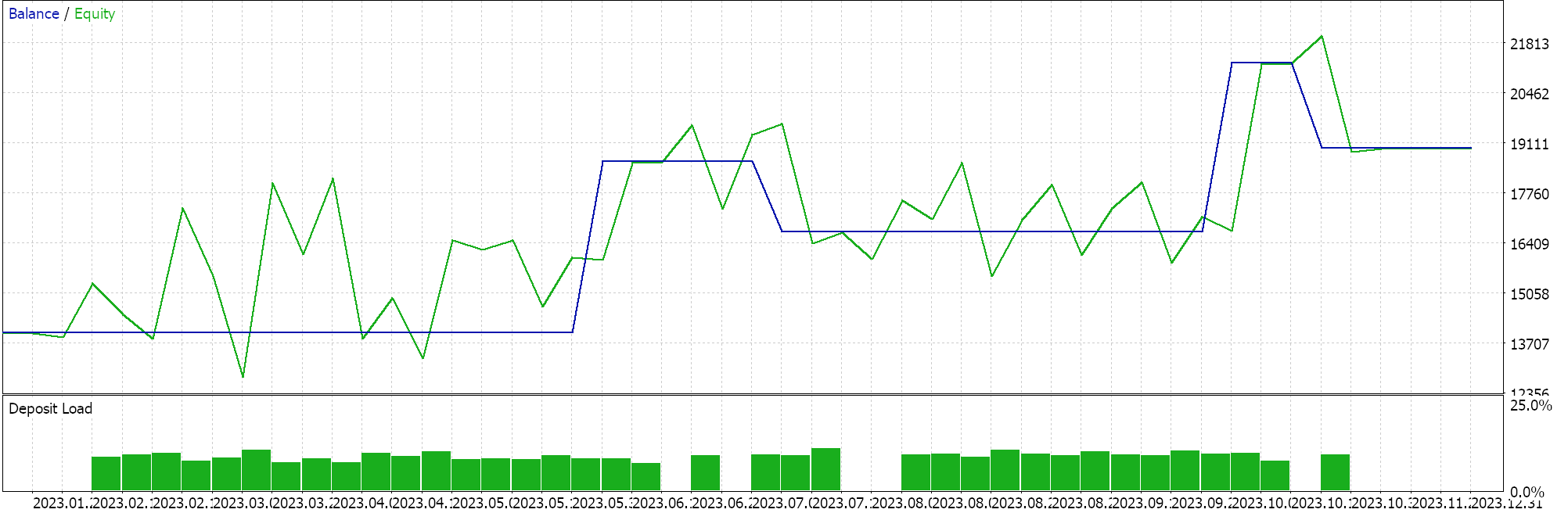
从我们上面的测试运行来看，在 H4 时间帧内，没有放置很多交易，这可能是一个好兆头，因为它所指是一个有辨别力的智能系统。然而，如常，在对智能系统的绩效做出任何决定之前，必须进行覆盖较长时间的测试，尤其要搭配前向漫游。
原生自相关作为对照
赫斯特指数声称能够充当自相关指标，来评估序列是否具有持久性状（值高于 0.5）、或抗拒持久性状（值低于 0.5）。但假设我们简单地衡量数据序列的相关性，而不费力地计算这个指数，并采用我们真实的相关性衡量结果来评估行情条件，那么我们的智能系统表现会有多大不同？
我们开发了这样一个自定义信号类，正如人们所期望的那样，它具有较少的函数，且简单地首先评估较长（较慢）平均周期内的任何正相关性。如果存在任何此类正相关，则据较慢周期的移动平均线来评估趋势跟踪设置，其中价格高于该平均值则看涨，低于该平均值则看跌。不过，如果在较长周期内不存在正相关，则在较短（较快）的平均周期处寻求负相关。在这种情况下，我们将寻找均值回归设置，其中价格低于快速移动平均线是看涨，而高于它则是看跌。我们的做多和做空条件的代码如下：
//+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalAC::LongCondition(void) { int result = 0; vector _new,_old; if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_slow_period, m_slow_period)) { vector _ma; if(_new.CorrCoef(_old) >= m_threshold) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period)) { if(m_symbol.Bid() > _ma.Mean()) { result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } else if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_fast_period, m_fast_period)) { if(_new.CorrCoef(_old) <= -m_threshold) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period)) { if(m_symbol.Bid() < _ma.Mean()) { result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } } } return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalAC::ShortCondition(void) { int result = 0; vector _new,_old; if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_slow_period, m_slow_period)) { vector _ma; if(_new.CorrCoef(_old) >= m_threshold) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_slow_period)) { if(m_symbol.Bid() < _ma.Mean()) { result = int(round(100.0 * ((_ma.Mean() - m_symbol.Bid())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } else if(_new.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period) && _old.CopyRates(m_symbol.Name(), m_period, 8, m_fast_period, m_fast_period)) { if(_new.CorrCoef(_old) <= -m_threshold) { if(_ma.CopyRates(m_symbol.Name(), m_period, 8, 0, m_fast_period)) { if(m_symbol.Bid() > _ma.Mean()) { result = int(round(100.0 * ((m_symbol.Bid() - _ma.Mean())/(fabs(m_symbol.Bid() - _ma.Mean()) + fabs(_ma.Max()-_ma.Min()))))); } } } } } return(result); }
我们针对同一 GBPCHF 货币对、2023 年的 H4 时间帧数据进行了几乎相似的测试运行，我们最佳运行的结果如下所示：
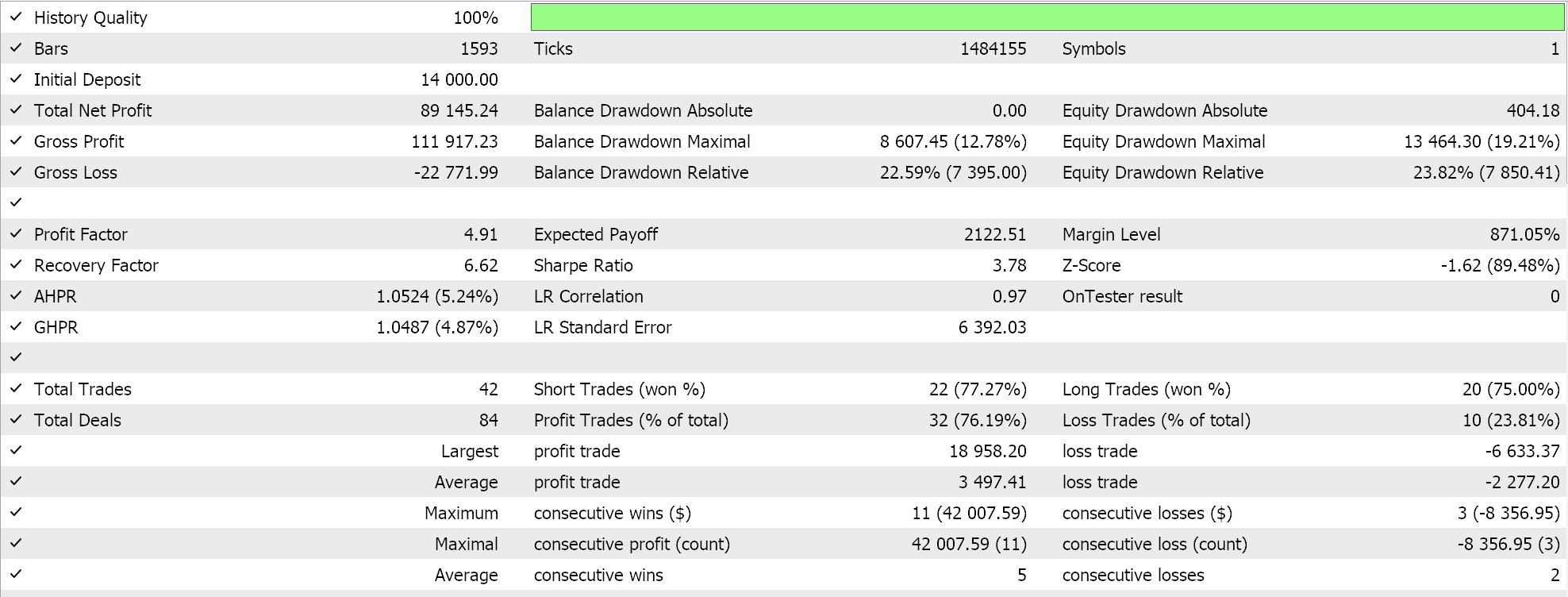
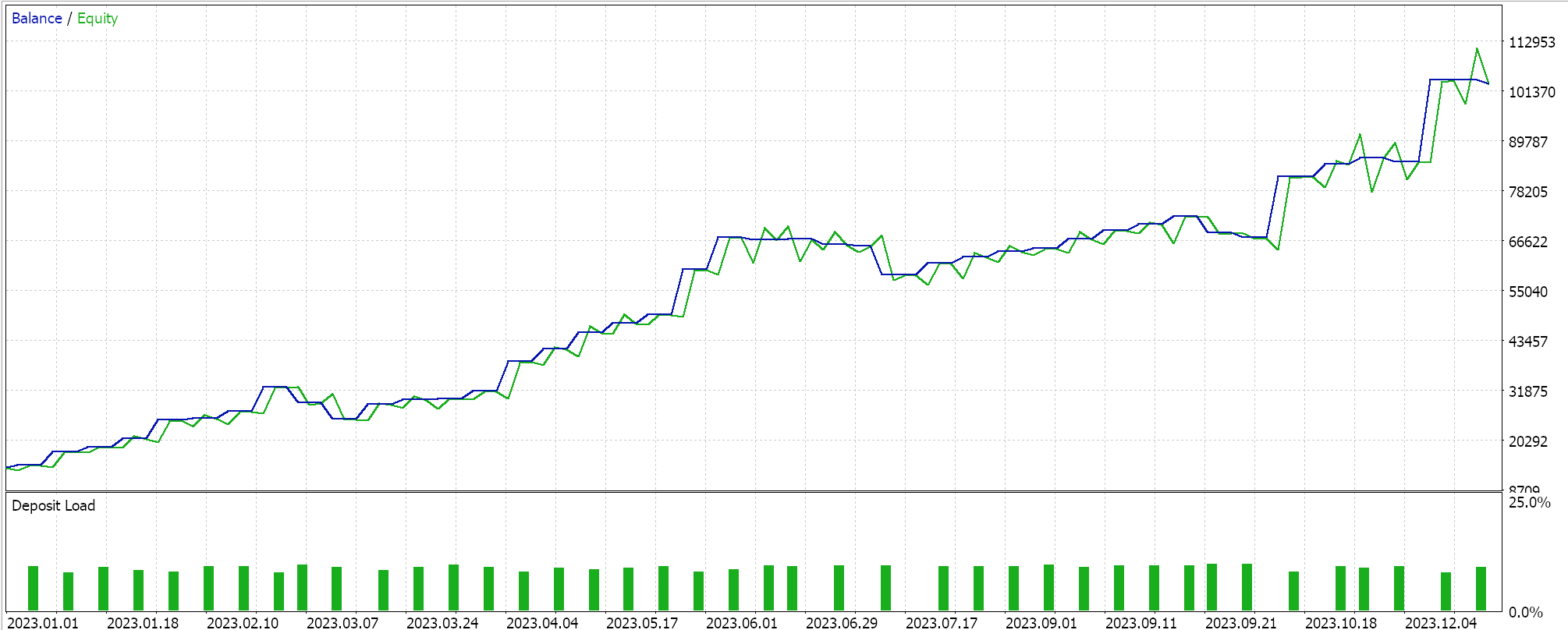
很清楚，这与赫斯特指数信号在性能上存在飞跃或差异。
结束语
赫斯特指数开发于上世纪初，主要作为一款有潜力预测尼罗河潮起潮落的工具，曾经拥有大量水文点数据集。自此，它已被更广泛的应用所采用，其中包括金融时间序列分析。至于本文，我们将其时间序列指数与移动平均线结伴，以便更好地区分趋势行情、和均值回归行情，以便创建自定义信号类。
尽管从我们上面进行的第一次测试运行中，它清晰表现出一些潜力，但考虑到其相对性能相较于原生自相关信号，显然仍有工作要做。它是计算密集型的，过度抑制其交易，且其最佳运行的回撤过大，考虑到这些运行给定的测试窗口相对较小，故这是一个要操心的问题。如常，独立测试运行可能会产生不同、甚至更有前景的结果，欢迎读者尝试一下。附带的源代码，遵循此处和此处的指南，可组装并编译成智能系统。建议深入的测试应该取用经纪商真实报价数据，并横贯数年保持健康。
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/15222
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
无政府社会优化（ASO）算法
将 MQL5 与数据处理包集成（第 1 部分）：高级数据分析和统计处理
使用MQL5中的动态时间规整进行模式识别
嗨，斯蒂芬、
我非常喜欢您写的《向导》一文。 Hurst 一文中介绍的自动相关性结果尤其有趣。 我下载了您的数据源，并对 Hurst CTL EA 进行了编译和测试。 结果令人失望，损失 3108 美元，而您的收益为 89 145 美元。
我将数据源与您的原始数据进行了比较，唯一的改动是包含语句。 我使用 Forex.com 作为数据源。
也许你能找出为什么两个结果会有如此大的差异。
干杯
科达角
嗨，斯蒂芬、
我非常喜欢你写的《向导》一文。 Hurst 一文介绍的自动相关性结果尤其有趣。 我下载了你的资料，并对 Hurst CTL EA 进行了编译和测试。 结果令人失望，损失了 3108 美元，而你的收益为 89 145 美元。
我将数据源与您的原文进行了比较，唯一的改动是包含语句。 我使用 Forex.com 作为数据源。
也许你能找出为什么这两个结果差别如此之大
干杯
科达角
你好、
我刚刚看到这个。您在策略测试器中得到的结果取决于对智能交易系统的输入。 通常情况下，我使用限价订单入市，并在不设止损的情况下设定获利目标。在考虑进一步采用这些想法时，这种设置并不理想，因为必须考虑止损或最长持有期，或一些减轻下行风险的策略。
这里介绍的想法纯粹是出于探索目的，并非交易建议，但如果你对输入进行微调，复制我的策略测试报告应该很容易。
感谢您的阅读。
感谢您的回复。
我推测下载的压缩包中指定的 EA 输入用于产生BackTest 中显示的利润。 我将检查输入并进行调整，以符合您的默认设置。