O Método de Agrupamento para Manipulação de Dados: Implementando o Algoritmo Iterativo Multicamadas em MQL5

Introdução

O Método de Agrupamento para Manipulação de Dados (GMDH) é uma família de algoritmos indutivos usados para modelagem de dados baseada em computador. Os algoritmos operam construindo e otimizando automaticamente modelos de redes neurais polinomiais a partir de dados, oferecendo uma abordagem única para descobrir relações entre variáveis de entrada e saída. Tradicionalmente, o arcabouço GMDH consistia em quatro algoritmos principais: o algoritmo combinatório (COMBI), o algoritmo combinatório seletivo (MULTI), o algoritmo iterativo multicamadas (MIA) e o algoritmo iterativo de relaxação (RIA). Neste artigo, exploraremos a implementação do algoritmo iterativo multicamadas em MQL5. Discutiremos seu funcionamento interno e também demonstraremos maneiras de aplicá-lo para construir modelos preditivos a partir de conjuntos de dados.

Compreendendo o GMDH: O Método de Grupo de Manipulação de Dados

O Método de Agrupamento para Manipulação de Dados é um tipo de algoritmo usado para análise e previsão de dados. É uma técnica de aprendizado de máquina que visa encontrar o melhor modelo matemático para descrever um determinado conjunto de dados. O GMDH foi desenvolvido pelo matemático soviético Alexey Ivakhnenko na década de 1960. Ele foi desenvolvido para abordar os desafios associados à modelagem de sistemas complexos com base em dados empíricos. Os algoritmos GMDH empregam uma abordagem orientada por dados para modelagem, onde os modelos são gerados e refinados com base em dados observados, em vez de suposições teóricas ou preconcebidas.

Uma das principais vantagens do GMDH é que ele automatiza o processo de construção de modelos, gerando e avaliando iterativamente modelos candidatos. Selecionando os modelos de melhor desempenho e refinando-os com base no feedback dos dados. Essa automação reduz a necessidade de intervenção manual e expertise na construção do modelo.

A ideia central por trás do GMDH é construir uma série de modelos de complexidade e precisão crescentes, selecionando e combinando variáveis iterativamente. O algoritmo começa com um conjunto de modelos simples (geralmente modelos lineares) e aumenta gradualmente sua complexidade adicionando variáveis e termos adicionais. Em cada etapa, o algoritmo avalia o desempenho dos modelos e seleciona os de melhor desempenho para formar a base da próxima iteração. Esse processo continua até que um modelo satisfatório seja obtido ou até que um critério de parada seja atendido.

O GMDH é particularmente bem adequado para modelagem de conjuntos de dados com um grande número de variáveis de entrada e relações complexas entre elas. As técnicas GMDH resultam em modelos que relacionam entradas a uma saída que pode ser representada por um polinômio Volterra-Kolmogorov-Gabor (VKG) infinito. Um polinômio Volterra-Kolmogorov-Gabor (VKG) é um tipo específico de polinômio usado na modelagem de sistemas não lineares e na aproximação de dados complexos. Um polinômio VKG assume a seguinte forma:

onde:

• Yn é a saída do sistema.
• Xi, Xj, e Xk são as variáveis de entrada nos tempos i, j e k, respectivamente.
• ai, aj, ak, etc. são os coeficientes do polinômio.

Esse tipo de polinômio pode ser considerado uma rede neural polinomial (PNN). As PNNs são um tipo de arquitetura de rede neural artificial (ANN) que usa funções de ativação polinomiais em seus neurônios. A estrutura de uma rede neural polinomial é semelhante à de outras redes neurais, com nós de entrada, camadas ocultas e nós de saída. No entanto, as funções de ativação aplicadas aos neurônios nas PNNs são funções polinomiais. Algoritmos GMDH paramétricos foram desenvolvidos especificamente para lidar com variáveis contínuas. Onde o objeto sendo modelado é caracterizado por propriedades que não apresentam ambiguidade em sua representação ou definição. O algoritmo iterativo multicamadas é um exemplo de um algoritmo GMDH paramétrico.

Algoritmo Iterativo Multicamadas

O MIA é uma variante do arcabouço GMDH para a construção de modelos de redes neurais polinomiais. Sua estrutura é quase idêntica a uma rede neural feedforward multicamadas. A informação flui da camada de entrada através das camadas intermediárias até a saída final. Com cada camada realizando transformações específicas nos dados. Em relação ao método geral do GMDH, a característica diferenciadora chave do MIA reside na seleção de subfunções ótimas do polinômio final que melhor descreve os dados. Isso significa que algumas informações obtidas durante o treinamento são descartadas de acordo com um critério predefinido.

Para construir um modelo usando o MIA, começamos dividindo o conjunto de dados que queremos estudar em conjuntos de treinamento e teste. Queremos ter o máximo de variedade possível no conjunto de treinamento para capturar adequadamente as características do processo subjacente. Iniciamos com a construção das camadas uma vez que essa divisão esteja feita. 

Construção de camadas

Semelhante a uma rede neural feedforward multicamadas, começamos com a camada de entrada, que é a coleção de preditores ou variáveis independentes. Essas entradas são tomadas duas a duas e enviadas para a primeira camada da rede. A primeira camada, portanto, será composta de "M combinações de 2" nós, onde M é o número de preditores.

A ilustração acima mostra um exemplo de como a camada de entrada e a primeira camada se parecerão ao lidar com 4 entradas (denotadas como x1..x4). Na primeira camada, modelos parciais serão construídos com base nas entradas de um nó usando o conjunto de dados de treinamento, e o modelo parcial resultante será avaliado em relação ao conjunto de dados de teste. O erro de previsão de todos os modelos parciais na camada é então comparado. Com os melhores N modelos sendo anotados e usados para gerar as entradas para a próxima camada. O erro de previsão dos melhores N modelos de uma camada é combinado de alguma maneira para chegar a uma medida única que indica o progresso geral na geração do modelo. Que é comparada com a medida da camada anterior. Se for menor, uma nova camada é criada e o processo é repetido. Caso contrário, se não houver melhoria, A geração do modelo é interrompida e os dados da camada atual são descartados, indicando que o treinamento do modelo estaria completo.

Nós e modelos parciais

Em cada nó de uma camada, é calculado um polinômio que estima as observações no conjunto de dados de treinamento dado o par de entradas provenientes da camada anterior. Isso é o que se refere como um modelo parcial. Um exemplo de uma equação usada para modelar saídas do conjunto de treinamento dadas as entradas do nó é mostrado abaixo.

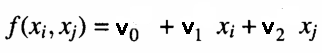
Onde os 'v's são os coeficientes do modelo linear ajustado. A qualidade do ajuste é testada determinando o erro quadrático médio das previsões em relação aos valores reais, no conjunto de dados de teste. Essas medidas de erro são então combinadas de alguma forma. Ou calculando sua média ou simplesmente selecionando o nó com o menor erro quadrático médio. Essa medida final dá uma indicação de se as aproximações estão melhorando ou não em relação a outras camadas. Ao mesmo tempo, os melhores N nós com o menor erro de previsão são anotados. E os coeficientes correspondentes são usados para gerar os valores de um novo conjunto de entradas para a próxima camada. Se as aproximações da camada atual forem melhores (neste caso menores) do que as da camada anterior, uma nova camada será construída.

Uma vez que a rede esteja completa, apenas os coeficientes dos nós que tiveram o menor erro de previsão em cada camada são retidos e usados para definir o modelo final que melhor descreve os dados. Na seção seguinte, nos aprofundamos no código que implementa o procedimento descrito. O código é adaptado de uma implementação em C++ do GMDH disponível no GitHub.

Implementação em MQL5

A implementação em C++ treina modelos e os salva em formato JSON em um arquivo de texto para uso posterior. Ela aproveita o multithreading para acelerar o treinamento e é construída usando as bibliotecas Boost e Eigen. Para nossa implementação em MQL5, a maioria dos recursos será mantida, exceto pelo treinamento multithread e pela disponibilidade de opções alternativas para decomposição QR para resolver equações lineares.

Nossa implementação consistirá em três arquivos de cabeçalho. O primeiro sendo gmdh_internal.mqh. Este arquivo contém definições para vários tipos de dados personalizados. Ele começa definindo três enumerações:

• PolynomialType - especifica o tipo de polinômio usado para transformar variáveis existentes antes de realizar outra rodada de treinamento.
  

  //+---------------------------------------------------------------------------------------------------------+
  //|  Enumeration for specifying the polynomial type to be used to construct new variables from existing ones|
  //+---------------------------------------------------------------------------------------------------------+
  enum PolynomialType
    {
     linear,
     linear_cov,
     quadratic
    };

  "PolynomialType" expõe três opções que representam as funções polinomiais abaixo, onde x1 e x2 são as entradas para a função f(x1,x2) e v0...vN são os coeficientes a serem encontrados. A enumeração representa o tipo de equações a partir das quais o conjunto de soluções será gerado:

Opção	Função f(x1,x2)
linear	equação linear: v0 + v1x1 + v2x2
linear_cov	equação linear com covariação: v0 + v1x1 + v2x2 + v3x1x2
quadratic	equação quadrática: v0 + v1x1 + v2x2 + v3x1x2 + v4x1^2 + v5x2^2

• Solver - determina o método de decomposição QR usado para resolver equações lineares. Nossa implementação terá apenas uma opção utilizável. A versão em C++ emprega variações do método de Householder para decomposição QR usando a biblioteca Eigen.
  

  //+-----------------------------------------------------------------------------------------------+
  //|  Enum  for specifying the QR decomposition method for linear equations solving in models.     |
  //+-----------------------------------------------------------------------------------------------+
  enum Solver
    {
     fast,
     accurate,
     balanced
    };

• CriterionType - permite que os usuários selecionem um critério externo específico que será usado como base para avaliar os modelos candidatos. A enumeração captura as opções que podem ser usadas como critérios de parada ao treinar um modelo.
  

  //+------------------------------------------------------------------+
  //|Enum for specifying the external criterion                        |
  //+------------------------------------------------------------------+
  enum CriterionType
    {
     reg,
     symReg,
     stab,
     symStab,
     unbiasedOut,
     symUnbiasedOut,
     unbiasedCoef,
     absoluteNoiseImmun,
     symAbsoluteNoiseImmun
    };

  As opções disponíveis são explicadas mais detalhadamente na tabela a seguir:

CriterionType	Descrição
reg	regularidade: aplica a soma regular dos erros quadráticos (SSE) com base na diferença entre os alvos do conjunto de dados de teste e as previsões feitas com os coeficientes calculados usando o conjunto de dados de treinamento em combinação com os preditores do conjunto de dados de teste.
symReg	regularidade simétrica: é a soma do SSE com base na diferença entre os alvos do conjunto de dados de teste e as previsões feitas com os coeficientes calculados usando o conjunto de dados de treinamento em combinação com os preditores do conjunto de dados de teste e o SSE com base na diferença entre os alvos do conjunto de dados de treinamento e as previsões feitas com os coeficientes calculados usando o conjunto de dados de teste em combinação com os preditores do conjunto de dados de treinamento
stab	estabilidade: usa o SSE com base na diferença entre todos os alvos e as previsões feitas com os coeficientes calculados usando o conjunto de dados de treinamento em combinação com todos os preditores
symStab	estabilidade simétrica: este critério combina o SSE calculado de maneira semelhante ao critério de 'estabilidade' e o SSE com base na diferença entre todos os alvos e as previsões feitas com os coeficientes calculados usando o conjunto de dados de teste em combinação com todos os preditores do conjunto de dados
unbiasedOut	saídas imparciais: é o SSE com base na diferença entre as previsões feitas com os coeficientes calculados usando o conjunto de dados de treinamento e as previsões feitas com os coeficientes calculados usando o conjunto de dados de teste, ambos utilizando os preditores do conjunto de dados de teste
symUnbiasedOut	saídas imparciais simétricas: calcula o SSE da mesma maneira que o critério 'unbiasedOutputs', mas desta vez usamos todos os preditores
unbiasedCoef	Coeficientes imparciais: a soma das diferenças quadráticas entre os coeficientes calculados usando os dados de treinamento e os coeficientes calculados usando os dados de teste
absoluteNoiseImmun	imunidade absoluta ao ruído: usando esta opção, o critério é calculado como o produto escalar das previsões do modelo treinado em todo o conjunto de dados menos as previsões do modelo treinado no conjunto de dados de treinamento quando aplicado ao conjunto de dados de teste e as previsões do modelo treinado no conjunto de dados de teste menos as previsões do modelo treinado no conjunto de dados de aprendizado quando aplicado ao conjunto de dados de teste
symAbsoluteNoiseImmun	imunidade absoluta ao ruído simétrica: aqui o critério é o produto escalar das previsões do modelo treinado em todo o conjunto de dados menos as previsões do modelo treinado no conjunto de dados de treinamento quando aplicado ao conjunto de dados de aprendizado e as previsões do modelo treinado em todo o conjunto de dados e as previsões do modelo treinado no conjunto de dados de teste quando aplicadas a todas as observações

As enumerações são seguidas por quatro estruturas personalizadas:

• BufferValues - é uma estrutura de vetores usada para armazenar coeficientes e valores previstos calculados de várias maneiras usando tanto os conjuntos de dados de teste quanto de treinamento.
  

  //+-------------------------------------------------------------------------------------+
  //| Structure for storing coefficients and predicted values calculated in different ways|
  //+--------------------------------------------------------------------------------------+
  struct BufferValues
    {
     vector            coeffsTrain; // Coefficients vector calculated using training data
     vector            coeffsTest; // Coefficients vector calculated using testing data
     vector            coeffsAll; // Coefficients vector calculated using learning data
     vector            yPredTrainByTrain; // Predicted values for *training* data calculated using coefficients vector calculated on *training* data
     vector            yPredTrainByTest; // Predicted values for *training* data calculated using coefficients vector calculated on *testing* data
     vector            yPredTestByTrain; // Predicted values for *testing* data calculated using coefficients vector calculated on *training* data
     vector            yPredTestByTest; //Predicted values for *testing* data calculated using coefficients vector calculated on *testing* data
  
                       BufferValues(void)
       {
  
       }
  
                       BufferValues(BufferValues &other)
       {
        coeffsTrain = other.coeffsTrain;
        coeffsTest =  other.coeffsTest;
        coeffsAll = other.coeffsAll;
        yPredTrainByTrain = other.yPredTrainByTrain;
        yPredTrainByTest = other.yPredTrainByTest;
        yPredTestByTrain = other.yPredTestByTrain;
        yPredTestByTest = other.yPredTestByTest;
       }
  
     BufferValues      operator=(BufferValues &other)
       {
        coeffsTrain = other.coeffsTrain;
        coeffsTest =  other.coeffsTest;
        coeffsAll = other.coeffsAll;
        yPredTrainByTrain = other.yPredTrainByTrain;
        yPredTrainByTest = other.yPredTrainByTest;
        yPredTestByTrain = other.yPredTestByTrain;
        yPredTestByTest = other.yPredTestByTest;
  
        return this;
       }
  
    };

  
  
• PairDVXd - encapsula uma estrutura de dados que combina um escalar e um vetor correspondente.
  

  //+------------------------------------------------------------------+
  //|  struct PairDV                                                   |
  //+------------------------------------------------------------------+
  struct PairDVXd
    {
     double            first;
     vector            second;
  
                       PairDVXd(void)
       {
        first = 0.0;
        second = vector::Zeros(10);
       }
  
                       PairDVXd(double &_f, vector &_s)
       {
        first = _f;
        second.Copy(_s);
       }
  
                       PairDVXd(PairDVXd &other)
       {
        first = other.first;
        second = other.second;
       }
  
     PairDVXd          operator=(PairDVXd& other)
       {
        first = other.first;
        second = other.second;
  
        return this;
       }
    };

  
  
• PairMVXd - é uma estrutura que combina uma matriz e um vetor. Juntos, eles armazenam as entradas e os valores de saída ou alvos correspondentes. As entradas são mantidas na matriz e o vetor é a coleção de saídas. Cada linha da matriz corresponde a um valor no vetor.
  

  //+------------------------------------------------------------------+
  //| structure PairMVXd                                               |
  //+------------------------------------------------------------------+
  struct PairMVXd
    {
     matrix            first;
     vector            second;
  
                       PairMVXd(void)
       {
        first = matrix::Zeros(10,10);
        second = vector::Zeros(10);
       }
  
                       PairMVXd(matrix &_f,  vector& _s)
       {
        first = _f;
        second = _s;
       }
  
                       PairMVXd(PairMVXd &other)
       {
        first = other.first;
        second = other.second;
       }
  
     PairMVXd          operator=(PairMVXd &other)
       {
        first = other.first;
        second = other.second;
  
        return this;
       }
    };

• SplittedData - esta estrutura de dados armazena os conjuntos de dados particionados para treinamento e teste.
  

  //+------------------------------------------------------------------+
  //|  Structure for storing parts of a split dataset                  |
  //+------------------------------------------------------------------+
  struct SplittedData
    {
     matrix            xTrain;
     matrix            xTest;
     vector            yTrain;
     vector            yTest;
  
                       SplittedData(void)
       {
        xTrain = matrix::Zeros(10,10);
        xTest = matrix::Zeros(10,10);
        yTrain = vector::Zeros(10);
        yTest = vector::Zeros(10);
       }
  
                       SplittedData(SplittedData &other)
       {
        xTrain = other.xTrain;
        xTest =  other.xTest;
        yTrain = other.yTrain;
        yTest =  other.yTest;
       }
  
     SplittedData      operator=(SplittedData &other)
       {
        xTrain = other.xTrain;
        xTest =  other.xTest;
        yTrain = other.yTrain;
        yTest =  other.yTest;
  
        return this;
       }
    };

  
  

Após as structs, chegamos às definições de classes:

• A classe Combination representa um modelo candidato. Ela armazena os critérios de avaliação, a combinação de entradas e os coeficientes calculados para um modelo.
  

  //+------------------------------------------------------------------+
  //| Сlass representing the candidate model of the GMDH algorithm     |
  //+------------------------------------------------------------------+
  class Combination
    {
     vector            _combination,_bestCoeffs;
     double            _evaluation;
  public:
                       Combination(void) { _combination = vector::Zeros(10); _bestCoeffs.Copy(_combination); _evaluation = DBL_MAX; }
                       Combination(vector &comb) : _combination(comb) { _bestCoeffs=vector::Zeros(_combination.Size()); _evaluation = DBL_MAX;}
                       Combination(vector &comb, vector &coeffs) : _combination(comb),_bestCoeffs(coeffs) { _evaluation = DBL_MAX; }
                       Combination(Combination &other) { _combination = other.combination(); _bestCoeffs=other.bestCoeffs(); _evaluation = other.evaluation();}
     vector            combination(void) { return _combination;}
     vector            bestCoeffs(void)  { return _bestCoeffs; }
     double            evaluation(void)  { return _evaluation; }
  
     void              setCombination(vector &combination) { _combination = combination; }
     void              setBestCoeffs(vector &bestcoeffs) { _bestCoeffs = bestcoeffs; }
     void              setEvaluation(double evaluation)  { _evaluation = evaluation; }
  
     bool              operator<(Combination &combi) { return _evaluation<combi.evaluation();}
     Combination       operator=(Combination &combi)
       {
        _combination = combi.combination();
        _bestCoeffs = combi.bestCoeffs();
        _evaluation = combi.evaluation();
  
        return this;
       }
    };

• CVector - define um contêiner personalizado semelhante a um vetor que armazena uma coleção de instâncias da classe Combination. Tornando-o um contêiner de modelos candidatos.

  //+------------------------------------------------------------------+
  //| collection of Combination instances                              |
  //+------------------------------------------------------------------+
  class CVector
    {
  protected:
     Combination       m_array[];
     int               m_size;
     int               m_reserve;
  public:
     //+------------------------------------------------------------------+
     //| default constructor                                              |
     //+------------------------------------------------------------------+
                       CVector(void) :m_size(0),m_reserve(1000) { }
     //+------------------------------------------------------------------+
     //| parametric constructor specifying initial size                   |
     //+------------------------------------------------------------------+
                       CVector(int size, int mem_reserve = 1000) :m_size(size),m_reserve(mem_reserve)
       {
        ArrayResize(m_array,m_size,m_reserve);
       }
     //+------------------------------------------------------------------+
     //| Copy constructor                                                 |
     //+------------------------------------------------------------------+
                       CVector(CVector &other)
       {
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]=other[i];
       }
  
  
     //+------------------------------------------------------------------+
     //| destructor                                                       |
     //+------------------------------------------------------------------+
                      ~CVector(void)
       {
  
       }
     //+------------------------------------------------------------------+
     //| Add element to end of array                                      |
     //+------------------------------------------------------------------+
     bool              push_back(Combination &value)
       {
        ResetLastError();
  
        if(ArrayResize(m_array,int(m_array.Size()+1),m_reserve)<m_size+1)
          {
           Print(__FUNCTION__," Critical error: failed to resize underlying array ", GetLastError());
           return false;
          }
  
        m_array[m_size++]=value;
  
        return true;
       }
     //+------------------------------------------------------------------+
     //| set value at specified index                                     |
     //+------------------------------------------------------------------+
     bool              setAt(int index, Combination &value)
       {
        ResetLastError();
  
        if(index < 0 || index >= m_size)
          {
           Print(__FUNCTION__," index out of bounds ");
           return false;
          }
  
        m_array[index]=value;
  
        return true;
  
       }
     //+------------------------------------------------------------------+
     //|access by index                                                   |
     //+------------------------------------------------------------------+
  
     Combination*      operator[](int index)
       {
        return GetPointer(m_array[uint(index)]);
       }
  
     //+------------------------------------------------------------------+
     //|overload assignment operator                                      |
     //+------------------------------------------------------------------+
  
     CVector           operator=(CVector &other)
       {
        clear();
  
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
  
  
        return this;
       }
     //+------------------------------------------------------------------+
     //|access last element                                               |
     //+------------------------------------------------------------------+
  
     Combination*      back(void)
       {
        return GetPointer(m_array[m_size-1]);
       }
     //+-------------------------------------------------------------------+
     //|access by first index                                             |
     //+------------------------------------------------------------------+
  
     Combination*      front(void)
       {
        return GetPointer(m_array[0]);
       }
     //+------------------------------------------------------------------+
     //| Get current size of collection ,the number of elements           |
     //+------------------------------------------------------------------+
  
     int               size(void)
       {
        return ArraySize(m_array);
       }
     //+------------------------------------------------------------------+
     //|Get the reserved memory size                                      |
     //+------------------------------------------------------------------+
     int               reserve(void)
       {
        return m_reserve;
       }
     //+------------------------------------------------------------------+
     //|set the reserved memory size                                      |
     //+------------------------------------------------------------------+
     void              reserve(int new_reserve)
       {
        if(new_reserve > 0)
           m_reserve = new_reserve;
       }
     //+------------------------------------------------------------------+
     //| clear                                                            |
     //+------------------------------------------------------------------+
     void              clear(void)
       {
        ArrayFree(m_array);
  
        m_size = 0;
       }
  
    };

• CVector2d - é outro contêiner personalizado semelhante a um vetor, que armazena uma coleção de instâncias de CVector.
  

  //+------------------------------------------------------------------+
  //| Collection of CVector instances                                  |
  //+------------------------------------------------------------------+
  class CVector2d
    {
  protected:
     CVector           m_array[];
     int               m_size;
     int               m_reserve;
  public:
     //+------------------------------------------------------------------+
     //| default constructor                                              |
     //+------------------------------------------------------------------+
                       CVector2d(void) :m_size(0),m_reserve(1000) { }
     //+------------------------------------------------------------------+
     //| parametric constructor specifying initial size                   |
     //+------------------------------------------------------------------+
                       CVector2d(int size, int mem_reserve = 1000) :m_size(size),m_reserve(mem_reserve)
       {
        ArrayResize(m_array,m_size,m_reserve);
       }
     //+------------------------------------------------------------------+
     //| Copy constructor                                                 |
     //+------------------------------------------------------------------+
                       CVector2d(CVector2d &other)
       {
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
       }
  
  
     //+------------------------------------------------------------------+
     //| destructor                                                       |
     //+------------------------------------------------------------------+
                      ~CVector2d(void)
       {
  
       }
     //+------------------------------------------------------------------+
     //| Add element to end of array                                      |
     //+------------------------------------------------------------------+
     bool              push_back(CVector &value)
       {
        ResetLastError();
  
        if(ArrayResize(m_array,int(m_array.Size()+1),m_reserve)<m_size+1)
          {
           Print(__FUNCTION__," Critical error: failed to resize underlying array ", GetLastError());
           return false;
          }
  
        m_array[m_size++]=value;
  
        return true;
       }
     //+------------------------------------------------------------------+
     //| set value at specified index                                     |
     //+------------------------------------------------------------------+
     bool              setAt(int index, CVector &value)
       {
        ResetLastError();
  
        if(index < 0 || index >= m_size)
          {
           Print(__FUNCTION__," index out of bounds ");
           return false;
          }
  
        m_array[index]=value;
  
        return true;
  
       }
     //+------------------------------------------------------------------+
     //|access by index                                                   |
     //+------------------------------------------------------------------+
  
     CVector*          operator[](int index)
       {
        return GetPointer(m_array[uint(index)]);
       }
  
     //+------------------------------------------------------------------+
     //|overload assignment operator                                      |
     //+------------------------------------------------------------------+
  
     CVector2d         operator=(CVector2d &other)
       {
        clear();
  
        m_size = other.size();
        m_reserve = other.reserve();
  
        ArrayResize(m_array,m_size,m_reserve);
  
        for(int i=0; i<m_size; ++i)
           m_array[i]= other[i];
  
        return this;
       }
     //+------------------------------------------------------------------+
     //|access last element                                               |
     //+------------------------------------------------------------------+
  
     CVector*          back(void)
       {
        return GetPointer(m_array[m_size-1]);
       }
     //+-------------------------------------------------------------------+
     //|access by first index                                             |
     //+------------------------------------------------------------------+
  
     CVector*          front(void)
       {
        return GetPointer(m_array[0]);
       }
     //+------------------------------------------------------------------+
     //| Get current size of collection ,the number of elements           |
     //+------------------------------------------------------------------+
  
     int               size(void)
       {
        return ArraySize(m_array);
       }
     //+------------------------------------------------------------------+
     //|Get the reserved memory size                                      |
     //+------------------------------------------------------------------+
     int               reserve(void)
       {
        return m_reserve;
       }
     //+------------------------------------------------------------------+
     //|set the reserved memory size                                      |
     //+------------------------------------------------------------------+
     void              reserve(int new_reserve)
       {
        if(new_reserve > 0)
           m_reserve = new_reserve;
       }
     //+------------------------------------------------------------------+
     //| clear                                                            |
     //+------------------------------------------------------------------+
     void              clear(void)
       {
  
        for(uint i = 0; i<m_array.Size(); i++)
           m_array[i].clear();
  
        ArrayFree(m_array);
  
        m_size = 0;
       }
  
    };

• Critério - esta classe implementa o cálculo de vários critérios externos com base em um tipo de critério selecionado.
  

  //+---------------------------------------------------------------------------------+
  //|Class that implements calculations of internal and individual external criterions|
  //+---------------------------------------------------------------------------------+
  class Criterion
    {
  protected:
     CriterionType     criterionType; // Selected CriterionType object
     Solver            solver; // Selected Solver object
  
  public:
     /**
     Implements the internal criterion calculation
     param xTrain Matrix of input variables that should be used to calculate the model coefficients
     param yTrain Target values vector for the corresponding xTrain parameter
     return Coefficients vector representing a solution of the linear equations system constructed from the parameters data
     */
     vector            findBestCoeffs(matrix& xTrain,  vector& yTrain)
       {
        vector solution;
  
        matrix q,r;
  
        xTrain.QR(q,r);
  
        matrix qT = q.Transpose();
  
        vector y = qT.MatMul(yTrain);
  
        solution = r.LstSq(y);
  
  
        return solution;
       }
  
     /**
      Calculate the value of the selected external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param _criterionType Selected external criterion type
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of external criterion and calculated model coefficients
      */
     PairDVXd          getResult(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                 CriterionType _criterionType, BufferValues& bufferValues)
       {
        switch(_criterionType)
          {
           case reg:
              return regularity(xTrain, xTest, yTrain, yTest, bufferValues);
           case symReg:
              return symRegularity(xTrain, xTest, yTrain, yTest, bufferValues);
           case stab:
              return stability(xTrain, xTest, yTrain, yTest, bufferValues);
           case symStab:
              return symStability(xTrain, xTest, yTrain, yTest, bufferValues);
           case unbiasedOut:
              return unbiasedOutputs(xTrain, xTest, yTrain, yTest, bufferValues);
           case symUnbiasedOut:
              return symUnbiasedOutputs(xTrain, xTest, yTrain, yTest, bufferValues);
           case unbiasedCoef:
              return unbiasedCoeffs(xTrain, xTest, yTrain, yTest, bufferValues);
           case absoluteNoiseImmun:
              return absoluteNoiseImmunity(xTrain, xTest, yTrain, yTest, bufferValues);
           case symAbsoluteNoiseImmun:
              return symAbsoluteNoiseImmunity(xTrain, xTest, yTrain, yTest, bufferValues);
          }
  
        PairDVXd pd;
        return pd;
       }
     /**
      Calculate the regularity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     param inverseSplit True, if it is necessary to swap the roles of training and testing data, otherwise false
     return The value of the regularity external criterion and calculated model coefficients
      */
     PairDVXd          regularity(matrix& xTrain, matrix& xTest, vector &yTrain, vector& yTest,
                                  BufferValues& bufferValues, bool inverseSplit = false)
       {
        PairDVXd pdv;
        vector f;
        if(!inverseSplit)
          {
           if(bufferValues.coeffsTrain.Size() == 0)
              bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
           if(bufferValues.yPredTestByTrain.Size() == 0)
              bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
           f = MathPow((yTest - bufferValues.yPredTestByTrain),2.0);
           pdv.first = f.Sum();
           pdv.second = bufferValues.coeffsTrain;
          }
        else
          {
           if(bufferValues.coeffsTest.Size() == 0)
              bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
           if(bufferValues.yPredTrainByTest.Size() == 0)
              bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
  
           f = MathPow((yTrain - bufferValues.yPredTrainByTest),2.0);
           pdv.first = f.Sum();
           pdv.second = bufferValues.coeffsTest;
          }
  
        return pdv;
       }
     /**
      Calculate the symmetric regularity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmertic regularity external criterion and calculated model coefficients
      */
     PairDVXd          symRegularity(matrix& xTrain, matrix& xTest, vector& yTrain, vector& yTest,
                                     BufferValues& bufferValues)
       {
        PairDVXd pdv1,pdv2,pdsum;
  
        pdv1 = regularity(xTrain,xTest,yTrain,yTest,bufferValues);
        pdv2 = regularity(xTrain,xTest,yTrain,yTest,bufferValues,true);
  
        pdsum.first = pdv1.first+pdv2.first;
        pdsum.second = pdv1.second;
  
        return pdsum;
       }
  
     /**
      Calculate the stability external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     param inverseSplit True, if it is necessary to swap the roles of training and testing data, otherwise false
     return The value of the stability external criterion and calculated model coefficients
      */
     PairDVXd          stability(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                 BufferValues& bufferValues, bool inverseSplit = false)
       {
        PairDVXd pdv;
        vector f1,f2;
        if(!inverseSplit)
          {
           if(bufferValues.coeffsTrain.Size() == 0)
              bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
           if(bufferValues.yPredTrainByTrain.Size() == 0)
              bufferValues.yPredTrainByTrain = xTrain.MatMul(bufferValues.coeffsTrain);
  
           if(bufferValues.yPredTestByTrain.Size() == 0)
              bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
           f1 = MathPow((yTrain - bufferValues.yPredTrainByTrain),2.0);
           f2 = MathPow((yTest - bufferValues.yPredTestByTrain),2.0);
  
           pdv.first = f1.Sum()+f2.Sum();
           pdv.second = bufferValues.coeffsTrain;
          }
        else
          {
           if(bufferValues.coeffsTest.Size() == 0)
              bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
           if(bufferValues.yPredTrainByTest.Size() == 0)
              bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
  
           if(bufferValues.yPredTestByTest.Size() == 0)
              bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
           f1 = MathPow((yTrain - bufferValues.yPredTrainByTest),2.0);
           f2 = MathPow((yTest - bufferValues.yPredTestByTest),2.0);
           pdv.first = f1.Sum() + f2.Sum();
           pdv.second = bufferValues.coeffsTest;
          }
  
        return pdv;
       }
  
     /**
      Calculate the symmetric stability external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmertic stability external criterion and calculated model coefficients
      */
     PairDVXd          symStability(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                    BufferValues& bufferValues)
       {
        PairDVXd pdv1,pdv2,pdsum;
  
        pdv1 = stability(xTrain, xTest, yTrain, yTest, bufferValues);
        pdv2 = stability(xTrain, xTest, yTrain, yTest, bufferValues, true);
  
        pdsum.first=pdv1.first+pdv2.first;
        pdsum.second = pdv1.second;
  
        return pdsum;
       }
  
     /**
      Calculate the unbiased outputs external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the unbiased outputs external criterion and calculated model coefficients
      */
     PairDVXd          unbiasedOutputs(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,
                                       BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        f = MathPow((bufferValues.yPredTestByTrain - bufferValues.yPredTestByTest),2.0);
        pdv.first = f.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the symmetric unbiased outputs external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmetric unbiased outputs external criterion and calculated model coefficients
      */
     PairDVXd          symUnbiasedOutputs(matrix &xTrain,  matrix &xTest,  vector &yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f1,f2;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
        if(bufferValues.yPredTrainByTrain.Size() == 0)
           bufferValues.yPredTrainByTrain = xTrain.MatMul(bufferValues.coeffsTrain);
        if(bufferValues.yPredTrainByTest.Size() == 0)
           bufferValues.yPredTrainByTest = xTrain.MatMul(bufferValues.coeffsTest);
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        f1 = MathPow((bufferValues.yPredTrainByTrain - bufferValues.yPredTrainByTest),2.0);
        f2 = MathPow((bufferValues.yPredTestByTrain - bufferValues.yPredTestByTest),2.0);
        pdv.first = f1.Sum() + f2.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the unbiased coefficients external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the unbiased coefficients external criterion and calculated model coefficients
      */
     PairDVXd          unbiasedCoeffs(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector f1;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        f1 = MathPow((bufferValues.coeffsTrain - bufferValues.coeffsTest),2.0);
        pdv.first = f1.Sum();
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the absolute noise immunity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the absolute noise immunity external criterion and calculated model coefficients
      */
     PairDVXd          absoluteNoiseImmunity(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        vector yPredTestByAll,f1,f2;
        PairDVXd pdv;
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.coeffsAll.Size() == 0)
          {
           matrix dataX(xTrain.Rows() + xTest.Rows(), xTrain.Cols());
  
           for(ulong i = 0; i<xTrain.Rows(); i++)
              dataX.Row(xTrain.Row(i),i);
  
           for(ulong i = 0; i<xTest.Rows(); i++)
              dataX.Row(xTest.Row(i),i+xTrain.Rows());
  
           vector dataY(yTrain.Size() + yTest.Size());
  
           for(ulong i=0; i<yTrain.Size(); i++)
              dataY[i] = yTrain[i];
  
           for(ulong i=0; i<yTest.Size(); i++)
              dataY[i+yTrain.Size()] = yTest[i];
  
           bufferValues.coeffsAll = findBestCoeffs(dataX, dataY);
          }
  
        if(bufferValues.yPredTestByTrain.Size() == 0)
           bufferValues.yPredTestByTrain = xTest.MatMul(bufferValues.coeffsTrain);
  
        if(bufferValues.yPredTestByTest.Size() == 0)
           bufferValues.yPredTestByTest = xTest.MatMul(bufferValues.coeffsTest);
  
        yPredTestByAll = xTest.MatMul(bufferValues.coeffsAll);
  
        f1 =  yPredTestByAll - bufferValues.yPredTestByTrain;
        f2 = bufferValues.yPredTestByTest - yPredTestByAll;
  
        pdv.first = f1.Dot(f2);
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
       }
  
     /**
      Calculate the symmetric absolute noise immunity external criterion for the given data
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     param bufferValues Temporary storage for calculated coefficients and target values
     return The value of the symmetric absolute noise immunity external criterion and calculated model coefficients
      */
     PairDVXd          symAbsoluteNoiseImmunity(matrix& xTrain,  matrix& xTest,  vector& yTrain,  vector& yTest,BufferValues& bufferValues)
       {
        PairDVXd pdv;
        vector yPredAllByTrain, yPredAllByTest, yPredAllByAll,f1,f2;
        matrix dataX(xTrain.Rows() + xTest.Rows(), xTrain.Cols());
  
        for(ulong i = 0; i<xTrain.Rows(); i++)
           dataX.Row(xTrain.Row(i),i);
  
        for(ulong i = 0; i<xTest.Rows(); i++)
           dataX.Row(xTest.Row(i),i+xTrain.Rows());
  
        vector dataY(yTrain.Size() + yTest.Size());
  
        for(ulong i=0; i<yTrain.Size(); i++)
           dataY[i] = yTrain[i];
  
        for(ulong i=0; i<yTest.Size(); i++)
           dataY[i+yTrain.Size()] = yTest[i];
  
        if(bufferValues.coeffsTrain.Size() == 0)
           bufferValues.coeffsTrain = findBestCoeffs(xTrain, yTrain);
  
        if(bufferValues.coeffsTest.Size() == 0)
           bufferValues.coeffsTest = findBestCoeffs(xTest, yTest);
  
        if(bufferValues.coeffsAll.Size() == 0)
           bufferValues.coeffsAll = findBestCoeffs(dataX, dataY);
  
        yPredAllByTrain = dataX.MatMul(bufferValues.coeffsTrain);
        yPredAllByTest = dataX.MatMul(bufferValues.coeffsTest);
        yPredAllByAll = dataX.MatMul(bufferValues.coeffsAll);
  
        f1 = yPredAllByAll - yPredAllByTrain;
        f2 = yPredAllByTest - yPredAllByAll;
  
        pdv.first = f1.Dot(f2);
        pdv.second = bufferValues.coeffsTrain;
  
        return pdv;
  
       }
  
     /**
      Get k models from the given ones with the best values of the external criterion
     param combinations Vector of the trained models
     param data Object containing parts of a split dataset used in model training. O parâmetro é usado no critério sequencial
  param func Função que retorna os novos dados de trem X e teste X construídos a partir dos dados originais usando a combinação fornecida de índices de coluna de variáveis ​​de entrada. Parameter is used in sequential criterion
     param k Number of best models
     return Vector containing k best models
      */
     virtual void      getBestCombinations(CVector &combinations, CVector &bestCombo,SplittedData& data, MatFunc func, int k)
       {
        double proxys[];
        int best[];
  
        ArrayResize(best,combinations.size());
        ArrayResize(proxys,combinations.size());
  
        for(int i = 0 ; i<combinations.size(); i++)
          {
           proxys[i] = combinations[i].evaluation();
           best[i] = i;
          }
  
        MathQuickSortAscending(proxys,best,0,combinations.size()-1);
  
        for(int i = 0; i<int(MathMin(MathAbs(k),combinations.size())); i++)
           bestCombo.push_back(combinations[best[i]]);
  
       }
     /**
      Calculate the value of the selected external criterion for the given data.
      For the individual criterion this method only calls the getResult() method
     param xTrain Input variables matrix of the training data
     param xTest Input variables matrix of the testing data
     param yTrain Target values vector of the training data
     param yTest Target values vector of the testing data
     return The value of the external criterion and calculated model coefficients
      */
     virtual PairDVXd  calculate(matrix& xTrain,  matrix& xTest,
                                 vector& yTrain,  vector& yTest)
       {
        BufferValues tempValues;
        return getResult(xTrain, xTest, yTrain, yTest, criterionType, tempValues);
       }
  
  public:
     ///  Construct a new Criterion object
                       Criterion() {};
  
     /**
      Construct a new Criterion object
     param _criterionType Selected external criterion type
     param _solver Selected method for linear equations solving
      */
                       Criterion(CriterionType _criterionType)
       {
        criterionType = _criterionType;
        solver = balanced;
       }
  
    };
  

Por fim, temos duas funções que marcam o final do arquivo gmdh_internal.mqh:

validateInputData() - é usada para garantir que os valores passados para métodos de classe ou outras funções independentes estejam corretamente especificados.

**
 *  Validar valores dos parâmetros de entrada
 *
 * param testSize Fração dos dados de entrada que deve ser colocada na segunda parte
 * param pAverage O número dos melhores modelos com base nos quais o critério externo para cada nível será calculado

 * param threads O número de threads usados para cálculos. Defina -1 para usar o máximo possível de threads
 * param verbose 1 se for necessário imprimir informações detalhadas sobre o processo de treinamento, caso contrário, 0
 * param limit O valor mínimo pelo qual o critério externo deve ser melhorado para continuar o treinamento


 * param kBest O número dos melhores modelos com base nos quais novos modelos do próximo nível serão construídos
 * retorno Status de saída do método
 */
int validateInputData(double testSize=0.0, int pAverage=0, double limit=0.0, int kBest=0)
  {
   int errorCode = 0;
//
   if(testSize <= 0 || testSize >= 1)
     {
      Print("testsize value must be in the (0, 1) range");
      errorCode |= 1;
     }
   if(pAverage && pAverage < 1)
     {
      Print("p_average value must be a positive integer");
      errorCode |= 4;
     }
   if(limit && limit < 0)
     {
      Print("limit value must be non-negative");
      errorCode |= 8;
     }
   if(kBest && kBest < 1)
     {
      Print("k_best value must be a positive integer");
      errorCode |= 16;
     }

   return errorCode;
  }

timeSeriesTransformation() - é uma função utilitária que recebe como entrada uma série em um vetor e a transforma em uma estrutura de dados de entradas e alvos de acordo com o número de lags escolhido.

/**
 *  Converter o vetor de série temporal para o formato de matriz 2D necessário para trabalhar com algoritmos GMDH
 *
 * param timeSeries Vetor de dados da série temporal
 * param lags Os lags (comprimento) dos subconjuntos da série temporal nos quais a série temporal original deve ser dividida
 * return Dados da série temporal transformados
 */
PairMVXd timeSeriesTransformation(vector& timeSeries, int lags)
  {
   PairMVXd p;

   string errorMsg = "";
   if(timeSeries.Size() == 0)
      errorMsg = "time_series value is empty";
   else
      if(lags <= 0)
         errorMsg = "lags value must be a positive integer";
      else
         if(lags >= int(timeSeries.Size()))
            errorMsg = "lags value can't be greater than  time_series  size";
   if(errorMsg != "")
      return p;

   ulong last = timeSeries.Size() - ulong(lags);
   vector yTimeSeries(last,slice,timeSeries,ulong(lags));
   matrix xTimeSeries(last, ulong(lags));
   vector vect;
   for(ulong i = 0; i < last; ++i)
     {
      vect.Init(ulong(lags),slice,timeSeries,i,i+ulong(lags-1));
      xTimeSeries.Row(vect,i);
     }

   p.first = xTimeSeries;
   p.second = yTimeSeries;

   return p;
  }

Aqui, "lags" se refere ao número de valores anteriores da série usados como preditores para calcular um termo subsequente.

Isso completa a descrição do arquivo gmdh_internal.mqh. Vamos seguir para o segundo arquivo de cabeçalho, gmdh.mqh.

Ele começa com a definição da função splitData().

/**
 *  Dividir os dados de entrada em 2 partes
 *
 * param x Matriz de dados de entrada contendo variáveis preditivas
 * param y Vetor dos valores-alvo correspondentes aos dados de x
 * param testSize Fração dos dados de entrada que deve ser colocada na segunda parte
 * param shuffle Verdadeiro se os dados devem ser embaralhados antes de serem divididos em 2 partes, caso contrário, falso 
 * param randomSeed Número de semente para o gerador aleatório para obter a mesma divisão todas as vezes
 * return Objeto SplittedData contendo 4 elementos de dados: train x, train y, test x, test y
 */
SplittedData splitData(matrix& x,  vector& y, double testSize = 0.2, bool shuffle = false, int randomSeed = 0)
  {
   SplittedData data;

   if(validateInputData(testSize))
      return data;
   
   string errorMsg = "";
   if(x.Rows() != y.Size())
      errorMsg = " x rows number and y size must be equal";
   else
      if(round(x.Rows() * testSize) == 0 || round(x.Rows() * testSize) == x.Rows())
         errorMsg = "Result contains an empty array. Change the arrays size or the  value for correct splitting";
   if(errorMsg != "")
     {
      Print(__FUNCTION__," ",errorMsg);
      return data;
     }


   if(!shuffle)
      data = GmdhModel::internalSplitData(x, y, testSize);
   else
     {
      if(randomSeed == 0)
         randomSeed = int(GetTickCount64());
      MathSrand(uint(randomSeed));

      int shuffled_rows_indexes[],shuffled[];
      MathSequence(0,int(x.Rows()-1),1,shuffled_rows_indexes);
      MathSample(shuffled_rows_indexes,int(shuffled_rows_indexes.Size()),shuffled);

      int testItemsNumber = (int)round(x.Rows() * testSize);


      matrix Train,Test;
      vector train,test;

      Train.Resize(x.Rows()-ulong(testItemsNumber),x.Cols());
      Test.Resize(ulong(testItemsNumber),x.Cols());

      train.Resize(x.Rows()-ulong(testItemsNumber));
      test.Resize(ulong(testItemsNumber));

      for(ulong i = 0; i<Train.Rows(); i++)
        {
         Train.Row(x.Row(shuffled[i]),i);
         train[i] = y[shuffled[i]];
        }

      for(ulong i = 0; i<Test.Rows(); i++)
        {
         Test.Row(x.Row(shuffled[Train.Rows()+i]),i);
         test[i] = y[shuffled[Train.Rows()+i]];
        }

      data.xTrain = Train;
      data.xTest = Test;
      data.yTrain = train;
      data.yTest = test;
     }

   return data;
  }  

Ela recebe como entrada uma matriz e um vetor representando variáveis e alvos, respectivamente. O parâmetro "testSize" define a fração do conjunto de dados a ser usada como conjunto de teste. "shuffle" permite o embaralhamento aleatório do conjunto de dados, e "randomSeed" especifica a semente para um gerador de números aleatórios usado no processo de embaralhamento.

Em seguida, temos a classe "GmdhModel", que define a lógica geral dos algoritmos GMDH.

//+------------------------------------------------------------------+
//| Class implementing the general logic of GMDH algorithms          |
//+------------------------------------------------------------------+

class  GmdhModel
  {
protected:

   string            modelName; // model name
   int               level; // Current number of the algorithm training level
   int               inputColsNumber; // The number of predictive variables in the original data
   double            lastLevelEvaluation; // The external criterion value of the previous training level
   double            currentLevelEvaluation; // The external criterion value of the current training level
   bool              training_complete; // flag indicator successful completion of model training
   CVector2d         bestCombinations; // Storage for the best models of previous levels

   /**
    *struct for generating vector sequence
    */
   struct unique
     {
   private:
      int            current;

      int            run(void)
        {
         return ++current;
        }

   public:
                     unique(void)
        {
         current = -1;
        }

      vector         generate(ulong t)
        {
         ulong s=0;
         vector ret(t);

         while(s<t)
            ret[s++] = run();

         return ret;
        }
     };

   /**
    *  Find all combinations of k elements from n
    *
    * param n Number of all elements
    * param k Number of required elements
    * return Vector of all combinations of k elements from n
    */
   void              nChooseK(int n, int k, vector &combos[])
     {
      if(n<=0 || k<=0 || n<k)
        {
         Print(__FUNCTION__," invalid parameters for n and or k", "n ",n , " k ", k);
         return;
        }

      unique q;

      vector comb = q.generate(ulong(k));

      ArrayResize(combos,combos.Size()+1,100);

      long first, last;

      first = 0;
      last = long(k);
      combos[combos.Size()-1]=comb;

      while(comb[first]!= double(n - k))
        {
         long mt = last;
         while(comb[--mt] == double(n - (last - mt)));
         comb[mt]++;
         while(++mt != last)
            comb[mt] = comb[mt-1]+double(1);
         ArrayResize(combos,combos.Size()+1,100);
         combos[combos.Size()-1]=comb;
        }

      for(uint i = 0; i<combos.Size(); i++)
        {
         combos[i].Resize(combos[i].Size()+1);
         combos[i][combos[i].Size()-1] = n;
        }

      return;
     }

   /**
    *  Get the mean value of extrnal criterion of the k best models
    *
    * param sortedCombinations Sorted vector of current level models
    * param k The numebr of the best models
    * return Calculated mean value of extrnal criterion of the k best models
    */
   double            getMeanCriterionValue(CVector &sortedCombinations, int k)
     {
      k = MathMin(k, sortedCombinations.size());

      double crreval=0;

      for(int i = 0; i<k; i++)
         crreval +=sortedCombinations[i].evaluation();
      if(k)
         return crreval/double(k);
      else
        {
         Print(__FUNCTION__, " Zero divide error ");
         return 0.0;
        }
     }

   /**
    *  Get the sign of the polynomial variable coefficient
    *
    * param coeff Selected coefficient
    * param isFirstCoeff True if the selected coefficient will be the first in the polynomial representation, otherwise false
    * return String containing the sign of the coefficient
    */
   string            getPolynomialCoeffSign(double coeff, bool isFirstCoeff)
     {
      return ((coeff >= 0) ? ((isFirstCoeff) ? " " : " + ") : " - ");
     }

   /**
    *  Get the rounded value of the polynomial variable coefficient without sign
    *
    * param coeff Selected coefficient
    * param isLastCoeff True if the selected coefficient will be the last one in the polynomial representation, otherwise false
    * return String containing the rounded value of the coefficient without sign
    */
   string            getPolynomialCoeffValue(double coeff, bool isLastCoeff)
     {
      string stringCoeff = StringFormat("%e",MathAbs(coeff));
      return ((stringCoeff != "1" || isLastCoeff) ? stringCoeff : "");
     }

   /**
    *  Train given subset of models and calculate external criterion for them
    *
    * param data Data used for training and evaulating models
    * param criterion Selected external criterion
    * param beginCoeffsVec Iterator indicating the beginning of a subset of models
    * param endCoeffsVec Iterator indicating the end of a subset of models
    * param leftTasks The number of remaining untrained models at the entire level
    * param verbose 1 if the printing detailed infomation about training process is needed, otherwise 0
    */
   bool              polynomialsEvaluation(SplittedData& data,  Criterion& criterion,  CVector &combos, uint beginCoeffsVec,
                                           uint endCoeffsVec)
     {
      vector cmb,ytrain,ytest;
      matrix x1,x2;
      for(uint i = beginCoeffsVec; i<endCoeffsVec; i++)
        {
         cmb = combos[i].combination();
         x1 = xDataForCombination(data.xTrain,cmb);
         x2 = xDataForCombination(data.xTest,cmb);
         ytrain = data.yTrain;
         ytest = data.yTest;
         PairDVXd pd = criterion.calculate(x1,x2,ytrain,ytest);

         if(pd.second.HasNan()>0)
            {
             Print(__FUNCTION__," No solution found for coefficient at ", i, "\n xTrain \n", x1, "\n xTest \n", x2, "\n yTrain \n", ytrain, "\n yTest \n", ytest);
             combos[i].setEvaluation(DBL_MAX);
             combos[i].setBestCoeffs(vector::Ones(3));
            }
         else
            {
             combos[i].setEvaluation(pd.first);
             combos[i].setBestCoeffs(pd.second);
            } 
        }

      return true;
     }

   /**
   *  Determine the need to continue training and prepare the algorithm for the next level
   *
   * param kBest The number of best models based of which new models of the next level will be constructed
   * param pAverage The number of best models based of which the external criterion for each level will be calculated
   * param combinations Trained models of the current level
   * param criterion Selected external criterion
   * param data Data used for training and evaulating models
   * param limit The minimum value by which the external criterion should be improved in order to continue training
   * return True if the algorithm needs to continue training, otherwise fasle
   */
   bool              nextLevelCondition(int kBest, int pAverage, CVector &combinations,
                                        Criterion& criterion, SplittedData& data, double limit)
     {
      MatFunc fun = NULL;
      CVector bestcombinations;
      criterion.getBestCombinations(combinations,bestcombinations,data, fun, kBest);
      currentLevelEvaluation = getMeanCriterionValue(bestcombinations, pAverage);

      if(lastLevelEvaluation - currentLevelEvaluation > limit)
        {
         lastLevelEvaluation = currentLevelEvaluation;
         if(preparations(data,bestcombinations))
           {
            ++level;
            return true;
           }
        }
      removeExtraCombinations();
      return false;

     }

   /**
    *  Fit the algorithm to find the best solution
    *
    * param x Matrix of input data containing predictive variables
    * param y Vector of the taget values for the corresponding x data
    * param criterion Selected external criterion
    * param kBest The number of best models based of which new models of the next level will be constructed
    * param testSize Fraction of the input data that should be used to evaluate models at each level
    * param pAverage The number of best models based of which the external criterion for each level will be calculated
    * param limit The minimum value by which the external criterion should be improved in order to continue training
    * return A pointer to the algorithm object for which the training was performed
    */
   bool              gmdhFit(matrix& x,  vector& y,  Criterion& criterion, int kBest,
                             double testSize, int pAverage, double limit)
     {
      if(x.Rows() != y.Size())
        {
         Print("X rows number and y size must be equal");
         return false;
        }

      level = 1; // reset last training
      inputColsNumber = int(x.Cols());
      lastLevelEvaluation = DBL_MAX;

      SplittedData data = internalSplitData(x, y, testSize, true) ;
      training_complete = false;
      bool goToTheNextLevel;
      CVector evaluationCoeffsVec;
      do
        {
         vector combinations[];
         generateCombinations(int(data.xTrain.Cols() - 1),combinations);
         
         if(combinations.Size()<1)
           {
            Print(__FUNCTION__," Training aborted");
            return training_complete;
           }  

         evaluationCoeffsVec.clear();

         int currLevelEvaluation = 0;
         for(int it = 0; it < int(combinations.Size()); ++it, ++currLevelEvaluation)
           {
            Combination ncomb(combinations[it]);
            evaluationCoeffsVec.push_back(ncomb);
           }

         if(!polynomialsEvaluation(data,criterion,evaluationCoeffsVec,0,uint(currLevelEvaluation)))
           {
            Print(__FUNCTION__," Training aborted");
            return training_complete;
           }

         goToTheNextLevel = nextLevelCondition(kBest, pAverage, evaluationCoeffsVec, criterion, data, limit); // checking the results of the current level for improvement
        }
      while(goToTheNextLevel);

      training_complete = true;

      return true;
     }

   /**
    *  Get new model structures for the new level of training
    *
    * param n_cols The number of existing predictive variables at the current training level
    * return Vector of new model structures
    */
   virtual void      generateCombinations(int n_cols,vector &out[])
     {
      return;
     }


   ///  Removed the saved models that are no longer needed
   virtual void      removeExtraCombinations(void)
     {
      return;
     }

   /**
    *  Prepare data for the next training level
    *
    * param data Data used for training and evaulating models at the current level
    * param _bestCombinations Vector of the k best models of the current level
    * return True if the training process can be continued, otherwise false
    */
   virtual bool      preparations(SplittedData& data, CVector &_bestCombinations)
     {
      return false;
     }

   /**
    *  Get the data constructed according to the model structure from the original data
    *
    * param x Training data at the current level
    * param comb Vector containing the indexes of the x matrix columns that should be used in the model
    * return Constructed data
    */
   virtual matrix    xDataForCombination(matrix& x,  vector& comb)
     {
      return matrix::Zeros(10,10);
     }

   /**
    *  Get the designation of polynomial equation
    *
    * param levelIndex The number of the level counting from 0
    * param combIndex The number of polynomial in the level counting from 0
    * return The designation of polynomial equation
    */
   virtual string    getPolynomialPrefix(int levelIndex, int combIndex)
     {
      return NULL;
     }

   /**
    *  Get the string representation of the polynomial variable
    *
    * param levelIndex The number of the level counting from 0
    * param coeffIndex The number of the coefficient related to the selected variable in the polynomial counting from 0
    * param coeffsNumber The number of coefficients in the polynomial
    * param bestColsIndexes Indexes of the data columns used to construct polynomial of the model
    * return The string representation of the polynomial variable
    */
   virtual string    getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber,
                                           vector& bestColsIndexes)
     {
      return NULL;
     }

   /*
    *  Transform model data to JSON format for further saving
    *
    * return JSON value of model data
    */
   virtual CJAVal    toJSON(void)
     {
      CJAVal json_obj_model;

      json_obj_model["modelName"] = getModelName();
      json_obj_model["inputColsNumber"] = inputColsNumber;
      json_obj_model["bestCombinations"] = CJAVal(jtARRAY,"");


      for(int i = 0; i<bestCombinations.size(); i++)
        {

         CJAVal Array(jtARRAY,"");

         for(int k = 0; k<bestCombinations[i].size(); k++)
           {
            CJAVal collection;
            collection["combination"] = CJAVal(jtARRAY,"");
            collection["bestCoeffs"] = CJAVal(jtARRAY,"");
            vector combination = bestCombinations[i][k].combination();
            vector bestcoeff = bestCombinations[i][k].bestCoeffs();
            for(ulong j=0; j<combination.Size(); j++)
               collection["combination"].Add(int(combination[j]));
            for(ulong j=0; j<bestcoeff.Size(); j++)
               collection["bestCoeffs"].Add(bestcoeff[j],-15);
            Array.Add(collection);
           }

         json_obj_model["bestCombinations"].Add(Array);

        }

      return json_obj_model;

     }

   /**
    *  Set up model from JSON format model data
    *
    * param jsonModel Model data in JSON format
    * return Method exit status
    */
   virtual bool      fromJSON(CJAVal &jsonModel)
     {
      modelName = jsonModel["modelName"].ToStr();
      bestCombinations.clear();
      inputColsNumber = int(jsonModel["inputColsNumber"].ToInt());

      for(int i = 0; i<jsonModel["bestCombinations"].Size(); i++)
        {
         CVector member;
         for(int j = 0; j<jsonModel["bestCombinations"][i].Size(); j++)
           {
            Combination cb;
            vector c(ulong(jsonModel["bestCombinations"][i][j]["combination"].Size()));
            vector cf(ulong(jsonModel["bestCombinations"][i][j]["bestCoeffs"].Size()));
            for(int k = 0; k<jsonModel["bestCombinations"][i][j]["combination"].Size(); k++)
               c[k] = jsonModel["bestCombinations"][i][j]["combination"][k].ToDbl();
            for(int k = 0; k<jsonModel["bestCombinations"][i][j]["bestCoeffs"].Size(); k++)
               cf[k] = jsonModel["bestCombinations"][i][j]["bestCoeffs"][k].ToDbl();
            cb.setBestCoeffs(cf);
            cb.setCombination(c);
            member.push_back(cb);
           }
         bestCombinations.push_back(member);
        }
      return true;
     }



   /**
    *  Compare the number of required and actual columns of the input matrix
    *
    * param x Given matrix of input data
    */
   bool              checkMatrixColsNumber(matrix& x)
     {
      if(ulong(inputColsNumber) != x.Cols())
        {
         Print("Matrix  must have " + string(inputColsNumber) + " columns because there were " + string(inputColsNumber) + " columns in the training  matrix");
         return false;
        }

      return true;
     }
     
     

public:
   ///  Construct a new Gmdh Model object
                     GmdhModel() : level(1), lastLevelEvaluation(0) {}

   /**
   *  Get full class name
   *
   * return String containing the name of the model class
   */
   string            getModelName(void)
     {
      return modelName;
     }
   /**
     *Get number of inputs required for model
     */
    int getNumInputs(void)
     {
      return inputColsNumber;
     }

   /**
    *  Save model data into regular file
    *
    * param path Path to regular file
    */
   bool              save(string file_name)
     {

      CFileTxt modelFile;

      if(modelFile.Open(file_name,FILE_WRITE|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print("failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         CJAVal js=toJSON();
         if(modelFile.WriteString(js.Serialize())==0)
           {
            Print("failed write to ",file_name,". Error -",::GetLastError());
            return false;
           }
        }

      return true;
     }

   /**
    *  Load model data from regular file
    *
    * param path Path to regular file
    */
   bool               load(string file_name)
     {
      training_complete = false;
      CFileTxt modelFile;
      CJAVal js;

      if(modelFile.Open(file_name,FILE_READ|FILE_COMMON,0)==INVALID_HANDLE)
        {
         Print("failed to open file ",file_name," .Error - ",::GetLastError());
         return false;
        }
      else
        {
         if(!js.Deserialize(modelFile.ReadString()))
           {
            Print("failed to read from ",file_name,".Error -",::GetLastError());
            return false;
           }
         training_complete = fromJSON(js);
        }
      return training_complete;
     }
   /**
    *  Divide the input data into 2 parts without shuffling
    *
    * param x Matrix of input data containing predictive variables
    * param y Vector of the taget values for the corresponding x data
    * param testSize Fraction of the input data that should be placed into the second part
    * param addOnesCol True if it is needed to add a column of ones to the x data, otherwise false
    * return SplittedData object containing 4 elements of data: train x, train y, test x, test y
    */
   static SplittedData internalSplitData(matrix& x,  vector& y, double testSize, bool addOnesCol = false)
     {
      SplittedData data;
      ulong testItemsNumber = ulong(round(double(x.Rows()) * testSize));
      matrix Train,Test;
      vector train,test;

      if(addOnesCol)
        {
         Train.Resize(x.Rows() - testItemsNumber, x.Cols() + 1);
         Test.Resize(testItemsNumber, x.Cols() + 1);

         for(ulong i = 0; i<Train.Rows(); i++)
            Train.Row(x.Row(i),i);

         Train.Col(vector::Ones(Train.Rows()),x.Cols());

         for(ulong i = 0; i<Test.Rows(); i++)
            Test.Row(x.Row(Train.Rows()+i),i);

         Test.Col(vector::Ones(Test.Rows()),x.Cols());

        }
      else
        {
         Train.Resize(x.Rows() - testItemsNumber, x.Cols());
         Test.Resize(testItemsNumber, x.Cols());

         for(ulong i = 0; i<Train.Rows(); i++)
            Train.Row(x.Row(i),i);

         for(ulong i = 0; i<Test.Rows(); i++)
            Test.Row(x.Row(Train.Rows()+i),i);
        }

      train.Init(y.Size() - testItemsNumber,slice,y,0,y.Size() - testItemsNumber - 1);
      test.Init(testItemsNumber,slice,y,y.Size() - testItemsNumber);

      data.yTrain = train;
      data.yTest = test;

      data.xTrain = Train;
      data.xTest = Test;

      return data;
     }

   /**
    *  Get long-term forecast for the time series
    *
    * param x One row of the test time series data
    * param lags The number of lags (steps) to make a forecast for
    * return Vector containing long-term forecast
    */
   virtual vector    predict(vector& x, int lags)
     {
      return vector::Zeros(1);
     }

   /**
    *  Get the String representation of the best polynomial
    *
    * return String representation of the best polynomial
    */
   string            getBestPolynomial(void)
     {
      string polynomialStr = "";
      int ind = 0;
      for(int i = 0; i < bestCombinations.size(); ++i)
        {
         for(int j = 0; j < bestCombinations[i].size(); ++j)
           {
            vector bestColsIndexes = bestCombinations[i][j].combination();
            vector bestCoeffs = bestCombinations[i][j].bestCoeffs();
            polynomialStr += getPolynomialPrefix(i, j);
            bool isFirstCoeff = true;
            for(int k = 0; k < int(bestCoeffs.Size()); ++k)
              {
               if(bestCoeffs[k])
                 {
                  polynomialStr += getPolynomialCoeffSign(bestCoeffs[k], isFirstCoeff);
                  string coeffValuelStr = getPolynomialCoeffValue(bestCoeffs[k], (k == (bestCoeffs.Size() - 1)));
                  polynomialStr += coeffValuelStr;
                  if(coeffValuelStr != "" && k != bestCoeffs.Size() - 1)
                     polynomialStr += "*";
                  polynomialStr += getPolynomialVariable(i, k, int(bestCoeffs.Size()), bestColsIndexes);
                  isFirstCoeff = false;
                 }
              }
            if(i < bestCombinations.size() - 1 || j < (bestCombinations[i].size() - 1))
               polynomialStr += "\n";
           }//j
         if(i < bestCombinations.size() - 1 && bestCombinations[i].size() > 1)
            polynomialStr += "\n";
        }//i
      return polynomialStr;
     }

                    ~GmdhModel()
     {
      for(int i = 0; i<bestCombinations.size(); i++)
         bestCombinations[i].clear();

      bestCombinations.clear();
     }
  };


//+------------------------------------------------------------------+

É a classe base da qual outros tipos de GMDH serão derivados. Ela fornece métodos para treinar ou construir um modelo e, subsequentemente, fazer previsões com ele. Os métodos "save" e "load" permitem salvar um modelo e carregá-lo de um arquivo para uso posterior. Os modelos são salvos em formato JSON em um arquivo de texto no diretório comum a todos os terminais MetaTrader.

O último arquivo de cabeçalho, mia.mqh, contém a definição da classe "MIA".

//+------------------------------------------------------------------+
//| Class implementing multilayered iterative algorithm MIA          |
//+------------------------------------------------------------------+
class MIA : public GmdhModel
  {
protected:
   PolynomialType    polynomialType; // Selected polynomial type

   void              generateCombinations(int n_cols,vector &out[])  override
     {
      GmdhModel::nChooseK(n_cols,2,out);
      return;
     }
   /**
   *  Get predictions for the input data
   *
   * param x Test data of the regression task or one-step time series forecast
   * return Vector containing prediction values
   */
   virtual vector    calculatePrediction(vector& x)
     {
      if(x.Size()<ulong(inputColsNumber))
         return vector::Zeros(ulong(inputColsNumber));

      matrix modifiedX(1,x.Size()+ 1);

      modifiedX.Row(x,0);

      modifiedX[0][x.Size()] = 1.0;

      for(int i = 0; i < bestCombinations.size(); ++i)
        {
         matrix xNew(1, ulong(bestCombinations[i].size()) + 1);
         for(int j = 0; j < bestCombinations[i].size(); ++j)
           {
            vector comb = bestCombinations[i][j].combination();
            matrix xx(1,comb.Size());
            for(ulong i = 0; i<xx.Cols(); ++i)
               xx[0][i] = modifiedX[0][ulong(comb[i])];
            matrix ply = getPolynomialX(xx);
            vector c,b;
            c = bestCombinations[i][j].bestCoeffs();
            b = ply.MatMul(c);
            xNew.Col(b,ulong(j));
           }
         vector n  = vector::Ones(xNew.Rows());
         xNew.Col(n,xNew.Cols() - 1);
         modifiedX = xNew;
        }

      return modifiedX.Col(0);

     }

   /**
    *  Construct vector of the new variable values according to the selected polynomial type
    *
    * param x Matrix of input variables values for the selected polynomial type
    * return Construct vector of the new variable values
    */
   matrix            getPolynomialX(matrix& x)
     {
      matrix polyX = x;
      if((polynomialType == linear_cov))
        {
         polyX.Resize(x.Rows(), 4);
         polyX.Col(x.Col(0)*x.Col(1),2);
         polyX.Col(x.Col(2),3);
        }
      else
         if((polynomialType == quadratic))
           {
            polyX.Resize(x.Rows(), 6);
            polyX.Col(x.Col(0)*x.Col(1),2) ;
            polyX.Col(x.Col(0)*x.Col(0),3);
            polyX.Col(x.Col(1)*x.Col(1),4);
            polyX.Col(x.Col(2),5) ;
           }

      return polyX;
     }

   /**
    *  Transform data in the current training level by constructing new variables using selected polynomial type
    *
    * param data Data used to train models at the current level
    * param bestCombinations Vector of the k best models of the current level
    */
   virtual void      transformDataForNextLevel(SplittedData& data,  CVector &bestCombs)
     {
      matrix xTrainNew(data.xTrain.Rows(), ulong(bestCombs.size()) + 1);
      matrix xTestNew(data.xTest.Rows(), ulong(bestCombs.size()) + 1);

      for(int i = 0; i < bestCombs.size(); ++i)
        {
         vector comb = bestCombs[i].combination();

         matrix train(xTrainNew.Rows(),comb.Size()),test(xTrainNew.Rows(),comb.Size());

         for(ulong k = 0; k<comb.Size(); k++)
           {
            train.Col(data.xTrain.Col(ulong(comb[k])),k);
            test.Col(data.xTest.Col(ulong(comb[k])),k);
           }

         matrix polyTest,polyTrain;
         vector bcoeff = bestCombs[i].bestCoeffs();
         polyTest = getPolynomialX(test);
         polyTrain = getPolynomialX(train);

         xTrainNew.Col(polyTrain.MatMul(bcoeff),i);
         xTestNew.Col(polyTest.MatMul(bcoeff),i);
        }

      xTrainNew.Col(vector::Ones(xTrainNew.Rows()),xTrainNew.Cols() - 1);
      xTestNew.Col(vector::Ones(xTestNew.Rows()),xTestNew.Cols() - 1);

      data.xTrain = xTrainNew;
      data.xTest =  xTestNew;
     }

   virtual void      removeExtraCombinations(void) override
     {

      CVector2d realBestCombinations(bestCombinations.size());
      CVector n;
      n.push_back(bestCombinations[level-2][0]);
      realBestCombinations.setAt(realBestCombinations.size() - 1,n);

      vector comb(1);
      for(int i = realBestCombinations.size() - 1; i > 0; --i)
        {
         double usedCombinationsIndexes[],unique[];
         int indexs[];
         int prevsize = 0;
         for(int j = 0; j < realBestCombinations[i].size(); ++j)
           {
            comb = realBestCombinations[i][j].combination();
            ArrayResize(usedCombinationsIndexes,prevsize+int(comb.Size()-1),100);
            for(ulong k = 0; k < comb.Size() - 1; ++k)
               usedCombinationsIndexes[ulong(prevsize)+k] = comb[k];
            prevsize = int(usedCombinationsIndexes.Size());
           }
         MathUnique(usedCombinationsIndexes,unique);
         ArraySort(unique);

         for(uint it = 0; it<unique.Size(); ++it)
            realBestCombinations[i - 1].push_back(bestCombinations[i - 1][int(unique[it])]);

         for(int j = 0; j < realBestCombinations[i].size(); ++j)
           {
            comb = realBestCombinations[i][j].combination();
            for(ulong k = 0; k < comb.Size() - 1; ++k)
               comb[k] = ArrayBsearch(unique,comb[k]);
            comb[comb.Size() - 1] = double(unique.Size());
            realBestCombinations[i][j].setCombination(comb);
           }

         ZeroMemory(usedCombinationsIndexes);
         ZeroMemory(unique);
         ZeroMemory(indexs);
        }

      bestCombinations = realBestCombinations;
     }
   virtual bool      preparations(SplittedData& data, CVector &_bestCombinations) override
     {
      bestCombinations.push_back(_bestCombinations);
      transformDataForNextLevel(data, bestCombinations[level - 1]);
      return true;
     }
   virtual matrix    xDataForCombination(matrix& x,  vector& comb)  override
     {
      matrix xx(x.Rows(),comb.Size());

      for(ulong i = 0; i<xx.Cols(); ++i)
         xx.Col(x.Col(ulong(comb[i])),i);

      return getPolynomialX(xx);
     }

   string            getPolynomialPrefix(int levelIndex, int combIndex)  override
     {
      return ((levelIndex < bestCombinations.size() - 1) ?
              "f" + string(levelIndex + 1) + "_" + string(combIndex + 1) : "y") + " =";
     }
   string            getPolynomialVariable(int levelIndex, int coeffIndex, int coeffsNumber,
                                           vector &bestColsIndexes)  override
     {
      if(levelIndex == 0)
        {
         if(coeffIndex < 2)
            return "x" + string(int(bestColsIndexes[coeffIndex]) + 1);
         else
            if(coeffIndex == 2 && coeffsNumber > 3)
               return "x" + string(int(bestColsIndexes[0]) + 1) + "*x" + string(int(bestColsIndexes[1]) + 1);
            else
               if(coeffIndex < 5 && coeffsNumber > 4)
                  return "x" + string(int(bestColsIndexes[coeffIndex - 3]) + 1) + "^2";
        }
      else
        {
         if(coeffIndex < 2)
            return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[coeffIndex]) + 1);
         else
            if(coeffIndex == 2 && coeffsNumber > 3)
               return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[0]) + 1) +
                      "*f" + string(levelIndex) + "_" + string(int(bestColsIndexes[1]) + 1);
            else
               if(coeffIndex < 5 && coeffsNumber > 4)
                  return "f" + string(levelIndex) + "_" + string(int(bestColsIndexes[coeffIndex - 3]) + 1) + "^2";
        }
      return "";
     }


   CJAVal            toJSON(void)  override
     {
      CJAVal json_obj_model = GmdhModel::toJSON();

      json_obj_model["polynomialType"] = int(polynomialType);
      return json_obj_model;

     }

   bool              fromJSON(CJAVal &jsonModel) override
     {
      bool parsed = GmdhModel::fromJSON(jsonModel);

      if(!parsed)
         return false;

      polynomialType = PolynomialType(jsonModel["polynomialType"].ToInt());

      return true;
     }

public:
   //+------------------------------------------------------------------+
   //| Constructor                                                      |
   //+------------------------------------------------------------------+

                     MIA(void)
     {
      modelName = "MIA";
     }

   //+------------------------------------------------------------------+
   //| model a time series                                              |
   //+------------------------------------------------------------------+

   virtual bool      fit(vector &time_series,int lags,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)
     {

      if(lags < 3)
        {
         Print(__FUNCTION__," lags must be >= 3");
         return false;
        }

      PairMVXd transformed = timeSeriesTransformation(time_series,lags);

      SplittedData splited = splitData(transformed.first,transformed.second,testsize);

      Criterion criter(criterion);

      if(kBest < 3)
        {
         Print(__FUNCTION__," kBest value must be an integer >= 3");
         return false;
        }

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      polynomialType = _polynomialType;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   //+------------------------------------------------------------------+
   //| model a multivariable data set  of inputs and targets            |
   //+------------------------------------------------------------------+

   virtual bool      fit(matrix &vars,vector &targets,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)
     {

      if(vars.Cols() < 3)
        {
         Print(__FUNCTION__," columns in vars must be >= 3");
         return false;
        }

      if(vars.Rows() != targets.Size())
        {
         Print(__FUNCTION__, " vars dimensions donot correspond with targets");
         return false;
        }

      SplittedData splited = splitData(vars,targets,testsize);

      Criterion criter(criterion);

      if(kBest < 3)
        {
         Print(__FUNCTION__," kBest value must be an integer >= 3");
         return false;
        }

      if(validateInputData(testsize, pAverage, limit, kBest))
         return false;

      polynomialType = _polynomialType;

      return GmdhModel::gmdhFit(splited.xTrain, splited.yTrain, criter, kBest, testsize, pAverage, limit);
     }

   virtual vector     predict(vector& x, int lags)  override
     {
      if(lags <= 0)
        {
         Print(__FUNCTION__," lags value must be a positive integer");
         return vector::Zeros(1);
        }

      if(!training_complete)
        {
         Print(__FUNCTION__," model was not successfully trained");
         return vector::Zeros(1);
        }

      vector expandedX = vector::Zeros(x.Size() + ulong(lags));
      for(ulong i = 0; i<x.Size(); i++)
         expandedX[i]=x[i];

      for(int i = 0; i < lags; ++i)
        {
         vector vect(x.Size(),slice,expandedX,ulong(i),x.Size()+ulong(i)-1);
         vector res = calculatePrediction(vect);
         expandedX[x.Size() + i] = res[0];
        }

      vector vect(ulong(lags),slice,expandedX,x.Size());
      return vect;
     }



  };
//+------------------------------------------------------------------+

Ela herda de "GmdhModel" para implementar o algoritmo iterativo multicamadas. "MIA" possui duas sobrecargas de "fit()" que podem ser chamadas para modelar um determinado conjunto de dados. Esses métodos se distinguem por seus primeiros e segundos parâmetros. Quando se deseja modelar uma série temporal usando apenas valores históricos, a "fit()" listada abaixo é usada.

fit(vector &time_series,int lags,double testsize=0.5,PolynomialType _polynomialType=linear_cov,CriterionType criterion=stab,int kBest = 10,int pAverage = 1,double limit = 0.0)

Enquanto o outro é útil ao modelar um conjunto de dados de variáveis dependentes e independentes. Os parâmetros de ambos os métodos são documentados na próxima tabela:

Tipo de dados	Nome do parâmetro	Descrição
vector	time_series	representa uma série temporal contida em um vetor
integer	lags	define o número de valores defasados a serem usados como preditores no modelo
matrix	vars	matriz de dados de entrada contendo variáveis preditivas
vector	targets	vetor dos valores-alvo para os membros correspondentes das linhas de "vars"
CriterionType	criterion	variável de enumeração que especifica o critério externo para o processo de construção do modelo
integer	kBest	define o número dos melhores modelos parciais com base nos quais novas entradas da camada subsequente serão construídas
PolynomialType	_polynomialType	Tipo de polinômio selecionado para ser usado na construção de novas variáveis a partir das existentes durante o treinamento
double	testSize	Fração dos dados de entrada que deve ser usada para avaliar os modelos
int	pAverage	O número dos melhores modelos parciais a serem considerados no cálculo dos critérios de parada
double	limit	O valor mínimo pelo qual o critério externo deve ser melhorado para continuar o treinamento

Uma vez que um modelo tenha sido treinado, ele pode ser usado para fazer previsões, chamando "predict()". O método requer um vetor de entradas e um valor inteiro que especifica o número desejado de previsões. Em caso de execução bem-sucedida, o método retorna um vetor contendo as previsões calculadas. Caso contrário, um vetor de zeros é retornado. Na seção seguinte, analisaremos alguns exemplos simples para ter uma ideia melhor de como usar o código descrito.

Exemplo:

Vamos passar por três exemplos implementados como scripts. Abrangendo como o MIA pode ser aplicado em diferentes cenários. O primeiro trata da construção de um modelo de uma série temporal. Onde um certo número de valores anteriores da série pode ser usado para determinar termos subsequentes. Este exemplo está contido no script MIA_Test.mq5, cujo código é mostrado abaixo.

//+------------------------------------------------------------------+
//|                                                     MIA_Test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>

input int NumLags = 3;
input int NumPredictions = 6;
input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input double DataSplitSize = 0.33;
input int NumBest = 10;
input int pAverge = 1;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---time series we want to model
   vector tms = {1,2,3,4,5,6,7,8,9,10,11,12};
//---
   if(NumPredictions<1)
     {
      Alert("Invalid setting for NumPredictions, has to be larger than 0");
      return;
     }
//---instantiate MIA object
   MIA mia;
//---fit the series according to user defined hyper parameters
   if(!mia.fit(tms,NumLags,DataSplitSize,polyType,critType,NumBest,pAverge,critLimit))
      return;
//---generate filename based on user defined parameter settings
   string modelname = mia.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_"+string(pAverge)+"_"+string(critLimit);
//---save the trained model
   mia.save(modelname+".json");
//---inputs from original series to be used for making predictions
   vector in(ulong(NumLags),slice,tms,tms.Size()-ulong(NumLags));
//---predictions made from the model
   vector out = mia.predict(in,NumPredictions);
//---output result of prediction
   Print(modelname, " predictions ", out);
//---output the polynomial that defines the model
   Print(mia.getBestPolynomial());
  }
//+------------------------------------------------------------------+

Ao executar o script, o usuário pode alterar vários aspectos do modelo. "NumLags" especifica o número de valores anteriores da série para calcular o próximo termo. "NumPredictions" indica o número de previsões a serem feitas além da série especificada. O restante dos parâmetros ajustáveis pelo usuário corresponde aos argumentos passados para o método "fit()". Quando um modelo é construído com sucesso, ele é salvo em um arquivo. E previsões são feitas e exibidas na aba Experts do terminal, junto com o polinômio final que representa o modelo. Os resultados da execução do script com as configurações padrão são mostrados abaixo. O polinômio mostrado representa o modelo matemático considerado o melhor para descrever a série temporal dada. É claramente desnecessariamente complicado, considerando a simplicidade da série. Embora, considerando os resultados da previsão, o modelo ainda capture a tendência geral da série.

PS      0       22:37:31.246    MIA_Test (USDCHF,D1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000004,16.00000000000005,17.0000000000001,18.0000000000001]
OG      0       22:37:31.246    MIA_Test (USDCHF,D1)    y = - 9.340179e-01*x1 + 1.934018e+00*x2 + 3.865363e-16*x1*x2 + 1.065982e+00

Em uma segunda execução do script. NumLags é aumentado para 4. Vamos ver qual efeito isso tem sobre o modelo.

Observe quanto mais complexidade é introduzida no modelo ao adicionar um preditor extra. Bem como o impacto que isso tem nas previsões. O polinômio agora abrange várias linhas, apesar de não haver uma melhoria perceptível nas previsões do modelo.

22:37:42.921    MIA_Test (USDCHF,D1)    MIA_stab_0.33_1_0.0 predictions [13.00000000000001,14.00000000000002,15.00000000000005,16.00000000000007,17.00000000000011,18.00000000000015]
ML      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_1 = - 1.666667e-01*x2 + 1.166667e+00*x4 + 8.797938e-16*x2*x4 + 6.666667e-01
CO      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_2 = - 6.916614e-15*x3 + 1.000000e+00*x4 + 1.006270e-15*x3*x4 + 1.000000e+00
NN      0       22:37:42.921    MIA_Test (USDCHF,D1)    f1_3 = - 5.000000e-01*x1 + 1.500000e+00*x3 + 1.001110e-15*x1*x3 + 1.000000e+00
QR      0       22:37:42.921    MIA_Test (USDCHF,D1)    f2_1 = 5.000000e-01*f1_1 + 5.000000e-01*f1_3 - 5.518760e-16*f1_1*f1_3 - 1.729874e-14
HR      0       22:37:42.921    MIA_Test (USDCHF,D1)    f2_2 = 5.000000e-01*f1_1 + 5.000000e-01*f1_2 - 1.838023e-16*f1_1*f1_2 - 8.624525e-15
JK      0       22:37:42.921    MIA_Test (USDCHF,D1)    y = 5.000000e-01*f2_1 + 5.000000e-01*f2_2 - 2.963544e-16*f2_1*f2_2 - 1.003117e-14

Para o nosso último exemplo, olhamos para um cenário diferente, onde queremos modelar saídas definidas por variáveis independentes. Neste exemplo, estamos tentando ensinar o modelo a somar 3 entradas. O código para este exemplo está em MIA_Multivariable_test.mq5.

//+------------------------------------------------------------------+
//|                                       MIA_miavariable_test.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>

input CriterionType critType = stab;
input PolynomialType polyType = linear_cov;
input double DataSplitSize = 0.33;
input int NumBest = 10;
input int pAverge = 1;
input double critLimit = 0;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---simple independent and dependent data sets we want to model
   matrix independent = {{1,2,3},{3,2,1},{1,4,2},{1,1,3},{5,3,1},{3,1,9}};
   vector dependent = {6,6,7,5,9,13};
//---declare MIA object     
   MIA mia;   
//---train the model based on chosen hyper parameters
   if(!mia.fit(independent,dependent,DataSplitSize,polyType,critType,NumBest,pAverge,critLimit))
      return;
//---construct filename for generated model
   string modelname = mia.getModelName()+"_"+EnumToString(critType)+"_"+string(DataSplitSize)+"_"+string(pAverge)+"_"+string(critLimit)+"_multivars";
//---save the model
   mia.save(modelname+".json");
//---input data to be used as input for making predictions
   matrix unseen = {{1,2,4},{1,5,3},{9,1,3}};
//---make predictions and output to the terminal
  for(ulong row = 0; row<unseen.Rows(); row++)
     {
       vector in = unseen.Row(row);
       Print("inputs ", in , " prediction ", mia.predict(in,1));
     }  
//---output the polynomial that defines the model
   Print(mia.getBestPolynomial()); 
  }
//+------------------------------------------------------------------+

Os preditores estão na matriz "vars". Cada linha corresponde a um alvo no vetor "targets". Como no exemplo anterior, temos a opção de definir vários aspectos dos hiperparâmetros de treinamento do modelo. Os resultados do treinamento com a configuração padrão são muito pobres, conforme mostrado abaixo.

RE      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [1,2,4] prediction [5.999999999999997]
JQ      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [1,5,3] prediction [7.5]
QI      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      inputs [9,1,3] prediction [13.1]
QK      0       22:38:57.445    MIA_Multivariable_test (USDCHF,D1)      y = 1.900000e+00*x1 + 1.450000e+00*x2 - 9.500000e-01*x1*x2 + 3.100000e+00

O modelo pode ser melhorado ajustando os parâmetros de treinamento. Os melhores resultados foram alcançados usando as configurações mostradas abaixo.

Usando essas configurações, o modelo finalmente consegue fazer previsões precisas em um conjunto de variáveis de entrada "não vistas". Mesmo que, assim como no primeiro exemplo, o polinômio gerado seja excessivamente complexo.

DM      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [1,2,4] prediction [6.999999999999998]
JI      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [1,5,3] prediction [8.999999999999998]
CD      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      inputs [9,1,3] prediction [13.00000000000001]
OO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_1 = 1.071429e-01*x1 + 6.428571e-01*x2 + 4.392857e+00
IQ      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_2 = 6.086957e-01*x2 - 8.695652e-02*x3 + 4.826087e+00
PS      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f1_3 = - 1.250000e+00*x1 - 1.500000e+00*x3 + 1.125000e+01
LO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_1 = 1.555556e+00*f1_1 - 6.666667e-01*f1_3 + 6.666667e-01
HN      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_2 = 1.620805e+00*f1_2 - 7.382550e-01*f1_3 + 7.046980e-01
PP      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f2_3 = 3.019608e+00*f1_1 - 2.029412e+00*f1_2 + 5.882353e-02
JM      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f3_1 = 1.000000e+00*f2_1 - 3.731079e-15*f2_3 + 1.155175e-14
NO      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      f3_2 = 8.342665e-01*f2_2 + 1.713326e-01*f2_3 - 3.359462e-02
FD      0       22:44:25.269    MIA_Multivariable_test (USDCHF,D1)      y = 1.000000e+00*f3_1 + 3.122149e-16*f3_2 - 1.899249e-15

Fica claro a partir dos exemplos simples que observamos, que o algoritmo iterativo multicamadas pode ser exagerado para conjuntos de dados elementares. Os polinômios gerados podem se tornar extremamente complicados. Esses modelos correm o risco de superajuste aos dados de treinamento. O algoritmo pode acabar capturando ruído ou outliers nos dados, levando a um desempenho de generalização ruim em amostras não vistas. O desempenho do MIA e dos algoritmos GMDH em geral depende muito da qualidade e das características dos dados de entrada. Dados ruidosos ou incompletos podem afetar negativamente a precisão e a estabilidade do modelo, potencialmente levando a previsões não confiáveis. Por fim, embora o processo de treinamento seja relativamente simples, ainda há algum nível de ajuste de hiperparâmetros necessário para obter os melhores resultados. Não é completamente automatizado.

Para nossa última demonstração, temos um script que carrega um modelo a partir de um arquivo e o utiliza para fazer previsões. Este exemplo é dado em LoadModelFromFile.mq5.

//+------------------------------------------------------------------+
//|                                            LoadModelFromFile.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <GMDH\mia.mqh>
//--- input parameters
input string   JsonFileName="";

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---declaration of MIA instance
    MIA mia;
//---load the model from file  
    if(!mia.load(JsonFileName))
      return;
//---get the number of required inputs for the loaded model     
    int numlags = mia.getNumInputs();
//---generate arbitrary inputs to make a prediction with  
    vector inputs(ulong(numlags),arange,21.0,1.0);
//---make prediction and output results to terminal    
    Print(JsonFileName," input ", inputs," prediction ", mia.predict(inputs,1));
//---output the model's polynomial    
    Print(mia.getBestPolynomial()); 
  }
//+------------------------------------------------------------------+

O gráfico a seguir ilustra como o script funciona e o resultado de uma execução bem-sucedida.

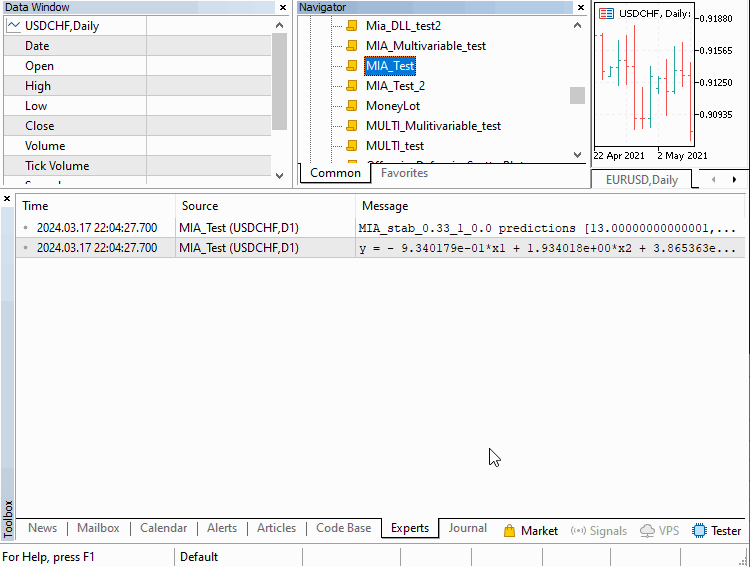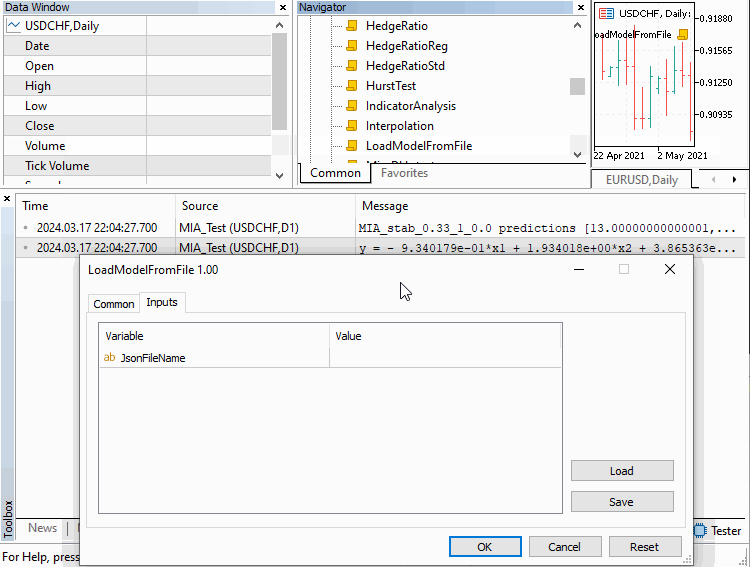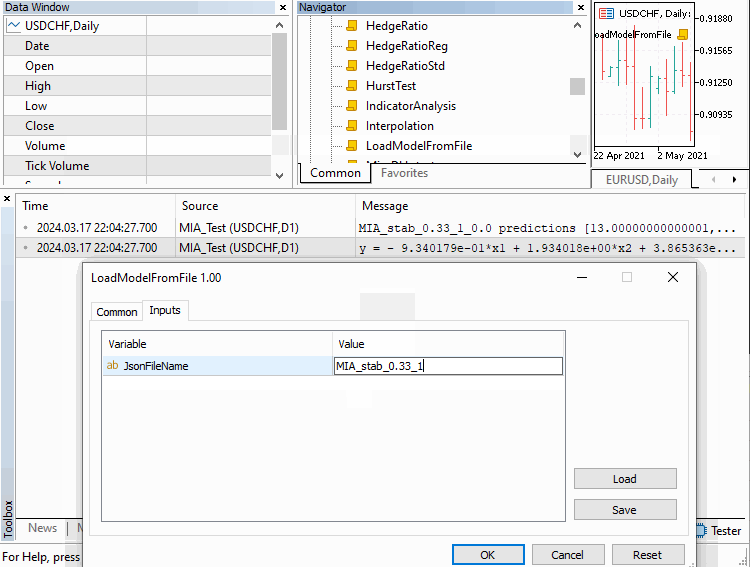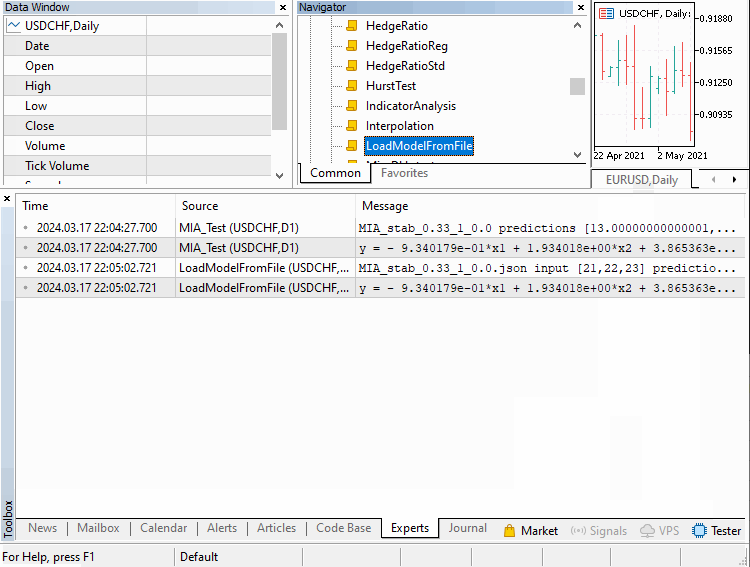
Conclusão

A implementação do algoritmo iterativo multicamadas do GMDH em MQL5 apresenta uma oportunidade para os traders aplicarem o conceito em suas estratégias. Oferecendo uma estrutura dinâmica, este algoritmo capacita os usuários com a capacidade de adaptar e refinar continuamente suas análises de mercado. No entanto, apesar de seu potencial, é essencial que os praticantes naveguem por suas limitações com prudência. Os usuários devem estar cientes das demandas computacionais inerentes aos algoritmos GMDH, especialmente ao lidar com conjuntos de dados extensos ou com alta dimensionalidade. A natureza iterativa do algoritmo exige múltiplos cálculos para determinar a estrutura ideal do modelo, consumindo tempo e recursos significativos no processo.

À luz dessas considerações, os praticantes são incentivados a abordar o uso do algoritmo iterativo multicamadas do GMDH com uma compreensão detalhada de seus pontos fortes e limitações. Embora ofereça uma ferramenta poderosa para a análise dinâmica de mercado, suas complexidades exigem uma navegação cuidadosa para desbloquear seu potencial completo de forma eficaz. Através de uma aplicação cuidadosa e da consideração de suas nuances, os traders podem aproveitar o algoritmo GMDH para enriquecer suas estratégias de negociação e obter insights valiosos dos dados de mercado.

Todo o código MQL5 está anexado ao final do artigo.

Arquivo	Descrição
Mql5\include\VectorMatrixTools.mqh	arquivo de cabeçalho com definições de funções usadas para manipular vetores e matrizes
Mql5\include\JAson.mqh	contém a definição dos tipos personalizados usados para analisar e gerar objetos JSON
Mql5\include\GMDH\gmdh_internal.mqh	arquivo de cabeçalho contendo definições de tipos personalizados usados na biblioteca GMDH
Mql5\include\GMDH\gmdh.mqh	arquivo include com definição da classe base GmdhModel
Mql5\include\GMDH\mia.mqh	contém a classe MIA que implementa o algoritmo iterativo multicamadas
Mql5\script\MIA_Test.mq5	um script que demonstra o uso da classe MIA construindo um modelo de uma série temporal simples
Mql5\script\MIA_Multivarible_test.mq5	outro script mostrando a aplicação da classe MIA para construir um modelo de um conjunto de dados multivariável
Script	script demonstrando como carregar um modelo a partir de um arquivo JSON