Funcionalidades do Assistente MQL5 que você precisa conhecer (Parte 16): Método de componentes principais com autovetores

Introdução

O método de componentes principais (Principal Component Analysis, PCA) foca apenas nos "componentes principais" entre as muitas dimensões de um conjunto de dados, onde as dimensões desse conjunto de dados são reduzidas ignorando as partes "não principais". Talvez o exemplo mais simples de redução dimensional seja uma matriz como a apresentada abaixo:

Se fosse um ponto de dados, poderia ser representado por um único valor:

Assim, esse valor único implica a redução da dimensionalidade de 9 para 1. Nossa ilustração acima reduz a matriz ao seu determinante, sendo um tipo de redução dimensional.

O PCA oferece uma abordagem mais profunda, utilizando autovalores e autovetores. Geralmente, os conjuntos de dados tratados com PCA têm estrutura matricial, e as componentes principais buscadas na matriz representam um vetor coluna (ou linha) que é o mais relevante entre os vetores da matriz, podendo ser suficiente como representante de toda a matriz. Como mencionado na introdução acima, esse vetor, por si só, conterá os componentes principais de toda a matriz, daí o nome PCA. No entanto, a identificação desse vetor não precisa, necessariamente, ocorrer por meio de autovetores e autovalores. Alternativas incluem a decomposição em valores singulares (singular value decomposition, SVD) e o método da potência.

A SVD permite a redução da dimensionalidade ao dividir o conjunto de dados matricial em três matrizes distintas, uma das quais, a matriz Σ, define as direções mais importantes de dispersão nos dados. Essa matriz, também chamada de matriz diagonal, contém valores singulares, que representam a variância em cada direção específica (registrada em outra das três matrizes, geralmente chamada de U). Quanto maior o valor singular, mais significativo é o respectivo direcionamento para explicar a variabilidade dos dados. Isso leva à escolha do vetor coluna de U com o maior valor singular como representativo de toda a matriz, efetivamente reduzindo a matriz a um único vetor.

Ao contrário, o método da potência ajusta iterativamente a estimativa do vetor, aproximando-o ao autovetor dominante. Esse autovetor fixa a direção com as mudanças mais significativas nos dados e representa a dimensão reduzida da matriz original.

No entanto, uma vez que neste artigo focamos em autovetores e autovalores, podemos transformar uma matriz de dimensão n x n em n vetores possíveis de tamanho n, onde a cada um desses vetores é atribuído um autovalor. Esse autovalor determina então a escolha de um autovetor que melhor representa a matriz, com um valor mais alto indicando novamente uma correlação positiva mais significativa ao explicar a variabilidade dos dados.

Qual é, então, o objetivo da redução dimensional em conjuntos de dados? Em resumo, eu diria que é a gestão do ruído branco. No entanto, uma resposta mais substantiva seria a melhoria da visualização, pois dados de alta dimensão são mais difíceis de exibir e representar em formatos comuns, como gráficos de dispersão e outros modos gráficos usuais. Nesse caso, a redução das dimensões (coordenadas do gráfico) para 2 ou 3 pode ser útil. Outro benefício importante é a diminuição dos custos computacionais ao comparar pontos de dados em previsões.

Essa comparação ocorre durante o treinamento de modelos, economizando tempo de treinamento e poder computacional. Isso leva à chamada "maldição da dimensionalidade", onde dados de alta dimensão tendem a produzir resultados precisos durante o teste em uma amostra no treinamento, mas essa eficiência diminui mais rapidamente do que com dados de baixa dimensão durante a validação cruzada. A redução dimensional pode ajudar a enfrentar esse problema. Além disso, a redução da dimensionalidade leva à diminuição do nível de ruído nos conjuntos de dados, o que teoricamente deve melhorar o desempenho. E finalmente, dados de menor dimensão ocupam menos espaço e, portanto, são mais eficientes para gerenciamento, especialmente ao treinar grandes modelos.

PCA e autovetores

Formalmente, os autovetores são definidos pela equação:

Av =λv

onde:

• A é a matriz de transformação
• v é o vetor que deve ser transformado
• λ é o coeficiente de escala aplicado ao vetor.

O princípio central dos autovetores é que para muitas (mas não todas) matrizes quadradas A de dimensão n x n, existem n vetores, cada um com dimensão n, de forma que, ao aplicar a matriz A a qualquer um desses vetores, a direção do produto resultante mantém a mesma direção do vetor original, com a única alteração sendo uma escala proporcional dos valores no vetor original. Na equação acima, essa escala é representada por lambda (λ), corretamente chamado de autovalor. Para cada autovetor, existe um autovalor correspondente.

Nem todas as matrizes produzem o número necessário de autovetores, pois algumas são deformadas; no entanto, para cada vetor obtido, existe um candidato para a redução dimensional da matriz original. A escolha do vetor "vencedor" entre esses candidatos é feita com base no autovalor, onde valores mais altos correspondem a uma melhor cobertura da dispersão do conjunto de dados e uma menor cobertura de seu ruído.

O processo de determinação do autovetor começa com a normalização da matriz do conjunto de dados. Isso pode ser feito de várias formas. Neste artigo, uso a normalização-z. Após a normalização dos dados matriciais, calcula-se o equivalente à matriz de covariância. Cada elemento da matriz reflete a covariância entre quaisquer dois elementos, e a diagonal reflete a covariância de cada elemento consigo mesmo. Além de ser mais eficiente em termos de cálculo para determinar autovetores e autovalores ao usar a matriz de covariância, os valores dos dados obtidos com ela refletem as relações lineares entre os pontos de dados na matriz, dando uma visão clara de como cada ponto de dados se compara aos demais na matriz.

O cálculo da matriz de covariância para tipos de dados matriciais é realizado por funções internas do MQL5, neste caso, a função Cov(). Após obter a matriz de covariância, os autovetores e autovalores podem ser calculados usando a função interna Eig(). Com os autovetores e seus respectivos valores em mãos, transpomos a matriz de autovetores e a multiplicamos pela matriz original de retornos. As linhas da matriz representam os pesos de dispersão de cada portfólio; portanto, o portfólio selecionado dependerá desses pesos. Isso se deve ao fato de que sua direção reflete a máxima dispersão dos dados dentro do conjunto de dados amostral.

Uma ilustração simples para explicar o conceito de fixação da dispersão máxima pode ser criada ao considerar as coordenadas x e y ao longo de uma curva elíptica como conjunto de dados, onde cada ponto de dados possui duas dimensões, x e y. Se traçássemos esse elipse em um gráfico, ele se pareceria com o seguinte:

fonte 

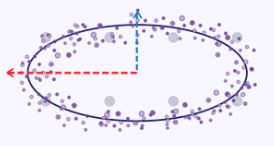
Assim, ao tentar reduzir essas dimensões x e y para um único (ou menor número de) dimensão, como mostrado no gráfico acima, os valores da coordenada x serão mais representativos, pois o elipse tende a se alongar mais ao longo de seu eixo x do que ao longo do eixo y.

No entanto, em geral, é necessário encontrar um equilíbrio entre a redução dimensional e a preservação da informação. Embora a redução da dimensionalidade ofereça vantagens, conforme discutido anteriormente, é importante ter em mente sua interpretabilidade e simplicidade de explicação.

Implementação com MQL5

Um sistema de negociação que utiliza PCA com autovetores normalmente faz isso por meio da seleção otimizada de um portfólio a partir de um ou mais conjuntos de diferentes iterações. Para ilustrar isso, podemos tomar a matriz mencionada na introdução acima como uma composição de vetores, onde cada vetor representa o retorno de um dólar investido em cada ativo sob três diferentes regimes de alocação. A distribuição real do peso de cada vetor (portfólio) torna-se importante apenas após a escolha do autovetor, e a alocação de ativos que deve ser adotada de acordo com esse vetor é então necessária para investimentos futuros.

Se nossos ativos forem SPY,TLT e PDBC, sua distribuição estimada, baseada no retorno de 5 anos de cada um desses ETFs, será:

Assim, o PCA com autovetores nos ajudará a escolher o portfólio ideal (alocação de ativos) entre essas 3 opções com base em seu desempenho nos últimos 5 anos. Listando os passos descritos acima, o primeiro que sempre precisamos realizar é a normalização do conjunto de dados, e, como mencionado, usamos a normalização-z para isso. O código-fonte está abaixo:

//+------------------------------------------------------------------+
//| Z-Normalization                                                  |
//+------------------------------------------------------------------+
matrix ZNorm(matrix &M)
{  matrix _z;
   _z.Init(M.Rows(), M.Cols());
   _z.Copy(M);
   if(M.Rows() > 0 && M.Cols() > 0)
   {  double _std_min = (M.Max() - M.Min()) / (M.Rows() * M.Cols());
      if(_std_min > 0.0)
      {  double _mean = M.Mean();
         double _std = fmax(_std_min, M.Std());
         for(ulong i = 0; i < M.Rows(); i++)
         {  for(ulong ii = 0; ii < M.Cols(); ii++)
            {  _z[i][ii] = (M[i][ii] - _mean) / _std;
            }
         }
      }
   }
   return(_z);
}

Após normalizarmos a matriz de retornos, calculamos a matriz de covariância daquilo que foi normalizado. O tipo de dados interno do MQL5 para matrizes pode fazer isso para nós com uma única linha de código:

   matrix _z = ZNorm(_m);
   matrix _cov_col = _z.Cov(false);

Com as relações de covariância de cada ponto de dados na matriz em mãos, podemos calcular os autovetores e autovalores. Esse cálculo também ocupa apenas uma linha:

   matrix _e_vectors;
   vector _e_values;
   _cov_col.Eig(_e_vectors, _e_values);

A saída da função mencionada acima é dupla. Nosso principal interesse está nos autovetores, retornados em forma de matriz. Essa matriz, uma vez transposta e multiplicada pela matriz original de retornos, nos dá o que procuramos — a matriz de projeção P. Essa é uma matriz com linhas para cada um dos portfólios possíveis, onde a coluna em cada linha representa o coeficiente de peso para cada um dos três autovetores gerados. Por exemplo, na primeira linha, o maior valor está na primeira coluna. Isso significa que a maioria da dispersão de retorno deste portfólio é explicada pelo primeiro autovetor. Se olharmos para o autovalor desse vetor, veremos que ele é o maior dos três. Isso indica, portanto, que entre todos os três portfólios, o primeiro portfólio é o responsável pela maioria das principais tendências (ou padrões) representadas na matriz de dados.

Em nosso caso, todos os portfólios geraram retorno positivo, se somarmos seus valores por colunas, uma vez que cada coluna representa um portfólio. A única perda ocorre quando se investe no ETF de commodities PDBC, independentemente da distribuição. Isso significa que, se alguém deseja "perpetuar" esse retorno com hedge, diversificado ou com uma boa beta, deve aderir ao portfólio 1. Novamente, a tendência geral da matriz de dados de retornos é um retorno positivo para ações e commodities e um retorno negativo para títulos. Assim, o PCA com autovetores pode classificar o portfólio entre aqueles que provavelmente continuarão essa tendência, como o portfólio 1, ou até mesmo fazer o oposto, que em nosso caso seria o portfólio 3, pois na matriz de projeção o valor máximo na 3ª linha está na coluna 3, e o 3º autovetor teve o menor valor.

É interessante notar que este portfólio não possui o maior retorno, e o processo em si não o seleciona como tal. Tudo o que ele faz é fornecer estimativas indicativas para a manutenção do status quo. À primeira vista, pode parecer um método desnecessariamente complexo para uma escolha que poderia ser feita facilmente ao analisar visualmente, mas, à medida que os dados de retorno ou as matrizes analisadas aumentam com mais linhas e colunas (o PCA com autovetores exige matrizes quadradas), esse processo começa a mostrar seu valor.

Para demonstrar o PCA em uma classe de sinais, estamos limitados ao teste de apenas um símbolo em um único período, o que significa que os conceitos de seleção de portfólio acima mencionados não são aplicáveis diretamente. Existem alternativas para contornar essas limitações, e, talvez, possamos abordá-las em um artigo futuro, mas, por agora, vamos trabalhar dentro dessas restrições.

Analisaremos as variações de preço para cada dia da semana de um único símbolo em um período diário. Como a semana tem 5 dias úteis, nossa matriz terá 5 colunas, e para obter as 5 linhas necessárias para a análise de autovetores no PCA, consideraremos 5 tipos de preços diferentes, a saber: abertura (Open), máxima (High), mínima (Low), fechamento (Close) e típica (Typical). A determinação dos autovetores e autovalores será feita seguindo os passos mencionados anteriormente.

O mesmo se aplica para a obtenção da matriz de projeção, e, uma vez que a tenhamos, poderemos identificar facilmente o dia da semana e o tipo de preço aplicado que refletem a maior dispersão. Seguindo o código de script abaixo:

   matrix _t = _e_vectors.Transpose();
   matrix _p = _m * _t;
   //Print(" projection: \n", _p);
   vector _max_row = _p.Max(0);
   vector _max_col = _p.Max(1);
   double _days[];
   _max_row.Swap(_days);
   PrintFormat(" best trade day is: %s", EnumToString(ENUM_DAY_OF_WEEK(ArrayMaximum(_days)+1)));
   ENUM_APPLIED_PRICE _price[__SIZE];
   _price[0] = PRICE_OPEN;
   _price[1] = PRICE_WEIGHTED;
   _price[2] = PRICE_MEDIAN;
   _price[3] = PRICE_CLOSE;
   _price[4] = PRICE_TYPICAL;
   double _prices[];
   _max_col.Swap(_prices);
   PrintFormat(" best applied price is: %s", EnumToString(_price[ArrayMaximum(_prices)]));
   PrintFormat(" worst trade day is: %s", EnumToString(ENUM_DAY_OF_WEEK(ArrayMinimum(_days)+1)));
   PrintFormat(" worst applied price is: %s", EnumToString(_price[ArrayMinimum(_prices)]));

As mensagens no log são apresentadas na seção "Teste de Estratégia e Resultados".

Assim, a partir dos logs acima, vemos que a maioria das variações de preço do símbolo ao qual o script está vinculado (EURJPY) ocorre nas quintas-feiras nos preços de fechamento. O que isso significa? Significa que, se alguém considera interessante a tendência geral e o comportamento de preços do EURJPY e deseja seguir uma estratégia semelhante no futuro, é recomendável concentrar suas operações nas quintas-feiras e utilizar a série de preços de fechamento. Suponha que o EURJPY faça parte de uma posição estabelecida no portfólio de alguém e, no futuro, a exposição ao EURJPY diminua. Como a matriz de posições pode ajudar? Os "piores" dias de negociação e séries de preços podem ser usados para determinar quando e como encerrar posições em EURJPY.

Assim, nossa matriz de posições recomenda dias de negociação e séries de preços; vamos, portanto, utilizar uma classe de sinais simples, descrita abaixo, que leva esses parâmetros em consideração.

   int _buffer_size = CopyRates(Symbol(), Period(), __start, __stop, _rates);
   PrintFormat(__FUNCSIG__+" buffered: %i",_buffer_size);
   if(_buffer_size >= 1)
   {  for(int i = 1; i < _buffer_size - 1; i++)
      {  TimeToStruct(_rates[i].time,_datetime);
         int _iii = int(_datetime.day_of_week)-1;
         if(_datetime.day_of_week == SUNDAY || _datetime.day_of_week == SATURDAY)
         {  _iii = 0;
         }
         for(int ii = 0; ii < __SIZE; ii++)
         {  
                ...

                ...
         }
      }
   }

Teste da estratégia e resultados

Para realizar um teste histórico com o EA criado no Assistente MQL5, primeiro precisamos executar o script no gráfico e período do símbolo que vamos testar. Em nosso exemplo, usamos EURUSD no H4. Quando executamos o script no gráfico, ele recomenda sexta-feira e o preço ponderado como os parâmetros "ideais" ou que melhor definem a dispersão para EURUSD no H4. As mensagens no log são apresentadas abaixo:

2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      best trade day is: FRIDAY
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      best applied price is: PRICE_WEIGHTED
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      worst trade day is: TUESDAY
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      worst applied price is: PRICE_OPEN

Nosso script também possui dois parâmetros de entrada que definem o período analisado: a hora de início e a hora de término, ambas variáveis do tipo datetime. Definimos essas variáveis como 2022.01.01 e 2023.01.01 para testar inicialmente nosso EA nesse intervalo e, em seguida, realizar uma validação cruzada com as mesmas configurações para o período de 2023.01.01 a 2024.01.01. O script recomenda sexta-feira e o preço ponderado como as melhores variáveis para definir a dispersão. Como usar essa informação no desenvolvimento da classe de sinal? Como sempre, temos algumas opções, mas vamos implementar um indicador simples de cruzamento de preço com uma média móvel. Utilizando a média móvel do preço recomendado e executando operações apenas no dia da semana sugerido, validaremos a lógica do nosso script. Assim, o código para nossa classe de sinal será bem direto:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalPCA::LongCondition(void)
{  int _result = 0;
   m_MA.Refresh(-1);
   m_close.Refresh(-1);
   m_time.Refresh(-1);
//
   if(m_MA.Main(StartIndex()+1) > m_close.GetData(StartIndex()+1) && m_MA.Main(StartIndex()) < m_close.GetData(StartIndex()))
   {  _result = 100;
      //PrintFormat(__FUNCSIG__);
   }
   if(m_pca)
   {  TimeToStruct(m_time.GetData(StartIndex()),__D);
      if(__D.day_of_week != m_day)
      {  _result = 0;
      }
   }
//
   return(_result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalPCA::ShortCondition(void)
{  int _result = 0;
   m_MA.Refresh(-1);
   m_close.Refresh(-1);
//
   if(m_MA.Main(StartIndex()+1) < m_close.GetData(StartIndex()+1) && m_MA.Main(StartIndex()) > m_close.GetData(StartIndex()))
   {  _result = 100;
      //PrintFormat(__FUNCSIG__);
   }
   if(m_pca)
   {  TimeToStruct(m_time.GetData(StartIndex()),__D);
      if(__D.day_of_week != m_day)
      {  _result = 0;
      }
   }
//
   return(_result);
}

Como de costume, não utilizamos níveis de preço para take-profit ou stop-loss, optando estritamente por ordens limitadas. Isso significa que, após a abertura de uma posição pelo EA, ela é encerrada apenas com uma reversão. Pode ser uma abordagem de alto risco, mas é suficiente para nossos objetivos. Se realizarmos um teste histórico no primeiro período, obteremos o seguinte relatório e curva de capital:

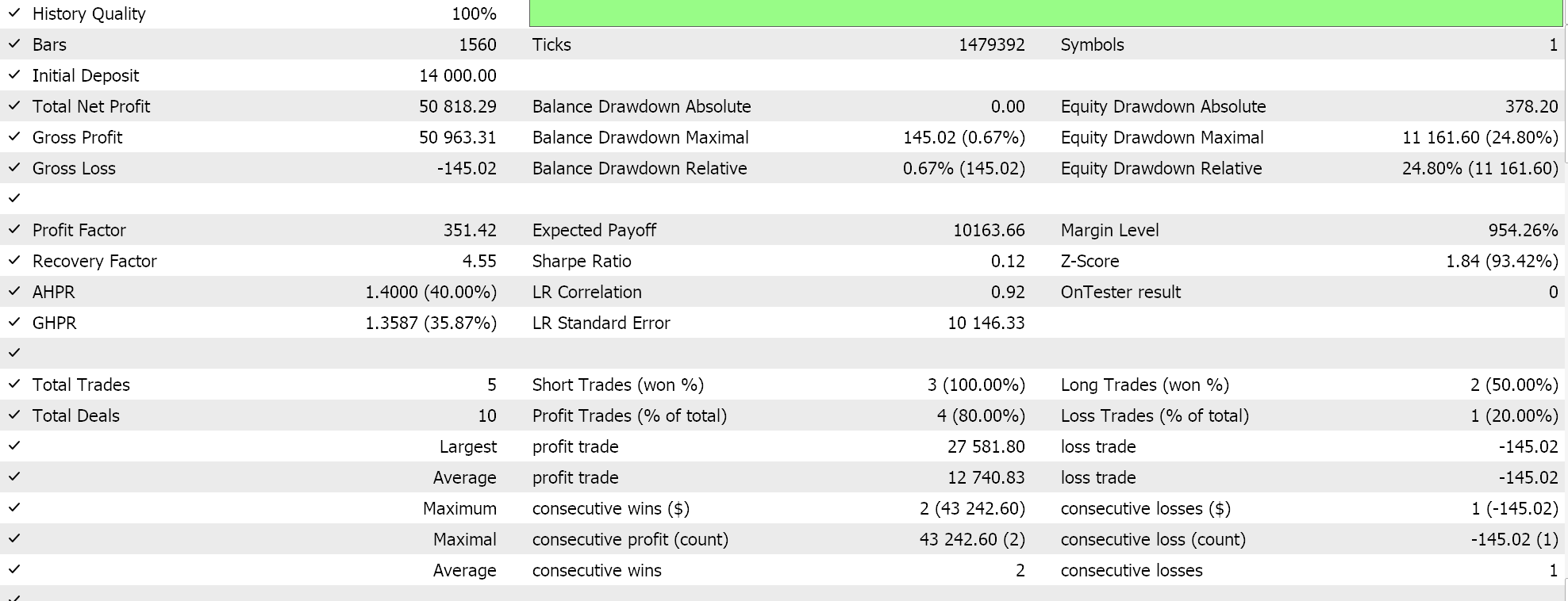
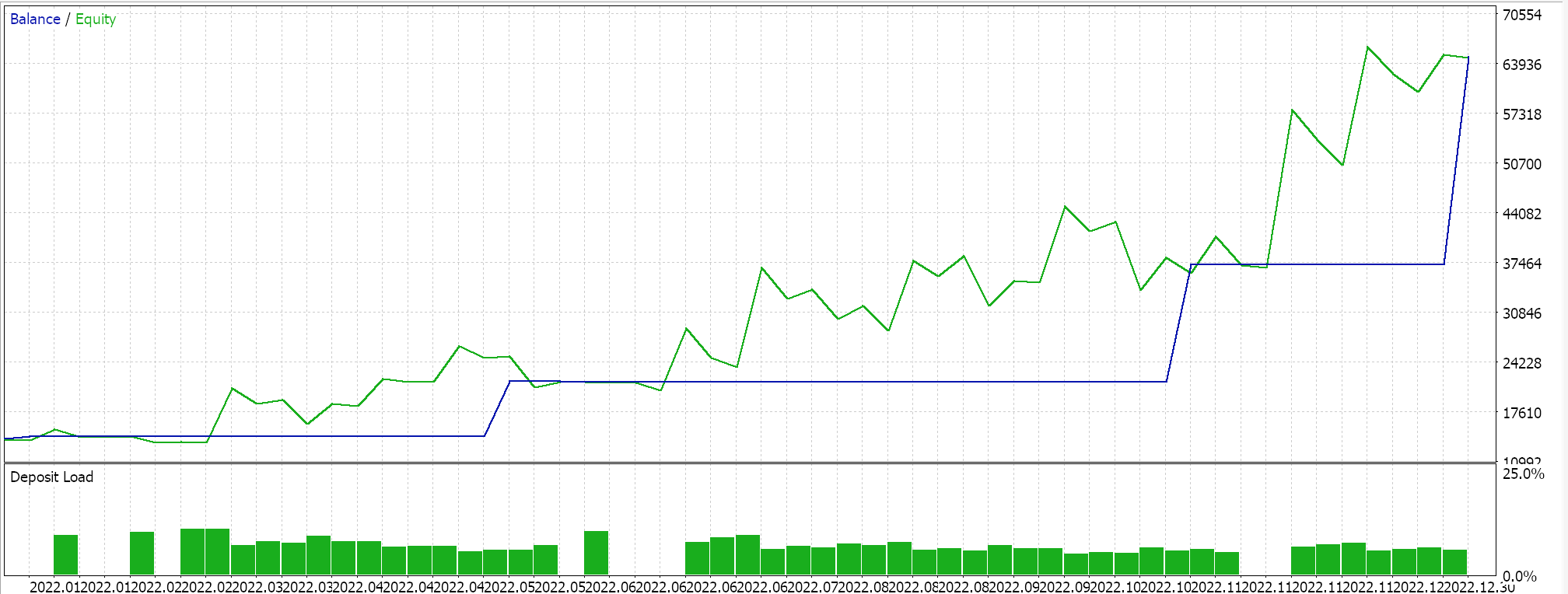
Os resultados acima se referem ao período de 01.01.2022 a 01.01.2023. Se tentarmos realizar um teste com as mesmas configurações por um período mais extenso, fora do intervalo de análise do script, de 2022.01.01 a 2024.01.01, os resultados serão os seguintes:

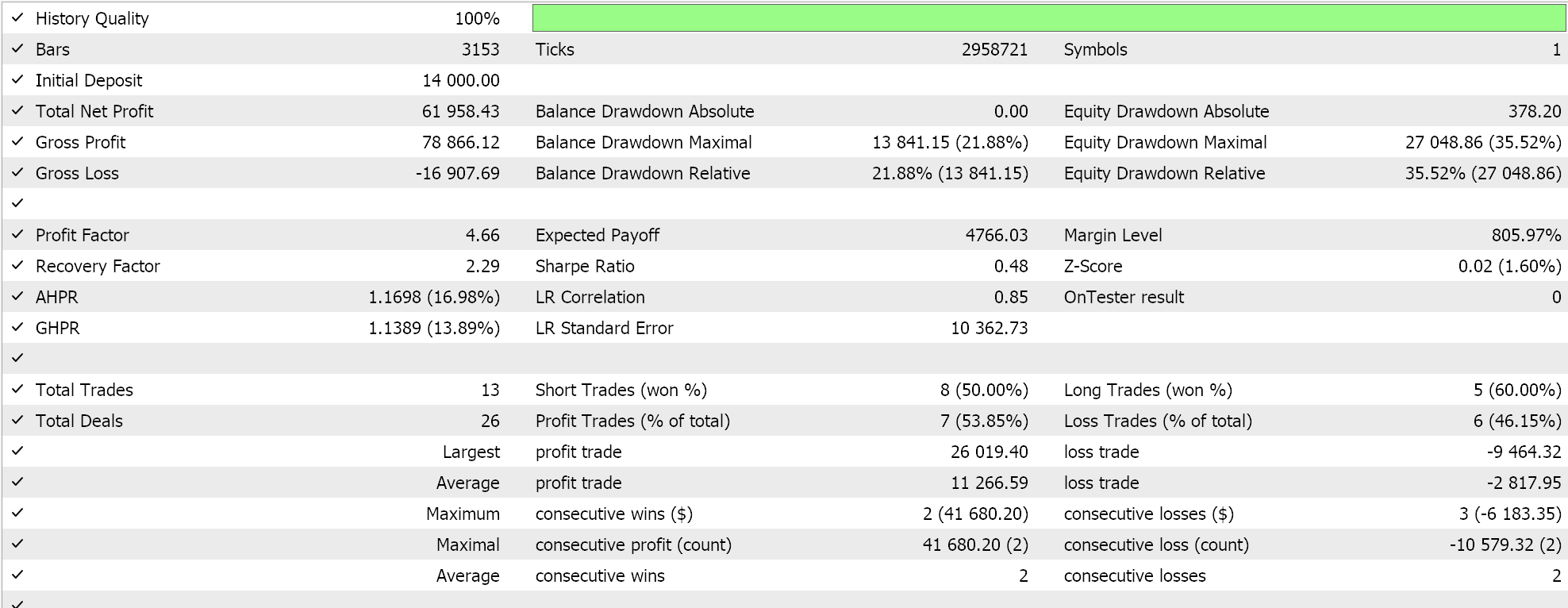
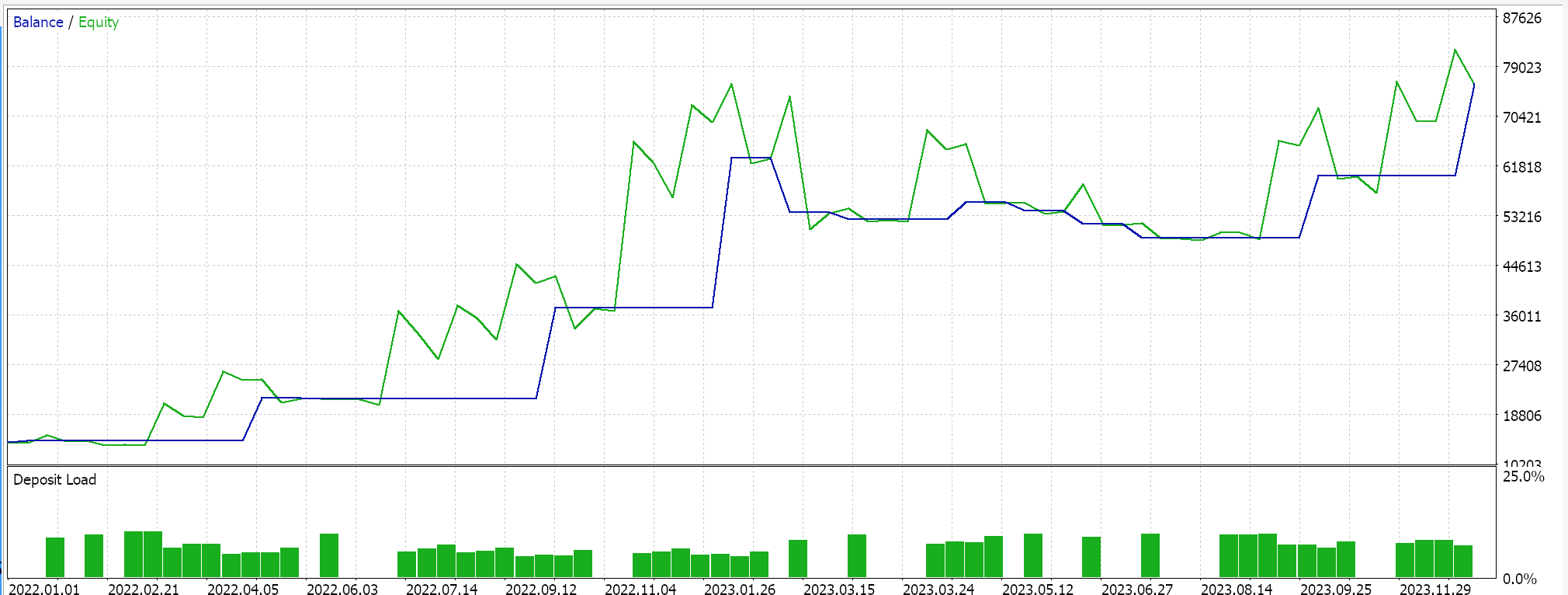
Nosso sinal possui diversas limitações, e o número de operações não é muito alto, o que coloca em dúvida a eficácia dos testes. Ainda assim, períodos de teste com vários anos nem sempre são confiáveis. Como controle, além da validação cruzada mencionada, também podemos realizar testes com diferentes preços aplicados em qualquer dia da semana usando as mesmas configurações do EA. Isso nos fornece os seguintes resultados:

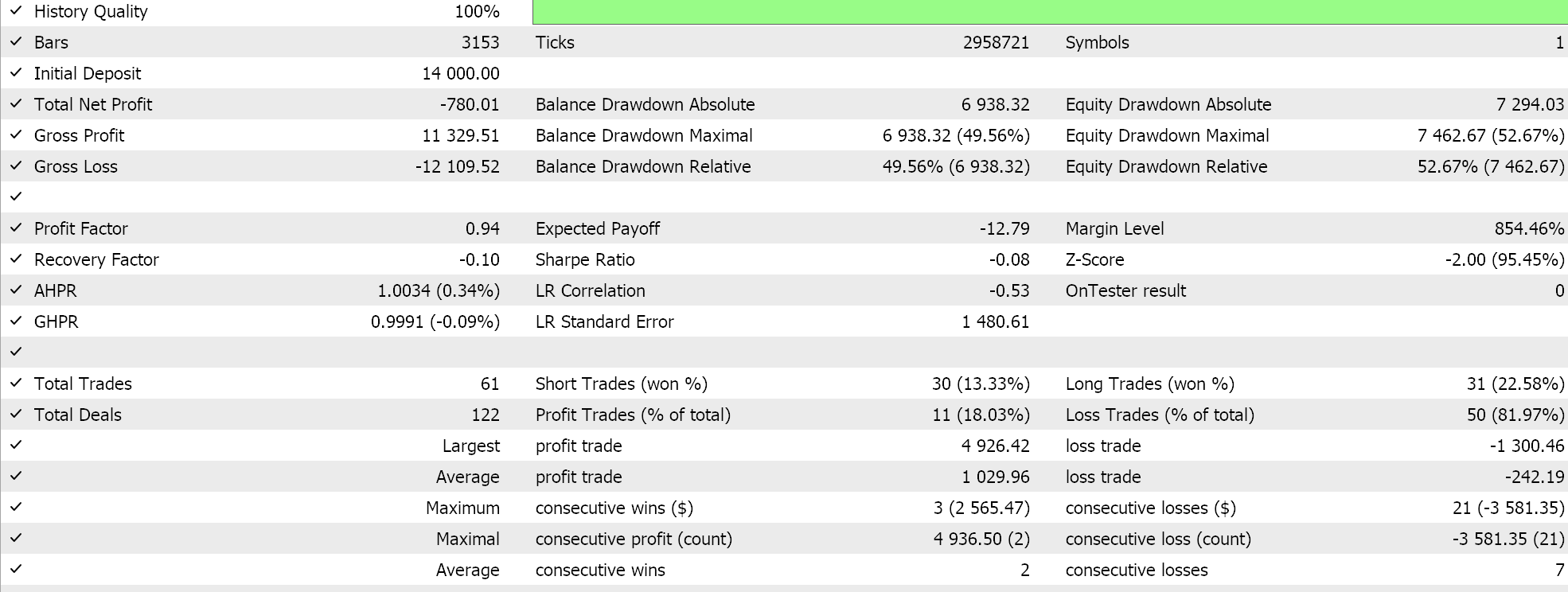
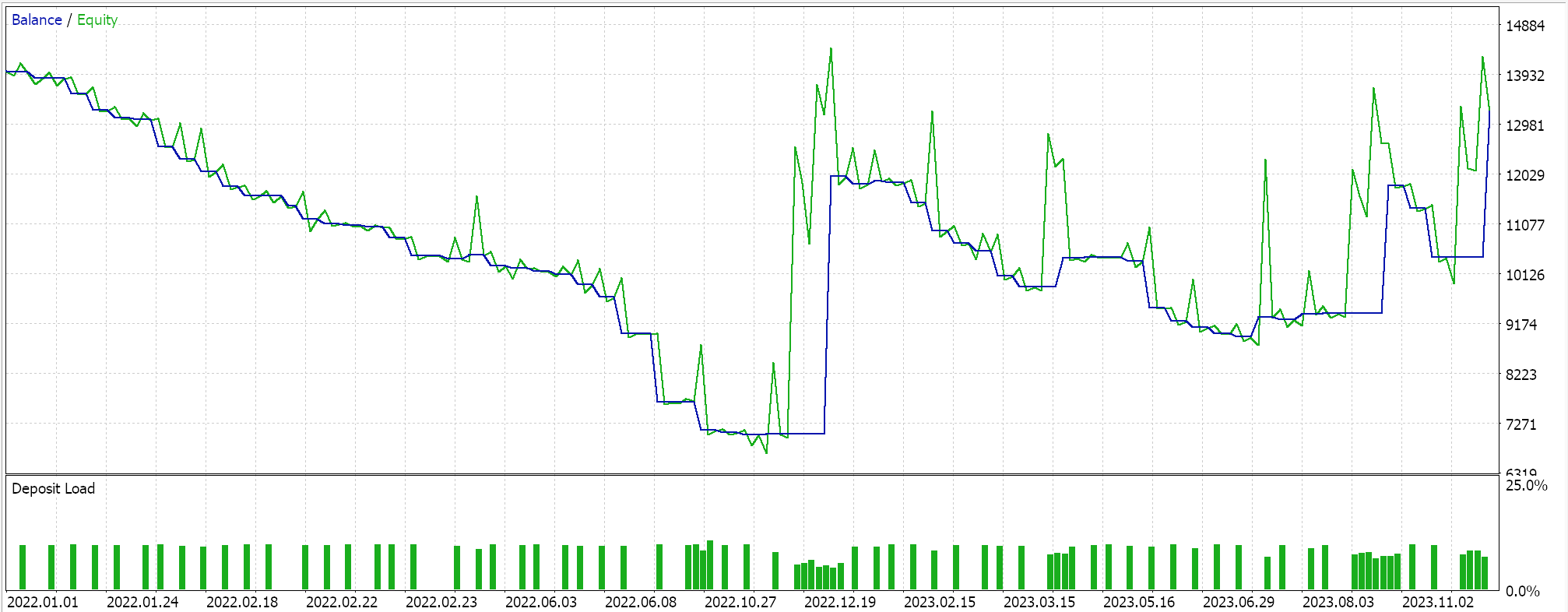
A performance geral claramente sofre quando saímos dos parâmetros recomendados pelo script PCA, mas por quê? Por que negociar apenas dentro dos parâmetros que definem a dispersão nos dá melhores resultados do que configurações ilimitadas? Esse é um questionamento relevante, pois a influência na dispersão não implica necessariamente uma maior lucratividade, já que a tendência geral do conjunto de dados estudado pode ser distorcida. Por isso, a escolha das configurações que melhor definem a dispersão deve ser feita apenas se as tendências básicas e gerais no conjunto de dados estudado estiverem alinhadas com os objetivos do trader.

Se analisarmos o gráfico do EURUSD, veremos que, durante o período de análise PCA de 2022.01.01 a 2023.01.01, o par exibiu principalmente uma tendência de queda, revertendo por um curto período em outubro. No entanto, no período de validação cruzada em 2023, o par oscilou bastante, sem formar grandes tendências como em 2022. Isso sugere que, ao realizar uma análise em períodos de tendência principal, é possível captar melhor os parâmetros de dispersão que definem a tendência, podendo até ser útil em situações de reversão acentuada, como ficou evidente em 2023.

Considerações finais

Vimos que o PCA é essencialmente uma ferramenta analítica focada em reduzir a dimensionalidade de conjuntos de dados, identificando as dimensões (ou componentes) que mais influenciam suas tendências básicas. Existem várias ferramentas disponíveis para redução dimensional, e o PCA pode parecer primitivo à primeira vista, mas exige análise e interpretação cuidadosas, pois está sempre fundamentado nas tendências básicas do conjunto de dados estudado.

No exemplo abordado nos testes, as tendências básicas do símbolo estudado eram baixistas, o que fez com que, na validação cruzada, a maioria das operações realizadas fora da amostra fossem posições vendidas. Se, hipoteticamente, estivéssemos analisando um mercado altista para o símbolo em questão, qualquer estratégia de negociação baseada nas configurações recomendadas pelo PCA deveria tirar proveito do ambiente altista. Da mesma forma, faria sentido escolher configurações que menos explicam a dispersão se o objetivo for lucrar em um mercado baixista, já que mercados altistas e baixistas são polos opostos. Além disso, o PCA gera mais de um conjunto de configurações, cada qual com um valor ponderado (ou autovalor), sugerindo a possibilidade de adotar mais de uma configuração se seus valores ponderados ultrapassarem um certo limiar. Esse ponto não foi explorado neste artigo, e o leitor pode aprofundar o tema usando o código fonte anexado abaixo. A utilização desse código no Assistente MQL5 para montar um EA pode ser visualizada aqui.

Uma abordagem que permite incorporar mais configurações do PCA no script de análise e no EA é normalizar os autovalores para que todos sejam positivos e fiquem no intervalo de 0,0 a 1,0. Com isso, você pode estabelecer limiares de seleção para os autovetores que serão escolhidos em cada análise. Por exemplo, se a análise PCA de uma matriz 3 x 3 fornece inicialmente os valores 2,94, 1,92 e 0,14, normalizamos esses valores para o intervalo de 0–1 da seguinte forma: 0,588, 0,384 e 0,028. Ao usar os valores normalizados, um limiar de, por exemplo, 0,3 pode permitir uma seleção imparcial dos autovetores em múltiplas análises. Análises repetidas com outros conjuntos de dados e até tamanhos de matrizes diferentes podem ainda assim ter autovetores selecionados de maneira semelhante. Para o script, isso significa iterar sobre os autovalores e adicionar duas propriedades cruzadas para cada valor correspondente na lista ou matriz de saída. Esse array pode ser uma estrutura que registra as propriedades x e y na matriz do conjunto de dados. No EA, será necessário introduzir as propriedades do filtro em forma de valores de texto separados por vírgulas, para maior escalabilidade. Isso exigirá a análise da string e a extração das propriedades para um formato padrão compreensível pelo EA.