Discussão do artigo "Funcionalidades do Assistente MQL5 que você precisa conhecer (Parte 16): Método de componentes principais com autovetores"
É muito útil saber disso, obrigado.
No entanto, para a matriz "_m", por que você não itera o índice "_rates" até "i<=_buffer_size"?
Sebastien Nicolas Paul Boulenc #:
É muito útil saber disso, obrigado.
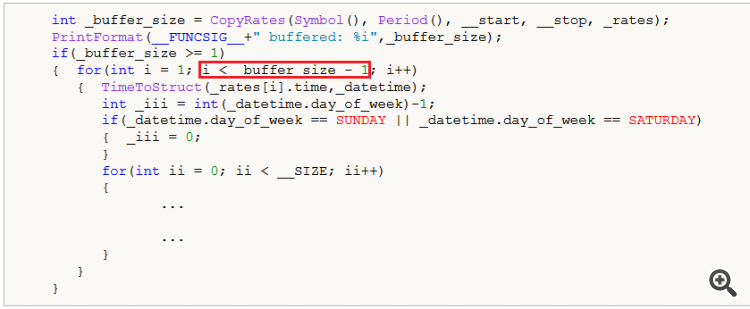
No entanto, para a matriz "_m", por que você não itera o índice "_rates" até "i<=_buffer_size"?
if(_buffer_size >= 2) { for(int i = 1; i <= _buffer_size - 1; i++) { ... } }
Deveria ter sido isso, mas como o tamanho do buffer é grande, acho que copiamos dados de um ano, o efeito desse erro foi mínimo. Obrigado pela observação.
Você está perdendo oportunidades de negociação:
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Registro
Login
Você concorda com a política do site e com os termos de uso
Se você não tem uma conta, por favor registre-se
Novo artigo Funcionalidades do Assistente MQL5 que você precisa conhecer (Parte 16): Método de componentes principais com autovetores foi publicado:
Este artigo discute o método de componentes principais, um método de redução da dimensionalidade ao analisar dados, e como ele pode ser implementado usando autovalores e vetores. Como sempre, vamos tentar desenvolver um protótipo da classe de sinais para EA que pode ser usado no Assistente MQL5.
A SVD permite a redução da dimensionalidade ao dividir o conjunto de dados matricial em três matrizes distintas, uma das quais, a matriz Σ, define as direções mais importantes de dispersão nos dados. Essa matriz, também chamada de matriz diagonal, contém valores singulares, que representam a variância em cada direção específica (registrada em outra das três matrizes, geralmente chamada de U). Quanto maior o valor singular, mais significativo é o respectivo direcionamento para explicar a variabilidade dos dados. Isso leva à escolha do vetor coluna de U com o maior valor singular como representativo de toda a matriz, efetivamente reduzindo a matriz a um único vetor.
Ao contrário, o método da potência ajusta iterativamente a estimativa do vetor, aproximando-o ao autovetor dominante. Esse autovetor fixa a direção com as mudanças mais significativas nos dados e representa a dimensão reduzida da matriz original.
No entanto, uma vez que neste artigo focamos em autovetores e autovalores, podemos transformar uma matriz de dimensão n x n em n vetores possíveis de tamanho n, onde a cada um desses vetores é atribuído um autovalor. Esse autovalor determina então a escolha de um autovetor que melhor representa a matriz, com um valor mais alto indicando novamente uma correlação positiva mais significativa ao explicar a variabilidade dos dados.
Autor: Stephen Njuki