MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 16): Hauptkomponentenanalyse mit Eigenvektoren

Einführung

Die Hauptkomponentenanalyse (Principal Component Analysis, PCA) konzentriert sich nur auf die „Hauptkomponenten“ unter den vielen Dimensionen eines Datensatzes, sodass man die Dimensionen dieses Datensatzes reduziert, indem man die „Nicht-Hauptkomponenten“ ignoriert. Das vielleicht einfachste Beispiel für eine Dimensionsreduzierung könnte eine Matrix wie die unten dargestellte sein:

Wenn es sich um einen Datenpunkt handelt, kann er als Einzelwert wiedergegeben werden:

Dieser eine Wert bedeutet also eine Verringerung der Dimensionen von 9 auf 1. Die obige Abbildung reduziert eine Matrix auf ihre Determinante, was in etwa einer Dimensionalitätsreduktion entspricht.

Die PCA-Methode mit Eigenwerten und Eigenvektoren verfolgt jedoch einen etwas tieferen Ansatz. Typischerweise liegen Datensätze, die im Rahmen der PCA verarbeitet werden, in einem Matrixformat vor, und die Hauptkomponenten, die in einer Matrix gesucht werden, ist eine einzelne Vektorspalte (oder -zeile), die unter den anderen Matrixvektoren am signifikantesten ist und als Repräsentant der gesamten Matrix ausreicht. Wie bereits in der Einleitung erwähnt, würde dieser Vektor allein die Hauptkomponenten der gesamten Matrix enthalten, daher der Name PCA. Die Identifizierung dieses Vektors muss jedoch nicht notwendigerweise durch Eigenvektoren und -werte erfolgen, da Singulärwertzerlegung (Singular Value Decomposition, SVD) und die Potenzmethode sind andere Alternativen.

SVD kann die Dimensionalität reduzieren, indem ein Matrixdatensatz in drei separate Matrizen aufgeteilt wird, wobei eine dieser drei, die Σ-Matrix, die wichtigsten Varianzrichtungen in den Daten identifiziert. Diese Matrix, die auch als Diagonalmatrix bezeichnet wird, enthält die Singulärwerte, die die Größen der Varianz entlang jeder vorher festgelegten Richtung darstellen (die in einer anderen der 3 Matrizen, die oft als U bezeichnet wird, aufgezeichnet werden). Je größer der Singulärwert ist, desto signifikanter ist die entsprechende Richtung bei der Erklärung der Variabilität der Daten. Dies führt dazu, dass die U-Spalte mit dem höchsten Singulärwert als repräsentativ für die gesamte Matrix ausgewählt wird, was zu einer Reduzierung der Dimensionen führt. Von einer Matrix zu einem einzelnen Vektor.

Umgekehrt verfeinert die Potenzmethode iterativ eine Vektorschätzung, um gegen den dominanten Eigenvektor zu konvergieren. Dieser Eigenvektor erfasst die Richtung mit der größten Variation in den Daten und entspricht einer reduzierten Dimension der ursprünglichen Matrix.

Mit Eigenvektoren und -werten, auf die wir uns in diesem Artikel konzentrieren, können wir jedoch eine n x n-Matrix in n mögliche n große Vektoren zerlegen, wobei jedem dieser Vektoren ein Eigenwert zugewiesen wird. Dieser Eigenwert dient dann als Grundlage für die Auswahl des einen Eigenvektors, der die Matrix am besten repräsentiert, wobei wiederum ein höherer Wert eine höhere positive Korrelation bei der Erklärung der Datenvariabilität anzeigt.

Welchen Sinn hat es also, die Dimensionen von Datensätzen zu reduzieren? Kurz gesagt, ich denke, die Antwort ist die Regelung von weißem Rauschen. Eine umfangreichere Antwort wäre jedoch: die Visualisierung zu verbessern, da hochdimensionale Daten umständlicher darzustellen und in Formaten wie Streudiagrammen und den typischen grafischen Möglichkeiten zu präsentieren sind. Die Reduzierung der Dimensionen (Zeichnungskoordinaten) auf 2 oder 3 kann dabei helfen. Ein weiterer großer Vorteil ist die Verringerung den Berechnungsaufwand für den Vergleich von Datenpunkten bei Prognosen.

Dieser Vergleich wird beim Trainieren der Modelle durchgeführt, sodass Zeit für das Trainieren der Modelle und Rechenleistung eingespart werden. Dies führt zu dem „Fluch der Dimensionalität“, bei dem hochdimensionierte Daten zu genauen Ergebnissen führen, wenn sie während des Trainings in Stichproben getestet werden, aber diese Leistung lässt bei der Kreuzvalidierung schneller nach als bei niedrigdimensionierten Daten. Eine Verringerung der Abmessungen kann dazu beitragen, dies zu bewältigen. Außerdem wird durch die Verringerung der Dimensionen das Rauschen in den Datensätzen tendenziell reduziert, was theoretisch die Leistung verbessern sollte. Und schließlich benötigen Daten mit weniger Dimensionen weniger Speicherplatz und sind daher effizienter zu verwalten, insbesondere beim Training großer Modelle.

PCA und Eigenvektoren

Formal sind die Eigenvektoren durch die Gleichung definiert:

Av =λv

wobei:

• A ist die Transformationsmatrix
• v ist der zu transformierende Vektor
• a und λ sind die Skalierungsfaktoren, der auf den Vektor angewendet wird.

Die zentrale These hinter den Eigenvektoren ist, dass es für viele (aber nicht alle) quadratische Matrizen A der Größe n x n n Vektoren gibt, die jeweils so groß sind, dass die Matrix A, wenn sie auf einen dieser Vektoren angewandt wird, die Richtung des resultierenden Produkts dieselbe Richtung beibehält wie der ursprüngliche Vektor, wobei die einzige Änderung eine proportionale Skalierung der Werte im ursprünglichen Vektor ist. Diese Skala wird in der obigen Gleichung als Lambda bezeichnet und ist besser als Eigenwert zu bezeichnen. Für jeden Eigenvektor gibt es einen Eigenwert.

Nicht alle Matrizen können die erforderliche Anzahl von Eigenvektoren berechnen, da einige deformiert sind, aber für jeden erzeugten Vektor gibt es eine mögliche reduzierte Dimension der ursprünglichen Matrix. Unter diesen Vektoren wird auf Basis des Eigenwerts ein Vektor ausgewählt, wobei höhere Werte eine bessere Erfassung der Varianz des Datensatzes und eine geringere Erfassung des Rauschens bedeuten.

Der Prozess der Identifizierung des Eigenvektors beginnt mit der Normalisierung der Matrix des Datensatzes, wofür es eine Reihe von Optionen gibt. Wir verwenden eine Standardisierung (Statistik) für diesen Artikel. Nach der Normalisierung der Matrixdaten wird dann das Äquivalent der Kovarianzmatrix berechnet. Jedes Element der Matrix erfasst die Kovarianz zwischen zwei beliebigen Elementen, wobei die Diagonale die Kovarianz jedes Elements mit sich selbst erfasst. Die Berechnung der Eigenvektoren und -werte ist bei Verwendung der Kovarianzmatrix nicht nur rechnerisch effizienter, sondern die aus der Kovarianzmatrix generierten Datenwerte erfassen auch die linearen Beziehungen zwischen den Datenpunkten in der Matrix und vermitteln ein klares Bild davon, wie jeder Datenpunkt innerhalb der Matrix mit anderen Datenpunkten zusammenhängt.

Die Berechnung der Kovarianzmatrix für Matrix-Datentypen wird mit den integrierten Funktionen in MQL5, in diesem Fall die Funktion „Cov()“, durchgeführt. Sobald wir die Kovarianzmatrix haben, können die Eigenvektoren und -werte auch über die eingebaute Funktion „Eig()“ berechnet werden. Sobald wir die Eigenvektoren und ihre jeweiligen Werte haben, transponieren wir die Eigenvektor-Matrix und multiplizieren sie mit der ursprünglichen Rückgabematrix. Die Zeilen in der Matrix stellen die Varianzgewichtung der einzelnen Portfolios dar, sodass das ausgewählte Portfolio von diesen Gewichtungen abhängt. Dies liegt daran, dass seine Richtung die maximale Varianz der Daten innerhalb des Stichproben-Datensatzes darstellt.

Eine einfache Veranschaulichung, um den Punkt der Erfassung der maximalen Varianz zu verdeutlichen, könnte gemacht werden, wenn wir die x- und y-Koordinaten entlang der Kurve einer Ellipse als Datensatz nehmen, wobei jeder Datenpunkt 2 Dimensionen x und y hat. Würde man diese Ellipse in ein Diagramm einzeichnen, würde sie wie unten dargestellt aussehen:

Quelle 

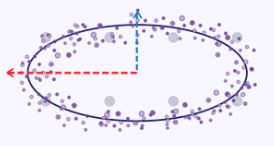
Bei der Aufgabe, diese x- und y-Dimensionen auf eine einzige (geringere Anzahl) von Dimensionen zu reduzieren, wären die x-Koordinatenwerte eindeutig repräsentativer, da die Ellipse dazu neigt, sich entlang ihrer x-Achse stärker zu dehnen als entlang ihrer y-Achse.

Im Allgemeinen muss jedoch ein Kompromiss und ein Gleichgewicht zwischen der Verringerung der Abmessungen und der Beibehaltung der Informationen gefunden werden. Die Dimensionsreduzierung hat zwar ihre Vorteile, die oben aufgeführt sind, aber ihre Interpretation und leichte Erklärbarkeit sollten nicht außer Acht gelassen werden.

Kodierung in MQL5

Ein Handelssystem, das die PCA mit Eigenvektoren nutzt, tut dies in der Regel durch die optimale Auswahl eines Portfolios aus einer Reihe verschiedener Iterationen. Um dies zu veranschaulichen, können wir die Matrix, die wir in der Einleitung betrachtet haben, einfach als Bestandteil von Vektoren betrachten, wobei jeder Vektor die Rendite eines investierten Dollars für jeden Vermögenswert unter drei verschiedenen Allokationsregimen darstellt. Die tatsächliche Allokationsgewichtung der einzelnen Vektoren (Portfolios) wird erst dann wichtig, wenn ein Eigenvektor ausgewählt wurde und die diesem Vektor entsprechende Vermögensallokation für künftige Investitionen erforderlich ist.

Wenn unsere Vermögenswerte SPY, TLT und PDBC sind, dann ist die implizite Allokation, basierend auf den 5-Jahres-Renditen für jeden dieser ETFs, wie folgt:

Die PCA mit Eigenvektoren würde uns also dabei helfen, ein ideales Portfolio (Asset Allocation) aus diesen drei Optionen auf der Grundlage ihrer Performance in den letzten fünf Jahren auszuwählen. Wenn wir die oben beschriebenen Schritte noch einmal durchgehen, müssen wir als Erstes den Datensatz normalisieren. Wie bereits erwähnt, verwenden wir dafür die z-Normalisierung, und der entsprechende Quellcode ist unten zu finden:

//+------------------------------------------------------------------+
//| Z-Normalization                                                  |
//+------------------------------------------------------------------+
matrix ZNorm(matrix &M)
{  matrix _z;
   _z.Init(M.Rows(), M.Cols());
   _z.Copy(M);
   if(M.Rows() > 0 && M.Cols() > 0)
   {  double _std_min = (M.Max() - M.Min()) / (M.Rows() * M.Cols());
      if(_std_min > 0.0)
      {  double _mean = M.Mean();
         double _std = fmax(_std_min, M.Std());
         for(ulong i = 0; i < M.Rows(); i++)
         {  for(ulong ii = 0; ii < M.Cols(); ii++)
            {  _z[i][ii] = (M[i][ii] - _mean) / _std;
            }
         }
      }
   }
   return(_z);
}

Sobald wir die Renditematrix normalisiert haben, würden wir die Kovarianzmatrix der normalisierten Werte berechnen. MQL5s integrierter Datentyp Matrix kann dies für uns in einer Zeile erledigen:

   matrix _z = ZNorm(_m);
   matrix _cov_col = _z.Cov(false);

Mit den Kovarianzbeziehungen der einzelnen Datenpunkte innerhalb der Matrix können wir dann die Eigenvektoren und Eigenwerte berechnen. Auch dies ist eine einzige Zeile:

   matrix _e_vectors;
   vector _e_values;
   _cov_col.Eig(_e_vectors, _e_values);

Die Ausgabe der obigen Funktion ist zweigeteilt, und unser Interesse gilt in erster Linie den Eigenvektoren, die als Matrix zurückgegeben werden. Transponiert man diese Matrix und multipliziert sie mit der ursprünglichen Renditematrix, erhält man die gesuchte Projektionsmatrix P. Dies ist eine Matrix mit Zeilen für jedes der möglichen Portfolios, wobei die Spalte in jeder Zeile eine Gewichtung für jeden der drei erzeugten Eigenvektoren darstellt. In der ersten Zeile befindet sich beispielsweise der größte Wert in der ersten Spalte. Das bedeutet, dass der größte Teil der Renditevarianz dieses Portfolios auf den ersten Eigenvektor zurückzuführen ist. Wenn wir uns den Eigenwert dieses Eigenvektors ansehen, sehen wir, dass er der größte der drei ist. Dies bedeutet also, dass bei allen drei Portfolios das erste für die Mehrzahl der in der Datenmatrix dargestellten signifikanten Muster (oder Trends) verantwortlich ist.

In unserem Fall haben alle Portfolios positive Renditen erzielt, wenn man ihre Werte spaltenweise zusammenzählt, da jede Spalte ein Portfolio darstellt. Die einzigen negativen Renditen entstehen, wenn man den Anleihen-ETF PDBC unabhängig von einer Allokation hält. Das bedeutet, dass man, wenn man diese abgesicherten oder diversifizierten oder Good-Beta-Renditen „verewigen“ will, bei Portfolio 1 bleiben muss. Auch hier zeigt die Renditematrix insgesamt positive Renditen bei Aktien und Rohstoffen und negative Renditen bei Anleihen. PCA mit Eigenvektoren kann also aus diesen ein Portfolio herausfiltern, das diesen Trend am ehesten fortsetzen wird, wie dies bei Portfolio 1 der Fall ist, oder man kann sogar das Gegenteil tun, was in unserem Fall Portfolio 3 wäre, da in der Projektionsmatrix der Höchstwert der dritten Zeile in Spalte 3 liegt und der dritte Eigenvektor den geringsten Wert hatte.

Bemerkenswert ist, dass dieses Portfolio nicht die besten Renditen aufweist und dieses Verfahren dies auch nicht per se auswählt. Sie bietet lediglich eine indikative Gewichtung für die Beibehaltung des Status quo. Das klingt alles unnötig kompliziert für eine Auswahl, die man leicht bei einer Inspektion treffen könnte, doch wenn die zurückgegebenen oder analysierten Matrizen größer werden und mehr Zeilen und Spalten aufweisen (PCA mit Eigenvektoren erfordert quadratische Matrizen), dann beginnt sich dieser Prozess auszuzahlen.

Um die PCA in einer Signalklasse zu präsentieren, sind wir insofern eingeschränkt, als dass standardmäßig nur ein Symbol auf einem einzigen Zeitrahmen getestet werden kann, was bedeutet, dass die obigen Überlegungen zur Portfolioauswahl nicht ohne Weiteres anwendbar sind. Es gibt Umgehungsmöglichkeiten für diese Einschränkungen und vielleicht können wir sie in einem anderen Artikel in der Zukunft behandeln, aber im Moment werden wir innerhalb dieser Einschränkungen arbeiten.

Wir werden für ein einzelnes Symbol auf dem täglichen Zeitrahmen die Preisänderungen für jeden Tag der Woche analysieren. Da es in einer Woche 5 Handelstage gibt, wird unsere Matrix 5 Spalten haben, und um die 5 Zeilen zu erhalten, die für die PCA-Eigenvektoranalyse erforderlich sind, werden wir 5 verschiedene Preistypen berücksichtigen, nämlich: Open, High, Low, Close und Typical. Die Bestimmung der Eigenvektoren und -werte erfolgt in den bereits oben erwähnten Schritten.

Das Gleiche gilt für den Erhalt der Projektionsmatrix, und sobald wir sie haben, können wir leicht den Handelstag der Woche und den angewandten Preistyp ablesen, die die größte Varianz erfassen. Wenn wir dem unten aufgeführten Skript folgen:

   matrix _t = _e_vectors.Transpose();
   matrix _p = _m * _t;
   //Print(" projection: \n", _p);
   vector _max_row = _p.Max(0);
   vector _max_col = _p.Max(1);
   double _days[];
   _max_row.Swap(_days);
   PrintFormat(" best trade day is: %s", EnumToString(ENUM_DAY_OF_WEEK(ArrayMaximum(_days)+1)));
   ENUM_APPLIED_PRICE _price[__SIZE];
   _price[0] = PRICE_OPEN;
   _price[1] = PRICE_WEIGHTED;
   _price[2] = PRICE_MEDIAN;
   _price[3] = PRICE_CLOSE;
   _price[4] = PRICE_TYPICAL;
   double _prices[];
   _max_col.Swap(_prices);
   PrintFormat(" best applied price is: %s", EnumToString(_price[ArrayMaximum(_prices)]));
   PrintFormat(" worst trade day is: %s", EnumToString(ENUM_DAY_OF_WEEK(ArrayMinimum(_days)+1)));
   PrintFormat(" worst applied price is: %s", EnumToString(_price[ArrayMinimum(_prices)]));

Unsere Logs sind unten unter Strategietests und Ergebnisse aufgeführt.

Aus den obigen Logs geht hervor, dass die Donnerstags- und Schlusskursreihen für den größten Teil der Kursschwankungen des Symbols verantwortlich sind, an dessen Chart das Skript angehängt ist (das Skript wurde an EURJPY angehängt). Was bedeutet das also? Das bedeutet, dass man, wenn man den allgemeinen Trend und die Kursentwicklung des EURJPY interessant findet und in Zukunft ähnliche Geschäfte machen möchte, sich besser auf den Donnerstag konzentrieren und die Close-Kursreihe verwenden sollte. Angenommen, EURJPY wäre Teil einer Reihe von Positionen im eigenen Portfolio und das Engagement in EURJPY soll demnächst reduziert werden, wie würde die Positionsmatrix helfen? Die „schlechtesten“ Handelstage und Preisreihen könnten bei der Entscheidung, wann und wie Positionen in EURJPY zu schließen sind, herangezogen werden.

Unsere Positionsmatrix empfiehlt also Handelstage und Preisserien, also verwenden wir die unten stehende einfache Signalklasse, die diese berücksichtigt.

   int _buffer_size = CopyRates(Symbol(), Period(), __start, __stop, _rates);
   PrintFormat(__FUNCSIG__+" buffered: %i",_buffer_size);
   if(_buffer_size >= 1)
   {  for(int i = 1; i < _buffer_size - 1; i++)
      {  TimeToStruct(_rates[i].time,_datetime);
         int _iii = int(_datetime.day_of_week)-1;
         if(_datetime.day_of_week == SUNDAY || _datetime.day_of_week == SATURDAY)
         {  _iii = 0;
         }
         for(int ii = 0; ii < __SIZE; ii++)
         {  
                ...

                ...
         }
      }
   }

Strategietests und Ergebnisse

Um unsere Backtests mit einem im MQL5-Assistenten zusammengestellten Expert Advisor durchzuführen, müssen wir das Skript zunächst auf dem Chart und dem Zeitrahmen des Symbols ausführen, das wir testen wollen. In unserem Beispiel handelt es sich um den EURUSD auf dem 4-Stunden-Zeitfenster. Wenn wir das Skript auf dem Chart ausführen, erhalten wir den Freitag und den gewichteten Preis als „ideale“ oder varianzbestimmende Parameter für EURUSD auf der 4-Stunden-Linie. Dies wird in den nachstehenden Protokollen angegeben:

2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      best trade day is: FRIDAY
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      best applied price is: PRICE_WEIGHTED
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      worst trade day is: TUESDAY
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      worst applied price is: PRICE_OPEN

Unser Skript hat auch 2 Eingabeparameter, die den zu analysierenden Zeitraum bestimmen, nämlich die Startzeit und die Stoppzeit. Beides sind Datetime-Variablen. Wir setzen diese auf 2022.01.01 und 2023.01.01, damit wir unseren Expert Advisor zunächst für diesen Zeitraum testen und dann mit denselben Einstellungen für den Zeitraum von 2023.01.01 bis 2024.01.01 eine Kreuzvalidierung durchführen können. Das Skript empfiehlt den Freitag und den gewichteten Preis als beste Varianzbestimmungsvariablen. Wie können wir diese Informationen bei der Entwicklung einer Signalklasse nutzen? Wie immer gibt es eine Reihe von Optionen, die man in Betracht ziehen kann. Wir werden uns jedoch den einfachen Preis – das Kreuzen zweier gleitender Durchschnitte. Indem wir den gleitenden Durchschnitt des empfohlenen angewandten Preises verwenden und außerdem nur an dem empfohlenen Wochentag handeln, versuchen wir, die These unseres Skripts zu überprüfen. Der Code für unsere Expertensignalklasse wird daher sehr einfach sein und wird im Folgenden vorgestellt:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalPCA::LongCondition(void)
{  int _result = 0;
   m_MA.Refresh(-1);
   m_close.Refresh(-1);
   m_time.Refresh(-1);
//
   if(m_MA.Main(StartIndex()+1) > m_close.GetData(StartIndex()+1) && m_MA.Main(StartIndex()) < m_close.GetData(StartIndex()))
   {  _result = 100;
      //PrintFormat(__FUNCSIG__);
   }
   if(m_pca)
   {  TimeToStruct(m_time.GetData(StartIndex()),__D);
      if(__D.day_of_week != m_day)
      {  _result = 0;
      }
   }
//
   return(_result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalPCA::ShortCondition(void)
{  int _result = 0;
   m_MA.Refresh(-1);
   m_close.Refresh(-1);
//
   if(m_MA.Main(StartIndex()+1) < m_close.GetData(StartIndex()+1) && m_MA.Main(StartIndex()) > m_close.GetData(StartIndex()))
   {  _result = 100;
      //PrintFormat(__FUNCSIG__);
   }
   if(m_pca)
   {  TimeToStruct(m_time.GetData(StartIndex()),__D);
      if(__D.day_of_week != m_day)
      {  _result = 0;
      }
   }
//
   return(_result);
}

Wie immer verwenden wir keine Kursziele für Take-Profit oder Stop-Loss und setzen ausschließlich Limit-Orders ein. Das bedeutet, dass eine Position, die von unserem Expertenberater eröffnet wurde, nur bei einer Umkehrung geschlossen wird. Dies ist zwar ein risikoreicher Ansatz, aber für unsere Zwecke reicht er aus. Wenn wir Backtests für den ersten Zeitraum durchführen, erhalten wir den folgenden Bericht und Kapitalkurven:

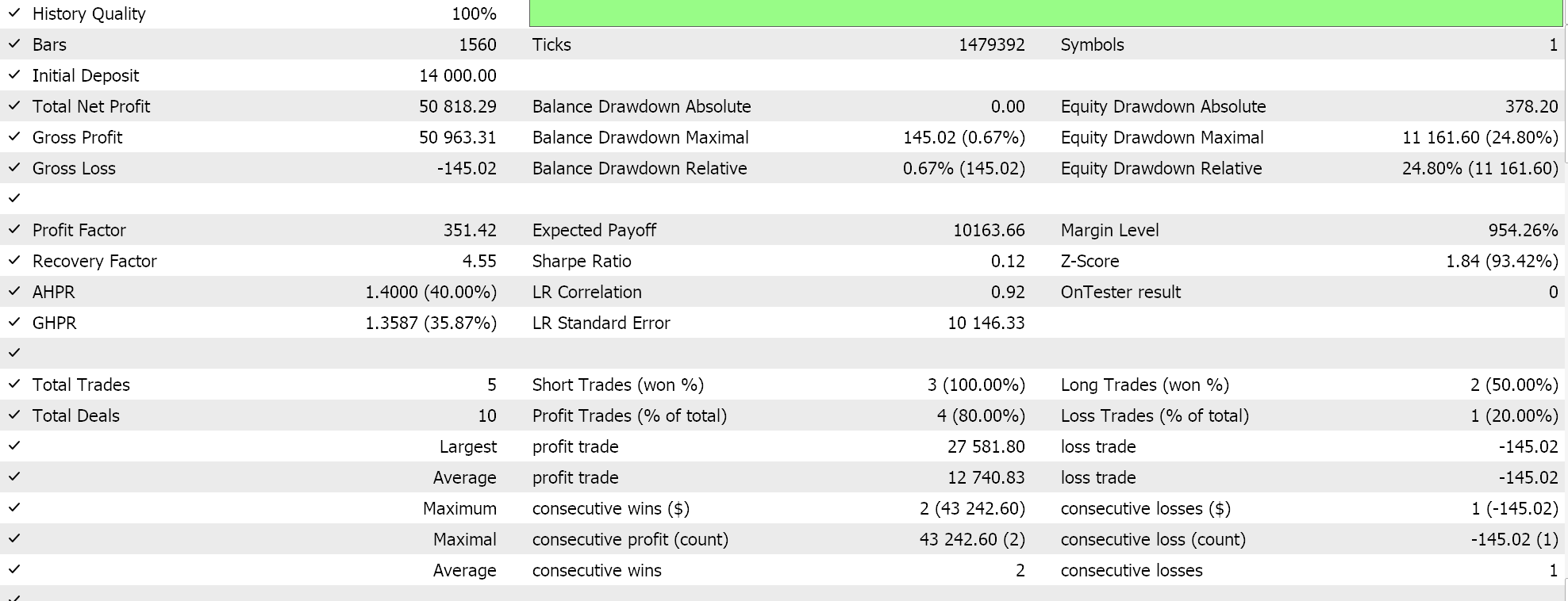
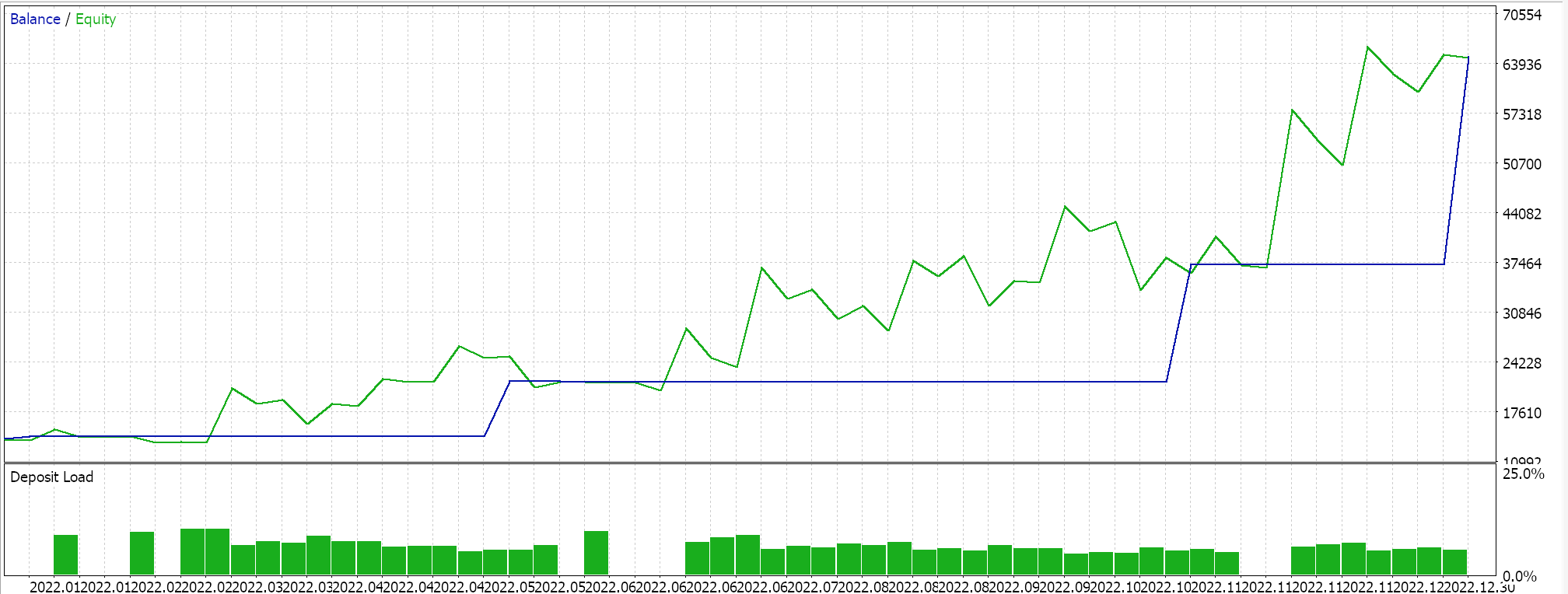
Die obigen Ergebnisse gelten für den Zeitraum 2022.01.01 bis 2023.01.01. Wenn wir versuchen, mit denselben Einstellungen über einen längeren Zeitraum zu testen, der über den Analysezeitraum des Skripts hinausgeht, indem wir ihn vom 2022.01.01 bis zum 2024.01.01 laufen lassen, erhalten wir die folgenden Ergebnisse:

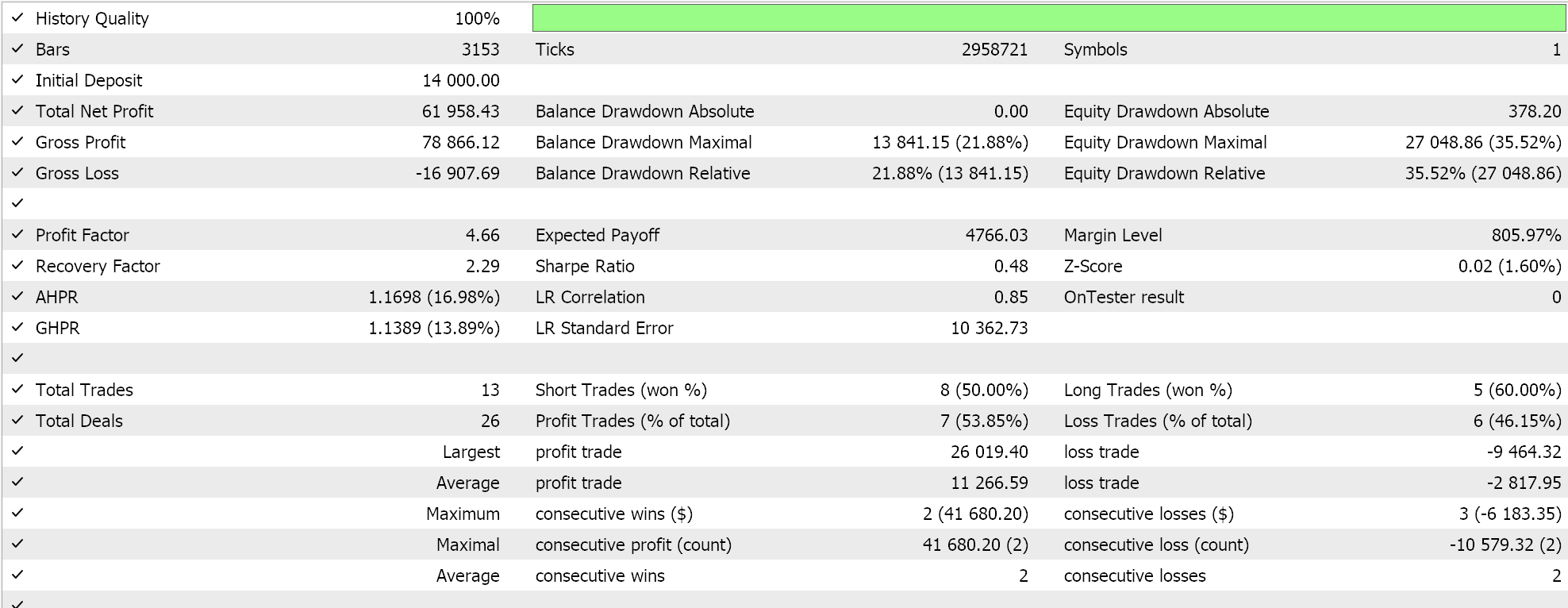
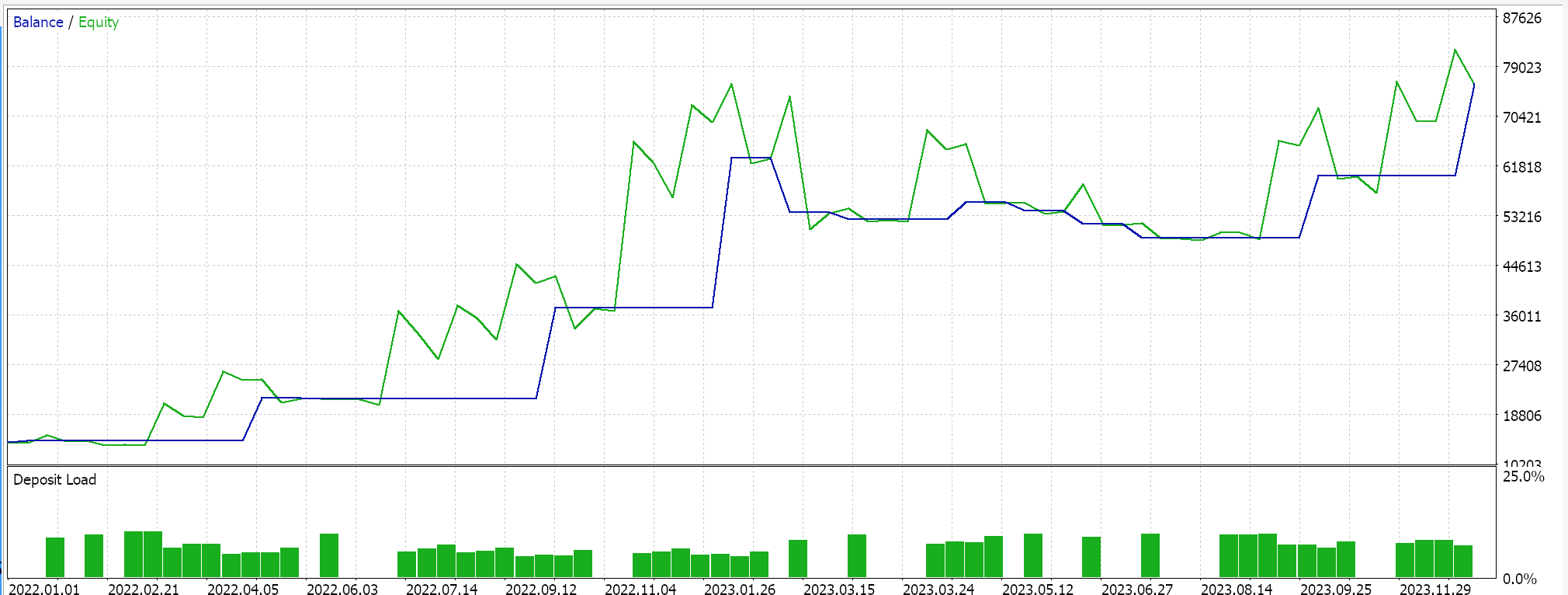
Unser Expertensignal ist etwas restriktiv und es werden nicht allzu viele Trades platziert, was man als unzureichenden Test bezeichnen könnte. Unabhängig davon sind Testzeiträume auch von einigen Jahren nicht verlässlich, wenn es um Live-Konten geht. Zur Kontrolle können wir neben der obigen Kreuzvalidierung auch Tests mit verschiedenen angewandten Preisen durchführen, während wir an einem beliebigen Wochentag mit denselben Expert Advisor-Einstellungen handeln. Dies führt zu den folgenden Ergebnissen:

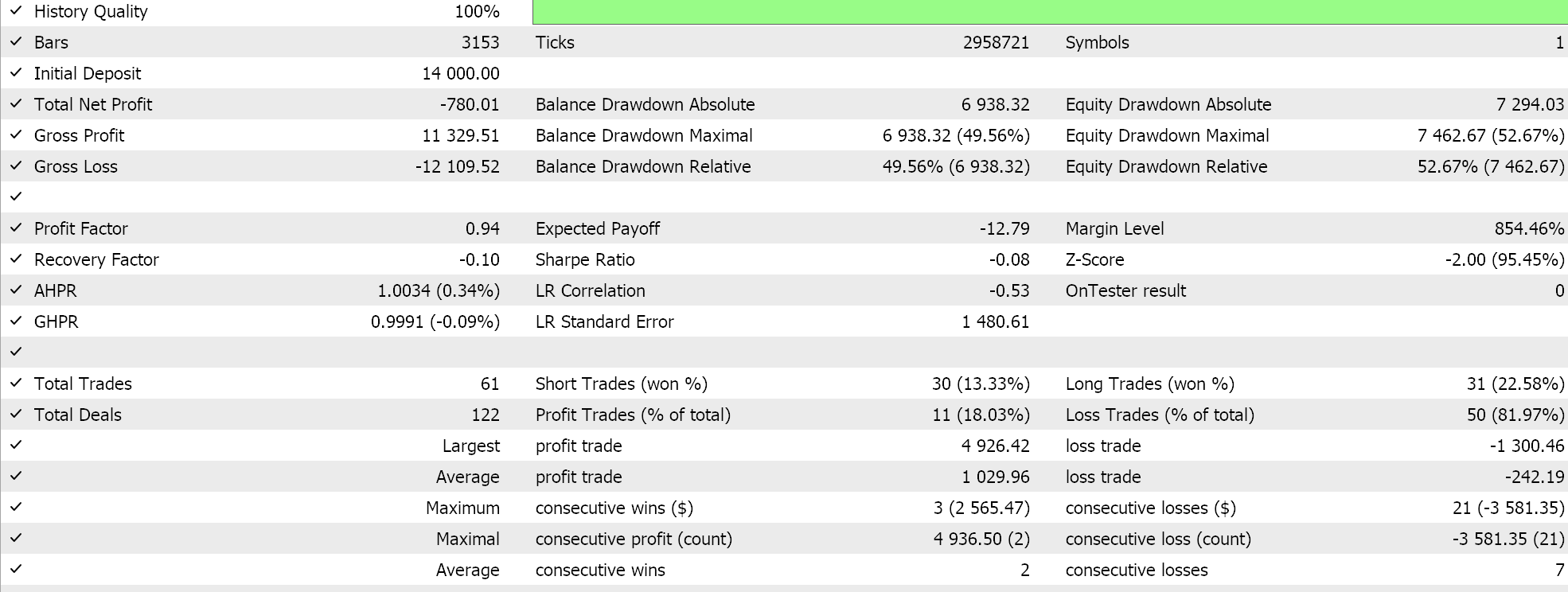
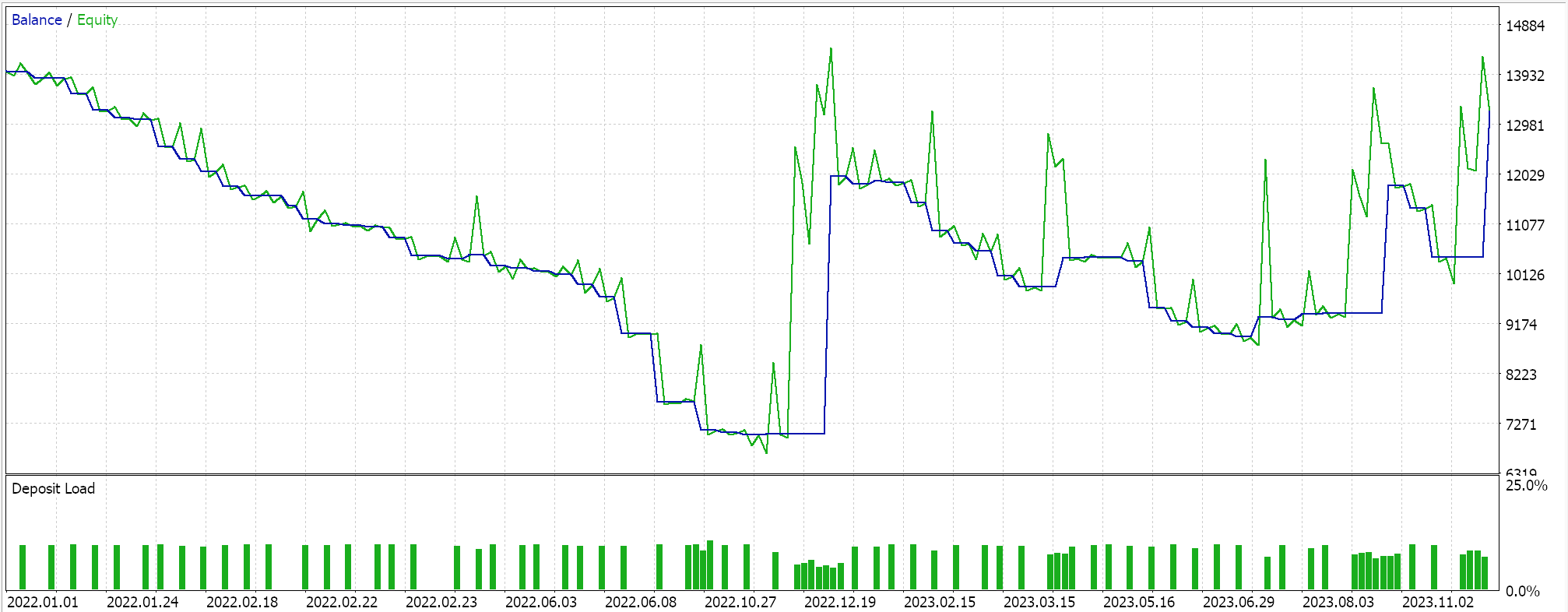
Die Gesamtleistung leidet eindeutig, sobald wir über die PCA-Skriptempfehlung hinausgehen, aber warum ist das so? Warum führt der Handel nur innerhalb der varianzbestimmenden Parameter zu besseren Ergebnissen als die nicht eingeschränkten Setups? Diese Frage ist meines Erachtens relevant, da eine Beeinflussung der Varianz nicht zwangsläufig zu einer höheren Rentabilität führt, da der Gesamttrend des untersuchten Datensatzes ins Wanken geraten könnte. Aus diesem Grund sollten die varianzbestimmenden Einstellungen nur dann gewählt werden, wenn die zugrunde liegenden und allgemeinen Trends im untersuchten Datensatz mit den allgemeinen Zielen des Händlers übereinstimmen.

Wenn wir den EURUSD-Kurs-Chart betrachten, können wir sehen, dass der EURUSD im PCA-Analysezeitraum vom 2022.01.01 bis 2023.01.01 überwiegend nach unten tendierte, bevor er im Oktober kurzzeitig umkehrte. Im Jahr 2023, dem Zeitraum der Kreuzvalidierung, schwankte das Paar jedoch stark, ohne dass sich wie im Jahr 2022 größere Trends abzeichneten. Dies könnte bedeuten, dass durch die Durchführung von Analysen über größere Trendperioden die trendbestimmenden Varianzparameter besser erfasst werden können, und sie könnten sogar in Situationen wie „Whipsaw“ (Zick-Zack) nützlich sein, wie dies im Jahr 2023 der Fall ist.

Schlussfolgerung

Zusammenfassend haben wir gesehen, dass die PCA von Natur aus ein Analysewerkzeug ist, das versucht, die Dimensionalität von Datensätzen zu reduzieren, indem es die Dimensionen (oder Komponenten des Datensatzes) identifiziert, die am meisten für die Bestimmung der zugrunde liegenden Trends verantwortlich sind. Es gibt viele Instrumente zur Verringerung der Dimensionalität von Daten, und auf den ersten Blick mag die PCA einfältig erscheinen, aber sie erfordert eine vorsichtige Analyse und Interpretation, da sie immer auf den zugrunde liegenden Trends des untersuchten Datensatzes basiert.

In dem von uns untersuchten Beispiel waren die zugrunde liegenden Trends für das untersuchte Symbol rückläufig, sodass bei der Kreuzvalidierung die Mehrheit der außerhalb der Stichprobe platzierten Trades short war. Wenn wir hypothetisch einen Aufwärtsmarkt für das betrachtete Symbol untersucht hätten, dann müssten alle Handelsstrategien, die auf der Grundlage der empfohlenen PCA-Einstellungen angenommen werden, von einem Aufwärtsumfeld profitieren. Umgekehrt könnte es in solchen Situationen sinnvoll sein, Einstellungen zu wählen, die die Varianz am wenigsten erklären, wenn man aus einer Baisse Kapital schlagen will, da eine Baisse und eine Hausse polare Gegensätze sind. Außerdem ergibt die PCA mehr als ein Paar von Einstellungen mit jeweils einer Gewichtung als eine Art Eigenwert, was bedeutet, dass mehr als eine Einstellung angenommen werden kann, wenn ihre Gewichtungen über einem ausreichenden Schwellenwert liegen. Dies wurde in diesem Artikel nicht untersucht, und der Leser ist herzlich eingeladen, sich damit zu befassen, da der Quellcode unten beigefügt ist. Die Verwendung dieses Codes im MQL5-Assistenten zur Erstellung eines Expert Advisors kann hier für diejenigen nachgelesen werden, die den Assistenten noch nicht kennen.

Eine Möglichkeit, mehr PCA-Einstellungen in das Analyseskript und den Expertenberater einzubauen, besteht darin, die Eigenwerte zunächst so zu normalisieren, dass sie beispielsweise alle positiv sind und im Bereich von 0,0 bis 1,0 liegen. Danach können Sie Auswahlschwellen für die Eigenvektoren festlegen, die Sie aus jeder Analyse auswählen. Wenn beispielsweise eine PCA-Analyse einer 3 x 3-Matrix anfänglich die Werte 2,94, 1,92, 0,14 ergibt, würden wir diese Werte auf einen Bereich von 0 bis 1 normalisieren: 0.588, 0.384, & 0.028. Mit den normalisierten Werten kann ein Schwellenwert wie 0,3 eine unparteiische Auswahl von Eigenvektoren über mehrere Analysen hinweg ermöglichen. Bei einer Wiederholung der Analyse mit einem anderen Datensatz und sogar einer anderen Matrixgröße können die Eigenvektoren immer noch auf ähnliche Weise ausgewählt werden. Für das Skript würde dies bedeuten, die Eigenwerte zu durchlaufen und die 2 Kreuzeigenschaften für jeden übereinstimmenden Wert zu einer Ausgabeliste oder einem Array hinzuzufügen. Dieses Array könnte eine Struktur sein, die die Eigenschaften sowohl von „x“ als auch von „y“- in der Datensatzmatrix protokolliert. Mit dem Expertenratgeber müssen Sie die Filtereigenschaften als durch Komma getrennte Zeichenfolgen eingeben, um die Skalierbarkeit zu gewährleisten. Dazu müsste die Zeichenkette geparst und die Eigenschaften in ein für den Expert Advisor lesbares Standardformat extrahiert werden.