Técnicas do MQL5 Wizard que você deve conhecer (Parte 24): Médias Móveis

Introdução

Damos continuidade a esta série sobre MQL5 Wizards analisando o indicador de média móvel e como ele pode ser adicionado à biblioteca de ferramentas já disponíveis de maneiras que podem ser novas para alguns traders. A Média Móvel possui muitas variantes, sendo uma série temporal única que pode ser anexada a um gráfico, mas também possui outras variantes como um oscilador e até outras como um indicador de envelopes.

Exploraremos essas múltiplas aplicações ou variantes dentro de uma categoria especial de 3 Médias Móveis (MA) chamada Médias Pitagóricas. As 3 MAs sob esse nome são Média Aritmética(AM), Média Geométrica(GM) e Média Harmônica(HM). A primeira delas, a média aritmética, é o que todos pensam inicialmente ao mencionar MA. É simplesmente a média de qualquer número de valores em um conjunto. A Wikipedia apresenta um resumo muito interessante dessas 3 médias em um diagrama. Ele é compartilhado abaixo:

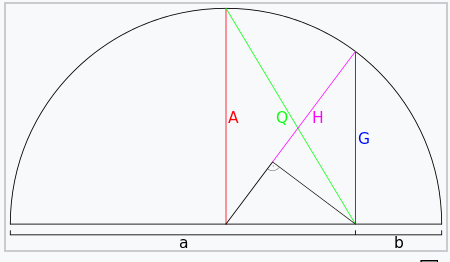
O que é apresentado acima é um semicírculo cujo diâmetro é dividido de forma desigual em dois valores a e b. A média aritmética desses dois valores é marcada como A em vermelho no diagrama, o que equivale ao raio do semicírculo, como seria de esperar. Para fins de completude, a fórmula da média aritmética é compartilhada abaixo como:

onde

• AM é a média aritmética
• x são os valores no conjunto cuja média é calculada
• n é o tamanho do conjunto

Agora, a média geométrica é dada pela fórmula:

onde

• GM é a média geométrica
• x e n representam o mesmo que na AM acima

O valor de GM no semicírculo acima é equivalente em comprimento à corda azul marcada como G, que o torna mais ponderado em direção ao menor valor b do que ao maior valor a. Além disso, é importante notar que o GM sempre será positivo, mesmo se todos os valores forem negativos! Esse cenário pode ser abordado atribuindo um valor negativo ao GM calculado se o conjunto tiver todos os números negativos, mas caso haja uma mistura de valores negativos e positivos, encontrar o GM real torna-se problemático.

Para a média harmônica, a representação no semicírculo é a linha marcada como H, cujo comprimento é equivalente à média de a e b. Sua fórmula é representada por:

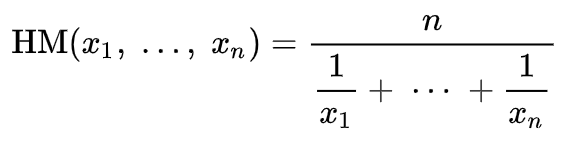
onde

• HM é, naturalmente, a média harmônica
• x e n representam o mesmo que acima

Se, por algum motivo, o valor b fosse zero, como pode ser visto no diagrama do semicírculo, tanto a média geométrica quanto a média harmônica seriam zero. (Isso ocorre apesar de gerar uma “divisão por zero” ao calcular a média harmônica). Curiosamente, isso seria verdadeiro independentemente da contagem (ou seja, se houver mais de 2) dos números cujas médias são calculadas; desde que qualquer um desses números seja zero, então a média geométrica e a média harmônica de todos os valores será zero.

Essa propriedade, em essência, mede o grau em que o menor valor de um conjunto está próximo de zero. Então, o que isso significa para os traders? Pode significar várias coisas, dependendo dos dados da média móvel que estão sendo considerados.

Se for apenas o preço dos ativos, então a média móvel pode atuar como um bom indicador de suporte. Por quê? Ela (a GM e HM) dá maior peso aos preços baixos. Isso poderia significar, por exemplo, que uma quebra de preço abaixo dessas médias teria mais relevância do que uma quebra abaixo de uma média móvel comum.Assim, GM e HM podem ser úteis no suporte da maioria das ações de preço. E no lado da resistência? Podemos obter um equivalente espelhado de ambas GM e HM a partir das seguintes fórmulas:

HM’ = AM + (AM - HM)

GM’ = AM + (AM - GM)

onde:

• HM’ é o espelho da média harmônica
• GM’ é o espelho da média geométrica
• AM, GM e HM são os mesmos que acima.

Ao introduzir equivalentes espelhados ou reflexos de GM e HM, estamos, em certo sentido, adicionando um equilíbrio às médias, pois as ponderações desses reflexos tendem a inclinar-se para os valores maiores em qualquer conjunto de valores cuja média está sendo calculada. Isso também significa que, para responder à questão da resistência, agora podemos usar tanto GM’ quanto HM’ como médias ponderadas por preços mais altos para servir como proxies mais eficazes na definição do nível de resistência.

A relevância de GM em comparação com HM para nossos propósitos será apenas uma questão de grau. Isso ocorre porque ambas são ponderadas para os valores menores, com a principal diferença de que a HM tem uma ponderação maior em direção a zero do que a GM.

Implementações Personalizadas

Agora, vamos ver como essas médias simples podem ser utilizadas no MQL5 para aproveitar suas propriedades únicas. Primeiro, temos a Média Aritmética básica. Dessas 3, esta é a mais comum, pois considera o básico das médias sem quaisquer modificações, e a maneira mais simples de usar essa média deve ser monitorando os cruzamentos de preço. Existem muitas aplicações de médias móveis ao rastrear a estrutura de preços, e esta provavelmente é a mais direta e comum. Portanto, essa aplicação é apresentada aqui principalmente para fins de comparação com as outras médias menos comuns de GM e HM já introduzidas acima.

Comparação e benchmarking são inerentes aos experts montados no MQL5 wizard, especialmente para as classes de sinais, pois cada classe de sinal escolhida no wizard pode receber um peso ou uma contribuição na determinação das condições de compra e venda de um ativo negociado. Graças aos tipos de dados vetoriais, obtemos facilmente o buffer de AM a partir desta função:

//+------------------------------------------------------------------+
//| Arithmetic Mean                                                  |
//+------------------------------------------------------------------+
double CSignalAM::AM(int Index, int Mask = 8)
{  vector _am;
   _am.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_fast);
   return(_am.Mean());
}

E também podemos medir a diferença de preço atual, que é fundamental para acompanhar o cruzamento de médias móveis, com a função abaixo:

   double            CrossOver(int Index)
   {                 m_close.Refresh(-1);
      return(AM(Index) - m_close.GetData(Index));
   }

Normalmente, em casos em que a negociação é feita manualmente, faz mais sentido ter tanto a GM quanto a HM codificadas como indicadores personalizados. Não estamos negociando manualmente, já que isso é para um Expert Advisor; portanto, uma função que acessa buffers de preço integrados da classe será suficiente.

A média HM, como a GM, é ponderada para valores menores e, como vimos acima, pode ser espelhada para criar outra média, HM’, que é ponderada para valores maiores. Assim, HM e HM’, sendo médias ponderadas para os extremos, se prestam à capacidade de detectar divergências. Agora, quando se pensa em divergências, a primeira coisa que pode vir à mente é uma diferença de tendência entre um oscilador e o preço do ativo. Essas oscilações ocorrem em períodos muito curtos e é preciso estar atento para captá-las. Alternativamente, pode ser uma divergência inteiramente nos preços de um ativo, mas em diferentes intervalos de tempo, como uma queda de preço no período de uma hora, enquanto em um período semanal uma forte tendência de alta está em vigor.

No entanto, para aproveitar os "viés" da média harmônica, analisaremos divergências em preços altos e baixos. Especificamente, abriremos posições apenas quando a mudança nos preços altos for diferente na direção da mudança nos preços baixos. Isso, no entanto, ainda pode ser explorado de duas maneiras. Podemos abrir uma posição em altos em queda e baixos em alta, ou podemos abrir em altos em alta e baixos em queda. Para este artigo, estamos explorando a última opção, mas como todo o código-fonte está anexado no final deste artigo, o leitor pode personalizá-lo e tentar explorar a divergência de "engolfo", mais popular, que não abordamos.

Assim, estaremos procurando uma elevação na média harmônica dos altos que seja simultânea a uma queda na média harmônica dos baixos para abrir posições. Um indicador complementar para orientar na abertura de uma posição longa ou curta pode ser personalizado aqui, mas o que usaremos como acompanhamento é simplesmente a mudança no preço de fechamento. Se tivermos uma alta no preço de fechamento, após uma divergência na barra anterior, então vamos abrir uma posição longa e vice-versa.

O código para implementar isso, como vimos com a AM, também é duplo. Primeiro, temos a função HM e seu espelho, que é apresentado abaixo:

//+------------------------------------------------------------------+
//| Harmonic Mean                                                    |
//+------------------------------------------------------------------+
double CSignalHM::HM(int Index, int Mask = 8)
{  vector _hm, _hm_i;
   _hm_i.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_slow);
   _hm = (1.0 / _hm_i);
   return(m_slow / _hm.Sum());
}
//+------------------------------------------------------------------+
//| Inverse Harmonic Mean                                            |
//+------------------------------------------------------------------+
double CSignalHM::HM_(int Index, int Mask = 8)
{  double _am = AM(Index, Mask);
   double _hm = HM(Index, Mask);
   return(_am + (_am - _hm));
}

Depois temos a função de divergência, que é a seguinte:

   double            Divergence(int Index)
   {                 return((HM_(Index, 2) - HM_(Index + 1, 2)) - (HM(Index, 4) - HM(Index + 1, 4)));
   }

Ao usar os vetores para copiar e carregar dados, o índice 'mask rates' é indispensável, pois nos permite alternar rapidamente entre vários preços (OHLC) e, ao mesmo tempo, o uso das funções estatísticas embutidas no tipo de dado vetorial economiza a necessidade de programar muitos códigos. Além disso, nossas funções de teste para essas médias pitagóricas utilizam dois períodos de médias móveis: um período rápido e um período lento. Isso é prática comum, especialmente ao usar a estratégia de cruzamento para determinar pontos de entrada e saída. Para os buffers de média harmônica e média geométrica, estamos confiando no período lento para calcular nossos valores. Os períodos rápidos estão sendo usados apenas para o buffer da média aritmética.

Isso, é claro, pode ser modificado ou ajustado para se adequar melhor à estratégia e abordagem de cada um, mas estamos mantendo isso aqui puramente para fins de teste.

Por fim, a média geométrica, que, assim como a harmônica, será aplicada de maneira semelhante às Bandas de Bollinger. Ela, como a harmônica, é ponderada mais para valores pequenos e em uma medida ligeiramente maior. É essa ponderação que a tornaria ideal para derivar um indicador semelhante às bandas de Bollinger, já que, como é bem conhecido, as bandas de Bollinger são uma média móvel mais 2 desvios padrão. Antes de chegarmos à implementação, no entanto, o código para obter uma média geométrica e seu espelho (equivalente ponderado para valores altos) seria o indicado abaixo:

//+------------------------------------------------------------------+
//| Geometric Mean                                                   |
//+------------------------------------------------------------------+
double CSignalGM::GM(int Index, int Mask = 8)
{  vector _gm;
   _gm.CopyRates(m_symbol.Name(), m_period, Mask, Index, m_slow);
   return(pow(_gm.Prod(), 1.0 / m_slow));
}
//+------------------------------------------------------------------+
//| Inverse Geometric Mean                                           |
//+------------------------------------------------------------------+
double CSignalGM::GM_(int Index, int Mask = 8)
{  double _am = AM(Index, Mask);
   double _gm = GM(Index, Mask);
   return(_am + (_am - _gm));
}

Mais uma vez, estamos usando os tipos de dados vetoriais e suas funções integradas para agilizar nosso processo de codificação. Os buffers das bandas são dois, consistindo em uma banda superior e uma banda inferior. Esses também são recuperados das duas funções listadas abaixo:

   double            BandsUp(int Index)
   {  vector _bu;
      _bu.CopyRates(m_symbol.Name(), m_period, 2, Index, m_slow);
      return(GM_(Index, 2) + (2.0 * _bu.Std()));
   }

   double            BandsDn(int Index)
   {  vector _bd;
      _bd.CopyRates(m_symbol.Name(), m_period, 4, Index, m_slow);
      return(GM(Index, 4) - (2.0 * _bd.Std()));
   }

As duas funções simplesmente retornam o preço da banda superior e o preço da banda inferior para as funções ‘BandsUp’ e ‘BandsDn’ respectivamente. Esses valores retornados podem ser facilmente reconstituídos em buffers paralelos para análise de várias formas. Estamos simplesmente usando-os de maneira cruzada para verificar se temos potencial de abertura para posições longas ou curtas. Para verificar uma posição longa, precisaríamos de confirmação de que o preço cruzou a banda inferior de baixo para cima, ou seja, estava abaixo da banda inferior, mas agora está acima dela. Da mesma forma, para verificar posições curtas, precisaríamos confirmar um cruzamento de preço da banda superior de cima para baixo, onde o preço estava acima da banda superior, mas em uma barra de preço subsequente agora está abaixo dela.

Classe de Sinal Personalizada

Cada uma dessas 3 MAs pitagóricas pode ser combinada em uma única classe com um parâmetro adicional que permite a seleção de uma delas para ser usada em um Expert Advisor. No entanto, implementamos essas médias como classes de sinal separadas, pois vamos explorar a configuração de peso das classes de sinal, realizando uma otimização para a ponderação ideal de cada média, a fim de ter uma ideia de qual desses sinais e, por extensão, qual das médias é mais útil na previsão e colocação de ordens com nosso Expert Advisor.

No entanto, antes de obtermos uma ideia da importância relativa, pode ser diligente realizar testes independentes de cada classe de sinal por conta própria, de forma que os pesos relativos obtidos ao final possam servir como validação (ou refutação) desses primeiros testes que teríamos realizado. Assim, começaremos desenvolvendo um Expert Advisor para cada uma das 3 médias e testando-as independentemente para avaliar seu desempenho. Uma vez que tivermos esses resultados, então executaremos testes em um Expert Advisor que combine todas as três médias e que otimizará as ponderações relativas de cada uma dessas médias.

Para desenvolver uma condição longa e curta para a classe de sinal da média aritmética, simplesmente verificaremos uma mudança no valor do cruzamento retornado pela função ‘Crossover’, cujo código é compartilhado acima. O código das condições de longo e curto é bem curto, e ambos estão compartilhados abaixo:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalAM::LongCondition(void)
{  int result = 0;
   if(CrossOver(StartIndex()) > 0.0 && CrossOver(StartIndex()+1) < 0.0)
   {  result = int(round(100.0 * ((CrossOver(StartIndex()) - CrossOver(StartIndex()+1))/fmax(fabs(CrossOver(StartIndex()))+fabs(CrossOver(StartIndex()+1)),fabs(CrossOver(StartIndex()+1))+fabs(CrossOver(StartIndex()+2))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalAM::ShortCondition(void)
{  int result = 0;
   if(CrossOver(StartIndex()) < 0.0 && CrossOver(StartIndex()+1) > 0.0)
   {  result = int(round(100.0 * ((CrossOver(StartIndex()+1) - CrossOver(StartIndex()))/fmax(fabs(CrossOver(StartIndex()))+fabs(CrossOver(StartIndex()+1)),fabs(CrossOver(StartIndex()+1))+fabs(CrossOver(StartIndex()+2))))));
   }
   return(result);
}

Como sempre, parece que o ponto crucial é normalizar o valor do resultado no caso de um sinal potencial. Para a AM, estamos usando a mudança atual nos valores de cruzamento dividida pelo maior valor em magnitude dos valores de cruzamento anteriores. Claramente, esta é uma área que pode ser muito personalizada, e o leitor é bem-vindo a implementar sua própria abordagem. Esta, no entanto, tende a capitalizar a média aritmética e, portanto, é utilizada.

A condição de longo e curto da média harmônica usará, por sua vez, as funções de "Divergência" para filtrar as possíveis aberturas de posições longas e curtas. Temos as condições de curto e longo indicadas abaixo:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalHM::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(Divergence(StartIndex()+1) > 0.0 && m_close.GetData(StartIndex()) > m_close.GetData(StartIndex()+1))
   {  result = int(round(100.0 * (Divergence(StartIndex()+1)/(fabs(Divergence(StartIndex()))+fabs(Divergence(StartIndex()+1))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalHM::ShortCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(Divergence(StartIndex()+1) > 0.0 && m_close.GetData(StartIndex()) < m_close.GetData(StartIndex()+1))
   {  result = int(round(100.0 * (Divergence(StartIndex()+1)/(fabs(Divergence(StartIndex()))+fabs(Divergence(StartIndex()+1))))));
   }
   return(result);
}

Com a média harmônica, estamos buscando qualquer divergência positiva onde os altos estejam subindo e os baixos caindo, seguida por uma alta no preço de fechamento para uma abertura de alta ou uma queda no preço de fechamento para uma abertura de baixa. Esses dois eventos acontecem sequencialmente e não na mesma barra. Essa divergência é, em muitos aspectos, o oposto do padrão de engolfo mais popular, que geralmente apresenta altos em queda e baixos em alta.

Depois que temos uma abertura, seja longa ou curta, a próxima questão é determinar o valor inteiro do resultado, que é sempre a saída para as condições de longo e curto dessas funções de classe de sinal. Mais uma vez, existem várias abordagens que podem ser adotadas aqui para quantificar o resultado, e várias dessas abordagens poderiam estar relacionadas a outros indicadores além da média harmônica. No entanto, para nossos propósitos, queremos nos apoiar ainda mais na média harmônica para estabelecer o valor do resultado. Por isso, estamos usando uma razão da divergência atual para a magnitude dos valores anteriores para obter um valor inteiro na faixa de 0 a 100.

Esse resultado, portanto, simplesmente significa que quanto maior a divergência atual, mais otimista ou pessimista seríamos. No denominador dessa razão de resultado (que normalizamos para a faixa de 0 a 100 via porcentagem) estão os valores de divergência atual e anteriores. Isso nos leva a aplicar a média geométrica.

A GM é implementada calculando os valores das bandas de Bollinger superior e inferior com base nos buffers de GM, conforme compartilhado acima. Para transformar isso em um sinal acionável, verificamos o cruzamento do preço da banda inferior e o cruzamento do preço da banda superior para as configurações de alta e baixa, respectivamente, como mencionado acima. Isso é codificado nas condições de longo e curto, conforme segue:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalGM::LongCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(m_close.GetData(StartIndex()) > m_close.GetData(StartIndex() + 1) && m_close.GetData(StartIndex()) > BandsDn(StartIndex()) && m_close.GetData(StartIndex() + 1) < BandsDn(StartIndex() + 1))
   {  result = int(round(100.0 * ((m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))/(fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1)) + fabs(BandsUp(StartIndex()) - BandsDn(StartIndex()))))));
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalGM::ShortCondition(void)
{  int result = 0;
   m_close.Refresh(-1);
   if(m_close.GetData(StartIndex()) < m_close.GetData(StartIndex() + 1) && m_close.GetData(StartIndex()) < BandsUp(StartIndex()) && m_close.GetData(StartIndex() + 1) > BandsUp(StartIndex() + 1))
   {  result = int(round(100.0 * ((m_close.GetData(StartIndex()+1) - m_close.GetData(StartIndex()))/(fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1)) + fabs(BandsUp(StartIndex()) - BandsDn(StartIndex()))))));
   }
   return(result);
}

O tamanho do resultado, como seguimos com a média aritmética e a média harmônica, também será mais inclinado para a média geométrica e não usará outro indicador. Assim, para esse fim, com a GM, o resultado é uma razão entre a mudança no preço de fechamento e a diferença entre as bandas superior e inferior das nossas bandas de Bollinger derivadas. Mais uma vez, esse resultado significa que um movimento de preço maior em relação à compressão da diferença das bandas deve indicar um sinal de entrada ou fechamento maior. Sinal de fechamento, pois as condições de longo e curto não apenas definem os limites de abertura, mas também determinam o limite no qual suas posições inversas são fechadas. Portanto, nas configurações de entrada, sempre temos um limite de abertura e um limite de fechamento. O último deve ser menor que o primeiro, pois você quer fechar posições longas antes de assumir posições curtas e vice-versa.

Além disso, possíveis implementações alternativas das bandas de Bollinger derivadas da GM para estabelecer um sinal poderiam considerar opções que acompanhem o tamanho da diferença entre as bandas superior e inferior com a inclinação da média base, entre outras variações. Nossa aplicação aqui não é a única forma de usar ou analisar as Bandas de Bollinger.

Teste de Estratégia e Avaliação de Desempenho

Vamos então realizar testes independentes com cada média móvel pitagórica individualmente em um Expert Advisor, e uma vez que tenhamos os resultados independentes de cada uma, faremos um teste com um Expert Advisor montado com todos os 3 sinais de média pitagórica e otimizaremos esse Expert Advisor para encontrar a ponderação relativa de cada uma das médias.

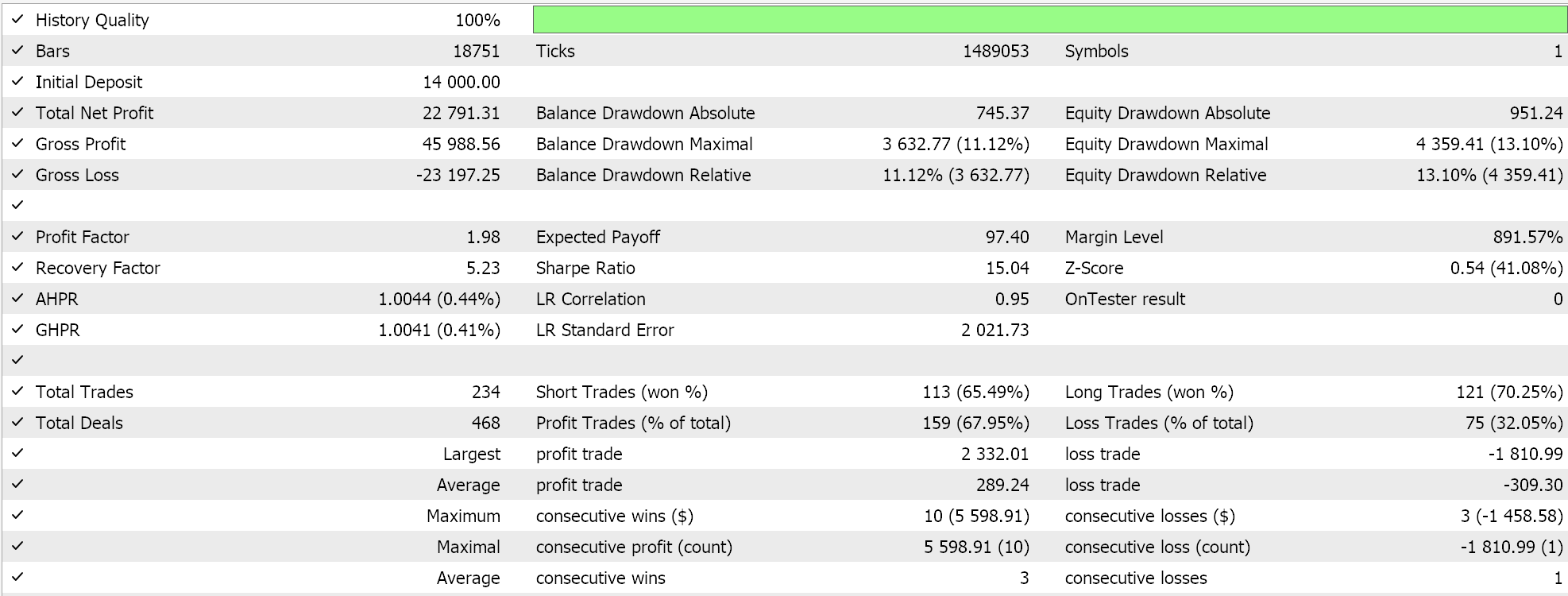
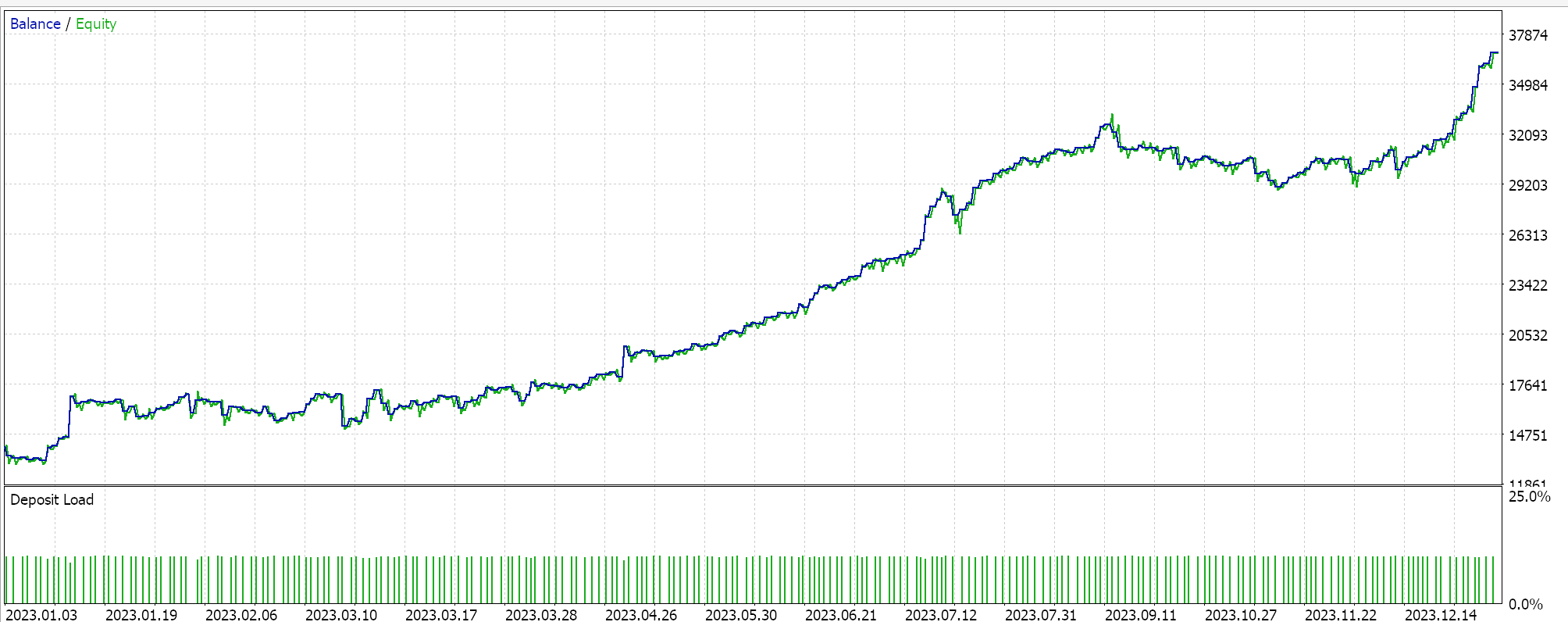
Para uniformidade, realizaremos testes em um símbolo EURJPY no intervalo de tempo de 20 minutos para o ano de 2023. Para a média aritmética, obtemos os seguintes resultados:

Para a média harmônica, obtemos o seguinte:

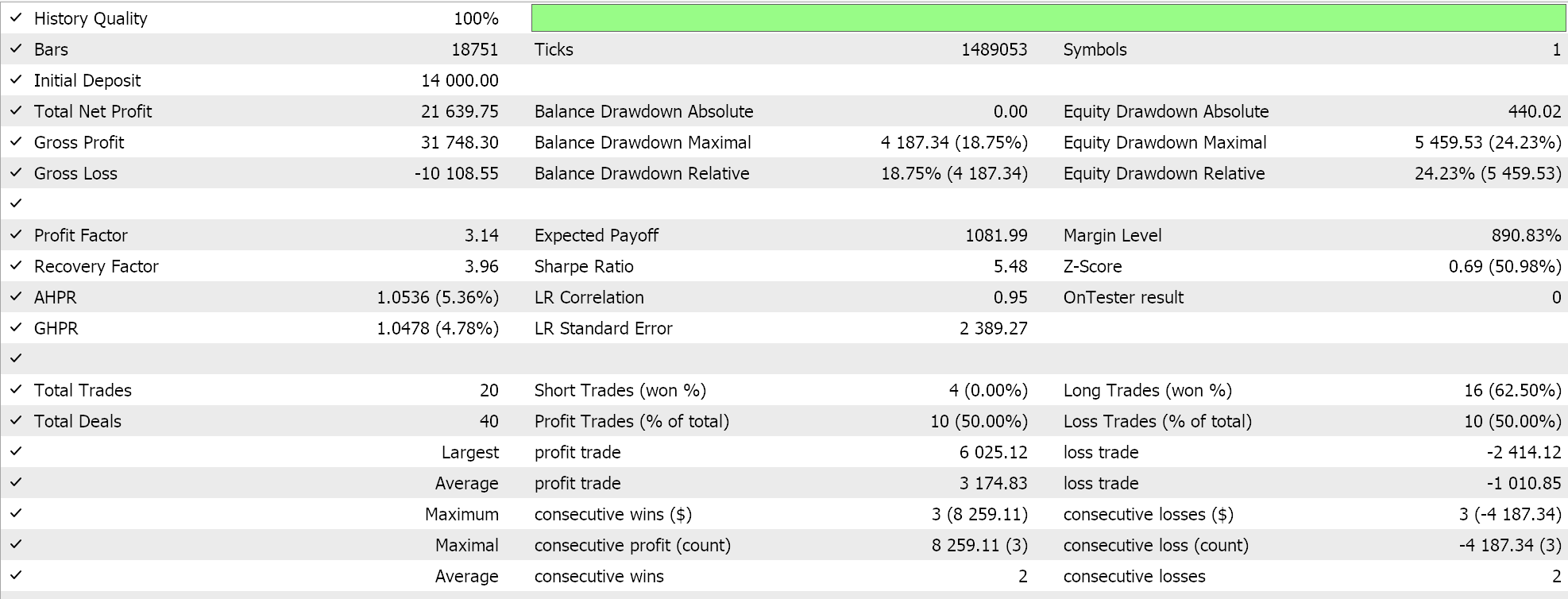
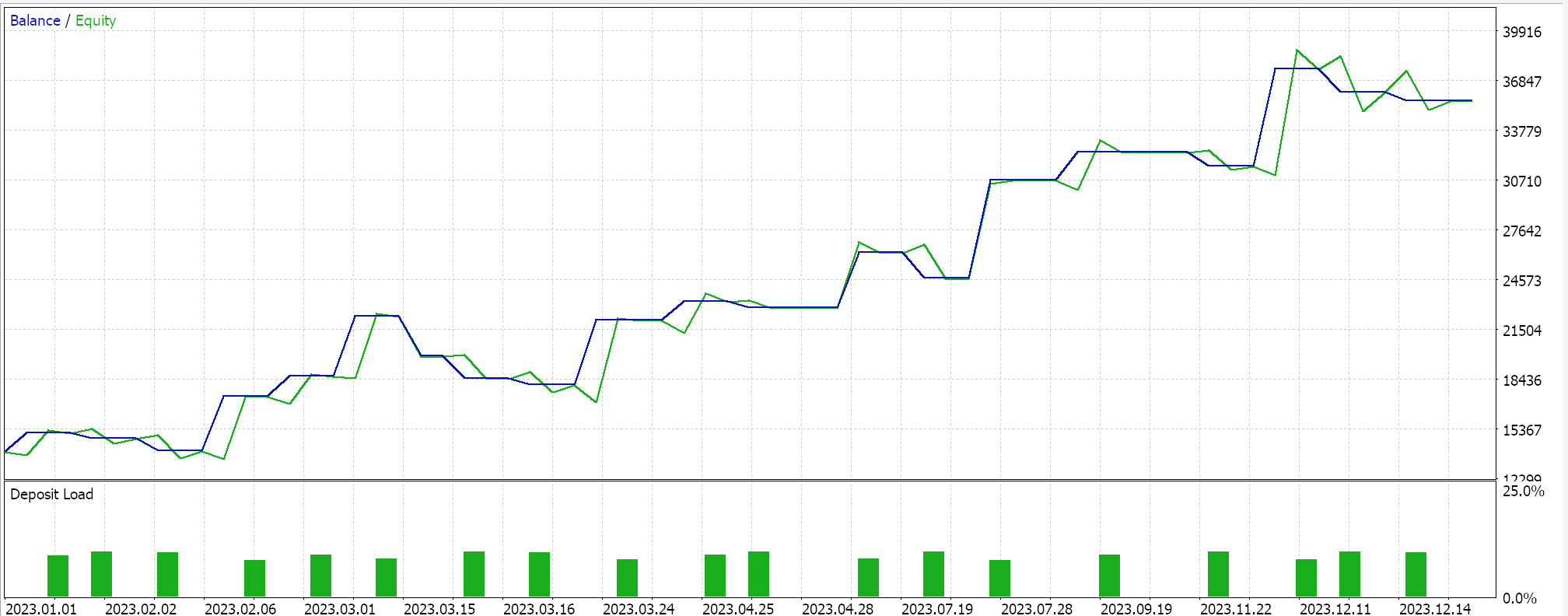
E, finalmente, para a média geométrica, temos:

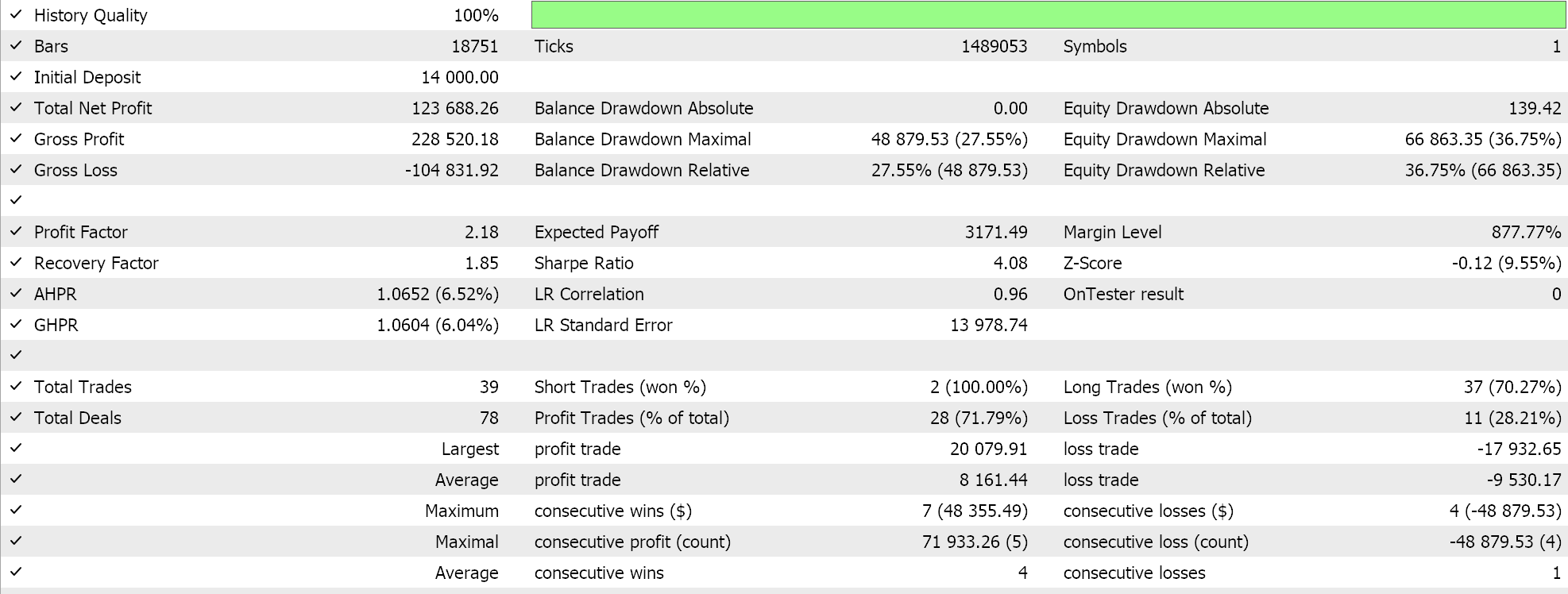
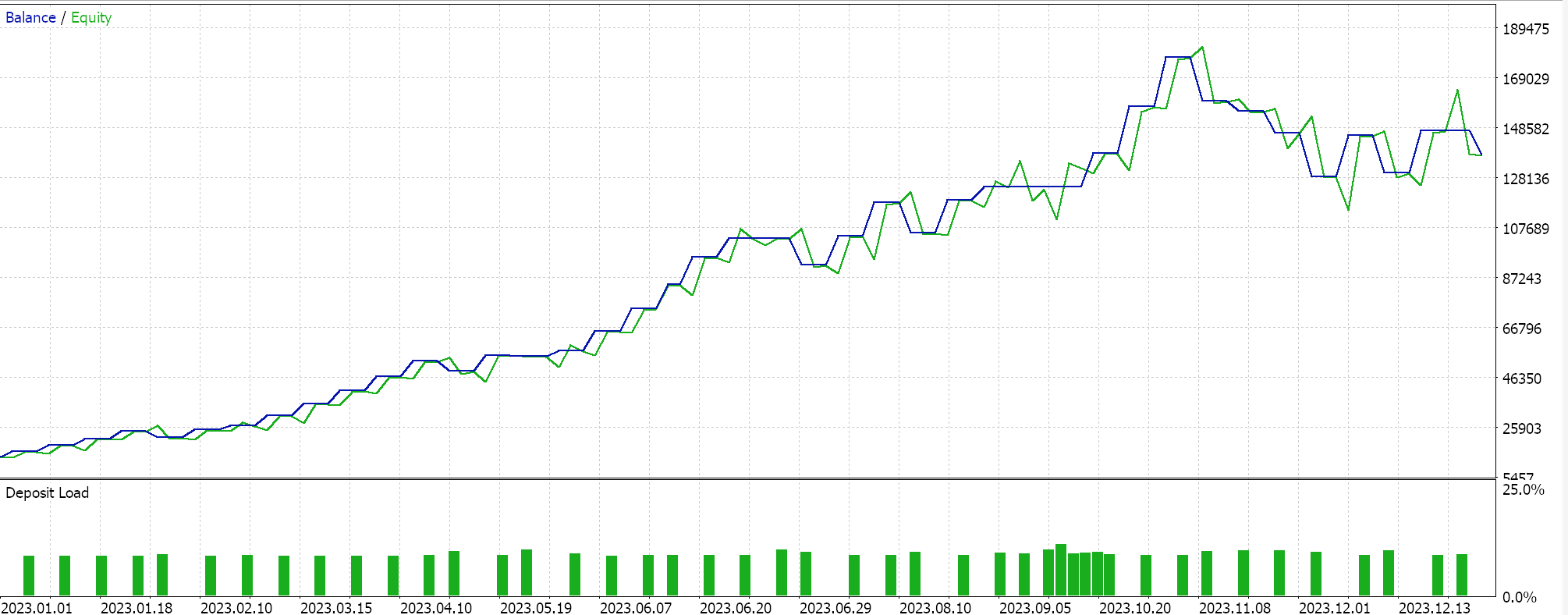
A partir do desempenho independente, parece que a média geométrica tem maior influência, seguida pela média aritmética de cruzamento simples, e a última é a divergência da média harmônica. Nossos resultados são, é claro, influenciados pelo fato de estarmos testando em um período muito curto e termos feito personalizações específicas em como interpretamos e implementamos os sinais de entrada para cada uma das médias. Mais testes são claramente necessários para tirar conclusões sobre o desempenho relativo, mas isso aponta para uma variabilidade relativamente ampla no desempenho, o que pode ser um sinal promissor em testes preliminares.

Se agora realizarmos testes com todas as três médias e tentarmos otimizá-las para a ponderação relativa, obtemos o seguinte como um dos melhores resultados:

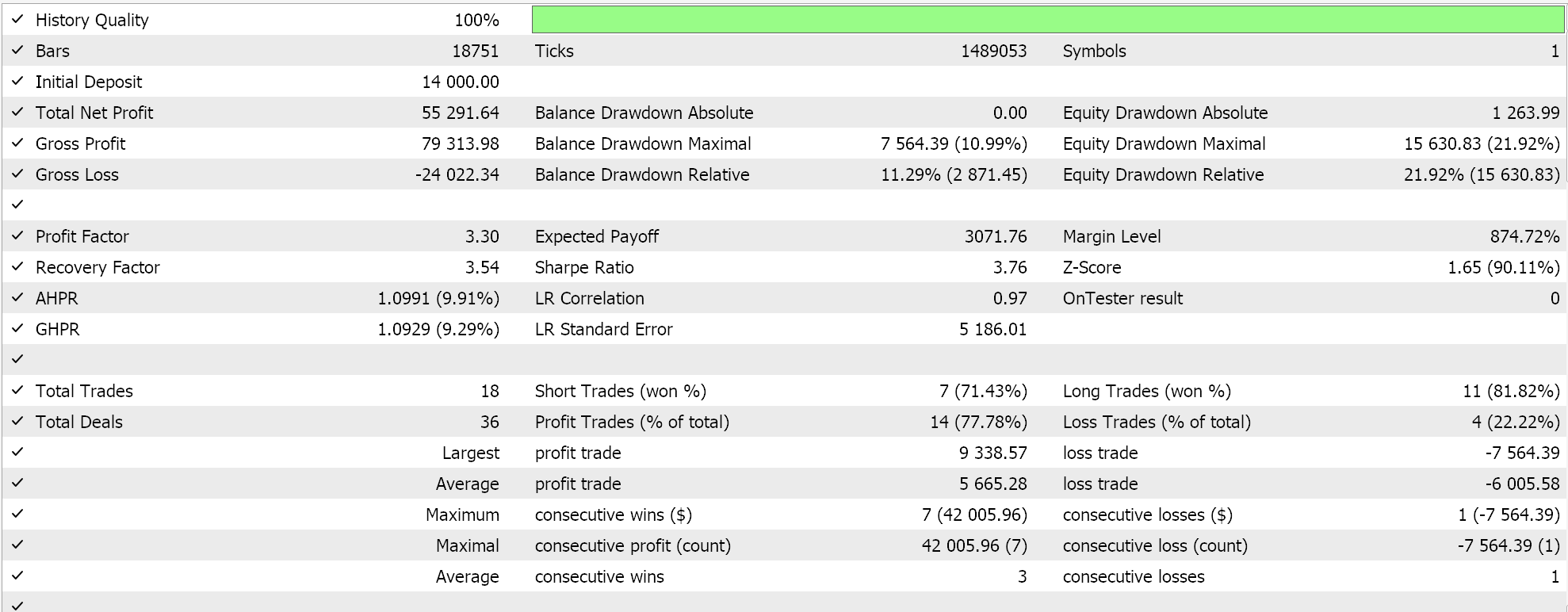
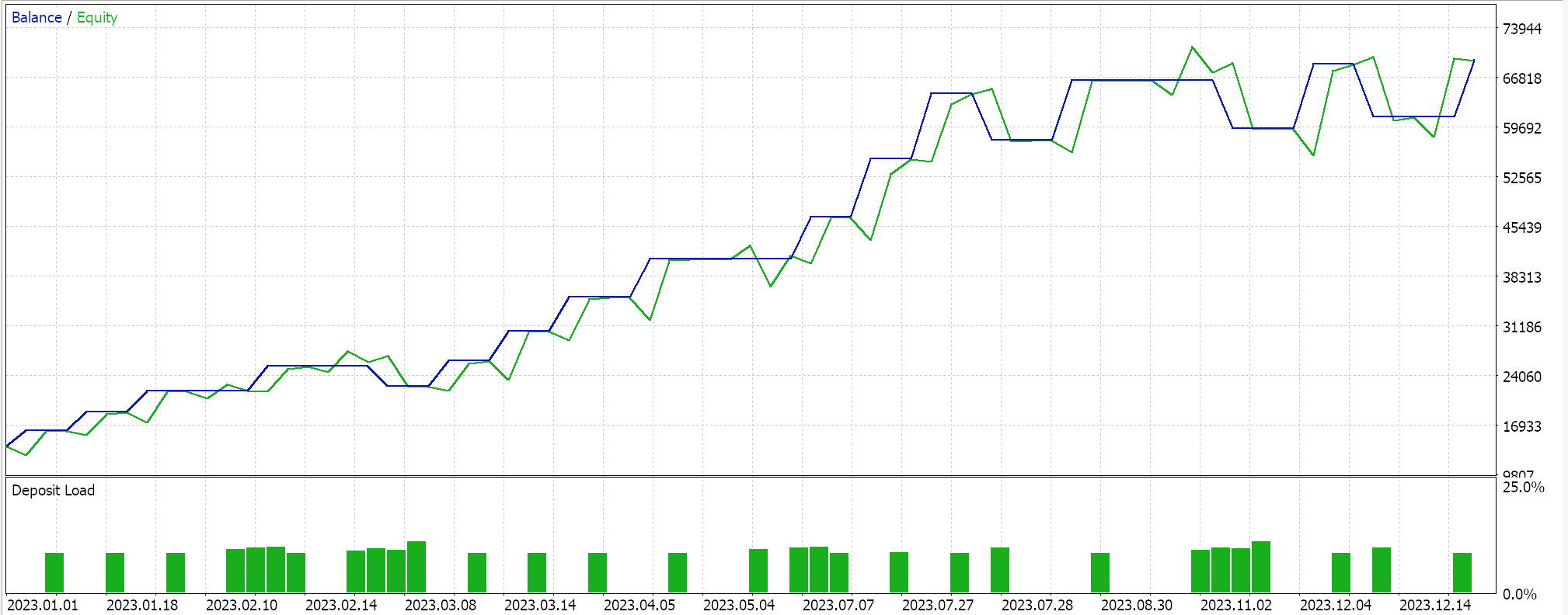
Claramente, os resultados independentes da média geométrica ainda são os melhores indicadores, embora sujeitos a testes em períodos mais longos. Interessante, ou ironicamente, para que os 3 sinais funcionem juntos, o melhor desempenho independente precisa receber a menor ponderação de 0,4. Os desempenhos independentes mais fracos da média harmônica e da média aritmética recebem ponderações maiores de 1,0 e 0,9, o que pode explicar por que o desempenho geral das três médias combinadas não é apenas menor que o desempenho independente da média geométrica, mas o desempenho da GM ainda é melhor, mesmo somando os desempenhos independentes da média aritmética e harmônica. As configurações para o Expert Advisor combinado estão compartilhadas abaixo:

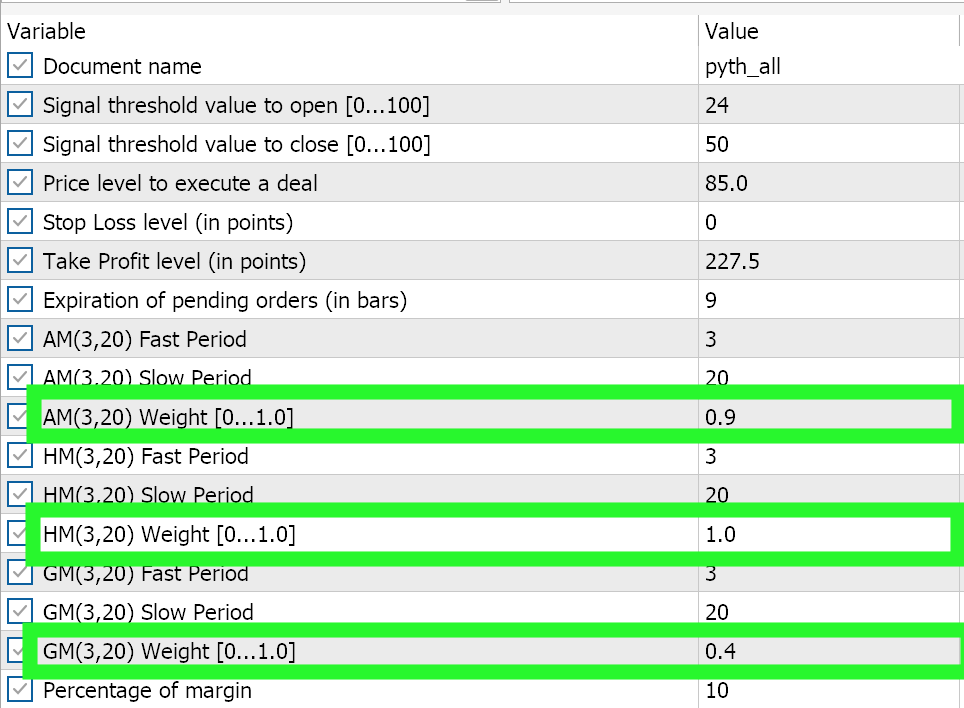
Conclusão

Desempenho passado não garante resultados futuros e, como já mencionado, testes extensivos, preferencialmente em períodos mais longos, são sempre recomendados e mais seguros do que realizar testes curtos, como o de um ano que temos aqui. Como sempre, montamos o código anexado para esses sinais seguindo as diretrizes compartilhadas nos artigos aqui e aqui. A média geométrica, que é a mais ponderada para valores menores das três médias consideradas neste artigo, mostra potencial na configuração das bandas de Bollinger. No entanto, não examinamos a média harmônica em uma configuração de bandas similar para ter conclusões mais definitivas sobre o desempenho relativo. E, além das Bandas de Bollinger, do cruzamento da AM ou da divergência da HM, existem outras implementações de médias móveis em forma de oscilador, como a OSMA ou o TRIX, que não exploramos. Esses e outros métodos podem ser considerados ao avaliar o potencial relativo das médias pitagóricas.