您应当知道的 MQL5 向导技术（第 16 部分）：配合本征向量进行主成分分析

概述

主成分分析（PCA）仅专注数据集众多维度中的“主成分”，如此这般通过忽略“非主成分”部分来降低该数据集的维度。或许最简单的降维示例就是如下所示的矩阵：

如果这是一个数据点，则可将其重新表示为单个值：

如此这般，一个值就意味着维度从 9 降到 1。我们上面的插图将矩阵简化为其行列式，这大致等同于降维。

然 PCA，配合本征值和向量，采取了稍微深入的方式。典型情况下，由 PCA 处理的数据集采用矩阵格式，自矩阵中查寻到的主成分，应当是其它矩阵向量中最重要的单列（或行），且足以代表整个矩阵。如上面的叙述中暗示，仅凭该向量即可包含整个矩阵的主成分，因此得名 PCA。识别这个向量并不一定必须通过本征向量和数值来完成，在于奇异值分解（SVD）和幂迭代都是其它备案。

SVD 能够将矩阵数据集拆分为 3 个单独的矩阵来达成降维，其中这 3 个矩阵之一，即 Σ 矩阵，标识数据中最重要的方差方向。这个矩阵也称为对角矩阵，包含奇异值，这些值表示沿每个预先确定的方向的方差量级（记录在 3 个矩阵中的另一个矩阵中，通常称为 U）。奇异值越大，在解释数据可变性时的相应方向就越重要。这导致了含有最高奇异值的 U 列被选作为整个矩阵的代表，其作为相当于将矩阵降维至单个向量。

相反，幂方法迭代细化向量估算，以便朝向主导本征向量收敛。该本征向量捕获数据中最明显变化的方向，并相当于一次原始矩阵的降维。

然而，配合本文所专注的本征向量和数值，我们能够将一个 n x n 矩阵简化为 n 个可能的 n 大小向量，每个向量都得以分配一个本征值。然后，由该本征值指导选择一个最能表示矩阵的本征向量，在解释数据可变性时，该值越高表示正相关程度越高。

如此，数据集降维的要点是什么呢？简言之，我觉得答案是管理白噪声。然而，一个更有谈资的响应是：提升可视化性，因为高维数据的绘制和呈现在散点图、和典型图形格式等媒体中更加麻烦。降维（绘图坐标）到 2 或 3，对此有所帮助。在预测时降低比较数据点的计算成本是另一个主要优势。

这种比较是在训练模型时完成的，如此可以节省训练模型的时间和算力。 这导致了“维数诅咒”，即在训练期间依据样本进行测试时，高维数据往往倾向准确的结果，但在交叉验证中，比之低维数据结果，这种性能磨损得更快。降维能帮助管理这种情况。此外，通过降维，数据集中的噪声趋于会减少，理论上应当会提高性能。最后，低维数据占用的存储空间更少，因此管理效率更高，尤其是在训练大型模型时。

PCA 和本征向量

形式上，本征向量由以下方程定义：

Av =λv

其中：

• A 是转换矩阵
• v 是要转换的向量
• a 和 λ 是应用于向量的比例因子。

本征向量背后的中心原则是，对于许多（但不是全部）大小为 n x n 的方阵 A，存在 n 个向量，每个向量的大小为 n，因此，当矩阵 A 应用于这些向量中的任何一个时，结果乘积的方向与原始向量的方向保持相同，唯一的变化是原始向量中数值的比例缩放。该缩放在上面的方程中称为莱姆德（λ），最好称为本征值。每个本征向量都有一个本征值。

并非所有矩阵都会产生所需数量的本征向量，因为有些矩阵会变形，不过对于每个生成的向量，都有一个候选原始矩阵的降维。在这些向量中选择获胜向量是基于本征值，数值越高表示能更好地捕获数据集的方差，且捕获的噪声较少。

识别本征向量的过程从归一化数据集矩阵开始，为此有少量选项可用。在本文中，我们使用 z-归一化。矩阵数据进行归一化后，然后计算协方差矩阵等效物。矩阵中的每个元素都捕获任意两个元素之间的协方差，对角线捕获每个元素与自身的协方差。使用协方差矩阵时，不光在计算本征向量和数值时计算效率更高，从协方差矩阵生成的数据值还捕获了矩阵中数据点之间的线性关系，并提供了矩阵中的每个数据点如何与其它数据点协变的清晰全貌。

针对矩阵数据类型的协方差矩阵的计算，由 MQL5 中的内置函数处理，在本例中为 'Cov()' 函数。一旦我们得到协方差矩阵，就可以通过内置函数 'Eig()' 来计算本征向量和数值。一旦我们得到本征向量及其各自的数值，我们转置本征向量矩阵，并将其与原始返回矩阵相乘。矩阵中的行表示每个组合的方差权重，如此所选组合将取决于这些权重。这是因为其方向表示采样数据集中数据的最大方差。

如果我们把椭圆曲线上的 x 和 y 坐标作为一个数据集，每个数据点都有 2 个维度 x 和 y，那么可以做一个简单的示例来概括捕获最大方差的点。如果我们在图表上绘制这个椭圆，它将如下所示：

源 

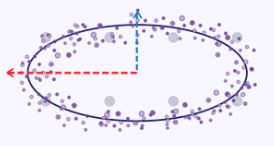
如此，当任务是将这些 x 和 y 维度降至单个（较少数量）维度的问题时，从上面的绘图中可以清晰地看到，x 坐标值将更好地代表两者，因为椭圆沿其 x 轴往往比其 y 轴伸展更多。

通常，仍需要在降维和保留信息之间权衡和平衡。而降维确实有它的益处，上面所列了阐述，且易于解释，都应当记住。

利用 MQL5 编码

使用 PCA 和本征向量的交易系统，典型做法是从一组不同的迭代中优化选择一个组合。为了概括这一点，我们可将上面讲述中看到的矩阵简单地视为向量的组成部分，其中每个向量代表在 3 种不同分配制度下，每种资产投资回报一美元。一旦选择了本征向量，且资产得以适度分配，则需要按向量排列，来进行未来投资，此刻每个向量（投资组合）的实际分配权重才变得重要。

如果我们的资产是 SPY、TLT 和 PDBC，那么基于这些 ETF 的 5 年回报率，其隐含分配为：

故此，带有本征向量的 PCA 的作用是帮助我们根据过去 5 年的表现，在这 3 个选项中选择一个理想的投资组合（资产配置）。如果我们回顾上述步骤，我们所要做的第一件事始终是归一化数据集，如前所述，我们为此采用了 z-归一化，以下源码执行该操作：

//+------------------------------------------------------------------+
//| Z-Normalization                                                  |
//+------------------------------------------------------------------+
matrix ZNorm(matrix &M)
{  matrix _z;
   _z.Init(M.Rows(), M.Cols());
   _z.Copy(M);
   if(M.Rows() > 0 && M.Cols() > 0)
   {  double _std_min = (M.Max() - M.Min()) / (M.Rows() * M.Cols());
      if(_std_min > 0.0)
      {  double _mean = M.Mean();
         double _std = fmax(_std_min, M.Std());
         for(ulong i = 0; i < M.Rows(); i++)
         {  for(ulong ii = 0; ii < M.Cols(); ii++)
            {  _z[i][ii] = (M[i][ii] - _mean) / _std;
            }
         }
      }
   }
   return(_z);
}

一旦我们归一化返回矩阵，我们就会计算我们已归一化对象的协方差矩阵。MQL5 内置的矩阵数据类型可在一行中为我们处理这个问题：

   matrix _z = ZNorm(_m);
   matrix _cov_col = _z.Cov(false);

有了矩阵中每个数据点的协方差关系，我们就可以计算出本征向量和本征值。同样是一行：

   matrix _e_vectors;
   vector _e_values;
   _cov_col.Eig(_e_vectors, _e_values);

上述函数的输出是双折叠的，我们感兴趣的是以矩阵形式返回的本征向量。当该矩阵与原始返回矩阵转置相乘时，为我们呈现出我们正在寻找的东西，即投影矩阵 P。这个矩阵的行，对应每个可能的投资组合，其中每行中的列代表对 3 个生成的本征向量中每个的权重。举例，在第一行中，最大值位于第一列。这意味着该投资组合回报的大部分方差都归因于第一个本征向量。如果我们查看这个本征向量的本征值，我们可以看到它是三个向量中最大的。因此，这意味着跨越所有三个投资组合，第一个投资组合占据了数据矩阵中所表示显著形态（或趋势）的主导。

在我们的案例中，如果它们的值按列求和，则所有投资组合都产生正回报，因为每列代表一个投资组合。事实上，唯一的负回报来自持有的债券 ETF PDBC，无关其分配。这意味着，如果打算“延续”这些对冲、或多元化、或良好的测试回报，他需要坚持使用投资组合-1。再一次，来自回报数据矩阵的总体主题，是股票和大宗商品的正回报，及来自债券的负回报。故此，带有本征向量的 PCA 可以从这些中筛选出最有可能延续这种趋势的投资组合，就像投资组合-1，甚或投资组合-1 的逆反情况所为，在我们的例子中是投资组合-3，因为在投影矩阵中，第 3 行的最大值在第 3 列中，而第 3 个本征向量的值最小。

值得注意的是，该投资组合未得到最好的回报，且该过程本身也未选择它。它的全部所为，只是为维持现状提供指示性权重。对于在调查时很容易做出的一个选择来说，这听起来太复杂且不必要，但是随着返回或所分析矩阵变得更大，行和列越来越多（具有本征向量的 PCA 需要方阵），那么该过程所做开始得到回报。

为了在信号类别中展示 PCA，我们受到约束，因为默认情况下，在单一时间帧上只能测试一个品种，这意味着我们上面关于投资组合选择的概念并非开箱即用的。有些做法能绕开这些约束，或许我们可以在将来的另一篇文章中涵盖它们，但现在我们要在这些限制内工作。

我们要做的是在日线时间帧上分析单个品种，一周中每天的价格变化。鉴于一周有 5 个交易日，我们的矩阵将有 5 列，为了获得 PCA 本征向量分析所需的 5 行，我们将研究 5 种不同的价格类型，即：开盘价、最高价、最低价、收盘价、和典型价。判定本征向量和数值将遵循上述步骤。

这同样适用于获取投影矩阵，一旦我们有了它，我们就可以轻松读取一周中的交易日，和应用的价格类型，这样可捕获大部分方差。如果我们遵循下面的脚本清单：

   matrix _t = _e_vectors.Transpose();
   matrix _p = _m * _t;
   //Print(" projection: \n", _p);
   vector _max_row = _p.Max(0);
   vector _max_col = _p.Max(1);
   double _days[];
   _max_row.Swap(_days);
   PrintFormat(" best trade day is: %s", EnumToString(ENUM_DAY_OF_WEEK(ArrayMaximum(_days)+1)));
   ENUM_APPLIED_PRICE _price[__SIZE];
   _price[0] = PRICE_OPEN;
   _price[1] = PRICE_WEIGHTED;
   _price[2] = PRICE_MEDIAN;
   _price[3] = PRICE_CLOSE;
   _price[4] = PRICE_TYPICAL;
   double _prices[];
   _max_col.Swap(_prices);
   PrintFormat(" best applied price is: %s", EnumToString(_price[ArrayMaximum(_prices)]));
   PrintFormat(" worst trade day is: %s", EnumToString(ENUM_DAY_OF_WEEK(ArrayMinimum(_days)+1)));
   PrintFormat(" worst applied price is: %s", EnumToString(_price[ArrayMinimum(_prices)]));

我们的策略测试和结果的日志打印输出，如下所示。

故此，从上面的日志中，我们可见周四和收盘价序列，担负了脚本所附图表品种的价格行为变化的大部分（脚本已附加到 EURJPY）。那么，这意味着什么呢？这意味着，如果一个人发现 EURJPY 的整体趋势和价格行为很有趣，且他愿意在未来进行类似的操作，那么他最好将交易集中在周四，并采用收盘价序列。假设 EURJPY 是一个人投资组合中一组持仓的一部分，且 EURJPY 正在前行的敞口正在缩小，如何做能对持仓矩阵有所帮助？“最差”的交易日和价格序列可用于判定何时、以及如何把 EURJPY 平仓。

故此，我们的持仓矩阵推荐交易日和价格序列，如此我们考虑到所有这些，使用下面的简单信号类。

   int _buffer_size = CopyRates(Symbol(), Period(), __start, __stop, _rates);
   PrintFormat(__FUNCSIG__+" buffered: %i",_buffer_size);
   if(_buffer_size >= 1)
   {  for(int i = 1; i < _buffer_size - 1; i++)
      {  TimeToStruct(_rates[i].time,_datetime);
         int _iii = int(_datetime.day_of_week)-1;
         if(_datetime.day_of_week == SUNDAY || _datetime.day_of_week == SATURDAY)
         {  _iii = 0;
         }
         for(int ii = 0; ii < __SIZE; ii++)
         {  
                ...

                ...
         }
      }
   }

策略测试和结果

为了执行利用 MQL5 向导组装的智能交易系统回溯测试，我们首先要在测试交易品种的图表和时间帧上运行脚本。至于我们的概括，这是 H4 时间帧上的 EURUSD。如果我们在图表上运行脚本，我们会得到周五和加权价格作为 4 小时 EURUSD 的“理想”或方差判定参数。如下日志中指示：

2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      best trade day is: FRIDAY
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      best applied price is: PRICE_WEIGHTED
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      worst trade day is: TUESDAY
2024.04.15 14:55:51.297 ev_5 (EURUSD.ln,H4)      worst applied price is: PRICE_OPEN

我们的脚本还有 2 个输入参数，用于判定所分析的区间，即开始时间和停止时间。两者都是 datetime 型变量。我们将这些设置为 2022.01.01 和 2023.01.01，以便我们可以首先在该期间测试我们的智能系统，然后在 2023.01.01 到 2024.01.01 期间按相同设置进行交叉验证。该脚本建议周五和加权价格作为最佳方差判定变量，如此，我们在开发信号类时如何使用这些信息呢？如常，有许多选项可以参考，我们将要查看的是简单价格 — 移动平均线交叉指标。按推荐采用应用价格的移动平均线，并且仅在推荐的工作日下单交易，我们将尝试交叉验证从脚本中呈现的论点。因此，我们的 EA 信号类的代码将非常简单，分享如下：

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalPCA::LongCondition(void)
{  int _result = 0;
   m_MA.Refresh(-1);
   m_close.Refresh(-1);
   m_time.Refresh(-1);
//
   if(m_MA.Main(StartIndex()+1) > m_close.GetData(StartIndex()+1) && m_MA.Main(StartIndex()) < m_close.GetData(StartIndex()))
   {  _result = 100;
      //PrintFormat(__FUNCSIG__);
   }
   if(m_pca)
   {  TimeToStruct(m_time.GetData(StartIndex()),__D);
      if(__D.day_of_week != m_day)
      {  _result = 0;
      }
   }
//
   return(_result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalPCA::ShortCondition(void)
{  int _result = 0;
   m_MA.Refresh(-1);
   m_close.Refresh(-1);
//
   if(m_MA.Main(StartIndex()+1) < m_close.GetData(StartIndex()+1) && m_MA.Main(StartIndex()) > m_close.GetData(StartIndex()))
   {  _result = 100;
      //PrintFormat(__FUNCSIG__);
   }
   if(m_pca)
   {  TimeToStruct(m_time.GetData(StartIndex()),__D);
      if(__D.day_of_week != m_day)
      {  _result = 0;
      }
   }
//
   return(_result);
}

如常，我们未使用止盈或止损的价格目标，并严格使用限价订单入场。这意味着一旦我们的智能系统开仓，它只会在逆转时平仓；可以说是一种高风险的方式，但出于我们的目的，这足矣。如果我们在第一个区间上进行回溯测试，我们会得到以下报告和净值曲线：

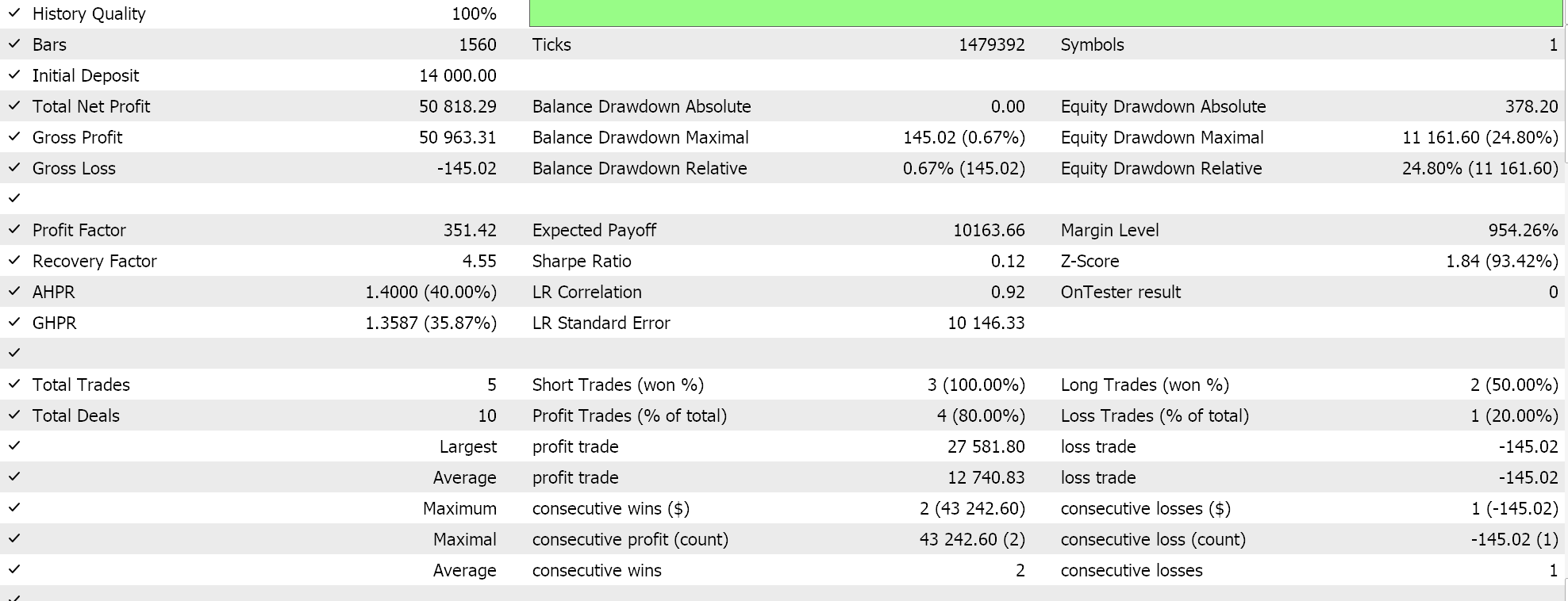
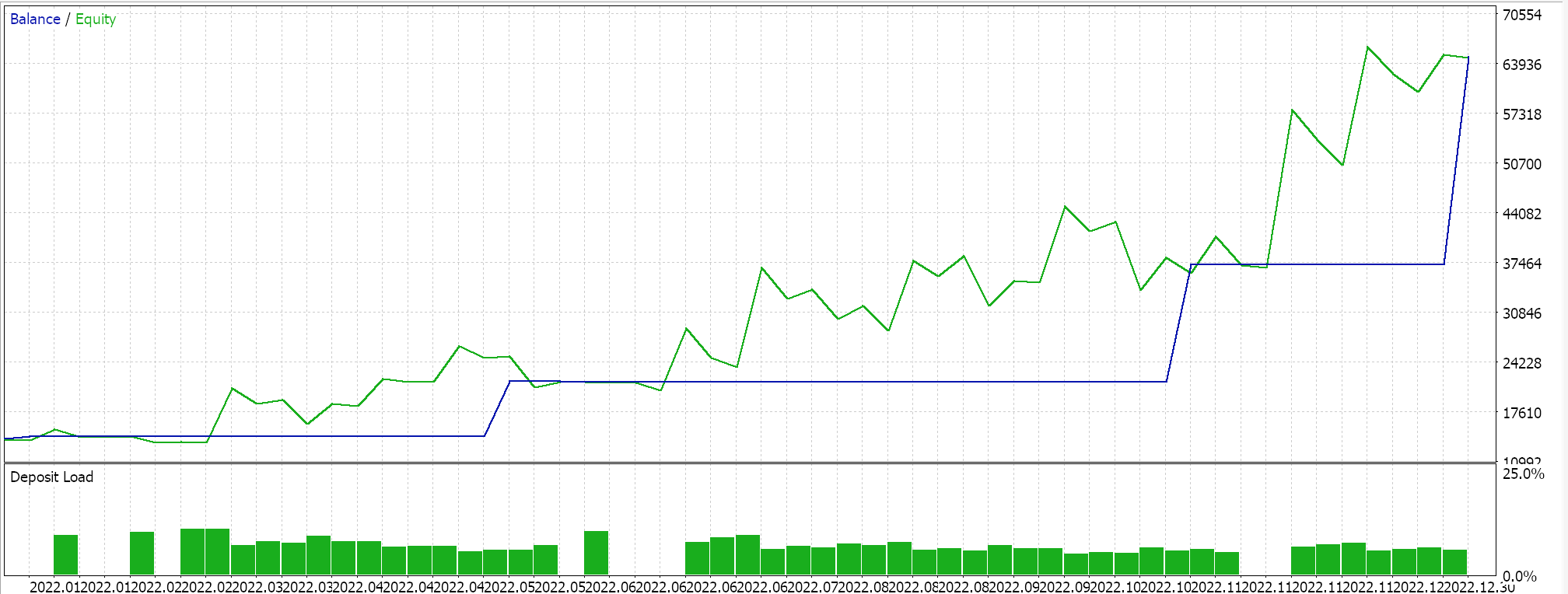
以上结果为 2022.01.01 至 2023.01.01。如果我们尝试覆盖 2022.01.01 到 2024.01.01 运行，在脚本分析区间之后的较长时间内按相同设置进行测试，我们将得到以下结果：

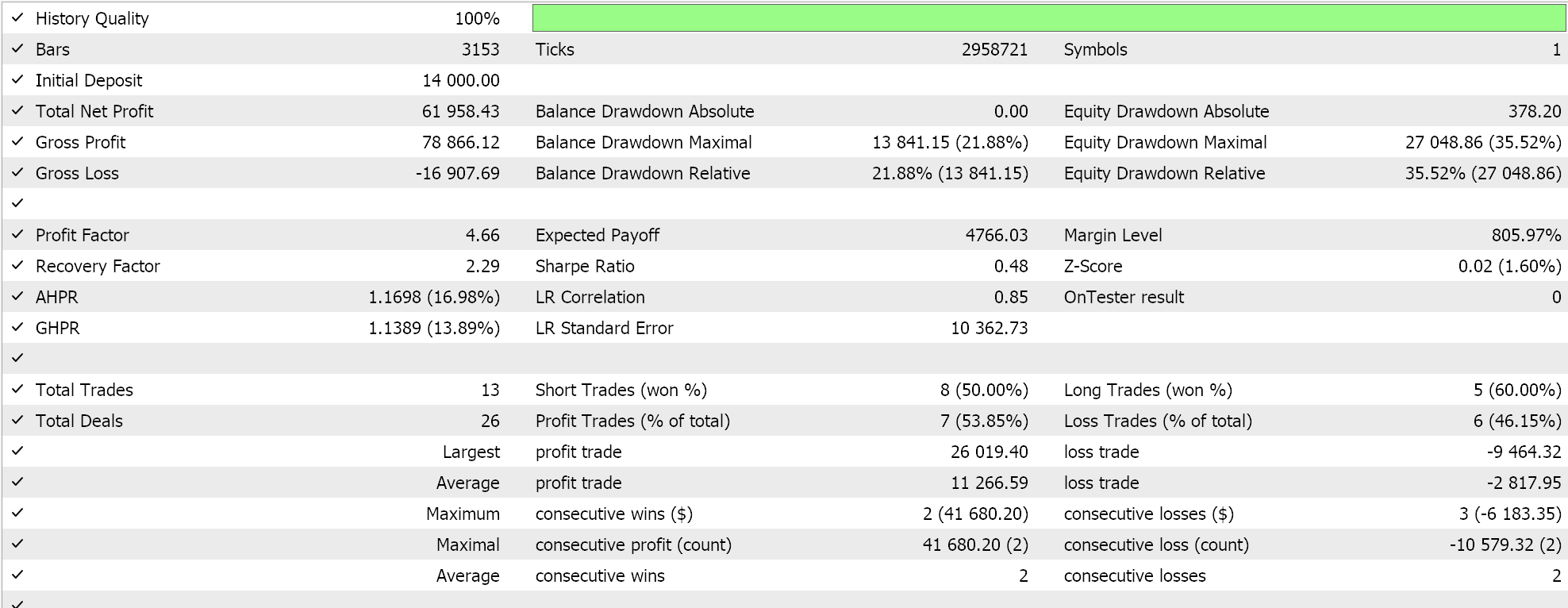
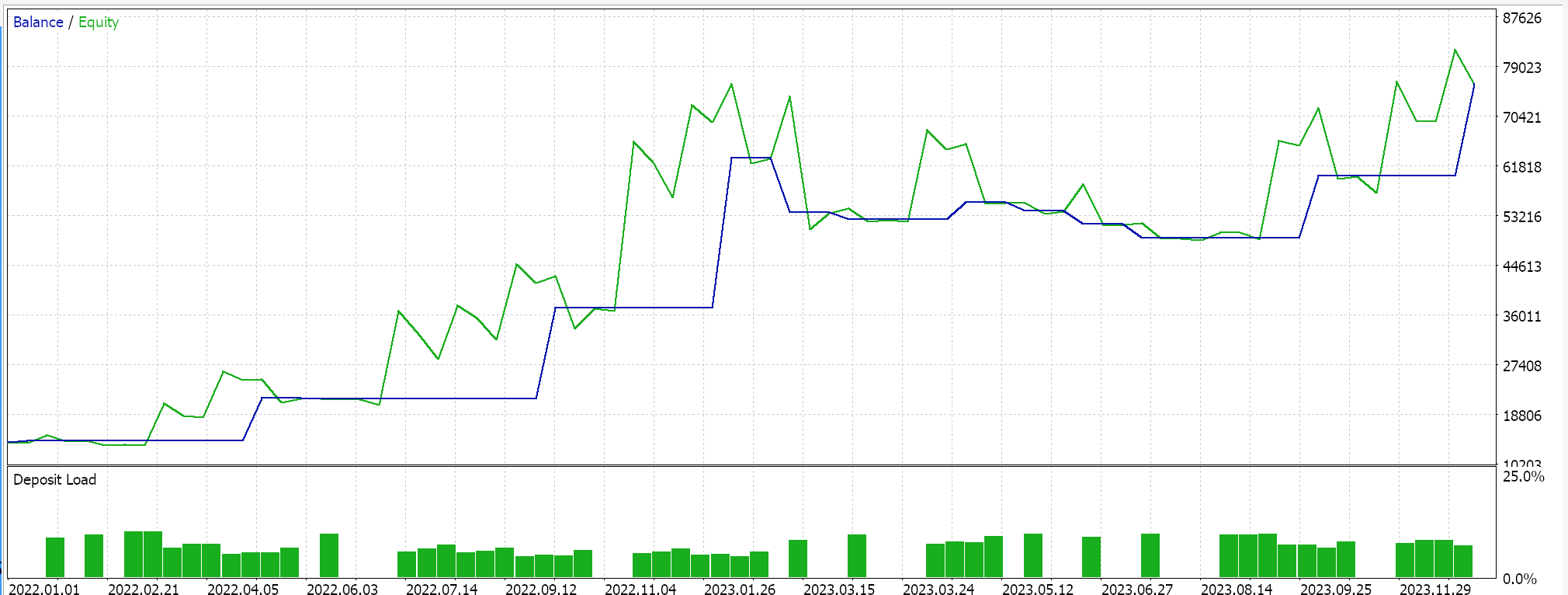
我们的智能系统有点受约束，没有太多交易，有人可能辩解说测试并不足够。无论如何，当考虑在真实账户运行时，太少年头的测试区间并不可靠。作为对照，除了上述交叉验证之外，我们还可以在一周中的任何一天按相同的智能交易系统设置进行交易，按不同的应用价格运行测试。这会产生以下结果：

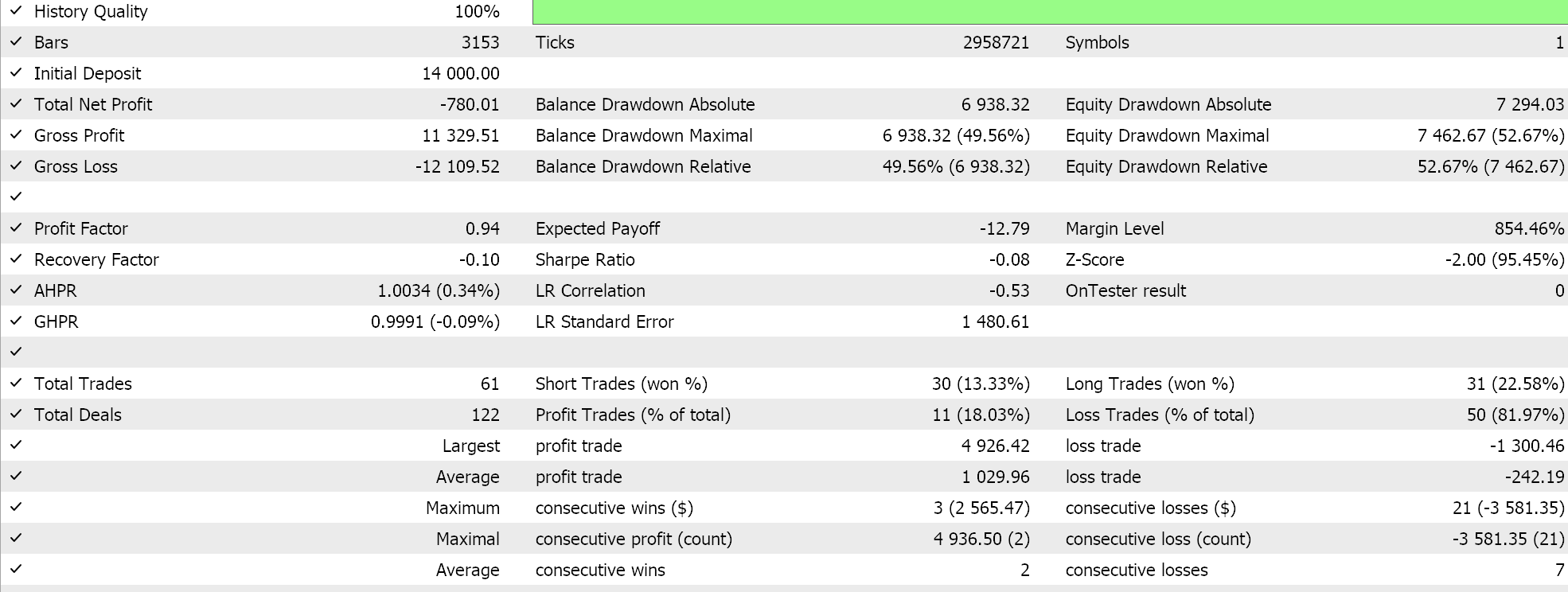
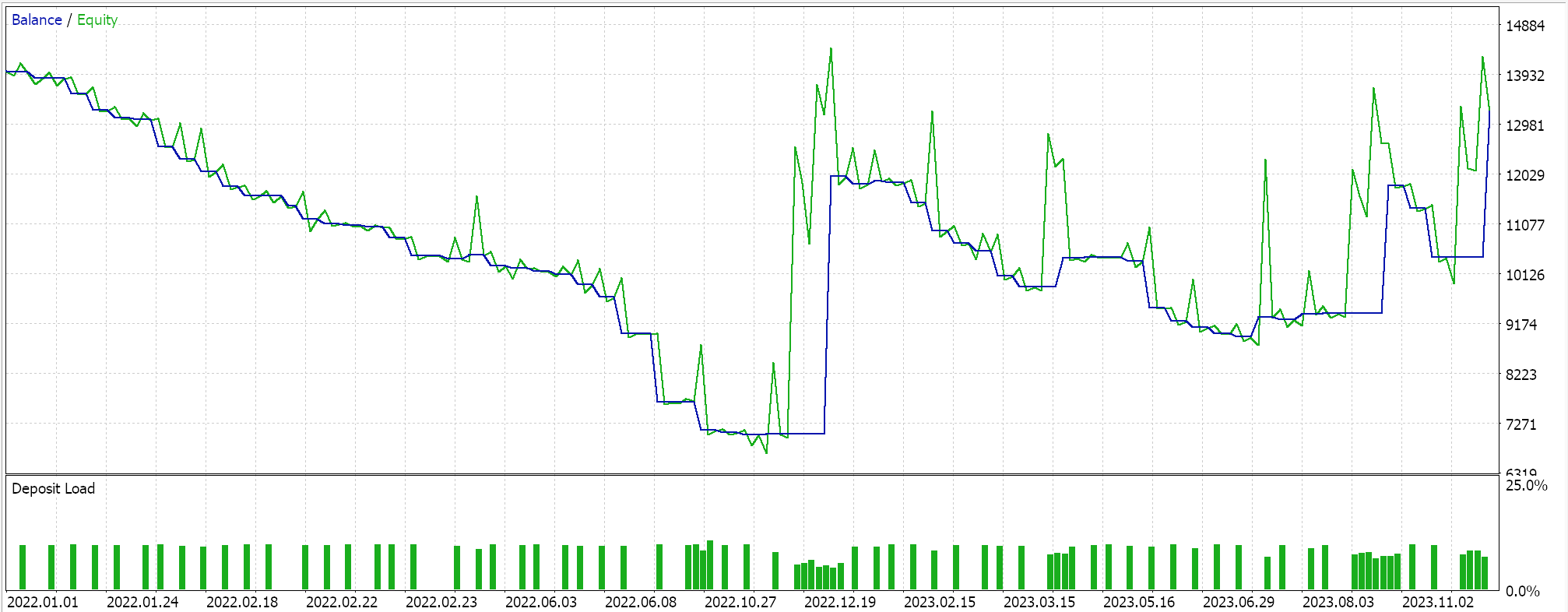
一旦我们偏离了 PCA 脚本的建议，整体性能清晰地遭受影响，但这是为什么呢？为什么仅在方差决定参数内进行交易给出我们的结果，比无约束设置更好？我觉得这是一个相关的问题，因为影响方差并不一定意味着更高的盈利能力，因为所研究数据集的整体趋势可能会反复折返。这就是为什么只有当所研究数据集中的潜在和整体趋势与交易者的总体意图一致时，才应该选择最大的方差决定设置。

如果我们查看 EURUSD 价格图表，我们可以看到在 2022.01.01 至 2023.01.01 的 PCA 分析区间，EURUSD 在 10 月份短暂逆转之前大多呈走低趋势。然而，在 2023 年的交叉验证期间，该货币对大幅波动，而没能像 2022 年那样出现任何主要趋势。这可能意味着，通过对主要趋势时期进行分析，可以更好地捕捉趋势设置方差参数，即使在 2023 年显而易见的状况下，它们也可能很实用。

结束语

总而言之，我们已见识到 PCA 本质上是一种分析工具，它试图通过识别判定其底层趋势主因的维度（或数据集的组成部分）来降低数据集的维度。有许多可用的工具可以降低数据维度，从表面上看，PCA 看似是空肠的，但它的所作所为需要谨慎的分析和解释，因为它总是基于所研究数据集的底层趋势。

在示例中，我们看到所研究品种在测试时的底层趋势是看跌的，且有基于此，在交叉验证中，样本以外的大多数交易都是空头。如果假设我们研究了所考虑品种的看涨行情，那么依据所推荐 PCA 设置，采用任何交易策略都必须立足于看涨环境。相反，在这些状况下，如果打算利用看跌行情，选择最不能解释方差的设置可能是有意义的，因为看跌行情和看涨行情是截然相反的。还有，PCA 会产生多对设置，每对设置都有一个权重，即本征值，这意味着如果它们的权重高于足够的阈值，则可以采用多个设置。本文没有对此进行探讨，欢迎读者进行研究，源代码附在下面。对于新手而言，可以在此处查找在 MQL5 向导中使用该代码组装智能交易系统的信息。

然而，在分析脚本和智能交易系统中可取的更多 PCA 设置时，应当首先归一化本征值，例如，它们都是正的，并且在 0.0 到 1.0 的范围内。完成该操作后，您就能定义选择阈值，以便从每个分析中选择本征向量。例如，如果 3 x 3 矩阵的 PCA 分析最初给出的值是 2.94、1.92、0.14，那么我们会将这些值归一化为 0 – 1 范围：0.588、0.384 和 0.028。配以归一化值，像 0.3 这样的阈值基准可以允许跨越多个分析公正地选择本征向量。配以不同数据集、甚至不同矩阵大小的重复分析，仍然可以按类似的方式选择其本征向量。对于脚本，这意味着遍历本征值，并将每个匹配值的 2 个交叉属性添加到输出列表或数组之中。该数组可以是在数据集矩阵中同时记录 'x' 和 'y' 属性的结构。配合智能系统，您需要在输入过滤器属性时，用逗号分隔字符串值，从而实现可伸缩性。这需要解析字符串，并提取属性，将其转换为智能系统可读的标准格式。