最適化におけるカスタム基準への新しいアプローチ（第1回）:活性化関数の例

はじめに

最適なパラメータの組み合わせを見つけるための理想的な最適化手法の追求は、今なお続いています。フォーラムでは、MetaTraderのオプティマイザにさまざまなパスを返し、それらをランク付けさせることで、開発者が安定したパラメータの組み合わせ（複数可）を選択できるようにするための提案が多数寄せられています。そこに、個人トレーダーに比べて遥かに厳格な制限を課すプロップファームが参入したことで、この課題はさらに難しくなりました。

カスタム基準の定義や、その背後にある不透明な方法論を持つ複雑な基準(Complex Criterion)の活用により、Excel、Python、R、または専用ソフトウェアを用いた結果の解析、もしくは少なくとも分析の手間を軽減し、最適なパラメータの組み合わせを導き出すことが可能になっています。

しかし問題は、依然としてreturn(0)を使用したカスタム基準が公開されることが珍しくない点です。これには、（わずかに）望ましくない結果を除外してしまう危険性や、さらに悪い場合には、遺伝的最適化プロセスを本来たどるべき有効な経路から逸らしてしまう可能性があり、実際的あるいは潜在的なリスクを伴います。

このような状況を踏まえ、基本に立ち返っていくつかの実験的な試みをおこない、いくつかの曲線方程式を探求しました。その過程で、「ニューラルネットワークにおける活性化関数」に着目し、いくつかの関数を本稿での活用を目的に採用・修正しました。さらに、それらをどのように実践に応用できるかについても提案しています。

本連載の計画は次のとおりです。

1. 標準的な活性化関数とMQL5コードの紹介
2. 修正、スケーリング、重み付け、および実例
3. 曲線の形状、スケーリング、重み付けを探索するツールの紹介
4. その他、関連する話題について

カスタム基準の現在の使用状況

私が深く敬意を抱いている2人の貢献者が、return(0)の使用や「複雑な基準」によって返される結果に対する懸念を述べ、この問題の本質を見事に指摘してくれました。フォーラムのモデレーターであるAlain Verleyen氏は、6,000の損失を出したパスが、1,736の利益を上げ、より多くの取引を含み、利益率・リカバリーファクター・シャープレシオ・ドローダウンのすべてで良好なスコアを記録したパスよりも高いスコアを得た事例を報告しています。Alain氏は、「この不可解な「複雑な基準」は奇妙な結果を返す」と述べています。私としては、それ以上に「複雑な基準」の背後にある方法論自体に重大な疑問を投げかけるものだと感じています。実際、同じスレッド内でMuhammad Fahad氏が後に述べているように（そして私も彼が正しいと確信しています）、「負のバランスの結果は最適化にとって必ずしも悪いものではなく、遺伝子が交差されるプロセスの中で、未来の世代が悪と最悪を見分ける判断基準として重要な役割を果たす」とのことです。そうであるなら、こうした損失パスに高スコアが与えられることは、遺伝的オプティマイザの判断を誤らせる原因となる可能性があるのです。

私が最後にMT4を使用したのは随分前のことですが、特定の結果統計に対して制約条件を設定できたように記憶しています。しかしMQL5では、一見したところ、それを実現するにはカスタム基準内でreturn(0)を使うという、非常に大雑把な方法しかないように思えます。そのリスクについてはすでに述べたとおりです。そこでふと思いついたのですが、もし各指標（比率やメトリック）が、設定した最低ライン以上・最高ライン以下、または特定のターゲット付近にあるときに、戻り値が1に近づくような関数を用意し、それらを掛け合わせた上で結果に100を掛けるという手法を取れば、何らかの有用な評価値が得られるのではないかと考えました。

ニューラルネットワークをインスピレーションの源にする理由

i) ニューラルネットワークとしての遺伝的最適化 

遺伝的アルゴリズムの背後にニューラルネットワークが存在するかどうかにかかわらず、その論理的なプロセスには類似性が見られます。すなわち、パラメータの組み合わせを試行し、それを（選択した最適化基準に従って）スコア付けし、将来的に有望な組み合わせを保持してさらなる改良に用い、残りを破棄する、というサイクルです。このプロセスは、スコアの改善が頭打ちになるまで繰り返されます。

ii) 谷、勾配爆発、重み付け、正規化、手動による選別 

非凸な誤差地形の問題は、機械学習の分野ではよく知られています。同様に、遺伝的最適化においてもreturn(0)のような文によって、アルゴリズムが有用な「知識」を捨ててしまい、局所的な最小値や鞍点に迷い込む可能性があると考えられます。

カスタム基準の構築において、複数のメトリクスを処理してスコアを生成する際には、多くの配慮が必要です。私の初期の試みは非常に粗削りで、さまざまな係数で割ったり掛けたり、指数関数を使ったりしていたため、スコアが異常に高くなる（いわゆる勾配爆発）という問題が発生していました。一方で、MetaTraderの「複雑な基準」スコアは、明らかにスコアを0〜100の範囲に収める関数を使用しており、これはシグモイド関数やロジスティック関数のようなものが使われている可能性を示唆しています。

カスタム基準の構成要素に対して重みを設定する必要性は明らかです。各メトリックの重要度を反映させるために重みを使い、また入力の正規化によってモデルの感度を調整し、出力の正規化によって異なるモデル間での比較を可能にする必要があります。これらの重み付けと正規化については、今後の記事で詳しく取り上げる予定です。

最適化の実行結果を、手動やスプレッドシートで確認する際、私たちはよく、各種の出力指標で並べ替えたり、フィルタをかけたり、主要なメトリックの色合いによってパラメータセットを直感的に選び出したりします。これはまさに、ここで述べてきた一連の処理を、私たち自身の知的判断プロセスを模倣する形で再適用しているに過ぎません。

ニューラルネットワークにおける活性化関数

私が探していた関数は、1、2年前に「Activation Functions in Neural Networks」を調べていたときに見つけた関数に似ていることに気づきました。

ニューラルネットワークの活性化関数は、大きく分けてバイナリ、線形、非線形の3種類に分類できます。

• バイナリ関数は、1または0を返すことで、値を2つのクラスのうちの1つに分類します。これらは私たちのユースケースではあまり有用ではありません。
• 線形関数は、単純な加算、乗算、減算、除算、またはそれらの組み合わせによって変換を返します。これらも、私たちのユースケースにはあまり役に立ちません。
• 非線形関数は、xの極端な値においては出力が制限されますが、0を中心とした範囲においてxの値を区別できるような曲線を返します。この範囲と中心は、オフセットによって調整することができます。

なお、

return(0);

のような記述や、複数の出力指標の積を無制限に返すような手法は、私自身も以前犯したことがあり、今でもフォーラムで見かけますが、いずれも前述の2種類（バイナリおよび線形）の問題を再現するような実装方法です。一方、非線形関数は、-∞から∞の範囲で勾配を保ちながらも、勾配爆発を防ぐよう制約されている傾向があります。

説明のために、いくつかの標準的な例を振り返っておきます。今回はReLU、Softplus、Sigmoid、Tanhについて見ていきます。また、次回の記事では、私自身が変更を加えたFlipped ReLU、Point ReLU、Flipped Sigmoid、Point Sigmoid、Flipped Tanh、Point Tanhについても取り上げる予定です。

a) ReLU活性化関数

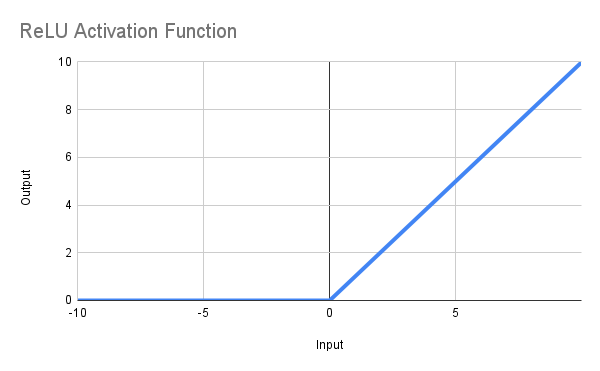
この関数の目的は、xが0以下の場合は0を返し、xが0より大きい場合にはxそのものを返すことです。数式で表すと、「f(x) = max(0, x)」となります。以下に示すような直線が得られ、MQL5での関数定義は次のように書くことができます。

double ReLU(double x) {
   return(MathMax(0, x));
}

ここまでは順調と言えるかもしれませんが、私はリカバリーファクターを最低でも5以上にしたいのです。そのためには、単にコードを次のように変更すればよいのです。*

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double ReLU(double x) {
   return(MathMax(0, x));
}

double ScoreRF = ReLU(DeviationRF);

このようにして線を右にシフトさせ、RF=5.0の地点を起点として、0から立ち上がるようになります（図に示す通り）。

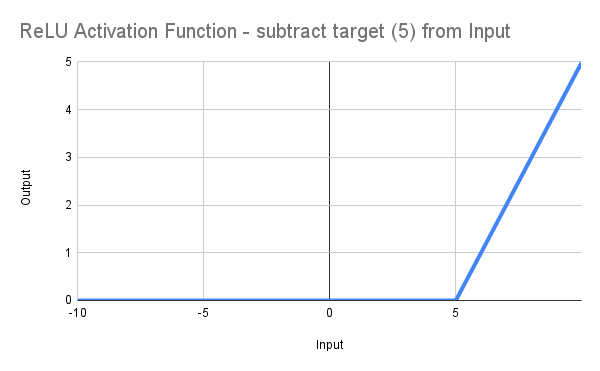
もちろん、これは*

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double ScoreRF = (RF - MinRF);

と書くのと大差ありませんが、出発点にはなります…

* 別の問題として、ターゲット値である5を入力しても、実際には0が返され、5を超える値のみが非ゼロを返すという点があります。ただしこの問題については、この関数には他にも多くの問題があるため、今回のユースケースでは実用性がないと判断し、深く掘り下げるつもりはありません。

問題点

やがて明らかになるのは、私たちが依然として2つの問題を抱えているということです。それはどちらも、コード自体が非常に単純であることに起因しています。先ほど、私は次のように述べました。

「もちろん、これは

input double MinRF = 5.0;
double RF = TesterStatistics(STAT_RECOVERY_FACTOR);


double ScoreRF = (RF - MinRF);

と書くのと大差ありませんが、これが出発点にはなります…」

ニューラルネットワークにおける問題点として、以下の2つは広く認識されています。

• Dying ReLU問題：ReLUの最大の弱点は、出力が常に0になることで、ニューロンが永続的に「死んでしまう」ことです。これは、入力が強く負の値になると勾配が0になり、その結果としてそのニューロンは活性化しなくなり、学習に寄与できなくなるという現象です。この問題はしばしば「勾配消失問題」とも呼ばれます。

• 出力の非制約性：ReLUは、正の入力に対して出力が無限に大きくなりうるという性質を持っています。一方で、SigmoidやTanhのような関数は、出力に上限（および下限）が存在するため、制約された動作になります。ReLUのように上限がない場合、深層ネットワークの学習中に勾配爆発が発生するリスクがあります。これは勾配爆発問題とも呼ばれます。

この2つ目の問題（出力の非制約性）は、統計学においては観測ウィンドウ全体で値を正規化することで対処されるのが一般的です。しかし、最適化アルゴリズムの制約下にある我々のケースでは、このような手法は利用できません。

したがって、私たちが必要としているのは以下のような機能を備えた関数です。

1. 数式的に制約を生成し、自動的な正規化を実現する
2. ある程度の線形性を保ち、入力が0未満のときのように完全に0を返すのではなく、サンプルの有意な範囲でスコアに差を出す

b) Softplus活性化関数

ここではこの関数について詳しく掘り下げるつもりはありませんが、ReLUとより高次の関数との中間段階として、参考までに簡単に触れておきます。Softplus関数についてはGeeksforgeeksでよく解説されており、ここでは図・数式・コードを以下に示すにとどめます。この関数はDying ReLU問題に対処していることは明らかですが、出力が無制限であるという問題は依然として残っています。さらに、Softplusには、左側の非常に緩やかなテール（尾部）から右側の傾きへと続く滑らかな遷移領域が存在するという特性があります。この点により、補正オフセットの検討が必要となるのです。この考え方については、後ほどあらためて取り上げます。

式はSoftplus( x ) = ln(1 + e ^x)で、MQL5コードは次の通りです。

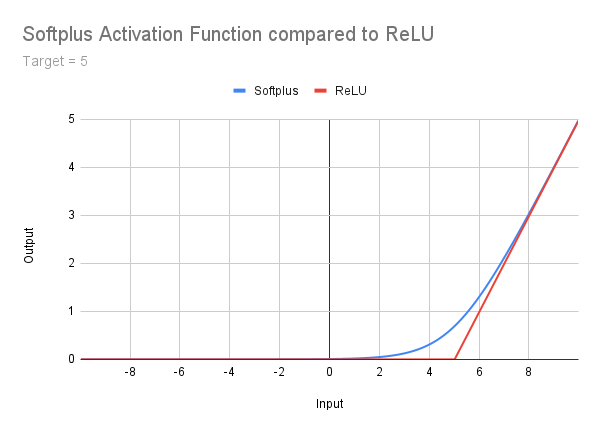
double Softplus(double x) {
   return(MathLog(1 + MathExp(x)));
}

興味があれば各自で詳しく調べてみてください。さて、ここからは出力が0から1の範囲に制約される関数を見ていくことにしましょう。

c) シグモイド活性化関数

シグモイド関数は数学的には「f( x ) = 𝛔( x ) = 1 / (1 + e ^(- x ))」と表されます。この関数は、Softplus関数の導関数と一致しており、MQL5では以下のように実装できます。

double Sigmoid(double x) {
   return(1 / (1 + MathExp(-x)));
}

下の曲線を見ると、すぐに次のことがわかります。

1. 出力が0から1の範囲に制限されており、Unconstrained Output（出力の非制約）問題を解決しています。

2. スケールの関係で視認しづらいものの、勾配は-∞から∞にわたって変化を保ち、決してゼロにはならない特性があります。 

3. シフトされていない元の曲線では、x=0のときにスコアが0.5になります。

3この3つ目の特性に対処するためには、xがしきい値（ターゲット値）に達したときにスコアが1に近づくように、曲線を左にシフトさせる必要があります。その際、単に閾値分だけでなく、補正値（通常は5以上）を加えてシフトすることで、実用上の調整をおこないます。 

よって、MQL5での実装は次のようになります。

input double MinRF = 5.0;
sinput double SigCorrection = 5;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double CorrectedSigmoid(double x) {
   return(1 / (1 + MathExp(-(x - SigCorrection))));
}

double ScoreRF = CorrectedSigmoid(DeviationRF);

以下に、ターゲット値を5とした場合の補正なしのシグモイド関数の曲線を示します。併せて、その導関数（4倍にスケーリングしたもの）も示しており、これは次に取り上げます。

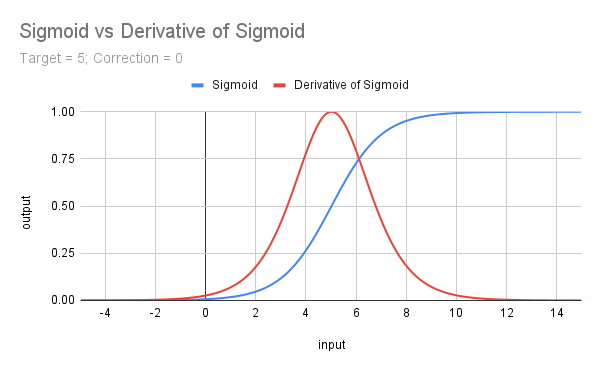
d) シグモイド関数の導関数（𝛔'）

この関数は、x=0を中心として最大値を持つ、きれいな形状をしています。これはシグモイド関数の傾きを表し、式はf(x) = 𝛔(x) - 𝛔^2(x) or 𝛔(x) * (1 - 𝛔(x))となります。 

この関数は（ここで取り上げる他の非線形関数と同様に）勾配消失問題の影響を受ける可能性があります。しかし、このリスクは、単純に関数を4倍することで軽減可能です（というのも、𝛔’(x)の最大値は0.25だからです）。この操作によって、結果が再び0〜1の範囲に制約されるという利点も得られます。また、この関数は特定のx値を中心に出力が集中するため、1つの点、あるいは正確にはその点を中心とした範囲をターゲットにすることが可能となります。

MQL5では次のようにできます。

input double TargetTrades = 100;

double Trades = TesterStatistics(STAT_TRADES);
double DeviationTrades = Trades - TargetTrades;

double Sigmoid(double x) {
   return(1 / (1 + MathExp(-x)));
}

double Deriv4Sigmoid(double x) {
   return(4 * (Sigmoid(x) * (1 - Sigmoid(x))));
}

double ScoreTrades = Deriv4Sigmoid(DeviationTrades);

補足：シグモイド関数、およびその導関数（4倍）、さらに次に紹介するTanh関数およびその導関数については、いずれも0〜1の範囲にスケーリングされているため、本番環境でさらにスカラー（重み係数）を加える必要はありません。もちろん、他の最適化指標と比較・統合する際には、それらに合わせて正規化したり、相対的な重要度を調整する目的で任意の係数を掛けることは可能です。この点については、次回の記事で詳しく取り上げることにします。

さて、最後に取り上げる標準関数が1つ残っています。それが、Tanh関数です。

e）双曲線正接関数(Tanh)

Tanhは、カスタム評価基準における実用性を探る本連載の中で、最後に取り上げる活性化関数です。これまでと同様の流れに沿って紹介しますが、説明は簡潔にしつつ、同じ原則を適用していきます。

以下のグラフは、Tanh関数とその導関数のプロットを示したものです。

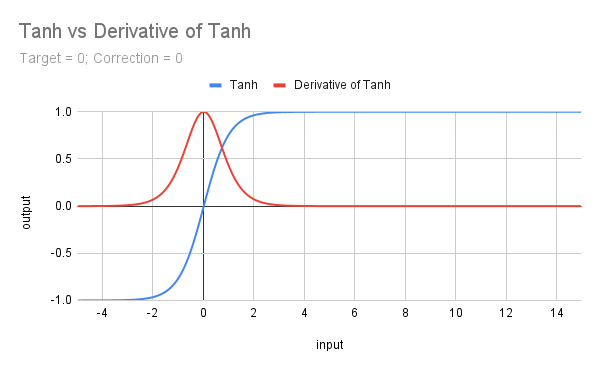
Tanh の式はf(x) = (e^x - e^(-x))/(e^x + e^(-x))であり、MQL5では独自の関数があるため、実装が簡単です。もちろん、ターゲット値や補正係数の扱いは必要ですが、それでも作業は簡単になります。

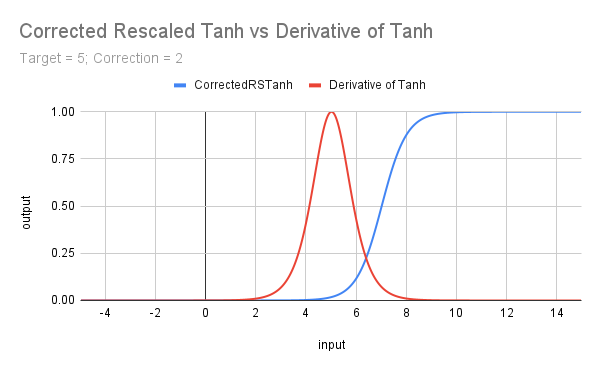
input double MinRF = 5.0;
sinput double TanhCorrection = 2.5; // Anything between 2 and 3 would be reasonable (see last figure)

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double CorrectedRSTanh(double x) {
   return((MathTanh(x  + TanhCorrection) + 1) / 2);  // rescaled and corrected
}

double ScoreRF = CorrectedRSTanh(DeviationRF);

上記のコードは、元の関数を0から1の範囲に収まるように（1を加えて2で割ることで）再スケールしています。また、補正係数とターゲット値を導入しており、その結果得られた曲線が、次のグラフに示すTanhの導関数**の形状となっています。Tanhの形状がシグモイド関数に似ており、またそれぞれの導関数も似通っている点は、見逃せない特徴です。これらの類似点については、次回の記事で詳しく探っていきます。

f) Tanhの導関数

Tanhの導関数の数式はf(x) = 1 - Tanh^2(x)です。

MQL5では次のようにできます。

input double TargetTrades = 100;

double Trades = TesterStatistics(STAT_TRADES);
double DeviationTrades = Trades - TargetTrades;

double DerivTanh(double x) {
   return(1 - MathPow(x, 2));

}double ScoreTrades = DerivTanh(DeviationTrades);

次のグラフは、Tanh関数をリスケールし、ターゲット（閾値）となるxの値に合わせて0からの立ち上がりを補正した効果を示しています。

まとめと今後のステップ

本記事では、一方で機械学習を、他方で遺伝的アルゴリズムや完全探索による最適化プロセス、さらにExcelや手動による後処理との関係について簡単に考察しました。また、様々な種類の活性化関数がカスタム基準の精緻化にどのように役立つか、その実装方法についても着手しました。

ReLUやSoftplusに見られる勾配消失や勾配爆発の問題を踏まえ、私たちはシグモイド関数やその導関数のような曲線を持つ関数に注目するようになりました。これらの関数は、スコアリングにおいて、単一の境界（例えばx > t）や二重境界（t1 < x < t2）の範囲を重視しつつ、勾配爆発の問題を解消し、勾配消失の問題を緩和することが可能であることがわかりました。

さらに、補正オフセットやターゲットオフセットの活用によって、評価対象の属性値の特定範囲に注目させる工夫についても考察しました。

次回の記事では、今回取り上げた標準的な関数群に対する、似ているが完全には同一でない改良版関数を検討します。また、スケーリングや重み付けの考え方を探り、最後に様々な関数を用いたカスタム評価基準の具体例も紹介する予定です。