パターン検索への総当たり攻撃アプローチ

はじめに

本稿では、市場パターンを検索し、特定されたパターンに基づいてエキスパートアドバイザーを作成し、これらのパターンが有効であるかどうかを確認します。この記事は、自己適応型の取引システムを作成する人にとって非常に役立つと思います。まず、外国為替取引における総当たり攻撃の概念の意味について説明します。一般に、総当たり攻撃アプローチでは、コードまたはその他の目的のために数値のシーケンスを決定する必要があります。このシーケンスを使用して、最終的に、最大の確率または最大の利用可能な確率で目的の結果を達成できます。暗号通貨を取得したり、アカウントやWi-Fiパスワードをハッキングするのが目的の場合もあります。適用範囲は非常に広いです。外国為替の場合、私たちのシーケンスは、可能な限り長く機能しながら最大の利益をもたらすはずです。シーケンスタイプと長さは任意です。唯一必要な条件はその効率です。シーケンスタイプは最終的にアルゴリズムに依存します。

このテクニックが特別で検討に値する理由

私は常に自分の考えを表現して、他のトレーダーにとって最大限の実用性を発揮できるようにしています。なぜそんなことをするかというのは、良い質問です。私は自分の経験を他のトレーダーと共有したいのです。見返りのあるなしに関係なく、誰かが私のアイデアを活用して、興味深く有益な何かを実装できれば幸いだと思いです。アイデアが完全に私のものではなく、車輪の再発明をしている場合があることはわかっています。私は、経験を共有し、可能な限り生産的に協力する必要性を信じています。おそらくこれが成功の秘訣です。他の人達から孤立して作業し、単独で重要なことを達成することは困難です。私の意見では、パターンのトピックは、市場の物理学を理解するために基本的に重要です。「トレーダーとしてのキャリア」というフレーズはおかしく聞こえるかもしれませんが、トレーダーとしてのキャリアは、基本的な考え方の理解に依存する可能性があります。私はこれらの質問を研究する人々の役に立つことを願っています。

総当たり攻撃とニューラルネットワークとの違いについて

ニューラルネットワークは本質的に一種の総当たり攻撃でもあります。しかし、そのアルゴリズムは単純な総当たり攻撃アルゴリズムとは大きく異なります。特定のニューラルネットワークアーキテクチャとその要素の詳細は提供しませんが、一般的な説明を提供しようとします。特定のアーキテクチャに固執する場合、事前にアルゴリズムの機能が制限されます。固定アーキテクチャは修復不可能な制限です。ニューラルネットワークは、私たちの場合、可能な戦略の一種のアーキテクチャです。その結果、ニューラルネットワークの構成は常にネットワークマップを持つ特定のファイルに対応します。これは常に特定のユニットのコレクションを指します。アイテムのパラメータを設定すると、プリンターがそれを生成するという、3Dプリンターの場合と同じです。したがって、ニューラルネットワークは、マップなしでは意味をなさない一般的なコードです。これは、高度なプログラミング言語を使用して、そのすべての機能を利用せずに空のプロジェクトを作成するようなものです。その結果、空のテンプレートは何もしません。ニューラルネットワークについても同じです。総当たり攻撃とは異なり、ニューラルネットワークは戦略にほぼ無制限の変動性、任意の数の基準、およびより高い効率を提供できます。このアプローチの唯一の欠点は、効率がコードの品質に大きく依存することです。システムの複雑さが増すと、プログラムのリソース集約度が高まる可能性があります。その結果、私たちの戦略は、同等のネットワークマップに変換されます。強引なアプローチでも同じことが行われますが、ここではいくつかの数字の単純なシーケンスを使用します。このシーケンスはネットワークマップよりもはるかに単純で、計算も簡単ですが、効率の点でも制限があります。以下のスキームは、上記の説明を表示します。

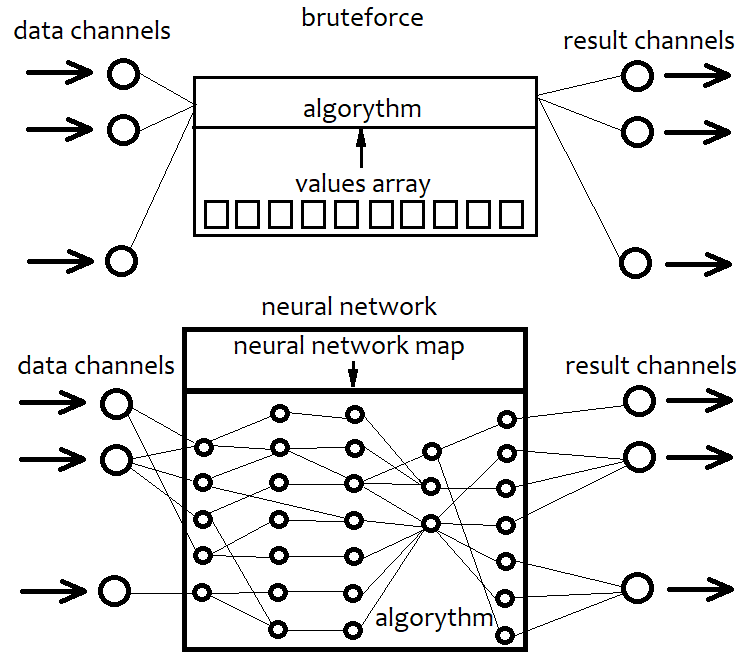
言い換えると、総当たり攻撃アプローチでは、コードと相互作用してさまざまな結果を生成する一連の数値を選択します。ただし、アルゴリズムは固定されているため、その柔軟性全体が数値の配列に含まれています。長さは固定されており、構造は非常に簡単です。ニューラルネットワークを使用する場合、最良の結果が得られるネットワークマップを検索します。いずれの場合も、特定のバイトシーケンス、または最終的に結果のアルゴリズムに変換されるデータを検索します。唯一の違いは、その機能と複雑さです。 

私の総当たり攻撃と最適化アルゴリズム

アルゴリズムで多変量テイラー展開を使用しました。これが私がこのアプローチを選択した理由です。非常に単純な、可能な限り可変のアルゴリズムを提供したかったのです。関数は最終的にテイラー級数またはフーリエ級数に展開できるため、特定の式に固執したくありませんでした。フーリエ級数はこの目的にはあまり適していないと思います。さらに、私は多次元フーリエには精通していないため、最初のバリアントを使用することにしました。さらに、その実装ははるかに簡単です。1次元のテイラー級数は次のようになります。

Y = Cs[0]+Cs[1]*(x-x0)^1 + Cs[2]*(x-x0) ^2 + ... + Cs[i]*(x-x0)^n

ここで、累乗の前の係数は、0からnまでの次数の導関数として機能します。これは、角かっこを展開することで、より単純な形式に変換できます。

Y = C[0]+C[1]*x^1 + C[2]*x^2 + ... + C[i]*x^n + ...= Sum(0,+infinity)(C[i]x^i)

この場合、変数は1つだけです。このシリーズは、選択したx0点の近くで連続的で微分可能な関数を模倣できます。式に含まれる用語が多いほど、関数はより正確に記述されます。それらの数が無限大に等しい場合が、私たちの関数と絶対的に等しいものです。ここでは、関数をテイラー級数に展開する方法については、ほとんど説明しません。この情報は、どの数学の本でも入手できます。しかし、一般式の変動性を高めるために複数のバーからのデータを使用したいので、1次元のバリアントでは十分ではありません。そのため、多次元バリアントを使用する必要があります。

Y = Sum(0,+Infinity)( C[i]*Product variant(x1^p1*x2^p2...*xN^pN) ) 

数式の他の変形はかなり難しいです。これは、1次元のバリアントと同じロジックを持っています。可能なすべての偏導関数を提供する必要があります。項の最大の累乗を制限すると、組み合わせと合計を使用してそのような項の総数を計算できます。私たちのアルゴリズムは、コンピューティングリソースの消費を制限するために、最高度の制限を使用します。 

しかし、これでも総当たり攻撃機能をより便利にするのに十分ではありません。最初の項C[0]を削除し、関数に入力する負または正の値に関して最大の対称性を持たせれば、より良くなります。また、便利な解決策は、正の関数値を買いシグナルとして解釈し、負の値を売りシグナルとして解釈することです。このシグナルのモジュラスの下限の増加は、理想的には期待されるペイオフと利益率の増加につながるはずですが、必然的にシグナルの数の減少にもつながります。関数がこれらの要件に近いほど、優れています。特定のローソク足の関数(Close[i]-Open[i])値を変数として入力します。

ここで行う必要があるのは、これらの係数のバリアントをランダムに生成し、そのバリアントがテスターでどのように動作するかを確認することです。もちろん、これらの係数を手動で繰り返す人は誰もいません。そのため、何千ものそのようなバリアントを維持しながらそのようなバリアントを生成できるエキスパートアドバイザー、またはストラテジーテスター機能の一部を実装するサードパーティソリューションが必要です。当初、私はそのようなエキスパートアドバイザーをMQL4で作成する必要がありました。このEAは、説明とともに記事に添付されているため、誰でも使用できます。ただし、C#で開発した別のアプリケーションを使用します。残念ながら、明らかな理由により、このアプリケーションを無料で提供することはできません。その機能は、研究分野をはるかに超えています。ただし、プログラミング方法を知っているすべての人がこのアプリケーションを再現できるように、そのすべての機能について説明およびデモンストレーションします。スクリーンショットは記事の後半で提供され、そこで操作結果を分析します。

アプリケーションの主な機能は次のとおりです。係数の配列の検索は2段階で実行されます。最初の段階では、ロードされた相場を検索して、次のローソク足で最大の期待ペイオフまたは最大の利益率を生成する配列を探します。ストラテジーテスターと同様のパスが実行されます。実際、それは単に次の小節の方向を最大の精度で予測する式を見つけようとしているだけです。最良の結果の特定の数は、アレイバリアントとしてメモリとディスクに保存されます。テストできるのは相場の一部のみです。ロードされた相場ファイルに対するパーセントをここで指定する必要があります。これは、第2段階でランダムな値を破棄できるようにするために使用されます。第2段階では、成行注文とバランス曲線をシミュレートします。これは、ロードされた領域全体に対して実行されます。同時に、シグナルの大きさの滑らかな増加が実行され、より良い品質のオプションが検索されます。このステージには、より滑らかなチャートを取得できるさまざまなフィルターもあります。チャートが滑らかであるほど、より良い式が見つかります。2番目の検索段階が完了すると、リストに視覚的に表示できる最適なオプションがいくつかあります。希望のオプションを選択すると、3番目のタブでMetaTrader4とMetaTrader5の自動売買ロボットを生成することができます。EAは、受信した番号が特定の場所で指定されている、コンパイル済みのテンプレートに従って生成されます。

タスクの簡単なテンプレートの作成

テンプレートは元々MQL4で作成され、その後MQL5に変換されました。コードは両方のプラットフォームに適合しています(前の記事のコードと同様)。解決策の適応にかかる時間を減らすために、この互換性を提供しようとしています。MQL4のように事前定義された配列を使用するには、以前の記事で説明したエキスパートアドバイザーにいくつかの追加コードを追加する必要があります。詳細については、その記事をご確認ください。この知識はこの記事に必要です。実際、それは難しいことではなく、どの開発者もそのような互換性を実装できます。ロボットの生成時に自動的に入力される変数と配列について説明することから始めましょう。

double C1[] = { %%%CVALUES%%% };//array of coefficients
int CNum=%%%CNUMVALUE%%%;//number of candlesticks in the formula
int DeepBruteX=%%%DEEPVALUE%%%;//formula depth
int DatetimeStart=%%%DATETIMESTART%%%;//start point in time
input bool bInvert=%%%INVERT%%%;//inverted trading
input double DaysToTrade=%%%DAYS%%%;//number of days into the future to trade

ここで、C1は、選択した度の前の係数の配列です。CNumは、多項式値の計算に使用される価格チャート上の最近のローソク足の数です。次は、多次元多項式の最大次数である式の深さです。私は通常1を使用します。これは、1次元のテイラー級数とは異なり、次数が増えると係数の総数が大幅に増えるため、次数が増えると計算がはるかに複雑になるためです。EAの操作時間を制限するには、操作の開始場所に関する情報が使用されるため、開始時点が必要です。逆関数は、多項式が正しい方向に機能することを保証するために使用されます。次数係数の前にあるすべての符号を反転すると、多項式自体は変化しませんが、多項式によって出力される数値のみが異なる符号を持ちます。ここで最も重要な部分は、係数の比率です。多項式の負の値が売りを示し、正の値が買いを意味する場合、inverse=falseです。そうでない場合は、trueです。したがって、アルゴリズムに「符号が反転した多項式の値を使用する」ように指示します。また、将来の取引の日数だけでなく、取引を反転できるようにする必要がある場合があるため、この変数を入力値にするtとより良くなります。

係数を使用して配列のサイズを計算する必要がある場合、これは次のように実行できます。

int NumCAll=0;//size of the array of coefficients
void DeepN(int Nums,int deepC=1)//intermediate fractal
   {
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {       
         DeepN(Nums,deepC-1);
         } 
      else 
         {
         NumCAll++;
         }
      }   
   }

void CalcDeepN(int Nums,int deepC=1)//to launch calculations
   {
   NumCAll=0;
   for ( int i=0; i<deepC; i++ )
      {
      DeepN(Nums,i+1);
      }   
   }

中間フラクタル関数は、すべての因子の合計次数が同じである項の数をカウントします。これは簡単にするために行われます。これは、用語を合計する順序はそれほど重要ではないためです。2番目の関数は、用語のタイプがある回数だけループ内の最初の関数を呼び出すだけです。たとえば、多次元級数展開がたとえば4に制限されている場合、1から4までのすべての自然数で最初の関数を呼び出します。

多項式値を計算する関数はほとんど同じです。ただし、この場合、配列はそれ自体で生成されるため、サイズを設定する必要はありません。これは次のようになります。

double ValW;//the number where everything is multiplied (and then added to ValStart)
uint NumC;//the current number for the coefficient
double ValStart;//the number where to add everything
void Deep(double &Ci0[],int Nums,int deepC=1,double Val0=1.0)//calculate the sum of one degree
   {
   for ( int i=0; i<Nums; i++ )
      {
      if (deepC > 1)
         {
         ValW=(Close[i+1]-Open[i+1])*Val0;      
         Deep(Ci0,Nums,deepC-1,ValW);
         } 
      else 
         {
         ValStart+=Ci0[NumC]*(Close[i+1]-Open[i+1])*Val0/Point;
         NumC++;
         }
      }   
   }
   
void CalcDeep(double &Ci0[],int Nums,int deepC=1)//calculate the entire polynomial
   {
   NumC=0;
   ValStart=0.0;
   for ( int i=0; i<deepC; i++ )
      {
      Deep(Ci0,Nums,i+1);
      }   
   }

計算されたものはすべてValStartに追加されます。つまり、結果はグローバル変数に追加されます。別のグローバル変数が必要で、これはValWです。これは、既存の製品に何らかの値を掛けるために使用されます。私たちの場合、これは対応するバーのポイント単位の動きです。動きは上下両方にできます。これは符号で示されています。したがって、これらの関数は非常に興味深い構造を持っています。それらは自分自身を内部で呼び出し、これらの呼び出しの数と構造は常に異なります。これは一種のコールツリーです。これらの関数は非常に可変であるため、私はこれらの関数を使用するのが本当に好きです。今回は、多次元テイラー級数をシンプルかつエレガントな方法で実装しました。

多項式の1次元バージョンのみが使用される場合に備えて、追加の関数を実装することもできます。この場合、シリーズ全体が非常に簡素化されます。これは、係数の合計に1次のバーの1つの動きを掛けたものになります。それらの数は使用済みバーの数と同じになります。これにより、すべての計算が簡素化されます。次数が1の場合、簡略化されたバージョンが使用されます。それ以外の場合は、あらゆる程度のより普遍的な方法が使用されます。

double Val;
double PolinomTrade()//optimized polynomial
   {
   Val=0;
   if ( DeepBruteX <= 1 )
      {
      for ( int i=0; i<ArraySize(C1); i++ )
         {
         Val+=C1[i]*(Close[i+1]-Open[i+1])/Point;
         }
      return Val;   
      }
   else
      {
      CalcDeep(C1,CNum,DeepBruteX);
      return ValStart;
      }      
   }

単純なバリアントを使用すると、結果がVal変数に追加されます。

次に、新しいバーが表示されたときに呼び出されるmainメソッドを記述しましょう。

void Trade()
   {
   double Value;
   Value=PolinomTrade();
   
   if ( Value > ValueCloseE)
      {
      if ( !bInvert )
         {
         CloseBuyF();
         }      
      else 
         {
         CloseSellF();
         }
      }
      
   if ( Value < -ValueCloseE)
      {
      if ( !bInvert )
         {
         CloseSellF();
         }      
      else 
         {
         CloseBuyF();
         }      
      }   
   
   if ( double(TimeCurrent()-DatetimeStart)/86400.0 <= DaysToTrade && Value > ValueOpenE && Value <= ValueOpenEMax )
      {
      if ( !bInvert ) SellF();
      else BuyF();
      }
      
   if ( double(TimeCurrent()-DatetimeStart)/86400.0 <= DaysToTrade && Value < -ValueOpenE && Value >= -ValueOpenEMax )
      {
      if ( !bInvert ) BuyF();
      else SellF();
      }

   }

この関数は非常に単純です。する必要があるのは望ましいポジション開閉関数を実装することです。

バーの出現は次のように検出できます。

void CalcTimer()
   {
   if ( Time[1] > PrevTimeAlpha )
       {
       if ( PrevTimeAlpha > 0 )
          {
          Trade();
          }
       PrevTimeAlpha=Time[1];
       }
   }

コードは非常に簡単で明確だと思います。

コードによって生成された係数は、上記で説明した4つのモデルを使用して作成されています。便宜上、値の比率は値自体よりも重要であるため、これらの係数はすべて[-1,1]の範囲にあります。MQL5プログラムのプロトタイプからこれらの数値を生成する関数は次のようになります。

   void GenerateC()
      {
      double RX;
      if ( DeepBrute > 1 ) CalcDeepN(CandlesE,DeepBrute);
      else NumCAll=CandlesE;
      for ( int j=0; j<VariantsE; j++ )
         {
         ArrayResize(Variants[j].Ci,NumCAll,0);
         Variants[j].CNum=CandlesE;
         Variants[j].ANum=NumCAll;
         Variants[j].DeepBruteX=DeepBrute;
         RX=MathRand()/32767.0;
         for ( int i=0; i<Variants[j].ANum; i++ )
            {
            if ( RE == RANDOM_TYPE_1 ) Variants[j].Ci[i]=double(MathRand())/32767.0;
            if ( RE == RANDOM_TYPE_2 )
               {
               if ( MathRand()/32767.0 >= 0.5  )
                  {
                  Variants[j].Ci[i]=double(MathRand())/32767.0;                  
                  }
               else
                  {
                  Variants[j].Ci[i]=double(-MathRand())/32767.0;                  
                  }
               }
            if ( RE == RANDOM_TYPE_3 )
               {
               if ( MathRand()/32767.0 >= RX  )
                  {
                  if ( MathRand()/32767.0 >= RX+(1.0-RX)/2.0  )
                     {
                     Variants[j].Ci[i]=double(MathRand())/32767.0;
                     ///Print(Variants[j].Ci[i]);
                     }
                  else
                     {
                     Variants[j].Ci[i]=double(-MathRand())/32767.0;                  
                     }        
                  }
               else
                  {
                  Variants[j].Ci[i]=0.0;                  
                  }
               }
            if ( RE == RANDOM_TYPE_4 )
               {
               if ( MathRand()/32767.0 >= RX  )
                  {
                  Variants[j].Ci[i]=double(MathRand())/32767.0;
                  }
               else
                  {
                  Variants[j].Ci[i]=0.0;                  
                  }
               }                              
            }
         }
      }

MQL4およびMQL5の総当たり攻撃プロトタイプは、記事の添付ファイルで入手できます。目的はテンプレートのフレームワーク内でアプローチを実装する方法を示すことだけなので、ここでは取引関数の実装を提供しません。実装全体を表示することに興味がある場合は、添付ファイルを確認してください。すべてのエキスパートアドバイザーおよびその他の必要な資料は、この記事の添付ファイルにあります。一般的に、私のテンプレートには、不要な関数や変数など、非常に多くの過剰なものがあり、何らかの方法で最適化できます。個人的には気にしません。動作に支障が生じた場合は削除します。私にとってもっと重要なことは、今ではすべてがうまく機能しているということです。私は常に何かを開発しているので、細部を完璧にする時間がありません。また、すべてのプロシージャと変数をクラスに格納する理由はありませんが、これによりコードの順序と読みやすさが向上する可能性があります。テンプレートは非常に簡単です。プログラムで使用される相場を持つファイルは、履歴を実行し、プログラムで簡単に読み取れる構造のテキストファイルにバーデータを書き込む特別なエキスパートアドバイザーによって生成されます。このEAのコードは簡単に開発できるため、ここでは提供しません。

パターンを見つけて分析するためのプログラムの使用

私は分析のために3つの市場領域を選択しました。それらはそれぞれ1か月の長さを持ち、互いに連続します。EURUSD, M5.

• 期間1:  2020.01.13 - 2020. 02.16
• 期間2:  2020.02.13 - 2020.03.15
• 期間3:  2020.03.13 - 2020.04.18

期間は、最終日が常に金曜日になるように選択されています。そして、ご存知のように、金曜日は週の最後の取引日です。このように間隔を選択すると、取引所が再び取引を開始するまで、丸2日でパターンを検索できます。これは一種の小さなライフハックです。私たちの場合、EAをテスターでテストするため、これは問題ではありません。ここでは、見つかったパターンの12のバリエーションについて説明することにしました。それらのうちの6つは、最大次数が1の多項式になります。他の6つは最大次数2になります。これで十分だと思います。

プログラムの最初のタブは次のようになります。

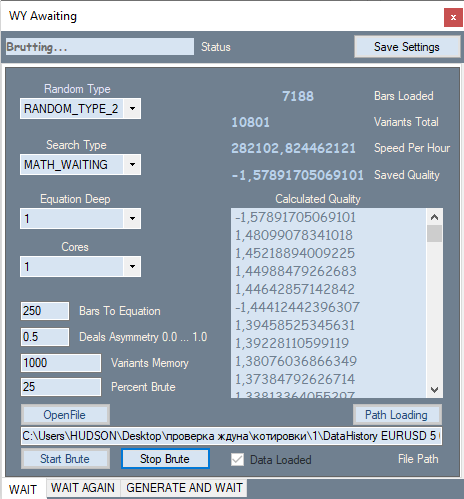
たとえば、正、正と負、正とゼロ、正と負、ゼロのみといった、数値生成タイプを変更することが可能性になります。検索基準は、2番目のComboBoxで構成されます。ポイントの期待値と利益係数式の私の2つの可能なオプションがあります。私の式では、この値の範囲は-1から+1です。また、除算誤差がゼロのため、利益率が計算できない場合もありません。

P_Factor=(Profit-Loss)/(Profit+Loss).

次に、計算に使用される多項式の最大次数とプロセッサコアの数が表示されます。テキストブロックで、多項式のバーの数または計算の数、および前の式と非常によく似た私自身が発明した取引非対称係数を指定します。

D_Asymmetry=|(BuyTrades-SellTrades)|/(BuyTrades+SellTrades).

その値は0から1の範囲です。このフィルターは、グローバルトレンド中にすべての取引が同じ方向に実行される状況を回避するために、同じ数の売買シグナルを持つようにプログラムに指示する必要がある場合に必要です。次は、メモリに保存する必要がある、見つかったすべてのバリアントからの最良のバリアントの数と、ロードされた見積もりの何パーセントが総当たり攻撃の反復に使用されるかです。このセクションは、最後のバーが開いた時間までに測定され、その後のセクションが最適化に使用されます。残りのインディケーターとバリアントを含むリストについては、十分に単純なので説明しません。

2番目のタブは次のようになります。

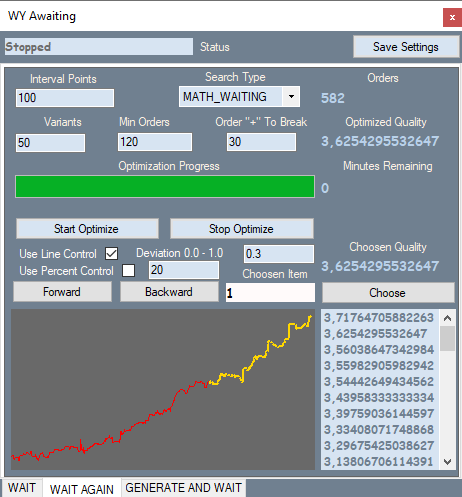
このタブは、ロボットの最初のセクションの最初のバリエーションに対応しています。私のプログラムのグラフをテスターグラフと比較することができます。これを以下に示します。総当たり攻撃が実行された相場の部分の注文は黄色で示され、他の注文は赤で示されています。ここでは、すべてのバリアントのスクリーンショットを提供しません。それらはすべて、添付ファイルで入手できます。

タブの内容を見てみましょう。区間ポイント — 多項式の値の区間を分割します。最初のタブで総当たり攻撃を実行すると、バリアントの主なパラメータと、この多項式のモジュロ最大値が計算されます。したがって、多項式の値のウィンドウがわかっており、このウィンドウを等しい部分に分割して、値を徐々に増やし、より強いシグナルを検出しようとすることができます。これは2番目のタブで行われます。このタブには、検索タイプと、最適化メモリに保存されている最適なバリアントの数もあります。さらにフィルターを使用すると、パターンの定義に適合しない不要なバリアントをフィルターで除外できます。Line Controlを使用すると、バリアントごとに追加の実行が可能になり、グラフの開始と終了を結ぶ直線からのグラフ線の相対偏差が計算されます。 

Deviation = Max(|Profit[i]-LineProfit[i]|)/EndProfit.

ここで、Profit[i]はi次のバランス曲線の値、LineProfit[i]は直線上の同じ値、EndProfitはグラフの最後の値です。

すべての値はポイントで測定されます。Use Percent Controlは、グラフの赤い部分のパーセンテージです(この場合、このフィルターは使用しませんでした)。最小注文数のフィルターもあります。

次の図は、ボット生成タブを示しています。

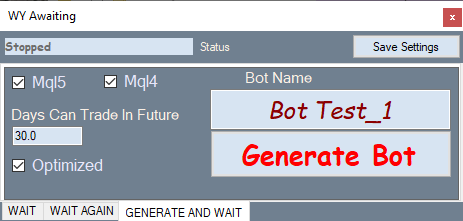
仕組み: [最適化]タブで目的のバリアントを選択し、このタブに切り替えて、エキスパートアドバイザーを生成します。

それでは、MetaTrader4ストラテジーテスターで生成されたロボットをテストしましょう。スプレッドを1に設定できるため、チャート表示への影響を実質的に排除できるため、これを選択しました。実際、この方法で見つかった大多数のロボットの予想ペイオフは、ペアの平均スプレッドよりもわずかに高いため、予想ペイオフが小さいパターンを視覚的に分析することはできません。各バリアントは約2時間にわたって総当たり攻撃を使用し、最適化されました。これは、高品質のパターンを見つけるには十分ではありません。1日か2日を過ごす方が良いです。しかし、この記事では、最良のものを見つけるのではなく、見つかったパターンを分析することを目的としているため、これで十分です。テスターでロボットをテストする場合は、DaysToTrade変数に注意してください。その値はデフォルトで3日に設定されています。したがって、総当たり攻撃セクションの後にはほとんど取引がない可能性があります。

まず、1次多項式に基づいて生成されたロボットについて考えます。

セクション1: 2020.01.13 - 2020. 02.16

ロボット1:

                                                             

総当たり攻撃セクション

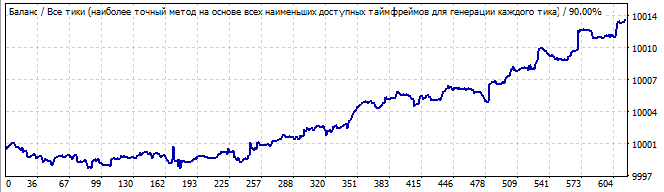
                                                              10日後 

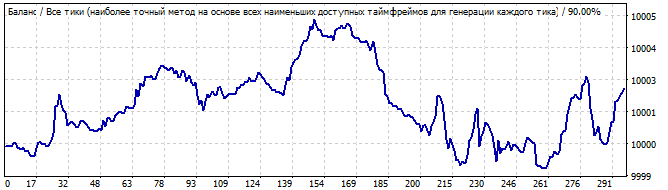
最初のグラフは、私のプログラムの2番目のタブのスクリーンショットからの変形を示しています。2番目のグラフは、同じロボットを10日間テストしたものです。それがどのように機能するかを見るには10日で十分だと思います。ご覧のとおり、パターンはしばらく続き、その後突然向きを変えて反対方向に進みます。このパターンは、2、3日間の利益を生み出すのに十分であるように思われるかもしれません。市場の同じ領域にある2番目のロボットを見てみましょう。

                                                             

総当たり攻撃セクション

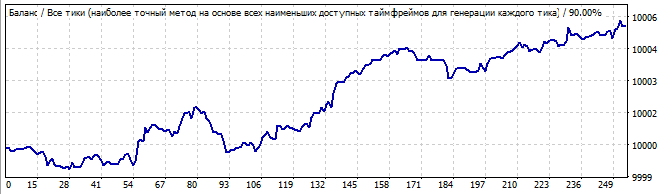
                                                             10日後

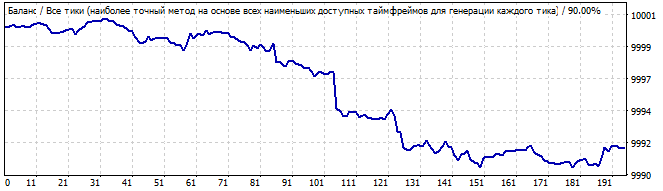
ここでは、結果はそれほど滑らかではありません。何故でしょうか。パターンは1日か2日は機能すると予想されていましたが、反転は非常に滑らかですが、最初の1秒から下がり始めます。おそらくこれはあなたが期待した結果ではありません。しかし、それは説明できるので、後で戻ります。

次に、2番目のテスト間隔に進みます。2020.02.13 - 2020.03.15

3番目のロボット:

                                                             

総当たり攻撃セクション

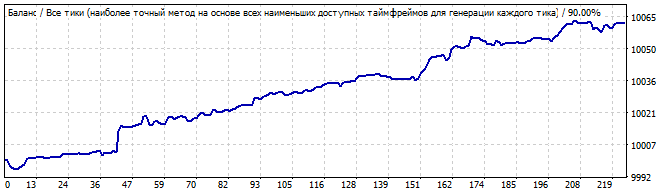
                                                             10日後

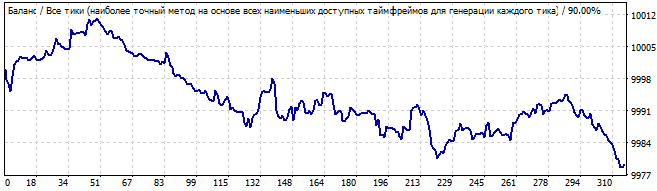
今回は状況が良くなりました。グラフはフラットで、直線に非常に近いです。これは、パターンが安定しており、しばらく続く可能性が高いことを示しています。そしてそれは続きました。将来の動きも線に似ています。つまり、パターンパラメータの多くは将来も機能し続けます。

これが4番目のロボットです。

                                                             

総当たり攻撃セクション

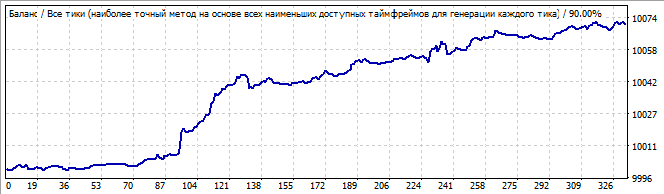
                                                             10日後

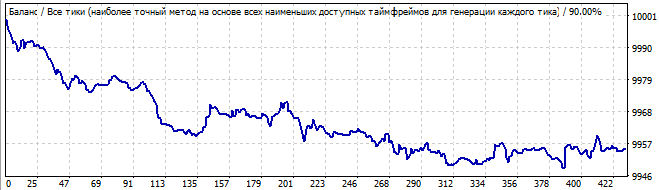
上向きの動きはかなり良く、チャートの最初の急激な上昇を除いて、すべてが滑らかで安定しているように見えます。しかし、この上昇は無視されるべきではありません。この非対称性は、これが単なる偶然または偶然の結果である可能性があることを示唆しています。当然、将来的にはパターン全体が反対方向に反転することがわかります。

次に、3番目のテスト間隔に進みます。2020.03.13 - 2020.04.18

5番目のロボット:

                                                             

総当たり攻撃セクション

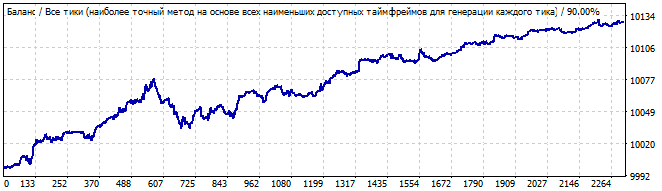
                                                             10日後

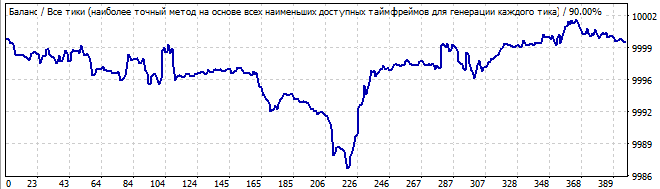
状況は似ています。目に見える非対称性、最初の波と最後の減衰が示されます。これは信頼できるパターンのようには見えません。パターン継続を取引するとは思えません。繰り返しになりますが、将来的には、数式全体のグラフの反転と反転が即座に発生します。ここでは6番目のロボットは示しません。そのグラフはアーカイブにあります。上記のグラフと非常によく似ています。

次に、2次多項式に基づいてロボットをテストしましょう。

セクション1:  2020.01.13 - 2020. 02.16

7番目のロボットは次の通りです。

                                                         

   

総当たり攻撃セクション

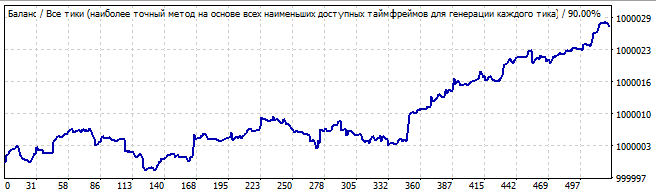
                                                             10日後

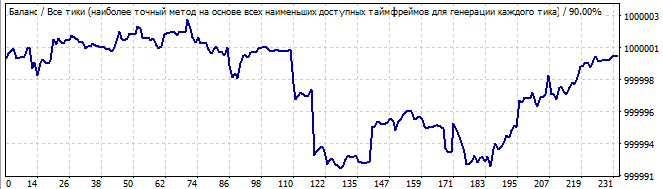
これらのロボットの特定の機能は、総当たり攻撃の間隔でよりよく機能することです。総当たり攻撃部分の前の間隔では、結果はあまり良くありません。総当たり攻撃間隔は常に鋭い正の半波を示します。しかし、残りの間隔は混乱しています。これらは特定の式の結果であり、動作は似ています。最初は少しランダムで、その後反対方向に動きます。

8番目のバリアント:

                                                             

総当たり攻撃セクション

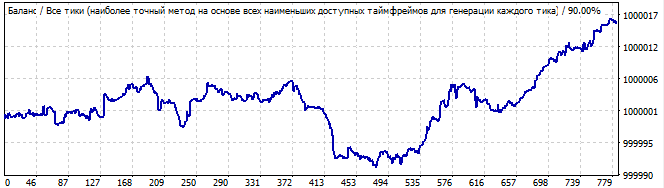
                                                             10日後

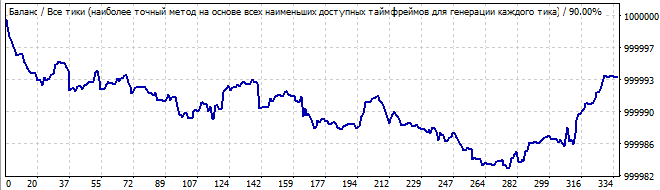
それははるかに悪いです。グローバルなパターンはありませんが、それでも総当たり攻撃間隔で上向きの動きを示しています。パターンではないので、グラフは下がっています。

次に、2番目のテスト間隔を確認します。 2020.02.13 - 2020.03.15

9番目のロボット:

                                                             

総当たり攻撃セクション

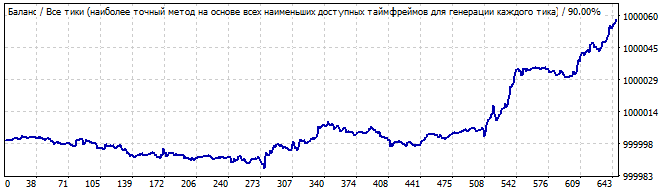
                                                             10日後

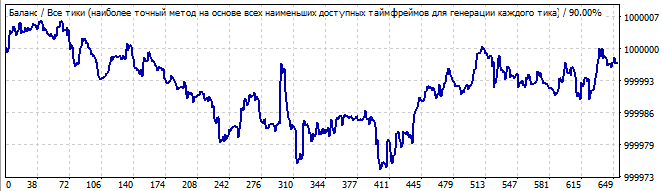
最初のグラフに波の始まりと将来の終わりが見えます。グローバルなパターンはありませんが、逆転はそれから利益を得ようとするのに十分スムーズです。

10番目のロボットは次のとおりです。

                                                             

総当たり攻撃セクション

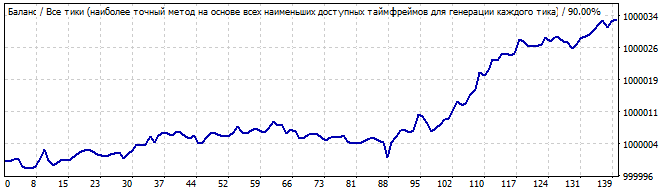
                                                             10日後

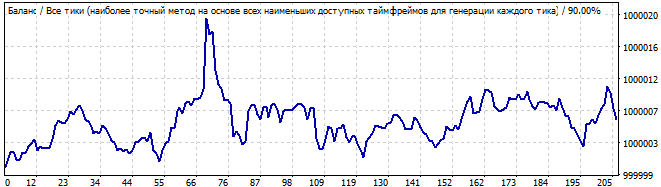
今回のグラフはより良いもので、パターンに似ています。パターンは最大1日か2日続きます。しかし、私はそのようなグラフを取引するリスクはとりません。それは直線から大きくずれています。 

次に、3番目のテスト間隔に進みます。2020.03.13 - 2020.04.18

11番目のロボット:

                                                       

     

  総当たり攻撃セクション

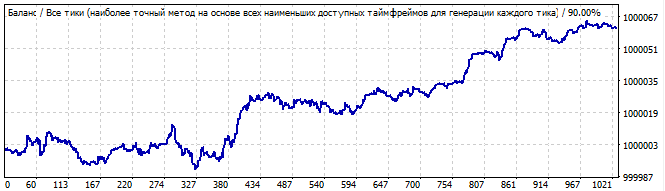
                                                              10日後

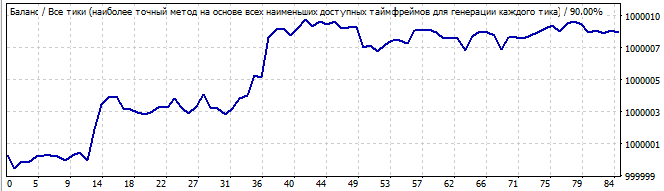
グラフはあまり美しくありませんが、直線に似ています。このパターンは今後も続きますが、ランダムノイズが多すぎるため、通常の結果ではなく運だと思います。または、これは完全なノイズではなく、小さな波である可能性があります。 

12番目のロボット:

                                                              

  総当たり攻撃セクション

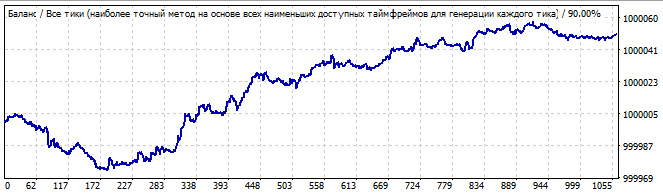
                                                               10日後

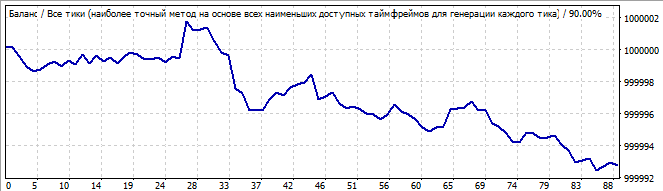
かなり醜いグラフですが、1つの波の終わりがはっきりしていて、それに続いて別の巨大な波があります。将来、この巨大な波はゆっくりと反転し、最終的にある時点で反転します。傾向の逆転は、次数が2よりも高い多項式を持つロボットでより滑らかに発生したように見えたので、あまり驚きではありません。時間をかけて3の次数をテストすることは理にかなっていると思います。規則性は、項内の因子の合計累乗が最も高い多項式によってより適切に説明できます。

私たちの研究からの結論と数学的真実

これで、エキスパートアドバイザーのすべてのテスト結果を要約できます。総当たり攻撃と最適化の間隔はパターンを示し、将来のセグメントは不明確な状況を示すため、これを行うのは難しいように思われるかもしれませんが、これはそうではありません。

• 将来の各テストでは、チャートが反転し、数式が反転するポイントが常にあります。
• 逆転は滑らかにまたは瞬時に発生する可能性がありますが、常に存在します。
• グラフの大部分は、一般的に将来的に下降します。
• パターンは最初にしばらく続くことがあります。
• 将来のすべてのテストでは、パターンが反対方向に機能することが示されています。
• バランス曲線が直線から外れると、継続の可能性ははるかに低くなります。
• 見つかった最良のバリアントでは、パターンは1日か2日機能し続けます。

これらの事実を今から説明しようと思います。ずっと前に、そのようなプログラムをまだ持っていなかったときに、最初のそして最も重要な事実を発見しました。これは単純な数学的真実です。以下に任意の戦略のバランスグラフを描きました。黒い線は小さな模様の線で、紫色の線は模様があります。グラフは、総当たり攻撃の間隔だけでなく、履歴全体でそれらを取引した場合の、それらのおおよその動作を示しています。

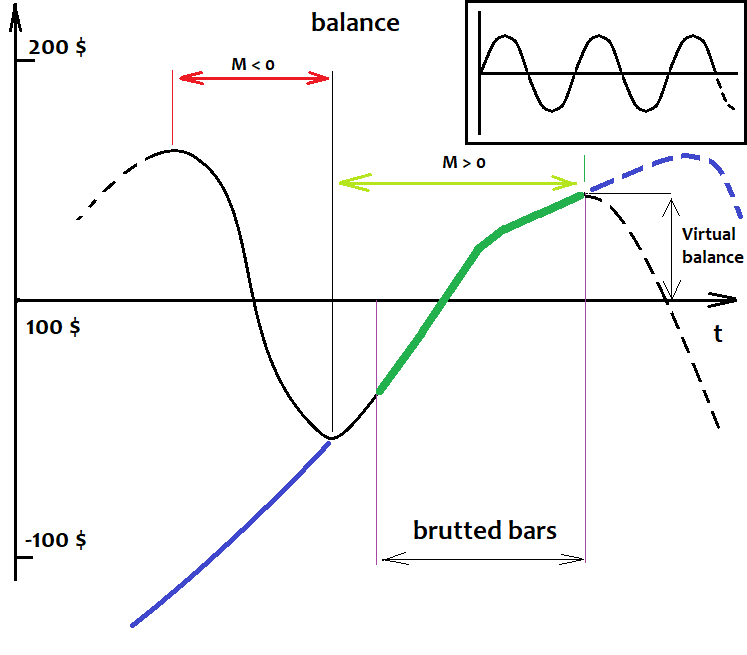
ここでのケースの分析の基礎はバランスグラフであるため、相場は挿入しません。この相場がどのように描かれても。相場には、戦略以上のものはありません。

履歴の最初から未来にかけて、すべてのロボットをテストしたと想像してみてください。将来の相場はありませんが、100％の精度で何が起こるかを想定できます。ナンセンスに聞こえるかもしれませんが、ナンセンスではありません。まず、利用可能な相場の履歴全体を使用してロボットをテストしていると想像してみましょう。何が見えますか。いくつかの紛らわしい動き、上下など。ここで何を認識できますか。波です。形状、波長、振幅は重要ではありません。正弦波ではありませんが、気にはしません。重要なのは、このプロセスが定期的であるということです。さらに、前回の記事で紹介した数学的調査に基づくと、履歴データの数が無限大になる傾向がある場合、ランダムな式に基づく戦略の期待値はゼロになる傾向があります。この効果は何でしょうか。上記の仮定に基づいて、取引数が無限のバランス曲線は、開始バランスラインを無限に横切ると言えます。何らかの理由で、バランスがすぐに上下し、常にそこにとどまっている場合でも、この線をわずかに上下にシフトして、バランスが変動する平衡点を見つけることができます。

歴史を通して顕著な利益または損失につながる公式は考慮しませんが、これらのバリアントはこのカテゴリに起因する可能性もあります。それは巨大な波の正または負の半波であり、ここでの履歴全体よりも大きいものです。これらの仮定によれば、見つかったパターンは正の半波の一部にすぎません。見つかった部分が大きいほど、平衡点がはるかに下にある可能性が高くなります。これによると、今正の半波がある場合、負の半波がすぐに現れるはずです。数学的な観点から、検出された半波が大きいほど、負の方向に移動する可能性が高くなります。逆に、負の半波を検出した場合、この半波が大きいほど、正の半波が始まる可能性が高くなります。もっと単純にできいます。履歴全体で期待ペイオフがゼロの戦略がある場合、このストーリー全体は、負と正の期待ペイオフを持つセグメントで構成され、互いに続き、常に交互になります。私には、この原則を実装するエキスパートアドバイザーがあり、これは、相場の履歴を通じて任意の通貨ペアで機能します。したがって、上記の仮定はエキスパートアドバイザーによっても確認されています。一般に、この原理はスケーリングできるだけでなく、無限に階層化できるため、システムの効率が向上します。もちろん、トレンドの継続を取引することは可能ですが、パターンが非常にはっきりしていて均一である場合にのみこれを行い、見つかったパターンの最大5〜10％を将来的に取引することをお勧めします。リスクは非常に高いです。さらに、数学に逆らって取引するのは愚かです。このパターンのおおよその残りの寿命をなんとかして見積もることができれば、試すこともできますが、パターンの性質が明確でないため、これは不可能です。また、パターンの性質が明確であっても、そのような分析を行うことは非常に困難です。

変動が発生する相対的なレベルを決定する方法

変動については、波とその動きを決定するためのレベルの定義方法についてお答えします。答えはとても簡単です。それを判断する方法はありません。レベルが存在せず、適切な取引を実行できないというわけではありません。このレベルは固定されておらず、私たちの頭の中にのみ存在します。次のことを理解することはさらに重要です。半波のサイズが無限大になる傾向がある場合、開始残高からのレベルの距離に対するこの半波のサイズの比率は無限大になる傾向があります。言い換えれば、半波が強いほど、このレベルがどこにあるかについて考えることができなくなります。これは、取引数が増えると、このレベルはゼロ点になる傾向があるためです。私たちが唯一する必要があるのは、非常に強い半波を見つけることです。同じことを示すもう1つの事実は、半波が大きくて優れているほど、残りの仮想テストで同等のサイズの波が見つかる可能性が低くなることです。言われたことを図で視覚的に示してみます。

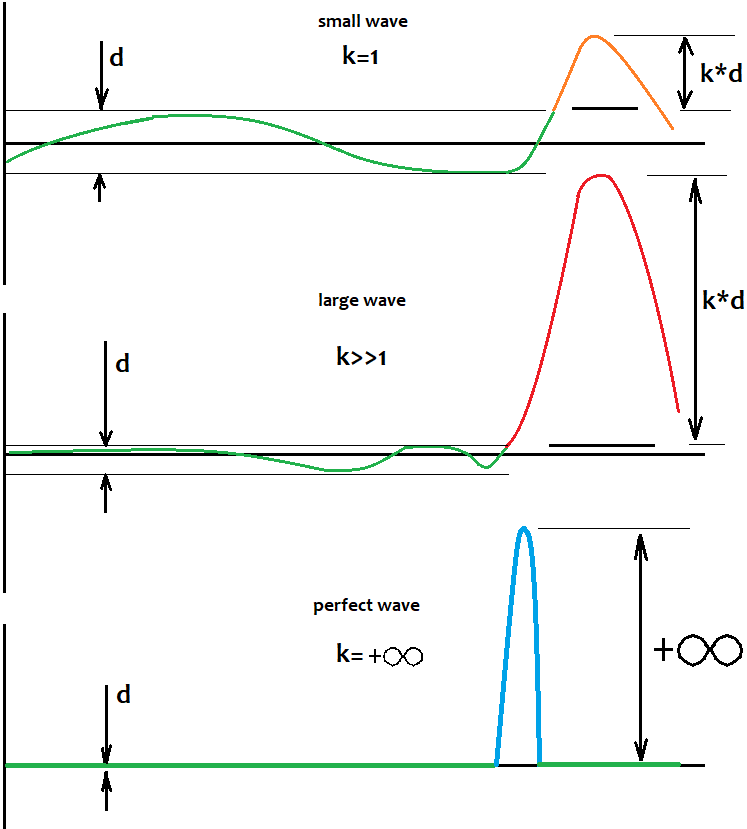
このレベルは、パターンが100％の確率で回転することを保証するものではありません。さらに重要なことに、半波の一部であるパターンが存在するという事実は、そのような波が複数存在する可能性が高く、歴史全体に存在する可能性があることを示しています。この場合、大きな引き戻し動作が発生する可能性が高くなるので、それを捕まえるように努めるべきです。グローバル規模では機能しないさまざまなエキスパートアドバイザーをテストした場合でも、これは直接または逆の方法でローカルで機能しました。鮮やかな波があり、チャートは明確に構成されていました。

この図を完成させるには

私の意見で、これらの波が最も効率的な方法で取引されるべき方法を示すことを試みます。最初にいくつかのイラストを紹介しましょう。

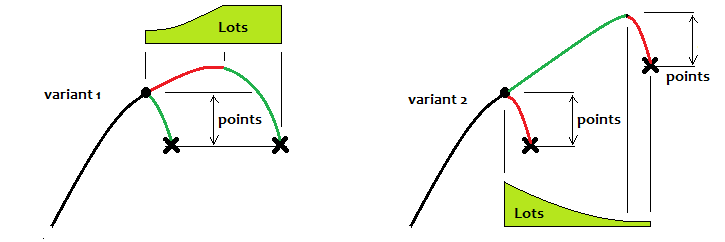
最初のオプションはパターン反転での取引であり、2番目のオプションは継続での取引です。最初のオプションを検討する場合、理想的には、常に特定のレベルに到達し、そこで取引サイクルを停止してから、次のサイクルを待つ必要があります。部分的なマーチンゲールを使用すると改善が見られますが、これはチャートがすぐに反転することがわかっている場合だけです。そうでない場合でも、期待されるペイオフは「0」になります。パターンが理想に近い場合にのみ、トレンド継続を取引できます。しかし、この取引は短期間である必要があります。2番目のバリアントでは、私の意見では、逆マーチンゲールを使用できます。正直なところ、私がテストしたすべての戦略は、数学的な事実を証明しています。固定ロットを取引し、将来の価格の振る舞いがわからない場合(そしてこれはほとんど知られていません)、結果は常に「0」になります。

しかし、誤ってグローバルパターンをキャッチし、それが非常にうまく機能する場合があります。しかし、私の意見では、そのような状況を待たない方が良いと思います。1つの取引スキームを選択してそれに従うことをお勧めします。統一されたソリューションはありません。デモアカウントでも2〜3か月かかるため、まだテストする時間がありません。月に4週間あり、毎週末に2日間のブルートフォースを実行する必要があります。そして、24時間稼働するコンピューターでテストする必要があります。私は今これをする可能性がありません。おそらく将来的には、デモアカウントで実験して、別のシグナルを作成する予定です。

終わりに

本稿では、市場に適用されるパターンとその物理学について、単純ですが非常に重要な結論を出しました。それらは次のとおりです。市場は混沌としておらず、チャートのさまざまな期間にその中に隠された多くのパターンがあります。それらは重なり合い、混沌の幻想を作り出します。パターンは、繰り返したり反転したりできる周期的なプロセスです。パターンが繰り返されるため、これらの波の振幅は制限される可能性があり、これは取引戦略で使用できます。私はこの記事をできるだけ明確にし、最小限の数学を提示するように努めました。この情報が取引システムの開発に役立つことを願っています。他の結論がある場合は、コメントを追加してください。残念ながら、時間がかかりすぎるため、より高い時間軸で総当たり攻撃を行うことができませんでした。読者の皆さんがより深い分析に興味がおありなら、このトピックをこれからの記事で続ける準備ができています。この記事では、トピックの紹介とデモンストレーションを提供します。