市場イベント予測のための因果ネットワーク分析(CNA)とベクトル自己回帰モデルの例

はじめに

因果ネットワーク分析(CNA)は、システム内の変数間の複雑な因果関係を理解し、モデル化するために用いられる手法です。金融市場に適用すれば、さまざまな市場イベントや要因が互いにどのように影響し合っているかを特定するのに役立ち、より正確な予測につながる可能性があります。

因果発見：因果発見とは、観察データから因果関係を推測するプロセスであり、金融市場の文脈では、どの変数（経済指標、市場価格、外部イベントなど）が他の変数に因果的な影響を及ぼすかを特定することを意味します。因果発見アルゴリズムにはいくつかの種類がありますが、最もポピュラーなもののひとつがPC (Peter-Clark)アルゴリズムです。

この取引ボットは「市場イベント予測のための因果ネットワーク分析」としてのシステムを名前付きコンポーネントとして明示的に実装しているわけではありませんが、概念的に類似した因果分析およびネットワークベースのアプローチの要素が取り入れられています。これを分解してみましょう。

因果分析：このボットは、因果発見アルゴリズムとしてPCアルゴリズムの代わりにFCI (Fast Causal Inference)アルゴリズムを使用しており、これはこれはFCIAlgorithm()関数で実装されています。

ネットワーク分析：このボットは、異なる金融商品や指標間の関係を表すためにネットワーク構造を使用しています。これはNode構造体とSetupNetwork()関数から明らかです。

イベント予想：明示的に「イベント予測」とは呼んでいませんが、このボットは自己回帰 (VAR) モデルを使って将来の市場状態を予測しています。これは、 TrainVARModel()やPredictVARValue()などの関数で実装されています。

因果ネットワーク分析：市場イベント予測の新境地

アルゴリズム取引の世界では、クオンツやトレーダーの間で「市場イベント予測のための因果ネットワーク分析」という新しいアプローチが人気を集めています。この洗練された手法は、因果推論、ネットワーク理論、予測分析の力を組み合わせ、かつてない精度で重要な市場イベントを予測します。

金融市場を相互接続された広大な網の目のように想像してみてください。各ストランドは、株価、経済指標、地政学的イベントなど、さまざまな市場変数の関係を表しています。従来の分析では相関関係に注目することが多いですが、経験豊富なトレーダーなら誰でも知っているように、相関関係が必ずしも因果関係を意味するとは限りません。

ここで因果ネットワーク分析の出番となります。因果ネットワーク分析は、この複雑な網の目の中にある真の因果関係を明らかにすることを目的としています。これにより、トレーダーは市場のダイナミクスをより深く理解し、従来の分析では見えなかった事象を予測できるようになります。

因果ネットワーク分析の核心には、以下の3つの重要なステップがあります。

1. ネットワークの構築：まず、各ノードが市場変数を表すネットワークを構築します。資産価格や取引量から、経済指標やセンチメントスコアまで、あらゆるものが含まれます。

2. 因果関係の発見：次に、高度なアルゴリズムを使って、これらのノード間の因果関係を決定します。単にどの変数が一緒に動くかを見るのではなく、どの変数が他の変数の変化を実際に促すかを明らかにします。

3. 出来事の予測：最後に、この因果ネットワークを用いて重要な市場イベントを予測します。市場の動きの真の原動力を理解することで、大きな変動や暴落、暴騰をより的確に予測することができます。

トレーダーにとっての利点

MQL5トレーダーにとって、因果ネットワーク分析を導入することは画期的なことです。以下がその理由です。

• リスク管理の改善：市場変動の根本原因を特定することで、潜在的な不況に備えることができます。
• より正確な予測：因果関係を理解することは、単なる相関関係に基づく予測よりも信頼性の高い予測につながります。
• 隠れたチャンスの発見：因果ネットワークは、一見しただけではわからないつながりを明らかにし、ユニークな取引機会をもたらす可能性があります。
• 適応戦略：市場が進化するにつれて、因果関係ネットワークも進化し、リアルタイムで戦略を適応させることができます。

MQL5での実装

完全な因果ネットワーク分析システムの実装は複雑ですが、MQL5はこの種の高度な分析のための堅牢なプラットフォームを提供しています。まずは以下から始めるといいです。

1. iCustom()関数を使用して、ネットワーク内の各ノードの指標を作成します。
2. PCアルゴリズムやグレンジャー因果性検定のような因果発見アルゴリズムを実装します（今回はFCIアルゴリズムを使用）。
3. MQL5のニューラルネットワーク機能を活用し、因果関係ネットワークに基づいた予測モデルを構築します。

なぜPCではなくFCIなのか？

FCI (Fast Causal Inference) とPC (Peter-Clark)は、観察データから因果関係を推測するために使用される因果発見アルゴリズムです。PCではなくFCIを選ぶ理由を以下に示します。

1. 潜在的交絡因子：PCに対するFCIの主な利点は、潜在的交絡因子を扱えることです。FCIは隠れた共通原因の存在を推測できますが、PCは因果充足性（潜在的交絡因子がないこと）を仮定します。
2. 選択バイアス：FCIは、PCでは対応できないデータの選択バイアスも考慮に入れることができます。
3. より一般的なモデル：FCIは、PCが生成する有向非循環グラフ(DAG:Directed Acyclic Graph)よりも幅広い因果構造を表現できる、部分祖語グラフ(PAG: Partial Ancestral Graph)と呼ばれる、より一般的なグラフモデルを生成します。
4. 健全性と完全性：FCIは因果的に不十分なシステムに対しても健全かつ完全であり、無限のサンプルサイズが与えられた場合、すべての可能な因果関係を正しく識別できます。
5. 堅牢性：FCIは、潜在的交絡因子や選択バイアスを扱えるため、隠れた変数が存在する可能性が高い実世界のデータに対して一般的により頑健です。

ただし、FCIにはPCと比較していくつかの欠点もあります。

1. 計算の複雑さ：FCIは一般にPCよりも計算コストが高く、大規模なデータセットでは特にその傾向が顕著です。
2. 決定的な出力が少ない：FCIによって生成されたPAGは、潜在的な交絡因子による追加的な不確実性を反映して、PCによるDAGよりも未確定のエッジ方向が多く含まれることがよくあります。
3. 解釈：PAGはDAGよりも専門家でない人にとっては解釈が難しいかもしれません。

実際、FCIとPCのどちらを選択するかは、因果推論タスクの具体的な要件やデータの性質、因果システムに関する仮定に依存します。隠れた交絡因子がなく、選択バイアスもないと確信できる場合は、PCで十分かつ効率的かもしれませんが、潜在変数や選択バイアスが疑われる場合はFCIが適切な選択となるでしょう。

自己回帰(VAR)モデル

VARは、2つ以上の時系列が互いに影響を与え合う場合に用いられる多変量予測アルゴリズムです。この取引システムでは、異なる金融商品や経済指標間の関係をモデル化するために使用される可能性が高いです。

VARの主な特徴

1. 複数の時系列間の線形相互依存関係を解析します。
2. 各変数は、それ自身の過去のラグおよび他の変数の過去のラグの一次関数として表現されます。
3. 複数の時系列システム内で豊かな動的関係をモデル化することができます。

この取引システムの文脈でのVARモデル

• VARモデルはTrainVARModel関数によって学習され、時系列データのパターンを捕捉します。
• PredictVARValue関数を使って、訓練済みのモデルから予測をおこないます。
• OptimizeVARModel関数を利用して、最適なラグや有意な変数の選択によりVARモデルを最適化します。

数学的表現

ラグ1の2変数VARモデルの場合：

y1,t = c1 + φ11y1,t-1 + φ12y2,t-1 + ε1,t

y2,t = c2 + φ21y1,t-1 + φ22y2,t-1 + ε2,t

ここで

• y1,tとy2,tは時刻tにおける2つの変数の値
• c1とc2は定数
• φijは係数
• ε1,tとε2,tは誤差項

システムは、VARモデルにより各変数間の係数を推定し、それを基に予測をおこないます。

単一の資産の将来価格を予測するだけでなく、相互に関連する複数の金融変数を同時に予測することを想像してみてください。それこそがVARの真価です。まるで、複数の未来が絡み合って見える水晶玉を手にしているようなものです。

VARの核心は、複数の時系列が互いに影響し合う場合に用いられる多変量予測アルゴリズムにあります。つまり、複数の時系列間の線形依存関係を捉える手法といえます。

VARはどのように機能するのか？

VARの機能は次のステップに分解できます。

1. データ収集：まず、モデルに含めるすべての変数の過去データを収集します。これは、複数の通貨ペア、商品、または経済指標の価格データなどが含まれるかもしれません。
2. モデル仕様：いくつのラグ（過去の期間）を含めるかを決定します。この設定には、過去の取引経験や市場の理解が役立ちます。
3. 推定：モデルは、各変数がそれ自身の過去の値および他の変数の過去の値からどのように影響を受けるかを推定します。
4. 予測：推定が完了すると、VARモデルは含まれるすべての変数について同時に予測を生成することができます。

MQL5でVARを実装する

MQL5には組み込みのVAR関数はありませんが、自分で実装することは可能です。以下は、コードをどのように構成するかの単純化した例です。

// Define your VAR model
struct VARModel {
    int lag;
    int variables;
    double[][] coefficients;
};

// Estimate VAR model
VARModel EstimateVAR(double[][] data, int lag) {
    // Implement estimation logic here
    // You might use matrix operations for efficiency
}

// Make predictions
double[] Forecast(VARModel model, double[][] history) {
    // Implement forecasting logic here
}

// In your EA or indicator
void OnTick() {
    // Collect your multivariate data
    double[][] data = CollectData();
    
    // Estimate model
    VARModel model = EstimateVAR(data, 5); // Using 5 lags
    
    // Make forecast
    double[] forecast = Forecast(model, data);
    
    // Use forecast in your trading logic
    // ...
}

VARの優位性

例えば、EUR/USDを取引しているとしましょう。従来のなアプローチでは、過去のEUR/USD価格だけを見て取引判断を下すかもしれません。しかし、VARを利用することで、具体的には、以下の変数をモデルに含めることができます。

• EUR/USD相場
• USD/JPY相場（米ドル全体の強さを捉える）
• 原油価格（多くの通貨にとって重要な要因）
• S&P500指数（市場全体のセンチメントを測る）
• 米欧金利差

これらを組み合わせることで、モデルはFX市場の状況をより豊かに捉えることができ、取引判断がより情報に基づいたものとなる可能性があります。

課題と考察

他の強力なツールと同様、VARにも課題があります。

1. データ要件：VARモデルは、大量のデータを必要とする場合があります。信頼性のある推定をおこなうためには、十分な過去のデータを確保することが重要です。
2. 計算強度：変数やラグの数を増やすと、計算量が増加します。したがって、効率化のためにコードを最適化する必要があります。
3. 定常性：VARモデルは定常時系列を前提としています。この仮定を満たすために、データの前処理（差分処理など）が必要になることがあります。
4. 解釈：複数の変数やラグがある場合、VARの結果の解釈は複雑になることがあります。そのため、統計的な洞察を得ることに加え、自分自身の取引知識と経験を組み合わせることを忘れないようにするべきです。

CNA取引システムにおけるネットワーク分析

このEAに実装されているネットワーク分析は、市場分析と予測戦略の基本的な要素です。異なる金融商品や市場変数間の複雑な関係を表現し、分析するために設計されています。

以下に、EAで使用されたネットワーク分析の要点をまとめます。

1. 構造：ネットワークはノードで構成され、各ノードは金融商品（通常は通貨ペア）を表します。
2. 目的：市場におけるさまざまな金融商品間の関係や相互依存関係をモデル化するために設計されています。
3. 因果発見：EAは、FCI (Fast Causal Inference)アルゴリズムを使用して、これらの商品間の潜在的な因果関係を明らかにします。
4. 表現：これらの関係は隣接行列で表され、因果的な影響力の観点からどの機器が直接リンクしているかを示します。
5. 分析：EAはこのネットワークに対して、V字構造（因果関係グラフに特有のパターン）の特定や、因果関係の理解をさらに深めるためのオリエンテーションルールの適用など、さまざまな分析をおこないます。
6. 予測との統合：この分析を通じて発見されたネットワーク構造と関係性は、予測に使用される自己回帰(VAR)モデルの入力となります。
7. 適応性：ネットワーク分析は静的なものではなく、EAは時間の経過とともに更新でき、変化する市場環境や金融商品間の関係に適応します。

このアプローチの背景にある重要な考え方は、金融商品は単独では動かないということです。さまざまな金融商品間の関係ネットワークをモデル化し分析することで、EAは市場のダイナミクスをより包括的に理解しようとしています。理論的には、これによりより正確な予測と、より良い情報に基づいた取引判断が可能になるはずです。

しかし、このアプローチは洗練されているとはいえ、金融市場は極めて複雑で、多くの要因に影響されることに注意が必要です。このネットワーク分析の有効性は、実際の市場ダイナミクスをどれだけうまく捉えられるか、そして取引戦略の他の構成要素とどのように統合されるかに依存します。

ネットワークの構造

ネットワークは以下の構造で表されます。

struct Node
{
    string name;
    double value;
};

Node g_network[];
int g_node_count = 0;

ネットワークの各ノードは特定の金融商品または市場変数を表します。nameフィールドは商品を識別し（例えばEURUSD、GBPUSD）、valueフィールドはそのノードの関連データを格納できます。

ネットワークの設定

ネットワークはSetupNetwork()関数で初期化されます。

void SetupNetwork()
{
    string symbols[] = {"EURUSD", "GBPUSD", "USDCAD", "USDCHF", "USDJPY", "AUDUSD"};
    for(int i = 0; i < ArraySize(symbols); i++)
    {
        AddNode(symbols[i]);
    }
}

void AddNode(string name)
{
    ArrayResize(g_network, g_node_count + 1);
    g_network[g_node_count].name = name;
    g_network[g_node_count].value = 0; // Initialize with default value
    g_node_count++;
}

この設定により、各ノードが異なる通貨ペアを表すネットワークが構築されます。

ネットワークの目的

ネットワークは、このEAにおいていくつかの重要な役割を果たしています。

1. 市場構造の表現：異なる通貨ペア間の相互関係をモデル化し、ある通貨ペアの動きが他の通貨ペアにどのような影響を与えるかをEAが考慮できるようにします。
2. 因果分析の基礎：ネットワーク構造は、ノード間の因果関係を発見しようとするFCI (Fast Causal Inference)アルゴリズムの基盤として使用されます。
3. 予測モデリングのための入力：因果分析によって発見されたネットワーク構造と関係性は、予測に使用される自己回帰(VAR)モデルの入力となります。

ネットワーク分析の実際

EAはこのネットワークに対していくつかの分析をおこないます。

1. 因果発見：FCIAlgorithm()関数は、ノード間の潜在的な因果関係を明らかにするために、FCIアルゴリズムを適用します。
2. 隣接行列：因果関係は隣接行列で表され、各項目は2つのノード間に直接的な因果関係があるかどうかを示します。
3. V字型構造の向き：OrientVStructures()関数は、因果グラフの重要なパターンであるネットワーク内のV字構造を特定し、方向付けます。
4. グラフ分析：最終的なグラフ構造は、因果関係のある商品が互いに予測情報を提供する可能性があることを前提に、取引の意思決定に役立てるために分析されます。

取引への影響

このネットワークベースのアプローチによって、EAで以下をおこなえるようになります。

1. 商品を単体で見たときにはわからないような、複雑な市場力学を考慮します。
2. 潜在的に分析対象商品の中から先行指標を特定できます。
3. より広い市場背景を考慮することで、より情報に基づいた予測をおこないます。
4. 因果構造が定期的に見直されるため、市場環境の変化に適応します。

このネットワーク分析を活用することで、EAは市場ダイナミクスをより深く理解し、より正確な予測と、より良い情報に基づいた取引判断につながる可能性があります。

コード例

このコードは、以下の2つのフロー図に従っています。

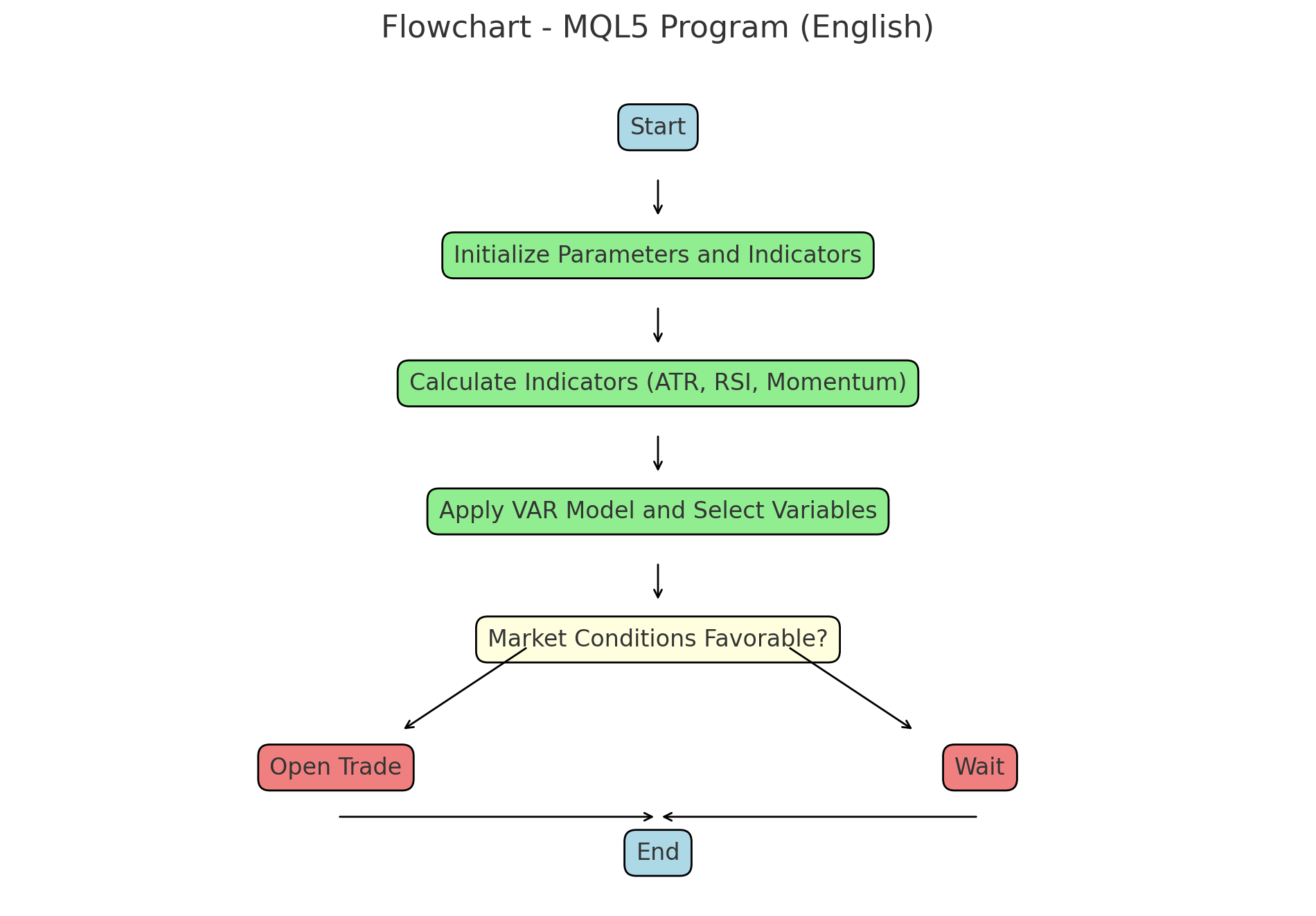
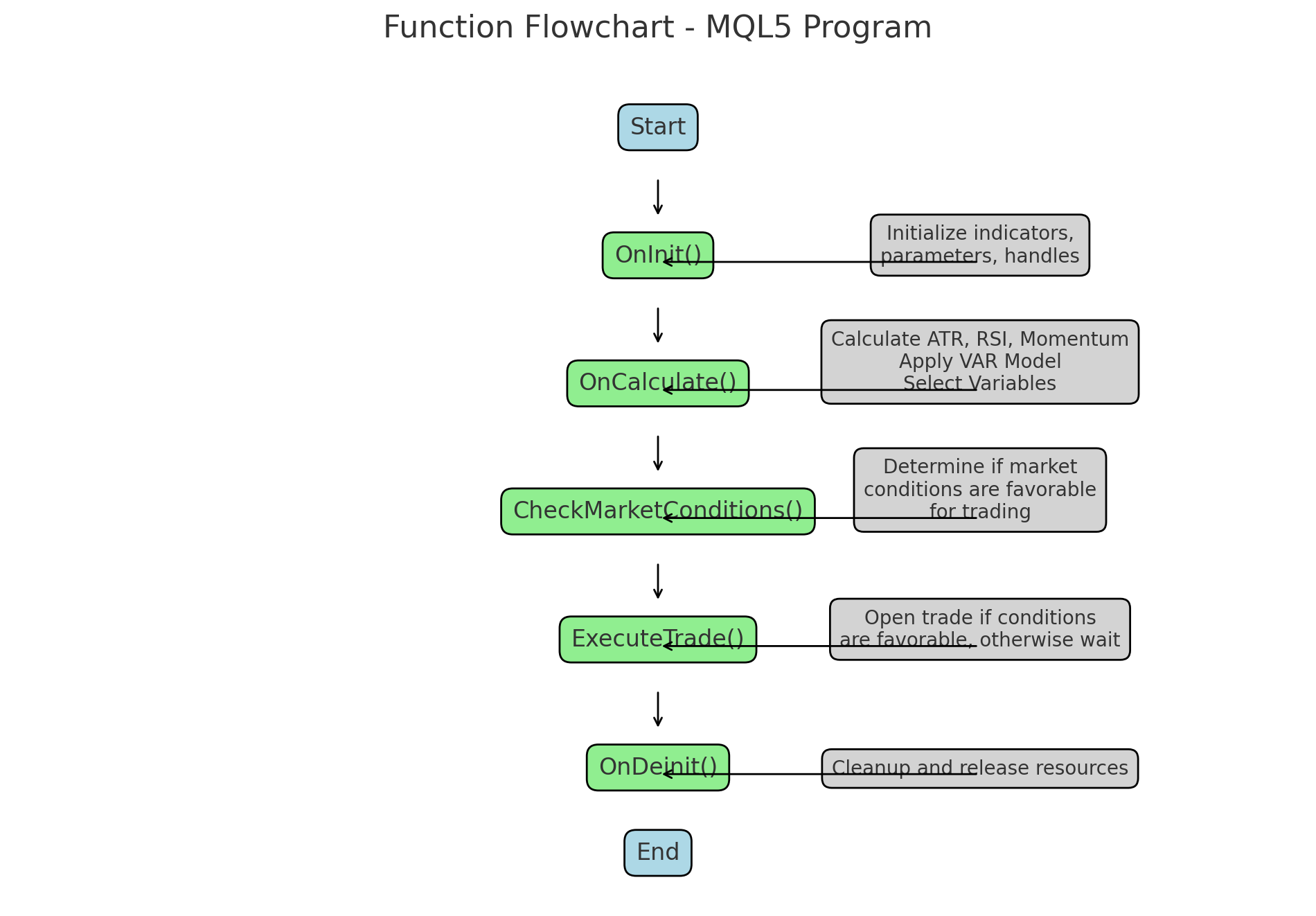
MQL5取引プログラムにおける主要関数の詳細説明

この取引EAは非常に洗練されており、いくつかの高度なアプローチを組み合わせています：

1. 予測には自己回帰(VAR)モデルを使用しています。
2. 異なる市場変数間の関係を理解するための因果発見アルゴリズム(FCI: Fast Causal Inference)を実装しています。
3. 複数の金融商品を同時に表現し、分析するためにネットワーク構造を採用しています。
4. ボラティリティ、RSI、トレンドの強さなど、さまざまなテクニカルフィルタが組み込まれています。
5. 適応的なリスク管理とポジションサイジングを採用しています。
6. モデルを継続的に更新し再学習させるために、スライディングウィンドウ戦略を実装しています。
7. これには、クロスバリデーションとモデルの最適化技術が含まれます。

EAの構造は、複雑な分析と意思決定を可能にすると同時に、将来的な改善や異なる市場環境に適応するための柔軟性を維持しています。

取引EAの主要機能の詳細説明

1. OnInit()

int OnInit()
  {
// Step 1: Set up your network structure
   SetupNetwork();

// Step 2: Run the causal discovery algorithm (e.g., PC or FCI)
   FCIAlgorithm();

// Step 3: Train the optimized causal model
   TrainOptimizedVARModel();

   ArrayResize(g_previous_predictions, g_node_count);
   ArrayInitialize(g_previous_predictions, 0);  // Initialize with zeros

   return(INIT_SUCCEEDED);
  }

これは、EAが最初に読み込まれたとき、またはチャート上で再ロードされたときに実行される初期化関数です。

主な機能

• SetupNetwork()を呼び出してネットワーク構造をセットアップする
• FCIAlgorithm()で因果発見アルゴリズム(FCI)を実行する
• TrainOptimizedVARModel()を使用して、最適化された因果モデルを訓練する
• 過去の予測値の配列を初期化する

この関数は、EAが実行するすべての分析と予測の基礎を築くものです。

2. OnTick()

void OnTick()
  {
   ENUM_TIMEFRAMES tf = ConvertTimeframe(InputTimeframe);

   static datetime lastBarTime = 0;
   datetime currentBarTime = iTime(Symbol(), tf, 0);

   if(currentBarTime == lastBarTime)
      return;

   lastBarTime = currentBarTime;

   Print("--- New bar on timeframe ", EnumToString(tf), " ---");

   UpdateModelSlidingWindow();

   for(int i = 0; i < g_node_count; i++)
     {
      string symbol = g_network[i].name;
      Print("Processing symbol: ", symbol);

      double prediction = PredictVARValue(i);
      Print("Prediction for ", symbol, ": ", prediction);

      int signal = GenerateSignal(symbol, prediction);
      Print("Signal for ", symbol, ": ", signal);

      // Imprimir más detalles sobre las condiciones
      Print("RSI: ", CustomRSI(symbol, ConvertTimeframe(InputTimeframe), 14, PRICE_CLOSE, 0));
      Print("Trend: ", DetermineTrend(symbol, ConvertTimeframe(InputTimeframe)));
      Print("Trend Strong: ", IsTrendStrong(symbol, ConvertTimeframe(InputTimeframe)));
      Print("Volatility OK: ", VolatilityFilter(symbol, ConvertTimeframe(InputTimeframe)));
      Print("Fast MA > Slow MA: ", (iMA(symbol, PERIOD_CURRENT, 14, 0, MODE_EMA, PRICE_CLOSE) > iMA(symbol, PERIOD_CURRENT, 24, 0, MODE_EMA, PRICE_CLOSE)));

      if(signal != 0)
        {
         Print("Attempting to execute trade for ", symbol);
         ExecuteTrade(symbol, signal);
        }
      else
        {
         g_debug_no_signal_count++;
         Print("No trade signal generated for ", symbol, ". Total no-signal count: ", g_debug_no_signal_count);
        }
      ManageOpenPositions();
      ManageExistingOrders(symbol);


      Print("Current open positions for ", symbol, ": ", PositionsTotal());
      Print("Current pending orders for ", symbol, ": ", OrdersTotal());
     }

   Print("--- Bar processing complete ---");
   Print("Total no-signal count: ", g_debug_no_signal_count);
   Print("Total failed trade count: ", g_debug_failed_trade_count);
  }

この関数は各ティックで呼び出されます。

主な機能

• 入力された時間枠を変換する
• UpdateModelSlidingWindow()でスライディングウィンドウを使用してモデルを更新する
• ネットワーク内の各銘柄について：
  • PredictVARValue()を使用して値を予測する
  • GenerateSignal()による売買シグナルを生成する
  • シグナルが発生したら取引を実行する
  • ポジションを管理する
  • 既存注文を管理する

これはEAの運用の中心であり、ここで売買の決定がおこなわれます。

3. OnCalculate()

提供されたコードには明示的に示されていませんが、この関数は通常、カスタム指標値を計算するために使用されます。このEAでは、この機能の一部がOnTick()に統合されているようです。

4. CheckMarketConditions()

int GenerateSignal(string symbol, double prediction)
  {
   int node_index = FindNodeIndex(symbol);
   if(node_index == -1)
      return 0;

   static bool first_prediction = true;
   if(first_prediction)
     {
      first_prediction = false;
      return 0; // No generar señal en la primera predicción
     }

   double current_price = SymbolInfoDouble(symbol, SYMBOL_BID);

// Calculate predicted change as a percentage
   double predicted_change = (prediction - current_price) / current_price * 100;

   bool volatility_ok = VolatilityFilter(symbol, ConvertTimeframe(InputTimeframe));
   double rsi = CustomRSI(symbol, ConvertTimeframe(InputTimeframe), 14, PRICE_CLOSE, 0);
   bool trend_strong = IsTrendStrong(symbol, ConvertTimeframe(InputTimeframe));
   int trend = DetermineTrend(symbol, ConvertTimeframe(InputTimeframe));

   double fastMA = iMA(symbol, PERIOD_CURRENT, 8, 0, MODE_EMA, PRICE_CLOSE);
   double slowMA = iMA(symbol, PERIOD_CURRENT, 24, 0, MODE_EMA, PRICE_CLOSE);

   Print("Debugging GenerateSignal for ", symbol);
   Print("Current price: ", current_price);
   Print("Prediction diff: ", prediction);
   Print("predicted_change: ", predicted_change);
   Print("RSI: ", rsi);
   Print("Trend: ", trend);
   Print("Trend Strong: ", trend_strong);
   Print("Volatility OK: ", volatility_ok);
   Print("Fast MA: ", fastMA, ", Slow MA: ", slowMA);

   bool buy_condition =  prediction >  0.00001 && rsi < 30 && trend_strong  && volatility_ok && fastMA > slowMA;
   bool sell_condition = prediction < -0.00001 && rsi > 70 && trend_strong && volatility_ok && fastMA < slowMA;

   Print("Buy condition met: ", buy_condition);
   Print("Sell condition met: ", sell_condition);

// Buy conditions
   if(buy_condition)
     {
      Print("Buy signal generated for ", symbol);
      int signal = 1;
      return signal;  // Buy signal
     }
// Sell conditions
   else
      if(sell_condition)
        {
         Print("Sell signal generated for ", symbol);
         int signal = -1;
         return signal; // Sell signal
        }
      else
        {
         Print("No signal generated for ", symbol);
         int signal = 0;
         return signal; // No signal
        }


  }

この関数はコード内で明示的に定義されていないが、その機能は主にGenerateSignal()内のいくつかの部分に分散されています。

• VolatilityFilter()でボラティリティを確認する
• RSIを確認する
• IsTrendStrong()でトレンドの強さを確認する
• DetermineTrend()でトレンド方向を決定する
• 高速移動平均と低速移動平均を比較する

これらの確認によって、市場の状況が取引に適しているかどうかを判断します。

5. ExecuteTrade()

void ExecuteTrade(string symbol, int signal)
  {
   if(!IsMarketOpen(symbol) || !IsTradingAllowed())
     {
      Print("Market is closed or trading is not allowed for ", symbol);
      return;
     }

   double price = (signal == 1) ? SymbolInfoDouble(symbol, SYMBOL_ASK) : SymbolInfoDouble(symbol, SYMBOL_BID);

   double stopLoss, takeProfit;
   CalculateAdaptiveLevels(symbol, signal, stopLoss, takeProfit);

   double lotSize = CalculateDynamicLotSize(symbol, stopLoss);

   if(lotSize <= 0)
     {
      Print("Invalid lot size for symbol: ", symbol);
      return;
     }

   trade.SetExpertMagicNumber(123456);
   trade.SetTypeFilling(ORDER_FILLING_FOK);

   bool result = false;
   int attempts = 3;

   for(int i = 0; i < attempts; i++)
     {
      if(signal == 1)
        {
         result = trade.Buy(lotSize, symbol, price, stopLoss, takeProfit, "CNA Buy");
         Print("Attempting Buy order: Symbol=", symbol, ", Lot Size=", lotSize, ", Price=", price, ", SL=", stopLoss, ", TP=", takeProfit);
        }
      else
         if(signal == -1)
           {
            result = trade.Sell(lotSize, symbol, price, stopLoss, takeProfit, "CNA Sell");
            Print("Attempting Sell order: Symbol=", symbol, ", Lot Size=", lotSize, ", Price=", price, ", SL=", stopLoss, ", TP=", takeProfit);
           }

      if(result)
        {
         Print("Order executed successfully for ", symbol, ", Type: ", (signal == 1 ? "Buy" : "Sell"), ", Lot size: ", lotSize);
         break;
        }
      else
        {
         int lastError = GetLastError();
         Print("Attempt ", i+1, " failed for ", symbol, ". Error: ", lastError, " - ", GetErrorDescription(lastError));

         if(lastError == TRADE_RETCODE_REQUOTE || lastError == TRADE_RETCODE_PRICE_CHANGED || lastError == TRADE_RETCODE_INVALID_PRICE)
           {
            price = (signal == 1) ? SymbolInfoDouble(symbol, SYMBOL_ASK) : SymbolInfoDouble(symbol, SYMBOL_BID);
            CalculateAdaptiveLevels(symbol, signal, stopLoss, takeProfit);
           }
         else
            break;
        }
     }

   if(!result)
     {
      Print("All attempts failed for ", symbol, ". Last error: ", GetLastError(), " - ", GetErrorDescription(GetLastError()));
     }
  }

この関数は、実際の取引の執行を処理します。

主な機能

• 市場が開いているか、取引が許可されているかを確認する
• 適応的な損切りと利食いのレベルを計算する
• リスク管理に基づいてロットサイズを決定する
• 注文の執行を試み、失敗した場合は再試行する
• 誤差を処理し、詳細なフィードバックを提供する

6. OnDeinit()

void OnDeinit(const int reason)
  {
   if(atr_handle != INVALID_HANDLE)
      IndicatorRelease(atr_handle);
   if(rsi_handle != INVALID_HANDLE)
      IndicatorRelease(rsi_handle);
   if(momentum_handle != INVALID_HANDLE)
      IndicatorRelease(momentum_handle);
   GenerateFinalSummary();
  }

この関数は、EAがチャートから削除されたとき、または端末が閉じられたときに呼び出されます。

主な機能

• 指標ハンドルをリリースする
• GenerateFinalSummary()を呼び出して、EAのパフォーマンスの最終サマリーを生成する

その他の重要な関数

UpdateModelSlidingWindow()

void UpdateModelSlidingWindow()
  {
   static int bars_since_update = 0;
   ENUM_TIMEFRAMES tf = ConvertTimeframe(InputTimeframe);

// Check if it's time to update
   if(bars_since_update >= g_update_frequency)
     {
      // Collect new data
      double training_data[];
      CollectTrainingData(training_data, g_window_size, tf);

      // Retrain model
      TrainModel(training_data);

      // Validate model
      double validation_score = ValidateModel();
      Print("Model updated. Validation score: ", validation_score);

      bars_since_update = 0;
     }
   else
     {
      bars_since_update++;
     }
  }

スライディングウィンドウのデータを使用してVARモデルを更新し、変化する市場環境に適応できるようにします。

TrainOptimizedVARModel()

void TrainOptimizedVARModel()
  {
   OptimizationResult opt_result = OptimizeVARModel();

   Print("Lag óptimo encontrado: ", opt_result.optimal_lag);
   Print("AIC: ", opt_result.aic);
   Print("Variables seleccionadas: ", ArraySize(opt_result.selected_variables));

// Usar opt_result.optimal_lag y opt_result.selected_variables para entrenar el modelo final
   TrainVARModel(opt_result.optimal_lag, opt_result.selected_variables);
  }

VARモデルの最適化と訓練、最適なラグ数と有意変数を選択します。

PredictVARValue()

double PredictVARValue(int node_index)
{
   if(node_index < 0 || node_index >= g_node_count)
   {
      Print("Error: Invalid node index: ", node_index);
      return 0;
   }

   double prediction = 0;
   int lag = g_var_params[node_index].lag;

   Print("Predicting for node: ", g_network[node_index].name, ", Lag: ", lag);

   // Retrieve the previous prediction
   double previous_prediction = g_previous_predictions[node_index];

   // Verify if there are enough coefficients
   int expected_coefficients = g_node_count * lag + 1; // +1 for the intercept
   if(ArraySize(g_var_params[node_index].coefficients) < expected_coefficients)
   {
      Print("Error: Not enough coefficients for node ", node_index, ". Expected: ", expected_coefficients, ", Actual: ", ArraySize(g_var_params[node_index].coefficients));
      return 0;
   }

   prediction = g_var_params[node_index].coefficients[0]; // Intercept
   Print("Intercept: ", prediction);

   double sum_predictions = 0;
   double sum_weights = 0;
   double current_price = iClose(g_network[node_index].name, PERIOD_CURRENT, 0);

   for(int l = 1; l <= lag; l++)
   {
      double time_weight = 1.0 - (double)(l-1) / lag; // Time-based weighting
      sum_weights += time_weight;

      double lag_prediction = 0;
      for(int j = 0; j < g_node_count; j++)
      {
         int coeff_index = (l - 1) * g_node_count + j + 1;
         if(coeff_index >= ArraySize(g_var_params[node_index].coefficients))
         {
            Print("Warning: Coefficient index out of range. Skipping. Index: ", coeff_index, ", Array size: ", ArraySize(g_var_params[node_index].coefficients));
            continue;
         }

         double coeff = g_var_params[node_index].coefficients[coeff_index];
         double raw_value = iClose(g_network[j].name, PERIOD_CURRENT, l);

         if(raw_value == 0 || !MathIsValidNumber(raw_value))
         {
            Print("Warning: Invalid raw value for ", g_network[j].name, " at lag ", l);
            continue;
         }

         // Normalize the value as a percentage change
         double normalized_value = (raw_value - current_price) / current_price;

         double partial_prediction = coeff * normalized_value;
         lag_prediction += partial_prediction;

         Print("Lag ", l, ", Node ", j, ": Coeff = ", coeff, ", Raw Value = ", raw_value,
               ", Normalized Value = ", normalized_value, ", Partial prediction: ", partial_prediction);
      }

      sum_predictions += lag_prediction * time_weight;
      Print("Lag ", l, " prediction: ", lag_prediction, ", Weighted: ", lag_prediction * time_weight);
   }

   Print("Sum of weights: ", sum_weights);

   // Calculate the final prediction
   if(sum_weights > 1e-10)
   {
      prediction = sum_predictions / sum_weights;
   }
   else
   {
      Print("Warning: sum_weights is too small (", sum_weights, "). Using raw sum of predictions.");
      prediction = sum_predictions;
   }

   // Calculate the difference between the current prediction and the previous prediction
   double prediction_change = prediction - previous_prediction;

   Print("Previous prediction: ", previous_prediction);
   Print("Current prediction: ", prediction);
   Print("Prediction change: ", prediction_change);

   // Convert the prediction to a percentage change
   double predicted_change_percent = (prediction - current_price) / current_price * 100;

   Print("Final prediction (as percentage change): ", predicted_change_percent, "%");

   // Update the current prediction for the next iteration
   g_previous_predictions[node_index] = prediction;

   // Return the difference in basis points
   return prediction_change * 10000; // Multiply by 10000 to convert to basis points
}

訓練済みのVARモデルを用いて、過去の値とモデル係数を考慮した予測をおこないます。

ManageOpenPositions() および ManageExistingOrders()

void ManageOpenPositions()
  {
   for(int i = PositionsTotal() - 1; i >= 0; i--)
     {
      ulong ticket = PositionGetTicket(i);
      if(PositionSelectByTicket(ticket))
        {
         string symbol = PositionGetString(POSITION_SYMBOL);
         double openPrice = PositionGetDouble(POSITION_PRICE_OPEN);
         double currentPrice = PositionGetDouble(POSITION_PRICE_CURRENT);
         double stopLoss = PositionGetDouble(POSITION_SL);
         ENUM_POSITION_TYPE positionType = (ENUM_POSITION_TYPE)PositionGetInteger(POSITION_TYPE);

         // Implement trailing stop
         if(positionType == POSITION_TYPE_BUY && currentPrice - openPrice > 2 * CustomATR(symbol, PERIOD_CURRENT, 14, 0))
           {
            double newStopLoss = NormalizeDouble(currentPrice - CustomATR(symbol, PERIOD_CURRENT, 14, 0), SymbolInfoInteger(symbol, SYMBOL_DIGITS));
            if(newStopLoss > stopLoss)
              {
               trade.PositionModify(ticket, newStopLoss, 0);
              }
           }
         else
            if(positionType == POSITION_TYPE_SELL && openPrice - currentPrice > 2 * CustomATR(symbol, PERIOD_CURRENT, 14, 0))
              {
               double newStopLoss = NormalizeDouble(currentPrice + CustomATR(symbol, PERIOD_CURRENT, 14, 0), SymbolInfoInteger(symbol, SYMBOL_DIGITS));
               if(newStopLoss < stopLoss || stopLoss == 0)
                 {
                  trade.PositionModify(ticket, newStopLoss, 0);
                 }
              }
        }
     }
  }

void ManageExistingOrders(string symbol)
  {
   for(int i = PositionsTotal() - 1; i >= 0; i--)
     {
      ulong ticket = PositionGetTicket(i);
      if(PositionSelectByTicket(ticket) && PositionGetString(POSITION_SYMBOL) == symbol)
        {
         double stopLoss = PositionGetDouble(POSITION_SL);
         double takeProfit = PositionGetDouble(POSITION_TP);
         double openPrice = PositionGetDouble(POSITION_PRICE_OPEN);
         double currentPrice = PositionGetDouble(POSITION_PRICE_CURRENT);
         ENUM_POSITION_TYPE positionType = (ENUM_POSITION_TYPE)PositionGetInteger(POSITION_TYPE);

         double atr = CustomATR(symbol, PERIOD_CURRENT, 14, 0);
         double newStopLoss, newTakeProfit;

         if(positionType == POSITION_TYPE_BUY)
           {
            newStopLoss = NormalizeDouble(currentPrice - 2 * atr, SymbolInfoInteger(symbol, SYMBOL_DIGITS));
            newTakeProfit = NormalizeDouble(currentPrice + 3 * atr, SymbolInfoInteger(symbol, SYMBOL_DIGITS));
            if(newStopLoss > stopLoss && currentPrice - openPrice > atr)
              {
               trade.PositionModify(ticket, newStopLoss, newTakeProfit);
              }
           }
         else
            if(positionType == POSITION_TYPE_SELL)
              {
               newStopLoss = NormalizeDouble(currentPrice + 2 * atr, SymbolInfoInteger(symbol, SYMBOL_DIGITS));
               newTakeProfit = NormalizeDouble(currentPrice - 3 * atr, SymbolInfoInteger(symbol, SYMBOL_DIGITS));
               if(newStopLoss < stopLoss && openPrice - currentPrice > atr)
                 {
                  trade.PositionModify(ticket, newStopLoss, newTakeProfit);
                 }
              }

         // Implementar cierre parcial
         double profit = PositionGetDouble(POSITION_PROFIT);
         double volume = PositionGetDouble(POSITION_VOLUME);
         if(profit > 0 && MathAbs(currentPrice - openPrice) > 2 * atr)
           {
            double closeVolume = volume * 0.5;
            if(IsValidVolume(symbol, closeVolume))
              {
               ClosePosition(ticket, closeVolume);
              }
           }
        }
     }
  }

未決済のポジションや既存の注文を管理し、トレーリングストップや部分決済などの戦略を実行します。

このEAは、伝統的なテクニカル分析と高度な統計モデリング(VAR)および機械学習技術（因果発見）を組み合わせて取引判断をおこないます。モジュール構造により、各コンポーネントの変更や改良が容易です。

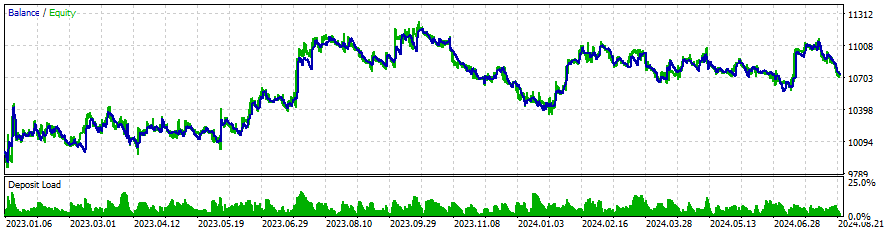
結果

以下はいくつかの銘柄についての結果です。設定と入力は調査したすべての銘柄について同じです。

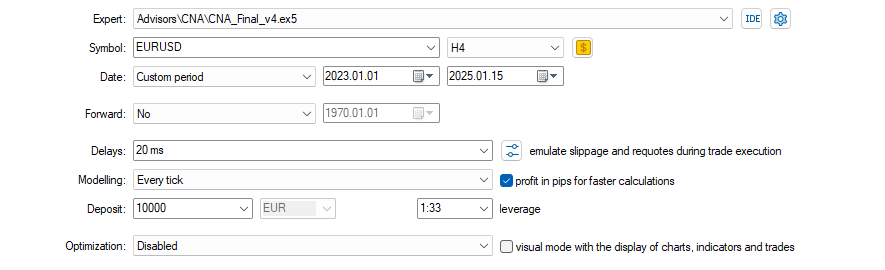
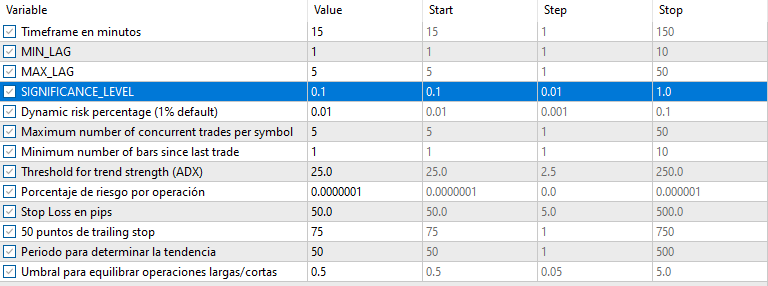
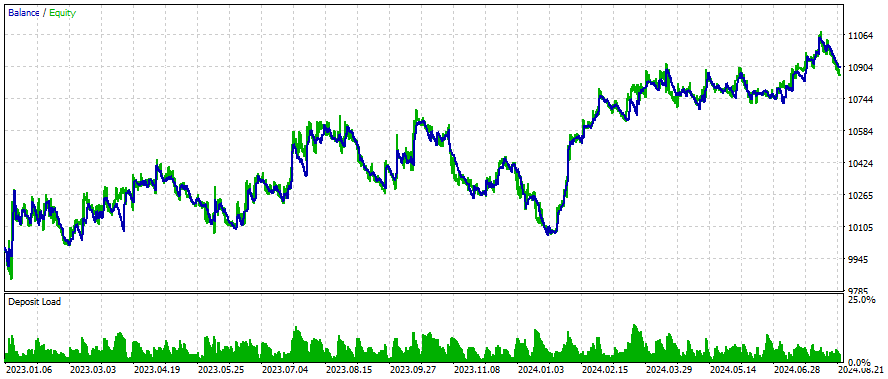
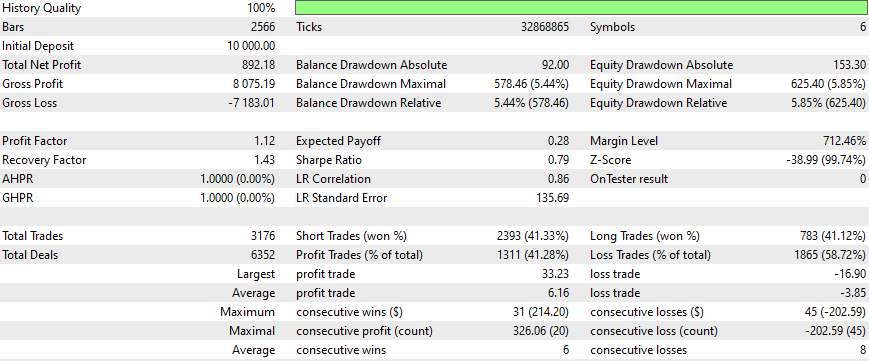
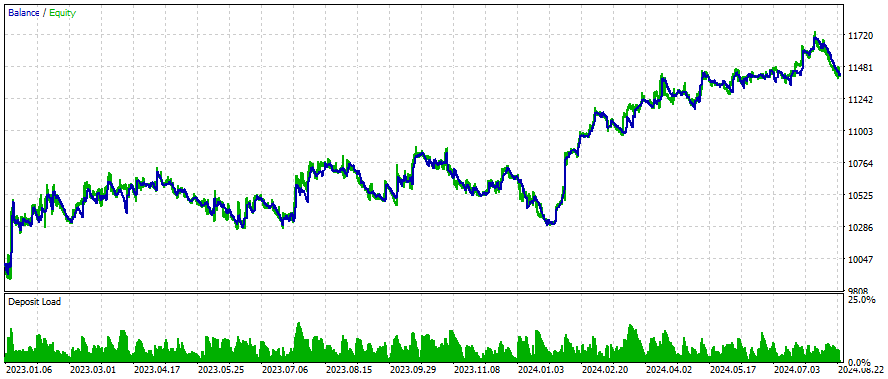
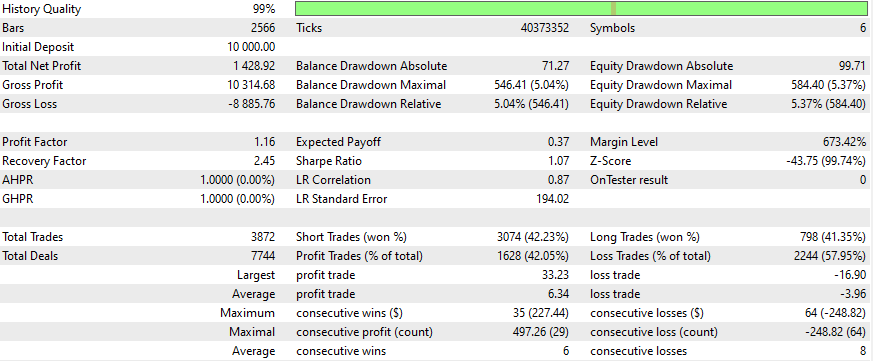
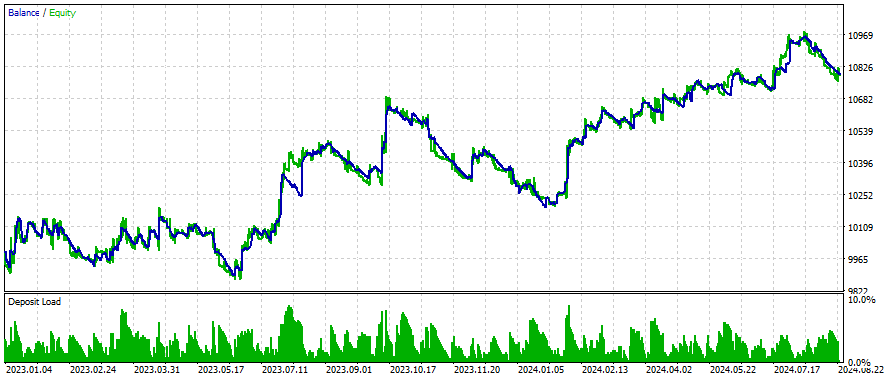
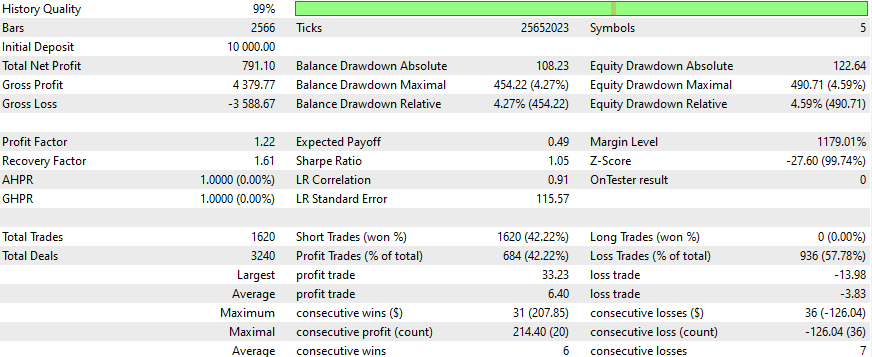
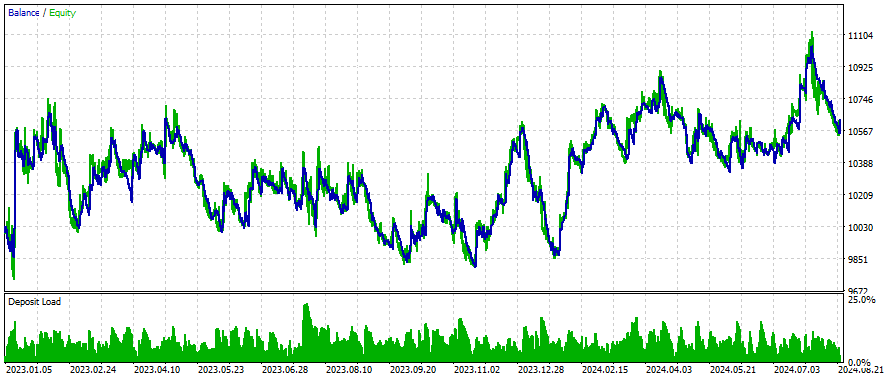
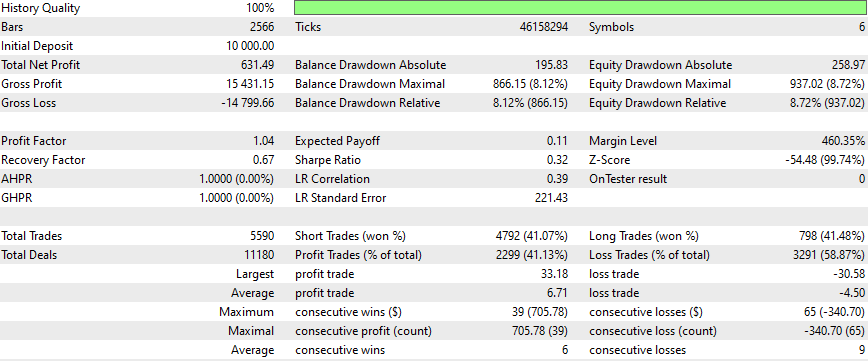
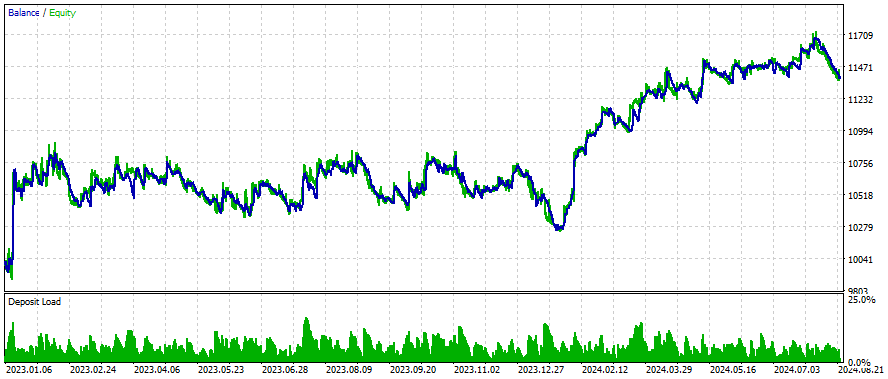
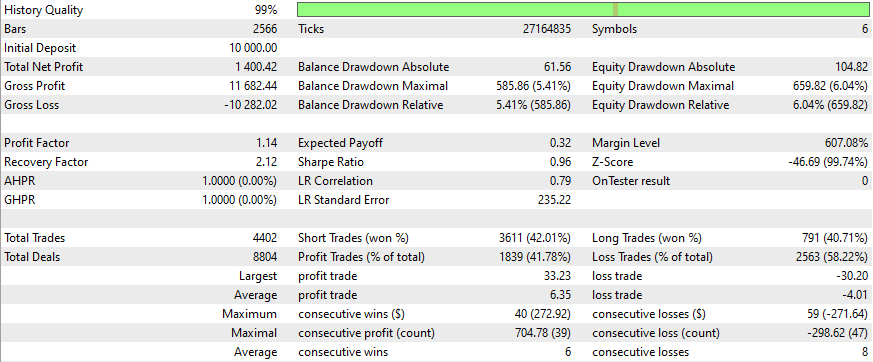
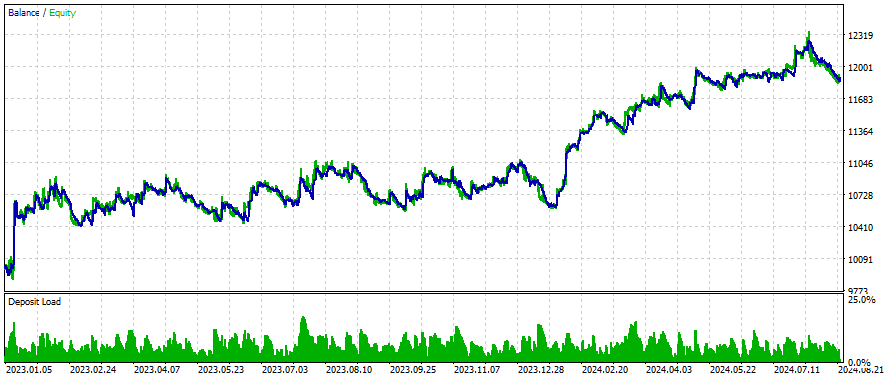
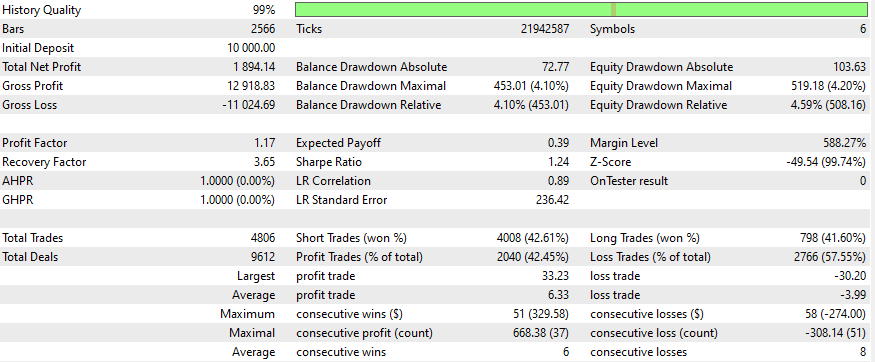
より良い結果を得るには？

銘柄ノードにさらに銘柄を追加し、共積分や相関のある銘柄を使用すれば、より良い結果を得ることができます。これらの銘柄が何なのかを知るには、  「取引におけるナッシュ均衡ゲーム理論のHMMフィルタリングの応用」稿にある私のPythonスクリプトを使うことができます。

また、戦略にディープラーニングを加えれば、より良い結果が得られます。「  Pythonを使ったEAとバックテストのための感情分析とディープラーニング」稿の様な例もあります。 

また、フィルタの最適化もおこなわれていません。さらにフィルタリングを追加してみるのもよいでしょう。

以下は、ネットワークに銘柄を増やすとグラフがどのように変化するかの例です。

void SetupNetwork()
  {
   string symbols[] = {"EURUSD", "GBPUSD", "USDCAD", "USDCHF", "USDJPY", "AUDUSD", "XAUUSD", "SP500m", "ND100m"};
   for(int i = 0; i < ArraySize(symbols); i++)
     {
      AddNode(symbols[i]);
     }
  }

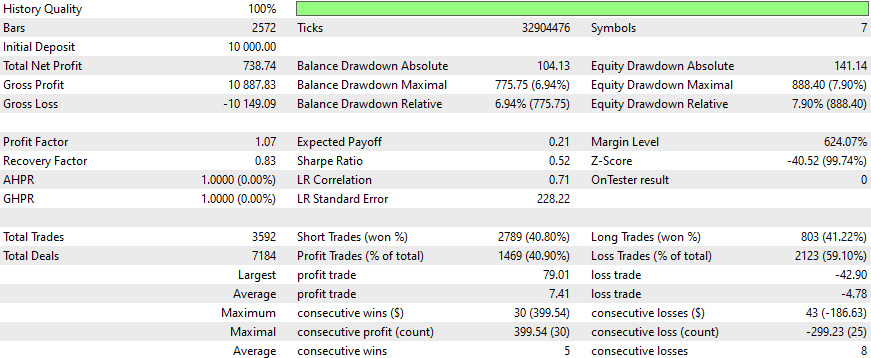
ネットワークに銘柄を増やすだけで、何とか改善することができました。

1. 取引活動（取引総数の増加）
2. ショート取引の勝率
3. 収益性の高い取引の割合
4. 最も収益性の高い取引の規模
5. 勝ち取引あたりの平均利益
6. 負け取引の割合の減少
7. 負け取引あたりの平均損失の減少

これらの改善は、いくつかの主要なパフォーマンス指標（プロフィットファクターやリカバリーファクターなど）が低いにもかかわらず、全体的な取引管理とリスクコントロールが改善されていることを示唆しています。

結論

この記事では、市場のイベントを予測し、取引の意思決定をおこなうための、因果ネットワーク分析(CNA: Causal Network Analysis)とベクトル自己回帰(VAR: Vector Autoregression)を統合した高度な取引システムについて説明しました。このシステムは、金融商品間の関係をモデル化するために、高度な統計技術と機械学習技術を活用しています。しかし、有望である一方で、強固なリスク管理と市場への深い理解を組み合わせることの重要性も強調しています。

より良い結果を求めるトレーダーには、より相関性の高い銘柄でネットワークを拡張し、ディープラーニングを取り入れ、フィルタリング方法を最適化することを提案しています。取引で長期的に成功するためには、継続的な学習と適応が不可欠です。

あなたのアルゴリズムが常に市場の一歩先を行くものでありますように。