知っておくべきMQL5ウィザードのテクニック（第64回）：ホワイトノイズカーネルでDeMarkerとEnvelope Channelsのパターンを活用する

はじめに

前回の記事では、モメンタム系インジケーターであるDeMarkerとサポート/レジスタンスを示すEnvelopesバンドを組み合わせ、そのシグナルを検証しました。今回はそれらを機械学習でどのように活用できるかを探ります。これまでにもインジケーターのペアリング手法を紹介してきましたので、導入的な内容に関心のある読者はそちらも参照ください。基本的には、MQL5で利用されるインジケーターをPython言語で実装し、さらにMetaTrader 5 Pythonモジュールを通じて取得した価格データを用います。このモジュールを利用すると、ブローカーのサーバーにログインして価格データや銘柄情報を取得できます。

Pythonにおけるインジケーター

Pythonには多様なテクニカル分析ライブラリがあり、インポートするだけで数多くのインジケーターを実装できます。しかし問題は、標準化されていないことや、一部のインジケーターがライブラリに含まれていないことです。たとえばこの記事の題材であるDeMarkerオシレーターはpandas technical analysisライブラリには存在せず、これは「ta」(technical analysis)モジュールには含まれています。一方で、Envelopesはpandas technical analysisライブラリにはあるものの、「ta」にはそのままの形では含まれておらず、代替としてBollinger BandsやDonchian Channelが用意されています。

そして興味深いことに、近年ではこうしたライブラリをインストールして使うのと同じくらい、あるいはそれ以下の労力でインジケーターを一から自作することが可能になっています。そのためこの記事ではDeMarkerとEnvelopesを自作関数として実装しました。これによりモジュール参照が減るため、理論的にはPythonの実行速度がわずかに向上するはずです。

DeMarker

DeMarkerインジケーターは、指定した期間における資産の買われ過ぎや売られ過ぎの極端な状態を追跡するオシレーターです。前回の記事で既に紹介したように、このインジケーターは0から1の範囲で変動し、0.7を超える値は買われ過ぎを示し、0.3を下回る値は売られ過ぎを意味します。これをPythonにおけるカスタム関数として実装することにします。

def DeMarker(df, period=14):
    """
    Calculate DeMarker indicator for a DataFrame with OHLC prices
    
    Args:
        df: Pandas DataFrame with columns ['open', 'high', 'low', 'close']
        period: Lookback period (default 14)
        
    Returns:
        Pandas Series with DeMarker values
    """
    # Calculate DeMax and DeMin
    demax = df['high'].diff().clip(lower=0)
    demin = -df['low'].diff().clip(upper=0)
    
    # Smooth the values using SMA
    demax_sma = demax.rolling(window=period).mean()
    demin_sma = demin.rolling(window=period).mean()
    
    # Calculate DeMarker
    demarker = demax_sma / (demax_sma + demin_sma)
    return pd.DataFrame({'main': demarker})

この関数の入力は、データフレーム「df」と「period」です。データフレーム「df」は始値、高値、安値、終値の価格データを含むpandasデータフレームであり、「period」はDeMarkerの計算に用いる過去の参照期間です。この関数はDeMarkerのロジックをカプセル化し、モジュール性と再利用性を持たせています。

DeMaxの計算は連続する高値の差分(df[‘high’].diff())を求めることでおこないます。このバッファにおいて差分が正の値であれば、それは高値が上昇していることを意味するためそのまま保持されますが、そうでなければゼロに設定されます。このゼロへの設定はclip関数(clip(lower=0))によって実現されます。同様に、安値の差分に対しては、差分が負（つまり現在の安値が前回の安値より低い）である場合には、その絶対値がバッファに保持され、そうでなければclip(upper=0)によってゼロに設定されます。

これらの絶対的な変化を追跡することが重要なのは、DeMaxが高値の上昇を記録することで上方向の価格モメンタムを測定し、一方DeMinが安値の下落を記録することで下方向の価格モメンタムを測定するからです。これら2つの指標はDeMarkerの中核であり、価格が前期間と比べてどれだけ動いたかを規定します。Pythonにおいてdiff関数を実装する際には、入力データフレームに十分なデータポイントが含まれていること、そして最初の行には必ずNaN値が発生することに注意する必要があります。

この後、それぞれのバッファ内の値を平滑化します。平滑化は各系列のノイズを減らし、短期的な価格変動に対するインジケーター値の感度を低くします。rolling(window=period).mean()メソッドは指定された期間の平均を計算し、この遅延がインジケーターの役割であるマクロトレンドの把握にしばしば合致します。開始からperiod-1までの値はローリングウィンドウに十分なデータがないためNaNとなり、これらはドロップするか、正規化された値で補う必要があります。期間の選択はDeMarkerの感度にも影響し、短い期間はより敏感になります。

次に、DeMaxの平均をDeMax平均とDeMin平均の合計で割ることでDeMarker値を計算します。このステップによってDeMarkerは0から1の範囲に正規化され、解釈が容易になります。この比率は事実上、上昇方向の価格変動の強さを、上昇と下降の両方を合わせた総変動に対する相対的な強さとして測定します。値が1に近ければ強い強気モメンタムを示し、0に近ければ弱気モメンタムが優勢であることを意味します。

実装に際しては、このステップでゼロ除算が発生しないようにすることが重要です。ただしこれは価格が常に変化しているため（特に高値と安値において）、稀なケースに留まります。最終的にこの関数は、「main」とラベル付けした単一列を持つpandasデータフレームとしてDeMarker値を返します。このデータフレーム形式にすることで、pandasベースの他の分析ツールとの互換性が確保され、より大きな取引システムへの統合も容易になります。

Envelopes

price-Envelopesはサポート/レジスタンス系のインジケーターで、価格の移動平均線の上下に2本のバンド（上部バンドと下部バンド）を描きます。バンドは一定の割合でオフセットされており、価格がこれらのバンドに触れることで、トレーダーにサポートおよびレジスタンスの目安を提供します。Pythonでの実装は次のとおりです。

def Envelopes(df, period=14, deviation=0.1):
    """
    Calculate Price Envelopes for a DataFrame with OHLC prices
    
    Args:
        df: Pandas DataFrame with columns ['open', 'high', 'low', 'close']
        period: MA period (default 20)
        deviation: Percentage deviation from MA (default 0.05 for 5%)
        
    Returns:
        DataFrame with columns ['upper', 'ma', 'lower']
    """
    # Calculate moving average (typically using close prices)
    ma = df['close'].rolling(window=period).mean()
    
    # Calculate upper and lower envelopes
    upper = ma * (1 + deviation)
    lower = ma * (1 - deviation)
    
    return pd.DataFrame({'upper': upper, 'ma': ma, 'lower': lower})

上記のコードは、異なる戦略に応じて期間や偏差の入力パラメータをカスタマイズできる柔軟な方法でEnvelopesを計算します。Envelopesを計算する最初のステップは移動平均の算出です。ここでは、指定期間の終値の単純移動平均(SMA)を使用します。移動平均はエンベロープの中心線であり、トレンドの平均価格として機能します。rolling(window=period).mean()によるバッファ計算は平均値ベクトルを返しますが、最初のperiod-1個の値はNaNとなります。これらは適切に処理する必要があります。

次に、上部および下部バンドの値を計算します。上部エンベロープは移動平均に(1 + deviation)を掛けることで算出されます。たとえば偏差が10%の場合、上部バンドは移動平均の110%となります。デフォルトの偏差値が0.1の場合、これは10%に相当します。下部エンベロープは移動平均に(1 - deviation)を掛けることで算出され、今回の例では90%となります。

上部および下部バンドは、価格が「通常の」条件下で変動すると予想される範囲を定義します。価格がいずれかのバンドに触れる場合、それはブレイクアウトか反転のシナリオを示します。これらのバンドをサポートおよびレジスタンスとして扱うため、トレンド継続や市場の買われ過ぎ/売られすぎ状態を示唆する状況となります。

偏差パラメータはEnvelopesの幅を制御します。偏差が大きいほどバンド幅が広くなり、ボラティリティの高い資産に適しています。一方、偏差が小さいと安定した資産向けの狭いバンドとなります。偏差は正の値である必要があり、無効なバンドを避けることができます。これらのエンベロープバンドは、上下のボラティリティが等しいことを前提として移動平均を中心に対称になります。非対称バンドが必要な場合は、ボリンジャーバンドを採用できます。

返されるpandasデータフレームにはupper、lower、maの3列が含まれます。このデータフレーム形式により、3つの構成要素すべてに簡単にアクセスでき、可視化、シグナル生成、さらなる解析が容易になります。

Pythonにおける特徴量

ここでいう特徴量とは、2つのインジケーターであるDeMarkerとEnvelopesから得られるシグナルをベクトル化した表現のことです。これらの特徴量は、機械学習モデルの入力として使用されます。モデルは回帰型ニューラルネットワーク(RNN)で、ホワイトノイズカーネルを用いる仕様です（詳細は後述）。このPythonにおける機械学習の実装は、前回の記事で扱った合計10個の特徴量に基づいています。そのうち、フォワードウォークで機能したのは6つ、すなわち0、1、5、6、7、8です。したがって、これらの特徴量のみを回帰型ニューラルネットワークでテストします。そのため、RNNに入力する前にPythonで手動でコード化する必要があります。

Feature_0

前回の記事で見たように、Feature_0、すなわちPattern_0は、DeMarkerが買われすぎ/売られすぎの閾値をクロスし、かつ価格が同時にEnvelopesの上部または下部バンドをクロスした際にシグナルを生成します。そこでこれをPythonで次のように実装します。

def feature_0(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:
    feature[:, 0] = ((dem_df['main'] <= 0.3) &
                     (price_df['close'] > env_df['lower']) &
                     (price_df['close'].shift(1) <= env_df['lower'].shift(1)) &
                     (price_df['close'].shift(2) >= env_df['lower'].shift(2))).astype(int)
    feature[:, 1] = ((dem_df['main'] >= 0.7) &
                     (price_df['close'] < env_df['upper']) &
                     (price_df['close'].shift(1) >= env_df['upper'].shift(1)) &
                     (price_df['close'].shift(2) <= env_df['upper'].shift(2))).astype(int)
    
    # Set first 2 rows to 0 (no previous values to compare)
    feature[0, :] = 0
    feature[1, :] = 0
    
    return feature

関数内の最初のコード行では、形状が(len(dem_df), 2)のゼロ埋めされたNumPy配列を作成しています。この配列は、強気と弱気のシグナルをカテゴリごとに格納するためのものです。すべての行を初期値ゼロで初期化しており、データフレームの長さと配列サイズを一致させることでインデックスのずれを防いでいます。

強気シグナルのチェックは配列の0列でおこなわれ、最初に評価されます。前回の記事で説明した通り、上記の実装では、DeMarkerが売られすぎ（通常0.3以下）であり、現在の終値が下部エンベロープを上回り、1期間前の終値が下部エンベロープ以下であり、2期間前の終値が下部エンベロープ以上である場合に強気シグナルが生成されます。

この強気条件は、DeMarkerの売られすぎ状態と価格の下部エンベロープ突破を組み合わせており、トレンドの継続や反転の可能性を示唆します。shift(1)およびshift(2)の条件により、価格が過去に下部エンベロープとどのように交わったかを確認でき、前回の記事で定義された動作を再現しています。実運用では、誤検出を減らすために複数期間のチェックや、特定の価格パターンを要求する追加条件を加えることも可能です。また、env_df['lower']とprice_df['close']のNaNを確認することで無効な比較を回避できます。

弱気シグナルの列は、DeMarkerが買われすぎ状態にあり、現在の終値が上部エンベロープを下回り、1期間前の終値が上部エンベロープ以上、2期間前の終値が上部エンベロープ以下である場合にシグナルを記録します。このパターンは、買われすぎ状態後の反転や押し戻しを捉えます。使用時には、shift操作に対応できる十分な過去データを確保することが重要です。

そのため、最初の2行の値はゼロに設定されています。これはshift(1)およびshift(2)を使用しているためです。

最後にreturn文でNumPy配列を返します。これにより、RNNへの入力に適した形式でシグナルパターンが提供されます。複数期間の価格とエンベロープの相互作用（shift(1)とshift(2)）は、時間的な確認層を追加するもので、他の単純なクロスオーバーシグナルと比べて独自性を高めています。

Feature_1

このパターンは、DeMarkerが買われすぎまたは売られすぎの極端なゾーンにあり、かつ価格が複数期間にわたってエンベロープの上部または下部バンドの外側に位置している場合にシグナルを生成します。Pythonでの実装は次のとおりです。

def feature_1(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:
    feature[:, 0] = ((dem_df['main'] > 0.7) &
                     (price_df['close'] > env_df['upper']) &
                     (price_df['close'].shift(1) > env_df['upper'].shift(1))).astype(int)
    feature[:, 1] = ((dem_df['main'] < 0.3) &
                     (price_df['close'] < env_df['lower']) &
                     (price_df['close'].shift(1) < env_df['lower'].shift(1))).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    feature[0, :] = 0
    
    return feature

最初のステップは、Feature_0と同様に、ゼロで埋めた配列を作成してサイズを設定することです。この初期化により、デフォルトではシグナルがない状態となり、NaNを扱うより安全です。次に各インデックスの値を定義します。最初のインデックス（列）では、強気条件をチェックします。コードは、DeMarkerが買われすぎ領域(>0.7)にあり、現在の終値が上部エンベロープより上に位置しており、かつ前回の終値も上部エンベロープを上回っている場合を確認します。 

これは、DeMarkerが買われすぎでも価格が上部エンベロープを維持している場合に強い上昇モメンタムを識別するため重要です。前回の記事でも述べたように、これは反転ではなくトレンド継続の可能性を示唆します。次に、コードは次のインデックス値を設定し、弱気条件をチェックします。こちらは、DeMarkerが売られすぎ領域(<0.3)にあり、現在の終値が下部エンベロープより下にあり、かつ前回の終値も下部エンベロープを下回っている場合を確認します。

強気シグナルの鏡像として期待され、下部エンベロープ下での価格維持により強い弱気モメンタムを捉えます。これは下降トレンドの継続を示します（前回の記事でも論じました）。shiftを使った比較をおこなうため、最初の行の値は0に設定する必要があります。この場合は比較が1つのインデックスのみなので、最初の行だけを設定します。return文では、NumPyフォーマットでシグナル配列を返します。

この関数は、DeMarkerの極値で確認されたエンベロープバンドを超えた持続的な価格ブレイクアウトを捉えます。これは強いトレンド継続のサインであり、反転を予測するというよりも、既存トレンドに乗る機会を示すものです。Feature_0とは異なり、クロスオーバーパターンを必要とせず、複数期間にわたるバンド外の価格に注目しています。

Feature_5

Feature_5は、前回の記事でフォワードウォークに成功したパターンの次のものです。上の2つの特徴量と少し似ていますが、シグナルはDeMarkerの極端な値から取得する点は同じでも、価格がバンドに触れることに注目するのではなく、エンベロープのバンドの方向性を用いる点が異なります。Pythonでの実装は次のとおりです。

def feature_5(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:
    feature[:, 0] = ((dem_df['main'] > 0.7) &
                     (env_df['upper'] > env_df['upper'].shift(1))).astype(int)
    feature[:, 1] = ((dem_df['main'] < 0.3) &
                     (env_df['lower'] < env_df['lower'].shift(1))).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    feature[0, :] = 0
    
    return feature

まず最初に、他の2つの関数と同様に、出力配列をゼロで初期化し、そのサイズを2に設定します。これは上記関数の最初の行で実現されています。次に、最初のインデックス値を設定します。これも他の特徴量と同様に、強気かどうかを確認する部分です。  条件は比較的シンプルで、DeMarkerが買われすぎ領域(>0.7)にあり、かつ上部エンベロープが上昇している場合、強気シグナルと判断します。次に、2番目のインデックス値を設定し、弱気かどうかを確認します。予想通り、DeMarkerが0.3未満で下部エンベロープが下降している場合は弱気シグナルとなります。最後に、shift比較によるNaNから生じる無効な比較を避けるため、最初の行の値をゼロに設定します。

Feature_6

Feature_6（またはPattern_6）は、前回の記事で紹介した通り、DeMarkerのモメンタム変化とエンベロープバンド上での価格波形の形成に基づいてシグナルを生成します。Pythonでの実装は次のとおりです。

def feature_6(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:
    feature[:, 0] = ((dem_df['main'] > dem_df['main'].shift(1)) &
                     (price_df['low'].shift(1) <= env_df['lower'].shift(1)) &
                     (price_df['low'].shift(2) >= env_df['lower'].shift(2)) &
                     (price_df['low'].shift(3) <= env_df['lower'].shift(3)) &
                     (price_df['low'].shift(4) >= env_df['lower'].shift(4))).astype(int)
    feature[:, 1] = ((dem_df['main'] < dem_df['main'].shift(1)) &
                     (price_df['high'].shift(1) >= env_df['upper'].shift(1)) &
                     (price_df['high'].shift(2) <= env_df['upper'].shift(2)) &
                     (price_df['high'].shift(3) >= env_df['upper'].shift(3)) &
                     (price_df['high'].shift(4) <= env_df['upper'].shift(4))).astype(int)
    
    # Set first 4 rows to 0 (no previous values to compare)
    feature[0, :] = 0
    feature[1, :] = 0
    feature[2, :] = 0
    feature[3, :] = 0
    
    return feature

初期化の手順は、上で見てきたものと同様ですが、配列に設定する値に違いがあります。まず、ブル（買い）シグナルを確認する最初のインデックスには、条件が満たされた場合に1（真に相当）を割り当てます。この条件は、DeMarkerが上昇しており、かつ過去4期間にわたって下部エンベロープに対する終値パターンが下、上、下、上と交互に形成されている場合です。次に、ベア（売り）シグナルを確認する2番目のインデックスでは、DeMarkerが下降しており、かつ買いの場合と同様に、上部エンベロープに対するM字型終値パターンを確認します。

無効な比較を避けるために初期行を0に設定する処理が続きます。これは、shift比較を使用しているため、デフォルトでNaNとなる値に対して比較をおこなうと無効な結果が生じるのを防ぐためです。今回の実装では、shiftで1～4インデックスを使用しているため、0行目から3行目までの4行に対して0を割り当てています。

Feature_7

この特徴量は、前回の記事でも述べたように、異なる時間ラグでのDeMarkerの値と、価格がエンベロープのバンドを横切る動きに基づいてシグナルを生成します。これにより、モメンタムの変化に注目することができます。Pythonでの実装は次のとおりです。

def feature_7(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:DEM(X()) >= 0.5 && DEM(X() + 2) <= 0.3 && Close(X()) > ENV_UP(X()) && Close(X() + 1) <= ENV_UP(X() + 1)
    feature[:, 0] = ((dem_df['main'] >= 0.5) &
                     (dem_df['main'].shift(2) <= 0.3) &
                     (price_df['close'] >= env_df['upper']) &
                     (price_df['close'].shift(1) <= env_df['upper'].shift(1))).astype(int)
    feature[:, 1] = ((dem_df['main'] <= 0.5) &
                     (dem_df['main'].shift(2) >= 0.8) &
                     (price_df['close'] <= env_df['lower']) &
                     (price_df['close'].shift(1) >= env_df['lower'].shift(1))).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    feature[0, :] = 0
    
    return feature

初期化では配列サイズを2に設定し、ゼロで埋めます。最初のインデックスはロングシグナルの確認に使用されます。コードでは、現在のDeMarkerがニュートラルまたは強気(>=0.5)で、2期間前のDeMarkerが売られ過ぎ(<=0.3)であり、かつ現在の終値が上部エンベロープ以下の場合に、強気シグナルを真としてマークします。この長い条件は、売られ過ぎからニュートラルまたは強気へのモメンタム変化を捉え、上部エンベロープのブレイクアウトによって確認されることを目的としています。これは通常、強い反転やトレンドの開始を示唆します。shift(2)条件は、最近の売られ過ぎ状態を必要とするラグを導入します。 

インデックス1での弱気条件チェックは、現在のDeMarkerがニュートラルから弱気(<=0.5)で、2期間前のDeMarkerが買われ過ぎ(>=0.8)であり、現在の終値が下部エンベロープ以下、さらに前回の終値が下部エンベロープ以上の場合に成立します。最後に、shiftインデックスが1つしか使用されていないため、最初の行のみをゼロに設定して終了します。

Feature_8

最後の特徴量は、DeMarkerが極端なゾーンにあり、かつ価格の安値/高値がエンベロープのバンドを大きく超えている場合にシグナルを生成します。つまり、極端な価格変動を捉えるものです。Pythonでの実装は次のとおりです。

def feature_8(dem_df, env_df, price_df):
    """
    """
    # Initialize empty array with 2 dimensions and same length as input
    feature = np.zeros((len(dem_df), 2))
    
    # Dimension 1:DEM(X()) > 0.7 && Low(X()) > ENV_UP(X())
    feature[:, 0] = ((dem_df['main'] > 0.7) &
                     (price_df['low'] > env_df['upper'])).astype(int)
    feature[:, 1] = ((dem_df['main'] < 0.3) &
                     (price_df['high'] < env_df['lower'])).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    # feature[0, :] = 0
    
    return feature

出力のNumPy配列をゼロで初期化し、サイズを2に設定した後、インデックス0の値を設定します。このインデックスは、上記の他のパターンと同様に、強気であるかどうかを示します。この場合、強気シグナルはDeMarkerが買われすぎ(>0.7)であり、かつ現在の安値がエンベロープ上限を上回っているときに発生します。このパターンは、その期間の最安値がエンベロープ上限を超えていることを示しているため、通常は強い上昇を意味します。これは大きな上昇モメンタムを示唆することが多いです。

インデックス1に割り当てられる弱気チェックは、DeMarkerが売られすぎ(<0.3)であり、かつ現在の高値が下部エンベロープを下回っている場合に確認されます。これは上記の強気セットアップの逆であり、どちらのシナリオもまれですが、前回の記事でのテストではいくつかの取引を確認することができました。ただし、実際の取引状況では、その希少性を考慮し、安全のために追加の確認フィルターを適用することも可能です。

PythonにおけるRNN

私たちの回帰型ニューラルネットワーク(RNN)は、上記のベクトル化されたインジケーター出力（特徴量0、1、5、6、7、8）を受け取るPyTorchのニューラルネットワークモジュールであり、標準的なRNNにノイズ注入機構を組み合わせて、ロバスト性を高めたり確率的プロセスをモデル化したりします。これは回帰タスク向けに調整されており、入力系列ごとに単一の出力値を生成します。ノイズ注入はRNNの隠れ状態に対しておこなわれ、射影層とシグモイド活性化によってその影響が調整されます。

このRNNへの入力は、形状（batch_size、input_size）のテンソルです。設計は、RNN層の後にノイズ用の線形射影層、さらに最終的な出力のための全結合層を持ちます。ノイズ注入は、RNNの隠れ状態にホワイトノイズカーネルを加えることで実行されます。これはオンザフライで生成することも、あらかじめ計算されたテンソルを与えることも可能です。出力は各系列ごとの単一の回帰値で、その形状は(batch_size,)です。Pythonでの実装は次のとおりです。

# Define the network as a class
class WhiteNoiseRNN(nn.Module):
    def __init__(self, input_size=5, hidden_size=64, num_layers=1):
        super().__init__()
        self.hidden_size = hidden_size
        self.rnn = nn.RNN(input_size, hidden_size, num_layers, batch_first=True)
        self.noise_proj = nn.Linear(hidden_size, hidden_size)  # Projects noise to hidden space
        self.fc = nn.Linear(hidden_size, 1)  # Single output for regression
        
    def forward(self, x, noise_std=0.05):
        """
        Args:
            x: Input tensor of shape (batch_size, seq_len, input_size)
            noise_std: Either:
                - float: Standard deviation for generated noise
                - tensor: Pre-computed noise (must match rnn_out shape: batch_size × seq_len × hidden_size)
        """
        # Ensure proper input dimensions
        if x.dim() == 2:
            x = x.unsqueeze(1)  # (batch, features) → (batch, 1, features)
            
        # RNN processing
        rnn_out, _ = self.rnn(x)  # (batch_size, seq_len, hidden_size)
        
        # Noise injection
        if isinstance(noise_std, torch.Tensor):
            noise_std = noise_std.float()
            if noise_std.dim() == 1:
                noise_std = noise_std.view(-1, 1, 1)  # (batch,) → (batch, 1, 1)
            noise = noise_std.expand_as(rnn_out)
        elif noise_std > 0:
            noise = torch.randn_like(rnn_out) * noise_std
        else:
            noise = 0
            
        if isinstance(noise, torch.Tensor):
            projected_noise = self.noise_proj(noise)
            rnn_out = rnn_out + torch.sigmoid(rnn_out) * projected_noise
            
        return self.fc(rnn_out[:, -1, :])  # (batch_size,)

上記のコードから、WhiteNoiseRNNクラスはnn.Moduleのサブクラスとして定義され、入力サイズ、隠れ層サイズ、層数の3つの入力パラメータで初期化されます。このステップでネットワークのアーキテクチャとハイパーパラメータが確立されます。

nn.Moduleを継承することで、PyTorchの自動微分やモデル管理機能（学習や評価など）を容易に活用できます。入力サイズは入力データの特徴量次元により決定されます。今回のケースではすべての特徴量が2次元なので、この値は2になります。

隠れ層のサイズはモデルの表現力を決定します。値を大きくするとモデルの表現力は増しますが、過学習や計算コスト増加のリスクがあります。層数は1に設定するだけでほとんどのシンプルなタスクには十分ですが、値を増やすと勾配消失の問題が生じやすくなります。

super()による初期化呼び出しで親クラス(nn.Module)を呼び出し、PyTorchのモジュール機能（パラメータ追跡やデバイス管理など）が正しくセットアップされます。この呼び出しを含めることは、初期化エラーを防ぐための定石です。隠れ層サイズはインスタンス変数として保存され、他のメソッドで使用できるようにしておきます。

RNN層は指定した入力サイズ、隠れ層サイズ、層数で初期化されます。batch_first=Trueとすることで、入力と出力のテンソル形状が「バッチサイズが先頭次元」となるため、処理が直感的になります。さらに、RNNの隠れ状態と同じ次元にノイズを射影するノイズ射影層を定義します。この層により、ノイズはスケーリングや回転などで変換されてから隠れ状態に加えられ、ノイズ注入が学習可能になります。これはモデルが学習中にノイズの影響を適応させるのに役立ちます。ただし線形層を追加するためパラメータ数が増え、モデルの複雑さも上がるため、十分な学習が必要です。

次に、RNNの最終隠れ状態を単一の出力値へマッピングする全結合層を定義します。これにより回帰出力が得られ、隠れ状態の次元が1つのスカラーに縮約されます。これは連続値の予測をおこなう回帰タスクでは不可欠であり、今回のケースでも特に重要です。

forwardメソッドはネットワークの順伝播を定義し、入力xを処理しつつ標準偏差noise_stdのノイズを適用します。この関数はRNNの処理、ノイズ注入、出力予測を組み合わせた主要計算を実装しています。入力xが正しい形状と前処理を満たしていることを常に確認することが重要です。デフォルトのnoise_std=0.05はハイパーパラメータであり、必要なノイズレベルに応じて調整します。事前計算されたノイズを使う場合は、その形状と型を検証し、ランタイムエラーを避ける必要があります。

最初の処理としてxに系列長の次元を追加して変形します。これにより、単一ステップ入力でも系列次元を持たせることができ、RNNの要求に適合します。これによって単一ステップ入力にもマルチステップ入力にも柔軟に対応できます。

次にRNNに入力xを通し、各タイムステップにおける隠れ状態を生成します。この処理の出力は2つあります。1つ目は隠れ状態を含むテンソルrnn_out、2つ目は最終層の隠れ状態であり、今回は使用しないため「_」に代入します。この処理は非常に重要で、RNNは入力系列の時間的依存関係を捉えることができ、モデルの系列処理の基盤を形成します。これらの隠れ状態こそが、ノイズ注入や出力予測の主要なメカニズムとなります。

その後、forward関数の最初のif文で、事前計算されたノイズの処理に移ります。ノイズテンソルは一貫性を保つためにfloat型に変換され、1次元テンソルであればブロードキャスト可能に変形され、さらにrnn_outと同じ形に拡張されます。一方で、ノイズを生成する場合は、隠れ状態にランダム性を導入し、確率的プロセスをモデル化する際のロバスト性を高めます。このノイズはnoise_stdによってスケーリングされ、その大きさが制御されます。もしnoise_stdが0または負の値である場合には、ノイズはゼロに設定されます。これにより、ノイズなしでもモデルを動作させることができ、決定論的な予測やデバッグ時に役立ちます。

ノイズ値を割り当てた後、ノイズをnoise_proj線形層に通してRNNの隠れ状態空間に整合させます。これにより、RNN出力のシグモイドを用いてノイズの影響を調整しつつ、それを隠れ状態に加えます。前述のとおり、この線形射影によってノイズ注入は学習可能となり、学習中にモデルがノイズの効果を適応できるようになります。torch.sigmoid(rnn_out)の項はノイズを0〜1にスケーリングし、隠れ状態を圧倒しないようにします。このアプローチは、制御された確率性を導入することでロバスト性を高め、過学習を防ぐのに寄与すると考えられます。

次に、最終タイムステップの隠れ状態を選択し、全結合層に通して系列ごとに単一の出力を生成します。最終タイムステップの隠れ状態は系列からの情報を要約しており、回帰タスクに適しています。fc層はこの隠れ状態を望まれる出力へマッピングします。

テスト実行

ネットワークを定義した上で、前回の記事でフォワードウォークに成功した6つのパターン（0、1、5、6、7、8）に対してテストを実施します。前回の記前回の記事以前では、強気あるいは弱気の条件にシグナルを組み合わせないまま、より長い入力系列をネットワークに与えて試行していました。

本記事ではそうしたことはしていません。すべてのパターンが明確に「強気チェックのインデックス」と「弱気チェックのインデックス」を持っているためです。これが、前回の記事でフォワードウォーク率がそれ以前の記事より高かった理由のひとつかもしれません。今回のテスト対象はGBP/USDです。訓練はPython上で2023年の4時間足データを使って実行しました。このPython訓練から得られるのは、「ロングに入るかショートに入るか」という判断の指針です。

その後、MetaTrader 5にインポートしたONNXモデルを、ウィザードで組み立てたエキスパートアドバイザー(EA)で利用します。このEAは加重されたロング/ショート条件を用いるため、これらの値も最適化する必要があります。そして、この最適化も2023年のデータで実施しました。

訓練と最適化を終えた後、2023.01.01から2025.01.01までのテスト実行をおこない、6つのパターン/特徴量すべてについて以下の結果が得られました。

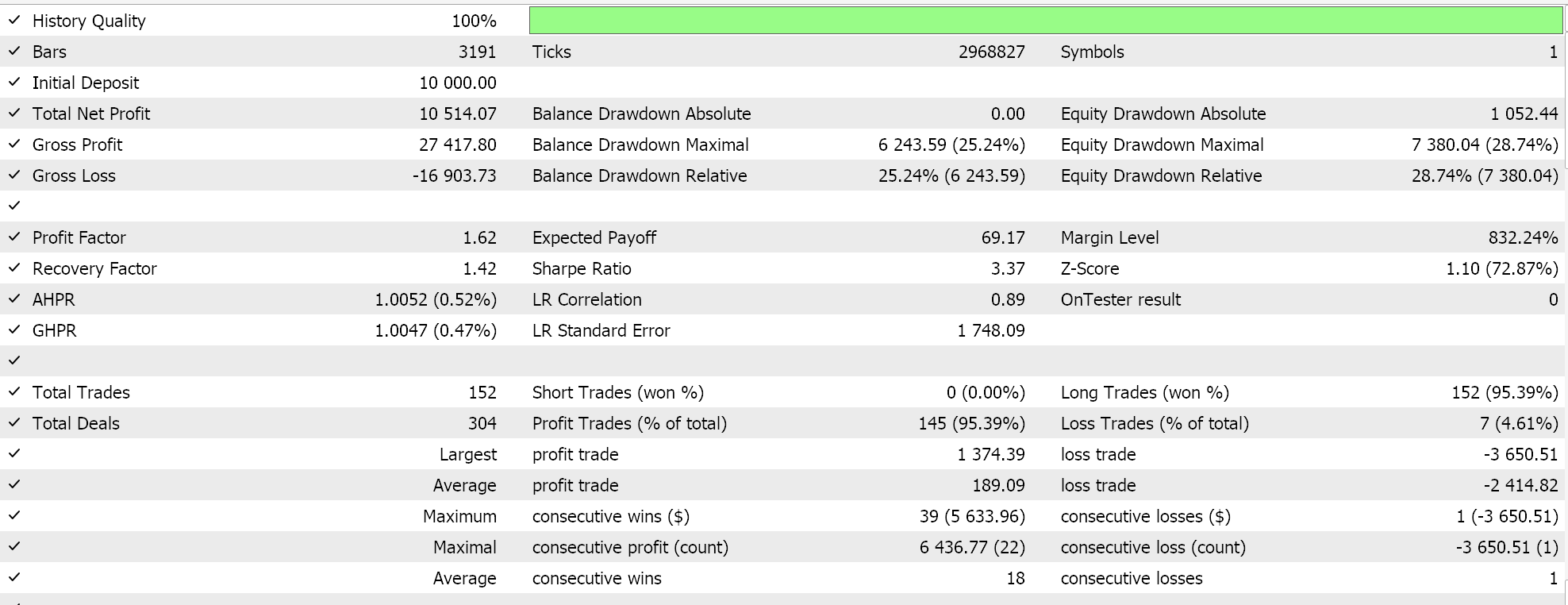
Feature_0のフォワードウォーク（失敗）

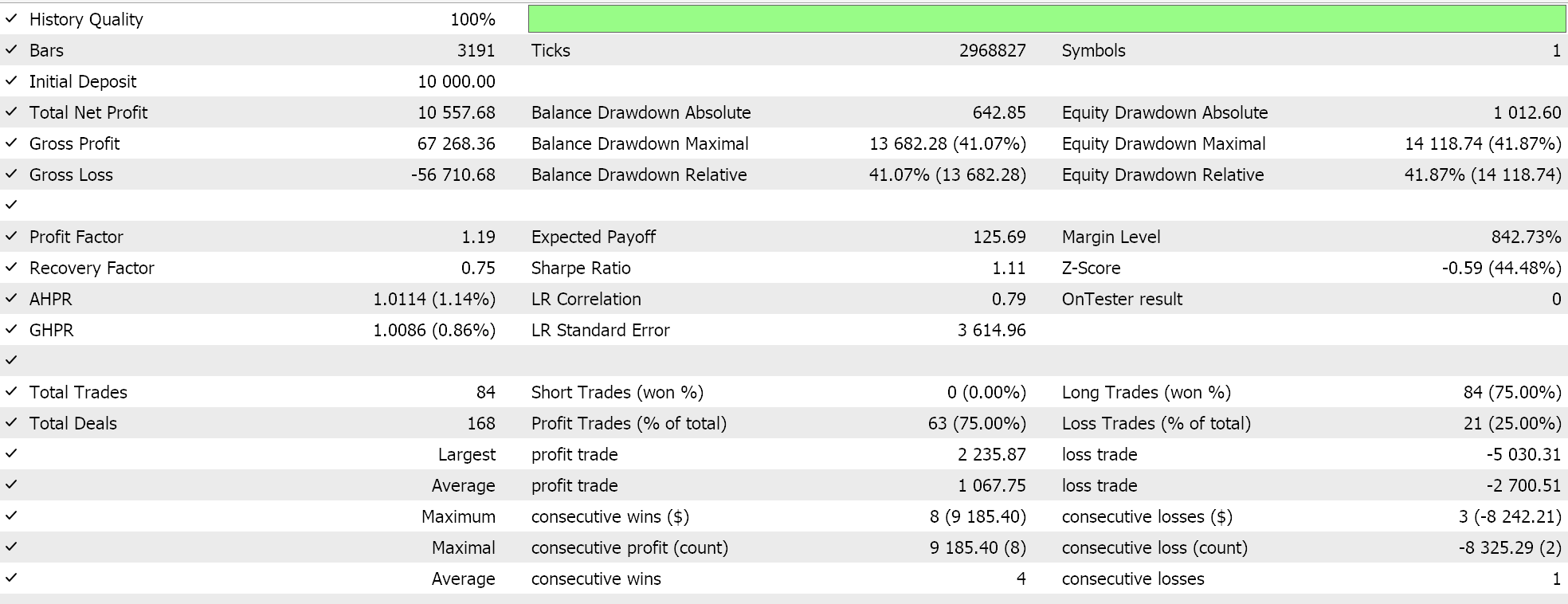
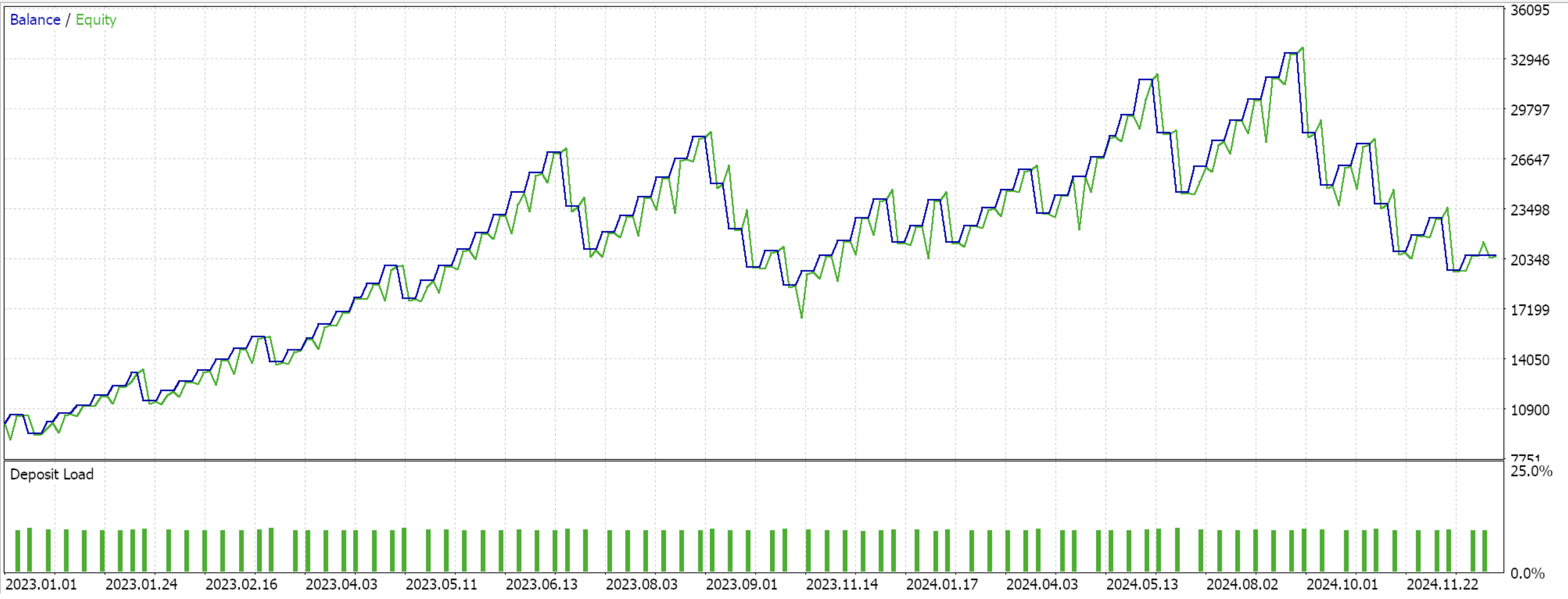
Feature_1のフォワードウォーク（失敗）

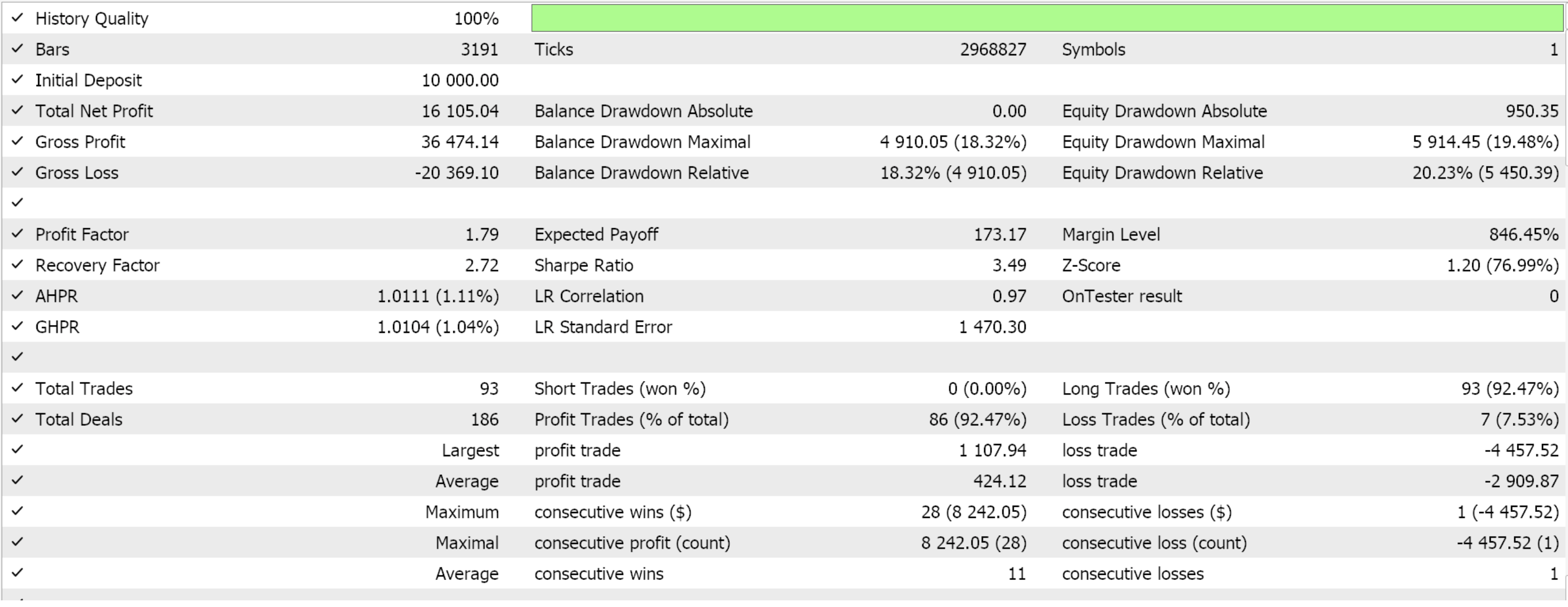
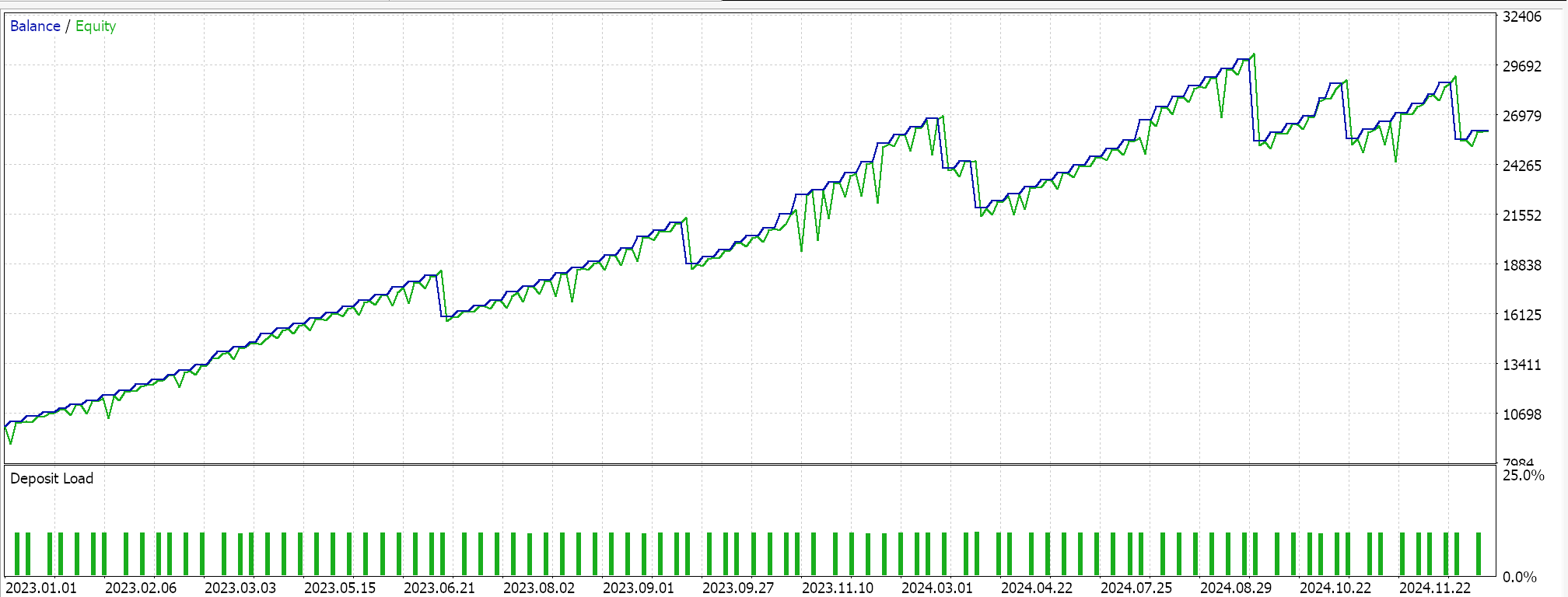
Feature_5のフォワードウォーク（成功）

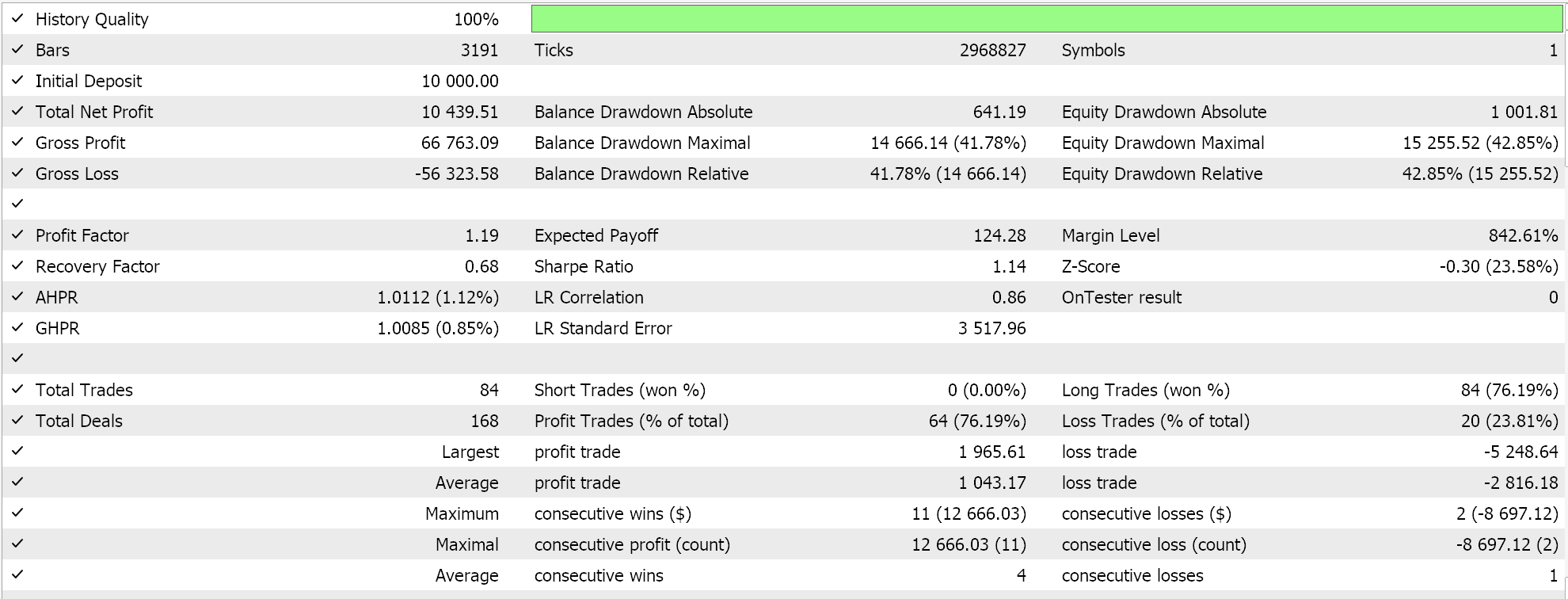
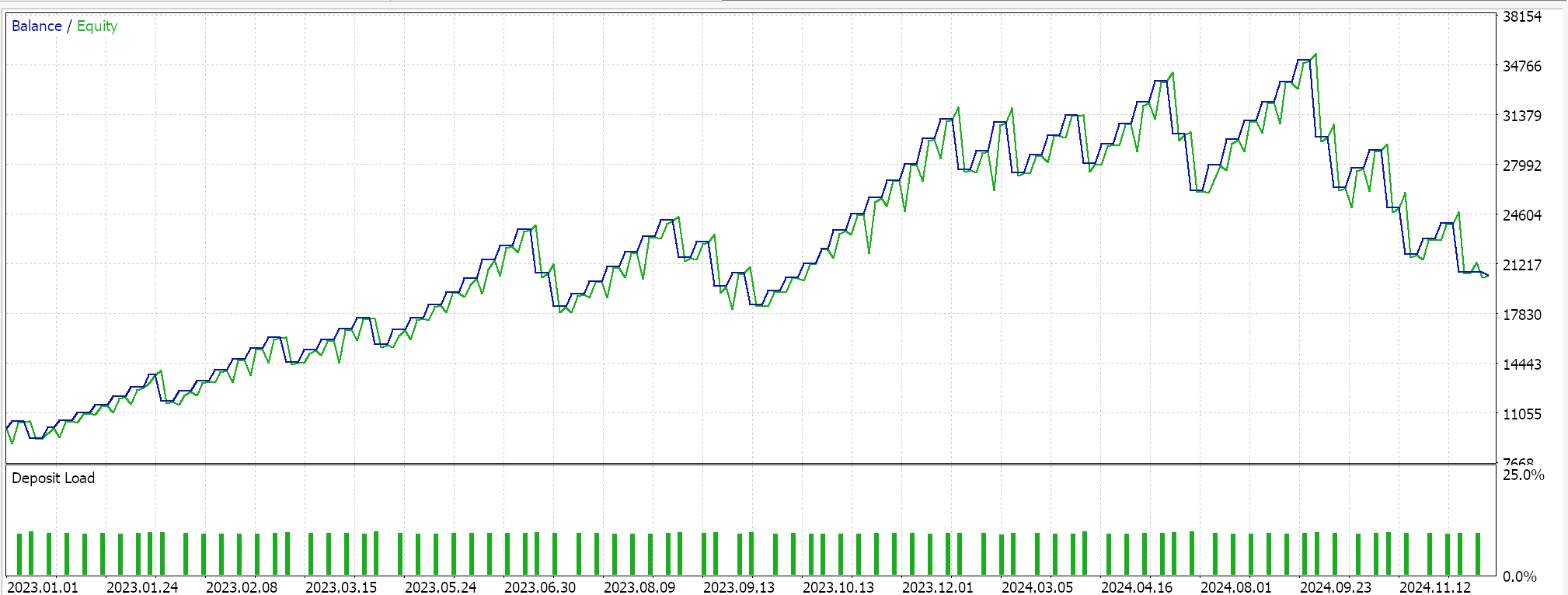
Feature_6のフォワードウォーク（失敗）

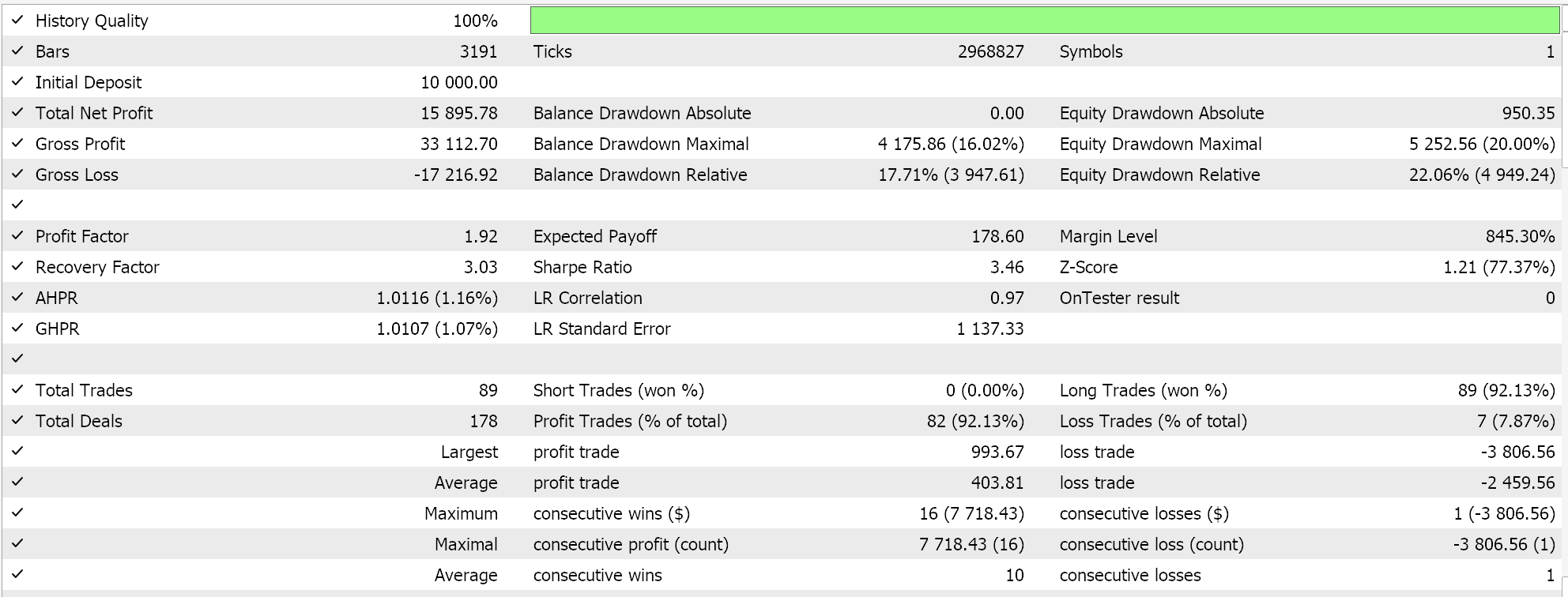
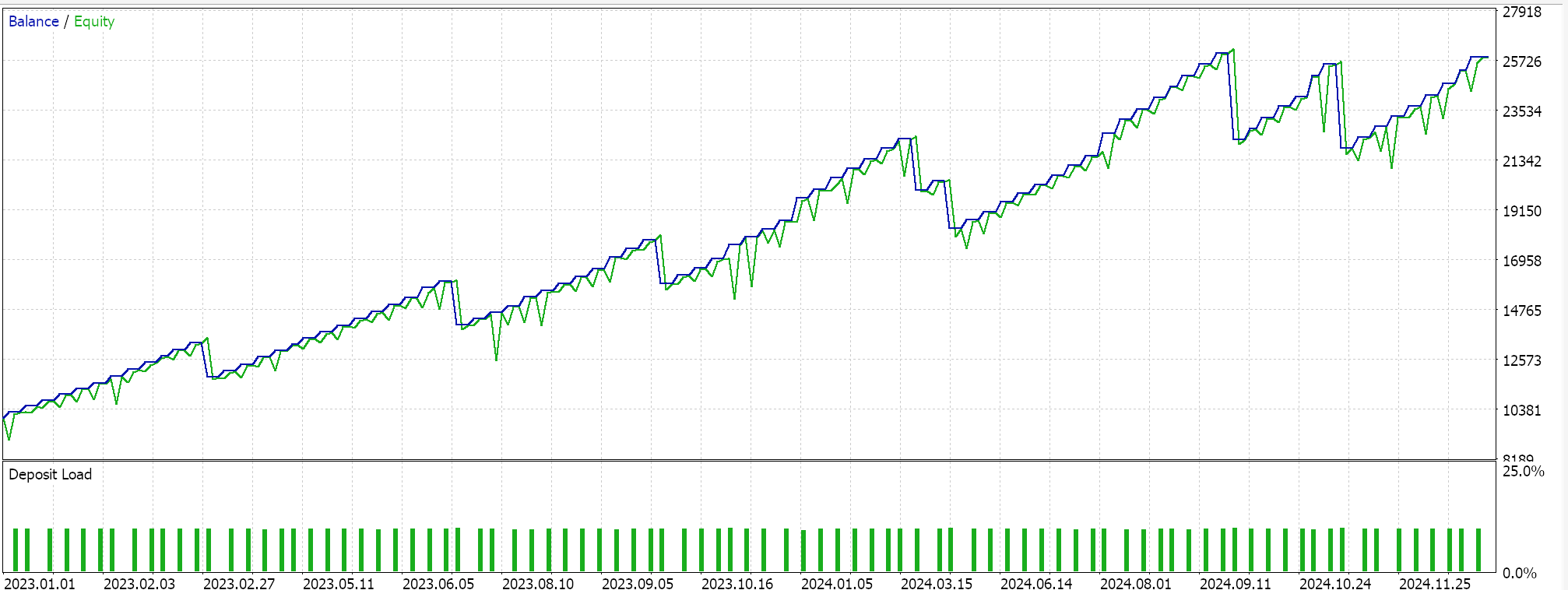
Feature_7のフォワードウォーク（成功）

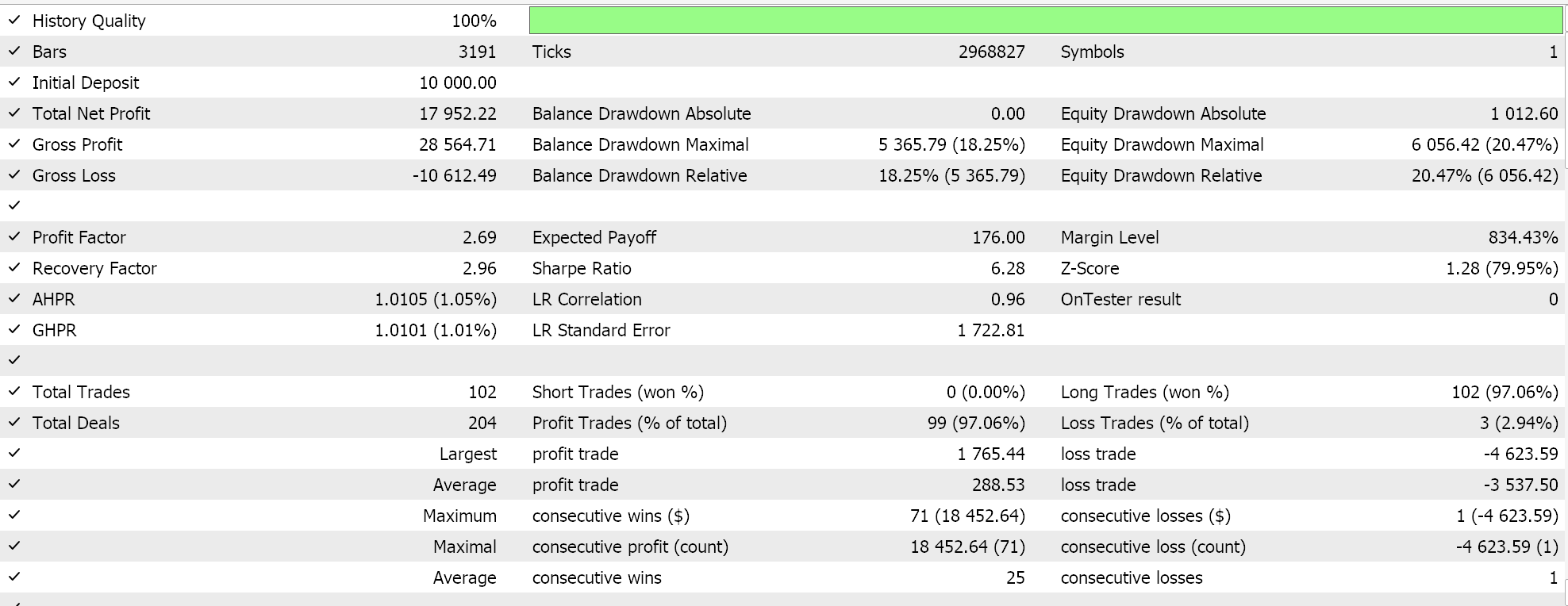
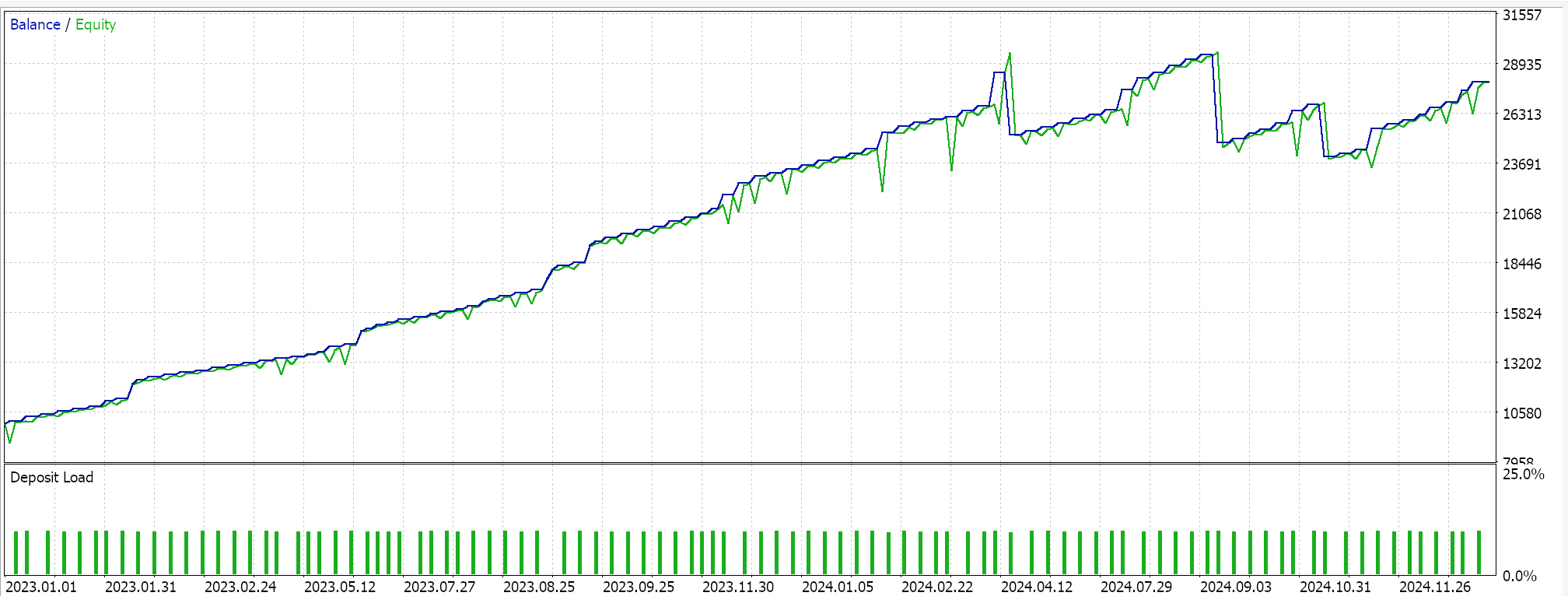
Feature_8のフォワードウォーク（成功）

結論

DeMarkerとEnvelopesのインジケーターを組み合わせて生成されたパターンを検証しました。モメンタムオシレーターとサポート/レジスタンスインジケーターという補完的な組み合わせは、前回の記事で初めてテストされ、その際はパターンそのものに基づいて取引をおこないました。この記事では、同じインジケーターパターンを処理するにあたり、ホワイトノイズカーネルを訓練に用いる回帰型ニューラルネットワークを通してパターンを処理しました。すべてのパターンをまとめて扱うニューラルネットワークについてはまだ検討していません。これは、生のシグナルパターンでは非現実的なことでした。今後の記事でこの点を取り上げることも考えられます。

名前	説明
wz64.mq5	ヘッダにインクルードファイルを示すウィザード組み立てEA
SignalWZ_64.mqh	カスタムシグナルクラスファイル
64_0.onnx	エクスポートされたFeature_0用ONNXモデル
64_1.onnx	エクスポートされたFeature_1用ONNXモデル
64_5.onnx	エクスポートされたFeature_5用ONNXモデル
64_6.onnx	エクスポートされたFeature_6用ONNXモデル
64_7.onnx	エクスポートされたFeature_7用ONNXモデル
64_8.onnx	エクスポートされたFeature_8用ONNXモデル