取引におけるナッシュ均衡ゲーム理論のHMMフィルタリングの応用

はじめに

数学的理論を応用することで、戦略的な優位性を獲得できます。著名な数学者ジョン・フォーブス・ナッシュ・ジュニアによって開発されたナッシュ均衡もその1つです。ゲーム理論への貢献で知られるナッシュの業績は、経済学にとどまらず、さまざまな分野に影響を与えています。この記事では、ナッシュの均衡理論が取引にどのように効果的に適用できるかを探ります。Pythonスクリプトや高度な統計モデルを活用することで、ナッシュのゲーム理論の原理を用いて取引戦略を最適化し、市場においてより情報に基づいた意思決定を行うことを目指します。

ナッシュ

ジョン・フォーブス・ナッシュ・ジュニアについて

ウィキペディアは彼についてこう書いています。

ジョン・フォーブス・ナッシュ・ジュニア（1928年6月13日 - 2015年5月23日）は、ジョン・ナッシュとして知られ、出版されたアメリカの数学者であり、ゲーム理論、実代数幾何学、微分幾何学、偏微分方程式に根本的な貢献をした。ナッシュとゲーム理論家のジョン・ハルサニ、ラインハルト・ゼルテンは1994年のノーベル経済学賞を受賞した。2015年、ナッシュとルイス・ニーレンバーグは偏微分方程式の分野への貢献により アーベル賞を受賞した。

プリンストン大学数学科の大学院生だったナッシュは、現在ではゲーム理論や様々な科学への応用において中心的概念とみなされている多くの概念（ナッシュ均衡やナッシュ交渉解など）を導入した。

彼の人生を題材にした映画『ビューティフルマインド』があります。 私たちは、彼のゲーム理論をMQL5を使った取引に応用するつもりです。

ナッシュのゲーム理論を取引にどう導入するのでしょうか。

ナッシュ均衡理論

ナッシュ均衡とは、ゲーム理論における概念で、各プレーヤーが他のプレーヤーの均衡戦略を知っていると仮定される状況です。このとき、どのプレーヤーも自分の戦略のみを変更しても利益を得ることはできません。

ナッシュ均衡では、各プレーヤーの戦略が、他のすべてのプレーヤーの戦略が与えられたときに最適となります。ゲームには、複数のナッシュ均衡が存在する場合もあれば、まったく存在しない場合もあります。

ナッシュ均衡はゲーム理論の基本的な概念であり、数学者ジョン・ナッシュにちなんで名付けられました。非協力ゲームにおいて、各プレーヤーが戦略を選択し、他のプレーヤーがその戦略を変更しない状態で、どのプレーヤーも一方的に戦略を変更して利益を得ることができない状況を表しています。

以下はその正式な定義です。

(N, S, u)を、以下を持つゲームとします。

• Nプレーヤー：N = {1, 2, ..., n}
• 各プレーヤーの戦略セット：S = (S₁, S₂, ..., Sₙ)
• 各プレーヤーの効用関数： u = (u₁, u₂, ..., uₙ)

戦略プロファイル「s* = (s₁*, s₂*, ..., sₙ*)」がナッシュ均衡であるのは、各プレーヤーiについて、そしてすべての代替戦略sᵢ∈ Sᵢについてです。

uᵢ(s₁*, ..., sᵢ*, ..., sₙ*) ≥ uᵢ(s₁*, ..., sᵢ, ..., sₙ*)

言い換えれば、他のすべてのプレーヤーが均衡戦略を維持している限り、どのプレーヤーiも均衡戦略sᵢ*から他の戦略sᵢに逸脱することによって一方的に効用を向上させることはできません。

二人用のゲームでは、これをもっと簡潔に表現できます。

(s₁*, s₂*)がナッシュ均衡である場合：

1. u₁(s₁*, s₂*) ≥ u₁(s₁, s₂*) for all s₁ ∈ S₁
2. u₂(s₁*, s₂*) ≥ u₂(s₁*, s₂) for all s₂ ∈ S₂

この定式化では、各プレーヤーの戦略が、均衡状態における相手プレーヤーの戦略に対する最善の対応であることが強調されています。

以下の点が重要です。

1. すべてのゲームが純粋戦略においてナッシュ均衡を持つわけではありません。
2. ゲームによっては、複数のナッシュ均衡が存在する場合があります。
3. ナッシュ均衡は、必ずしもパレート最適であるとは限らず、全プレーヤーにとって最も望ましい結果であるとも限りません。

ナッシュ均衡の概念は、経済学や政治学など、合理的な主体間の戦略的相互作用が研究される分野で幅広く応用されています。

ナッシュ均衡においては、他のプレーヤーが戦略を変えない限り、いずれのプレーヤーも一方的に利益を増やすことはできません。しかし、金融市場は動的であり、完全な均衡が成立することはまれです。一時的な非効率性、情報の優位性、優れたリスク管理、他のプレーヤーよりも速やかな反応力などにより、利益を得るチャンスが生まれます。また、外的要因や予測不可能な事象がバランスを崩し、準備が整っている者に新たな機会をもたらすこともあります。

まず最初に、取引する通貨ペアを選択する必要があります（ナッシュ均衡を適用するため、2つの銘柄を選び、できれば負の相関を持つものを選びます）。以下が使用したスクリプトです。

import MetaTrader5 as mt5
import pandas as pd
from scipy.stats import pearsonr
from statsmodels.tsa.stattools import coint
import numpy as np
import datetime

# Connect with MetaTrader 5
if not mt5.initialize():
    print("Failed to initialize MT5")
    mt5.shutdown()

# Get the list of symbols
symbols = mt5.symbols_get()
symbols = [s.name for s in symbols if s.name.startswith('EUR') or s.name.startswith('USD') or s.name.endswith('USD')]  # Filter symbols by example

# Download historical data and save in dictionary
data = {}
for symbol in symbols:
    start_date = "2020-01-01"
    end_date = "2023-12-31"
    timeframe = mt5.TIMEFRAME_H4
    start_date = datetime.datetime.strptime(start_date, "%Y-%m-%d")
    end_date = datetime.datetime.strptime(end_date, "%Y-%m-%d")
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    
    if rates is not None:
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        data[symbol] = df.set_index('time')['close']

# Close connection with MT5
mt5.shutdown()

# Calculate the Pearson coefficient and test for cointegration for each pair of symbols
cointegrated_pairs = []
for i in range(len(symbols)):
    for j in range(i + 1, len(symbols)):
        if symbols[i] in data and symbols[j] in data:
            common_index = data[symbols[i]].index.intersection(data[symbols[j]].index)
            if len(common_index) > 30:  # Ensure there are enough data points
                corr, _ = pearsonr(data[symbols[i]][common_index], data[symbols[j]][common_index])
                if abs(corr) > 0.8:  # Strong correlation
                    score, p_value, _ = coint(data[symbols[i]][common_index], data[symbols[j]][common_index])
                    if p_value < 0.05:  # P-value less than 0.05
                        cointegrated_pairs.append((symbols[i], symbols[j], corr, p_value))

# Filter and show only cointegrated pairs with p-value less than 0.05
print(f'Total pairs with strong correlation and cointegration: {len(cointegrated_pairs)}')
for sym1, sym2, corr, p_val in cointegrated_pairs:
    print(f'{sym1} - {sym2}: Correlation={corr:.4f}, P-Cointegration value={p_val:.4f}')

このスクリプトは、まずMetaTrader 5を初期化し、EURまたはUSDで始まる、あるいはUSDで終わるすべての銘柄を取得します。その後、これらの銘柄のデータをダウンロードし、MetaTrader 5をシャットダウンします。次に、すべての銘柄を比較し、相関の強いものだけを抽出します。その後、強い共積分関係があるペアに対して別のフィルタを適用します。最後に、フィルタを通過した銘柄リストを端末に表示して終了します。

相関とは、2つの要素がどのように関連しているかを測る指標です。あなたと親友が土曜日にいつも一緒に映画を観に行くとします。これは相関関係の例です。あなたが映画館に行くと、あなたの友人もそこにいます。正の相関関係は、一方が上昇すれば他方も上昇することを意味します。負の場合は、一方が増加すると他方が減少します。相関がゼロであれば、両者の間には何の関係もありません。

共和分とは、2つ以上の変数が、短期的には独立して変動していても長期的には何らかの関係を持っているという状況を説明するために使用される統計的概念です。ロープで結ばれた2人のスイマーを想像してください。2人はプールで自由に泳ぐことができますが、互いに遠くへ移動することはできません。共和分は、一時的な差異にもかかわらず、これらの変数が常に共通の長期的均衡またはトレンドに戻ることを示します。

ピアソン係数は、2つの変数がどの程度線形に関連しているかを測定します。係数が+1に近い場合は、一方の変数が増加すると他方の変数も増加するという直接的な依存関係を示しています。係数が-1に近いということは、一方が増加すると他方が減少することを意味し、逆の関係を示しています。0は線形のつながりがないことを意味します。例えば、気温と冷たい飲み物の販売数を測定することで、ピアソン係数を用いてこれらの要因がどのように関連しているかを理解することができます。

このスクリプトの結果は以下のようになるはずです（以下はスクリプトの初期条件から得られたサンプル結果です）。

    start_date = "2020-01-01"
    end_date = "2023-12-31"
    timeframe = mt5.TIMEFRAME_H4

Total pairs with strong correlation and cointegration: 40
USDJPY - EURCHF: Correlation=-0.9416, P-Cointegration value=0.0165
USDJPY - EURN.NASDAQ: Correlation=0.9153, P-Cointegration value=0.0008
USDCNH - USDZAR: Correlation=0.8474, P-Cointegration value=0.0193
USDRUB - USDRUR: Correlation=0.9993, P-Cointegration value=0.0000
AUDUSD - USDCLP: Correlation=-0.9012, P-Cointegration value=0.0280
AUDUSD - USDILS: Correlation=-0.8686, P-Cointegration value=0.0026
NZDUSD - USDNOK: Correlation=-0.9353, P-Cointegration value=0.0469
NZDUSD - USDILS: Correlation=-0.8514, P-Cointegration value=0.0110
...
EURSEK - XPDUSD: Correlation=-0.8200, P-Cointegration value=0.0269
EURZAR - USDP.NASDAQ: Correlation=-0.8678, P-Cointegration value=0.0154
USDMXN - EURCNH: Correlation=-0.8490, P-Cointegration value=0.0389
EURL.NASDAQ - EURSGD: Correlation=0.9157, P-Cointegration value=0.0000
EURN.NASDAQ - EURSGD: Correlation=-0.8301, P-Cointegration value=0.0358

すべての結果から、次の2つの銘柄を選択します。負の相関は、一方が上昇するともう一方が下落し、逆も同様に動く関係を示します。一方で、正の相関は、2つの銘柄が連動して同じ方向に動くことを意味します。ここでは、USDJPY銘柄を選択します。これは、ナッシュ均衡に基づき、USDが外国為替市場の主要な原動力であるためです。このため、USDに強く相関する他の通貨がその動向に追随する可能性があると考えられます。

USDJPY - EURCHF: Correlation=-0.9416, P-Cointegration value=0.0165

デモ口座でMetaTrader 5を使用して、すべてのデータを取得し、EAをバックテストしました。

HMM（隠れマルコフモデル）

隠れマルコフモデル（HMM）は、部分的にランダムであり、部分的に隠れた状態に依存して時間と共に変化するシステムを記述するために使用される統計モデルです。想像してみてください。観察可能な特定の結果のみが見えるものの、その結果は直接観察できない根本的な要因（または状態）に影響されています。

HMMは、過去のデータを利用して市場のパターンを予測するモデルを作成するために、取引で活用されています。

HMMモデルを取得するためにはPythonスクリプトを使用します。スクリプトの使用には、時間枠（EAと同じ時間枠を推奨）、隠れた状態の数、予測するデータ量（多い方が望ましい）を考慮する必要があります。

このPythonスクリプトの実行結果として、EAで使用するための3つの行列（.txt形式）と3つのグラフが出力されます。

以下が.pyスクリプトです。

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
from hmmlearn import hmm
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import datetime
import os
import sys

# Number of models to train
n_models = 10

# Redirect stdout to a file
def redirect_output(symbol):
    output_file = f"{symbol}_output.txt"
    sys.stdout = open(output_file, 'w')

# Connect to MetaTrader 5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# Get and process data
def get_mt5_data(symbol, timeframe, start_date, end_date):
    """Get historical data from MetaTrader 5."""
    start_date = datetime.datetime.strptime(start_date, "%Y-%m-%d")
    end_date = datetime.datetime.strptime(end_date, "%Y-%m-%d")
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    return df

def calculate_features(df):
    """Calculate important features like returns, volatility, and trend."""
    df['returns'] = df['close'].pct_change()
    df['volatility'] = df['returns'].rolling(window=50).std()
    df['trend'] = df['close'].pct_change(periods=50)
    return df.dropna()

# Main script
symbol = "USDJPY"
timeframe = mt5.TIMEFRAME_H4
start_date = "2020-01-01"
end_date = "2023-12-31"
current_date = datetime.datetime.now().strftime("%Y-%m-%d")

# Redirect output to file
redirect_output(symbol)

# Get historical data for training
df = get_mt5_data(symbol, timeframe, start_date, end_date)
df = calculate_features(df)

features = df[['returns', 'volatility', 'trend']].values
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# Lists to store the results of each model
state_predictions = np.zeros((scaled_features.shape[0], n_models))
strategy_returns = np.zeros((scaled_features.shape[0], n_models))
transition_matrices = np.zeros((10, 10, n_models))
means_matrices = np.zeros((n_models, 10, 3))
covariance_matrices = np.zeros((n_models, 10, 3, 3))

# Train multiple models and store the results
for i in range(n_models):
    model = hmm.GaussianHMM(n_components=10, covariance_type="full", n_iter=10000, tol=1e-6, min_covar=1e-3)
    X_train, X_test = train_test_split(scaled_features, test_size=0.2, random_state=i)
    model.fit(X_train)

    # Save the transition matrix, emission means, and covariances
    transition_matrices[:, :, i] = model.transmat_
    means_matrices[i, :, :] = model.means_
    covariance_matrices[i, :, :, :] = model.covars_

    # State prediction
    states = model.predict(scaled_features)
    state_predictions[:, i] = states

    # Generate signals and calculate strategy returns for this model
    df['state'] = states
    df['signal'] = 0
    for j in range(10):
        df.loc[df['state'] == j, 'signal'] = 1 if j % 2 == 0 else -1
    df['strategy_returns'] = df['returns'] * df['signal'].shift(1)
    strategy_returns[:, i] = df['strategy_returns'].values

# Average of matrices
average_transition_matrix = transition_matrices.mean(axis=2)
average_means_matrix = means_matrices.mean(axis=0)
average_covariance_matrix = covariance_matrices.mean(axis=0)

# Save the average matrices in the output file in appropriate format
print("Average Transition Matrix:")
for i, row in enumerate(average_transition_matrix):
    for j, val in enumerate(row):
        print(f"average_transition_matrix[{i}][{j}] = {val:.8f};")

print("\nAverage Means Matrix:")
for i, row in enumerate(average_means_matrix):
    for j, val in enumerate(row):
        print(f"average_means_matrix[{i}][{j}] = {val:.8f};")

print("\nAverage Covariance Matrix:")
for i in range(10):  # For each state
    for j in range(3):  # For each row of the covariance matrix
        for k in range(3):  # For each column of the covariance matrix
            print(f"average_covariance_matrix[{i}][{j}][{k}] = {average_covariance_matrix[i, j, k]:.8e};")

# Average of state predictions and strategy returns
average_states = np.round(state_predictions.mean(axis=1)).astype(int)
average_strategy_returns = strategy_returns.mean(axis=1)

# Store the average results in the original dataframe
df['average_state'] = average_states
df['average_strategy_returns'] = average_strategy_returns

# Calculate cumulative returns using the average strategy
df['cumulative_market_returns'] = (1 + df['returns']).cumprod()
df['cumulative_strategy_returns'] = (1 + df['average_strategy_returns']).cumprod()

# Plot cumulative returns (training)
plt.figure(figsize=(7, 6))
plt.plot(df.index, df['cumulative_market_returns'], label='Market Returns')
plt.plot(df.index, df['cumulative_strategy_returns'], label='Strategy Returns (Average)')
plt.title('Cumulative Returns with Average Strategy')
plt.xlabel('Date')
plt.ylabel('Cumulative Returns')
plt.legend()
plt.grid(True)
plt.savefig(f'average_strategy_returns_{symbol}.png')
plt.close()

# Additional plots for averages
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(12, 15), sharex=True)

# Plot closing price and average HMM states
ax1.plot(df.index, df['close'], label='Closing Price')
scatter = ax1.scatter(df.index, df['close'], c=df['average_state'], cmap='viridis', s=30, label='Average HMM States')
ax1.set_ylabel('Price')
ax1.set_title('Closing Price and Average HMM States')
ax1.legend(loc='upper left')

# Add color bar for states
cbar = plt.colorbar(scatter, ax=ax1)
cbar.set_label('Average HMM State')

# Plot returns
ax2.bar(df.index, df['returns'], label='Market Returns', alpha=0.5, color='blue')
ax2.bar(df.index, df['average_strategy_returns'], label='Average Strategy Returns', alpha=0.5, color='red')
ax2.set_ylabel('Return')
ax2.set_title('Daily Returns')
ax2.legend(loc='upper left')

# Plot cumulative returns
ax3.plot(df.index, df['cumulative_market_returns'], label='Cumulative Market Returns')
ax3.plot(df.index, df['cumulative_strategy_returns'], label='Cumulative Average Strategy Returns')
ax3.set_ylabel('Cumulative Return')
ax3.set_title('Cumulative Returns')
ax3.legend(loc='upper left')

# Adjust layout
plt.tight_layout()
plt.xlabel('Date')

# Save figure
plt.savefig(f'average_returns_{symbol}.png')
plt.close()

# Calculate cumulative returns for each average state
state_returns = {}
for state in range(10):  # Assuming 10 states
    state_returns[state] = df[df['average_state'] == state]['returns'].sum()

# Create lists for states and their cumulative returns
states = list(state_returns.keys())
returns = list(state_returns.values())

# Create bar chart
plt.figure(figsize=(7, 6))
bars = plt.bar(states, returns)

# Customize chart
plt.title('Cumulative Returns by Average HMM State', fontsize=7)
plt.xlabel('State', fontsize=7)
plt.ylabel('Cumulative Return', fontsize=7)
plt.xticks(states)

# Add value labels above each bar
for bar in bars:
    height = bar.get_height()
    plt.text(bar.get_x() + bar.get_width()/2., height,
             f'{height:.4f}',
             ha='center', va='bottom')

# Add horizontal line at y=0 for reference
plt.axhline(y=0, color='r', linestyle='-', linewidth=0.5)

# Adjust layout and save chart
plt.tight_layout()
plt.savefig(f'average_bars_{symbol}.png')
plt.close()

# Get recent data to test the model
df_recent = get_mt5_data(symbol, timeframe, end_date, current_date)
df_recent = calculate_features(df_recent)

# Apply the same scaler to recent data
scaled_recent_features = scaler.transform(df_recent[['returns', 'volatility', 'trend']].values)

# Lists to store the results of each model for recent data
recent_state_predictions = np.zeros((scaled_recent_features.shape[0], n_models))
recent_strategy_returns = np.zeros((scaled_recent_features.shape[0], n_models))

# Apply the trained model to recent data
for i in range(n_models):
    model = hmm.GaussianHMM(n_components=10, covariance_type="full", n_iter=10000, tol=1e-4, min_covar=1e-3)
    X_train, X_test = train_test_split(scaled_features, test_size=0.2, random_state=i)
    model.fit(X_train)
    
    recent_states = model.predict(scaled_recent_features)
    recent_state_predictions[:, i] = recent_states

    df_recent['state'] = recent_states
    df_recent['signal'] = 0
    for j in range(10):
        df_recent.loc[df_recent['state'] == j, 'signal'] = 1 if j % 2 == 0 else -1
    df_recent['strategy_returns'] = df_recent['returns'] * df_recent['signal'].shift(1)
    recent_strategy_returns[:, i] = df_recent['strategy_returns'].values

# Average of state predictions and strategy returns for recent data
average_recent_states = np.round(recent_state_predictions.mean(axis=1)).astype(int)
average_recent_strategy_returns = recent_strategy_returns.mean(axis=1)

# Store the average results in the recent dataframe
df_recent['average_state'] = average_recent_states
df_recent['average_strategy_returns'] = average_recent_strategy_returns

# Calculate cumulative returns using the average strategy on recent data
df_recent['cumulative_market_returns'] = (1 + df_recent['returns']).cumprod()
df_recent['cumulative_strategy_returns'] = (1 + df_recent['average_strategy_returns']).cumprod()

# Plot cumulative returns (recent test)
plt.figure(figsize=(7, 6))
plt.plot(df_recent.index, df_recent['cumulative_market_returns'], label='Market Returns')
plt.plot(df_recent.index, df_recent['cumulative_strategy_returns'], label='Strategy Returns (Average)')
plt.title('Cumulative Returns with Average Strategy (Recent Data)')
plt.xlabel('Date')
plt.ylabel('Cumulative Returns')
plt.legend()
plt.grid(True)
plt.savefig(f'average_recent_strategy_returns_{symbol}.png')
plt.close()

# Close MetaTrader 5
mt5.shutdown()


# Assign descriptive names to the hidden states
state_labels = {}
for state in range(10):  # Assuming 10 states
    if state in df['average_state'].unique():
        label = f"State {state}: "  # You can customize this description based on your observations
        if state_returns[state] > 0:
            label += "Uptrend"
        else:
            label += "Downtrend"
        state_labels[state] = label
    else:
        state_labels[state] = f"State {state}: Not present"

# Print the states and their descriptive labels
print("\nDescription of Hidden States:")
for state, label in state_labels.items():
    print(f"{label} (State ID: {state})")

# Close MetaTrader 5 connection
mt5.shutdown()

# Finally, close the output file
sys.stdout.close()
sys.stdout = sys.__stdout__

このスクリプトをこの初期条件で実行したところ、このような結果が得られました。

timeframe = mt5.TIMEFRAME_H4
start_date = "2020-01-01"
end_date = "2023-12-31"

Average Transition Matrix:
average_transition_matrix[0][0] = 0.15741321;
average_transition_matrix[0][1] = 0.07086962;
average_transition_matrix[0][2] = 0.16785905;
average_transition_matrix[0][3] = 0.08792403;
average_transition_matrix[0][4] = 0.11101073;
average_transition_matrix[0][5] = 0.05415263;
average_transition_matrix[0][6] = 0.08019415;
.....
average_transition_matrix[9][3] = 0.13599698;
average_transition_matrix[9][4] = 0.12947508;
average_transition_matrix[9][5] = 0.06385211;
average_transition_matrix[9][6] = 0.09042617;
average_transition_matrix[9][7] = 0.16088280;
average_transition_matrix[9][8] = 0.06588065;
average_transition_matrix[9][9] = 0.04559230;

Average Means Matrix:
average_means_matrix[0][0] = 0.06871601;
average_means_matrix[0][1] = 0.14572210;
average_means_matrix[0][2] = 0.05961646;
average_means_matrix[1][0] = 0.06903949;
average_means_matrix[1][1] = 1.05226034;
.....
average_means_matrix[7][2] = 0.00453701;
average_means_matrix[8][0] = -0.38270747;
average_means_matrix[8][1] = 0.86916742;
average_means_matrix[8][2] = -0.58792329;
average_means_matrix[9][0] = -0.16057267;
average_means_matrix[9][1] = 1.17106076;
average_means_matrix[9][2] = 0.18531821;

Average Covariance Matrix:
average_covariance_matrix[0][0][0] = 1.25299224e+00;
average_covariance_matrix[0][0][1] = -4.05453267e-02;
average_covariance_matrix[0][0][2] = 7.95036804e-02;
average_covariance_matrix[0][1][0] = -4.05453267e-02;
average_covariance_matrix[0][1][1] = 1.63177290e-01;
average_covariance_matrix[0][1][2] = 1.58609858e-01;
average_covariance_matrix[0][2][0] = 7.95036804e-02;
average_covariance_matrix[0][2][1] = 1.58609858e-01;
average_covariance_matrix[0][2][2] = 8.09678270e-01;
average_covariance_matrix[1][0][0] = 1.23040552e+00;
average_covariance_matrix[1][0][1] = 2.52108300e-02;
....
average_covariance_matrix[9][0][0] = 5.47457383e+00;
average_covariance_matrix[9][0][1] = -1.22088743e-02;
average_covariance_matrix[9][0][2] = 2.56784647e-01;
average_covariance_matrix[9][1][0] = -1.22088743e-02;
average_covariance_matrix[9][1][1] = 4.65227101e-01;
average_covariance_matrix[9][1][2] = -2.88257686e-01;
average_covariance_matrix[9][2][0] = 2.56784647e-01;
average_covariance_matrix[9][2][1] = -2.88257686e-01;
average_covariance_matrix[9][2][2] = 1.44717234e+00;

Description of Hidden States:
State 0: Not present (State ID: 0)
State 1: Downtrend (State ID: 1)
State 2: Uptrend (State ID: 2)
State 3: Downtrend (State ID: 3)
State 4: Uptrend (State ID: 4)
State 5: Uptrend (State ID: 5)
State 6: Uptrend (State ID: 6)
State 7: Downtrend (State ID: 7)
State 8: Uptrend (State ID: 8)
State 9: Not present (State ID: 9)

このスクリプトを使用するには、まずデータの取得先、状態の数、日付を調整する必要があります。また、EAの設定を調整し、PythonスクリプトとEAで共通の期間（時間枠）を設定する必要があります（すべてのスクリプトとEAで統一することが推奨されます）。

このスクリプトでは、10個のモデルを作成し、それらの平均を取り入れることでロバストなモデルを構築します（もしモデルが2つしかなければ、行列の両グループが異なるものとなり、一貫性が得られない可能性があります）。行列の作成には時間がかかりますが、最終的に行列データ、3つのグラフ（重要性については後述）、隠れ状態の説明、および行列を含む.txtファイルが出力されます。

結果

最初の画像には、平均化したHMMモデルを用いたバックテストの結果が示されています。このバックテスト期間の価格動向とHMMを用いた戦略の結果が確認できます。

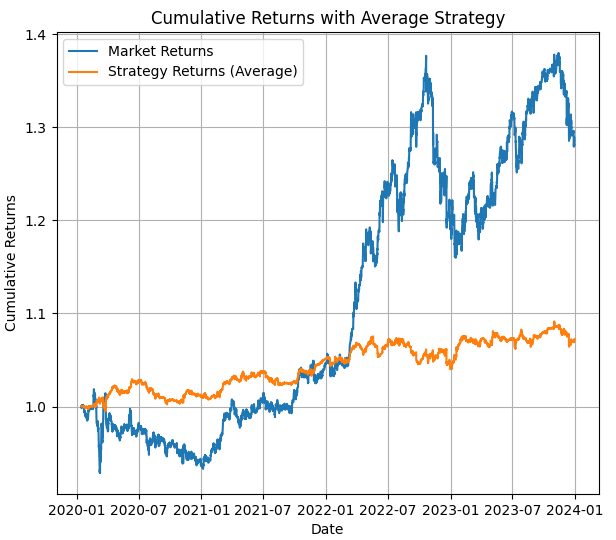
2つ目の画像には、テスト期間中におけるバックテストの結果が示されています。また、隠れ状態がどこで使用されているかを示す重要な視覚情報も確認できます。この画像から、上昇トレンド、下降トレンド、レンジ相場、または中立状態が取得された箇所が分かります。

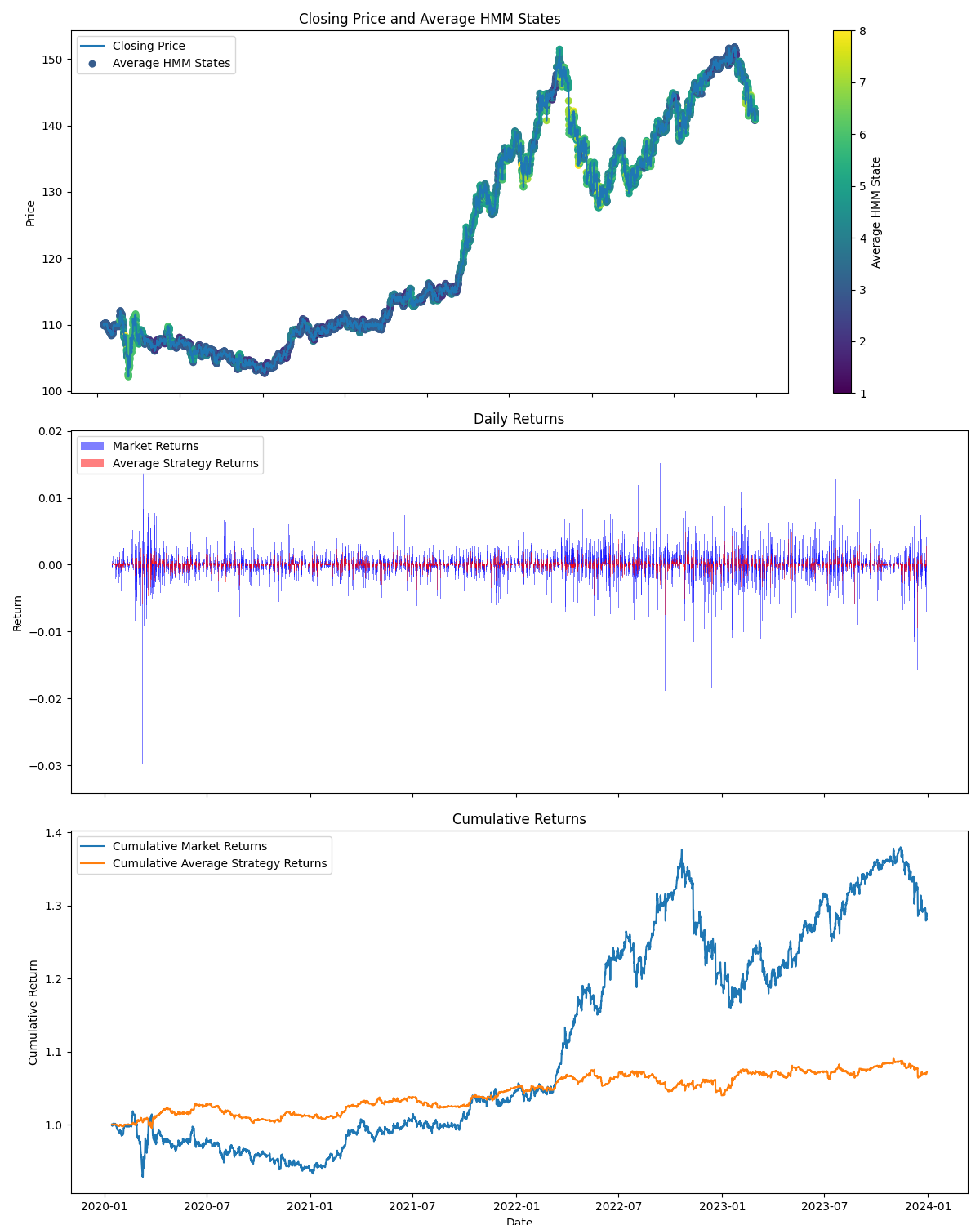
3つ目の画像では、各隠れ状態の利益を棒グラフで見ることができます。

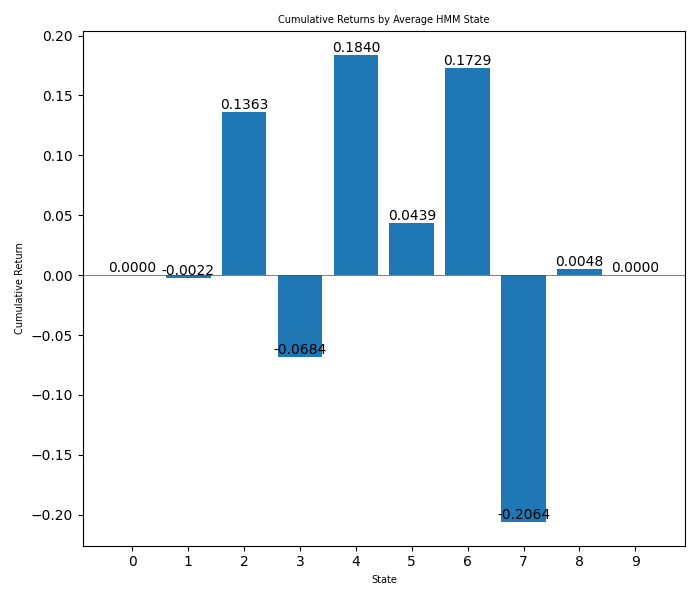
4番目の画像では、最終日付から現在までの期間における戦略の平均リターンが示されています。これは、MetaTrader 5のバックテストにおいて、隠れ状態の調整をおこなわない場合に期待される戦略リターンを可視化したものです。

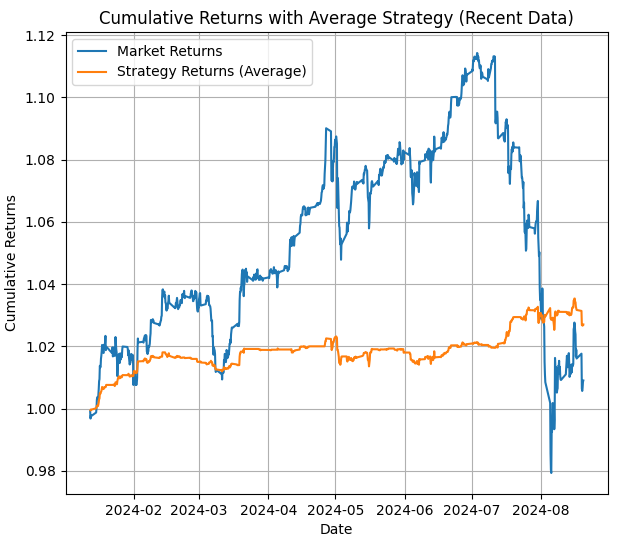
得られたすべての情報をもとに、適切な隠れ状態を選択して、（2つ目の画像から）トレンドや（棒グラフから）勝利をもたらす隠れ状態を特定できます。この情報を使用して、EAの状態を切り替えることが可能です。

棒グラフから、使用すべき隠れ状態が「2（保合）」「3（上昇トレンド）」「7（下降トレンド）」であることがわかります。これにより、EAに最適な戦略を設定でき、利益を生まない他の隠れ状態を除外する判断がしやすくなります。どれが最適かを確認するため、複数回のバックテストも有効です。

なお、PythonスクリプトはすべてPython 3.10で実行しています。

行列をEAに追加することも可能ですが、Pythonでは行列の表示が異なるため、コンポーネントごとに表示させる手間があります。そのため、行列をEAで使用するためのMQl5形式に変換する次のスクリプトを利用します。これは行列の書式設定を簡便におこなうためのEAです。

import re
import os

def read_file(filename):
    if not os.path.exists(filename):
        print(f"Error: The file {filename} does not exist.")
        return None
    try:
        with open(filename, "r") as file:
            return file.read()
    except Exception as e:
        print(f"Error reading the file: {str(e)}")
        return None

def parse_matrix(file_content, matrix_name):
    pattern = rf"{matrix_name}\[(\d+)\]\[(\d+)\]\s*=\s*([-+]?(?:\d*\.\d+|\d+)(?:e[-+]?\d+)?)"
    matches = re.findall(pattern, file_content)
    matrix = {}
    for match in matches:
        i, j, value = int(match[0]), int(match[1]), float(match[2])
        if i not in matrix:
            matrix[i] = {}
        matrix[i][j] = value
    return matrix

def parse_covariance_matrix(file_content):
    pattern = r"average_covariance_matrix\[(\d+)\]\[(\d+)\]\[(\d+)\]\s*=\s*([-+]?(?:\d*\.\d+|\d+)(?:e[-+]?\d+)?)"
    matches = re.findall(pattern, file_content)
    matrix = {}
    for match in matches:
        i, j, k, value = int(match[0]), int(match[1]), int(match[2]), float(match[3])
        if i not in matrix:
            matrix[i] = {}
        if j not in matrix[i]:
            matrix[i][j] = {}
        matrix[i][j][k] = value
    return matrix

def format_matrix(matrix, is_3d=False):
    if not matrix:
        return "{     };"
    
    formatted = "{\n"
    for i in sorted(matrix.keys()):
        if is_3d:
            formatted += "        {  "
            for j in sorted(matrix[i].keys()):
                formatted += "{" + ", ".join(f"{matrix[i][j][k]:.8e}" for k in sorted(matrix[i][j].keys())) + "}"
                if j < max(matrix[i].keys()):
                    formatted += ",\n           "
            formatted += "}"
        else:
            formatted += "        {" + ", ".join(f"{matrix[i][j]:.8f}" for j in sorted(matrix[i].keys())) + "}"
        if i < max(matrix.keys()):
            formatted += ","
        formatted += "\n"
    formatted += "     };"
    return formatted

def main():
    input_filename = "USDJPY_output.txt"
    output_filename = "formatted_matrices.txt"
    content = read_file(input_filename)
    
    if content is None:
        return

    print(f"Input file size: {len(content)} bytes")
    print("First 200 characters of the file:")
    print(content[:200])

    transition_matrix = parse_matrix(content, "average_transition_matrix")
    means_matrix = parse_matrix(content, "average_means_matrix")
    covariance_matrix = parse_covariance_matrix(content)

    print(f"\nElements found in the transition matrix: {len(transition_matrix)}")
    print(f"Elements found in the means matrix: {len(means_matrix)}")
    print(f"Elements found in the covariance matrix: {len(covariance_matrix)}")

    output = "Transition Matrix:\n"
    output += format_matrix(transition_matrix)
    output += "\n\nMeans Matrix:\n"
    output += format_matrix(means_matrix)
    output += "\n\nCovariance Matrix:\n"
    output += format_matrix(covariance_matrix, is_3d=True)

    try:
        with open(output_filename, "w") as outfile:
            outfile.write(output)
        print(f"\nFormatted matrices saved in '{output_filename}'")
    except Exception as e:
        print(f"Error writing the output file: {str(e)}")

    print(f"\nFirst lines of the output file '{output_filename}':")
    output_content = read_file(output_filename)
    if output_content:
        print("\n".join(output_content.split("\n")[:20]))  # Display the first 20 lines

if __name__ == "__main__":
    main()

また、ソケットを使用して（ソケットは外部データを使用してmt5と対話する良い方法です）行列をインポートすることもできます。「  ソケットを使ったツイッターのセンチメント分析」稿で説明されている通りにすれば大丈夫です。さらに（記事で説明されているように）センチメント分析を追加して、より良いトレンドポジションを得ることもできます。

このスクリプトを実行すると、次のような.txtが得られます。

Transition Matrix:
{
        {0.15741321, 0.07086962, 0.16785905, 0.08792403, 0.11101073, 0.05415263, 0.08019415, 0.12333382, 0.09794255, 0.04930020},
        {0.16646033, 0.11065086, 0.10447035, 0.13332935, 0.09136784, 0.08351764, 0.06722600, 0.09893912, 0.07936700, 0.06467150},
        {0.14182826, 0.15400641, 0.13617941, 0.08453877, 0.09214389, 0.04040276, 0.09065499, 0.11526167, 0.06725810, 0.07772574},
        {0.15037837, 0.09101998, 0.09552059, 0.10035540, 0.12851236, 0.05000596, 0.09542873, 0.12606514, 0.09394759, 0.06876588},
        {0.15552336, 0.08663776, 0.15694344, 0.09219379, 0.08785893, 0.08381830, 0.05572122, 0.10309824, 0.08512219, 0.09308276},
        {0.19806868, 0.11292565, 0.11482367, 0.08324432, 0.09808519, 0.06727817, 0.11549253, 0.10657752, 0.06889919, 0.03460507},
        {0.12257742, 0.11257625, 0.11910078, 0.07669820, 0.16660657, 0.04769350, 0.09667861, 0.12241177, 0.04856867, 0.08708823},
        {0.14716725, 0.12232022, 0.11135735, 0.08488571, 0.06274817, 0.07390905, 0.10742571, 0.12550373, 0.11431005, 0.05037277},
        {0.11766333, 0.11533807, 0.15497601, 0.14017237, 0.11214274, 0.04885795, 0.08394306, 0.12864406, 0.06945878, 0.02880364},
        {0.13559147, 0.07444276, 0.09785968, 0.13599698, 0.12947508, 0.06385211, 0.09042617, 0.16088280, 0.06588065, 0.04559230}
     };

Means Matrix:
{
        {0.06871601, 0.14572210, 0.05961646},
        {0.06903949, 1.05226034, -0.25687024},
        {-0.04607112, -0.00811718, 0.06488246},
        {-0.01769149, 0.63694700, 0.26965491},
        {-0.01874345, 0.58917438, -0.22484670},
        {-0.02026370, 1.09022869, 0.86790417},
        {-0.85455759, 0.48710677, 0.08980023},
        {-0.02589947, 0.84881170, 0.00453701},
        {-0.38270747, 0.86916742, -0.58792329},
        {-0.16057267, 1.17106076, 0.18531821}
     };

Covariance Matrix:
{
        {  {1.25299224e+00, -4.05453267e-02, 7.95036804e-02},
           {-4.05453267e-02, 1.63177290e-01, 1.58609858e-01},
           {7.95036804e-02, 1.58609858e-01, 8.09678270e-01}},
        {  {1.23040552e+00, 2.52108300e-02, 1.17595322e-01},
           {2.52108300e-02, 3.00175953e-01, -8.11027442e-02},
           {1.17595322e-01, -8.11027442e-02, 1.42259217e+00}},
        {  {1.76376507e+00, -7.82189996e-02, 1.89340073e-01},
           {-7.82189996e-02, 2.56222155e-01, -1.30202288e-01},
           {1.89340073e-01, -1.30202288e-01, 6.60591043e-01}},
        {  {9.08926052e-01, 3.02606081e-02, 1.03549625e-01},
           {3.02606081e-02, 2.30324420e-01, -5.46541678e-02},
           {1.03549625e-01, -5.46541678e-02, 7.40333449e-01}},
        {  {8.80590495e-01, 7.21102489e-02, 3.40982555e-02},
           {7.21102489e-02, 3.26639817e-01, -1.06663221e-01},
           {3.40982555e-02, -1.06663221e-01, 9.55477387e-01}},
        {  {3.19499555e+00, -8.63552078e-02, 5.03260281e-01},
           {-8.63552078e-02, 2.92184645e-01, 1.03141313e-01},
           {5.03260281e-01, 1.03141313e-01, 1.88060098e+00}},
        {  {3.22276957e+00, -6.37618091e-01, 3.80462477e-01},
           {-6.37618091e-01, 4.96770891e-01, -5.79521882e-02},
           {3.80462477e-01, -5.79521882e-02, 1.05061090e+00}},
        {  {2.16098355e+00, 4.02611831e-02, 3.01261346e-01},
           {4.02611831e-02, 4.83773367e-01, 7.20003108e-02},
           {3.01261346e-01, 7.20003108e-02, 1.32262495e+00}},
        {  {4.00745050e+00, -3.90316434e-01, 7.28032792e-01},
           {-3.90316434e-01, 6.01214190e-01, -2.91562862e-01},
           {7.28032792e-01, -2.91562862e-01, 1.30603500e+00}},
        {  {5.47457383e+00, -1.22088743e-02, 2.56784647e-01},
           {-1.22088743e-02, 4.65227101e-01, -2.88257686e-01},
           {2.56784647e-01, -2.88257686e-01, 1.44717234e+00}}
     };

これがEAで使用する行列の形式です。

負の相関があり共分散している2つの銘柄があります。このうち1つの銘柄に対してHMMを実行します（2つの銘柄に相関があることが分かっているため、1つだけで十分です）。負の相関があるため、HMMによって一方が上がると仮定した場合、ナッシュ均衡を適用し、条件が正しければもう一方の銘柄を売る、という戦略が成り立ちます。

この手法は、複数の銘柄でも同様に応用可能です。相関がある場合には同じ方向に買い、負の相関がある場合には売るといったアプローチを取ります。

実際に戦略を適用する前に、Pythonでスクリプトを作成し、隠れ状態を用いた実験をおこない、結果を確認しました。以下がそのスクリプトです。

import MetaTrader5 as mt5
import numpy as np
import pandas as pd
from hmmlearn import hmm
import matplotlib.pyplot as plt
from datetime import datetime

# Function to load matrices from the .txt file
def parse_matrix_block(lines, start_idx, matrix_type="normal"):
    matrix = []
    i = start_idx
    while i < len(lines) and not lines[i].strip().startswith("};"):
        line = lines[i].strip().replace("{", "").replace("}", "").replace(";", "")
        if line:  # Ensure the line is not empty
            if matrix_type == "covariance":
                # Split the line into elements
                elements = [float(x) for x in line.split(',') if x.strip()]
                matrix.append(elements)
            else:
                row = [float(x) for x in line.split(',') if x.strip()]  # Filter out empty values
                matrix.append(row)
        i += 1
    return np.array(matrix), i

def load_matrices(file_path):
    with open(file_path, 'r') as file:
        lines = file.readlines()
    
    transition_matrix = []
    means_matrix = []
    covariance_matrix = []
    
    i = 0
    while i < len(lines):
        line = lines[i].strip()
        
        if line.startswith("Transition Matrix:"):
            transition_matrix, i = parse_matrix_block(lines, i + 1)
            i += 1  # Move forward to avoid repeating the same block

        elif line.startswith("Means Matrix:"):
            means_matrix, i = parse_matrix_block(lines, i + 1)
            i += 1

        elif line.startswith("Covariance Matrix:"):
            covariance_matrix = []
            i += 1
            while i < len(lines) and not lines[i].strip().startswith("};"):
                block, i = parse_matrix_block(lines, i, matrix_type="covariance")
                covariance_matrix.append(block)
                i += 1
            covariance_matrix = np.array(covariance_matrix)
            covariance_matrix = covariance_matrix.reshape(-1, 3, 3)

        i += 1
    
    return transition_matrix, means_matrix, covariance_matrix

# Load the matrices from the .txt file
transition_matrix, means_matrix, covariance_matrix = load_matrices('formatted_matrices.txt')

# Connect to MetaTrader 5
if not mt5.initialize():
    print("initialize() failed, error code =", mt5.last_error())
    quit()

# Set parameters to retrieve data
symbol = "USDJPY"  # You can change to your desired symbol
timeframe = mt5.TIMEFRAME_H4  # You can change the timeframe
start_date = datetime(2024, 1, 1)
end_date = datetime.now()

# Load data from MetaTrader 5
rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
mt5.shutdown()

# Convert the data to a pandas DataFrame
data = pd.DataFrame(rates)
data['time'] = pd.to_datetime(data['time'], unit='s')
data.set_index('time', inplace=True)

# Use only the closing prices column
prices = data['close'].values.reshape(-1, 1)

# Create and configure the HMM model
n_components = len(transition_matrix)
model = hmm.GaussianHMM(n_components=n_components, covariance_type="full")
model.startprob_ = np.full(n_components, 1/n_components)  # Initial probabilities
model.transmat_ = transition_matrix
model.means_ = means_matrix
model.covars_ = covariance_matrix

# Fit the model using the loaded prices
model.fit(prices)

# Predict hidden states
hidden_states = model.predict(prices)

# Manual configuration of states
bullish_states = [2,4,5,6,8]  # States considered bullish
bearish_states = [1,3,7]  # States considered bearish
exclude_states = [0,9]  # States to exclude (neither buy nor sell)

# HMM strategy:
hmm_returns = np.zeros_like(prices)
for i in range(1, len(prices)):
    if hidden_states[i] in bullish_states:  # Buy if the state is bullish
        hmm_returns[i] = prices[i] - prices[i-1]
    elif hidden_states[i] in bearish_states:  # Sell if the state is bearish
        hmm_returns[i] = prices[i-1] - prices[i]
    # If the state is in exclude_states, do nothing

# Buy and hold strategy (holding)
holding_returns = prices[-1] - prices[0]

# Plot results
plt.figure(figsize=(7, 8))
plt.plot(data.index, prices, label='Price of '+str(symbol), color='black', linestyle='--')
plt.plot(data.index, np.cumsum(hmm_returns), label='HMM Strategy', color='green')
plt.axhline(holding_returns, color='blue', linestyle='--', label='Buy and Hold Strategy (Holding)')
plt.title('Backtesting Comparison: HMM vs Holding and Price')
plt.legend()
plt.savefig("playground.png")

# Print accumulated returns of both strategies
print(f"Accumulated returns of the HMM strategy: {np.sum(hmm_returns)}")
print(f"Accumulated returns of the Holding strategy: {holding_returns[0]}")

このスクリプトを見ていきましょう。まず、行列が含まれた.txtファイルを開き、対象銘柄のMetaTrader 5データをダウンロードします。その後、他のスクリプトで使用した最後の日付から今日までのデータを使い、HMMがどのように機能するかを確認します。結果は.png形式で表示され、状態を変更することが可能です。また、2つ目のスクリプトの指示に従い、すべての状態を使用した結果も確認してみましょう。

以下が2つ目のスクリプトです。

Description of Hidden States:
State 0: Not present (State ID: 0)
State 1: Downtrend (State ID: 1)
State 2: Uptrend (State ID: 2)
State 3: Downtrend (State ID: 3)
State 4: Uptrend (State ID: 4)
State 5: Uptrend (State ID: 5)
State 6: Uptrend (State ID: 6)
State 7: Downtrend (State ID: 7)
State 8: Uptrend (State ID: 8)
State 9: Not present (State ID: 9)

以下がその出力です。

Accumulated returns of the HMM strategy: -1.0609999999998365
Accumulated returns of the Holding strategy: 5.284999999999997

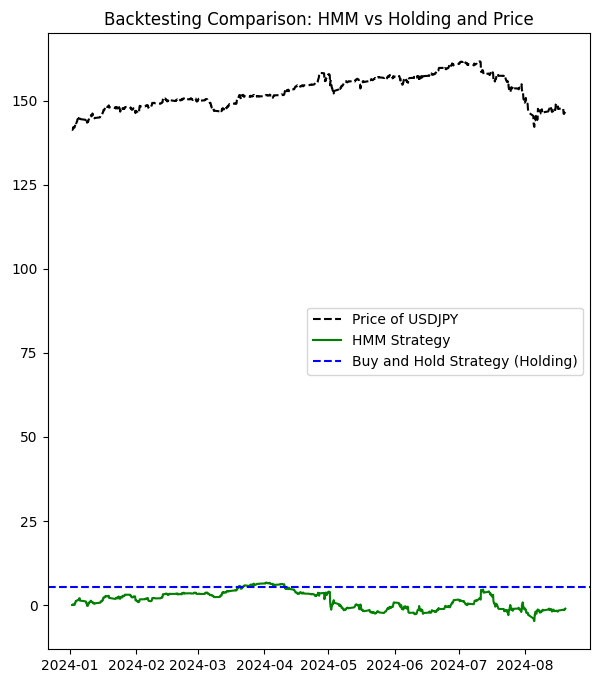
お分かりの通り、この戦略はあまり効果的ではありません。それでは、隠れ状態を非表示にし（ここでは棒グラフを用いて7番目の状態を除外します）、この設定で試してみましょう。

# Manual configuration of states
bullish_states = [2,4,5,6,8]  # States considered bullish
bearish_states = [1,3]  # States considered bearish
exclude_states = [0,7,9]  # States to exclude (neither buy nor sell)

Accumulated returns of the HMM strategy: 7.978000000000122
Accumulated returns of the Holding strategy: 5.284999999999997

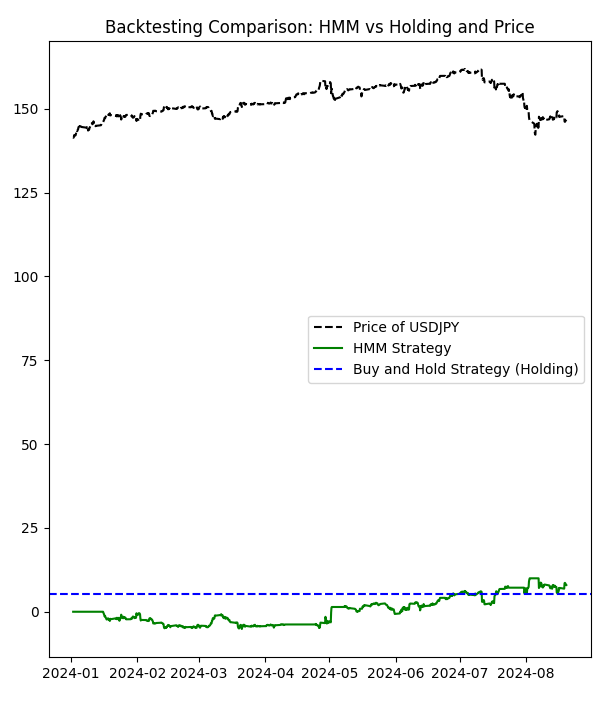
ここから、最悪の隠れ状態を使用しないことで、より収益性の高い戦略が取れることがわかります。

再度強調しますが、これにディープラーニングを適用すれば、最初の銘柄（この場合はUSDJPY）のパターンをより効果的に検出できるでしょう。もしかしたら、別の機会にその実験をおこなうかもしれません。

MQL5での実装

ナッシュEAは、MetaTrader 5プラットフォーム用に設計された高度なアルゴリズム取引システムです。このEAは、外国為替市場での取引決定を行うために、隠れマルコフモデル(HMM)、対数尤度分析、トレンドの強さの評価、およびナッシュ均衡の概念を組み込んだマルチ戦略アプローチを採用しています。

EAはまず、重要なパラメータと指標を初期化します。具体的には、指数移動平均(EMA)、相対力指数(RSI)、平均トゥルーレンジ(ATR)、ボリンジャーバンドを設定します。これらのテクニカル指標はEAの市場分析の基盤となります。また、初期化プロセスでは、EAの予測能力の中心となる隠れマルコフモデルのパラメータも設定します。

EAの主な特徴の一つは市場レジーム検出システムです。このシステムはHMM法と対数尤度法の両方を利用して、現在の市場の状態を上昇トレンド、下降トレンド、または中立の3つのカテゴリに分類します。レジーム検出プロセスには、排出確率と状態遷移の複雑な計算が含まれ、市場状況に対する詳細な理解を提供します。

EAはHMMベース、対数尤度ベース、トレンドの強さ、ナッシュ均衡の4つの異なる取引戦略を実装しています。各戦略はそれぞれ独自の売買シグナルを生成し、それを重み付けして組み合わせることで、総合的な売買判断を行います。特にナッシュ均衡戦略は、他の戦略との最適なバランスを見つけることを目的としており、より強固な取引決定を導く可能性があります。

リスク管理はナッシュEAの重要な側面です。口座残高と戦略パフォーマンスに基づく動的なロットサイズ、ストップロスレベル、テイクプロフィットレベル、トレーリングストップメカニズムなどが組み込まれています。これらのリスク管理ツールは、資本を保護しつつ、有利な市場環境において潜在的な利益を得ることを目指しています。

このEAにはバックテスト機能も備わっており、トレーダーは過去のデータからそのパフォーマンスを評価できます。この機能は、利益、総取引数、勝ち取引数、勝率など、各戦略のさまざまなパフォーマンス指標を計算します。こうした包括的なテスト機能により、トレーダーはEAのパラメータを微調整して最適なパフォーマンスを得ることが可能です。

ナッシュEAのメインループでは、新しい価格バーごとに市場データを処理します。市場レジームを再計算し、戦略シグナルを更新し、有効化されたすべての戦略の総合的な出力に基づいて取引判断を下します。このEAはペアでポジションを建てるように設計されており、プライマリ銘柄とEURCHFの両方を同時に取引する可能性があります。

最後に、EAには堅牢なエラーハンドリングとログ機能があります。有効な指標値を継続的に確認し、端末とEAの設定で取引が許可されていることを確認し、操作と意思決定プロセスの詳細なログを提供します。この透明性により、デバッグやパフォーマンス分析が容易になります。

ここで、いくつかの重要な関数とナッシュ均衡について見てみましょう。

このEAでナッシュ均衡の概念を実装するために使用される主な関数は以下の通りです。

1. CalculateStrictNashEquilibrium()

これは厳密なナッシュ均衡を計算するための主要関数です。以下がその実装です。

void CalculateStrictNashEquilibrium()
{
   double buySignal = 0;
   double sellSignal = 0;

   // Sum the weighted signals of the enabled strategies
   for(int i = 0; i < 3; i++) // Consider only the first 3 strategies for Nash equilibrium
   {
      if(strategies[i].enabled)
      {
         buySignal += strategies[i].weight * (strategies[i].signal > 0 ? 1 : 0);
         sellSignal += strategies[i].weight * (strategies[i].signal < 0 ? 1 : 0);
      }
   }

   // If there's a stronger buy signal than sell signal, set Nash Equilibrium signal to buy
   if(buySignal > sellSignal)
   {
      strategies[3].signal = 1; // Buy signal
   }
   else if(sellSignal > buySignal)
   {
      strategies[3].signal = -1; // Sell signal
   }
   else
   {
      // If there's no clear signal, force a decision based on an additional criterion
      double closePrice = iClose(_Symbol, PERIOD_CURRENT, 0);
      double openPrice = iOpen(_Symbol, PERIOD_CURRENT, 0);
      strategies[3].signal = (closePrice > openPrice) ? 1 : -1;
   }
}

説明

• この関数は、最初の3つの戦略のシグナルを加重平均して売買シグナルを計算します。
• 買いシグナルと売りシグナルを比較し、ナッシュ均衡の行動を決定します。
• シグナルが等しい場合、現在の価格の方向に基づいて判断します。

2. SimulateTrading()

ナッシュ均衡専用ではありませんが、この関数はナッシュ均衡を含む取引ロジックを実装しています。

void SimulateTrading(MarketRegime actualTrend, datetime time, string symbol)
{
   double buySignal = 0;
   double sellSignal = 0;

   for(int i = 0; i < ArraySize(strategies); i++)
   {
      if(strategies[i].enabled)
      {
         if(strategies[i].signal > 0)
            buySignal += strategies[i].weight * strategies[i].signal;
         else if(strategies[i].signal < 0)
            sellSignal -= strategies[i].weight * strategies[i].signal;
      }
   }

   // ... (code to simulate trades and calculate profits)
}

説明

• この関数は、ナッシュ均衡戦略を含むすべての戦略からのシグナルに基づいて取引をシミュレートします。
• すべての有効な戦略の売買シグナルを加重計算します。

3. OnTick()

OnTick()関数では、ナッシュ均衡に基づいて取引を実行するロジックが実装されています。

void OnTick()
{
   // ... (other code)

   // Check if the Nash Equilibrium strategy has generated a signal
   if(strategies[3].enabled && strategies[3].signal != 0)
   {
      if(strategies[3].signal > 0)
      {
         OpenBuyOrder(strategies[3].name);
      }
      else if(strategies[3].signal < 0)
      {
         OpenSellOrder(strategies[3].name);
      }
   }

   // ... (other code)
}

説明

• この関数は、ナッシュ均衡戦略（戦略配列の3番目の戦略）が有効で、シグナルが発生しているかどうかを確認します。
• 買いシグナルがあれば（シグナル＞0）、買い注文を出します。
• 売りシグナルがあれば（シグナル＜0）、売り注文を出します。

ナッシュ均衡は、本EAの取引戦略の1つとして実装されています。CalculateStrictNashEquilibrium()関数は、他の戦略からのシグナルに基づいてナッシュ均衡シグナルを決定します。このシグナルは、OnTick()関数で取引判断に使われます。この実装の目的は、さまざまな戦略のバランスを見つけることで、より強固な取引決定をおこなうことです。

ナッシュ均衡を取引戦略に導入するこのアプローチは、ゲーム理論を金融市場に応用する興味深い試みです。異なる取引シグナル間の相互作用を考慮し、最適な戦略を見つけようとするものであり、各「プレーヤー」が異なる取引戦略を取るマルチプレーヤーゲームにおける均衡を見つけることに似ています。

DetectMarketRegime関数：この関数は、EAの意思決定プロセスにとって極めて重要です。テクニカル指標と複雑な統計モデルを用いて現在の市場状況を分析し、市場体制を決定します。

void DetectMarketRegime(MarketRegime &hmmRegime, MarketRegime &logLikelihoodRegime)
{
    // Calculate indicators
    double fastEMA = iMAGet(fastEMAHandle, 0);
    double slowEMA = iMAGet(slowEMAHandle, 0);
    double rsi = iRSIGet(rsiHandle, 0);
    double atr = iATRGet(atrHandle, 0);
    double price = SymbolInfoDouble(_Symbol, SYMBOL_BID);

    // Calculate trend strength and volatility ratio
    double trendStrength = (fastEMA - slowEMA) / slowEMA;
    double volatilityRatio = atr / price;

    // Normalize RSI
    double normalizedRSI = (rsi - 50) / 25;

    // Calculate features for HMM
    double features[3] = {trendStrength, volatilityRatio, normalizedRSI};

    // Calculate log-likelihood and HMM likelihoods
    double logLikelihood[10];
    double hmmLikelihoods[10];
    CalculateLogLikelihood(features, symbolParams.emissionMeans, symbolParams.emissionCovs);
    CalculateHMMLikelihoods(features, symbolParams.emissionMeans, symbolParams.emissionCovs, symbolParams.transitionProb, 10, hmmLikelihoods);

    // Determine regimes based on maximum likelihood
    int maxLogLikelihoodIndex = ArrayMaximum(logLikelihood);
    int maxHmmLikelihoodIndex = ArrayMaximum(hmmLikelihoods);

    logLikelihoodRegime = InterpretRegime(maxLogLikelihoodIndex);
    hmmRegime = InterpretRegime(maxHmmLikelihoodIndex);

    
    // ... (confidence calculation code)
}

この関数は、テクニカル指標、隠れマルコフモデル、対数尤度分析を組み合わせて、現在の市場体制を判断します。これは市場分析に対する洗練されたアプローチであり、市場状況に対する深い理解を提供します。

CalculateStrategySignals関数：この関数は、現在の市場レジームとテクニカル指標に基づいて、EAの各戦略の売買シグナルを計算します。

void CalculateStrategySignals(string symbol, datetime time, MarketRegime hmmRegime, MarketRegime logLikelihoodRegime)
{
    if(strategies[0].enabled) // HMM Strategy
    {
        CalculateHMMSignal();
    }
    
    if(strategies[1].enabled) // LogLikelihood Strategy
    {
        CalculateLogLikelihoodSignal();
    }
    
    if(strategies[2].enabled) // Trend Strength
    {
        double trendStrength = CalculateTrendStrength(PERIOD_CURRENT);
        strategies[2].signal = NormalizeTrendStrength(trendStrength);
    }
    
    if(strategies[3].enabled) // Nash Equilibrium
    {
        CalculateStrictNashEquilibrium();
    }
}

この関数は、有効化された各戦略のシグナルを計算し、様々な分析手法を統合して総合的な取引判断をおこないます。

SimulateTrading関数：この関数は、計算されたシグナルに基づいて取引をシミュレートし、各戦略のパフォーマンス指標を更新します。

void SimulateTrading(MarketRegime actualTrend, datetime time, string symbol)
{
    double buySignal = 0;
    double sellSignal = 0;

    for(int i = 0; i < ArraySize(strategies); i++)
    {
        if(strategies[i].enabled)
        {
            if(strategies[i].signal > 0)
                buySignal += strategies[i].weight * strategies[i].signal;
            else if(strategies[i].signal < 0)
                sellSignal -= strategies[i].weight * strategies[i].signal;
        }
    }

    // Simulate trade execution and calculate profits
    // ... (trade simulation code)

    // Update strategy performance metrics
    // ... (performance update code)
}

この関数は、バックテストやEAのパフォーマンスを評価するために非常に重要です。計算されたシグナルに基づいて取引をシミュレートし、各戦略のパフォーマンス指標を更新します。

CalculateHMMLikelihoods関数：この関数は、隠れマルコフモデルを用いて、さまざまな市場の状態の尤度を計算します。

void CalculateHMMLikelihoods(const double &features[], const double &means[], const double &covs[], const double &transitionProb[], int numStates, double &hmmLikelihoods[])
{
    // Initialize and calculate initial likelihoods
    // ... (initialization code)

    // Forward algorithm to calculate HMM likelihoods
    for(int t = 1; t < ArraySize(features) / 3; t++)
    {
        // ... (HMM likelihood calculation code)
    }

    // Normalize and validate likelihoods
    // ... (normalization and validation code)
}

この関数は、隠れマルコフモデルの順方向アルゴリズムを実装し、異なる市場状態の尤度を計算します。これは、観察された特徴に基づいて市場の動きを予測する高度な手法です。

これらの関数は、ナッシュEAの分析および意思決定プロセスの中心を成しています。EAの強みは、伝統的なテクニカル分析と、隠れマルコフモデルやナッシュ均衡のような高度な統計的手法との組み合わせにあります。このマルチ戦略アプローチは、強固なバックテストとリスク管理機能を兼ね備え、外国為替市場におけるアルゴリズム取引の強力なツールとなり得ます。

このEAの最も重要な点は、その適応性です。市場環境を継続的に評価し、パフォーマンスに基づいて戦略の重みを調整することで、さまざまな市場環境においても有効性を維持することを目指しています。しかし、こうしたシステムは洗練されているとはいえ、刻々と変化する市場環境の中で効果を持ち続けるためには、注意深い監視と定期的な再調整が必要であることに留意することが重要です。

結果

以下が設定です。

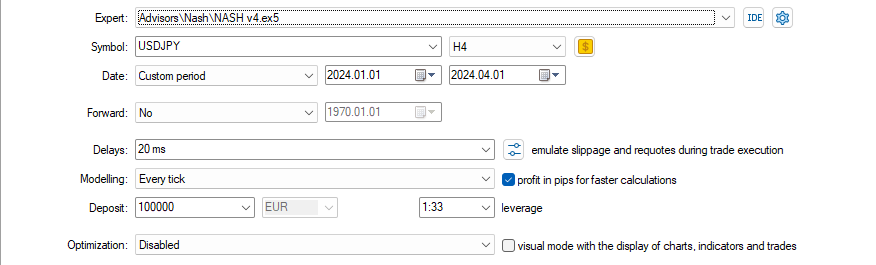
以下が入力です。

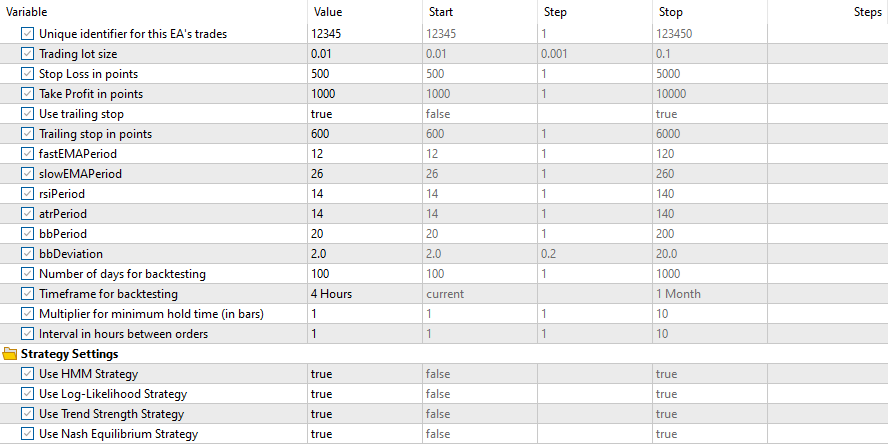
すべての戦略の結果は以下の通りです。

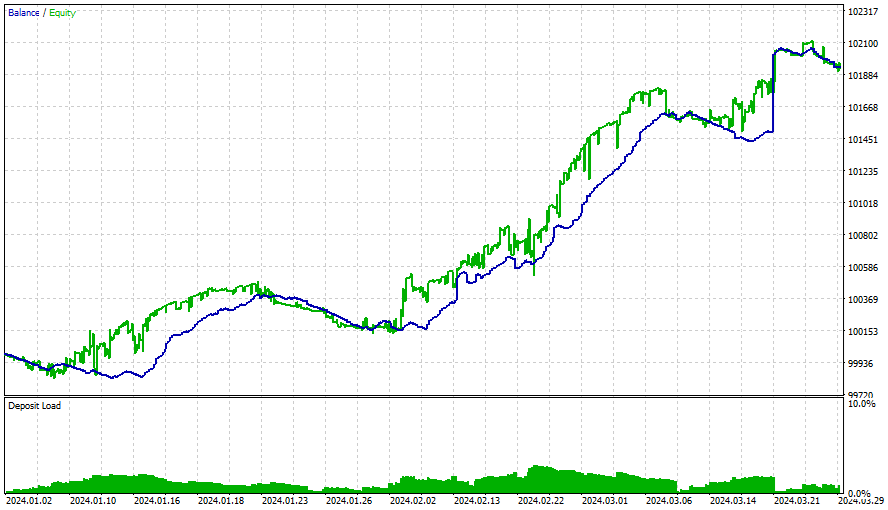
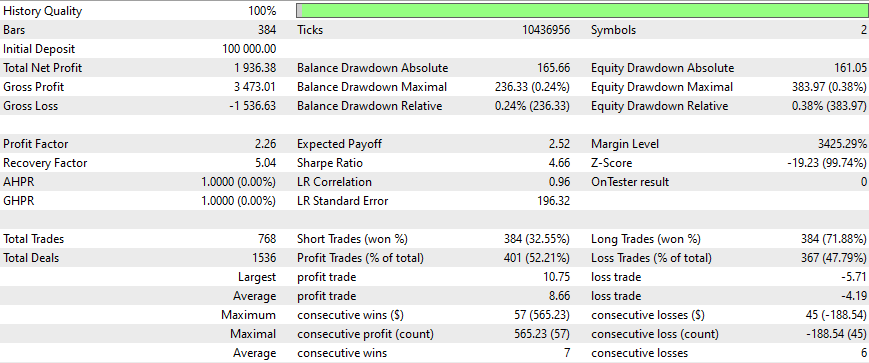
この期間を過ぎると、勝ち星は伸び悩み、最適化は3カ月ごとにおこなうべきでした（このようなスタート条件をすべて満たした状態で）。戦略はシンプルで、トレーリングストップを使用していますが、これは非常にシンプルで固定されたものです。さらなる最適化、より新しい行列、そしてより洗練された戦略を取り入れることで、より良い結果が得られるでしょう。また、このEAにセンチメント分析とディープラーニングを加えることも検討する必要があります。

すべての戦略にはナッシュ均衡が不可欠です。

結論

ゲーム理論と取引が交わることで、市場戦略を強化するエキサイティングな機会が生まれます。ナッシュ均衡理論を応用することで、トレーダーは市場内の他者の潜在的な行動を考慮し、より計算された決定を下すことができます。この記事では、PythonとMetaTrader 5を使用してこれらのコンセプトを実装する方法を概説し、取引アプローチの高度化を目指す人々に強力なツールセットを提供します。市場が進化し続ける中、ナッシュ均衡のような数学的理論を統合することは、取引で一貫した成功を収めるための重要な差別化要因となり得ます。

この記事を読んでいただき、あるいは再生することで、読者自身のEAに役立つことを願っています。このテーマは非常に興味深く、読者の期待に応えられることを願っています。私自身が制作を楽しんだように、皆さんにも楽しんでいただければ幸いです。