知っておくべきMQL5ウィザードのテクニック（第68回）： コサインカーネルネットワークでTRIXとWPRのパターンを使用する

はじめに

前回の記事で検討した10種類のシグナルパターンのうち、フォワードウォークに成功したのはわずか3パターンでした。これらのパターンは、トレンド指標であるTRIXと、サポート/レジスタンスオシレーターであるWilliams Percent Range (WPR)の指標シグナルを組み合わせて生成されました。エキスパートアドバイザー(EA)の学習・最適化は2023年の1年間に限定され、フォワードウォークは翌年の2024年で実施されました。テスト対象はCHF/JPYの4時間足です。

フォワードウォーク可能なパターンを機械学習で拡張する際には、通常Pythonを使用します。Pythonはネットワークのコーディングや学習を非常に効率的におこなえるためであり、GPUがなくても十分に効果を発揮します。過去の記事では、フォワードウォーク可能なパターンの関数をPythonで実装する方法を前置きとして示してきました。本記事では指標のPython実装にも触れますが、主に指標シグナルを入力とするネットワークの構築に重点を置きます。このネットワークは1次元の畳み込みニューラルネットワークで、設計にコサインカーネルを使用しています。

Pythonにおけるインジケーター

ネットワークで指標シグナルをPythonで利用するには、Pythonのライブラリを使用することも、自分でコーディングすることも可能です。ここでは、TRIX関数をPythonで次のように実装します。

def TRIX(df: pd.DataFrame, period: int) -> pd.DataFrame:
    """
    Calculate TRIX indicator and append it as 'TRIX' column to the input DataFrame.
    
    Args:
        df (pd.DataFrame): DataFrame with 'close' column
        period (int): Lookback period for EMA calculation
        
    Returns:
        pd.DataFrame: Input DataFrame with new 'TRIX' column
    """
    # Input validation
    if not all(col in df.columns for col in ['close']):
        raise ValueError("DataFrame must contain 'close' column")
    if period < 1:
        raise ValueError("Period must be positive")
        
    # Create a copy to avoid modifying the input DataFrame
    result_df = df.copy()
    
    # Calculate triple EMA
    ema1 = df['close'].ewm(span=period, adjust=False).mean()
    ema2 = ema1.ewm(span=period, adjust=False).mean()
    ema3 = ema2.ewm(span=period, adjust=False).mean()
    
    # Calculate TRIX: percentage rate of change of triple EMA
    result_df['main'] = ema3.pct_change() * 100
    
    return result_df

TRIXは、三重平滑化EMA (Exponential Moving Average)の変化率を計算します。入力としては、close列を持つpandasデータフレームと、EMA計算に使用する整数の期間を指定します。出力は同じデータフレームで、計算された指標値を格納する列が追加されます。主に、価格データを平滑化しつつモメンタムの変化を強調することで、トレンドの方向性や潜在的な反転を識別するために使用されます。

上記のコードは、まず関数を定義し、入力に型ヒントを付けることで明確性と型安全性を確保します。その後、終値に対して1回目のEMAを計算し、この価格データをさらに平滑化してEMAの重み付けを一貫させます。次に、1回目のEMAに対して2回目のEMAを計算し、データのノイズを減らすためにさらに平滑化します。これをema2に代入します。続いて3回目のEMAを計算し、三重平滑化のプロセスを完了させます。この段階でTRIXはモメンタムの変化に敏感になります。出力はema3です。

このema3を用いて、入力のpandasデータフレームにTRIXを計算した列を追加します。TRIXは、三重EMA (ema3)の前値に対する百分率変化として表現されます。100を掛けることで、結果を解釈しやすくし、0〜100％の範囲で扱えるようにスケーリングしています。TRIXの定義が終わったら、次にWilliams Percent Range (WPR)に移ります。WPRはPythonで次のように実装します。

def WPR(df: pd.DataFrame, period: int) -> pd.DataFrame:
    """
    Calculate Williams %R indicator and append it as 'WPR' column to the input DataFrame.
    
    Args:
        df (pd.DataFrame): DataFrame with 'high', 'low', 'close' columns
        period (int): Lookback period for calculation
        
    Returns:
        pd.DataFrame: Input DataFrame with new 'WPR' column
    """
    # Input validation
    if not all(col in df.columns for col in ['high', 'low', 'close']):
        raise ValueError("DataFrame must contain 'high', 'low', 'close' columns")
    if period < 1:
        raise ValueError("Period must be positive")
        
    # Create a copy to avoid modifying the input DataFrame
    result_df = df.copy()
    
    # Calculate highest high and lowest low over the period
    high_max = df['high'].rolling(window=period).max()
    low_min = df['low'].rolling(window=period).min()
    
    # Calculate Williams %R
    result_df['main'] = ((high_max - df['close']) / (high_max - low_min)) * -100
    
    return result_df

WPRは、サポート/レジスタンスのオシレーターであり、価格が買われ過ぎ（レジスタンス）にあるのか、売られ過ぎ（サポート）にあるのかを判断するのに役立ちます。本関数の入力はpandasデータフレームで、使用する列はhigh、low、closeに加え、指標の参照期間を決定する整数の期間です。出力もpandasデータフレームで、追加の列としてWPRをラベル付けします。この列には[-100, 0]の範囲の値が格納されます。

コードはTRIXと同様に、まず入力に型ヒントを付けて定義します。その後、指定された期間の最高値を計算し、WPR計算の上限を形成します。同様に、同じ参照期間における最安値も計算します。次に、入力データフレームに追加する列としてWPRを定義し、標準的なWPRの計算式を用いて値を計算します。 

Pythonでは、計算結果をバッファとして簡単に扱える点が非常に便利です。C言語系の言語から移行してくるプログラマーにとっては驚くべき点です。

両関数には追加の検証を組み込むことも可能です。これらの関数は、入力データフレームに必要な列が存在し、十分な行数があることを前提としています。本記事ではMetaTrader 5のPythonモジュールから取得したデータを使用していますが、欠損列についてはMetaTrader 5側で常に存在するため問題ありません。しかし、行数が少ない場合に備えたエラーハンドリングを追加することで、関数の堅牢性を向上させることができます。さらに、大規模データセットに対しては、ローリングウィンドウの事前計算や、pandasで実装されているベクトル化処理を活用して最適化することが重要です。テスト段階では、MetaTraderなどのプラットフォームで既知の指標値と出力を照合することで、計算結果の正確性を確認することも推奨されます。

Conv1Dアーキテクチャにおけるコサインカーネル使用の利点

Conv1Dネットワークは、金融時系列やテキストのようなシーケンスデータに対して一次元の畳み込み演算をおこなう特殊な畳み込みニューラルネットワークです。この過程では、入力データにフィルターを適用してスライドさせ、入力データの重要なパターン、トレンド、モチーフを抽出します。この抽出の結果、入力シーケンスの次元は本質的に削減されます。ただし、各フィルターは入力データの特定の重要な特徴量を出力することを目的としています。ネットワークは畳み込み層、活性化層、プーリング層、全結合層を含みます。Conv1Dは、時間的または順序的差異を持つ順序データの処理に効率的です。

一方、コサインカーネルは類似度の測定手法です。2つのベクトル間の角度のコサイン値を計算し、方向の類似性を定量化します。2つのベクトルの内積をそれぞれの大きさで正規化することで求められ、出力値は-1（逆方向）から+1（同方向）までの範囲になります。この類似度は、テキストのように大きさよりも方向性が重要な高次元データの処理に非常に有効です。

Conv1D設計にコサインカーネルを使用する利点はいくつかあります。まず、カーネルサイズに滑らかな変化を与えられる点です。コサイン関数はカーネルサイズに対して滑らかな振動パターンを生成し、CNNが急激な変化なく異なるスケールで特徴を捉えることを可能にします。適応的なチャネル進行も利点の一つで、コサインベースのチャネルスケーリングによりフィルター数を段階的に増加させることができ、全層におけるモデルの複雑性と特徴抽出能力のバランスを取ることができます。

さらに、コサインカーネルは堅牢な特徴抽出を可能にします。これは、その振動的性質が金融時系列などの平均回帰的な時系列の自然パターンを模倣するためで、CNNが周期的または循環的パターンを検出するのに役立ちます。最後に、カーネルサイズとチャネルの変化によって正則化効果が生じます。この正則化により、アーキテクチャに制御された変動を導入でき、過学習のリスクを低減します。

Conv1Dでコサインカーネルを使用する場合、入力データは通常、batch_size × input_channels × input_lengthの3次元テンソルである必要があります。単変量時系列を使用する場合、input_channelsは1となります。十分な入力長があれば、カーネルサイズを扱う際に過剰な次元削減を避けることができます。 

本モデルで調整が必要な主要ハイパーパラメータは5つです。まずbase_channelsがあります。これは初期値として16〜32程度が理想的です。2番目はレイヤー数で、通常は3〜5層が適切で、多すぎると勾配消失や計算量の増大を招きます。3番目の最大カーネルサイズも重要で、長いシーケンスの場合は7以上が適切であり、対称性を保つために奇数に設定します。

さらに、周波数(frequency)はカーネルサイズとチャネルの振動を制御し、0.5で中程度の振動となり、0.1〜1.0の範囲で調整可能です。最後にドロップアウト率は0.2〜0.5の範囲で設定し、正則化に重要です。高めの値は過学習を抑制しますが、損失関数の最小化精度に影響を与える場合があります。

学習時には、Adamなどの標準的なオプティマイザと学習率スケジューラを用いることで、高速かつ精度の高い収束が可能です。バッチ正規化やドロップアウトは十分におこない、特に小規模データセットでは過学習防止に重要です。コサイン類似度でカーネルサイズを決定した場合、出力は分類タスクなら単一ニューロン＋シグモイド活性化のバイナリが理想です。他のタスク（多クラス分類や回帰）の場合は、全結合層を適宜修正します。適用例としては、周期的・振動的パターンが予想される時系列データが最適です。

一方、このカーネルをCNNに適用する際の制約として、すべてのデータセットに最適とは限らない点があります。標準Conv1Dアーキテクチャと比較して性能を確認することが重要です。また、グローバル平均プーリングは固定出力サイズを前提としており、シーケンス出力が必要なタスクには適さない場合があります。

ネットワーク

TRIXとWPRからのシグナルをバイナリ入力ベクトルとして受け取る我々のネットワークは、先に紹介したようにコサイン類似度を用いてカーネルサイズを決定する畳み込みニューラルネットワークです。これを次のように実装します。

class CosineConv1D(nn.Module):
    """
    A 1D Convolutional Neural Network with kernel sizes and channels based on cosine functions.
    Outputs a scalar float in [0,1] using sigmoid activation.
    """
    def __init__(self, input_channels: int, base_channels: int, num_layers: int, input_length: int,
                 max_kernel_size: int = 7, frequency: float = 0.5, dropout_rate: float = 0.3):
        super(CosineConv1D, self).__init__()
        
        if input_channels < 1 or base_channels < 1 or num_layers < 1:
            raise ValueError("Input channels, base channels, and num layers must be positive")
        if input_length < 1:
            raise ValueError("Input length must be positive")
        if max_kernel_size < 1:
            raise ValueError("Max kernel size must be positive")
        if not (0 <= dropout_rate < 1):
            raise ValueError("Dropout rate must be between 0 and 1")
        
        self.layers = nn.ModuleList()
        self.input_length = input_length
        current_length = input_length
        
        for i in range(num_layers):
            kernel_size = int(3 + (max_kernel_size - 3) * (1 + np.cos(2 * np.pi * frequency * i)) / 2)
            kernel_size = max(3, min(kernel_size, max_kernel_size))
            channels = int(base_channels * (1 + 0.5 * np.cos(np.pi * i / num_layers)))
            channels = max(base_channels, channels)
            padding = kernel_size // 2
            
            conv_layer = nn.Sequential(
                nn.Conv1d(
                    in_channels=input_channels if i == 0 else self.layers[-1][0].out_channels,
                    out_channels=channels,
                    kernel_size=kernel_size,
                    padding=padding
                ),
                nn.BatchNorm1d(channels),
                nn.ReLU(),
                nn.Dropout(dropout_rate)
            )
            self.layers.append(conv_layer)
            current_length = (current_length - kernel_size + 2 * padding) // 1 + 1
            
        self.global_pool = nn.AdaptiveAvgPool1d(1)
        self.fc = nn.Sequential(
            nn.Linear(channels, 1),
            nn.Sigmoid()
        )
        
    def forward(self, x: torch.Tensor) -> torch.Tensor:
        for layer in self.layers:
            x = layer(x)
        x = self.global_pool(x)
        x = x.squeeze(-1)
        x = self.fc(x)
        return x

    def get_output_length(self) -> int:
        return self.layers[-1][0].out_channels

本ネットワークは、TRIXとWPRからのシグナルをバイナリ入力ベクトルとして受け取り、前述したようにコサイン類似度を用いてカーネルサイズを決定する1次元畳み込みニューラルネットワーク(1D CNN)です。出力はシグモイド活性化関数を通じて[0,1]の範囲に収まるスカラー値となります。これはPyTorchのnn.Moduleを継承したカスタムモジュールとして実装されており、カーネルサイズとチャネル数を調整するアーキテクチャによって、入力パターンに適応可能です。シグモイド活性化によって、出力は0から1の確率的なスカラーとして表現されます。

ネットワークの初期化は検証と組み合わせておこなわれます。これにより、チャネル数、レイヤー数、カーネルサイズ、ドロップアウト率といった入力パラメータが有効であることを保証します。主な確認点は、入力値が正であること、ドロップアウト率が0から1の範囲内であることです。これは、無効な設定によって発生する実行時エラーやパフォーマンス低下を防ぐ上で不可欠です。また、これらのカスタマイズ可能なパラメータによってネットワーク設計に柔軟性が加わります。 

実装に際しては、入力チャネルは入力データの次元と一致させる必要があります。ベースチャネルは「モデルのキャパシティ」を制御し、レイヤー数は深さと計算要件のバランスを取ります。最大カーネルサイズや周波数は、順伝播の各段階における特徴抽出を最適化するために調整することができます。

初期化と検証を終えると、次はカーネルサイズとチャネル数の決定に進みます。すでに述べたように、各レイヤーにおいてコサイン関数を用いてカーネルサイズとチャネル数を動的に調整します。したがって、コサイン関数を使用して各レイヤーのカーネルサイズとチャネル数を計算します。カーネルサイズは3から最大カーネルサイズの範囲で変動し、  チャネル数はベースチャネルの値から始まり、コサイン関数によって変動します。

これによって受容野や特徴抽出能力に動的な変化が導入され、ネットワークは多様なパターンを捉えることが可能になります。コサインによる変調は、カーネル間のスムーズな遷移を保証し、急激な変化を避けます。周波数は通常0.1から1.0の範囲で調整し、カーネルサイズの振動を制御します。より複雑な多次元データセットには、より大きなベースチャネルが適しています。さらに、過剰なパディングを避けるため、最大カーネルサイズのパラメータは入力データの長さに合わせる必要があります。ここまでを踏まえ、次に畳み込み層の構築へと進みます。これは堅牢性を高めるために、バッチ正規化、ReLU、そしてドロップアウトを組み合わせておこないます。

各レイヤーは、1次元畳み込み、バッチ正規化、ReLU活性化、ドロップアウトのシーケンスとして構築されます。最初のレイヤーは入力チャネルを使い、以降のレイヤーは前のレイヤーの出力チャネルを用います。パディングによって入力長が維持されます。この構成の重要性は、各要素が果たす役割にあります。畳み込みは特徴抽出のためにあり、バッチ正規化は学習の安定性を高め、ReLU活性化関数は非線形性を確保し、ドロップアウトは正則化によって過学習を防ぎます。実装時には、ドロップアウト率は0.2から0.5の範囲で設定するのがよいでしょう。入力チャネルがデータと一致していることを確認することも重要であり、nn.ModuleListを活用すれば動的なレイヤー管理が可能になります。次にグローバルプーリングと出力処理がおこなわれます。

ここでは適応平均プーリングによって空間次元を1に縮小します。その後、線形層を通じて単一の出力に変換し、シグモイド活性化によって0から1の範囲に制約します。プーリングはシーケンス全体の特徴を要約し、入力長に依存せず固定サイズの出力を可能にします。線形層とシグモイドは、分類タスクに適したスカラーを出力します。このネットワークでは単一出力を扱うため、原則として、最終レイヤーのチャネル数が線形層の入力と一致することを確認する必要があります。

次にフォワードパス関数を定義します。この重要な関数は、入力をレイヤー、プーリング、最終的な出力変換を通して処理します。これは入力xを処理するネットワークのフォワードパスを定義するものであり、畳み込み層、空間次元を圧縮するグローバルプーリング、そして最終的に全結合層を通じて実行されます。この関数の重要性は、データフローを明確に指定する点にあります。これにより、入力から出力までの正しい変換が保証されます。空間次元の圧縮は、線形層との互換性を保つために余分な次元を省略します。実装にあたってはテンソルの形状が正しいことを確認する必要があり、形状の不一致をデバッグする際には各レイヤーの出力を確認することで対応できます。

最後に、出力長を追跡する関数があります。この追跡は互換性を保証し、前述のようにデバッグにも利用できます。この関数は最終畳み込み層からの出力チャネル数を返します。これはネットワークの出力に関する重要なメタデータを提供するもので、後続のタスクやデバッグに役立ちます。また、この関数は後続のレイヤーやモデルとの互換性を検証するためにも使用でき、さらにデータなど追加のメタデータが必要な場合には拡張することも可能です。

シーケンスと学習

ネットワークにデータを前処理するためのcreate_sequences関数も用意しています。この関数は、入力データとラベルを1D CNN処理用のシーケンスに整える役割を果たします。これをPythonで次のように実装します。

def create_sequences(data, labels, sequence_length):
    num_samples, num_features = data.shape
    sequences = []
    seq_labels = []
    
    # Ensure labels is 1D
    labels = labels.flatten()
    
    for i in range(num_samples - sequence_length + 1):
        sequences.append(data[i:i+sequence_length].T)  # Transpose to (num_features, sequence_length)
        seq_labels.append(labels[i+sequence_length-1])  # Use label of last sample in sequence
    
    sequences = np.array(sequences)  # Shape: (num_sequences, num_features, sequence_length)
    seq_labels = np.array(seq_labels).reshape(-1, 1)  # Shape: (num_sequences, 1)
    
    return torch.tensor(sequences, dtype=torch.float32), torch.tensor(seq_labels, dtype=torch.float32)

シーケンスを作成する際には、まず入力データ（形状は[samples, features]）から、入力パラメータであるsequence-lengthに一致する長さのシーケンスと対応するラベルを作成します。その後、このデータはCNNの入力フォーマットである[features, sequence-length]に一致するよう転置されます。ラベルは各シーケンスの最後のタイムステップから取得されます。これは、データを「シーケンス」と呼んでいる関連性のあるデータのまとまりに構造化することで、1D CNNに適した形に準備するために重要です。これにより、上記の「CosineConv1D」ネットワークとの互換性要件が満たされます。

シーケンス長の設定は時間的依存関係に基づきます。つまり、時系列データにおいて繰り返し可能で追跡可能なパターンが現れる遅延距離に基づいています。特徴量の数が入力チャネル数と一致することを確認することが重要です。また、複雑なデータセットを扱う教師ありタスクでは、ラベルの整合性も検証する必要があります。

create_sequences関数を定義したところで、次にtrain_and_evaluate関数を見ていきます。ここで最初におこなうのはハイパーパラメータの設定です。この関数の冒頭4行のコードで、学習用ハイパーパラメータを定義しています。設定する必要があるのは、ミニバッチ処理のためのバッチサイズ、ロングとショートの条件に対応する入力チャネル、シーケンス長、エポック数、そして学習率です。我々のシーケンス長は1に設定されています。これは価格バー同士が遅延なしに直接関係していることを意味します。したがって、1週間のラグにおけるパターン内関係を仮定していることになります。学習関数を次のように実装します。

def train_and_evaluate(x_train, y_train):
    # Hyperparameters
    batch_size = 32
    input_channels = 2  # TRIX and WPR
    sequence_length = 1  # Adjustable based on your needs
    num_epochs = 10
    learning_rate = 0.0005

    # Create sequences
    X_tensor, y_tensor = create_sequences(x_train, y_train, sequence_length)
    num_sequences = X_tensor.shape[0]
    
    # Initialize model
    model = CosineConv1D(
        input_channels=input_channels,
        base_channels=128,
        num_layers=16,
        input_length=sequence_length,
        max_kernel_size=7,
        frequency=0.5,
        dropout_rate=0.03
    )
    
    # Loss and optimizer
    criterion = nn.BCELoss()
    optimizer = optim.Adam(model.parameters(), lr=learning_rate)
    
    # Training loop
    model.train()
    for epoch in range(num_epochs):
        total_loss = 0
        for i in range(0, num_sequences, batch_size):
            batch_X = X_tensor[i:i+batch_size]  # Shape: (batch_size, 2, sequence_length)
            batch_y = y_tensor[i:i+batch_size]
            
            outputs = model(batch_X)
            loss = criterion(outputs, batch_y)
            
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            
            total_loss += loss.item()
        
        avg_loss = total_loss / (num_sequences // batch_size)
        print(f"Epoch [{epoch+1}/{num_epochs}], Loss: {avg_loss:.4f}")
    
    # Export model to ONNX
    model.eval()
    dummy_input = torch.randn(1, input_channels, sequence_length)
    torch.onnx.export(
        model,
        dummy_input,
        inp_model_name,
        export_params=True,
        opset_version=11,
        do_constant_folding=True,
        input_names=['input'],
        output_names=['output'],
        dynamic_axes={'input': {0: 'batch_size'}, 'output': {0: 'batch_size'}}
    )
    print("\nModel exported to: ", inp_model_name)

    # Load and verify ONNX model
    try:
        onnx_model = onnx.load(inp_model_name)
        onnx.checker.check_model(onnx_model)
        print(f" ONNX model '{inp_model_name}' has been successfully exported and validated!")

        session = ort.InferenceSession(inp_model_name)

        for i in session.get_inputs():
            print(f" Input: {i.name}, Shape: {i.shape}, Type: {i.type}")

        for o in session.get_outputs():
            print(f" Output: {o.name}, Shape: {o.shape}, Type: {o.type}")

    except onnx.onnx_cpp2py_export.checker.ValidationError as e:
        print(f" ONNX model validation failed: {e}")
    except Exception as e:
        print(f" An error occurred: {e}")
        
    
    # Evaluate on a single sample
    with torch.no_grad():
        single_input = X_tensor[0:1]  # Shape: (1, 2, 50)
        scalar_output = model(single_input).squeeze()
        print(f"\nSingle sample input shape: {single_input.shape}")
        print(f"Single sample output shape: {scalar_output.shape}")
        print(f"Single sample output value: {scalar_output.item():.4f}")

これらのステップは重要です。なぜならハイパーパラメータは、学習効率、モデルのキャパシティ、収束速度を制御するからです。短いシーケンス長は入力を単純化し、一方で学習率は最適化の安定性に影響を与えます。バッチサイズはメモリ制約に応じて16〜64程度にするのが良い考えです。入力チャネルはすでに強調したようにデータの特徴量数と一致する必要があります。また、エポック数を増やしたり、学習率を0.0001〜0.001の範囲で調整することで収束を改善することも可能です。

次に、学習関数内でモデルのインスタンスを初期化します。ここではベースチャネル数128、レイヤー数16、ドロップアウト率0.03という設定でモデルをインスタンス化します。学習は典型的なCPU環境でおこなっており、GPUは使用していません。このネットワークアーキテクチャ構成は、シーケンス長1の入力を処理し、複雑さと正則化のバランスを取ります。

続いて損失関数とオプティマイザを定義します。ここでは二項分類のためにバイナリ交差エントロピー損失(BCELoss)を使い、指定した学習率でAdamオプティマイザを使用します。これは重要です。なぜならBCELossはモデルのシグモイド出力に適しているからです。Adamは適応的な学習率で効率的に動作します。BCELossは二値タスクに理想的であり、本ケースでは0から1の範囲の単一スカラー値を出力するため適合しています。ただし、収束が遅い場合はSGDや学習率スケジューラなど他の最適化手法を検討することも可能です。

次に学習ループです。これはエポックとバッチに渡って繰り返し処理し、モデルをトレーニングモードに設定します。予測を計算し、損失を算出し、逆伝播を行い、重みを更新します。その後、各エポックの平均損失を出力します。学習ループは損失を最小化することでモデルを最適化する中核的なロジックなので重要です。バッチ処理を使うことで効率が大きく向上します。実行時には損失値を監視し、収束速度を評価することが重要です。損失が停滞する場合には、エポック数やバッチサイズを調整する必要があります。また、勾配をリセットするためにzero_gradを必ず呼び出すことも大切です。

その後、検証とモデルのONNX形式へのエクスポートをおこないます。学習が完了したら、ダミー入力を用いてモデルをONNX形式に変換し、モデルを検証し、ONNXランタイムセッションを作成します。これは動的なバッチサイズをサポートします。ONNXへのエクスポートは、モデルをさまざまなプラットフォームに展開できるようにするために重要です。特にここで関心があるのはMQL5です。このステップではエクスポートの整合性も検証し、後でモデルを使用する際のエラーを回避します。エクスポート時には、opset-versionが対象プラットフォームに適合していることを確認することが重要です。現在のところMQL5ではバージョン12が問題なく動作します。検証エラーが出る場合には、モデルの互換性を確認する必要があります。

次に、学習済みモデルを評価またはテストするためのコードがあります。これは勾配計算をおこなわずに単一のシーケンスで評価を実行し、入力と出力の形状、そしてスカラー出力を出力します。これにより、学習済みの重みに基づいたモデルの機能や単一サンプルに対する出力形式が確認できます。デバッグにも役立ちますし、モデルの挙動を確認することもできます。使用時には入力形状が学習データと一致していることを確認することが重要です。また、出力が0から1の範囲に収まっているかも確認する必要があります。

まとめると、ネットワーククラスに付随するこれら2つの補助関数（create-sequences関数とtrain-and-evaluate関数）は、データを準備し、CosineConv1Dモデルを二項分類用に学習させるためのものです。これはコサイン変調アーキテクチャを用いて実行されます。重要なステップは、シーケンスの作成、ハイパーパラメータの調整、モデルの学習、ONNX形式へのエクスポート、そして評価です。これらをおこなう際には、シーケンス長、学習率、エポック数を調整して最適な性能を得ることが必要です。さらに、エクスポート前にONNXモデルを検証することも不可欠です。

MQL5での実装

これまでの記事では、インジケーターシグナルパターンの活用を機械学習で拡張することを考察しましたが、MQL5での実装については紙幅の都合でほとんど触れてきませんでした。今回の記事では、Pythonでの関数実装がやや繰り返し的になってきたこともあり、エクスポートしたONNXモデルをインポートして使用する際にMQL5側で考慮すべきいくつかの側面を取り上げたいと思います。 

ONNXモデルをインポートし、MQL5ウィザードを通じてEAに組み込まれるカスタムシグナルクラスでは、ロングとショートの条件が次のように形成されます。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalML_TRX_WPR::LongCondition(void)
{  int result  = 0, results = 0;
   vectorf _x;
   _x.Init(2);
   _x.Fill(0.0);
//--- if the model 1 is used
   if(((m_patterns_usage & 0x02) != 0) && IsPattern_1(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_1;
         results++;
      }
   }
//--- if the model 4 is used
   if(((m_patterns_usage & 0x10) != 0) && IsPattern_4(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_4;
         results++;
      }
   }
//--- if the model 5 is used
   if(((m_patterns_usage & 0x20) != 0) && IsPattern_5(POSITION_TYPE_BUY))
   {  _x[0] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_BUY, _x);
      if(_y > 0.0)
      {  result += m_pattern_5;
         results++;
      }
   }
//--- return the result
//if(result > 0)printf(__FUNCSIG__+" result is: %i",result);
   if(results > 0 && result > 0)
   {  return(int(round(result / results)));
   }
   return(0);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalML_TRX_WPR::ShortCondition(void)
{  int result  = 0, results = 0;
   vectorf _x;
   _x.Init(2);
   _x.Fill(0.0);
//--- if the model 1 is used
   if(((m_patterns_usage & 0x02) != 0) && IsPattern_1(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_1;
         results++;
      }
   }
//--- if the model 4 is used
   if(((m_patterns_usage & 0x10) != 0) && IsPattern_4(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_4;
         results++;
      }
   }
//--- if the model 5 is used
   if(((m_patterns_usage & 0x20) != 0) && IsPattern_5(POSITION_TYPE_SELL))
   {  _x[1] = 1.0f;
      double _y = RunModel(0, POSITION_TYPE_SELL, _x);
      if(_y < 0.0)
      {  result += m_pattern_5;
         results++;
      }
   }
//--- return the result
//if(result > 0)printf(__FUNCSIG__+" result is: %i",result);
   if(results > 0 && result > 0)
   {  return(int(round(result / results)));
   }
   return(0);
}

これら2つの関数から明らかなように、RunModel関数を頻繁に参照します。コードは次のとおりです。

//+------------------------------------------------------------------+
//| Forward Feed Network, to Get Forecast State.                     |
//+------------------------------------------------------------------+
double CSignalML_TRX_WPR::RunModel(int Index, ENUM_POSITION_TYPE T, vectorf &X)
{  vectorf _y(1);
   _y.Fill(0.0);
   ResetLastError();
   if(!OnnxRun(m_handles[Index], ONNX_NO_CONVERSION, X, _y))
   {  printf(__FUNCSIG__ + " failed to get y forecast, err: %i", GetLastError());
      return(double(_y[0]));
   }
   //printf(__FUNCSIG__ + " y: "+DoubleToString(_y[0],5));
   if(T == POSITION_TYPE_BUY && _y[0] > 0.5f)
   {  _y[0] = 2.0f * (_y[0] - 0.5f);
   }
   else if(T == POSITION_TYPE_SELL && _y[0] < 0.5f)
   {  _y[0] = 2.0f * (0.5f - _y[0]);
   }
   return(double(_y[0]));
}

このアンカークラスは、これらすべての関数に対して、MQL5 EAのシグナル処理用の基底クラスであるCExpertSignalを継承しています。これにより、ウィザードで組み立てられたEAで使用されるエコシステムやクラスファイルとの統合が可能になります。フォワードウォークが可能であったPattern_1、4、5それぞれに対して3つのモデルを学習させ、MQL5にインポートしてテストをおこなったところ、次のレポートが得られました。

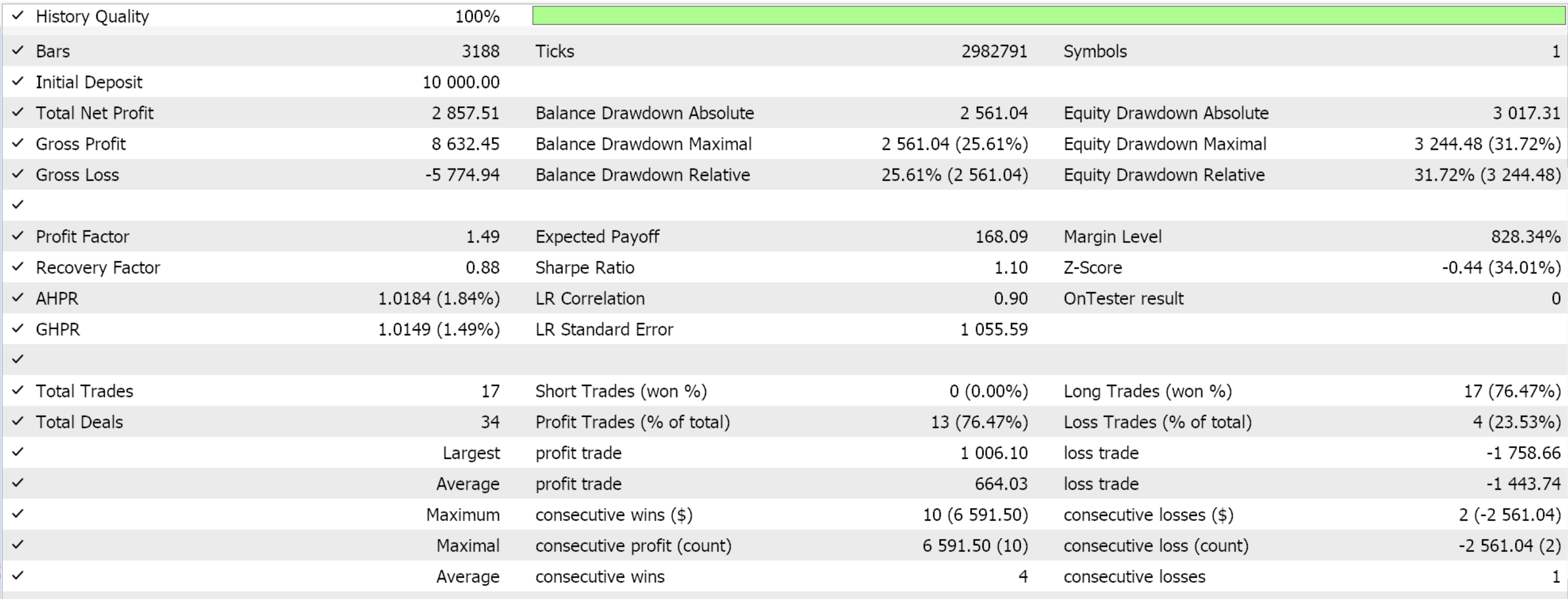
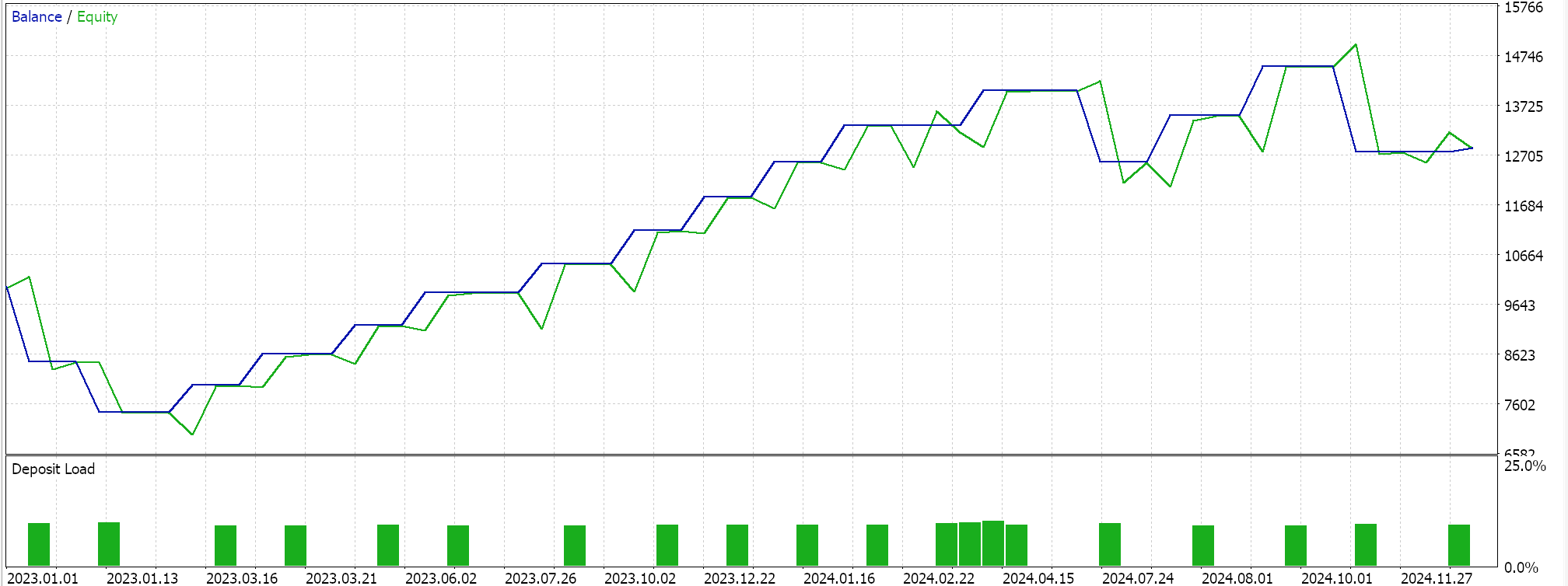
Pattern_1の場合

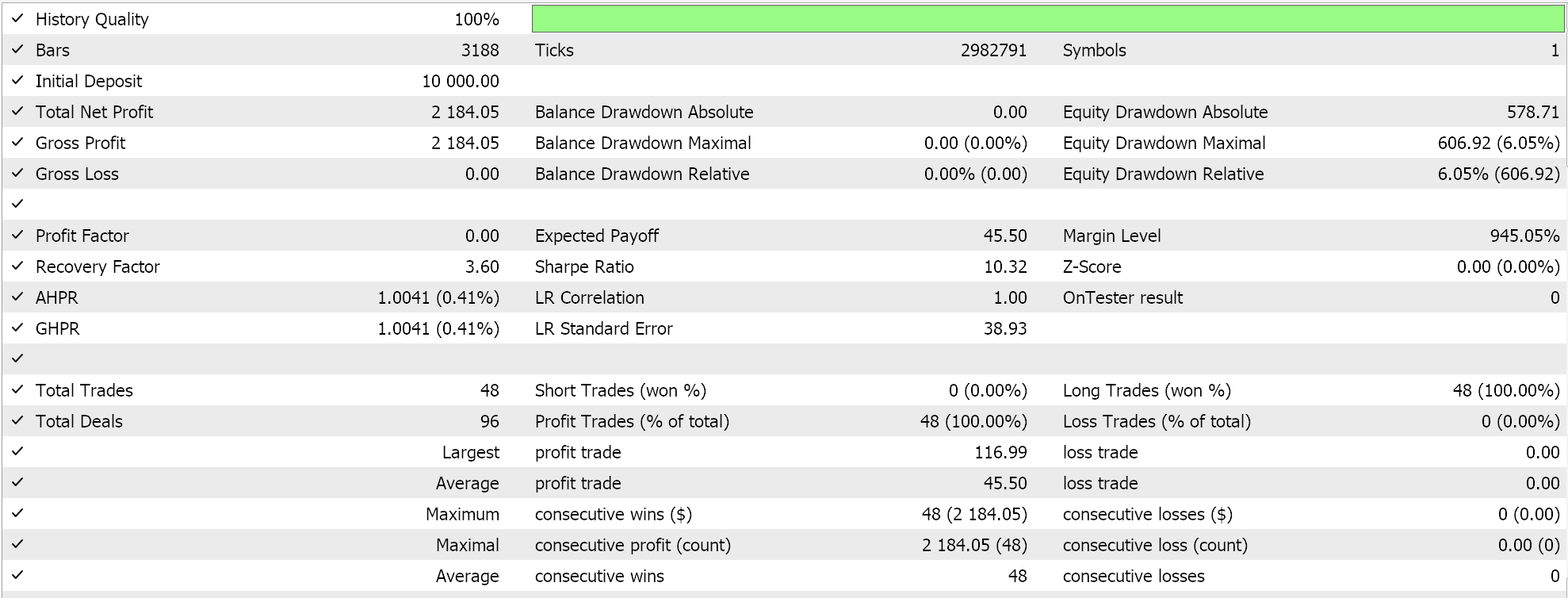
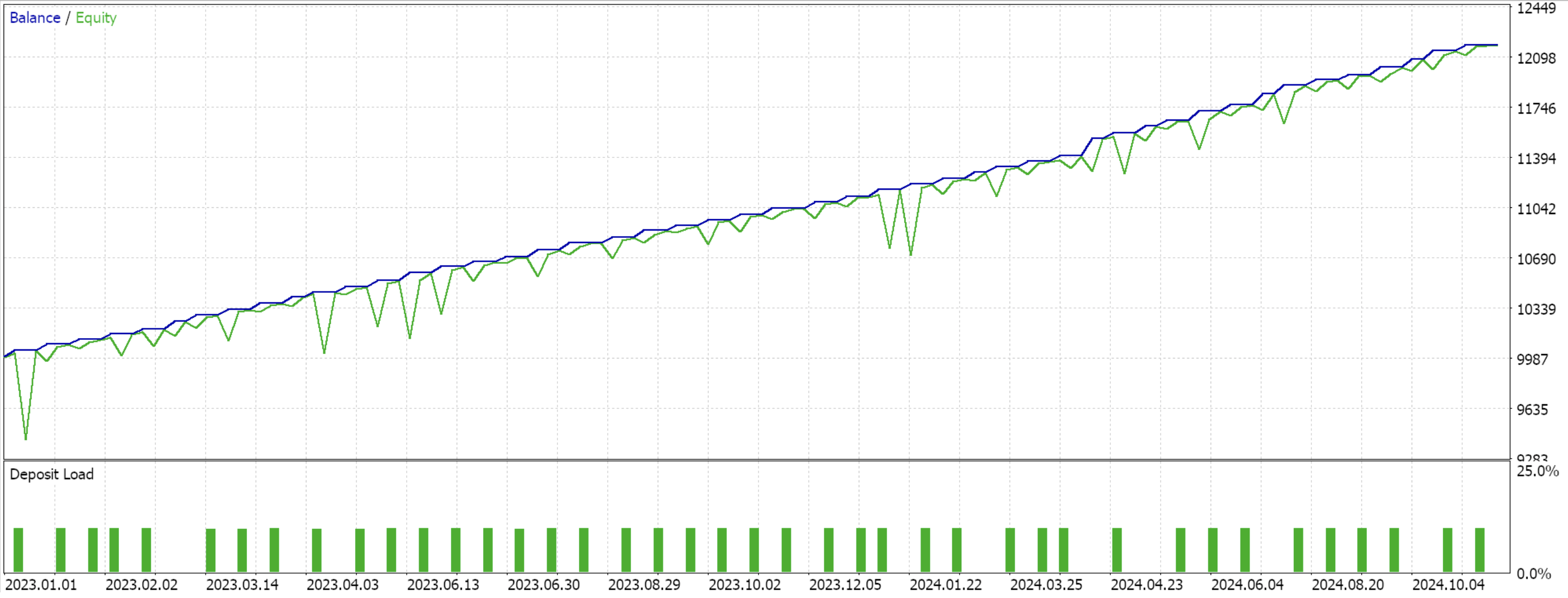
Pattern_4の場合

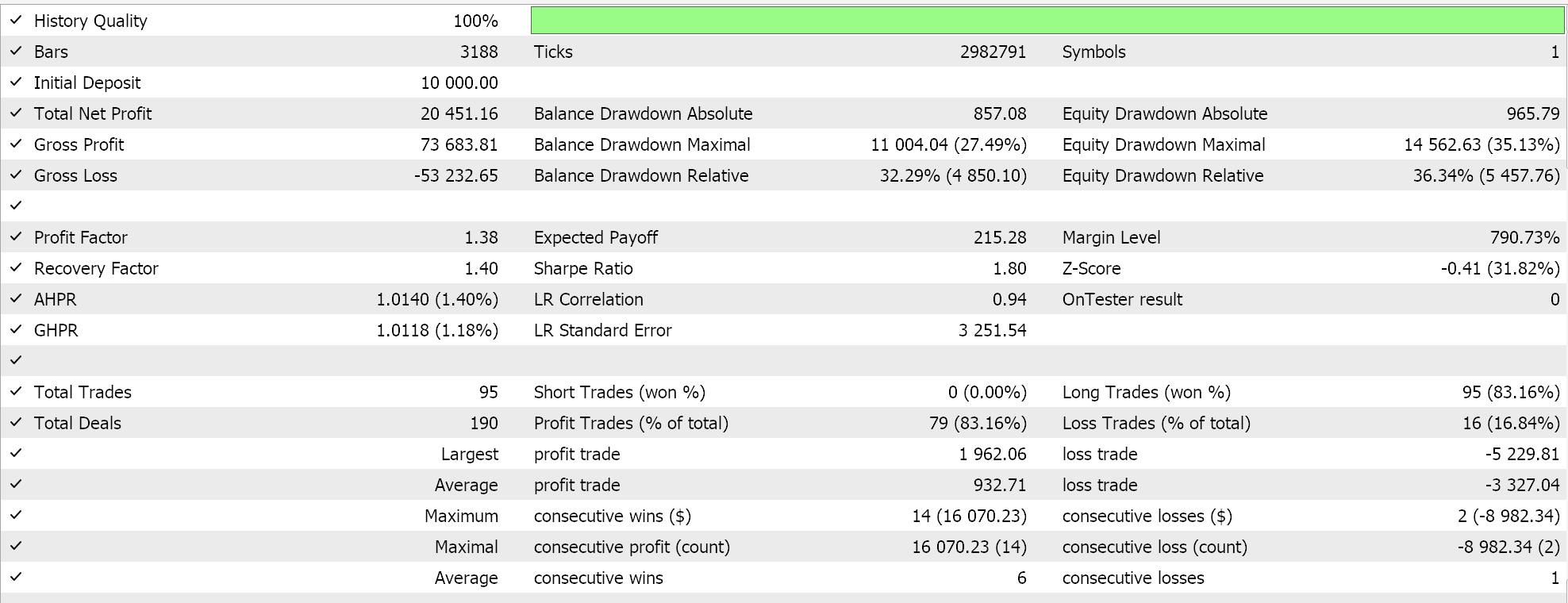
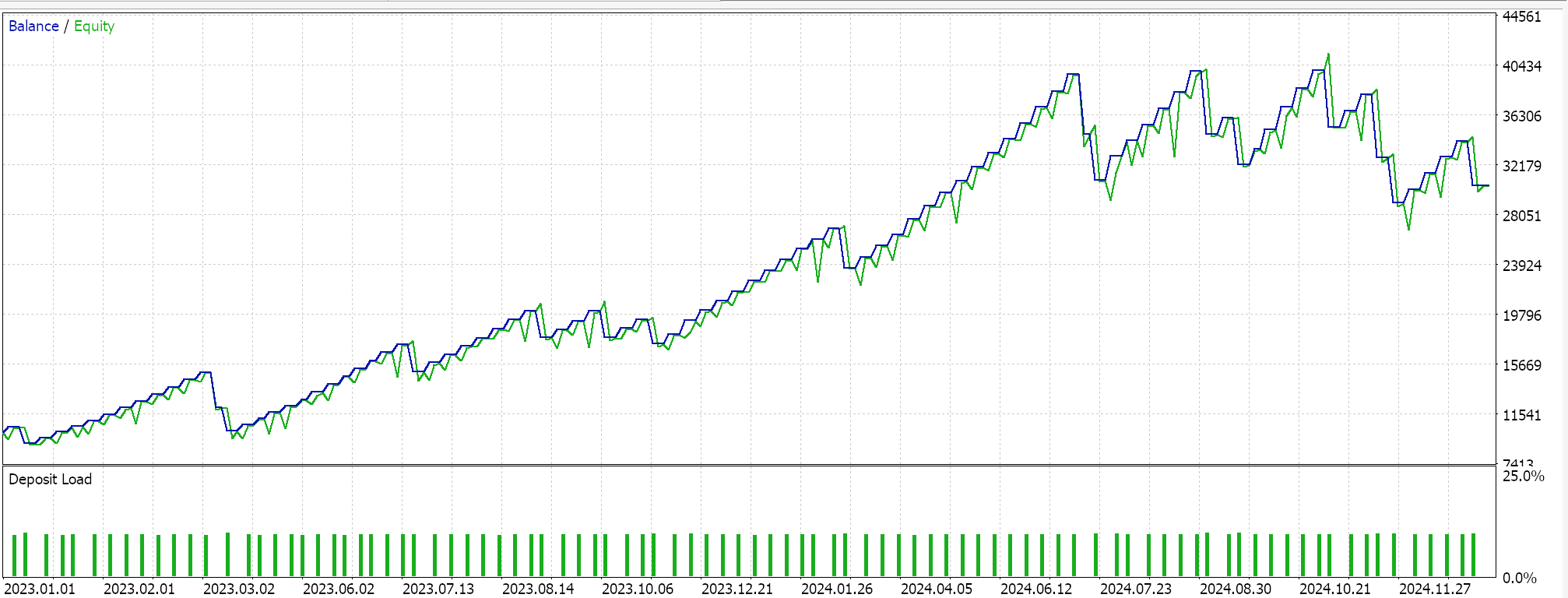
Pattern_5の場合

新しい読者向けに、こちらには入門ガイドがあり、付属のコードを用いてMQL5ウィザード経由でEAを組み立てる方法についての二次リンクもあります。私たちが作成したカスタムシグナルクラスは、MQL5ウィザードとの容易な統合を念頭に設計されており、異なるEA間で再利用可能です。ONNXモデルを用いてEAの予測能力を強化できるため、機械学習の統合が可能になりました。これには、堅牢な学習データセットが必要です。過学習を避けるためにはアウトオブサンプルでのモデル検証が重要であり、そのため展示目的では、データを50/50に分割し、1年間で学習、次の年でフォワードウォークをおこなっています。

テスト結果を見ると、Pattern_1、4、5のすべてがウォーク可能であったようですが、より「説得力がある」結果を示したのはPattern_4のみのようです。ただし、これらのテストには短期間のテストウィンドウ以外にも大きな制約があります。主な注意点としては、オープンポジションにはストップロスが設定されず、テイクプロフィットのみがある環境でテストがおこなわれたことです。また、エントリーに指値注文を使用しているため、結果が実際よりも有利に見える傾向があります。これらの点は、読者が添付のソースコードをさらに開発するかどうかを判断する際に留意すべき事項です。

結論

三重指数移動平均オシレーター(TRIX)のシグナルとウィリアムズ％レンジ(WPR)オシレーターのシグナルを組み合わせ、機械学習モデルで処理して予測をおこなう方法を見てきました。考慮したパターンはすでにフォワードウォーク可能であったため、我々の機械学習モデルは本質的に、テスト年にフォワードウォークできることがわかっている取引に対するフィルターとして機能しました。パフォーマンスはわずかに改善されましたが、今後の記事では、フォワードウォークできなかったパターンを用いたMLによるテストも検討していきます。

名前	説明
wz-68.mq5	ヘッダにインクルードファイルを示すウィザード組み立てEA
SignalWZ_68.mqh	ウィザードアセンブリで使用されるカスタムシグナルクラスファイル
68_1.mqh	エクスポートされたPattern_1用のONNXモデル
68_4.mqh	エクスポートされたPattern_4用のONNXモデル
68_5.mqh	エクスポートされたPattern_5用のONNXモデル