知っておくべきMQL5ウィザードのテクニック（第33回）：ガウス過程カーネル

はじめに

ガウス過程カーネルは、時系列などのデータポイント間の関係を測定するためにガウス過程で使用される共分散関数です。このカーネルはデータ内の関係性を捉える行列を生成し、データが正規分布に従うと仮定することで、ガウス過程による予測や推定を可能にします。本連載では、新しいアイデアを探求し、その活用方法を模索しており、今回はガウス過程(GP)カーネルを用いたカスタムシグナルの構築に焦点を当てています。

これまで5回にわたり機械学習に関連する記事を多く取り上げてきたため、今回は少し視点を変え、古典的な統計学に立ち返ってみましょう。システム開発においては機械学習と統計学が組み合わさることが多いですが、今回のカスタムシグナル開発では、機械学習アルゴリズムを直接取り入れることはありません。GPカーネルの特筆すべき点は、その柔軟性にあります。

GPカーネルは、周期性、トレンド、非線形な関係といったさまざまなデータパターンをモデル化するのに適しており、単に単一の予測値を提供するだけでなく、希望値に加え、上限値や下限値を含む不確かさの推定値も提供します。これらの推定値はしばしば信頼区間とともに示され、予測値に基づくトレーダーの意思決定プロセスをより明確にサポートします。また、異なる信頼度で示された複数の予測バンドを比較する際にも役立ち、取引対象の証券についての洞察を深めることができます。

さらに、K行列にノイズ値を加えることができるため（後述）、ノイズの多いデータに対しても適応力が高く、事前知識を組み込むことも可能で、非常にスケーラブルです。カーネルの種類は多岐にわたり、例えば二乗指数カーネル（RBF）、線形カーネル、周期カーネル、有理二次カーネル、Maternカーネル、指数カーネル、多項式カーネル、ホワイトノイズカーネル、ドット積カーネル、スペクトル混合カーネル、定数カーネル、コサインカーネル、ニューラルネットワーク（アークコサイン）カーネル、積和カーネルなどがあります。

この記事では、RBFカーネル（別名Radial Basis Functionカーネル、放射基底カーネル）について説明します。多くのカーネルと同様に、RBFカーネルは2つのデータポイント間の類似性を測定します。これは、2点間の距離に基づいており、距離が遠いほど類似性が低く、近いほど高いという基本的な仮定に基づいています。RBFカーネルの挙動は、以下の式に従います。

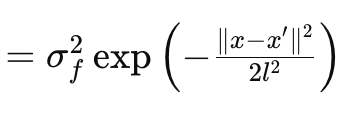
ここで

• xとx′：入力ベクトル、または入力空間内の点
• σ f ²：カーネルの分散パラメータで、あらかじめ決定された、あるいは最適化可能なパラメータとして機能します。
• l：しばしば長さスケールパラメータと呼ばれ、結果となる関数の滑らかさを制御します。lが小さい（つまりスケールが短い）と関数は急激に変化し、l が大きい（つまりスケールが長い）と関数はより滑らかになります。
• exp： 指数関数

このカーネルはMQL5で次のように簡単にコーディングできます。

//+------------------------------------------------------------------+
// RBF Kernel Function
//+------------------------------------------------------------------+
matrix CSignalGauss::RBF_Kernel(vector &Rows, vector &Cols)
{  matrix _rbf;
   _rbf.Init(Rows.Size(), Cols.Size());
   for(int i = 0; i < int(Rows.Size()); i++)
   {  for(int ii = 0; ii < int(Cols.Size()); ii++)
      {  _rbf[i][ii] = m_variance * exp(-0.5 * pow(Rows[i] - Cols[ii], 2.0) / pow(m_next, 2.0));
      }
   }
   return(_rbf);
}

金融時系列におけるガウス過程

ガウス過程(GP)は確率的な枠組みであり、予測は固定された値ではなく、分布の観点からおこなわれます。そのため、ノンパラメトリックフレームワークとも呼ばれています。出力予測には、平均予測値と、その予測値を取り囲む分散（または不確実性）が含まれます。GPの分散は、予測の不確実性や信頼性を示しており、GPが正規分布に基づいていることから、理論上はランダムであると考えられます。しかし、これは区間と信頼度（通常95%）を意味するため、すべての予測がその範囲内に収まるわけではありません。ARIMAなどの他の統計的予測手法と比較すると、GPは非常に柔軟で、不確実性を定量化しながら複雑な非線形関係をモデル化することができます。一方、ARIMAは特定の構造を持つ定常時系列データにおいて最も効果的に機能します。GPの主な欠点は、計算コストが高い点にあり、ARIMAのような手法はその点で優れています。

RBFカーネル

GPカーネルの計算には、主に6つの行列と2つのベクトルが含まれます。これらの行列とベクトルはすべてGetOutput関数で使われます。下記はコードの概要です。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalGauss::GetOutput(double BasisMean, vector &Output)
{  
   ...

   matrix _k = RBF_Kernel(_past_time, _past_time);
   matrix _noise;
   _noise.Init(_k.Rows(), _k.Cols());
   _noise.Fill(fabs(0.05 * _k.Min()));
   _k += _noise;
   matrix _norm;
   _norm.Init(_k.Rows(), _k.Cols());
   _norm.Identity();
   _norm *= 0.0005;
   _k += _norm;
   vector _next_time;
   _next_time.Init(m_next);
   for(int i = 0; i < m_next; i++)
   {  _next_time[i] = _past_time[_past_time.Size() - 1] + i + 1;
   }
   matrix _k_s = RBF_Kernel(_next_time, _past_time);
   matrix _k_ss = RBF_Kernel(_next_time, _next_time);
// Compute K^-1 * y
   matrix _k_inv = _k.Inv();
   if(_k_inv.Rows() > 0 && _k_inv.Cols() > 0)
   {  vector _alpha = _k_inv.MatMul(_past);
      // Compute mean predictions: mu_* = K_s * alpha
      vector _mu_star = _k_s.MatMul(_alpha);
      vector _mean;
      _mean.Init(_mu_star.Size());
      _mean.Fill(BasisMean);
      _mu_star += _mean;
   // Compute covariance: Sigma_* = K_ss - K_s * K_inv * K_s^T
      matrix _v = _k_s.MatMul(_k_inv);
      matrix _sigma_star = _k_ss - (_v.MatMul(_k_s.Transpose()));
      vector _variances = _sigma_star.Diag();
      //Print(" sigma star: ",_sigma_star);
      Print(" pre variances: ",_variances);
      Output = _mu_star;
      SetOutput(Output);
      SetOutput(_variances);
      Print(" variances: ",_variances);
   }
}

箇条書きにすると、以下のようになります。

• _k
• _k_s
• _k_ss
• _k_inv
• _v
• _sigma_star

_kはアンカーとメインの共分散行列であり、使用するカーネル関数に基づいて、2つの入力ベクトル間の関係を捉える役割を果たします。ここではRBF（Radial Basis Function）カーネルを使用しており、そのソースは前述の通りです。時系列データの予測をおこなう場合、RBFカーネルへの入力として使用するのは、予測対象のデータ系列に対応する2つの時間ベクトルです。これらのベクトルは、時点間の類似性を符号化し、データの全体的な構造を決定するための基礎となります。前述の14種類のカーネル形式からも分かるように、多様なカーネルが存在し、今後の記事ではこれらの代替カーネルをカスタムシグナルクラスで検討していく予定です。

このプロセスを通じて、共分散行列_k_sにたどり着きます。この行列は、_k 行列と同様にRBFカーネルを通して生成され、次の時間インデックスへの橋渡しとして機能します。これらの時間インデックスの長さや数は、投影されるデータの数を決定し、length-scale入力パラメータによって定義されます。カスタムシグナルクラスでは、このパラメータをm_nextと呼んでいます。過去のインデックスと次回のインデックスをつなぐことで、_k_sは既知のデータと次に予測する未知のデータとの関係を予測でき、予測精度の向上に貢献します。この特殊な行列は投影の影響を非常に受けやすいため、その精度は極めて重要ですが、私たちのコードとRBFカーネルはこの処理をシームレスにおこなっています。それでも、分散と長さスケールという2つの調整可能なパラメータは、投影の精度を最大化するために細心の注意を払って調整する必要があります。

この行列は次のように定義できます。

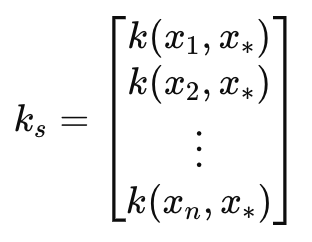
ここで

• k(x i , y i )：インデックスiにおけるベクトルxとyの2つの値の間の放射基底関数。この場合、xとyは同じ入力時間ベクトルであるため、どちらのベクトルもxとラベル付けされます。通常、xは学習データであり、yはテストデータのプレースホルダーです。
• k s：訓練データとテスト点x＊の間の共分散ベクトル（偶数長スケールまたは投影数が1を超える場合は行列）
• x 1 , x 2 ,..., xn：入力訓練データ点
• x∗：予測をおこなう入力テストデータ点

これにより、本質的には_k行列の鏡像である_k_ss行列が得られます。主な違いは、k_ssが予測時間インデックスの共分散行列である点です。そのため、この行列の次元は、長さスケールに対応する入力パラメータと一致します。k_ssは、予測の不確実性推定部分を計算する際に重要な役割を果たします。具体的には、データが組み込まれる前の予測時間インデックスにおける分散を測定するために使用されます。これを数式で表すとこうなります。

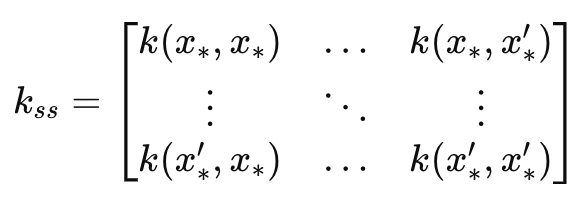
ここで

• k ss：テストデータ点の共分散行列
• x∗, x∗ ′：予測をおこなう入力テストデータ点
• k(x∗,x∗′)：テスト点𝑥∗と𝑥∗′のペアに適用されるカーネル関数

k_inv行列は、その名の通りk行列の逆行列です。逆行列の計算は組み込みの関数で処理されますが、場合によっては逆行列を求められないこともあります。そのため、このコードでは、逆行列の計算が正しくおこなわれたかどうかを確認するために、行や列が存在するかどうかを確認しています。もし行や列が1つも存在しない場合、逆行列の計算が失敗したことを意味します。逆行列の計算は、予測時に訓練データに適用される重み付けを計算する上で重要なステップです。例えば、コレスキー分解のような逆行列の計算に使える別の方法も考えられますが（これは組み込みではないアプローチを前提としている）、その実装は読者の判断に委ねられます。

重みベクトルは、訓練の出力を共分散構造に基づいて結合するために使用されます。_alpha(α)は、新しいデータ点がテスト点や長さスケールの点に対して予測にどの程度影響を与えるかを決定する重要なパラメータです。αは、逆行列 k と古いデータを基にした行列積から得られます。この時点で、目的の_mu_starベクトルが明確に見えてきます。これは、カスタムシグナルクラスの入力パラメータ m_pastに基づき、過去のデータに対して長さスケールの期間における予測を記録するものです。予測される平均値の数は、クラスで m_nextと呼ばれる長さスケールによって決定されます。なお、MQL5 のベクトルはシリーズとして並び替えられないため（コピーしてレートを処理する場合）、この予測ベクトルの最高インデックスは最後に発生する値であり、ゼロインデックスは直近に発生することが想定されます。このことは、次に発生する値の推定だけでなく、長さスケールのパラメータに応じて、その後に続くトレンドも予測できることを示しています。これらの予測値は「テストポイント」とも呼ばれます。

指標となる平均値を得た後、GPでは、_sigma_star行列を使用して、これらの予測値に対する不確実性の範囲も提供します。この行列は、将来の異なる時点やテストポイント間の予測に関連する共分散を表します。各テストポイントに対して1つの予測がおこなわれるため、関心があるのは、この行列の対角部分にあたる値のみです。予測間の共分散自体には関心がありません。この行列は以下の式で表されます。

ここで

• k ss：新しいデータ点の共分散行列（上記_k_ss）
• k s：新しいデータ点と学習データの間の共分散行列（上記_k_s）
• K：訓練データの共分散行列で、最初に定義した行列

上の式から、_v行列は_k_s とK^-1の積として示されます。この場合、私たちは95%の信頼度でテストをおこなっているため、正規分布表を基に、各テストポイントの上限値は予測平均にσ_star行列の分散値の1.96倍を加えたものとなります。逆に、下限値は予測平均から_sigma_star 行列の分散値の1.96倍を引いた値です。この分散は、予測の信頼性を定量化するのに役立ち、値が大きいほど不確実性が高いことを示します。つまり、（上限値から下限値までの）信頼範囲が広ければ広いほど、予測に対する自信度は低くなるということです。

ここで重要なのは、GPカーネルの計算には逆行列の計算が含まれており、すでに述べたように、計算誤差や NaNを最小化するために、コレスキー分解のようなアプローチを使用することも検討できます。さらに、GPカーネル過程の初期段階で_k行行列に対して一般的に行われる正規化手法として、対角要素に小さな非ゼロ値を追加することが挙げられます。これにより、_sigma_star行列で負の値が発生するのを防ぎます。この行列は標準偏差の二乗、つまり分散を示すため、すべての値が正であるべきです。この小さな足し算を省略すると、負の値が現れる可能性があるため、重要なステップといえます。上記のGetOutput関数のコードにも示されています。

このプロセスにより、私たちの予測は、単なる数値予測に留まらず、その予測に対する自信度も示してくれます。今回のテストでは、_sigma_star行列が示す信頼度は考慮せず、生の予測結果のみを評価していますが、これはGPカーネルの潜在能力を十分に活かしきれていないともいえます。では、カスタムシグナルに予測の信頼性をどのように組み込むかという問題が残ります。これを実現するための方法は複数ありますが、まずはポジションサイジングの基準として信頼度を使用するのが手っ取り早いアプローチです。これは通常、カスタムシグナルクラスの外で実装されますが、効果的です。

この方法をさらに発展させるためには、カスタムシグナルクラスにGPカーネルを使用するだけでなく、カスタムマネーマネジメントクラスにもGPカーネルを導入することが考えられます。この場合、シグナルクラスとマネーマネジメントクラスの両方が、同じデータセット、共分散、そして長さスケールのパラメータを共有する必要があります。カスタムシグナルクラス内でこれを実装するためには、まず_sigma_star行列の対角要素をコピーし、分散ベクトルを作成してから、それをSetOutput関数で正規化し、最も低い値を持つインデックスを特定します。このインデックスを_mu_starベクトルで使用し、カスタムシグナルの条件を決定します。なお、mu_starも同様に正規化され、0.5未満の値は弱気なシグナルを、0.5以上の値は強気なシグナルを示します。

カスタムシグナルクラス内で定量化された不確実性を活用するもう1つの方法は、すべてのテストポイントにわたる予測の加重平均を取る際に、正規化された分散値を逆重みとして使用することです。つまり、分散値を1から引くか反転させ、分母には小さな値を加えながら計算します。前述したように、分散が大きいほど不確実性が高いことを意味するため、この逆転が重要になります。不確実性を活用したこのアプローチは、ここで言及されているだけであり、コードやテスト実行にはまだ実装されていません。読者の皆さんがこの方法を自分でテストしてみることで、さらに次のステップへ進むことができるでしょう。

データの前処理と正規化

GPカーネルは、さまざまな金融時系列データに適用可能です。一般的には、このデータは絶対価格のような絶対的な形式で表される場合もあれば、価格変動のような増分形式で表されることもあります。今回の記事では、後者の形式でGPカーネルRBFをテストします。そのため、まず_pastベクトルを、異なる時点における終値をコピーした2つのベクトルの差で埋めます（これは、上記のGetOutputのコードに記載されている通りです）。

さらに、この価格変動データを変換し、-1.0から+1.0の範囲に正規化することも可能です。データの事後正規化には、SetOutput関数やその他のカスタムメソッドを使用することができますが、今回のテストでは、生データの価格変動（floatまたはdouble形式）をそのまま使用し、予測値に対してのみ正規化を適用しています。この正規化は、SetOutput関数で実行されます。以下がコードです。

//+------------------------------------------------------------------+
//|
//+------------------------------------------------------------------+
void CSignalGauss::SetOutput(vector &Output)
{  vector _copy;
   _copy.Copy(Output);
   if(Output.HasNan() == 0 && _copy.Max() - _copy.Min() > 0.0)
   {  for (int i = 0; i < int(Output.Size()); i++)
      {  if(_copy[i] >= 0.0)
         {  Output[i] = 0.5 + (0.5 * ((_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min())));
         }
         else if(_copy[i] < 0.0)
         {  Output[i] = (0.5 * ((_copy[i] - _copy.Min()) / (_copy.Max() - _copy.Min())));
         }
      }
   }
   else
   {  Output.Fill(0.5);
   }
}

この正規化は、本連載の以前の記事でも使用されており、今回行っているのは、投影ベクトル値を0.0から+1.0の範囲に再スケーリングすることだけです。ここでの重要なポイントは、値が0.5未満の場合は正規化前のシリーズで負となり、0.5以上の場合は正となることです。

テストと評価

GPカーネルRBFによるテストでは、2023年の日足時間枠でEURUSDペアを対象にしています。よくあることですが（常にそうとは限りません）、これらの設定は非常に短い最適化作業から得られたものであり、フォワードウォークによる検証はおこなわれていません。私たちのウィザードが組み立てたエキスパートアドバイザー(EA)を実際の市場環境に適用するには、より多くの履歴データとフォワードウォーク（交差検証）による広範なテストを確実に実施するために、読者自身が注意を払う必要があります。結果は以下の通りです。

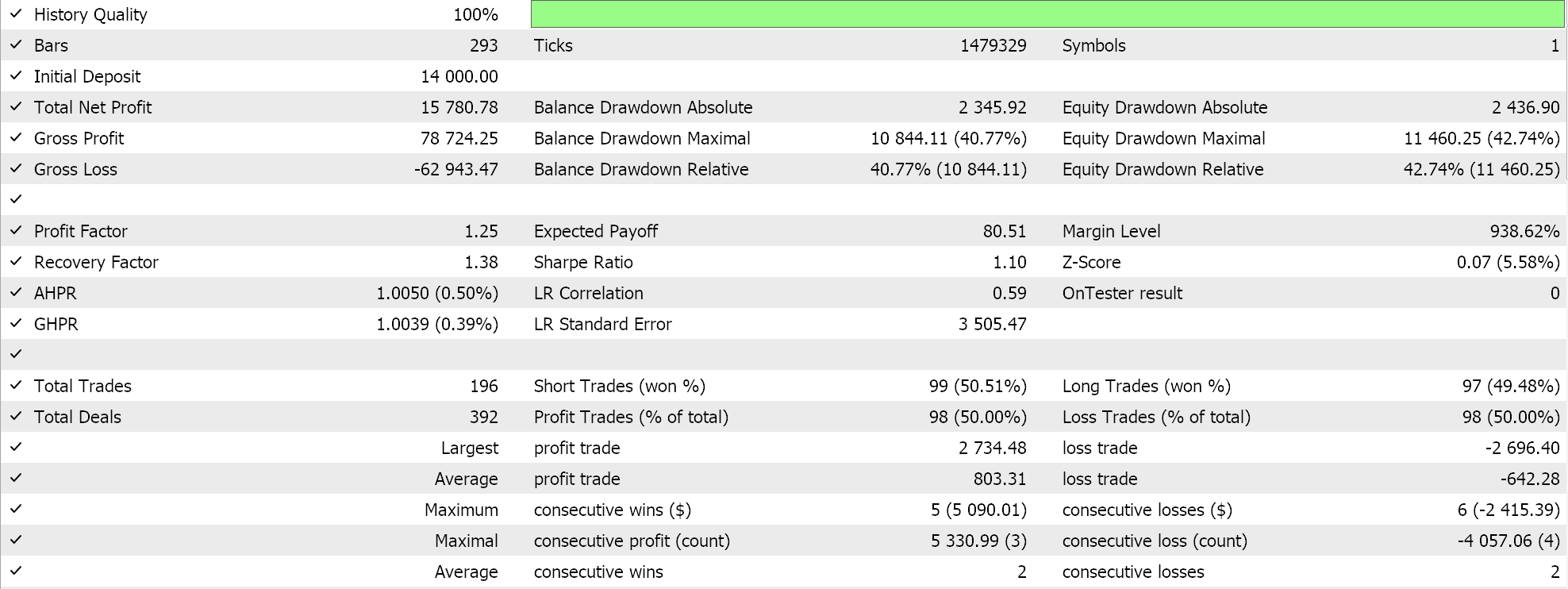
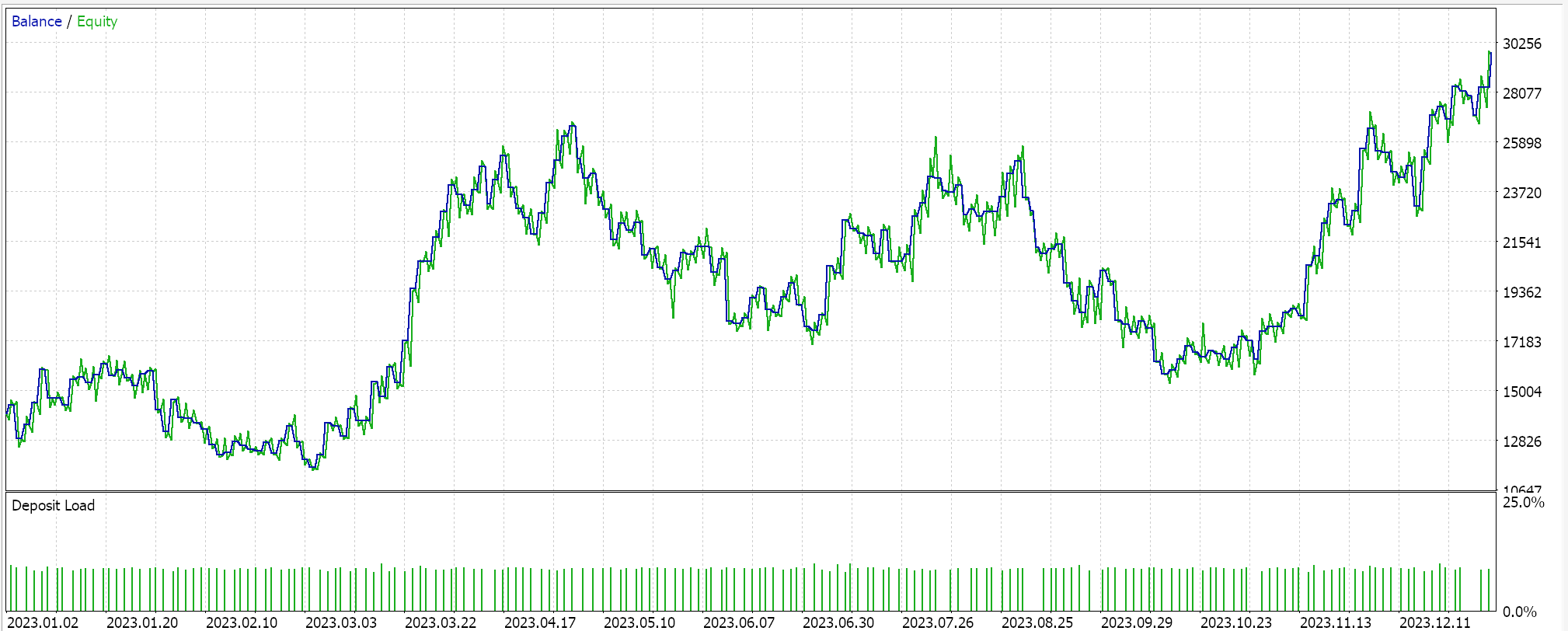
結論

ガウス過程カーネルを取引システムへの潜在的なシグナルとして考察してきました。「ガウス分布」はしばしばランダム性や、システムがその環境をランダムであると仮定していることを示唆し、その結果、50対50の確率に賭けていることになります。しかし、その支持者たちは、提供されたデータサンプルを用いて、確率論的な枠組みの中であらかじめ定義された期間にわたって予測を行うことを主張しています。この手法は、調査されたデータの性質を仮定しない（つまり、ノンパラメトリックである）ため、より柔軟性が高いとされます。唯一の包括的な仮定は、データがガウス分布に従うということです。したがって、不確実性がプロセスと結果に組み込まれる理由は、プロセスが単なるランダム性に依存しないと主張されています。

さらに、ガウス過程カーネルのコーディングとテストにおいては、他の予測手法とは異なる不確実性の定量化がおこなわれていません。しかし、正規分布の使用とその依存性は、ガウス過程カーネルが単独で使用されるべきなのか、あるいは別のシグナルと組み合わせた方が最適なのかという疑問を引き起こします。MQL5ウィザード（新しい読者はこちらおよび こちらのガイダンスを参照できます）は、選択した各シグナルを適切な重み付けで最適化できるため、1つのEAで複数のシグナルを簡単にテストできます。これらのカーネルと組み合わせる価値のある代替シグナルには何が考えられるでしょうか。この質問に対する最良の答えは、読者自身が試行錯誤を通じて見出すしかありませんが、私が提案するのは、RSIのようなオシレーターやストキャスティックオシレーター、オンバランスボリューム、さらにはいくつかのニュースセンチメント指標です。さらに、単純移動平均や移動平均クロスオーバー、プライスチャネル、および一般的に大幅なラグを持つ指標は、ガウス過程カーネルと組み合わせると効果的でないことがあります。

ここでは放射基底関数という1種類のカーネルのみを検証しましたが、今後は他の形式についても設定を変えて検証する予定です。