とても良い作品だ!
あっという間に読んでしまった。
ありがとう!
この記事は信用できる。)
この論文は複雑で矛盾している。一方では、著者は確率論的な用語や統計的な道具を使い、価格の上昇とボラティリティを確率変数として特徴づけ、さまざまなボラティリティ尺度の分布を構築するなどしているが、他方ではボラティリティの確率モデルを好まない。
一方で著者は、ボラティリティ系列における相関はデータの非定常性に起因する統計的な人工物であると考え、他方で、時間の滑らかな決定論的関数を用いてボラティリティを予測することは将来の問題であると考えている。
Evgeniy Chernish #:
この記事は複雑で矛盾している。一方では、著者は確率論的な用語、統計的な道具を使い、価格上昇とボラティリティを確率変数として特徴づけ、さまざまなボラティリティ尺度の分布を構築するなどしているが、他方では確率的なボラティリティ・モデルを好まない。
彼の論文からは矛盾も感じられる。市場のセッション制の性質上、日中の変動については彼の仮説が正しいのは明らかだが、日中の変動について彼の仮説が現実的に役に立つかどうかはわからない。
この記事は複雑で矛盾している。一方では、著者は確率論的な用語、統計的な道具を使い、価格上昇とボラティリティを確率変数として特徴づけ、さまざまなボラティリティ尺度の分布を構築するなどしているが、他方では確率的なボラティリティ・モデルを好まない。
一方では、ボラティリティ系列における相関はデータの非定常性に起因する統計的な人工物であると考え、他方では、時間の滑らかな決定論的関数を用いてボラティリティを予測することは将来の問題であると考えている。
神の 助けを借りてLLM DeepSeekを作りました。自分のデータで代用できます。
説明
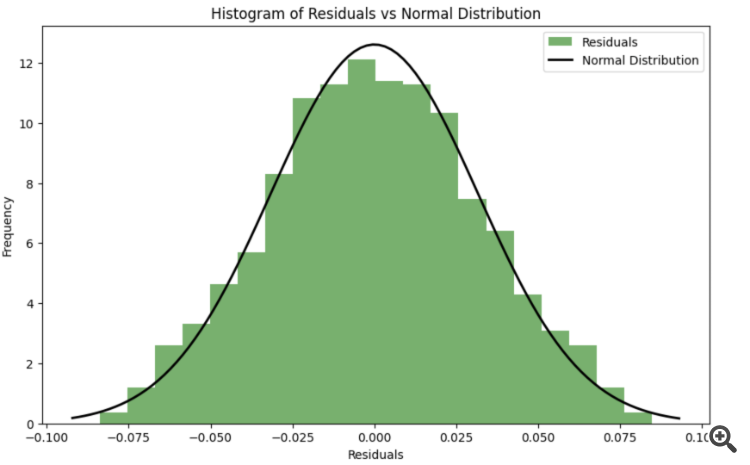
最適化の過程で残差をできるだけ正規分布に近づけるために、一致の基準(Shapiro-Wilk 基準やKolmogorov-Smirnov 基準など)を使って残差の正規性を評価することができます。そして,残差の正規分布からの偏差が最小になる ように , パラメータ k k および s sを最適化できる.
-
残差の正規性を考慮した誤差関数:残差を計算し,その正規性を評価するためにShapiro-Wilk 基準を使用する新しい 関数 spline_error_with_normality が導入された.負のp値が最小化され,残差の正規性が最大化される.
-
最適化:新しい誤差 関数に基づいて パラメータ k k および s s を最適化する ために 使用される 。
このアプローチでは、残差が正規分布を最大化するようにスプライン・パラメータを調整することができ、モデルの品質と結果の解釈可能性を向上させることができる。
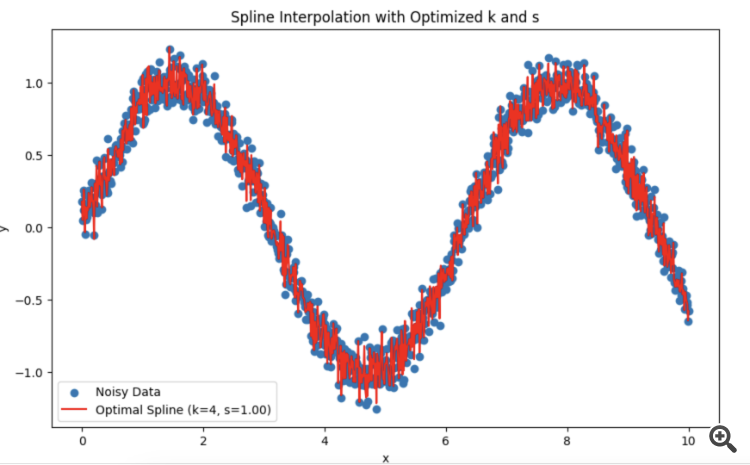
スプラインは新しいデータでは機能しないので、HPや他のフィルターでやり直すことが可能である。特定のモデルを構築したいという要望がある場合。
取引の機会を逃しています。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
新しい記事「ボラティリティを予測するための計量経済学ツール:GARCHモデル」はパブリッシュされました:
この記事では、条件付き異分散性(GARCH)という非線形モデルの特性について説明します。また、このモデルを基に、一歩先のボラティリティを予測するためのiGARCHインジケーターを構築しました。モデルのパラメータ推定には、ALGLIB数値解析ライブラリを使用しています。
ボラティリティは、金融資産の価格変動性を評価するための重要な指標です。価格変動の分析において、大きな値動きはさらなる大きな変動を引き起こしやすいことが、特に金融危機時に顕著に見られます。逆に、小さな変動はその後も小さい変動が続く傾向にあります。このように、相場が落ち着いている期間の後には、不安定な期間が訪れることが一般的です。
この現象を説明しようとした最初のモデルがEngleによって開発されたARCH(自己回帰条件付き異分散性)モデルです。このモデルは、リターンのクラスタリング効果(大きな値と小さな値がまとまって発生する特性)を説明するだけでなく、価格変動の分布に見られる厚い裾(ファットテール)や正の尖度(クルトシス)の発生要因を解明しました。 ARCH条件付きガウスモデルの成功により、さらに多くの一般化モデルが開発されました。それらの目的は、金融時系列データの分析において観察されるさまざまな現象を説明することでした。こうした一般化モデルの中で、最も初期に登場したものの一つが、GARCH(Generalized ARCH:一般化ARCH)モデルです。
GARCHモデルの最大の利点は、ARCHモデルに比べてよりコンパクトであり、サンプルデータに適合させる際に長いラグ構造を必要としないことです。本記事では、GARCHモデルについて説明し、さらに本モデルを活用したボラティリティ予測ツールを紹介します。特に、財務データ分析における主要な目的の一つである「予測」に焦点を当てます。
作者: Evgeniy Chernish