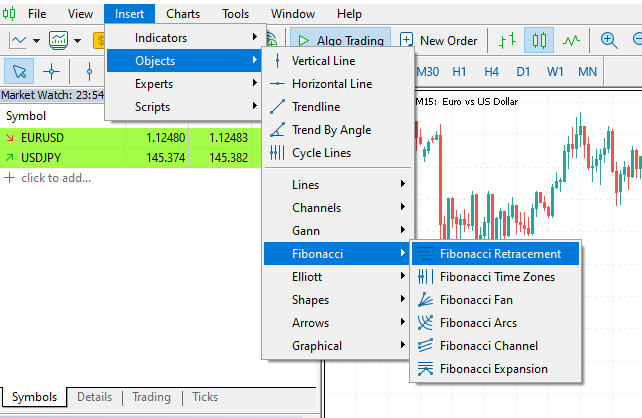
データサイエンスとML（第40回）：機械学習データにおけるフィボナッチリトレースメントの利用

MetaTrader 5 — エキスパートアドバイザー | YYYY年09月DD日, 07:02

Omega J Msigwa

内容

フィボナッチ数の起源

フィボナッチ数は、中世の数学者レオナルド・ピサ（通称フィボナッチ）にまでさかのぼります。

1202年に出版された彼の著書『算盤の書(Liber Abaci)』において、現在フィボナッチ数列として知られる数列が紹介されました。この数列は0と1から始まり、その後の各数は直前の2つの数の合計として算出されます。

この数列は非常に強力で、植物や動物の成長パターンなど、多くの自然現象に現れます。

生物学的には、完全一致ではないものの、一部の動物や昆虫の殻に見られる対数螺旋がフィボナッチ数に近似しています。

また、兎の個体数の増加や蜜蜂の家系図など、フィボナッチ的な成長パターンが見られるケースもあります。

さらに、哺乳類や人間のDNA構造の中にもフィボナッチ数のパターンが見られることがあります。

画像出典：unsplash.com

フィボナッチ数は極めて普遍的で、自然界や人工物の至る所で観察されます。以下は、フィボナッチ数を扱う際に頻繁に出てくる用語です。

フィボナッチ数列

数学において、フィボナッチ数列とは「各要素が直前の2つの要素の合計で表される数列」を指します。この数列に含まれる数をフィボナッチ数と呼びます。

フィボナッチ数列、黄金長方形

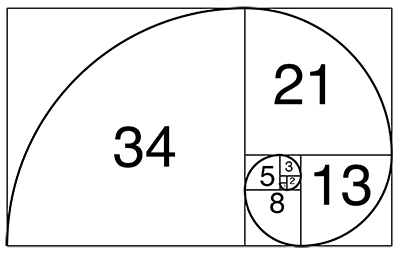
フィボナッチ数列は次の式で表されます

ここで、nは1より大きくなります(n>1)。

黄金比

黄金比は2つの量の関係を示す数学的概念であり、「小さい方の量と大きい方の量の比率」が「大きい方の量と両方の合計の比率」と等しくなる関係を指します。

黄金比はおおよそ1.6180339887で、ギリシャ文字φ（ファイ）で表されます。

黄金比はφと完全に一致するわけではありませんが非常に近似しており、フィボナッチ数列の隣接する2つの数の比として表すことができます。

大きい方を小さい方で割ると、その結果はφに近づきます。数列が進むにつれてその値はますますφに近づきますが、完全に等しくなることはありません。これはφが分数で表すことができない無理数であるためです。

黄金比の計算イラスト

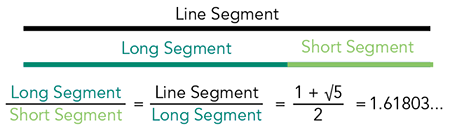
黄金比は自然界や人工構造物に多く見られ、普遍的な美と調和の原理として認識されています。

取引におけるフィボナッチリトレースメントレベルの理解

フィボナッチリトレースメントレベルは、価格が反転する可能性のあるサポートやレジスタンスの位置を示す水平線です。これらのレベルは、前章で説明したフィボナッチ数の原理に基づいて作成されます。

これはトレーダーがMetaTrader 5で広く使用するツールで、取引目標（ストップロスやテイクプロフィット）の設定や、価格が反転する可能性が高いサポート・レジスタンスラインの検出など、さまざまな目的で利用されます。

MetaTrader 5では、[挿入]タブ > [オブジェクト] > [フィボナッチ係数]の下にあります。

下図は、EURUSDの1時間足チャートにフィボナッチリトレースメントをプロットした例です。

フィボナッチリトレースメントツールは、市場の反転を検出したり、取引目標を設定したりする際に便利で信頼性のあるレベルを提供します。しかし今回は、フィボナッチレベルが機械学習や人工知能(AI)の観点でどの程度有効かを検証します。特に黄金比（61.8％、または0.618）に注目します。

続いて、フィボナッチレベルを数学的に計算し、それを用いて機械学習モデルが市場の方向性を理解し予測するための目的変数を作成する方法を探っていきます。

フィボナッチリトレースメントを用いた目的変数の作成

教師あり機械学習を用いてデータ内の関係性をモデルに学習させるには、適切に設計された目的変数が必要です。フィボナッチレベルは特定の価格レベルを表す単なる数値ですので、必要なフィボナッチレベルにおける市場価格を収集し、回帰問題の目的変数として利用することが可能です。

分類問題の場合は、フィボナッチラインに基づいた市場の動きに応じてクラスラベルを作成します。具体的には、たとえば上昇トレンドで市場があるバー数先に動き、計算したフィボナッチレベルを超えた場合は強気シグナル(1)と見なし、逆に市場が下落して設定したフィボナッチレベルを下回った場合は弱気シグナル(0)と見なします。その他のシグナルについては保留(-1)として割り当てることができます。

分類問題の場合

以下がImportです。

import pandas as pd
import numpy as np

以下が関数です。

def create_fib_clftargetvar(price: pd.Series, lookback_window: int=10, lookahead_window: int=10, fib_level: float=0.618):
    """
    Creates a target variable based on Fibonacci breakthroughs in price data.
    
    Parameters:
    - price: pd.Series of price data (close, open, high, or low)
    - lookback_window: int - number of past periods to calculate high/low
    - lookahead_window: int - number of future periods to assess breakout
    - fib_level: float - Fibonacci retracement level (e.g. 0.618)
    
    Returns:
    - pd.Series: with values
        1 => Bullish fib level reached
        0 => Bearish fib level reached
       -1 => False breakthrough or no fib hit
    """


    high = price.rolling(lookback_window).max()
    low = price.rolling(lookback_window).min()

    fib_level_value = high - (high - low) * fib_level # calculate the Fibonacci level in market price
    
    price_ahead = price.shift(-lookahead_window) # future price values
    
    target_var = []
    
    for i in range(len(price)):
        
        if np.isnan(price_ahead.iloc[i]) or np.isnan(fib_level_value.iloc[i]) or np.isnan(price.iloc[i]):
            target_var.append(np.nan)
            continue
        
        # let's detect bull and bearish movement afterwards
        
        if price_ahead.iloc[i] > price.iloc[i]: # The market went bullish
            if price_ahead.iloc[i] >= fib_level_value.iloc[i]:
                target_var.append(1) # bullish Fibonacci target reached
            else:
                target_var.append(-1) # false breakthrough
            
        else: # The market went bearish
            if price_ahead.iloc[i] <= fib_level_value.iloc[i]:
                target_var.append(0) # bearish Fibonacci target reached
            else:
                target_var.append(-1) # false breakthrough
                
    return target_var

市場におけるフィボナッチレベルは、次の式で計算されます。

fib_level_value = high - (high - low) * fib_level

分類問題として、市場の反応を前回のフィボナッチレベルに基づいて予測したい場合、将来の動向を考慮してトレンドを検出する必要があります。その後、lookahead_windowに基づく将来価格がフィボナッチレベルを上回ったか（上昇トレンドの場合）、または下回ったか（下降トレンドの場合）を確認し、それぞれ買い・売りシグナルを生成します。価格がどちらの方向にもフィボナッチレベルに到達しなかった場合は、保留シグナルを割り当てます。

この関数を使用して目的変数を作成し、結果をデータフレームに追加しましょう。

df["Fib signals"] = create_fib_clftargetvar(price=df["Close"], 
                                             lookback_window=10, 
                                             lookahead_window=5,
                                             fib_level=0.618)

df.dropna(inplace=True) # drop nan(s) caused by the shifting operation

df

以下が結果です。

	Open	High	Low	Close	Fib signals
9	1.3492	1.3495	1.3361	1.3362	0.0
10	1.3364	1.3405	1.3350	1.3371	0.0
11	1.3370	1.3376	1.3277	1.3300	0.0
12	1.3302	1.3313	1.3248	1.3279	-1.0
13	1.3279	1.3293	1.3260	1.3266	0.0

回帰問題の場合

def create_fib_regtargetvar(price: pd.Series, lookback_window: int=10, fib_level: float=0.618):
    """
    This function helps us in calculating the target variable based on fibonacci breakthroughs given a price
    
    price:
        Can be close, open, high, low
    
    """
    
    high = price.rolling(lookback_window).max()
    low = price.rolling(lookback_window).min()

    return high - (high - low) * fib_level

回帰問題の場合、将来の情報を取得するために値をシフトする必要はありません。なぜなら、裁量取引では、前回のウィンドウ(lookback_window)で計算したフィボナッチレベルを基準として、将来の価格がそのレベルを上回ったか下回ったかを確認するからです。

私たちの目的は、回帰モデルを学習させ、lookback_windowに基づいて次のフィボナッチレベルの値を予測できるようにすることです。

df["Fibonacci Level"] = create_fib_regtargetvar(price=df["Close"], 
                                         lookback_window=10,
                                         fib_level=0.618)

df.dropna(inplace=True)

df.head(5)

以下は、フィボナッチレベル列を追加した後の結果のデータフレームです。

	Open	High	Low	Close	Fibonacci Level
9	1.3492	1.3495	1.3361	1.3362	1.343840
10	1.3364	1.3405	1.3350	1.3371	1.342923
11	1.3370	1.3376	1.3277	1.3300	1.339015
12	1.3302	1.3313	1.3248	1.3279	1.337717
13	1.3279	1.3293	1.3260	1.3266	1.335195

フィボナッチを基にした目的変数に基づく分類モデルの学習

「Fib signals」という名前の分類目的変数から始めて、このデータを単純なRandomForestClassifierモデルで学習させてみましょう。

以下がImportです。

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
from sklearn.utils.class_weight import compute_class_weight
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import RobustScaler

学習用データとテスト用データに分割します。

X = df.drop(columns=[
    "Fib signals"
])

y = df["Fib signals"]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, shuffle=False)

以下がモデルです。

class_weights = compute_class_weight('balanced', classes=np.unique(y_train), y=y_train)
weight_dict = dict(zip(np.unique(y_train), class_weights))

model = RandomForestClassifier(n_estimators=100,
                               min_samples_split=2,
                               max_depth=10,
                               class_weight=weight_dict,
                               random_state=42
                              )

clf_pipeline = Pipeline(steps=[
    ("scaler", RobustScaler()),
    ("rfc", model)
])

clf_pipeline.fit(X_train, y_train)

ランダムフォレストモデルは決定木ベースのモデルであり、必ずしもスケーリング手法を必要としません。しかし、Open、High、Low、Close (OHLC)の値は連続変数であり、時間の経過とともに変動するため、モデルに外れ値が入り込む可能性があります。そのため、RobustScalerを用いることで、データ中の外れ値の影響を抑制することができます。

最後に、この分類モデルを学習用データとテスト用データの両方で検証します。

y_train_pred = clf_pipeline.predict(X_train)

print("Train Classification report\n",classification_report(y_train, y_train_pred))

y_test_pred = clf_pipeline.predict(X_test)

print("Test Classification report\n",classification_report(y_test, y_test_pred))

以下が結果です。

Train Classification report
               precision    recall  f1-score   support

        -1.0       0.53      0.55      0.54      4403
         0.0       0.59      0.64      0.61      7122
         1.0       0.67      0.60      0.64      8294

    accuracy                           0.61     19819
   macro avg       0.60      0.60      0.60     19819
weighted avg       0.61      0.61      0.61     19819

Test Classification report
               precision    recall  f1-score   support

        -1.0       0.22      0.22      0.22      1810
         0.0       0.38      0.60      0.46      3181
         1.0       0.42      0.20      0.27      3504

    accuracy                           0.35      8495
   macro avg       0.34      0.34      0.32      8495
weighted avg       0.36      0.35      0.33      8495

学習用データでは結果が非常に良好に見えますが、テスト用データでは極めて悪い結果となりました。この原因としては、モデルが学習に使用したサンプル以外のパターンを十分に捉えられなかったことが考えられます。

たとえば、市場の有意なパターンを捕捉するための特徴量が不足している場合があります。OHLCの値のみでは十分な情報を提供できない可能性があります。また、目的変数を作成する際に使用した、次のlookahead_windowバーに基づく粗いトレンド検出方法が適切でなかったことも要因として挙げられます。この方法では、価格がフィボナッチレベルを中間のバーで超えた場合を見逃してしまう可能性があります。

このプロセスは、将来の価格がフィボナッチレベルを超えるかどうかを予測するモデルを学習させることを目的としているため、分類レポートの結果が完璧である必要はありません。現時点ではこのモデルを使用し、実際の取引環境におけるテストデータでの結果を分析していきます。

最後に、この学習済みモデルをONNX形式で保存し、MQL5プログラミング言語で外部利用できるようにします。

import skl2onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

# Define the initial type of the model’s input
initial_type = [('input', FloatTensorType([None, X_train.shape[1]]))]

# Convert the pipeline to ONNX
onnx_model = convert_sklearn(clf_pipeline, initial_types=initial_type, target_opset=13)

# Save the ONNX model to a file
with open(f"{symbol}.{timeframe}.Fibonnacitarg-RFC.onnx", "wb") as f:
    f.write(onnx_model.SerializeToString())

フィボナッチに基づく目的変数を用いた回帰モデルの学習

回帰モデルを学習させる場合も同じ原則に従うことができますが、この場合はモデルのタイプと目的変数のみが異なります。

以下がImportです。

from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score

学習用データとテスト用データに分割します。

X = df.drop(columns=[
    "Fibonacci Level"
])

y = df["Fibonacci Level"]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, shuffle=False)

以下は、ランダムフォレスト回帰モデルです。

model = RandomForestRegressor(n_estimators=100,
                               min_samples_split=2,
                               max_depth=10,
                               random_state=42
                              )

reg_pipeline = Pipeline(steps=[
    ("scaler", RobustScaler()),
    ("rfr", model)
])

reg_pipeline.fit(X_train, y_train)

最後に、回帰モデルを学習用データとテスト用データの両方で検証します。

y_train_pred = reg_pipeline.predict(X_train)

print("Train accuracy score:",r2_score(y_train, y_train_pred))

y_test_pred = reg_pipeline.predict(X_test)

print("Test accuracy score:",r2_score(y_test, y_test_pred))

以下が結果です。

Train accuracy score: 0.9990321734526452
Test accuracy score: 0.9565827587164671

回帰モデルから得られたR²スコアの結果だけでは多くを判断することはできませんが、テスト用データで0.9565という値は十分に良好な結果です。

最後に、この学習済みモデルをONNX形式で保存し、MQL5プログラミング言語で外部利用できるようにします。

# Define the initial type of the model’s input
initial_type = [('input', FloatTensorType([None, X_train.shape[1]]))]

# Convert the pipeline to ONNX
onnx_model = convert_sklearn(reg_pipeline, initial_types=initial_type, target_opset=13)

# Save the ONNX model to a file
with open(f"{symbol}.{timeframe}.Fibonnacitarg-RFR.onnx", "wb") as f:
    f.write(onnx_model.SerializeToString())

では、これら2つのモデルの予測能力を、実際の取引環境でテストしてみます。

ストラテジーテスターでのフィボナッチベース機械学習モデルのテスト

まず、ONNX形式のランダムフォレストモデルをリソースとしてエキスパートアドバイザー(EA)に追加します。

#resource "\\Files\\EURUSD.PERIOD_H4.Fibonnacitarg-RFC.onnx" as uchar rfc_onnx[]
#resource "\\Files\\EURUSD.PERIOD_H4.Fibonnacitarg-RFR.onnx" as uchar rfr_onnx[]

続いて、ランダムフォレスト分類モデルと回帰モデルの両方をONNX形式で読み込むのに役立つライブラリをインポートします。

#include <Random Forest.mqh>

CRandomForestClassifier rfc;
CRandomForestRegressor rfr;

学習データで使用したのと同じlookback_windowおよびlookahead_windowの値が必要です。これらの値は、取引をどのくらいの期間保持するか、またいつ決済するかを判断する際に役立ちます。

input group "Models configs";

input target_var_type fib_target = CLASSIFIER; //Model type
input int lookahead_window = 5;
input int lookback_window = 10;

変数fib_targetの入力は、使用するモデルのタイプを選択するのに役立ちます。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Setting the symbol and timeframe
   
   if (!MQLInfoInteger(MQL_TESTER) && !MQLInfoInteger(MQL_DEBUG))
     if (!ChartSetSymbolPeriod(0, symbol_, timeframe_))
       {
         printf("%s failed to set symbol %s and timeframe %s",__FUNCTION__,symbol_,EnumToString(timeframe_));
         return INIT_FAILED;
       }

//---

   m_trade.SetExpertMagicNumber(magic_number);
   m_trade.SetDeviationInPoints(slippage);
   m_trade.SetMarginMode();
   m_trade.SetTypeFillingBySymbol(Symbol());
   
//---
   
   switch(fib_target)
     {
      case  REGRESSOR:
      
         if (!rfr.Init(rfr_onnx))
            {
               printf("%s failed to initialize the random forest regressor",__FUNCTION__);
               return INIT_FAILED;
            }
                    
        break;
      case CLASSIFIER:
            
         if (!rfc.Init(rfc_onnx))
            {
               printf("%s failed to initialize the random forest classifier",__FUNCTION__);
               return INIT_FAILED;
            }
            
        break;
     }

//---

   return(INIT_SUCCEEDED);
  }

OnTick関数内では、学習データで使用したのと同じ形でOHLCの値をモデルに渡した後、モデルからシグナルを取得します。

これらのシグナルは売買取引を開始するために使用されます。

void OnTick()
  {
//--- Getting signals from the model
   
   if (!isNewBar())
      return;
      
    vector x = {
       iOpen(Symbol(), Period(), 1),
       iHigh(Symbol(), Period(), 1),
       iLow(Symbol(), Period(), 1),
       iClose(Symbol(), Period(), 1)
    };
    
    long signal = 0;
    
    switch(fib_target)
      {
       case  REGRESSOR:
         {
            double pred_fib = rfr.predict(x);         
            signal = pred_fib>iClose(Symbol(), Period(), 0)?1:0; //If the predicted fibonacci is greater than the current close price, thats bullish otherwise thats bearish signal
         }
         
         break;
       case CLASSIFIER:
       
         signal = rfc.predict(x).cls;         
         
         break;
      }

//--- Trading based on the signals received from the model
   
   MqlTick ticks;
   if (!SymbolInfoTick(Symbol(), ticks))
      {
         printf("Failed to obtain ticks information, Error = %d",GetLastError());
         return;
      }
      
   double volume_ = SymbolInfoDouble(Symbol(), SYMBOL_VOLUME_MIN);
   
   if (signal == 1)
     {        
        if (!PosExists(POSITION_TYPE_BUY) && !PosExists(POSITION_TYPE_SELL))  
            m_trade.Buy(volume_, Symbol(), ticks.ask);
     }
     
   if (signal == 0)
     {        
        if (!PosExists(POSITION_TYPE_SELL) && !PosExists(POSITION_TYPE_BUY))  
             m_trade.Sell(volume_, Symbol(), ticks.bid);
     } 

//--- Closing trades 
   
   switch(fib_target)
     {
      case CLASSIFIER:
        
        CloseTradeAfterTime((Timeframe2Minutes(Period())*lookahead_window)*60); //Close the trade after a certain lookahead and according the the trained timeframe  
        
        break;
        
      case REGRESSOR:
      
        CloseTradeAfterTime((Timeframe2Minutes(Period())*lookback_window)*60); //Close the trade after a certain lookahead and according the the trained timeframe
        
        break;
     }
  }

取引の決済は、選択したモデルタイプ、lookahead_window、lookback_windowの値によって異なります。

分類モデルを選択した場合、取引は現在の時間軸でlookahead_windowに相当するバー数が経過した後に決済されます。

回帰モデルを選択した場合、取引は現在の時間軸でlookback_windowに相当するバー数が経過した後に決済されます。

これは、Pythonスクリプト内で目的変数を作成した方法に基づいています。

最後に、これら2つのモデルをストラテジーテスター上でテストします。

学習データは2005年1月1日から2023年1月1まで収集したため、モデルの結果は2023年1月1日から2023年12月31日までのアウトオブサンプルデータでテストします。

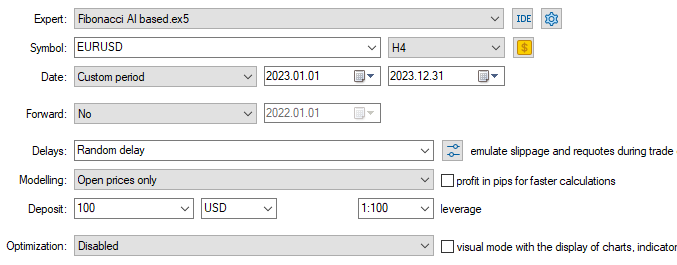
モデルタイプ：分類モデル

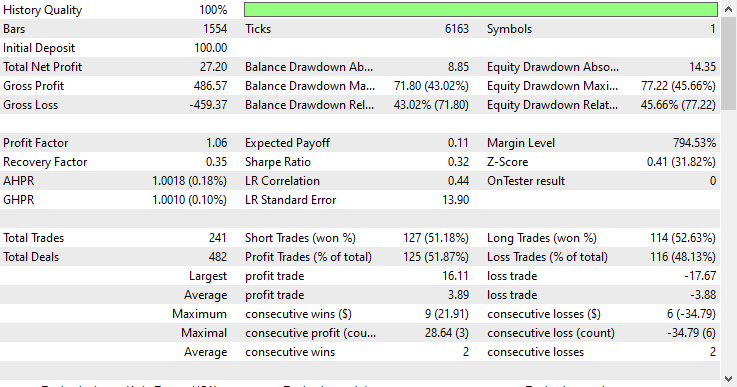
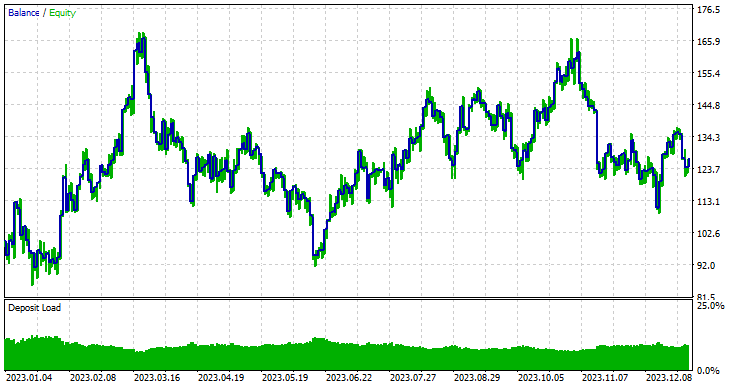
モデルタイプ：回帰モデル

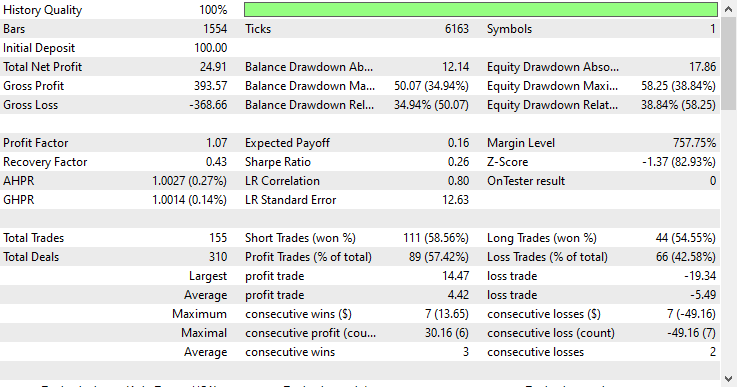
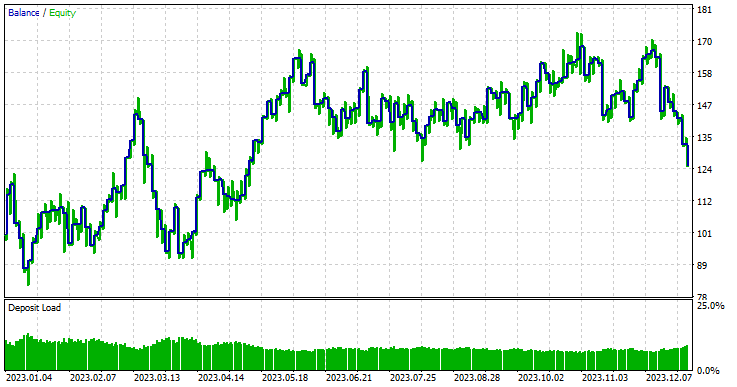
回帰モデルは、アウトオブサンプルデータであるにもかかわらず非常に優れた成績を示し、57.42%の勝率を記録しました。

自動売買ロボット内で回帰モデルを有効活用するために、ランダムフォレスト回帰モデルが出力する連続値を二値信号に変換しました。

signal = pred_fib>iClose(Symbol(), Period(), 0)?1:0; //If the predicted Fibonacci is greater than the current close price, that's bullish otherwise that's bearish signal

これにより、予測されたフィボナッチレベルの解釈方法は従来の裁量取引とは全く異なります。裁量取引では通常、トレンド確認シグナルを受け取った後に取引を開始し、取引目標を特定のフィボナッチレベル（通常は61.8%）に設定します。

今回のアプローチでは、機械学習モデルが学習データにおける指定されたlookback_windowおよびlookahead_windowを通じて既にこのパターンを理解していると仮定し、取引を開始して指定されたバー数に従って保持するだけで済みます。

ここで重要なのは、lookback_windowおよびlookahead_windowの値です。裁量取引でフィボナッチツールを使用する際、通常は計算に用いるバーの数（高値や安値）は考慮せず、直感的にツールを配置します。

ツール自体は裁量取引で機能しますが、正しい位置にツールを置いていると錯覚してしまい、実際には明確なルールなしに自分の意図で配置しているだけの場合があります。

機械学習を用いて目的変数を作成する場合、そしてフィボナッチレベルの有効性を検証する場合は、このlookback_windowおよびlookahead_windowの値を最適化することが重要です。

最後に

フィボナッチリトレースメントやフィボナッチレベルは、機械学習における目的変数作成のための強力な手法であることが、回帰モデルによってストラテジーテスターで得られたレポートからも示されています。Open、High、Low、Closeのわずかな予測変数しか使用していない場合でも、市場パターンが多く含まれていないにもかかわらず、モデルはフィボナッチレベルから学習した情報を基に、有用なパターンを検出し、ランダム推測に比べて良好な結果を出すことができました。

結果をどのように見ても、個人的には非常に印象的だと思います。

ただし現時点では、このアイデアはまだ十分に洗練されていません。データにインジケーターの値や取引戦略の確認情報など、より多くの特徴量を追加することで、フィボナッチを基にしたモデルが市場で発生する複雑なパターンを捉えやすくなるでしょう。また、他のフィボナッチレベルを探索してみることも推奨されます。

さらにこのアイデアを改良すれば、特に株式や指数市場において、強気の長期トレンド中に定期的に発生するプルバックの予測に非常に効果的になると考えられます。また、データのノイズが比較的少ない日足などの高時間軸でも有効性が高まるでしょう。

添付ファイルの表

ファイル名とパス	説明と使用法
Experts\Fibonacci AI based.mq5	機械学習モデルテスト用のメインのEA
Include\Random Forest.mqh	.ONNX形式で存在するランダムフォレスト分類モデルと回帰モデルを読み込み、展開するためのクラス
Files\*.onnx	ONNX形式の機械学習モデル
Files\*.csv	機械学習モデル学習用データセットを含むCSVファイル
Python\fibbonanci-in-ml.ipynb	データを処理し、ランダムフォレストモデルを学習させるためのPythonスクリプト

情報源と参考文献

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/18078

添付されたファイル |

ZIPをダウンロード

Attachments.zip (1525.28 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動

MQL5における高度な注文執行アルゴリズム：TWAP、VWAP、アイスバーグ注文

MQL5フレームワークで、機関投資家向けの高度な執行アルゴリズム（TWAP、VWAP、アイスバーグ注文）を小口トレーダー向けに提供します。統合された実行マネージャーとパフォーマンスアナライザーを用いて、注文の分割（スライシング）や分析をよりスムーズかつ正確に行える環境を提供します。

データサイエンスとML（第39回）：ニュース × 人工知能、それに賭ける価値はあるか

ニュースは金融市場を動かす力を持っており、特に非農業部門雇用者数(NFP)のような主要指標の発表は大きな影響を与えます。私たちは、単一のヘッドラインが急激な価格変動を引き起こす様子を何度も目にしてきました。本記事では、ニュースデータと人工知能(AI)の強力な融合について探っていきます。

エラー 146 (「トレードコンテキストビジー」) と、その対処方法

この記事では、MT4において複数のEAの衝突をさける方法を扱います。ターミナルの操作、MQL4の基本的な使い方がわかる人にとって、役に立つでしょう。

MQL5経済指標カレンダーを使った取引（第8回）：ニュース駆動型バックテストの最適化 - スマートなイベントフィルタリングと選択的ログ

本記事では、スマートなイベントフィルタリングと選択的ログ出力を用いて経済カレンダーを最適化し、ライブおよびオフラインモードでのバックテストをより高速かつ明確に実施できるようにします。イベント処理を効率化し、ログを重要な取引やダッシュボードイベントに絞ることで、戦略の可視化を向上させます。これらの改善により、ニュース駆動型取引戦略のテストと改善をシームレスにおこなえるようになります。