
ニューラルネットワークが簡単に(第75回):軌道予測モデルのパフォーマンス向上
はじめに
今後の値動きの軌跡を予測することは、おそらく、希望する計画期間の取引プランを構築するプロセスにおいて重要な役割を果たします。このような予測の精度は非常に重要です。軌道予測モデルは軌道予測の質を向上させるために、複雑になっています。
しかし、この過程には別の側面もあります。より複雑なモデルは、より多くのコンピューティングリソースを必要とします。つまり、モデルの訓練とその運用の両方にコストがかかるということです。モデル訓練の費用も考慮する必要があります。しかし、運営費に関しては、これらはさらに重要な意味を持ちます。特に、ボラティリティの高い市場で成行注文を使用したリアルタイム取引となるとなおさらです。そのような場合、モデルのパフォーマンスを向上させる手法を検討します。理想的には、このような最適化は将来の軌道予測の質に影響を与えないべきです。
最近の記事で取り上げた軌道予測法は、自律走行車業界から拝借したものです。現場の研究者も同じ問題に直面しています。自動車のスピードは、意思決定に要する時間を増大させます。軌道予測や意思決定に高価なモデルを使用することは、意思決定に費やす時間の増加につながるだけでなく、より高価なハードウェアの設置が必要となるため、使用する機器のコスト増加にもつながります。この文脈では、「Efficient Baselines for Motion Prediction in Autonomous Driving(自律走行における動作予測のためのベースライン)」稿で紹介されているアイデアを検討することをお勧めします。著者は「軽量」な軌道予測モデルを構築することを課題とし、以下の成果を強調しています。
- リアルタイム推論とリソースに制約のあるデバイスへの展開に影響を与える、動作予測モデルのサイズにおける重要な課題を特定する
- 車両交通予測のためのいくつかの効果的なベースラインの提案:このベースラインは、高品質のコンテキスト地図の徹底的な分析に明示的に依存するのではなく、簡単な前処理ステップで得られる事前の地図情報を予測のガイドとして利用する
- より少ないパラメータと操作で、より低い計算コストで競争力のあるパフォーマンスを達成する
1.パフォーマンス向上テクニック
分析されたソースデータとモデルの複雑さのバランスを考慮しながら、この手法の著者は、注意メカニズムやグラフニューラルネットワーク(GNN)を含む強力な深層学習技術を使用して、競争力のある結果を達成するよう努めています。これにより、他の手法と比べ、パラメータや操作の数が減ります。特に、この論文の著者はモデルの入力データとして以下のものを使用しています。
- エージェントの過去の軌跡とそれに対応するインタラクションを、社会的ベースレベルブロックへの唯一の入力とする
- 拡張機能(エージェントの許容範囲の簡略化された表現を地図データベースへの追加入力として追加)
したがって、提案するモデルは、物理的コンテキストを計算するために、高品質の完全な注釈付き地図やラスタライズされたシーン表現を必要としません。
この手法の著者は、シンプルながら強力な地図前処理アルゴリズムの使用を提案しており、そこではターゲットエージェントの軌跡が最初にフィルタリングされます。そして、地図の幾何学的情報のみを考慮して、ターゲットエージェントが対話可能な実行可能領域を計算します。
社会的ベースラインは、最も重要な障害物の過去の軌跡を入力として使用し、相対的な変位としてエンコーダモジュールに与えます。そして、社会的情報はグラフニューラルネットワーク(GNN)を使用して計算されます。彼らの論文では、エージェント間の最も重要な相互作用を得るために、Convolutional Network(Crystal-GCN)とMulti-Head Self Attention(MHSA)層を使用しています。その後、デコーダモジュールで、i番目のステップの出力が前のステップに依存する自己回帰戦略を用いて、この潜在情報がデコードされます。
提案手法の特徴の1つは、全期間Th = Tobs + Tlenの情報を持つエージェントとの相互作用の分析です。同時に、複雑なトラフィックシナリオで考慮する必要のあるエージェントの数を減らすことができます。上からの絶対的な2Dビューを使用する代わりに、エージェントiの入力は一連の相対的な変位です。
![]()
この手法の著者は、シーケンス内のエージェントの数を制限したり固定したりしていません。すべてのエージェントの相対的な変位を考慮するために、1つのLSTMブロックを使用し、シーケンス内の各エージェントの時間情報を計算します。
各車両の分析履歴を順番に符号化した後、最も関連性の高い社会情報を得るためにエージェント間の相互作用が計算されます。この目的のために、相互作用グラフが構築されます。Crystal-GCN層はグラフの構築に使用されます。次に、エージェントとエージェントの相互作用の学習を改善するためにMHSAが適用されます。
インタラクションの仕組みを作成する前に、このメソッドの著者たちは一時的な情報を適切なシーンに分解します。これは、移動シナリオごとにエージェントの数が異なることを考慮したものです。相互作用メカニズムは双方向完全連結グラフとして定義され、初期ノード特徴量v0iは、運動履歴エンコーダによって計算された各車両hi,outの潜在的な時間情報によって表されます。一方、ノードkからノードlへのエッジは、ある時点tobs,lenにおける対応するエージェント間の距離ベクトルek,lによって絶対座標で表されます。
![]()
相互作用のグラフ(ノードとエッジ)が与えられると、Crystal-GCNは次のように定義されます。
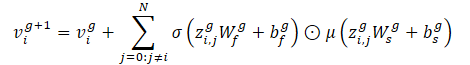
この演算子は、車間距離に基づいてノード特徴量を更新するためにエッジ特徴量を埋め込むことを可能にします。この手法の著者は、層間の非線形性としてReLUとバッチ正規化を用いた2層のCrystal-GCNを使用しています。
σとμはそれぞれシグモイドとソフトプラスの活性化関数です。また、zi,j=(vi‖vj‖ei,j) はGNN層の2つのノードと対応するエッジの特徴量の連結であり、Nはシーン内のエージェントの総数を表し、Wとbは対応する層の重みと変位です。
インタラクショングラフを通過した後、更新された各ノード特徴量viは、エージェントの時間的社会的コンテキストiに関する情報を含みます。しかし、現在の位置と過去の軌跡によっては、エージェントは特定の社会的情報に注意を払う必要があるかもしれません。この手法をモデル化するために、この手法の著者は4つのヘッドを持つMulti-Head Self Attentionメカニズムを使用しています。これは、ノードviの特徴量を文字列として含み、更新されたノード特徴量行列Vに適用されます。
最終的な社会的注意行列SATT(GNNメカニズムとMHSAメカニズムの後の社会的注意モジュールの出力)の各行は、内部の時間情報を考慮した、エージェントiと周囲のエージェントとの相互作用の特徴量を表します。
次に、この手法の著者は、地図に関する最小限の情報を用いて社会的基本モデルを拡張し、そこからターゲットエージェントの領域Pを、最後の観測フレームにおけるターゲットエージェントのスピードと加速度を考慮しながら、妥当な中央線(高レベルで構造化された特徴量)の周りのランダムに選択されたr個の点 {p0, p1...pr} の部分集合として離散化します。これは地図の前処理ステップであり、モデルが高解像度地図を見ることはありません。
物理法則に基づき、この手法の著者は、連続するタイムスタンプの間に急激な動きの変化がない剛体構造として車両を扱っています。したがって、道路を運転するというタスクを説明する場合、通常、最も重要な特徴量は特定の方向(進行方向前方)にあります。これにより、簡略化された地図を得ることができます。
軌跡に関する情報には、実世界のデータ収集プロセスに関連するノイズが含まれていることが多いです。最後の観測フレームtobs,lenにおけるターゲットエージェントの動的変数を推定するために、この手法の著者は、まず、各軸に沿って最小二乗アルゴリズムを用いてターゲットエージェントの過去の観測値をフィルタリングすることを提案します。エージェントが一定の加速度で移動していると仮定し、ターゲットエージェントの動的特性(速度と加速度)を計算することができます。そして、速度と加速度の推定ベクトルを計算します。さらに、これらのベクトルは、最初の観測により少ない重み(より高い忘却因子λ)を割り当てて、スムーズな推定を得るためにスカラーとして合計されます。このように、最新の観察結果は、エージェントの現在の運動状態を決定する上で重要な役割を果たします。
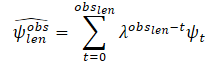
ここで
obslen 観測フレーム数 ψt フレームtにおける推定速度/加速度 λ ∈ (0, 1) 忘却因子
運動状態を計算した後、どの時間tでも一定の旋回スピードで加速する物理モデルを仮定して、移動距離を推定します。
そして、これらの車線の軌跡候補は、妥当な物理情報として使用されるように処理されます。まず、ターゲットエージェントが最後に観測した地点のうち、もっとも妥当な中央線の始点に最も近い地点を見つけます。そして、元の中心線に沿って移動した距離を推定します。そして、累積距離(各点間のユークリッド距離を考慮)が事前に計算された偏差以上となる点を中央線mの終点インデックスpとして決定します。
そして、対応する中央線mの始点と終点の間で三次補間をおこない、計画期間のステップを求めます。この手法の著者がおこなった実験では、ターゲットエージェントの真の軌道の終点とフィルタリングされた中央線の終点との間の検証セット全体の平均距離と中央値距離L2を考慮した最良のアプリオリ情報は、運動状態における速度と加速度を考慮し、最小二乗法を用いて入力をフィルタリングすることによって達成されることが実証されました。
これらのハイレベルで構造化された中央線に加えて、この手法の著者は、正規分布N(0, 0.2)に従って、すべての妥当な中央線に点の歪みを適用することを提案しています。これは、妥当な領域Pを、妥当な中央線の周りにランダムに選ばれたr個の点{p0, p1...pr}の部分集合として離散化します。こうして、低レベルの特徴量として特定される可能性の高い領域の大まかな見当をつけることができます。この手法の著者は、車線の境界を使用する代わりに、正規化項の追加として正規分布Nを使用します。これにより、エンコーディングモジュールでの過剰適合を防ぐことができます。
エリアエンコーダと中央線エンコーダは、潜在地図情報を計算するために使用されます。それぞれ低レベルと高レベルの地図特徴量を処理します。これらのエンコーダはそれぞれ多層パーセプトロン(MLP)で表されます。まず、点の次元に沿って情報を平滑化し、座標軸に沿って情報を交互に並べます。そして、対応するMLP(3層、バッチ正規化、ReLU、ドロップアウトを使用)は、解釈された原点周りの絶対座標を代表的な潜在的物理情報に変換します。静的な物理的コンテキスト(領域エンコーダからの出力)は、異なるモードに対する共通の潜在的表現として機能し、一方、特定の物理的コンテキストは、各モードに対する特定の地図情報を示します。
未来軌道デコーダは、提案されたベースラインモデルの第3の構成要素です。このモジュールはLSTMブロックで構成され、運動履歴エンコーダで過去の相対運動を学習したのと同じ方法で、将来の時間ステップの相対運動を再帰的に推定します。社会的ベースの場合、モデルは、ターゲットエージェントのデータのみに注目し、社会的インタラクションモジュールによって計算された社会的コンテキストを使用します。社会的コンテキストは、シナリオ内のすべてのトラフィックを表し、自己回帰LSTM予測変数の入力潜在ベクトルを表します。
この手法の著者は、モードmの地図的な基本ケースの観点から、潜在的な交通コンテキストを、社会的コンテキスト、静的な物理的コンテキスト、特定の物理的コンテキストの連結として特定することを提案しています。これはLSTMデコーダの入力隠れベクトルとして機能します。
社会的な場合のLSTMブロックのオリジナルデータと比較すると、空間埋め込み後のターゲットエージェントの過去n回の相対的な動きが符号化されて表現され、地図的なベースラインでは、ターゲットエージェントの現在の絶対位置と現在の中央線の間の符号化された距離ベクトルと、現在のスカラータイムスタンプtが追加されます。どちらの場合も(社会的および地図)、LSTMブロックの結果は標準的な全結合層を使用して処理されます。
ある時間ステップtにおける相対予測を得た後、最後に計算した相対移動がベクトルの最後に来るように、過去の観測の初期データをシフトさせ、最初のデータを削除します。
マルチモーダル予測が計算された後、連結され、信頼度を得るためにMLP残差によって処理されます(信頼度が高いほど、そのレジームは可能性が高く、真実に近い)。
論文の著者によって発表された手法の元の可視化を以下に示します。ここでは青の線は社会情報を表し、赤の線はカードに関する情報の伝達を表しています。
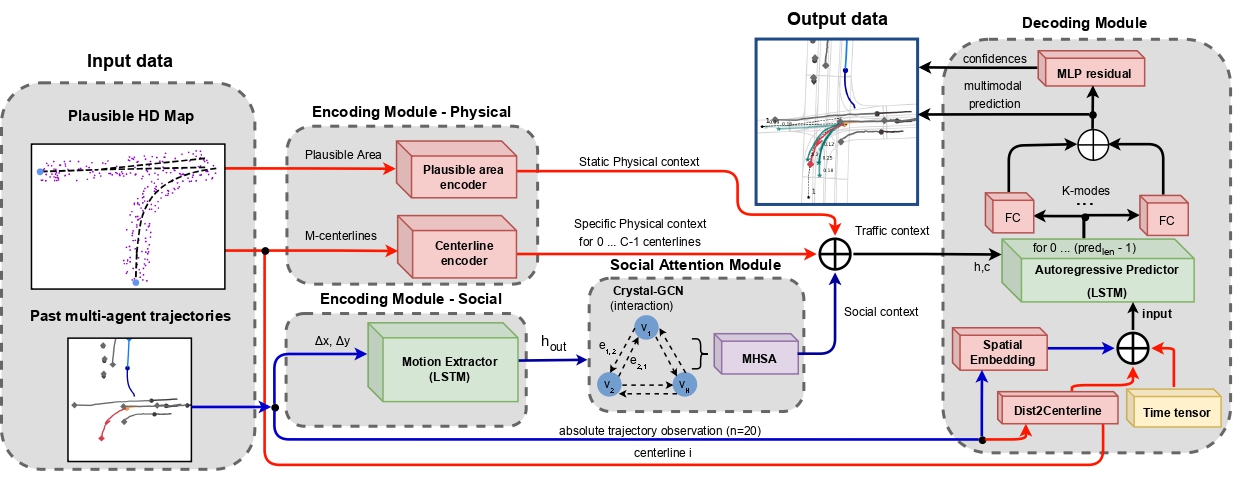
2.MQL5を使用した実装
提案された方法の理論的側面について検討したので、次に、MQL5を使用して実装してみましょう。ご覧のように、このメソッドの著者はモデルをブロックに分割しました。各ブロックは最小限の層数を使用します。同時に、個々のブロックのアーキテクチャを単純化することは、分析環境に関する先験的な情報を用いた追加的なデータ分析を伴います。特に、地図は前処理され、通過した軌跡はフィルタリングされます。これにより、予測軌道の構築の質を落とすことなく、初期データのノイズと量を減らすことができます。
2.1 CrystalGraph畳み込みネットワーク層の作成
さらに、提案された方法の中で、私たちはこれまで出会ったことのないグラフニューラル層に出会います。したがって、提案アルゴリズムの構築に移る前に、ライブラリに新しい層を作成します。
この手法の著者が提案したCrystalGraph畳み込みネットワーク層は、以下の式で表すことができます。
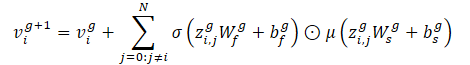
基本的に、ここでは2つの全結合層の作業結果の要素ごとの乗算が見られます。そのうちの1つはシグモイドによって活性化され、グラフの頂点間の接続の有無を表す訓練可能なバイナリ行列を表します。第2層は、ReLUのソフトアナログであるSoftPlus関数によって活性化されます。
CrystalGraph畳み込みネットワークを実装するために、CNeuronBaseOCLから基本機能を継承した新しいクラスCNeuronCGConvOCLを作成します。
class CNeuronCGConvOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL cInputF; CNeuronBaseOCL cInputS; CNeuronBaseOCL cF; CNeuronBaseOCL cS; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronCGConvOCL(void) {}; ~CNeuronCGConvOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronCGConvOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual CLayerDescription* GetLayerInfo(void); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
新しいクラスは、親クラスからオーバーライドのための標準的なメソッドセットと基本的な機能を受け取ります。グラフ畳み込みアルゴリズムを実装するために、4つの内部全結合層を作成します。
- 2層は、バックプロパゲーションパスの間、元のデータと誤差勾配を書き込む(cInputFとcInputS)
- 2層は機能を実行する(cFおよびcS)
すべての内部オブジェクトを静的に作成するので、クラスのコンストラクタとデストラクタは「空」のままです。
Initクラスの初期化メソッドでは、まず親クラスの関連メソッドを呼び出し、外部プログラムから受け取ったデータに対して必要な制御をすべて実装し、継承したオブジェクトと変数を初期化します。
bool CNeuronCGConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch)) return false; activation = None;
その後、追加された内部オブジェクトの初期化メソッドを呼び出して、順次初期化していきます。
if(!cInputF.Init(numNeurons, 0, OpenCL, window, optimization, batch)) return false; if(!cInputS.Init(numNeurons, 1, OpenCL, window, optimization, batch)) return false; cInputF.SetActivationFunction(None); cInputS.SetActivationFunction(None); //--- if(!cF.Init(0, 2, OpenCL, numNeurons, optimization, batch)) return false; cF.SetActivationFunction(SIGMOID); if(!cS.Init(0, 3, OpenCL, numNeurons, optimization, batch)) return false; cS.SetActivationFunction(LReLU); //--- return true; }
ソースデータ記録の内部層については、活性化関数がないことを指定しました。機能層については、作成された層のアルゴリズムが提供する活性化関数を含めました。CNeuronCGConvOCL層自体は活性化関数を持ちません。
オブジェクトを初期化した後、フィードフォワードメソッドfeedForwardの作成に移ります。メソッドはパラメータで前のニューラル層のオブジェクトへのポインタを受け取ります。その出力には初期データが含まれます。
bool CNeuronCGConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getOutput() || NeuronOCL.getOutputIndex() < 0) return false;
メソッド本体では、受け取ったポインタの妥当性を即座に確認します。
コントロールブロックの受け渡しに成功したら、ソースデータを前の層のバッファから2つの内部ソースデータ層のバッファに転送する必要があります。ニューラル層のすべての操作はOpenCLコンテキスト側でおこなうということを忘れないでください。したがって、OpenCLコンテキストのメモリにもデータをコピーする必要がありますが、ここではもう少し踏み込んで、物理的にデータを転送することなく「コピー」を実行します。内部層の結果バッファへのポインタを単純に置き換え、前の層の結果バッファへのポインタを渡します。ここでは、前の層の活性化関数も示します。
if(cInputF.getOutputIndex() != NeuronOCL.getOutputIndex()) { if(!cInputF.getOutput().BufferSet(NeuronOCL.getOutputIndex())) return false; cInputF.SetActivationFunction((ENUM_ACTIVATION)NeuronOCL.Activation()); } if(cInputS.getOutputIndex() != NeuronOCL.getOutputIndex()) { if(!cInputS.getOutput().BufferSet(NeuronOCL.getOutputIndex())) return false; cInputS.SetActivationFunction((ENUM_ACTIVATION)NeuronOCL.Activation()); }
このように、内部層を扱う場合、データを物理的にコピーすることなく、前の層の結果バッファに直接アクセスすることができます。最小限のリソースでデータ転送のタスクを実装しました。さらに、OpenCLコンテキストに2つの追加バッファを作成する必要がないため、メモリ使用量を最適化できます。
そして、単純に内部機能層のフィードフォワードメソッドを呼び出します。
if(!cF.FeedForward(GetPointer(cInputF))) return false; if(!cS.FeedForward(GetPointer(cInputS))) return false;
これらの操作の結果、文脈とグラフのつながりの行列が得られたので、それらの要素ごとの乗算を実行します。この演算を実行するためにはDropoutカーネルを使用します。これは、元データをマスクで要素ごとに乗算するために作成したものです。私たちの場合、同じ数学的操作でも背景が違います。
必要なパラメータと初期データをカーネルに渡しましょう。
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(Neurons() + 3) / 4; ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cF.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cS.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, Output.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
その後、実行キューに入れます。
次のステップは、バックプロパゲーション機能を実装することです。ここではまず、OpenCL側のカーネルを作成するところから始めます。ポイントは、前の層からの誤差勾配の分布は、最終結果への影響に従って内部層への移動から始まるということです。そのためには、結果として得られる誤差勾配に、第2機能層のフィードフォワードパスの結果を掛け合わせる必要があります。上記で使用した要素ごとの乗算カーネルを2回呼び出すのを避けるため、1回のパスで両方の層の誤差勾配を求める新しいカーネルを作成します。
CGConv_HiddenGradientカーネルパラメータでは、5つのデータバッファへのポインタと、両方の層の活性化関数のタイプを渡します。
__kernel void CGConv_HiddenGradient(__global float *matrix_g,///<[in] Tensor of gradients at current layer __global float *matrix_f,///<[in] Previous layer Output tensor __global float *matrix_s,///<[in] Previous layer Output tensor __global float *matrix_fg,///<[out] Tensor of gradients at previous layer __global float *matrix_sg,///<[out] Tensor of gradients at previous layer int activationf,///< Activation type (#ENUM_ACTIVATION) int activations///< Activation type (#ENUM_ACTIVATION) ) { int i = get_global_id(0);
層のニューロン数に基づいて、1次元のタスク空間でカーネルを起動します。カーネル本体では、スレッド識別子に基づいて、解析対象の要素へのデータバッファ内のオフセットを即座に決定します。
次に、GPUのグローバルメモリにアクセスする「集中的な」操作を減らすために、解析された要素のデータをローカル変数に格納します。
float grad = matrix_g[i]; float f = matrix_f[i]; float s = matrix_s[i];
この時点で、両層の誤差勾配を計算するのに必要なデータがすべて揃ったので、それを計算します。
float sg = grad * f; float fg = grad * s;
ただし、得られた値をグローバルデータバッファの要素に書き込む前に、見つかった誤差勾配を対応する活性化関数に調整する必要があります。
switch(activationf) { case 0: f = clamp(f, -1.0f, 1.0f); fg = clamp(fg + f, -1.0f, 1.0f) - f; fg = fg * max(1 - pow(f, 2), 1.0e-4f); break; case 1: f = clamp(f, 0.0f, 1.0f); fg = clamp(fg + f, 0.0f, 1.0f) - f; fg = fg * max(f * (1 - f), 1.0e-4f); break; case 2: if(f < 0) fg *= 0.01f; break; default: break; }
switch(activations) { case 0: s = clamp(s, -1.0f, 1.0f); sg = clamp(sg + s, -1.0f, 1.0f) - s; sg = sg * max(1 - pow(s, 2), 1.0e-4f); break; case 1: s = clamp(s, 0.0f, 1.0f); sg = clamp(sg + s, 0.0f, 1.0f) - s; sg = sg * max(s * (1 - s), 1.0e-4f); break; case 2: if(s < 0) sg *= 0.01f; break; default: break; }
カーネルの操作が終了したら、操作結果をグローバルデータバッファの対応する要素に保存します。
matrix_fg[i] = fg; matrix_sg[i] = sg; }
カーネルを作成したら、クラスのメソッドに戻ります。誤差勾配分布はcalcInputGradientsメソッドで実装されます。そのパラメータに前の層のオブジェクトへのポインタを渡します。メソッド本体では、受け取ったポインタの妥当性を即座に確認します。
bool CNeuronCGConvOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer || !prevLayer.getGradient() || prevLayer.getGradientIndex() < 0) return false;
次に、内部層に勾配を分散させるために、上述のカーネルCGConv_HiddenGradientを呼び出す必要があります。ここでは、まずタスク空間を定義します。
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = Neurons();
そして必要なパラメータをカーネルに渡します。
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_f, cF.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_fg, cF.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_s, cS.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_sg, cS.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_g, getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activationf, cF.Activation())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activations, cS.Activation())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
カーネルを実行キューに入れます。
if(!OpenCL.Execute(def_k_CGConv_HiddenGradient, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
次に、誤差勾配を内部全結合層を通して伝播させる必要があります。そのために、対応するメソッドを呼び出します。
if(!cInputF.calcHiddenGradients(GetPointer(cF))) return false; if(!cInputS.calcHiddenGradients(GetPointer(cS))) return false;
この段階で、元データの2つの内部層の誤差勾配の2つのストリームの結果が得られます。単純にそれらを合計し、結果を前の層のレベルに移します。
if(!SumAndNormilize(cF.getOutput(), cS.getOutput(), prevLayer.getOutput(), 1, false)) return false; //--- return true; }
この場合、前の層の活性化関数は明示的には考慮しません。これは誤差勾配を正しく伝えるために重要です。ただし、ここにはニュアンスがあります。すべてのクラスのニューラル層は、活性化関数の微分の調整が、前の層のバッファに勾配を伝搬する前に実行されるように構築されています。これらの目的のために、フィードフォワードパスの間に、ソースデータの内部層のために、前の層の活性化関数を指定しました。したがって、誤差勾配が内部機能層を通して伝搬されたとき、直ちに誤差勾配を活性化関数の微分に調整しました。これは両方のストリームの勾配で同じです。出力では、活性化関数の微分で調整済みの誤差勾配を合計します。
2番目のバックプロパゲーションメソッドのアルゴリズム(重み行列updateInputWeightsの更新)は非常に単純です。ここでは、機能内部層の対応するメソッドを呼び出すだけです。
bool CNeuronCGConvOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cF.UpdateInputWeights(cInputF.AsObject())) return false; if(!cS.UpdateInputWeights(cInputS.AsObject())) return false; //--- return true; }
CNeuronCGConvOCLクラスの残りのメソッドの実装は、私の意見では、特に面白くありません。この連載ですでに何度も説明してきた、対応するメソッドの通常のアルゴリズムを使用しました。添付ファイルをご覧ください。また、記事執筆時に使用したすべてのプログラムの完全なコードも掲載されています。では、モデルのアーキテクチャを構築し、それらを訓練する上で、提案された方法の実装に移りましょう。
2.2 モデルアーキテクチャ
モデルのアーキテクチャを作成するために、元データの構造を維持したまま、以前の記事のモデルを使用します。これは意図的です。ADAPT構造では、特徴エンコーディングとして表示されるエンコーダモジュールを選択することもできます。また、Multi-Head Attentionの連続層からの社会的注意のブロックも含まれます。終点予測ブロックは、提案された中央線と比較することができます。信頼度ブロックは、軌道確率の予測に似ています。これによって、新しいモデルでの仕事がさらに面白くなります。
bool CreateTrajNetDescriptions(CArrayObj *encoder, CArrayObj *endpoints, CArrayObj *probability) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!endpoints) { endpoints = new CArrayObj(); if(!endpoints) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; }
エンコーダのモデルから始めましょう。モデルには、環境の状態に関する生データを入力します。
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
生のソースデータは、バッチデータ正規化ユニットで前処理されます。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
次に、著者が提案したLSTMブロックの代わりに、位置符号化を用いた 埋め込み層を残しました。この方法では、より深い履歴を保存して分析することができるからです。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; { int temp[] = {prev_count}; ArrayCopy(descr.windows, temp); } prev_count = descr.count = GPTBars; int prev_wout = descr.window_out = EmbeddingSize; if(!encoder.Add(descr)) { delete descr; return false; }
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPEOCL; descr.count = prev_count; descr.window = prev_wout; if(!encoder.Add(descr)) { delete descr; return false; }
また、エンコーダのモデルには社会的注目のブロックも入れました。元の手法に従い、これは2つの連続したグラフ畳み込み層で構成され、バッチ正規化層で区切られています。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCGConvOCL; descr.count = prev_count * prev_wout; descr.window = descr.count; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count*prev_wout; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCGConvOCL; descr.count = prev_count * prev_wout; descr.window = descr.count; if(!encoder.Add(descr)) { delete descr; return false; }
社会的注意ブロックの出力は、1つのMulti-Head Attention層を使用します。
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLMHAttentionOCL; descr.count = prev_count; descr.window = prev_wout; descr.step = 4; descr.window_out = 16; descr.layers = 1; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
私たちの場合、今後の値動きについて最も可能性の高い選択肢のいくつかを分析的に導き出せるような環境地図がありません。したがって、中央線の代わりに終点予測ブロックを残します。社会的注目度ブロックの結果をソースデータとして使用します。
//--- Endpoints endpoints.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = (prev_count * prev_wout); descr.activation = None; descr.optimization = ADAM; if(!endpoints.Add(descr)) { delete descr; return false; }
しかし、その前に全結合層でデータを前処理する必要があります。
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!endpoints.Add(descr)) { delete descr; return false; }
次に、軌跡解読ブロックには、この手法の著者が提案したLSTMブロックを使用します。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronLSTMOCL; descr.count = 3 * NForecast; descr.activation = None; descr.optimization = ADAM; if(!endpoints.Add(descr)) { delete descr; return false; }
ブロックの出力では、与えられたオプションの数に対して、終点のマルチモーダル表現を生成します。
軌道を選択する確率を予測するモデルに変化はありませんでした。前の2つのモデルの結果をモデルに与えます。
//--- Probability probability.Clear(); //--- Input layer if(!probability.Add(endpoints.At(0))) return false; //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = 3 * NForecast; descr.optimization = ADAM; descr.activation = SIGMOID; if(!probability.Add(descr)) { delete descr; return false; }
全結合層のブロックで処理します。
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!probability.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NForecast; descr.activation = None; descr.optimization = ADAM; if(!probability.Add(descr)) { delete descr; return false; }
SoftMax層を使用して、結果を確率の領域に変換します。
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = NForecast; descr.step = 1; descr.activation = None; descr.optimization = ADAM; if(!probability.Add(descr)) { delete descr; return false; } //--- return true; }
前作同様、値動きの詳細な軌跡を予測しようとはしません。主な目標は、金融市場で利益を上げることです。そこで、予測された値動きの終点に基づいて最適な行動方針を生成できるActorモデルを訓練します。
モデルアーキテクチャは、前回の記事から完全にコピーしたもので、添付ファイル「...\Experts\BaseLines\Trajectory.mqh」のCreateDescriptionsメソッドに記載されています。その詳しい説明は前回の記事でおこなっています。
2.3 モデルの訓練
提示されたモデルのアーキテクチャからわかるように、環境と相互作用するEAにおけるモデルの使用順序は変わっていません。したがって、この記事では、訓練データを収集し、訓練済みモデルをテストするためのプログラムのアルゴリズムの検討には触れません。モデル訓練アドバイザーに直行します。前回の記事と同様に、すべてのモデルを1つのEA「...\Experts\BaseLines\Study.mq5」で訓練します。
EA初期化メソッドでは、まずモデル訓練用の例データベースを読み込みます。
int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
そして、事前に訓練されたモデルを読み込み、必要に応じて新しいモデルを作成します。
//--- load models float temp; if(!BLEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !BLEndpoints.Load(FileName + "Endp.nnw", temp, temp, temp, dtStudied, true) || !BLProbability.Load(FileName + "Prob.nnw", temp, temp, temp, dtStudied, true) ) { CArrayObj *encoder = new CArrayObj(); CArrayObj *endpoint = new CArrayObj(); CArrayObj *prob = new CArrayObj(); if(!CreateTrajNetDescriptions(encoder, endpoint, prob)) { delete endpoint; delete prob; delete encoder; return INIT_FAILED; } if(!BLEncoder.Create(encoder) || !BLEndpoints.Create(endpoint) || !BLProbability.Create(prob)) { delete endpoint; delete prob; delete encoder; return INIT_FAILED; } delete endpoint; delete prob; delete encoder; }
if(!StateEncoder.Load(FileName + "StEnc.nnw", temp, temp, temp, dtStudied, true) || !EndpointEncoder.Load(FileName + "EndEnc.nnw", temp, temp, temp, dtStudied, true) || !Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true)) { CArrayObj *actor = new CArrayObj(); CArrayObj *endpoint = new CArrayObj(); CArrayObj *encoder = new CArrayObj(); if(!CreateDescriptions(actor, endpoint, encoder)) { delete actor; delete endpoint; delete encoder; return INIT_FAILED; } if(!Actor.Create(actor) || !StateEncoder.Create(encoder) || !EndpointEncoder.Create(endpoint)) { delete actor; delete endpoint; delete encoder; return INIT_FAILED; } delete actor; delete endpoint; delete encoder; //--- }
すべてのモデルを1つのOpenCLコンテキストに転送します。
OpenCL = Actor.GetOpenCL(); StateEncoder.SetOpenCL(OpenCL); EndpointEncoder.SetOpenCL(OpenCL); BLEncoder.SetOpenCL(OpenCL); BLEndpoints.SetOpenCL(OpenCL); BLProbability.SetOpenCL(OpenCL);
モデルのアーキテクチャをコントロールします。
Actor.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; }
BLEndpoints.getResults(Result); if(Result.Total() != 3 * NForecast) { PrintFormat("The scope of the Endpoints does not match forecast endpoints (%d <> %d)", 3 * NForecast, Result.Total()); return INIT_FAILED; }
BLEncoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; }
メソッドの最後に、補助データバッファを作成し、モデルの訓練開始のためのカスタムイベントを生成します。
if(!bGradient.BufferInit(MathMax(AccountDescr, NForecast), 0) || !bGradient.BufferCreate(OpenCL)) { PrintFormat("Error of create buffers: %d", GetLastError()); return INIT_FAILED; }
if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
非初期化メソッドでは、訓練済みモデルを保存し、動的オブジェクトのメモリをクリアします。
void OnDeinit(const int reason) { //--- if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE)) { Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true); StateEncoder.Save(FileName + "StEnc.nnw", 0, 0, 0, TimeCurrent(), true); EndpointEncoder.Save(FileName + "EndEnc.nnw", 0, 0, 0, TimeCurrent(), true); BLEncoder.Save(FileName + "Enc.nnw", 0, 0, 0, TimeCurrent(), true); BLEndpoints.Save(FileName + "Endp.nnw", 0, 0, 0, TimeCurrent(), true); BLProbability.Save(FileName + "Prob.nnw", 0, 0, 0, TimeCurrent(), true); } delete Result; delete OpenCL; }
モデルの訓練プロセスはTrainメソッドで実行されます。メソッドの本体では、まず軌道を選択する確率のベクトルを生成します。
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
その後、ローカル変数を作成します。
vector<float> result, target; matrix<float> targets, temp_m; bool Stop = false; //--- uint ticks = GetTickCount();
モデルの訓練ループのシステムを作成します。
for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++) { int tr = SampleTrajectory(probability); int batch = GPTBars + 48; int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - PrecoderBars - batch)); if(state <= 0) { iter--; continue; }
外側ループの本体では、経験リプレイバッファから軌跡をサンプリングし、その上で学習開始時の状態をサンプリングします。
ここで、選択された軌道上の訓練パッケージの最後の状態を決定し、再帰データバッファをクリアします。
BLEncoder.Clear(); BLEndpoints.Clear(); int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);
ネストされたループの本体では、経験リプレイバッファから1つの環境状態を取り出し、終点予測モデルとその確率のフィードフォワードパスを実行します。
for(int i = state; i < end; i++) { bState.AssignArray(Buffer[tr].States[i].state); //--- Trajectory if(!BLEncoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
if(!BLEndpoints.feedForward((CNet*)GetPointer(BLEncoder), -1, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
if(!BLProbability.feedForward((CNet*)GetPointer(BLEncoder), -1, (CNet*)GetPointer(BLEndpoints))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
ご覧の通り、上記の操作は前回の記事と大差ありません。ただし、変化はあるでしょう。これらは特に、訓練過程におけるモデルへの先験的知識の伝達に関するものです。というのも、環境に関する先験的な知識を用いることで、この手法の著者は、モデル自体のアーキテクチャを単純化しつつ、予測の精度を高めることに努めているからです。
実際、先験的な知識をモデルに伝達するには、いくつかの方法があります。生データを前処理して圧縮し、より有益なものにすることができます。これは、中央線を使用する手法の著者によって提案されました。
モデルを訓練する過程で目標値を生成する際に、先験的な知識を利用することもできます。これによってモデルは、ソースデータ中の最も重要なオブジェクトにより注意を払うようになります。もちろん、両方の方法を同時に使用することも可能です。
この記事では、2番目の方法を使用することにします。終点予測モデルの訓練のための目標値を準備するために、まずリプレイバッファから今後の値動きデータを収集します。
targets = matrix<float>::Zeros(PrecoderBars, 3); for(int t = 0; t < PrecoderBars; t++) { target.Assign(Buffer[tr].States[i + 1 + t].state); if(target.Size() > BarDescr) { matrix<float> temp(1, target.Size()); temp.Row(target, 0); temp.Reshape(target.Size() / BarDescr, BarDescr); temp.Resize(temp.Rows(), 3); target = temp.Row(temp.Rows() - 1); } targets.Row(target, t); } target = targets.Col(0).CumSum(); targets.Col(target, 0); targets.Col(target + targets.Col(1), 1); targets.Col(target + targets.Col(2), 2);
先験的知識の例として、MACD指標のシグナルを使用します。主線のデータは、環境の状態を表す配列の要素7に格納されています。シグナル線の値は、同じ配列の要素8にあります。シグナル線が主線を上回れば、現在のトレンドは強気と判断します。それ以外は弱気です。
int direct = (Buffer[tr].States[i].state[8] >= Buffer[tr].States[i].state[7] ? 1 : -1);
この方法はかなり単純化されており、トレンドを特定するためにもっと多くのシグナルや指標を使用するべきだという点には同意しますが、論文の枠組み内での明確な実施例を提供し、方法の影響を評価することを可能にするのは、まさにこのシンプルさです。最適な結果を得るためには、プロジェクトにおいてより包括的な方法を用いることをお勧めします。
トレンドの方向を決定した後、この方向における極値を決定します。また、今後の値動きの行列を、発見された極値に限定します。
ulong extr=(direct>0 ? target.ArgMax() : target.ArgMin()); if(extr==0) { direct=-direct; extr=(direct>0 ? target.ArgMax() : target.ArgMin()); } targets.Resize(extr+1, 3);
MACDシグナルはトレンドの変化より遅れていることに注意すべきです。したがって、極値を決定する際に、行列の最初の行に極値を見つけた場合は、トレンドの方向を反対に変え、極値を定義し直す。
環境に関する先験的な知識を用いて決定されたトレンドを用いることで、以前は次の最初のローソク足の方向を用いた場合に観察された目標値の確率性をいくらか軽減することができます。一般的に、これはモデルがトレンドと将来の値動きの方向性をより正しく判断するのに役立つはずです。
今後の値動きの切り捨て行列から、今後の値動きの極値によって目標値を決定します。
if(direct >= 0) { target = targets.Max(AXIS_HORZ); target[2] = targets.Col(2).Min(); } else { target = targets.Min(AXIS_HORZ); target[1] = targets.Col(1).Max(); }
以前と同様に、マルチモーダル終点空間全体から最も正確なモデル予測を決定し、バックプロパゲーション実行で、選択された予測のみを調整します。
BLEndpoints.getResults(result); targets.Reshape(1, result.Size()); targets.Row(result, 0); targets.Reshape(NForecast, 3); temp_m = targets; for(int i = 0; i < 3; i++) temp_m.Col(temp_m.Col(i) - target[i], i); temp_m = MathPow(temp_m, 2.0f); ulong pos = temp_m.Sum(AXIS_VERT).ArgMin(); targets.Row(target, pos); Result.AssignArray(targets);
こうして用意された目標値によって、終点予測モデルのパラメータと初期環境状態エンコーダを更新することができます。
if(!BLEndpoints.backProp(Result, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } if(!BLEncoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
ここでは確率予測モデルを調整しますが、このモデルの誤差勾配は、終点予測モデルやエンコーダには伝えません。
bProbs.AssignArray(vector<float>::Zeros(NForecast)); bProbs.Update((int)pos, 1); bProbs.BufferWrite(); if(!BLProbability.backProp(GetPointer(bProbs), GetPointer(BLEndpoints))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
次のステップは、Actor方策の訓練です。ここではまず、口座状況と未決済ポジションに関する情報を準備します。
//--- Policy float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bAccount.Clear(); bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance); bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bAccount.Add(Buffer[tr].States[i].account[2]); bAccount.Add(Buffer[tr].States[i].account[3]); bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance); double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(bAccount.GetIndex() >= 0) bAccount.BufferWrite();
次に、状態と予測される終点の埋め込みを作成します。
//--- State embedding if(!StateEncoder.feedForward((CNet *)GetPointer(BLEncoder), -1, (CBufferFloat*)GetPointer(bAccount))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } //--- Endpoint embedding if(!EndpointEncoder.feedForward((CNet *)GetPointer(BLEndpoints), -1, (CNet*)GetPointer(BLProbability))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
これまでの研究とは異なり、予測終点の埋め込みを生成するためには、目標値ではなく、訓練済みモデルの上のフィードフォワードパスの結果を使用します。これにより、終点予測モデルの結果に合わせてActorのパフォーマンスを調整できるようになります。
埋め込みを準備した後、Actorモデルをフィードフォワードで通過させます。
//--- Actor if(!Actor.feedForward((CNet *)GetPointer(StateEncoder), -1, (CNet*)GetPointer(EndpointEncoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
フィードフォワードパスの実行に成功すると、モデルのパラメータを更新するバックワードパスが続きます。ここで、Actorモデルを訓練するための目標値を用意する際に、先験的な知識も加えます。特に、ある方向または別の方向に取引を開始する前に、環境状態記述配列の4番目と5番目の要素にそれぞれ格納されているRSIとCCI指標の値を確認します。
if(direct > 0) { if(Buffer[tr].States[i].state[4] > 30 && Buffer[tr].States[i].state[5] > -100 ) { float tp = float(target[1] / _Point / MaxTP); result[1] = tp; int sl = int(MathMax(MathMax(target[1] / 3, -target[2]) / _Point, MaxSL / 10)); result[2] = float(sl) / MaxSL; result[0] = float(MathMax(risk / (value * sl), 0.01)) + FLT_EPSILON; } }
else { if(Buffer[tr].States[i].state[4] < 70 && Buffer[tr].States[i].state[5] < 100 ) { float tp = float((-target[2]) / _Point / MaxTP); result[4] = tp; int sl = int(MathMax(MathMax((-target[2]) / 3, target[1]) / _Point, MaxSL / 10)); result[5] = float(sl) / MaxSL; result[3] = float(MathMax(risk / (value * sl), 0.01)) + FLT_EPSILON; } }
この場合、MACD指標のシグナルを明示的に確認していません。今後の動きの方向を決定する際に、すでに考慮されているからです。
これらの準備された目標値があれば、複合Actorモデルを通してバックプロパゲーションを実行することができます。
Result.AssignArray(result); if(!Actor.backProp(Result, (CNet *)GetPointer(EndpointEncoder)) || !StateEncoder.backPropGradient(GetPointer(bAccount), (CBufferFloat *)GetPointer(bGradient)) || !EndpointEncoder.backPropGradient((CNet*)GetPointer(BLProbability)) ) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Actor誤差勾配を使用してエンコーダのパラメータを更新しますが、終点予測モデルは更新しません。
if(!BLEncoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
ループシステム内の操作が終了したら、訓練の進行状況をユーザーに知らせます。
if(GetTickCount() - ticks > 500) { double percent = (double(i - state) / ((end - state)) + iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Endpoints", percent, BLEndpoints.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Probability", percent, BLProbability.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
モデルの訓練が完了したら、チャートのコメント欄を消去します。モデルの訓練結果をログに出力し、EAの終了処理を開始します。
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Endpoints", BLEndpoints.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Probability", BLProbability.getRecentAverageError()); ExpertRemove(); //--- }
以上で、軌道予測モデルを最適化するための基本的な方法を提案するアルゴリズムの考察を終えます。また、ここで使用されているすべてのプログラムの完全なコードは添付ファイルにあります。
3.テスト
MQL5を用いて軌道予測モデルを最適化するための基本的な方法を実装しました。特に、グラフ畳み込み層を作成し、モデル訓練時の目標設定に環境に関する先験的知識を利用する方法を適用しました。これにより、モデルの層数が減り、モデルの複雑さが軽減され、動作スピードが向上する可能性があります。MetaTrader 5のストラテジーテスターで、訓練済みモデルを実際のデータで訓練テストする過程で、提案された方法の影響を評しました。
前回と同様に、モデルの訓練とテストは、EURUSD H1の2023年の最初の7ヶ月で実施されています。
モデルのアーキテクチャを構築する際、ソースデータ構造を保存することはすでに述べました。これにより、過去の記事で収集した経験リプレイバッファを訓練に使用することができました。以前に収集したデータファイルの名前をBaseLines.bdに変更するだけです。新しい訓練データセットを作成する場合は、環境相互作用EAを使用して、以前に説明した手法のいずれかを使用することができます。
モデルの訓練過程で目標値を生成するプロセスにより、訓練データセットを更新補完することなく、最適な結果が得られるまで使用することができました。
ただし、訓練の結果は期待したほど期待できないことが判明しました。訓練済みモデルをテストする際、テスト期間を1ヶ月から3ヶ月に増やしました。
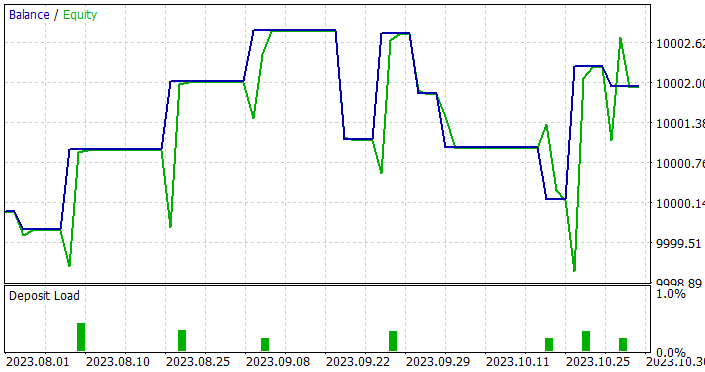
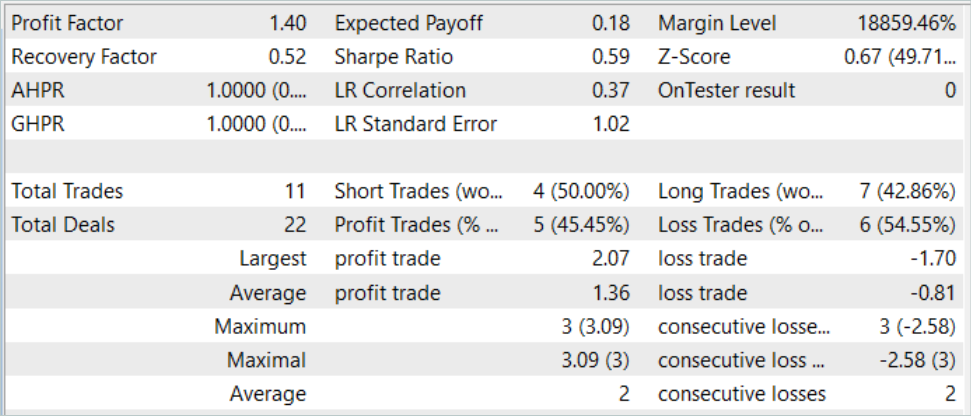
訓練サンプルとテストサンプルの両方で利益を生み出すことができるモデルができました。さらに、得られたモデルはプロフィットファクターが1.4と良好な安定性を示しました。過去のデータで7ヶ月間訓練した後、モデルは少なくとも3ヶ月間利益を生み出すことができます。これは、モデルがかなり安定した予測因子を特定できたことを示しているのかもしれません。
ただし、このモデルは取引回数という点ではかなり劣っていました。3ヶ月で11回の取引は非常に少ないです。これは私たちが望んだ結果ではありません。
結論
本稿では、軌道予測モデルのパフォーマンスを最適化するための基本的な方法を検討しました。提案された方法の実装により、ソースデータ中の真に有意な予測因子を識別できるモデルを訓練することが可能になります。これにより、訓練後、かなり長期間にわたって安定した運用が可能になります。
しかし、私たちの結果は、モデルによる決定が非常に保守的であることを示しています。これは取引件数の少なさに反映されています。この方向で研究を続けなければなりません。
参照文献
記事で使用されているプログラム
| # | ファイル名 | 種類 | 詳細 |
|---|---|---|---|
| 1 | Research.mq5 | EA | コレクションEAの例 |
| 2 | ResearchRealORL.mq5 | EA | Real-ORL法による事例収集のためのEA |
| 3 | Study.mq5 | EA | モデル訓練EA |
| 4 | Test.mq5 | EA | モデルテストEA |
| 5 | Trajectory.mqh | クラスライブラリ | システム状態記述の構造体 |
| 6 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークを作成するためのクラスのライブラリ |
| 7 | NeuroNet.cl | コードベース | OpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14187
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 多通貨エキスパートアドバイザーの開発(第2回):取引戦略の仮想ポジションへの移行
多通貨エキスパートアドバイザーの開発(第2回):取引戦略の仮想ポジションへの移行
 母集団最適化アルゴリズム:人工多社会的検索オブジェクト(MSO)
母集団最適化アルゴリズム:人工多社会的検索オブジェクト(MSO)
 MQL5入門(第7回):MQL5でEAを構築し、AI生成コードを活用するための初心者ガイド
MQL5入門(第7回):MQL5でEAを構築し、AI生成コードを活用するための初心者ガイド
 母集団最適化アルゴリズム:社会集団の進化(ESG)
母集団最適化アルゴリズム:社会集団の進化(ESG)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索