
Нейросети — это просто (Часть 75): Повышение производительности моделей прогнозирования траекторий
Введение
Прогнозирование траектории предстоящего ценового движения играет, наверное, одну из ключевых ролей в процессе построения торговых планов на рассматриваемый горизонт планирования. Точность таких прогнозов критически важна. С целью повышения качества прогнозирования траекторий мы приходим к усложнению наших моделей прогнозирования траекторий.
Однако, у этого процесса есть и «обратная сторона медали». Более сложные модели требуют больших вычислительных ресурсов. А значит повышаются затраты как на обучение моделей, так и на их эксплуатацию. Да, затраты на обучение моделей нужно учитывать. Но, порой, затраты на эксплуатацию могут оказаться критичными. Особенно если речь идет о торговле рыночными ордерами в режиме реального времени на высоко волатильном рынке. В подобных случаях мы обращаем внимание на методы повышения производительности наших моделей. И, желательно, без снижения качества прогнозирования будущих траекторий.
Методы прогнозирования траекторий, которые мы рассматривали в последних статьях, были заимствованы из индустрии построения моделей автономного движения. И, как ни странно, исследователи в данной отрасли сталкиваются с той же проблемой. Скорости движения транспортных средств предъявляют повышенные требования к времени принятия решения. А использования затратных моделей прогнозирования траекторий и принятия решений приводит не только к увеличению затрат времени на принятие решения, но и к удорожанию эксплуатируемого средства. Так как требуется установка более дорогого "железа". В данном контексте особый интерес представляет статья "Efficient Baselines for Motion Prediction in Autonomous Driving". Её авторы ставят перед собой задачу построения "легкой" модели прогнозирования траектории и выделяют следующие свои достижения:
- Выявление ключевой проблемы в размере моделей прогнозирования движения с последствиями для вывода в реальном времени и развертывания на устройствах с ограниченными ресурсами.
- Предложение нескольких эффективных базовых вариантов прогнозирования движения транспортных средств, которые не полагаются явно на исчерпывающий анализ контекстной карты высокого качества, а на предварительную информацию о карте, полученную в простом предварительном этапе обработки, служащем в качестве руководства в прогнозировании.
- Использование меньшего количества параметров и операций для достижения конкурентоспособной производительности с более низкой вычислительной стоимостью.
1. Методы повышения производительности
С учетом баланса между анализируемыми исходными данными и сложностью модели, авторы метода стремятся достичь конкурентоспособных результатов, используя мощные техники глубокого обучения, включая механизмы внимания и графовые нейронные сети (GNN). При этом уменьшается количество параметров и операций по сравнению с другими методами. В частности, в качестве исходных данных для своих моделей они используют:
- прошлые траектории агентов и их соответствующие взаимодействия, в качестве единственного входа для блока социального базового уровня;
- расширение, где добавляется упрощенное представление области допустимости агента в качестве дополнительного входа для картографической базы.
Таким образом, предлагаемые модели не требуют полностью аннотированных карт высокого качества или растеризованных представлений сцены для вычисления физического контекста.
Авторы метода предлагают использовать простой, но мощный алгоритм предварительной обработки карты, где траектория целевого агента изначально фильтруется. А затем вычисляется область допустимости, в которой целевой агент может взаимодействовать, учитывая только геометрическую информацию карты.
Социальный базовый уровень использует в качестве исходных данных прошлые траектории наиболее значимых препятствий в виде относительных смещений для подачи в модуль Кодировщика. Затем социальная информация вычисляется с использованием графовой нейронной сети. В своей работе авторы метода используют слои CrystalGraph Convolutional Network (Crystal-GCN), и Multi-Head Self Attention (MHSA) для выделения наиболее значимых взаимодействий между агентами. После чего в модуле Декодера эта латентная информация декодируется с использованием авторегрессивной стратегии, в которой вывод на i-м шаге зависит от предыдущего.
Одной из особенностей предложенного метода является анализ взаимодействия с агентами, о которых есть информация на всем временном горизонте Th = Tobs + Tlen. В то же время уменьшается количество агентов, которые нужно учитывать в сложных сценариях движения. Вместо использования абсолютных 2D-представлений сверху, входом для агента i является серия относительных смещений:
![]()
Авторы метода не ограничивают и не фиксируют количество агентов в последовательности. Для учета относительных смещений всех агентов используется один LSTM-блок, в котором вычисляется временная информации каждого агента в последовательности.
После кодирования анализируемой истории каждого транспортного средства в последовательности вычисляются взаимодействия между агентами, с целью получения наиболее значимой социальной информации. Для этого строится граф взаимодействий. На практике для построения графа используется слой Crystal-GCN. Затем применяется MHSA для улучшения обучения взаимодействий агент-агент.
Прежде чем создать механизм взаимодействия, авторы метода разбивают временную информацию на соответствующие сцены. При этом учитывается, что каждый сценарий движения может иметь разное количество агентов. Механизм взаимодействия определен как двунаправленный полностью связанный граф, где начальные признаки узла v0i представлены латентной временной информацией для каждого транспортного средства hi,out, вычисленной кодировщиком истории движения. С другой стороны, ребра от узла k к узлу l представлены вектором расстояния ek,l между соответствующими агентами в момент времени tobs,len в абсолютных координатах:
![]()
Учитывая граф взаимодействий (узлы и ребра), Crystal-GCN определяется как:
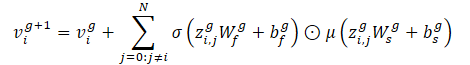
Этот оператор позволяет внедрять признаки ребра для обновления признаков узла на основе расстояния между транспортными средствами. Авторы метода используют 2 слоя Crystal-GCN с ReLU и батч-нормализацией как нелинейностями между слоями.
σ и μ - это функции активации сигмоида и софтплюс соответственно. Кроме того, zi,j=(vi‖vj‖ei,j) представляет собой конкатенацию признаков двух узлов в слое GNN и соответствующего ребра, N представляет собой общее количество агентов на сцене, а W и b - веса и смещения соответствующих слоев.
После прохождения графа взаимодействия каждый обновленный признак узла vi содержит информацию о временном и социальном контексте агента i. Тем не менее, в зависимости от текущего положения и прошлой траектории агенту может потребоваться обращать внимание на конкретную социальную информацию. Для моделирования этого авторы метода используют механизм много-голового Self-Attention c 4 головами, который применяется к обновленной матрице признаков узла V, содержащей признаки узла vi в виде строк.
Каждая строка окончательной матрицы социального внимания SATT (выход модуля социального внимания, после механизмов GNN и MHSA) представляет собой признак взаимодействия для агента i с окружающими агентами, учитывая информацию о времени под капотом.
Далее авторы метода расширяют социальную базовую модель, используя минимальную информацию о карте, из которой дискретизируется область P целевого агента как подмножество r случайно выбранных точек {p0, p1...pr} вокруг вероятных центральных линий (высокоуровневые и структурированные признаки), учитывая скорость и ускорение целевого агента в последнем кадре наблюдения. Это шаг предварительной обработки карты, поэтому модель никогда не видит карту высокого разрешения.
Основываясь на законах физики, авторы метода рассматривают транспортное средство как жесткую структуру без резких изменений движения между последовательными метками времени. Соответственно, при описании задачи движения по дороге обычно наиболее важные признаки находятся в конкретном направлении (впереди по ходу движения). Это позволяет получить упрощенную версию карты.
Информация о пройденных траекториях часто содержат шум, связанный с процессом сбора данных в реальном мире. Чтобы оценить динамические переменные целевого агента в последнем кадре наблюдения tobs,len, авторы метода предлагают сначала фильтровать прошлые наблюдения целевого агента, используя алгоритм наименьших квадратов по каждой из осей. Предполагается, что агент движется с постоянным ускорением и мы можем вычислить динамические характеристики (скорость и ускорение) целевого агента. Затем вычисляется вектор оценки скорости и ускорения. Кроме того, эти векторы суммируются как скаляры для получения плавной оценки, присваивая меньший вес (больший коэффициент забывания λ) первым наблюдениям. Таким образом, последние наблюдения играют ключевую роль для определения текущего кинематического состояния агента:
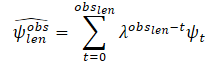
где
obslen количество наблюдаемых кадров, ψt оцененная скорость/ускорение на кадре t, λ ∈ (0, 1) коэффициент забывания.
После вычисления кинематического состояния оценивается пройденное расстояние, предполагая физическую модель на основе ускорения с постоянной скоростью поворота в любой момент времени t.
Затем эти кандидаты в правдоподобные траектории полосы обрабатываются для использования их в качестве правдоподобной физической информации. Сначала находим ближайшую точку к последним данным наблюдения целевого агента, которая будет представлять начальную точку правдоподобной центральной линии. После чего оцениваем пройденное расстояние вдоль исходных центральных линий. Определяем индекс конечной точки p центральной линии m как точку, где накопленное расстояние (учитывая евклидово расстояние между каждой точкой) больше или равно предварительно вычисленному отклонению.
А далее выполняется кубическая интерполяцию между начальной и конечной точками соответствующей центральной линии m, чтобы получить шаги на горизонт планирования. Проведенные авторами метода эксперименты демонстрируют, что лучшая априорная информация, учитывая среднее и медианное расстояние L2 по всему набору валидации между конечной точкой истинной траектории целевого агента и конечными точками отфильтрованных центральных линий, достигается при учете скорости и ускорения в кинематическом состоянии и фильтрации входа методом наименьших квадратов.
В дополнение к этим высокоуровневым и структурированным центральным линиям авторы метода предлагают применять искажения положения точек ко всем правдоподобным центральным линиям в соответствии с нормальным распределением N(0, 0.2). Это позволит дискретизировать правдоподобную область P как подмножество r случайно выбранных точек {p0, p1...pr} вокруг правдоподобных центральных линий. И таким образом получить общее представление о правдоподобной области, определенной как признаки низкого уровня. Авторы метода используют нормальное распределение N в качестве дополнительного регуляризационного члена, вместо использования границ полос. Это позволит предотвратить переобучение в модуле кодирования, аналогично тому, как к предыдущим траекториям применяется аугментация данных.
Для вычисления латентной картографической информации используются кодировщики области и центральной линии. Которые обрабатывают признаки карты низкого и высокого уровня, соответственно. Каждый из этих кодировщиков представлен многослойным перцептроном (MLP). Сначала сглаживаем информацию вдоль размерности точек, чередуя информацию по осям координат. Затем соответствующий MLP (3 слоя, с батч-нормализацией, ReLU и DropOut в первом слое) преобразует интерпретируемые абсолютные координаты вокруг начала координат в представительную латентную физическую информацию. Статический физический контекст (вывод от кодировщика области) будет служить общим латентным представлением для различных режимов, в то время как конкретный физический контекст будет иллюстрировать конкретную картографическую информацию для каждого режима.
Декодер будущей траектории представляет собой третий компонент предлагаемых базовых моделей. Модуль состоит из LSTM-блока, который рекурсивно оценивает относительные перемещения для будущих временных шагов так же, как изучались пройденные относительные перемещения в Кодировщике истории движения. В отношении социального базового варианта модель использует социальный контекст, вычисленный модулем социального взаимодействия, обращая внимание только на данные целевого агента. Только социальный контекст представляет собой весь трафик в сценарии, представляя входной скрытый вектор авторегрессионного предиктора LSTM.
С точки зрения картографического базового варианта для режима m авторы метода предлагают выявлять латентный контекст трафика как конкатенацию социального контекста, статического физического контекста и конкретного физического контекста, который будет служить входным скрытым вектором LSTM-декодера.
Относительно исходных данных LSTM-блока в социальном случае он представлен закодированными прошлыми n относительными перемещениями целевого агента после пространственного вложения, тогда как картографический базовый вариант добавляет закодированный вектор расстояния между текущим абсолютным положением целевого агента и текущей центральной линией, а также текущий скалярный временной штамп t. В обоих случаях (социальный и картографический) результаты LSTM-блока обрабатываются с использованием стандартного полносвязанного слоя.
После получения относительного прогноза на временном шаге t, сдвигаем начальные данные прошлого наблюдения таким образом, чтобы внести наше последнее вычисленное относительное перемещение в конец вектора, удаляя первые данные.
После вычисления многомодальных прогнозов они конкатенируются и обрабатываются с использованием остаточной MLP для получения уверенности (чем выше уверенность, тем более вероятен режим, и ближе к истине).
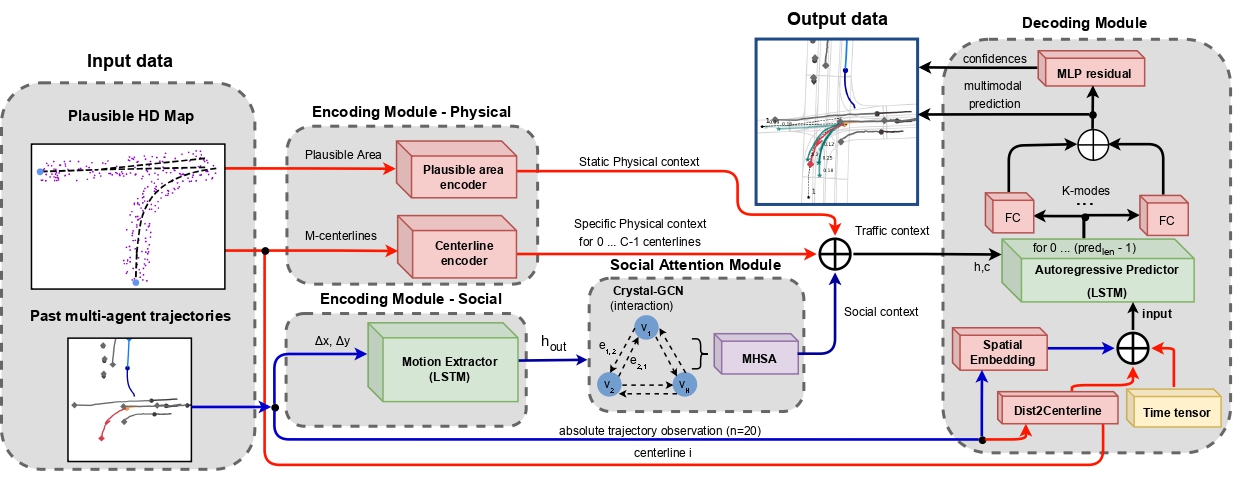
Авторская визуализация метода представлена ниже. На ней синими линиями представлен поток социальной информации, а красными отображается передача информации о карте.
2. Реализация средствами MQL5
После рассмотрения теоретических аспектов предложенных подходов мы переходим к их практической реализации средствами MQL5. Как можно заметить, авторы метода разделили модель на блоки. В каждом блоке используется минимальное количество слоев. При этом упрощение архитектуры отдельных блоков сопровождается дополнительным анализом данных с использованием априорной информации об анализируемой среде. В частности, осуществляется предварительная обработка карты и фильтрация пройденных траекторий. Что позволяет снизить шум и объем исходных данных, без потери качества построения прогнозных траекторий.
2.1 Создание слоя CrystalGraph Convolutional Network
Кроме того, среди предложенных подходов мы встречаем графовые нейронные слои, с которыми не встречались ранее. Соответственно, прежде чем перейти к построению предложенного алгоритма нам предстоит создать новый слой в нашей библиотеке.
Предложенный авторами метода к использованию слой CrystalGraph Convolutional Network можно представить формулой.
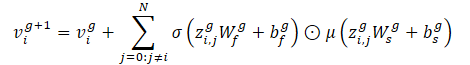
По существу, мы здесь видим поэлементное умножение результатов работы 2 полносвязных слоев. Один из них активируется сигмоидой и представляет обучаемую бинарную матрицу наличия связей между вершинами графа. Второй слой активируется функцией SoftPlus, которая является мягким аналогом ReLU.
Для реализации CrystalGraph Convolutional Network мы создадим новый класс CNeuronCGConvOCL с наследованием базового функционала от CNeuronBaseOCL.
class CNeuronCGConvOCL : public CNeuronBaseOCL { protected: CNeuronBaseOCL cInputF; CNeuronBaseOCL cInputS; CNeuronBaseOCL cF; CNeuronBaseOCL cS; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL); //--- virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL); public: CNeuronCGConvOCL(void) {}; ~CNeuronCGConvOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch); virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer); //--- virtual int Type(void) const { return defNeuronCGConvOCL; } //--- methods for working with files virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); virtual CLayerDescription* GetLayerInfo(void); virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); };
Наш новый класс получает стандартный набор методов для переопределения и базовый функционал от родительского класса. Для реализации же алгоритма графовой свертки мы создадим 4 внутренних полносвязных слоя:
- 2 для записи исходных данных и градиентов ошибки при обратном проходе (cInputF и cInputS)
- 2 для выполнения функционала (cF и cS).
Все внутренние объекты мы создадим статическими, поэтому конструктор и деструктор класса останутся «пустыми».
В методе инициализации нашего класса Init мы сначала вызовем аналогичный метод родительского класса, в котором реализованы все необходимые контроли данных, полученных от внешней программы, и инициализируются унаследованные объекты и переменные.
bool CNeuronCGConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint numNeurons, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, numNeurons, optimization_type, batch)) return false; activation = None;
После чего мы последовательно инициализируем добавленные внутренние объекты путем вызова их методов инициализации.
if(!cInputF.Init(numNeurons, 0, OpenCL, window, optimization, batch)) return false; if(!cInputS.Init(numNeurons, 1, OpenCL, window, optimization, batch)) return false; cInputF.SetActivationFunction(None); cInputS.SetActivationFunction(None); //--- if(!cF.Init(0, 2, OpenCL, numNeurons, optimization, batch)) return false; cF.SetActivationFunction(SIGMOID); if(!cS.Init(0, 3, OpenCL, numNeurons, optimization, batch)) return false; cS.SetActivationFunction(LReLU); //--- return true; }
Обратите внимание, что для внутренних слоев записи исходных данных мы указали отсутствие функции активации. А для функциональных слоев указали функции активации, предусмотренные алгоритмом создаваемого слоя. При этом сам слой CNeuronCGConvOCL не имеет функции активации.
После инициализации объекта мы переходим к созданию метода прямого прохода feedForward. В параметрах метод получает указатель на объект предыдущего нейронного слоя, на выходе которого содержатся для нас исходные данные.
bool CNeuronCGConvOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL || !NeuronOCL.getOutput() || NeuronOCL.getOutputIndex() < 0) return false;
И в теле метода мы сразу проверяем актуальность полученного указателя.
После успешного прохождения блока контролей нам предстоит осуществить перенос исходных данных из буфера предыдущего слоя в буферы наших 2 внутренних слоев исходных данных. При этом мы помним, что все операции с нашими нейронными слоями мы осуществляем на стороне OpenCL контекста. Соответственно, копирование данных нам так же предстоит осуществить на в памяти OpenCL контекста. Но мы пойдем немного дальше и осуществим "копирование" без физического переноса данных. Мы просто осуществим подмену указателя на буфер результатов во внутренних слоях и передадим им указатель на буфер результатов предыдущего слоя. Одновременно укажем функцию активации предыдущего слоя.
if(cInputF.getOutputIndex() != NeuronOCL.getOutputIndex()) { if(!cInputF.getOutput().BufferSet(NeuronOCL.getOutputIndex())) return false; cInputF.SetActivationFunction((ENUM_ACTIVATION)NeuronOCL.Activation()); } if(cInputS.getOutputIndex() != NeuronOCL.getOutputIndex()) { if(!cInputS.getOutput().BufferSet(NeuronOCL.getOutputIndex())) return false; cInputS.SetActivationFunction((ENUM_ACTIVATION)NeuronOCL.Activation()); }
Таким образом, при работе с внутренними слоями мы получаем прямой доступ к буферу результатов предыдущего слоя без физического копирования данных. Задача переноса данных выполнена с минимальными затратами ресурсов. Более того, мы исключили создание двух дополнительных буферов в OpenCL контексте, тем самым оптимизировали использование памяти.
И далее мы просто вызываем методы прямого прохода внутренних функциональных слоев.
if(!cF.FeedForward(GetPointer(cInputF))) return false; if(!cS.FeedForward(GetPointer(cInputS))) return false;
В результате данных операций мы получили матрицы контекста и связей графа. И далее нам предстоит осуществить их поэлементное умножение. Для выполнения этой операции мы воспользуемся кернелом Dropout, который мы создавали для поэлементного умножения исходных данных на маску. В нашем случае мы имеем иную подоплеку на ту же математическую операцию.
Передадим необходимые параметры и исходные данные в кернел.
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = int(Neurons() + 3) / 4; ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_input, cF.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_map, cS.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_Dropout, def_k_dout_out, Output.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_Dropout, def_k_dout_dimension, Neurons())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.Execute(def_k_Dropout, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
После чего поставим его в очередь выполнения.
Следующим этапом нам предстоит реализовать функционал обратного прохода. И здесь нам предстоит начать работу с создания кернела на стороне OpenCL программы. Дело в том, что распределение градиента ошибки от предыдущего слоя начинается с передачи его на внутренние слои в соответствии с их влиянием на конечный результат. Для этого нам предстоит умножить полученный градиент ошибки на результаты прямого прохода второго функционального слоя. И, чтобы не вызывать выше используемый кернел поэлементного умножения 2 раза, мы создадим новый кернел, в котором получим градиенты ошибок для обоих слоев за 1 проход.
В параметрах кернела CGConv_HiddenGradient мы будем передавать указатели на 5 буферов данных и типы функций активации обоих слоёв.
__kernel void CGConv_HiddenGradient(__global float *matrix_g,///<[in] Tensor of gradients at current layer __global float *matrix_f,///<[in] Previous layer Output tensor __global float *matrix_s,///<[in] Previous layer Output tensor __global float *matrix_fg,///<[out] Tensor of gradients at previous layer __global float *matrix_sg,///<[out] Tensor of gradients at previous layer int activationf,///< Activation type (#ENUM_ACTIVATION) int activations///< Activation type (#ENUM_ACTIVATION) ) { int i = get_global_id(0);
Запускать кернел мы будем в одномерном пространстве задач по числу нейронов в наших слоях. И в теле кернела мы сразу определяем смещение в буферах данных до анализируемого элемента по идентификатору потока.
Далее, с целью уменьшения "дорогих" операций по обращению к глобальной памяти GPU мы сохраним данные анализируемого элемента в локальных переменных, обращение к которым осуществляется в разы быстрее.
float grad = matrix_g[i]; float f = matrix_f[i]; float s = matrix_s[i];
На данном этапе у нас есть все данные, необходимые для вычисления градиентов ошибки на обоих слоях, и мы их вычисляем.
float sg = grad * f; float fg = grad * s;
Но прежде, чем записать полученные значения в элементы глобальных буферов данных, нам предстоит скорректировать найденные градиенты ошибки на соответствующие функции активации.
switch(activationf) { case 0: f = clamp(f, -1.0f, 1.0f); fg = clamp(fg + f, -1.0f, 1.0f) - f; fg = fg * max(1 - pow(f, 2), 1.0e-4f); break; case 1: f = clamp(f, 0.0f, 1.0f); fg = clamp(fg + f, 0.0f, 1.0f) - f; fg = fg * max(f * (1 - f), 1.0e-4f); break; case 2: if(f < 0) fg *= 0.01f; break; default: break; }
switch(activations) { case 0: s = clamp(s, -1.0f, 1.0f); sg = clamp(sg + s, -1.0f, 1.0f) - s; sg = sg * max(1 - pow(s, 2), 1.0e-4f); break; case 1: s = clamp(s, 0.0f, 1.0f); sg = clamp(sg + s, 0.0f, 1.0f) - s; sg = sg * max(s * (1 - s), 1.0e-4f); break; case 2: if(s < 0) sg *= 0.01f; break; default: break; }
В завершении работы кернела мы сохраняем результаты операций в соответствующие элементы глобальных буферов данных.
matrix_fg[i] = fg; matrix_sg[i] = sg; }
После создания кернела мы возвращаемся к работе над методами нашего класса. Функционал распределения градиента ошибки реализован в методе calcInputGradients, в параметрах которого мы передадим указатель на объект предыдущего слоя. И в теле метода мы сразу проверяем актуальность полученного указателя.
bool CNeuronCGConvOCL::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer || !prevLayer.getGradient() || prevLayer.getGradientIndex() < 0) return false;
Далее нам предстоит вызвать выше описанный кернел распределения градиента по внутренним слоям CGConv_HiddenGradient. Здесь мы сначала определяем пространство задач.
uint global_work_offset[1] = {0}; uint global_work_size[1]; global_work_size[0] = Neurons();
Затем передаем необходимые параметры в кернел.
ResetLastError(); if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_f, cF.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_fg, cF.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_s, cS.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_sg, cS.getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_CGConv_HiddenGradient, def_k_cgc_matrix_g, getGradientIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activationf, cF.Activation())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_CGConv_HiddenGradient, def_k_cgc_activations, cS.Activation())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
И ставим кернел в очередь выполнения.
if(!OpenCL.Execute(def_k_CGConv_HiddenGradient, 1, global_work_offset, global_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; }
Далее нам предстоит провести градиент ошибки через внутренние полносвязные слои. Для этого мы просто вызываем их соответствующие методы.
if(!cInputF.calcHiddenGradients(GetPointer(cF))) return false; if(!cInputS.calcHiddenGradients(GetPointer(cS))) return false;
На данном этапе мы имеем результаты 2 потоков градиентов ошибки на 2 внутренних слоях исходных данных. Мы просто суммируем их и результат передаем на уровень предыдущего слоя.
if(!SumAndNormilize(cF.getOutput(), cS.getOutput(), prevLayer.getOutput(), 1, false)) return false; //--- return true; }
Обратите внимание, что в данном случае мы нигде явно не учитываем функцию активации предыдущего слоя. А это важно для правильной передачи градиента ошибки. Но здесь есть один момент. Все наши классы нейронных слоев построены таким образом, что корректировка на производную функции активации осуществляется перед передачей градиента в буфер предыдущего слоя. Именно для этих целей при прямом проходе мы указали на для наших внутренних слоев исходных данных функцию активации предыдущего слоя. Таким образом, при прохождении градиента ошибка через наши внутренние функциональные слои мы сразу скорректировали градиент ошибки на производную функции активации, которая одинакова для градиентов обоих потоков. И на выходе мы суммируем градиенты ошибки уже скорректированные на производную функции активации.
Алгоритм второго метода обратного прохода (обновления матрицы весовых коэффициентов updateInputWeights) довольно прост. Здесь мы лишь вызываем соответствующие методы функциональных внутренних слоев.
bool CNeuronCGConvOCL::updateInputWeights(CNeuronBaseOCL *NeuronOCL) { if(!cF.UpdateInputWeights(cInputF.AsObject())) return false; if(!cS.UpdateInputWeights(cInputS.AsObject())) return false; //--- return true; }
Реализация остальных методов нашего класса CNeuronCGConvOCL, на мой взгляд, не представляет особого интереса. В них я использовал обычные алгоритмы для соответствующих методов, которые уже многократно были описаны в рамках данной серии статей. И я предлагаю Вам самостоятельно ознакомиться с ними во вложении. Там же Вы найдете полный код всех программ, используемых при подготовке данной статьи. А мы переходим к реализации предложенных подходов в построении архитектуры моделей и их обучении.
2.2 Архитектура моделей
Начиная работу над архитектурой моделей сразу скажу, что за основу мы взяли модели из предыдущей статьи и сохранили структуру исходных данных. Это не случайно. В структуре ADAPT так же можно выделить модуль кодировщика, который представлен в виде Feature Encoding. Он же включает блок социального внимания из последовательных слоев много-голового внимания. Блок прогнозирования конечных точек можно сопоставить с предложенными центральными линиями. А блок уверенности аналогичен прогнозированию вероятностей траекторий. И тем интереснее будет посмотреть на результаты работы моделей.
bool CreateTrajNetDescriptions(CArrayObj *encoder, CArrayObj *endpoints, CArrayObj *probability) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!endpoints) { endpoints = new CArrayObj(); if(!endpoints) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; }
И начнем работу с модели кодировщика. На вход модели мы подаем сырые исходные данные о состоянии окружающей среды.
//--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Сырые исходные данные проходят первичную обработку в блоке пакетной нормализации данных.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Далее вместо предложенного авторами LSTM-блока я оставил слой Эмбединга с позиционным кодированием, так как такой подход позволяет сохранять и анализировать более глубокую историю.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronEmbeddingOCL; { int temp[] = {prev_count}; ArrayCopy(descr.windows, temp); } prev_count = descr.count = GPTBars; int prev_wout = descr.window_out = EmbeddingSize; if(!encoder.Add(descr)) { delete descr; return false; }
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronPEOCL; descr.count = prev_count; descr.window = prev_wout; if(!encoder.Add(descr)) { delete descr; return false; }
В модель Энкодера я так же включил блок социального внимания. Который в соответствии с предложениями авторов метода состоит из 2 последовательных слоев графовой свертки, разделенных слоем пакетной нормализации.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCGConvOCL; descr.count = prev_count * prev_wout; descr.window = descr.count; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count*prev_wout; descr.batch = MathMax(1000, GPTBars); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCGConvOCL; descr.count = prev_count * prev_wout; descr.window = descr.count; if(!encoder.Add(descr)) { delete descr; return false; }
На выходе блока социального внимания используется 1 слой много-голового внимания.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMLMHAttentionOCL; descr.count = prev_count; descr.window = prev_wout; descr.step = 4; descr.window_out = 16; descr.layers = 1; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
В нашем случае отсутствует карта окружающей среды, по которой мы бы могли аналитическим способом вывести какие-то наиболее вероятные варианты предстоящего ценового движения. Поэтому вместо центральных линий мы оставляем блок прогнозирования конечных точек. В качестве исходных данных он будет использовать результаты работы блока социального внимания.
//--- Endpoints endpoints.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = (prev_count * prev_wout); descr.activation = None; descr.optimization = ADAM; if(!endpoints.Add(descr)) { delete descr; return false; }
Которые мы сначала обработаем полносвязным слоем.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = SIGMOID; descr.optimization = ADAM; if(!endpoints.Add(descr)) { delete descr; return false; }
А затем воспользуемся LSTM-блоком, как было предложено авторами метода для блока декодирования траекторий.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronLSTMOCL; descr.count = 3 * NForecast; descr.activation = None; descr.optimization = ADAM; if(!endpoints.Add(descr)) { delete descr; return false; }
На выходе блока мы генерируем мульти-модальное представление конечных точек для заданного количества вариантов.
Модель прогнозирования вероятностей выбора траекторий осталась без изменений. На вход модели мы подаем результаты работы 2 предыдущих моделей.
//--- Probability probability.Clear(); //--- Input layer if(!probability.Add(endpoints.At(0))) return false; //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = 3 * NForecast; descr.optimization = ADAM; descr.activation = SIGMOID; if(!probability.Add(descr)) { delete descr; return false; }
Обрабатываем их блоком полносвязных слоев.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!probability.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NForecast; descr.activation = None; descr.optimization = ADAM; if(!probability.Add(descr)) { delete descr; return false; }
А результаты переводим в область вероятностей с использованием слоя SoftMax.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = NForecast; descr.step = 1; descr.activation = None; descr.optimization = ADAM; if(!probability.Add(descr)) { delete descr; return false; } //--- return true; }
Как и в предыдущей работе, мы не будем пытаться спрогнозировать детальную траекторию ценового движения. Наша основная задача получение прибыли на финансовых рынках. И поэтому мы обучим модель Актера, способного генерировать оптимальную политику поведения на основе прогнозных конечных точек ценового движения.
Архитектура модели полностью перенесена из предыдущей работы и представлена во вложении в методе CreateDescriptions файла «...\Experts\BaseLines\Trajectory.mqh». А ее детальное описание представлено в предыдущей статье.
2.3 Обучение моделей
Как можно заметить из представленной архитектуры моделей, последовательность их использования в советниках взаимодействия с окружающей средой осталась без изменений. Поэтому в рамках данной статьи мы не будем останавливаться на рассмотрении алгоритмов программ сбора обучающих данных и тестирования обученных моделей. Мы сразу переходим к советнику обучения моделей. Как и в прошлой работе, все модели обучаются в одном советнике «...\Experts\BaseLines\Study.mq5»
В методе инициализации советника мы сначала загружаем базу примеров для обучения моделей.
int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
После чего загружаем предварительно обученные модели и, при необходимости, создаем новые.
//--- load models float temp; if(!BLEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !BLEndpoints.Load(FileName + "Endp.nnw", temp, temp, temp, dtStudied, true) || !BLProbability.Load(FileName + "Prob.nnw", temp, temp, temp, dtStudied, true) ) { CArrayObj *encoder = new CArrayObj(); CArrayObj *endpoint = new CArrayObj(); CArrayObj *prob = new CArrayObj(); if(!CreateTrajNetDescriptions(encoder, endpoint, prob)) { delete endpoint; delete prob; delete encoder; return INIT_FAILED; } if(!BLEncoder.Create(encoder) || !BLEndpoints.Create(endpoint) || !BLProbability.Create(prob)) { delete endpoint; delete prob; delete encoder; return INIT_FAILED; } delete endpoint; delete prob; delete encoder; }
if(!StateEncoder.Load(FileName + "StEnc.nnw", temp, temp, temp, dtStudied, true) || !EndpointEncoder.Load(FileName + "EndEnc.nnw", temp, temp, temp, dtStudied, true) || !Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true)) { CArrayObj *actor = new CArrayObj(); CArrayObj *endpoint = new CArrayObj(); CArrayObj *encoder = new CArrayObj(); if(!CreateDescriptions(actor, endpoint, encoder)) { delete actor; delete endpoint; delete encoder; return INIT_FAILED; } if(!Actor.Create(actor) || !StateEncoder.Create(encoder) || !EndpointEncoder.Create(endpoint)) { delete actor; delete endpoint; delete encoder; return INIT_FAILED; } delete actor; delete endpoint; delete encoder; //--- }
Затем переносим все модели в единый контекст OpenCL.
OpenCL = Actor.GetOpenCL(); StateEncoder.SetOpenCL(OpenCL); EndpointEncoder.SetOpenCL(OpenCL); BLEncoder.SetOpenCL(OpenCL); BLEndpoints.SetOpenCL(OpenCL); BLProbability.SetOpenCL(OpenCL);
И осуществляем контроль архитектуры моделей.
Actor.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; }
BLEndpoints.getResults(Result); if(Result.Total() != 3 * NForecast) { PrintFormat("The scope of the Endpoints does not match forecast endpoints (%d <> %d)", 3 * NForecast, Result.Total()); return INIT_FAILED; }
BLEncoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; }
В завершении метода создаем вспомогательные буфера данных и генерируем пользовательское событие начала обучения моделей.
if(!bGradient.BufferInit(MathMax(AccountDescr, NForecast), 0) || !bGradient.BufferCreate(OpenCL)) { PrintFormat("Error of create buffers: %d", GetLastError()); return INIT_FAILED; }
if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
В методе деинициализации не забываем сохранить обученные модели и очистить память динамических объектов.
void OnDeinit(const int reason) { //--- if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE)) { Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true); StateEncoder.Save(FileName + "StEnc.nnw", 0, 0, 0, TimeCurrent(), true); EndpointEncoder.Save(FileName + "EndEnc.nnw", 0, 0, 0, TimeCurrent(), true); BLEncoder.Save(FileName + "Enc.nnw", 0, 0, 0, TimeCurrent(), true); BLEndpoints.Save(FileName + "Endp.nnw", 0, 0, 0, TimeCurrent(), true); BLProbability.Save(FileName + "Prob.nnw", 0, 0, 0, TimeCurrent(), true); } delete Result; delete OpenCL; }
Непосредственно обучение моделей осуществляется в методе Train. В теле метода мы сначала генерируем вектор вероятностей выбора траекторий.
void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
После чего мы создаем локальные переменные.
vector<float> result, target; matrix<float> targets, temp_m; bool Stop = false; //--- uint ticks = GetTickCount();
И создаем систему циклов обучения моделей.
for(int iter = 0; (iter < Iterations && !IsStopped() && !Stop); iter ++) { int tr = SampleTrajectory(probability); int batch = GPTBars + 48; int state = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2 - PrecoderBars - batch)); if(state <= 0) { iter--; continue; }
В теле внешнего цикла мы сэмплируем траекторию из буфера воспроизведения опыта и состояние начала обучения на ней.
Тут же мы определим последнее состояния пакета обучения на выбранной траектории и очистим рекуррентные буфера данных.
BLEncoder.Clear(); BLEndpoints.Clear(); int end = MathMin(state + batch, Buffer[tr].Total - PrecoderBars);
В теле вложенного цикла мы возьмем одно состояние окружающей среды из буфера воспроизведения опыта и осуществим прямые проходы моделей прогнозирования конечных точек и их вероятностей.
for(int i = state; i < end; i++) { bState.AssignArray(Buffer[tr].States[i].state); //--- Trajectory if(!BLEncoder.feedForward((CBufferFloat*)GetPointer(bState), 1, false, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
if(!BLEndpoints.feedForward((CNet*)GetPointer(BLEncoder), -1, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
if(!BLProbability.feedForward((CNet*)GetPointer(BLEncoder), -1, (CNet*)GetPointer(BLEndpoints))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Как можно заметить, описанные выше операции мало чем отливаются от аналогичных в предыдущей статье. Но изменения все же будут. И коснутся они именно передачи априорных знаний модели в процессе обучения. Ведь именно использованием априорных знаний об окружающей среде авторы метода стремятся повысить точность прогнозов при упрощении архитектуры самих моделей.
На самом деле есть несколько подходов в передаче априорных знаний модели. Мы можем осуществлять предварительную обработку исходных данных, чтобы сжать их и сделать более информативными. Как это предложено авторами метода с использованием центральных линий.
А можем использовать априорные знания при генерации целевых значений в процессе обучения моделей. Это поможет модели больше обращать внимания на наиболее значимые объекты исходных данных. И, конечно, возможно использование обоих подходов одновременно.
В рамках данной статьи мы будем использовать второй подход. Для подготовки целевых значений обучения модели прогнозирования конечных точек мы сначала соберем данные о предстоящем ценовом движении из буфера воспроизведения.
targets = matrix<float>::Zeros(PrecoderBars, 3); for(int t = 0; t < PrecoderBars; t++) { target.Assign(Buffer[tr].States[i + 1 + t].state); if(target.Size() > BarDescr) { matrix<float> temp(1, target.Size()); temp.Row(target, 0); temp.Reshape(target.Size() / BarDescr, BarDescr); temp.Resize(temp.Rows(), 3); target = temp.Row(temp.Rows() - 1); } targets.Row(target, t); } target = targets.Col(0).CumSum(); targets.Col(target, 0); targets.Col(target + targets.Col(1), 1); targets.Col(target + targets.Col(2), 2);
В качестве примера априорных знаний мы воспользуемся сигналами индикатора MACD. Данные основной линии у нас хранятся в элементе 7 массива описания состояния окружающей среды. А значение сигнальной линии в элементе 8 того же массива. Если сигнальная линия выше основной, то мы считаем текущую тенденцию бычьей. В противном случае — медвежьей.
int direct = (Buffer[tr].States[i].state[8] >= Buffer[tr].States[i].state[7] ? 1 : -1);
Согласен, что такой подход довольно упрощен и мы могли бы использовать больше сигналов и индикаторов для определения тенденций. Но именно такая простота даст наглядный пример реализации в рамках статьи и позволит оценить влияние подхода на результат. В своих работах я предлагаю Вам использовать более комплексные подходы для получения оптимальных результатов.
После определения направления тенденции мы определяем экстремум в данном направлении. И ограничиваем матрицу предстоящего ценового движения до найденного экстремума.
ulong extr=(direct>0 ? target.ArgMax() : target.ArgMin()); if(extr==0) { direct=-direct; extr=(direct>0 ? target.ArgMax() : target.ArgMin()); } targets.Resize(extr+1, 3);
Здесь надо отметить, что сигнал MACD несколько запаздывает за изменением тенденций. Поэтому, если при определении экстремума мы обнаруживаем его в первой строке матрицы, то изменяем направление тенденции на противоположную и переопределяем экстремум.
При использовании тенденций, определенных с помощью априорных знаний об окружающей среде мы несколько снижаем стохастичность целевых значений, которая наблюдалась ранее при использовании направления первой предстоящей свечи. И в целом это должно помочь нашей моделе более корректно определять тенденции и будущие направления ценового движения.
Из усеченной матрицы предстоящего ценового мы определяем целевые значения экстремумом предстоящего ценового движения.
if(direct >= 0) { target = targets.Max(AXIS_HORZ); target[2] = targets.Col(2).Min(); } else { target = targets.Min(AXIS_HORZ); target[1] = targets.Col(1).Max(); }
Как и ранее, мы определяем наиболее точный прогноз модели из всего пространства много-модальных конечных точек и при обратном проходе корректируем только выбранный прогноз.
BLEndpoints.getResults(result); targets.Reshape(1, result.Size()); targets.Row(result, 0); targets.Reshape(NForecast, 3); temp_m = targets; for(int i = 0; i < 3; i++) temp_m.Col(temp_m.Col(i) - target[i], i); temp_m = MathPow(temp_m, 2.0f); ulong pos = temp_m.Sum(AXIS_VERT).ArgMin(); targets.Row(target, pos); Result.AssignArray(targets);
Подготовленные таким образом целевые значения позволяют нам осуществить обновление параметров модели прогнозирования конечных точек и Энкодера исходного состояния окружающей среды.
if(!BLEndpoints.backProp(Result, (CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } if(!BLEncoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Тут же мы корректируем модели прогнозирования вероятностей. Только градиент ошибки данной модели мы не передаем ни на модель прогнозирования конечных точек, ни на Энкодер.
bProbs.AssignArray(vector<float>::Zeros(NForecast)); bProbs.Update((int)pos, 1); bProbs.BufferWrite(); if(!BLProbability.backProp(GetPointer(bProbs), GetPointer(BLEndpoints))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Следующим этапом мы переходим к обучению политики Актера. Здесь мы сначала подготовим информацию о состоянии счета и открытых позиций.
//--- Policy float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; bAccount.Clear(); bAccount.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[1] / PrevBalance); bAccount.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); bAccount.Add(Buffer[tr].States[i].account[2]); bAccount.Add(Buffer[tr].States[i].account[3]); bAccount.Add(Buffer[tr].States[i].account[4] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[5] / PrevBalance); bAccount.Add(Buffer[tr].States[i].account[6] / PrevBalance); double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); bAccount.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); bAccount.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(bAccount.GetIndex() >= 0) bAccount.BufferWrite();
Затем создадим Эмбединги состояний и прогнозных конечных точек.
//--- State embedding if(!StateEncoder.feedForward((CNet *)GetPointer(BLEncoder), -1, (CBufferFloat*)GetPointer(bAccount))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; } //--- Endpoint embedding if(!EndpointEncoder.feedForward((CNet *)GetPointer(BLEndpoints), -1, (CNet*)GetPointer(BLProbability))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Обратите внимание, что в отличии от предыдущей работы, для генерации эмбединга прогнозных конечных точек мы используем результаты прямого прохода выше обучаемых моделей, а не целевые значения. Это позволит нам адаптировать работу Актера к результатам модели прогнозирования конечных точек.
После подготовки эмбедингов мы осуществляем прямой проход модели Актера.
//--- Actor if(!Actor.feedForward((CNet *)GetPointer(StateEncoder), -1, (CNet*)GetPointer(EndpointEncoder))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
За успешным выполнением прямого прохода следует этап обратного прохода с обновлением параметров моделей. И здесь при подготовке целевых значений для обучения модели актера мы так же добавим некоторые априорные знания. В частности, перед открытием сделки в том или ином направлении мы проверим значения индикаторов RSI и CCI, которые хранятся в 4 и 5 элементе массива описания состояния окружающей среды, соответственно.
if(direct > 0) { if(Buffer[tr].States[i].state[4] > 30 && Buffer[tr].States[i].state[5] > -100 ) { float tp = float(target[1] / _Point / MaxTP); result[1] = tp; int sl = int(MathMax(MathMax(target[1] / 3, -target[2]) / _Point, MaxSL / 10)); result[2] = float(sl) / MaxSL; result[0] = float(MathMax(risk / (value * sl), 0.01)) + FLT_EPSILON; } }
else { if(Buffer[tr].States[i].state[4] < 70 && Buffer[tr].States[i].state[5] < 100 ) { float tp = float((-target[2]) / _Point / MaxTP); result[4] = tp; int sl = int(MathMax(MathMax((-target[2]) / 3, target[1]) / _Point, MaxSL / 10)); result[5] = float(sl) / MaxSL; result[3] = float(MathMax(risk / (value * sl), 0.01)) + FLT_EPSILON; } }
Обратите внимание, что в данном случае мы не проверяем явно сигналы индикатора MACD. Так как они уже учтены при определении направления предстоящего движения direct ранее.
Подготовленные таким образом целевые значения позволяют нам осуществить обратный проход составной модели Актера.
Result.AssignArray(result); if(!Actor.backProp(Result, (CNet *)GetPointer(EndpointEncoder)) || !StateEncoder.backPropGradient(GetPointer(bAccount), (CBufferFloat *)GetPointer(bGradient)) || !EndpointEncoder.backPropGradient((CNet*)GetPointer(BLProbability)) ) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
Градиент ошибки Актера мы используем для обновления параметров Энкодера, но не обновляем модель прогнозирования конечных точек.
if(!BLEncoder.backPropGradient((CBufferFloat*)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); Stop = true; break; }
В завершении операций внутри системы циклов нам остается лишь проинформировать пользователя о ходе процесса обучения.
if(GetTickCount() - ticks > 500) { double percent = (double(i - state) / ((end - state)) + iter) * 100.0 / (Iterations); string str = StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Actor", percent, Actor.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Endpoints", percent, BLEndpoints.getRecentAverageError()); str += StringFormat("%-14s %6.2f%% -> Error %15.8f\n", "Probability", percent, BLProbability.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } } }
После завершения процесса обучения моделей мы очищаем поле комментариев на графике. Выводим в журнал результаты обучения моделей и инициализируем процесс завершения работы программы.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Actor", Actor.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Endpoints", BLEndpoints.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Probability", BLProbability.getRecentAverageError()); ExpertRemove(); //--- }
На этом мы завершаем рассмотрение алгоритмов реализации предложенных базовых подходов по оптимизации моделей прогнозирования траекторий. А с полным кодом всех программ, используемых при подготовке данной статьи, Вы можете ознакомиться во вложении.
3. Тестирование
Выше была проведена работа по реализации базовых подходов к оптимизации моделей прогнозирования траекторий средствами MQL5. В частности, был создан слой графовой свертки и применены подходы по использованию априорных знаний об окружающей среде при постановке целей в процессе обучения моделей. При этом было уменьшено количество слоев в моделях, что потенциально должно снизить сложность моделей и повысить скорость их работы. Влияние предложенных подходов мы оценивали в процессе обучения и тестирования обученных моделей на реальных данных в тестере стратегий MetaTrader 5.
Как всегда, обучение моделей осуществлялось на исторических данных за первые 7 месяцев 2023 года инструмента EURUSD тайм-фрейм Н1.
Выше при построении архитектуры моделей уже было сказано о сохранении структуры исходных данных. Это позволило нам в процессе обучения использовать буфер воспроизведения опыта, собранный при подготовке предыдущих статей. Для этого достаточно переименовать файл собранных ранее данных в «BaseLines.bd». Если же Вы хотите создать новую обучающую выборку, то можете воспользоваться любым из рассмотренных ранее методов с использованием советников взаимодействия с окружающей средой.
Генерация целевых значений в процессе обучения моделей позволило использовать нам обучающую выборку до получения оптимальных результатов без необходимости её актуализации и дополнения.
Однако, результаты обучения оказались не столь радужными как хотелось. В процессе тестирования обученных моделей мы даже увеличили период тестирования с 1 до 3 месяцев.
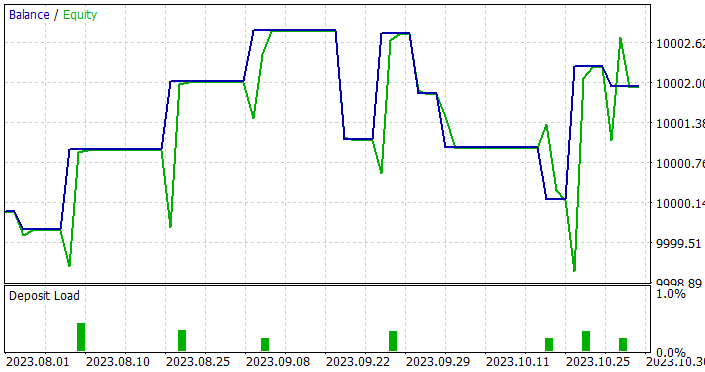
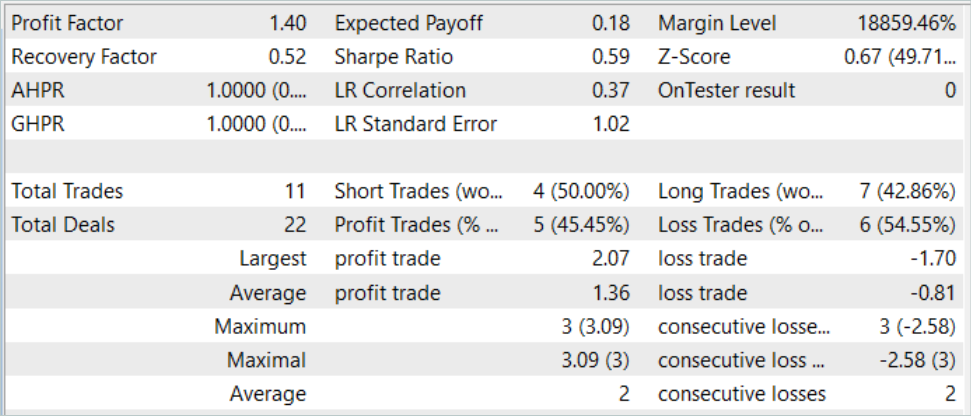
Да, нам удалось получить модель, способную генерировать прибыль как на обучающей, так и на тестовой выборке. Более того, полученная модель продемонстрировала хорошую стабильность работы с профит-фактором 1.4. После обучения на исторических данных в 7 месяцев она способна генерировать прибыль на протяжении как минимум 3 месяцев. Это может свидетельствовать о том, что модели удалось определить довольно стабильные предикторы.
Однако, количество сделок оставляет желать лучшего. Совершенные 11 сделок за 3 месяца — это очень мало. И это не тот результат, который мы хотели получить.
Заключение
В данной статье мы рассмотрели базовые подходы по оптимизации работы моделей прогнозирования траекторий. Внедрение предложенных подходов позволяет обучать модели, способные выделять действительно значимые предикторы в исходных данных. Что позволяет им работать стабильно на довольно длительном временном отрезке после обучения.
Однако, полученные нами результаты говорят о сильном консерватизме решений, принимаемых моделей. Что выражается в очень малом количестве совершаемых сделок. И это то направление, в котором нам предстоит продолжить исследования.
Ссылки
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения Моделей |
| 4 | Test.mq5 | Советник | Советник для тестирования модели |
| 5 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода программы OpenCL |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Популяционные алгоритмы оптимизации: Эволюция социальных групп (Evolution of Social Groups, ESG)
Популяционные алгоритмы оптимизации: Эволюция социальных групп (Evolution of Social Groups, ESG)
 Популяционные алгоритмы оптимизации: Искусственные мультисоциальные поисковые объекты (artificial Multi-Social search Objects, MSO)
Популяционные алгоритмы оптимизации: Искусственные мультисоциальные поисковые объекты (artificial Multi-Social search Objects, MSO)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования