
Métodos de conjunto para mejorar las tareas de clasificación en MQL5
Introducción
En un artículo anterior, exploramos métodos de combinación de modelos para predicciones numéricas. Este artículo amplía esa exploración centrándose en técnicas de conjunto diseñadas específicamente para tareas de clasificación. A lo largo del camino, también examinamos estrategias para utilizar clasificadores de componentes que generan rangos de clase en una escala ordinal. Aunque las técnicas de combinación numérica pueden aplicarse en ocasiones a tareas de clasificación en las que los modelos se basan en resultados numéricos, muchos clasificadores adoptan un enfoque más rígido y solo producen decisiones de clase discretas. Además, los clasificadores basados en números suelen presentar inestabilidad en las predicciones, lo que subraya la necesidad de métodos de combinación especializados.
Los conjuntos de clasificación que se analizan en este artículo funcionan bajo supuestos específicos sobre los modelos que los componen. En primer lugar, se supone que estos modelos se entrenan con datos con objetivos de clase mutuamente excluyentes y exhaustivos, lo que garantiza que cada instancia pertenezca exactamente a una clase. Cuando se requiere una opción «ninguna de las anteriores», debe tratarse como una clase independiente o gestionarse mediante un método de combinación numérica con un umbral de pertenencia definido. Además, cuando se les proporciona un vector de entrada de predictores, se espera que los modelos de componentes produzcan N salidas, donde N representa el número de clases. Estos resultados pueden ser probabilidades o puntuaciones de confianza que indican la probabilidad de pertenencia a cada una de las clases. También podrían ser decisiones binarias, en las que un resultado es 1.0 (verdadero) y los demás son 0.0 (falso), o los resultados del modelo podrían ser clasificaciones enteras del 1 al N, que reflejan la probabilidad relativa de pertenencia a una clase.
Algunos de los métodos de conjunto que veremos se benefician enormemente de los clasificadores de componentes que producen resultados clasificados. Los modelos capaces de estimar con precisión las probabilidades de pertenencia a una clase suelen ser muy valiosos, pero existe un riesgo significativo al tratar los resultados como probabilidades cuando no lo son. Cuando hay dudas sobre lo que representan los resultados del modelo, puede ser beneficioso convertirlos en rangos. La utilidad de la información sobre la clasificación aumenta con el número de clases. En la clasificación binaria, los rangos no ofrecen información adicional, y su valor para los problemas de tres clases sigue siendo modesto. Sin embargo, en escenarios que involucran numerosas clases, la capacidad de interpretar las opciones secundarias de un modelo resulta muy beneficiosa, especialmente cuando las predicciones individuales están plagadas de incertidumbre. Por ejemplo, las máquinas de vectores de soporte (Support Vector Machines, SVM) podrían mejorarse para producir no solo clasificaciones binarias, sino también distancias de límite de decisión para cada clase, lo que ofrecería una mayor comprensión de la confianza en la predicción.
Las clasificaciones también abordan un reto clave en los métodos de conjunto: normalizar los resultados de diversos modelos de clasificación. Consideremos dos modelos que analizan los movimientos del mercado: uno se especializa en las fluctuaciones de precios a corto plazo en mercados altamente líquidos, mientras que el otro se centra en las tendencias a largo plazo a lo largo de semanas o meses. El enfoque más amplio del segundo modelo podría introducir ruido en las predicciones a corto plazo. Convertir la confianza en las decisiones de clase en rangos mitiga este problema, garantizando que las valiosas perspectivas a corto plazo no se vean eclipsadas por señales de tendencias más amplias. Este enfoque conduce a predicciones conjuntas más equilibradas y eficaces.
Objetivos alternativos para la combinación de clasificadores
El objetivo principal de aplicar clasificadores de conjunto suele ser mejorar la precisión de la clasificación. No siempre tiene por qué ser así, algunas tareas de clasificación también pueden beneficiarse de mirar más allá de este objetivo específico. Además de la precisión básica de la clasificación, se pueden implementar medidas de éxito más sofisticadas para abordar situaciones en las que la decisión inicial puede ser incorrecta. Teniendo esto en cuenta, la clasificación puede abordarse a través de dos objetivos distintos pero complementarios, cualquiera de los cuales puede servir como métrica de rendimiento para las estrategias de combinación de clases:
- Reducción del conjunto de clases: este enfoque tiene como objetivo identificar el subconjunto más pequeño de las clases originales que conserve una alta probabilidad de incluir la clase verdadera. Aquí, la clasificación interna dentro del subconjunto es secundaria para garantizar que el subconjunto sea compacto y tenga probabilidades de contener la clasificación correcta.
- Ordenación de clases: este método se centra en clasificar las probabilidades de pertenencia a una clase para situar la clase verdadera lo más cerca posible de la parte superior. En lugar de utilizar umbrales de rango fijos, el rendimiento se evalúa midiendo la distancia media entre la clase real y la posición más alta en la clasificación.
En determinadas aplicaciones, dar prioridad a uno de estos esquemas sobre el otro puede proporcionar ventajas significativas. Incluso cuando dicha preferencia no se requiera explícitamente. Seleccionar el objetivo más relevante e implementar su medida de error correspondiente suele proporcionar métricas de rendimiento más fiables que basarse únicamente en la precisión de la clasificación. Además, estos dos objetivos no tienen por qué ser mutuamente excluyentes. Un enfoque híbrido puede resultar especialmente eficaz: en primer lugar, aplicar un método combinado centrado en la reducción del conjunto de clases para identificar un subconjunto pequeño y altamente probable de clases. A continuación, utilice un método secundario para clasificar las clases dentro de este subconjunto refinado. La clase mejor clasificada de este proceso de dos pasos se convierte en la decisión final, beneficiándose tanto de la eficiencia de la reducción del conjunto como de la precisión de la clasificación ordenada. Esta estrategia de doble objetivo podría ofrecer un marco de clasificación más sólido que los métodos tradicionales de predicción de una sola clase, especialmente en escenarios complejos en los que la certeza de la clasificación varía considerablemente. Con esto en mente, comenzamos nuestra exploración de los clasificadores de conjunto.
Conjuntos basados en la regla de la mayoría
La regla de la mayoría es un enfoque sencillo e intuitivo para la clasificación de conjuntos, derivado del concepto familiar de votación. El método consiste en seleccionar la clase que recibe más votos de los modelos de componentes. Este sencillo método ofrece un valor especial en situaciones en las que los modelos solo pueden proporcionar selecciones de clases discretas, lo que lo convierte en una excelente opción para sistemas con modelos de sofisticación limitada. La representación matemática formal de la regla de la mayoría se describe en la siguiente ecuación.
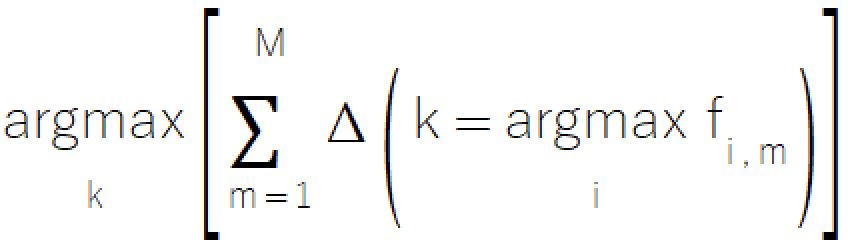
La implementación de la regla de la mayoría reside en el archivo ensemble.mqh, donde la clase CMajority gestiona su funcionalidad principal a través del método classify().
//+------------------------------------------------------------------+ //| Compute the winner via simple majority | //+------------------------------------------------------------------+ class CMajority { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMajority(void); ~CMajority(void); ulong classify(vector &inputs, IClassify* &models[]); };
Este método toma como entrada un vector de predictores y una matriz de modelos componentes proporcionados como punteros IClassify. La interfaz IClassify estandariza la manipulación de modelos de forma muy similar a la interfaz IModel descrita en el artículo anterior.
//+------------------------------------------------------------------+ //| IClassify interface defining methods for manipulation of | //|classification algorithms | //+------------------------------------------------------------------+ interface IClassify { //train a model bool train(matrix &predictors,matrix&targets); //make a prediction with a trained model vector classify(vector &predictors); //get number of inputs for a model ulong getNumInputs(void); //get number of class outputs for a model ulong getNumOutputs(void); };
La función classify() devuelve un entero que representa la clase seleccionada, que va desde cero hasta uno menos que el número total de clases posibles. La clase devuelta corresponde a la que recibe el mayor número de «votos» de los modelos de componentes. La aplicación de la regla de la mayoría puede parecer sencilla a primera vista, pero su aplicación práctica plantea un problema importante. ¿Qué ocurre cuando dos o más clases reciben el mismo número de votos? En entornos democráticos, una situación así conduce a otra ronda de votaciones, pero eso no funcionará en este contexto. Para resolver los empates de manera justa, el método introduce pequeñas perturbaciones aleatorias en el recuento de votos de cada clase durante el proceso de comparación. Esta técnica garantiza que las clases empatadas tengan las mismas probabilidades de selección, lo que mantiene la integridad del método y evita sesgos.
//+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CMajority::classify(vector &inputs,IClassify *&models[]) { double best, sum, temp; ulong ibest; best =0; ibest = 0; CHighQualityRandStateShell state; CHighQualityRand::HQRndRandomize(state.GetInnerObj()); m_output = vector::Zeros(models[0].getNumOutputs()); for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); m_output[classification.ArgMax()] += 1.0; } sum = 0.0; for(ulong i=0 ; i<m_output.Size() ; i++) { temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state); if((i == 0) || (temp > best)) { best = temp ; ibest = i ; } sum += m_output[i] ; } if(sum>0.0) m_output/=sum; return ibest; }
A pesar de su utilidad, la regla de la mayoría presenta varias limitaciones que merecen ser tenidas en cuenta:
- El método solo tiene en cuenta la primera opción de cada modelo, lo que puede descartar información valiosa contenida en las clasificaciones inferiores. Aunque utilizar una simple media aritmética de los resultados de las clases podría parecer una solución, este enfoque puede introducir complicaciones adicionales relacionadas con el ruido y el escalado.
- En situaciones en las que intervienen varias clases, es posible que el mecanismo de votación simple no refleje las sutiles relaciones entre las diferentes opciones de clase.
- El enfoque trata todos los modelos de componentes por igual, independientemente de sus características de rendimiento individuales o su fiabilidad en diferentes contextos.
El siguiente método que analizaremos es otro sistema basado en el «voto», que busca superar algunos de los inconvenientes de la regla de la mayoría mediante el empleo de un sistema un poco más sofisticado.
El método de recuento de Borda
El método de recuento de Borda calcula una puntuación para cada clase agregando, en todos los modelos, el número de clases clasificadas por debajo de ella en la evaluación de cada modelo. Este método logra un equilibrio óptimo entre la utilización y la moderación de la influencia de las opciones con menor puntuación, lo que proporciona una alternativa más refinada a los mecanismos de votación más simples. En un sistema con «m» modelos y «k» clases, el rango de puntuación está bien definido: una clase que ocupa sistemáticamente el último lugar en todos los modelos recibe una puntuación Borda de cero, mientras que una que ocupa el primer lugar en todos los modelos alcanza una puntuación máxima de m(k-1).

Este método representa un avance significativo con respecto a los métodos de votación más simples, ya que ofrece una mayor capacidad para capturar y utilizar todo el espectro de predicciones del modelo, al tiempo que mantiene la eficiencia computacional. Aunque el método gestiona eficazmente los empates dentro de las clasificaciones de los modelos individuales, los empates en los recuentos finales de Borda entre los modelos requieren una consideración cuidadosa. Para tareas de clasificación binaria, el método de recuento Borda es funcionalmente equivalente a la regla de la mayoría. Por lo tanto, sus ventajas distintivas se hacen evidentes principalmente en escenarios que involucran tres o más clases. La eficiencia del método se deriva de su enfoque basado en la clasificación, que permite un procesamiento optimizado de los resultados de las clases, al tiempo que mantiene asociaciones de índices precisas.
La implementación del recuento de Borda comparte similitudes estructurales con la metodología de la regla de la mayoría, pero incorpora eficiencias computacionales adicionales. El proceso se gestiona a través de la clase CBorda dentro de ensemble.mqh y funciona sin necesidad de una fase de entrenamiento preliminar.
//+------------------------------------------------------------------+ //| Compute the winner via Borda count | //+------------------------------------------------------------------+ class CBorda { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; long m_indices[]; public: CBorda(void); ~CBorda(void); ulong classify(vector& inputs, IClassify* &models[]); };
El procedimiento de clasificación comienza con la inicialización del vector de salida, destinado a almacenar los recuentos acumulativos de Borda. A continuación, se evalúan todos los modelos componentes dados el vector de entrada. Se establece una serie de índices para realizar un seguimiento de las relaciones entre clases. Los resultados de la clasificación de cada modelo se ordenan en orden ascendente. Y, por último, los votos Borda se acumulan sistemáticamente en función de las clasificaciones ordenadas.
//+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CBorda::classify(vector &inputs,IClassify *&models[]) { double best=0, sum, temp; ulong ibest=0; CHighQualityRandStateShell state; CHighQualityRand::HQRndRandomize(state.GetInnerObj()); if(m_indices.Size()) ArrayFree(m_indices); m_output = vector::Zeros(models[0].getNumOutputs()); if(ArrayResize(m_indices, int(m_output.Size()))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return ULONG_MAX; } for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(long j = 0; j<long(classification.Size()); j++) m_indices[j] = j; if(!classification.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong k =0; k<classification.Size(); k++) m_output[m_indices[k]] += double(k); } sum = 0.0; for(ulong i=0 ; i<m_output.Size() ; i++) { temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state); if((i == 0) || (temp > best)) { best = temp ; ibest = i ; } sum += m_output[i] ; } if(sum>0.0) m_output/=sum; return ibest; }
En las secciones siguientes consideramos conjuntos que incorporan la mayor parte, si no toda, la información generada por los modelos de componentes a la hora de tomar la decisión final sobre la clase.
Promediando los resultados del modelo de componentes
Cuando los modelos de componentes generan resultados con valores relativos significativos y comparables entre modelos, la incorporación de estas mediciones numéricas mejora significativamente el rendimiento del conjunto. Mientras que los métodos de la regla mayoritaria y el recuento de Borda ignoran una parte sustancial de la información disponible, el promedio de los resultados de los componentes proporciona un enfoque más completo para la utilización de los datos. El método calcula la salida media para cada clase en todos los modelos componentes. Dado que el número de modelos permanece constante, este enfoque es matemáticamente equivalente a la suma de resultados. Esta técnica trata eficazmente cada modelo de clasificación como un predictor numérico, combinándolos mediante métodos de promediado simples. La decisión final sobre la clasificación se determina identificando la clase con el mayor rendimiento agregado.
Existe una diferencia significativa entre el promedio en tareas de predicción numérica y en tareas de clasificación. En la predicción numérica, los modelos de componentes suelen compartir un objetivo de entrenamiento común, lo que garantiza la coherencia de los resultados. Sin embargo, las tareas de clasificación, en las que solo las clasificaciones de salida tienen importancia para los modelos individuales, pueden producir inadvertidamente resultados incomparables. A veces, esta incoherencia puede dar lugar a que la combinación se convierta efectivamente en una media ponderada implícita en lugar de una verdadera media aritmética. Por otra parte, los modelos individuales pueden tener un efecto desproporcionado en la suma final, comprometiendo la eficacia del conjunto. Por lo tanto, para mantener la integridad del metamodelo, es fundamental verificar la coherencia de los resultados en todos los modelos componentes.
Partiendo de la hipótesis de que los resultados de los modelos de componentes son, en realidad, probabilidades, se han desarrollado métodos de combinación alternativos, conceptualmente similares al promedio. Una de ellas es la regla del producto. ¿Qué sustituye la suma por la multiplicación de los resultados del modelo? El problema es que este enfoque demuestra una sensibilidad extrema incluso ante pequeñas violaciones de los supuestos de probabilidad. La subestimación significativa de la probabilidad de una clase por parte de un único modelo puede penalizar irreversiblemente a esa clase, ya que la multiplicación por valores cercanos a cero produce resultados insignificantes independientemente de otros factores. Esta mayor sensibilidad hace que la regla del producto resulte poco práctica para la mayoría de las aplicaciones, a pesar de su elegancia teórica. Sirve principalmente como ejemplo cautelar de cómo los enfoques matemáticamente sólidos pueden resultar problemáticos en las aplicaciones prácticas.
La implementación de la regla Average (Promedio) reside en la clase CAvgClass, que refleja estructuralmente el marco de la clase CMajority.
//+------------------------------------------------------------------+ //| full resolution' version of majority rule. | //+------------------------------------------------------------------+ class CAvgClass { private: ulong m_outputs; ulong m_inputs; vector m_output; public: CAvgClass(void); ~CAvgClass(void); ulong classify(vector &inputs, IClassify* &models[]); };
Durante la clasificación, el método classify() recopila las predicciones de todos los modelos componentes y acumula sus respectivas salidas. La calificación final se basa en la puntuación acumulada máxima.
//+------------------------------------------------------------------+ //| make classification with consensus model | //+------------------------------------------------------------------+ ulong CAvgClass::classify(vector &inputs, IClassify* &models[]) { m_output=vector::Zeros(models[0].getNumOutputs()); vector model_classification; for(uint i =0 ; i<models.Size(); i++) { model_classification = models[i].classify(inputs); m_output+=model_classification; } double sum = m_output.Sum(); ulong min = m_output.ArgMax(); m_output/=sum; return min; }
La mediana
La agregación media tiene la ventaja de permitir una utilización exhaustiva de los datos, pero ello conlleva una mayor sensibilidad a los valores atípicos, lo que puede comprometer el rendimiento del conjunto. La mediana presenta una alternativa sólida que, a pesar de una reducción marginal en la utilización de la información, proporciona mediciones fiables de la tendencia central, al tiempo que mantiene la resistencia a los valores extremos. El método de conjunto mediano, implementado a través de la clase CMedian en ensemble.mqh, ofrece un enfoque sencillo pero eficaz para la clasificación de conjuntos. Esta implementación aborda los retos que plantean la gestión de predicciones atípicas y la preservación de un orden relativo significativo entre las clases. Los valores atípicos se tratan mediante la implementación de una transformación basada en rangos. Los resultados de cada modelo componente se clasifican de forma independiente y, a continuación, se calcula la media de estas clasificaciones para cada clase. Este enfoque reduce eficazmente la influencia de las predicciones extremas, al tiempo que preserva la relación jerárquica esencial entre las predicciones de clase.
El enfoque mediano mejora la estabilidad en presencia de predicciones extremas ocasionales. Sigue siendo eficaz incluso cuando se trata de distribuciones de predicción asimétricas o sesgadas, y logra un equilibrio entre la utilización de información completa y la gestión robusta de los valores atípicos. Al aplicar la regla de la mediana, los profesionales deben evaluar los requisitos específicos de cada caso de uso. En situaciones en las que es probable que se produzcan predicciones extremas ocasionales o en las que la estabilidad de las predicciones es primordial, el método de la mediana suele ofrecer un equilibrio óptimo entre fiabilidad y rendimiento.
//+------------------------------------------------------------------+ //| median of predications | //+------------------------------------------------------------------+ class CMedian { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMedian(void); ~CMedian(void); ulong classify(vector &inputs, IClassify* &models[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMedian::CMedian(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMedian::~CMedian(void) { } //+------------------------------------------------------------------+ //| consensus classification | //+------------------------------------------------------------------+ ulong CMedian::classify(vector &inputs,IClassify *&models[]) { m_out = matrix::Zeros(models[0].getNumOutputs(),models.Size()); vector model_classification; for(uint i = 0; i<models.Size(); i++) { model_classification = models[i].classify(inputs); if(!m_out.Col(model_classification,i)) { Print(__FUNCTION__, " ", __LINE__, " failed row insertion ", GetLastError()); return ULONG_MAX; } } m_output = vector::Zeros(models[0].getNumOutputs()); for(ulong i = 0; i<m_output.Size(); i++) { vector row = m_out.Row(i); if(!row.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortd(0,row.Size()-1,row); m_output[i] = row.Median(); } double sum = m_output.Sum(); ulong mx = m_output.ArgMax(); if(sum>0.0) m_output/=sum; return mx; }
Clasificadores de conjunto MaxMax y MaxMin
A veces, dentro de un conjunto de modelos componentes, los modelos individuales pueden haber sido diseñados para tener experiencia en subconjuntos específicos del conjunto de clases. Cuando operan dentro de sus ámbitos especializados, estos modelos generan resultados de alta fiabilidad, mientras que producen valores moderados menos significativos para clases fuera de su ámbito de especialización. La regla MaxMax aborda este escenario evaluando cada clase en función de su rendimiento máximo en todos los modelos. Este enfoque da prioridad a las predicciones de alta confianza, mientras que descarta los resultados moderados que pueden ser menos informativos. Sin embargo, los profesionales deben tener en cuenta que este método resulta inadecuado para situaciones en las que los resultados secundarios tienen un valor analítico significativo.
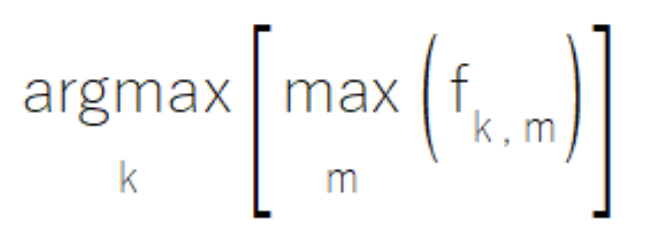
La implementación de la regla MaxMax reside en la clase CMaxmax dentro de ensemble.mqh, lo que proporciona un marco estructurado para aprovechar los patrones de especialización de modelos.
//+------------------------------------------------------------------+ //|Compute the maximum of the predictions | //+------------------------------------------------------------------+ class CMaxMax { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMaxMax(void); ~CMaxMax(void); ulong classify(vector &inputs, IClassify* &models[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMaxMax::CMaxMax(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMaxMax::~CMaxMax(void) { } //+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CMaxMax::classify(vector &inputs,IClassify *&models[]) { double sum; ulong ibest; m_output = vector::Zeros(models[0].getNumOutputs()); for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(ulong j = 0; j<classification.Size(); j++) { if(classification[j] > m_output[j]) m_output[j] = classification[j]; } } ibest = m_output.ArgMax(); sum = m_output.Sum(); if(sum>0.0) m_output/=sum; return ibest; }
Por el contrario, algunos sistemas conjuntos cuentan con modelos que destacan por excluir clases específicas en lugar de identificarlas. En estos casos, cuando una instancia pertenece a una clase concreta, al menos un modelo del conjunto generará un resultado claramente bajo para cada clase incorrecta, lo que las elimina de forma efectiva de la consideración.
La regla MaxMin aprovecha esta característica evaluando la pertenencia a una clase basándose en el resultado mínimo de todos los modelos para cada clase.
Este enfoque, implementado en la clase CMaxmin dentro de ensemble.mqh, proporciona un mecanismo para aprovechar las fortalezas excluyentes de modelos específicos.
//+------------------------------------------------------------------+ //| Compute the minimum of the predictions | //+------------------------------------------------------------------+ class CMaxMin { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMaxMin(void); ~CMaxMin(void); ulong classify(vector &inputs, IClassify* &models[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMaxMin::CMaxMin(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMaxMin::~CMaxMin(void) { } //+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CMaxMin::classify(vector &inputs,IClassify *&models[]) { double sum; ulong ibest; for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); if(i == 0) m_output = classification; else { for(ulong j = 0; j<classification.Size(); j++) if(classification[j] < m_output[j]) m_output[j] = classification[j]; } } ibest = m_output.ArgMax(); sum = m_output.Sum(); if(sum>0.0) m_output/=sum; return ibest; }
Al implementar el enfoque MaxMax o MaxMin, los profesionales deben evaluar cuidadosamente las características de su conjunto de modelos. Para el enfoque MaxMax, es esencial confirmar que los modelos muestran patrones de especialización claros. Es especialmente importante garantizar que los resultados moderados representen ruido en lugar de información secundaria valiosa y, por último, garantizar que el conjunto proporcione una cobertura completa de todas las clases relevantes. Al aplicar el enfoque MaxMin, los profesionales deben asegurarse de que el conjunto aborde colectivamente todos los posibles escenarios de clasificación errónea y estar atentos a cualquier laguna en la cobertura de exclusión.
El método de intersección
El método de intersección representa un enfoque especializado para la combinación de clasificadores, diseñado principalmente para la reducción de conjuntos de clases en lugar de la clasificación de uso general. Es cierto que su aplicación directa puede ser limitada, pero se incluye en este texto para que sirva como precursor fundamental de métodos más sólidos, en particular el método de unión. Este enfoque requiere modelos de componentes para generar clasificaciones completas de clases para cada caso de entrada, desde el más probable hasta el menos probable. Muchos clasificadores pueden cumplir este requisito, y el proceso de clasificación de resultados con valores reales suele mejorar el rendimiento al filtrar eficazmente el ruido y conservar al mismo tiempo la información valiosa. La fase de entrenamiento del método identifica el número mínimo de resultados mejor clasificados que cada modelo componente debe conservar para garantizar la inclusión coherente de la clase verdadera en todo el conjunto de entrenamiento. Para los casos nuevos, la decisión combinada comprende un subconjunto mínimo que contiene la clase verdadera, determinada por la intersección de los subconjuntos mínimos de todos los modelos componentes.
Consideremos un ejemplo práctico con varias clases y cuatro modelos. El examen de las cinco muestras del conjunto de entrenamiento revela patrones de clasificación variables para la clase verdadera en todos los modelos.
| Muestra | Modelo 1 | Modelo 2 | Modelo 3 | Modelo 4 |
|---|---|---|---|---|
| 1 | 3 | 21 | 4 | 5 |
| 2 | 8 | 4 | 8 | 9 |
| 3 | 1 | 17 | 12 | 3 |
| 4 | 7 | 16 | 2 | 8 |
| 5 | 7 | 8 | 6 | 1 |
| Máximo | 8 | 21 | 12 | 9 |
La tabla muestra que la clase real de la segunda muestra fue clasificada en octavo lugar por el primer modelo, en cuarto lugar por el segundo modelo y en noveno lugar por el cuarto modelo. La última fila de la tabla muestra los rangos máximos por columna, que son 8, 21, 12 y 9, respectivamente. Al evaluar casos desconocidos, el conjunto selecciona e intersecta las clases mejor clasificadas de cada modelo según estos umbrales, produciendo un subconjunto final de clases comunes a todos los conjuntos.
La clase CIntersection gestiona la implementación del método de intersección, con un procedimiento de entrenamiento diferenciado a través de su función fit(). Esta función analiza los datos de entrenamiento para determinar las clasificaciones más desfavorables para cada modelo, realizando un seguimiento del número mínimo de clases mejor clasificadas necesarias para incluir de forma sistemática clasificaciones correctas.
//+------------------------------------------------------------------+ //| Use intersection rule to compute minimal class set | //+------------------------------------------------------------------+ class CIntersection { private: ulong m_nout; long m_indices[]; vector m_ranks; vector m_output; public: CIntersection(void); ~CIntersection(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
Al invocar el método classify() de la clase CIntersection, se evalúan secuencialmente todos los modelos componentes en los datos de entrada. Para cada modelo, se ordena su vector de salida y se utilizan los índices del vector ordenado para calcular la intersección de las clases que pertenecen al subconjunto mejor clasificado para cada modelo.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool CIntersection::fit(matrix &inputs,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_output = vector::Ones(m_nout); m_ranks = vector::Zeros(models.Size()); double best = 0.0; ulong nbad; if(ArrayResize(m_indices,int(m_nout))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k; for(ulong i = 0; i<inputs.Rows(); i++) { vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); best = trow[k]; for(uint j = 0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); best = classification[k]; nbad = 1; for(ulong ii = 0; ii<m_nout; ii++) { if(ii == k) continue; if(classification[ii] >= best) ++nbad; } if(nbad > ulong(m_ranks[j])) m_ranks[j] = double(nbad); } } return true; } //+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CIntersection::classify(vector &inputs,IClassify *&models[]) { for(long j =0; j<long(m_nout); j++) m_indices[j] = j; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); ArraySort(m_indices); qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong j = 0; j<m_nout-ulong(m_ranks[i]); j++) { m_output[m_indices[j]] = 0.0; } } ulong n=0; double cut = 0.5; for(ulong i = 0; i<m_nout; i++) { if(m_output[i] > cut) ++n; } return n; }
A pesar de su elegancia teórica, el método de intersección tiene varias limitaciones importantes. Si bien garantiza la inclusión de clases verdaderas del conjunto de entrenamiento, esta ventaja se ve atenuada por sus limitaciones inherentes. El método también puede producir subconjuntos de clases vacíos para casos fuera del conjunto de entrenamiento, especialmente cuando los subconjuntos mejor clasificados carecen de elementos comunes entre los modelos. Lo más importante es que la dependencia del método en el peor rendimiento posible a menudo da lugar a subconjuntos de clases excesivamente grandes, lo que disminuye tanto su eficacia como su eficiencia.
El método de intersección puede resultar útil en contextos específicos en los que todos los modelos de componentes funcionan de manera consistente en todo el conjunto de clases. Sin embargo, su sensibilidad al bajo rendimiento de los modelos en áreas no especializadas a menudo limita su utilidad práctica, especialmente en aplicaciones que dependen de modelos especializados para diferentes subconjuntos de clases. En última instancia, el valor principal de este método reside en su contribución conceptual a enfoques más sólidos, como el método de unión, más que en su aplicación directa en la mayoría de las tareas de clasificación.
La regla de unión
La regla de unión representa una mejora estratégica del método de intersección, ya que aborda su principal limitación: la excesiva dependencia de los peores resultados posibles. Esta modificación resulta especialmente valiosa cuando se combinan modelos especializados con diferentes áreas de experiencia, desplazando el enfoque de los peores escenarios de rendimiento a los mejores. El proceso inicial refleja el enfoque del método de intersección: analizar los casos del conjunto de entrenamiento para determinar las clasificaciones reales de las clases en los modelos componentes. Sin embargo, la regla sindical se desvía al identificar y rastrear el modelo con mejor rendimiento para cada caso, en lugar de supervisar los peores rendimientos. A continuación, el método evalúa el menos favorable de estos resultados óptimos en el conjunto de datos de entrenamiento. Para la clasificación de casos desconocidos, el sistema construye un subconjunto de clase combinado unificando los subconjuntos óptimos de cada modelo componente. Consideremos nuestro ejemplo anterior de conjunto de datos, ahora mejorado con columnas de seguimiento del rendimiento con el prefijo «Perf».
| Muestra | Modelo 1 | Modelo 2 | Modelo 3 | Modelo 4 | Perf_Model 1 | Perf_Model 2 | Perf_Model 3 | Perf_Model 4 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 21 | 4 | 5 | 3 | 0 | 0 | 0 |
| 2 | 8 | 4 | 8 | 9 | 0 | 4 | 0 | 0 |
| 3 | 1 | 17 | 12 | 3 | 1 | 0 | 0 | 0 |
| 4 | 7 | 16 | 2 | 8 | 0 | 0 | 2 | 0 |
| 5 | 7 | 8 | 6 | 1 | 0 | 0 | 0 | 1 |
| Máximo | 3 | 4 | 2 | 1 |
Las columnas adicionales registran los casos en los que cada modelo muestra un rendimiento superior, y la fila inferior indica los valores máximos de estos escenarios óptimos.
La regla de unión ofrece varias ventajas claras sobre el método de intersección. Elimina la posibilidad de subconjuntos vacíos, ya que al menos un modelo funcionará de manera óptima de forma consistente para cualquier caso dado. El método también gestiona eficazmente los modelos especializados al ignorar el bajo rendimiento fuera de sus áreas de especialización durante el entrenamiento, lo que permite que los especialistas adecuados tomen el control. Por último, proporciona un mecanismo natural para identificar y, potencialmente, excluir los modelos con un rendimiento consistentemente bajo, tal y como indican las columnas de ceros en la matriz de seguimiento.
La implementación del método de union mantiene una similitud estructural significativa con el método de intersección, utilizando el contenedor m_ranks para supervisar los valores máximos de las columnas de seguimiento del rendimiento.
//+------------------------------------------------------------------+ //| Use union rule to compute minimal class set | //+------------------------------------------------------------------+ class CUnion { private: ulong m_nout; long m_indices[]; vector m_ranks; vector m_output; public: CUnion(void); ~CUnion(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
Sin embargo, surgen diferencias clave en el manejo de las clasificaciones de clases y la inicialización de indicadores. Durante el entrenamiento, el sistema realiza un seguimiento de las clasificaciones mínimas en todos los modelos para cada caso, actualizando los valores máximos en m_ranks cuando es necesario.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool CUnion::fit(matrix &inputs,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_output = vector::Zeros(m_nout); m_ranks = vector::Zeros(models.Size()); double best = 0.0; ulong nbad; if(ArrayResize(m_indices,int(m_nout))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k, ibestrank=0, bestrank=0; for(ulong i = 0; i<inputs.Rows(); i++) { vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); for(uint j = 0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); best = classification[k]; nbad = 1; for(ulong ii = 0; ii<m_nout; ii++) { if(ii == k) continue; if(classification[ii] >= best) ++nbad; } if(j == 0 || nbad < bestrank) { bestrank = nbad; ibestrank = j; } } if(bestrank > ulong(m_ranks[ibestrank])) m_ranks[ibestrank] = double(bestrank); } return true; }
La fase de clasificación incluye progresivamente clases que cumplen criterios de rendimiento específicos.
//+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CUnion::classify(vector &inputs,IClassify *&models[]) { for(long j =0; j<long(m_nout); j++) m_indices[j] = j; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); ArraySort(m_indices); qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong j =(m_nout-ulong(m_ranks[i])); j<m_nout; j++) { m_output[m_indices[j]] = 1.0; } } ulong n=0; double cut = 0.5; for(ulong i = 0; i<m_nout; i++) { if(m_output[i] > cut) ++n; } return n; }
A pesar de la capacidad de la regla de unión para abordar eficazmente muchas limitaciones del método de intersección, sigue siendo vulnerable a casos atípicos en los que todos los modelos componentes generan clasificaciones deficientes. Este escenario, aunque supone un reto, debería seguir siendo poco frecuente en aplicaciones bien diseñadas y, a menudo, puede mitigarse mediante un diseño adecuado del sistema y una selección adecuada del modelo. La eficacia del método destaca especialmente en entornos con modelos especializados, en los que cada componente destaca en ámbitos específicos, pero puede tener un rendimiento deficiente en otros. Esta característica lo hace especialmente valioso para tareas de clasificación complejas que requieren conocimientos especializados diversos.
Combinaciones de clasificadores basadas en regresión logística
De todos los clasificadores conjuntos analizados hasta ahora, el método de recuento de Borda es una solución universalmente eficaz para combinar clasificadores con un rendimiento similar, ya que asume una capacidad predictiva uniforme en todos los modelos. Cuando el rendimiento varía significativamente entre los modelos, puede ser conveniente aplicar ponderaciones diferenciales basadas en el rendimiento individual de cada modelo. La regresión logística proporciona un marco sofisticado para este enfoque de combinación ponderada.
La implementación de la regresión logística para la combinación de clasificadores se basa en los principios de la regresión lineal ordinaria, pero aborda los retos específicos de la clasificación. En lugar de predecir directamente valores continuos, la regresión logística calcula probabilidades de pertenencia a una clase, lo que ofrece un enfoque refinado para las tareas de clasificación. El proceso comienza transformando los datos de entrenamiento originales a un formato compatible con la regresión. Consideremos un sistema con tres clases y cuatro modelos que generan los siguientes resultados.
| Modelo 1 | Modelo 2 | Modelo 3 | Modelo 4 | |
|---|---|---|---|---|
| 1 | 0.7 | 0.1 | 0.8 | 0.4 |
| 2 | 0.8 | 0.3 | 0.9 | 0.3 |
| 3 | 0.2 | 0.2 | 0.7 | 0.2 |
Estos datos generan tres nuevos casos de entrenamiento de regresión para cada caso original, con la variable objetivo establecida en 1.0 para la clase correcta y en 0.0 para las clases incorrectas. Los predictores utilizan clasificaciones proporcionales en lugar de resultados brutos, lo que mejora la estabilidad numérica.
La clase CLogitReg en ensemble.mqh gestiona la implementación de un enfoque de combinación ponderada para conjuntos de clasificadores.
//+------------------------------------------------------------------+ //| Use logistic regression to find best class | //| This uses one common weight vector for all classes. | //+------------------------------------------------------------------+ class ClogitReg { private: ulong m_nout; long m_indices[]; matrix m_ranks; vector m_output; vector m_targs; matrix m_input; logistic::Clogit *m_logit; public: ClogitReg(void); ~ClogitReg(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
El método fit() construye el conjunto de entrenamiento de regresión procesando sistemáticamente casos individuales. En primer lugar, se determina la verdadera pertenencia a la clase de cada muestra de entrenamiento. A continuación, los resultados de la evaluación de cada modelo componente se organizan en la matriz m_ranks. Esta matriz se procesa para generar las variables dependientes e independientes para el problema de regresión, que posteriormente se resuelve utilizando el objeto m_logit.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool ClogitReg::fit(matrix &inputs,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_input = matrix::Zeros(inputs.Rows(),models.Size()); m_targs = vector::Zeros(inputs.Rows()); m_output = vector::Zeros(m_nout); m_ranks = matrix::Zeros(models.Size(),m_nout); double best = 0.0; ulong nbelow; if(ArrayResize(m_indices,int(m_nout))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k; if(CheckPointer(m_logit) == POINTER_DYNAMIC) delete m_logit; m_logit = new logistic::Clogit(); for(ulong i = 0; i<inputs.Rows(); i++) { vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); best = trow[k]; for(uint j = 0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); if(!m_ranks.Row(classification,j)) { Print(__FUNCTION__, " ", __LINE__, " failed row insertion ", GetLastError()); return false; } } for(ulong j = 0; j<m_nout; j++) { for(uint jj =0; jj<models.Size(); jj++) { nbelow = 0; best = m_ranks[jj][j]; for(ulong ii =0; ii<m_nout; ii++) { if(m_ranks[jj][ii]<best) ++nbelow; } m_input[i][jj] = double(nbelow)/double(m_nout); } m_targs[i] = (j == k)? 1.0:0.0; } } return m_logit.fit(m_input,m_targs); }
Esta implementación representa un enfoque sofisticado para la combinación de clasificadores, que ofrece un valor especial en escenarios en los que los modelos de componentes muestran distintos niveles de eficacia en diferentes tareas de clasificación.
El proceso de clasificación ponderada se basa en la metodología del recuento de Borda, integrando ponderaciones específicas del modelo. El algoritmo comienza inicializando los vectores de acumulación y procesando los casos desconocidos a través de cada modelo componente. Los pesos óptimos, calculados por el objeto m_logit, se aplican para ajustar las contribuciones de los clasificadores de componentes. La clase final se determina como el índice correspondiente al valor más grande en m_output.
//+------------------------------------------------------------------+ //| classify with ensemble model | //+------------------------------------------------------------------+ ulong ClogitReg::classify(vector &inputs,IClassify *&models[]) { double temp; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(long j =0; j<long(classification.Size()); j++) m_indices[j] = j; if(!classification.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,classification.Size()-1,classification,m_indices); temp = m_logit.coeffAt(i); for(ulong j = 0 ; j<m_nout; j++) { m_output[m_indices[j]] += j * temp; } } double sum = m_output.Sum(); ulong ibest = m_output.ArgMax(); double best = m_output[ibest]; if(sum>0.0) m_output/=sum; return ibest; }
La implementación hace hincapié en los pesos universales debido a su mayor estabilidad y menor riesgo de sobreajuste. Sin embargo, las ponderaciones específicas por clase siguen siendo una opción viable para aplicaciones con grandes cantidades de datos de entrenamiento. En la siguiente sección se analiza un método que emplea ponderaciones específicas para cada clase. Por ahora, desviamos la atención hacia cómo se obtienen los pesos óptimos, concretamente el modelo de regresión logística.
Un elemento fundamental de la regresión logística es la transformación logística o logit que se muestra a continuación.
Esta función asigna un dominio ilimitado al intervalo [0, 1]. Cuando x en la ecuación anterior es extremadamente negativo, el resultado se aproxima a cero. Por el contrario, a medida que x se hace más grande, el valor de la función se aproxima a la unidad. Si x=0, la función devuelve un valor exactamente a mitad de camino entre los dos extremos. Si x representa la variable predicha en el modelo de regresión, significa que cuando x es cero, hay un 50 % de probabilidades de que una muestra pertenezca a una clase concreta. A medida que el valor de x aumenta desde 0, el porcentaje de probabilidad aumenta en consecuencia. Por otro lado, a medida que x disminuye en valor desde 0, el porcentaje disminuye.
Una forma alternativa de expresar la probabilidad son las cuotas. Esto se conoce formalmente como la razón de probabilidades, que es la probabilidad de que ocurra un evento dividida por la probabilidad de que no ocurra. Expresando e^x en la transformación logit, en términos de f(x), se obtiene la siguiente ecuación.
Si eliminamos los exponentes de esta ecuación aplicando logaritmos a ambos lados y dejando que x sea la variable predicha del problema de regresión, obtenemos la ecuación que se muestra a continuación.
Esta expresión, formulada en el contexto de conjuntos de clasificadores, estipula que, para cada muestra del conjunto de entrenamiento, una combinación lineal de predictores de los clasificadores componentes proporciona el logaritmo de las probabilidades para la etiqueta de clase correspondiente. Los pesos óptimos, w, pueden obtenerse utilizando la estimación de máxima verosimilitud o minimizando una función objetivo. Los detalles al respecto exceden el alcance de este artículo.
Al principio resultó difícil encontrar una implementación completa de la regresión logística en MQL5. La versión MQL5 de la librería Alglib cuenta con herramientas específicas para la regresión logística, pero este autor nunca ha conseguido compilarlas con éxito. Tampoco hay ejemplos de su uso en los programas de demostración que muestran las herramientas de Alglib. Afortunadamente, la biblioteca Alglib resultó útil para implementar la clase Clogit definida en el archivo logistic.mqh. El archivo incluye la definición de la clase CFg que implementa la interfaz CNDimensional_Grad.
//+------------------------------------------------------------------+ //| function and gradient calculation object | //+------------------------------------------------------------------+ class CFg:public CNDimensional_Grad { private: matrix m_preds; vector m_targs; ulong m_nclasses,m_samples,m_features; double loss_gradient(matrix &coef,double &gradients[]); void weight_intercept_raw(matrix &coef,matrix &x, matrix &wghts,vector &intcept,matrix &rpreds); void weight_intercept(matrix &coef,matrix &wghts,vector &intcept); double l2_penalty(matrix &wghts,double strenth); void sum_exp_minus_max(ulong index,matrix &rp,vector &pr); void closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &intout_2); public: //--- constructor, destructor CFg(matrix &predictors,vector &targets, ulong num_classes) { m_preds = predictors; vector classes = np::unique(targets); np::sort(classes); vector checkclasses = np::arange(classes.Size()); if(checkclasses.Compare(classes,1.e-1)) { double classv[]; np::vecAsArray(classes,classv); m_targs = targets; for(ulong i = 0; i<targets.Size(); i++) m_targs[i] = double(ArrayBsearch(classv,m_targs[i])); } else m_targs = targets; m_nclasses = num_classes; m_features = m_preds.Cols(); m_samples = m_preds.Rows(); } ~CFg(void) {} virtual void Grad(double &x[],double &func,double &grad[],CObject &obj); virtual void Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj); }; //+------------------------------------------------------------------+ //| this function is not used | //+------------------------------------------------------------------+ void CFg::Grad(double &x[],double &func,double &grad[],CObject &obj) { matrix coefficients; arrayToMatrix(x,coefficients,m_nclasses>2?m_nclasses:m_nclasses-1,m_features+1); func=loss_gradient(coefficients,grad); return; } //+------------------------------------------------------------------+ //| get function value and gradients | //+------------------------------------------------------------------+ void CFg::Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj) { double xarray[],garray[]; x.ToArray(xarray); Grad(xarray,func,garray,obj); grad = garray; return; } //+------------------------------------------------------------------+ //| loss gradient | //+------------------------------------------------------------------+ double CFg::loss_gradient(matrix &coef,double &gradients[]) { matrix weights; vector intercept; vector losses; matrix gradpointwise; matrix rawpredictions; matrix gradient; double loss; double l2reg; //calculate weights intercept and raw predictions weight_intercept_raw(coef,m_preds,weights,intercept,rawpredictions); gradpointwise = matrix::Zeros(m_samples,rawpredictions.Cols()); losses = vector::Zeros(m_samples); double sw_sum = double(m_samples); //loss gradient calculations if(m_nclasses>2) { double max_value, sum_exps; vector p(rawpredictions.Cols()+2); //--- for(ulong i = 0; i< m_samples; i++) { sum_exp_minus_max(i,rawpredictions,p); max_value = p[rawpredictions.Cols()]; sum_exps = p[rawpredictions.Cols()+1]; losses[i] = log(sum_exps) + max_value; //--- for(ulong k = 0; k<rawpredictions.Cols(); k++) { if(ulong(m_targs[i]) == k) losses[i] -= rawpredictions[i][k]; p[k]/=sum_exps; gradpointwise[i][k] = p[k] - double(int(ulong(m_targs[i])==k)); } } } else { for(ulong i = 0; i<m_samples; i++) { closs_grad_halfbinmial(m_targs[i],rawpredictions[i][0],losses[i],gradpointwise[i][0]); } } //--- loss = losses.Sum()/sw_sum; l2reg = 1.0 / (1.0 * sw_sum); loss += l2_penalty(weights,l2reg); gradpointwise/=sw_sum; //--- if(m_nclasses>2) { gradient = gradpointwise.Transpose().MatMul(m_preds) + l2reg*weights; gradient.Resize(gradient.Rows(),gradient.Cols()+1); vector gpsum = gradpointwise.Sum(0); gradient.Col(gpsum,m_features); } else { gradient = m_preds.Transpose().MatMul(gradpointwise) + l2reg*weights.Transpose(); gradient.Resize(gradient.Rows()+1,gradient.Cols()); vector gpsum = gradpointwise.Sum(0); gradient.Row(gpsum,m_features); } //--- matrixToArray(gradient,gradients); //--- return loss; } //+------------------------------------------------------------------+ //| weight intercept raw preds | //+------------------------------------------------------------------+ void CFg::weight_intercept_raw(matrix &coef,matrix &x,matrix &wghts,vector &intcept,matrix &rpreds) { weight_intercept(coef,wghts,intcept); matrix intceptmat = np::vectorAsRowMatrix(intcept,x.Rows()); rpreds = (x.MatMul(wghts.Transpose()))+intceptmat; } //+------------------------------------------------------------------+ //| weight intercept | //+------------------------------------------------------------------+ void CFg::weight_intercept(matrix &coef,matrix &wghts,vector &intcept) { intcept = coef.Col(m_features); wghts = np::sliceMatrixCols(coef,0,m_features); } //+------------------------------------------------------------------+ //| sum exp minus max | //+------------------------------------------------------------------+ void CFg::sum_exp_minus_max(ulong index,matrix &rp,vector &pr) { double mv = rp[index][0]; double s_exps = 0.0; for(ulong k = 1; k<rp.Cols(); k++) { if(mv<rp[index][k]) mv=rp[index][k]; } for(ulong k = 0; k<rp.Cols(); k++) { pr[k] = exp(rp[index][k] - mv); s_exps += pr[k]; } pr[rp.Cols()] = mv; pr[rp.Cols()+1] = s_exps; } //+------------------------------------------------------------------+ //| l2 penalty | //+------------------------------------------------------------------+ double CFg::l2_penalty(matrix &wghts,double strenth) { double norm2_v; if(wghts.Rows()==1) { matrix nmat = (wghts).MatMul(wghts.Transpose()); norm2_v = nmat[0][0]; } else norm2_v = wghts.Norm(MATRIX_NORM_FROBENIUS); return 0.5*strenth*norm2_v; } //+------------------------------------------------------------------+ //| closs_grad_half_binomial | //+------------------------------------------------------------------+ void CFg::closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &inout_2) { if(raw <= -37.0) { inout_2 = exp(raw); inout_1 = inout_2 - y_true * raw; inout_2 -= y_true; } else if(raw <= -2.0) { inout_2 = exp(raw); inout_1 = log1p(inout_2) - y_true * raw; inout_2 = ((1.0 - y_true) * inout_2 - y_true) / (1.0 + inout_2); } else if(raw <= 18.0) { inout_2 = exp(-raw); // log1p(exp(x)) = log(1 + exp(x)) = x + log1p(exp(-x)) inout_1 = log1p(inout_2) + (1.0 - y_true) * raw; inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2); } else { inout_2 = exp(-raw); inout_1 = inout_2 + (1.0 - y_true) * raw; inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2); } }
Esto es necesario para el procedimiento de minimización de la función LBFGS. Clogit cuenta con métodos conocidos para el entrenamiento y la inferencia.
//+------------------------------------------------------------------+ //| logistic regression implementation | //+------------------------------------------------------------------+ class Clogit { public: Clogit(void); ~Clogit(void); bool fit(matrix &predictors, vector &targets); double predict(vector &preds); vector proba(vector &preds); matrix probas(matrix &preds); double coeffAt(ulong index); private: ulong m_nsamples; ulong m_nfeatures; bool m_trained; matrix m_train_preds; vector m_train_targs; matrix m_coefs; vector m_bias; vector m_classes; double m_xin[]; CFg *m_gradfunc; CObject m_dummy; vector predictProba(double &in); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ Clogit::Clogit(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ Clogit::~Clogit(void) { if(CheckPointer(m_gradfunc) == POINTER_DYNAMIC) delete m_gradfunc; } //+------------------------------------------------------------------+ //| fit a model to a dataset | //+------------------------------------------------------------------+ bool Clogit::fit(matrix &predictors, vector &targets) { m_trained = false; m_classes = np::unique(targets); np::sort(m_classes); if(predictors.Rows()!=targets.Size() || m_classes.Size()<2) { Print(__FUNCTION__," ",__LINE__," invalid inputs "); return m_trained; } m_train_preds = predictors; m_train_targs = targets; m_nfeatures = m_train_preds.Cols(); m_nsamples = m_train_preds.Rows(); m_coefs = matrix::Zeros(m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1); matrixToArray(m_coefs,m_xin); m_gradfunc = new CFg(m_train_preds,m_train_targs,m_classes.Size()); //--- CMinLBFGSStateShell state; CMinLBFGSReportShell rep; CNDimensional_Rep frep; //--- CAlglib::MinLBFGSCreate(m_xin.Size(),m_xin.Size()>=5?5:m_xin.Size(),m_xin,state); //--- CAlglib::MinLBFGSOptimize(state,m_gradfunc,frep,true,m_dummy); //--- CAlglib::MinLBFGSResults(state,m_xin,rep); //--- if(rep.GetTerminationType()>0) { m_trained = true; arrayToMatrix(m_xin,m_coefs,m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1); m_bias = m_coefs.Col(m_nfeatures); m_coefs = np::sliceMatrixCols(m_coefs,0,m_nfeatures); } else Print(__FUNCTION__," ", __LINE__, " failed to train the model ", rep.GetTerminationType()); delete m_gradfunc; return m_trained; } //+------------------------------------------------------------------+ //| get probability for single sample | //+------------------------------------------------------------------+ vector Clogit::proba(vector &preds) { vector predicted; if(!m_trained) { Print(__FUNCTION__," ", __LINE__," no trained model available "); predicted.Fill(EMPTY_VALUE); return predicted; } predicted = ((preds.MatMul(m_coefs.Transpose()))); predicted += m_bias; if(predicted.Size()>1) { if(!predicted.Activation(predicted,AF_SOFTMAX)) { Print(__FUNCTION__," ", __LINE__," errror ", GetLastError()); predicted.Fill(EMPTY_VALUE); return predicted; } } else { predicted = predictProba(predicted[0]); } return predicted; } //+------------------------------------------------------------------+ //| get probability for binary classification | //+------------------------------------------------------------------+ vector Clogit::predictProba(double &in) { vector out(2); double n = 1.0/(1.0+exp(-1.0*in)); out[0] = 1.0 - n; out[1] = n; return out; } //+------------------------------------------------------------------+ //| get probabilities for multiple samples | //+------------------------------------------------------------------+ matrix Clogit::probas(matrix &preds) { matrix output(preds.Rows(),m_classes.Size()); vector rowin,rowout; for(ulong i = 0; i<preds.Rows(); i++) { rowin = preds.Row(i); rowout = proba(rowin); if(rowout.Max() == EMPTY_VALUE || !output.Row(rowout,i)) { Print(__LINE__," probas error ", GetLastError()); output.Fill(EMPTY_VALUE); break; } } return output; } //+------------------------------------------------------------------+ //| get probability for single sample | //+------------------------------------------------------------------+ double Clogit::predict(vector &preds) { vector prob = proba(preds); if(prob.Max() == EMPTY_VALUE) { Print(__LINE__," predict error "); return EMPTY_VALUE; } return m_classes[prob.ArgMax()]; } //+------------------------------------------------------------------+ //| get model coefficient at specific index | //+------------------------------------------------------------------+ double Clogit::coeffAt(ulong index) { if(index<(m_coefs.Rows())) { return (m_coefs.Row(index)).Sum(); } else { return 0.0; } } } //+------------------------------------------------------------------+
Combinaciones de conjuntos basadas en regresión logística con ponderaciones específicas por clase.
El enfoque de conjunto de pesos único descrito en la sección anterior ofrece estabilidad y eficacia, pero tiene la limitación de que puede no aprovechar al máximo la especialización del modelo. Si los modelos individuales demuestran un rendimiento superior para clases específicas, ya sea por diseño o por desarrollo natural, la implementación de conjuntos de pesos separados para cada clase puede aprovechar estas capacidades especializadas de manera más eficaz. La transición a conjuntos de pesos específicos para cada clase introduce una complejidad significativa en el proceso de optimización. En lugar de optimizar un único conjunto de pesos, el conjunto debe gestionar K conjuntos (uno por clase), cada uno de los cuales contiene M parámetros, lo que da un total de K*M parámetros. Este aumento de los parámetros exige un análisis minucioso de los requisitos de datos y los riesgos de implementación.
Una aplicación sólida de conjuntos de pesos separados requiere una cantidad considerable de datos de entrenamiento para mantener la validez estadística. Como pauta general, cada clase debe tener al menos diez veces más casos de entrenamiento que modelos. Incluso con datos suficientes, este enfoque debe aplicarse con cautela y solo cuando haya pruebas claras que sugieran una especialización significativa del modelo entre clases.
La clase CLogitRegSep gestiona la implementación de conjuntos de pesos separados, difiriendo de CLogitReg en su asignación de objetos Clogit individuales para cada clase. El proceso de entrenamiento distribuye los casos de regresión entre conjuntos de entrenamiento específicos para cada clase, en lugar de consolidarlos en un único conjunto.
//+------------------------------------------------------------------+ //| Use logistic regression to find best class. | //| This uses separate weight vectors for each class. | //+------------------------------------------------------------------+ class ClogitRegSep { private: ulong m_nout; long m_indices[]; matrix m_ranks; vector m_output; vector m_targs[]; matrix m_input[]; logistic::Clogit *m_logit[]; public: ClogitRegSep(void); ~ClogitRegSep(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
La clasificación de los casos desconocidos sigue un proceso similar al enfoque de ponderación única, con una diferencia clave: durante el cálculo del recuento de Borda se aplican ponderaciones específicas para cada clase. Esta especialización permite al sistema aprovechar de manera más eficaz los conocimientos específicos de los modelos de cada clase.
//+------------------------------------------------------------------+ //| classify with ensemble model | //+------------------------------------------------------------------+ ulong ClogitRegSep::classify(vector &inputs,IClassify *&models[]) { double temp; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(long j =0; j<long(classification.Size()); j++) m_indices[j] = j; if(!classification.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong j = 0 ; j<m_nout; j++) { temp = m_logit[j].coeffAt(i); m_output[m_indices[j]] += j * temp; } } double sum = m_output.Sum(); ulong ibest = m_output.ArgMax(); double best = m_output[ibest]; if(sum>0.0) m_output/=sum; return ibest; }
La implementación de conjuntos de pesos separados requiere procedimientos de validación rigurosos. Los profesionales deben supervisar las distribuciones de peso en busca de valores extremos inexplicables, asegurándose de que las disparidades de peso se ajusten a las características conocidas del modelo. Se deben implementar medidas de seguridad para evitar inestabilidades en el proceso de regresión. Todo ello puede aplicarse de manera eficaz mediante el mantenimiento de protocolos de pruebas exhaustivos.
La implementación exitosa de conjuntos de pesos específicos para cada clase depende de prestar especial atención a varios factores críticos: garantizar que haya suficientes datos de entrenamiento para cada clase, verificar que los patrones de especialización justifiquen pesos separados, supervisar la estabilidad de los pesos y confirmar que la precisión de la clasificación haya mejorado con respecto a los enfoques de peso único. Si bien esta implementación avanzada de la regresión logística ofrece capacidades de clasificación mejoradas, requiere una gestión cuidadosa para abordar la mayor complejidad y los riesgos potenciales.
Conjuntos que aprovechan la precisión local
Para aprovechar aún más las fortalezas de los modelos individuales, podemos considerar su precisión local dentro del espacio del predictor. A veces, los clasificadores de componentes muestran un rendimiento superior en regiones específicas del espacio predictivo. Esta especialización se manifiesta cuando los modelos destacan en condiciones particulares de variables predictivas; por ejemplo, un modelo puede funcionar de manera óptima con valores variables más bajos, mientras que otro destaca con valores más altos. Estos patrones de especialización, ya sean diseñados intencionadamente o surgidos de forma natural, pueden mejorar significativamente la precisión de la clasificación cuando se utilizan adecuadamente.
La implementación sigue un enfoque sencillo pero eficaz. Al evaluar un caso desconocido, el sistema recopila clasificaciones de todos los modelos componentes y selecciona el modelo que considera más fiable para ese caso específico. El conjunto evalúa la fiabilidad de un modelo mediante el empleo de un método propuesto en el artículo «Combinación de múltiples clasificadores utilizando estimaciones de precisión locales», escrito por Woods, Kegelmeyer y Bowyer. Este enfoque funciona a través de varios pasos definidos:
- Calcula las distancias euclidianas entre el caso desconocido y todos los casos de entrenamiento.
- Identificar un número predefinido de casos de entrenamiento más cercanos para realizar un análisis comparativo.
- Evalúa el rendimiento de cada modelo específicamente en estos casos cercanos, centrándote en los casos en los que el modelo asigna la misma clasificación que en el caso desconocido.
- Calcular un criterio de rendimiento basado en la proporción de clasificaciones correctas entre los casos en los que el modelo predijo la misma clase para el caso desconocido y sus vecinos.
Consideremos un escenario en el que se analizan los diez vecinos más cercanos. Tras identificar a estos vecinos mediante cálculos de distancia euclidiana, el conjunto presenta un caso desconocido a un modelo, que lo asigna a la clase 3. A continuación, el sistema evalúa el rendimiento de este modelo en los diez casos de entrenamiento cercanos. Si el modelo clasifica seis de estos casos como clase 3, y cuatro de estas clasificaciones son correctas, el modelo alcanza un criterio de rendimiento de 0,67 (4/6). Este proceso de evaluación se aplica a todos los modelos componentes, y el modelo con la puntuación más alta determina finalmente la clasificación definitiva. Este enfoque garantiza que las decisiones de clasificación aprovechen el modelo más fiable para cada contexto específico.
Para abordar los empates, seleccionamos el modelo con mayor certeza, calculada como la relación entre su resultado máximo y la suma de todos los resultados. Es necesario determinar el tamaño de este subconjunto local, ya que los subconjuntos más pequeños son más sensibles a las variaciones locales, mientras que los subconjuntos más grandes son más robustos, pero pueden reducir la naturaleza «local» de la evaluación. La validación cruzada puede ayudar a determinar el tamaño óptimo del subconjunto, priorizándose normalmente los tamaños más pequeños por motivos de eficiencia en caso de empates. Al aplicar este enfoque, el conjunto utiliza eficazmente la experiencia en modelos específicos del dominio, al tiempo que mantiene la eficiencia computacional. El método permite que el conjunto se adapte dinámicamente a las diferentes regiones del espacio predictivo, y la medida de fiabilidad puede aprovecharse para proporcionar una métrica transparente para la selección de modelos.
La clase ClocalAcc en ensemble.mqh está diseñada para determinar la clase más probable a partir de un conjunto de clasificadores basándose en la precisión local.
//+------------------------------------------------------------------+ //| Use local accuracy to choose the best model | //+------------------------------------------------------------------+ class ClocalAcc { private: ulong m_knn; ulong m_nout; long m_indices[]; matrix m_ranks; vector m_output; vector m_targs; matrix m_input; vector m_dist; matrix m_trnx; matrix m_trncls; vector m_trntrue; ulong m_classprep; bool m_crossvalidate; public: ClocalAcc(void); ~ClocalAcc(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[], bool crossvalidate = false); vector proba(void) { return m_output;} };
El método fit() entrena el objeto ClocalAcc. Toma los datos de entrada (inputs), los valores objetivo (targets), una matriz de modelos clasificadores (models) y un indicador opcional para la validación cruzada (crossvalidate). Durante el entrenamiento, fit() calcula la distancia entre cada punto de datos de entrada y todos los demás puntos de datos. A continuación, determina los k vecinos más cercanos para cada punto, donde k se determina mediante validación cruzada si crossvalidate se establece en true. Para cada vecino, el método evalúa el rendimiento de cada clasificador del conjunto.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool ClocalAcc::fit(matrix &inputs,matrix &targets,IClassify *&models[], bool crossvalidate = false) { m_crossvalidate = crossvalidate; m_nout = targets.Cols(); m_input = matrix::Zeros(inputs.Rows(),models.Size()); m_targs = vector::Zeros(inputs.Rows()); m_output = vector::Zeros(m_nout); m_ranks = matrix::Zeros(models.Size(),m_nout); m_dist = vector::Zeros(inputs.Rows()); m_trnx = matrix::Zeros(inputs.Rows(),inputs.Cols()); m_trncls = matrix::Zeros(inputs.Rows(),models.Size()); m_trntrue = vector::Zeros(inputs.Rows()); double best = 0.0; if(ArrayResize(m_indices,int(inputs.Rows()))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k, knn_min,knn_max,knn_best=0,true_class, ibest=0; for(ulong i = 0; i<inputs.Rows(); i++) { np::matrixCopyRows(m_trnx,inputs,i,i+1,1); vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); best = trow[k]; m_trntrue[i] = double(k); for(uint j=0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); ibest = classification.ArgMax(); best = classification[ibest]; m_trncls[i][j] = double(ibest); } } m_classprep = 1; if(!m_crossvalidate) { m_knn=3; return true; } else { ulong ncases = inputs.Rows(); if(inputs.Rows()<20) { m_knn=3; return true; } knn_min = 3; knn_max = 10; vector testcase(inputs.Cols()) ; vector clswork(m_nout) ; vector knn_counts(knn_max - knn_min + 1) ; for(ulong i = knn_min; i<=knn_max; i++) knn_counts[i-knn_min] = 0; --ncases; for(ulong i = 0; i<=ncases; i++) { testcase = m_trnx.Row(i); true_class = ulong(m_trntrue[i]); if(i<ncases) { if(!m_trnx.SwapRows(ncases,i)) { Print(__FUNCTION__, " ", __LINE__, " failed row swap ", GetLastError()); return false; } m_trntrue[i] = m_trntrue[ncases]; double temp; for(uint j = 0; j<models.Size(); j++) { temp = m_trncls[i][j]; m_trncls[i][j] = m_trncls[ncases][j]; m_trncls[ncases][j] = temp; } } m_classprep = 1; for(ulong knn = knn_min; knn<knn_max; knn++) { ulong iclass = classify(testcase,models); if(iclass == true_class) { ++knn_counts[knn-knn_min]; } m_classprep=0; } if(i<ncases) { if(!m_trnx.SwapRows(i,ncases) || !m_trnx.Row(testcase,i)) { Print(__FUNCTION__, " ", __LINE__, " error ", GetLastError()); return false; } m_trntrue[ncases] = m_trntrue[i]; m_trntrue[i] = double(true_class); double temp; for(uint j = 0; j<models.Size(); j++) { temp = m_trncls[i][j]; m_trncls[i][j] = m_trncls[ncases][j]; m_trncls[ncases][j] = temp; } } } ++ncases; for(ulong knn = knn_min; knn<=knn_max; knn++) { if((knn==knn_min) || (ulong(knn_counts[knn-knn_min])>ibest)) { ibest = ulong(knn_counts[knn-knn_min]); knn_best = knn; } } m_knn = knn_best; m_classprep = 1; } return true; }
El método classify() predice la etiqueta de clase para un vector de entrada dado. Calcula las distancias entre el vector de entrada y todos los puntos de datos de entrenamiento e identifica los k vecinos más cercanos. Para cada clasificador del conjunto, determina la precisión del clasificador en estos vecinos. Se selecciona el clasificador con mayor precisión en los vecinos más cercanos y se devuelve su etiqueta de clase prevista.
//+------------------------------------------------------------------+ //| classify with an ensemble model | //+------------------------------------------------------------------+ ulong ClocalAcc::classify(vector &inputs,IClassify *&models[]) { double dist=0, diff=0, best=0, crit=0, bestcrit=0, conf=0, bestconf=0, sum ; ulong k, ibest, numer, denom, bestmodel=0, bestchoice=0 ; if(m_classprep) { for(ulong i = 0; i<m_input.Rows(); i++) { m_indices[i] = long(i); dist = 0.0; for(ulong j = 0; j<m_trnx.Cols(); j++) { diff = inputs[j] - m_trnx[i][j]; dist+= diff*diff; } m_dist[i] = dist; } if(!m_dist.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0, m_dist.Size()-1, m_dist,m_indices); } for(uint i = 0; i<models.Size(); i++) { vector vec = models[i].classify(inputs); sum = vec.Sum(); ibest = vec.ArgMax(); best = vec[ibest]; conf = best/sum; denom = numer = 0; for(ulong ii = 0; ii<m_knn; ii++) { k = m_indices[ii]; if(ulong(m_trncls[k][i]) == ibest) { ++denom; if(ibest == ulong(m_trntrue[k])) ++numer; } } if(denom > 0) crit = double(numer)/double(denom); else crit = 0.0; if((i == 0) || (crit > bestcrit)) { bestcrit = crit; bestmodel = ulong(i); bestchoice = ibest; bestconf = conf; m_output = vec; } else if(fabs(crit-bestcrit)<1.e-10) { if(conf > bestconf) { bestcrit= crit; bestmodel = ulong(i); bestchoice = ibest; bestconf = conf; m_output = vec; } } } sum = m_output.Sum(); if(sum>0) m_output/=sum; return bestchoice; }
Conjuntos combinados utilizando la integral difusa
La lógica difusa es un marco matemático que se ocupa de grados de verdad en lugar de valores absolutos de verdadero o falso. En el contexto de la combinación de clasificadores, la lógica difusa se puede utilizar para integrar los resultados de múltiples modelos, teniendo en cuenta la fiabilidad de cada uno de ellos. La integral difusa, propuesta originalmente por Sugeno (1977), implica una medida difusa que asigna valores a subconjuntos de un universo. Esta medida satisface ciertas propiedades, incluyendo condiciones de contorno, monotonía y continuidad. Sugeno amplió este concepto con la medida difusa λ, que incorpora un factor adicional para combinar las medidas de conjuntos disjuntos.
La integral difusa en sí misma se calcula utilizando una fórmula específica que involucra la función de pertenencia y la medida difusa. Aunque es posible realizar un cálculo por fuerza bruta, existe un método más eficiente para conjuntos finitos, que implica un cálculo recursivo. El valor de λ se determina asegurándose de que la medida final sea igual a uno. En el contexto de la combinación de clasificadores, la integral difusa se puede aplicar tratando cada clasificador como un elemento del universo, con su fiabilidad como valor de pertenencia. A continuación, se calcula la integral difusa para cada clase y se selecciona la clase con la integral más alta. Este método combina eficazmente los resultados de múltiples clasificadores, teniendo en cuenta su fiabilidad individual.
La clase CFuzzyInt implementa el método integral difuso para combinar clasificadores.
//+------------------------------------------------------------------+ //| Use fuzzy integral to combine decisions | //+------------------------------------------------------------------+ class CFuzzyInt { private: ulong m_nout; vector m_output; long m_indices[]; matrix m_sort; vector m_g; double m_lambda; double recurse(double x); public: CFuzzyInt(void); ~CFuzzyInt(void); bool fit(matrix &predictors, matrix &targets, IClassify* &models[]); ulong classify(vector &inputs, IClassify* &models[]); vector proba(void) { return m_output;} };
El núcleo de este método reside en la función recurse(), que calcula iterativamente la medida difusa. El parámetro clave, λ, se determina hallando el valor que garantiza que la medida difusa de todos los modelos converge en uno. Comenzamos con un valor inicial y lo ajustamos gradualmente hasta que la medida difusa de todos los modelos converge en uno. Esto suele implicar el uso de un intervalo para el valor λ correcto y, a continuación, refinar la búsqueda utilizando un método de bisección.
//+------------------------------------------------------------------+ //| recurse | //+------------------------------------------------------------------+ double CFuzzyInt::recurse(double x) { double val ; val = m_g[0] ; for(ulong i=1 ; i<m_g.Size() ; i++) val += m_g[i] + x * m_g[i] * val ; return val - 1.0 ; }
Para estimar la fiabilidad de cada modelo, evaluamos su precisión en el conjunto de entrenamiento. A continuación, ajustamos esta precisión restando la precisión esperada de una respuesta aleatoria y reescalando el resultado a un valor entre cero y uno. Existen formas más sofisticadas de estimar la fiabilidad de los modelos, pero se prefiere este enfoque por su simplicidad.
//+------------------------------------------------------------------+ //| fit ensemble model | //+------------------------------------------------------------------+ bool CFuzzyInt::fit(matrix &predictors,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_output = vector::Zeros(m_nout); m_sort = matrix::Zeros(models.Size(), m_nout); m_g = vector::Zeros(models.Size()); if(ArrayResize(m_indices,int(models.Size()))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k=0, iclass =0 ; double best=0, xlo=0, xhi=0, y=0, ylo=0, yhi=0, step=0 ; for(ulong i = 0; i<predictors.Rows(); i++) { vector trow = targets.Row(i); vector inrow = predictors.Row(i); k = trow.ArgMax(); best = trow[k]; for(uint ii = 0; ii< models.Size(); ii++) { vector vec = models[ii].classify(inrow); iclass = vec.ArgMax(); best = vec[iclass]; if(iclass == k) m_g[ii] += 1.0; } } for(uint i = 0; i<models.Size(); i++) { m_g[i] /= double(predictors.Rows()) ; m_g[i] = (m_g[i] - 1.0 / m_nout) / (1.0 - 1.0 / m_nout) ; if(m_g[i] > 1.0) m_g[i] = 1.0 ; if(m_g[i] < 0.0) m_g[i] = 0.0 ; } xlo = m_lambda = -1.0 ; ylo = recurse(xlo) ; if(ylo >= 0.0) // Theoretically should never exceed zero return true; // But allow for pathological numerical problems step = 1.0 ; for(;;) { xhi = xlo + step ; yhi = recurse(xhi) ; if(yhi >= 0.0) // If we have just bracketed the root break ; // We can quit the search if(xhi > 1.e5) // In the unlikely case of extremely poor models { m_lambda = xhi ; // Fudge a value return true ; // And quit } step *= 2.0 ; // Keep increasing the step size to avoid many tries xlo = xhi ; // Move onward ylo = yhi ; } for(;;) { m_lambda = 0.5 * (xlo + xhi) ; y = recurse(m_lambda) ; // Evaluate the function here if(fabs(y) < 1.e-8) // Primary convergence criterion break ; if(xhi - xlo < 1.e-10 * (m_lambda + 1.1)) // Backup criterion break ; if(y > 0.0) { xhi = m_lambda ; yhi = y ; } else { xlo = m_lambda ; ylo = y ; } } return true; }
Durante la clasificación, se selecciona la clase con la integral difusa más alta. La integral difusa para cada clase se calcula comparando iterativamente la salida del modelo con la medida difusa calculada recursivamente y seleccionando el valor mínimo en cada paso. La integral difusa final para una clase representa la confianza combinada de los modelos en esa clase.
//+------------------------------------------------------------------+ //| classify with ensemble | //+------------------------------------------------------------------+ ulong CFuzzyInt::classify(vector &inputs,IClassify *&models[]) { ulong k, iclass; double sum, gsum, minval, maxmin, best ; for(uint i = 0; i<models.Size(); i++) { vector vec = models[i].classify(inputs); sum = vec.Sum(); vec/=sum; if(!m_sort.Row(vec,i)) { Print(__FUNCTION__, " ", __LINE__, " row insertion error ", GetLastError()); return false; } } for(ulong i = 0; i<m_nout; i++) { for(uint ii =0; ii<models.Size(); ii++) m_indices[ii] = long(ii); vector vec = m_sort.Col(i); if(!vec.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,long(vec.Size()-1), vec, m_indices); maxmin = gsum = 0.0; for(int j = int(models.Size()-1); j>=0; j--) { k = m_indices[j]; if(k>=vec.Size()) { Print(__FUNCTION__," ",__LINE__, " out of range ", k); } gsum += m_g[k] + m_lambda * m_g[k] * gsum; if(gsum<vec[k]) minval = gsum; else minval = vec[k]; if(minval > maxmin) maxmin = minval; } m_output[i] = maxmin; } iclass = m_output.ArgMax(); best = m_output[iclass]; return iclass; }
Acoplamiento por pares
El acoplamiento por pares es un enfoque único para la clasificación multiclase que aprovecha la potencia de los clasificadores binarios especializados. Combina un conjunto de K(K−1)/2 clasificadores binarios (donde K es el número de clases), cada uno diseñado para distinguir entre un par específico de clases. Imaginemos que tenemos un conjunto de datos compuesto por objetivos con 3 clases. Para compararlos, creamos un conjunto de 3*(3-1)/2 = 3 modelos. Cada modelo está diseñado para decidir entre solo dos clases. Si las clases se designaron, los identificadores (A, B y C). Los 3 modelos se configurarían de la siguiente manera:
- Modelo 1: Decide entre la clase A y la clase B.
- Modelo 2: Decide entre la clase A y la clase C.
- Modelo 3: Decide entre la clase B y la clase C.
Los datos de entrenamiento tendrían que dividirse para incluir las muestras relevantes para la tarea de clasificación de cada modelo. La evaluación de estos modelos daría como resultado un conjunto de probabilidades que podrían organizarse en una matriz K por K. A continuación se muestra un ejemplo hipotético de dicha matriz.
| A | B | C | |
| A | ---- | 0.2 | 0.7 |
| B | 0.8 | ---- | 0.4 |
| C | 0.3 | 0.6 | ---- |
En esta matriz, el modelo que discrimina entre las clases A y B asigna una probabilidad de 0.2 de que la muestra pertenezca a la clase A. Los elementos diagonales superiores derechos de la matriz representan el conjunto completo de probabilidades calculadas para decidir entre las clases emparejadas, ya que la matriz es simétrica. Dados los resultados del modelo, el objetivo es calcular una estimación de la probabilidad de que un caso fuera de la muestra pertenezca a una clase concreta. Esto significa que debemos encontrar un conjunto de probabilidades cuya distribución se corresponda con la de las probabilidades por pares observadas o, como mínimo, se acerque lo más posible a ellas. Se emplea un enfoque iterativo para refinar estas estimaciones de probabilidad iniciales, sin tener que utilizar un procedimiento de minimización de funciones.
Este proceso iterativo refina gradualmente las estimaciones iniciales de probabilidad de clase, asegurando que se alineen mejor con las predicciones por pares de los clasificadores individuales. En esencia, es como refinar gradualmente un mapa hasta que refleje con precisión el mundo real. Empezamos con un boceto aproximado y luego hacemos pequeños ajustes basados en la nueva información hasta obtener un mapa muy preciso. Este enfoque iterativo es eficiente y, por lo general, converge rápidamente hacia una solución.
La clase CPairWise implementa el algoritmo de acoplamiento por pares.
//+------------------------------------------------------------------+ //| Use pairwise coupling to combine decisions | //+------------------------------------------------------------------+ class CPairWise { private: ulong m_nout; ulong m_npairs; vector m_output; vector m_rij; vector m_uij; public: CPairWise(void); ~CPairWise(void); ulong classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[]); vector proba(void) { return m_output;} };
El cálculo central se realiza dentro del método classify(), que sigue un proceso estructurado para calcular las probabilidades de clase a partir de los resultados de los clasificadores por pares. El método comienza evaluando todos los modelos por pares para un caso de prueba determinado. Cada modelo corresponde a un par específico de clases y genera un resultado que representa la probabilidad de que el caso de prueba pertenezca a una de las dos clases del par.
//+------------------------------------------------------------------+ //| classify using ensemble model | //+------------------------------------------------------------------+ ulong CPairWise::classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[]) { m_nout=numclasses; m_npairs = m_nout*(m_nout-1)/2; m_output = vector::Zeros(m_nout); m_rij = vector::Zeros(m_npairs); m_uij = vector::Zeros(m_npairs); long k; ulong iclass=0 ; double rr, best=0, numer, denom, sum, delta, oldval ; for(ulong i = 0; i<m_npairs; i++) { vector vec = models[i].classify(inputs); rr = vec[0]; if(vec[0]> 0.999999) vec[0] = 0.999999 ; if(vec[0] < 0.000001) vec[0] = 0.000001 ; m_rij[i] = vec[0] ; } k = 0 ; for(ulong i=0 ; i<m_nout-1 ; i++) { for(ulong j=i+1 ; j<m_nout ; j++) { rr = m_rij[k++] ; m_output[i] += rr ; m_output[j] += 1.0 - rr ; } } for(ulong i=0 ; i<m_nout ; i++) m_output[i] /= double(m_npairs) ; k = 0 ; for(ulong i=0 ; i<m_nout-1 ; i++) { for(ulong j=i+1 ; j<m_nout ; j++) m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ; } for(int iter=0 ; iter<10000 ; iter++) { delta = 0.0 ; for(ulong i=0 ; i<m_nout ; i++) { numer = denom = 0.0 ; for(ulong j=0 ; j<m_nout ; j++) { if(i < j) { k = (long(i) * (2 * long(m_nout) - long(i) - 3) - 2) / 2 + long(j) ; numer += samplesPerModel[k] * m_rij[k] ; denom += samplesPerModel[k] * m_uij[k] ; } else if(i > j) { k = (long(j) * (2 * long(m_nout) - long(j) - 3) - 2) / 2 + long(i) ; //Print(__FUNCTION__," ",__LINE__," k ", k); numer += samplesPerModel[k] * (1.0 - m_rij[k]) ; denom += samplesPerModel[k] * (1.0 - m_uij[k]) ; } } oldval = m_output[i] ; m_output[i] *= numer / denom ; sum = 0.0 ; for(ulong j=0 ; j<m_nout ; j++) sum += m_output[j] ; for(ulong j=0 ; j<m_nout ; j++) m_output[j] /= sum ; if(fabs(m_output[i]-oldval) > delta) delta = fabs(m_output[i]-oldval) ; k = 0 ; for(ulong i=0 ; i<m_nout-1 ; i++) { for(ulong j=i+1 ; j<m_nout ; j++) m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ; } } if(delta < 1.e-6) break ; } return m_output.ArgMax() ; }
Una vez obtenidos los resultados iniciales (probabilidades), se utilizan como estimaciones iniciales para las probabilidades de clase. A continuación, el método refina estas estimaciones de forma iterativa para mejorar la precisión. Después de refinar las probabilidades de clase, el paso final es identificar la clase con la mayor probabilidad. La clase con la probabilidad más alta se considera la clase más probable para el caso de prueba dado, y su índice se devuelve como resultado del método classify().
Conclusión: Comparación de métodos combinados
El script ClassificationEnsemble_Demo.mq5 está diseñado para comparar el rendimiento de los algoritmos de conjunto analizados en este artículo en diversos escenarios. Al ejecutar múltiples réplicas de Monte Carlo, el script permite evaluar el rendimiento de cada método de conjunto en diferentes condiciones. El script permite a los usuarios especificar el número de muestras de entrenamiento utilizadas en cada ejecución, lo que permite realizar pruebas en conjuntos de datos de distintos tamaños, desde pequeños hasta grandes. El número de clases se puede ajustar para comprobar la escalabilidad de los métodos de conjunto a medida que aumenta la complejidad del problema. El número de clasificadores base (modelos) utilizados en el conjunto puede variar para evaluar el rendimiento de los algoritmos con diferentes niveles de complejidad.
Los usuarios pueden especificar el número de réplicas de Monte Carlo para cada escenario con el fin de evaluar la estabilidad y la coherencia de los algoritmos de conjunto. La probabilidad de clasificación errónea fuera de la muestra se utiliza como métrica de rendimiento, lo que garantiza que los modelos se evalúen con datos no vistos para simular tareas de clasificación del mundo real. Si se emplean cuatro o más modelos, uno de ellos se inutiliza deliberadamente (por ejemplo, haciéndole realizar predicciones aleatorias o producir resultados constantes). Esto pone a prueba la solidez de los algoritmos de conjunto, evaluando su capacidad para gestionar la inclusión de modelos irrelevantes o no informativos.
Si se utilizan cinco o más modelos, el quinto modelo se configura para producir ocasionalmente predicciones extremas o erráticas, simulando un escenario real en el que un modelo podría ser inestable o ruidoso. Esta función evalúa cómo los métodos de conjunto gestionan los modelos poco fiables y si pueden mantener un buen rendimiento de clasificación ponderando o restando peso adecuadamente a los modelos problemáticos. El factor de dificultad de clasificación define la dispersión entre clases, que controla la dificultad del problema para los modelos de componentes. Una diferencia mayor facilita la distinción entre las clases, mientras que una diferencia menor aumenta la dificultad. Esto permite comprobar el rendimiento de los métodos de conjunto en distintos niveles de dificultad, evaluando su capacidad para mantener la precisión en situaciones complejas.
//+------------------------------------------------------------------+ //| ClassificationEnsemble_Demo.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs #include<ensemble.mqh> #include<multilayerperceptron.mqh> //--- input parameters input int NumSamples=10; input int NumClasses=3; input int NumModels=3; input int NumReplications=1000; input double ClassificationDifficultyFactor=0.0; //+------------------------------------------------------------------+ //| normal(rngstate) | //+------------------------------------------------------------------+ double normal(CHighQualityRandStateShell &state) { return CAlglib::HQRndNormal(state); } //+------------------------------------------------------------------+ //| unifrand(rngstate) | //+------------------------------------------------------------------+ double unifrand(CHighQualityRandStateShell &state) { return CAlglib::HQRndUniformR(state); } //+------------------------------------------------------------------+ //|Multilayer perceptron | //+------------------------------------------------------------------+ class CMLPC:public ensemble::IClassify { private: CMlp *m_mlfn; double m_learningrate; double m_tolerance; double m_alfa; double m_beyta; uint m_epochs; ulong m_in,m_out; ulong m_hl1,m_hl2; public: CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2); ~CMLPC(void); void setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs); bool train(matrix &predictors,matrix&targets); vector classify(vector &predictors); ulong getNumInputs(void) { return m_in;} ulong getNumOutputs(void) { return m_out;} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMLPC::CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2) { m_in = ins; m_out = outs; m_alfa = 0.3; m_beyta = 0.01; m_learningrate=0.001; m_tolerance=1.e-8; m_epochs= 1000; m_hl1 = numhl1; m_hl2 = numhl2; m_mlfn = new CMlp(); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMLPC::~CMLPC(void) { if(CheckPointer(m_mlfn) == POINTER_DYNAMIC) delete m_mlfn; } //+------------------------------------------------------------------+ //| set other hyperparameters of the i_model | //+------------------------------------------------------------------+ void CMLPC::setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs) { m_alfa = alpha_; m_beyta = beta_; m_learningrate=learning_rate; m_tolerance=tolerance; m_epochs= num_epochs; } //+------------------------------------------------------------------+ //| fit a i_model to the data | //+------------------------------------------------------------------+ bool CMLPC::train(matrix &predictors,matrix &targets) { if(m_in != predictors.Cols() || m_out != targets.Cols()) { Print(__FUNCTION__, " failed training due to invalid training data"); return false; } return m_mlfn.fit(predictors,targets,m_alfa,m_beyta,m_hl1,m_hl2,m_epochs,m_learningrate,m_tolerance); } //+------------------------------------------------------------------+ //| make a prediction with the trained i_model | //+------------------------------------------------------------------+ vector CMLPC::classify(vector &predictors) { return m_mlfn.predict(predictors); } //+------------------------------------------------------------------+ //| clean up dynamic array pointers | //+------------------------------------------------------------------+ void cleanup(ensemble::IClassify* &array[]) { for(uint i = 0; i<array.Size(); i++) if(CheckPointer(array[i])==POINTER_DYNAMIC) delete array[i]; } //+------------------------------------------------------------------+ //| global variables | //+------------------------------------------------------------------+ int nreplications, nsamps,nmodels, divisor, nreps_done ; int n_classes, nnn, n_pairs, nh_g ; ulong ntrain_pair[]; matrix xdata, xbad_data, xtainted_data, test[],x_targ,xbad_targ,xwild_targ; vector inputdata; double cd_factor, err_score, err_score_1, err_score_2, err_score_3 ; vector classification_err_raw, output_vector; double classification_err_average ; double classification_err_median ; double classification_err_maxmax ; double classification_err_maxmin ; double classification_err_intersection_1 ; double classification_err_intersection_2 ; double classification_err_intersection_3 ; double classification_err_union_1 ; double classification_err_union_2 ; double classification_err_union_3 ; double classification_err_majority ; double classification_err_borda ; double classification_err_logit ; double classification_err_logitsep ; double classification_err_localacc ; double classification_err_fuzzyint ; double classification_err_pairwise ; //+------------------------------------------------------------------+ //| ensemble i_model objects | //+------------------------------------------------------------------+ ensemble::CAvgClass average_ensemble ; ensemble::CMedian median_ensemble ; ensemble::CMaxMax maxmax_ensemble ; ensemble::CMaxMin maxmin_ensemble ; ensemble::CIntersection intersection_ensemble ; ensemble::CUnion union_rule ; ensemble::CMajority majority_ensemble ; ensemble::CBorda borda_ensemble ; ensemble::ClogitReg logit_ensemble ; ensemble::ClogitRegSep logitsep_ensemble ; ensemble::ClocalAcc localacc_ensemble ; ensemble::CFuzzyInt fuzzyint_ensemble ; ensemble::CPairWise pairwise_ensemble ; int n_hid = 4 ; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { CHighQualityRandStateShell rngstate; CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj()); //--- nsamps = NumSamples ; n_classes = NumClasses ; nmodels = NumModels ; nreplications = NumReplications ; cd_factor = ClassificationDifficultyFactor ; if((nsamps <= 3) || (n_classes <= 1) || (nmodels <= 0) || (nreplications <= 0) || (cd_factor < 0.0)) { Alert(" Invalid inputs "); return; } divisor = 1 ; ensemble::IClassify* models[]; ensemble::IClassify* model_pairs[]; /* Allocate memory and initialize */ n_pairs = n_classes * (n_classes-1) / 2 ; if(ArrayResize(models,nmodels)<0 || ArrayResize(model_pairs,n_pairs)<0 || ArrayResize(test,10)<0 || ArrayResize(ntrain_pair,n_pairs)<0) { Print(" Array resize errors ", GetLastError()); cleanup(models); cleanup(model_pairs); return; } ArrayInitialize(ntrain_pair,0); for(int i=0 ; i<nmodels ; i++) models[i] = new CMLPC(2,ulong(n_classes),4,0) ; xdata = matrix::Zeros(nsamps,(2+n_classes)); xbad_data = matrix::Zeros(nsamps,(2+n_classes)); xtainted_data = matrix::Zeros(nsamps,(2+n_classes)); inputdata = vector::Zeros(3); for(uint i = 0; i<test.Size(); i++) test[i] = matrix::Zeros(nsamps,(2+n_classes)); classification_err_raw = vector::Zeros(nmodels); classification_err_average = 0.0 ; classification_err_median = 0.0 ; classification_err_maxmax = 0.0 ; classification_err_maxmin = 0.0 ; classification_err_intersection_1 = 0.0 ; classification_err_intersection_2 = 0.0 ; classification_err_intersection_3 = 0.0 ; classification_err_union_1 = 0.0 ; classification_err_union_2 = 0.0 ; classification_err_union_3 = 0.0 ; classification_err_majority = 0.0 ; classification_err_borda = 0.0 ; classification_err_logit = 0.0 ; classification_err_logitsep = 0.0 ; classification_err_localacc = 0.0 ; classification_err_fuzzyint = 0.0 ; classification_err_pairwise = 0.0 ; for(int i_rep=0 ; i_rep<nreplications ; i_rep++) { nreps_done = i_rep + 1 ; if(i_rep>0) xdata.Fill(0.0); //--- for(int i=0, z=0; i<nsamps ; i++) { xdata[i][0] = normal(rngstate) ; xdata[i][1] = normal(rngstate) ; if(i < n_classes) z = i ; else z = (int)(unifrand(rngstate) * n_classes) ; if(z >= n_classes) z = n_classes - 1 ; xdata[i][2+z] = 1.0 ; xdata[i][0] += double(z) * cd_factor ; xdata[i][1] -= double(z) * cd_factor ; } if(nmodels >= 4) { xbad_data = xdata; matrix arm = np::sliceMatrixCols(xbad_data,2); for(int i = 0; i<nsamps; i++) for(int z = 0; z<n_classes; z++) arm[i][z] = (unifrand(rngstate)<(1.0/double(n_classes)))?1.0:0.0; np::matrixCopy(xbad_data,arm,0,xbad_data.Rows(),1,2); } if(nmodels >= 5) { xtainted_data = xdata; matrix arm = np::sliceMatrixCols(xtainted_data,2); for(int i = 0; i<nsamps; i++) for(int z = 0; z<n_classes; z++) if(unifrand(rngstate)<0.1) arm[i][z] = xdata[i][2+z] * 1000.0 - 500.0 ; np::matrixCopy(xtainted_data,arm,0,xtainted_data.Rows(),1,2); } for(int i=0 ; i<10 ; i++) // Build a test dataset { if(i_rep>0) test[i].Fill(0.0); for(int j=0,z=0; j<nsamps; j++) { test[i][j][0] = normal(rngstate) ; test[i][j][1] = normal(rngstate) ; z = (int)(unifrand(rngstate) * n_classes) ; if(z >= n_classes) z = n_classes - 1 ; test[i][j][2+z] = 1.0 ; test[i][j][0] += double(z) * cd_factor ; test[i][j][1] -= double(z) * cd_factor ; } } for(int i_model=0 ; i_model<nmodels ; i_model++) { matrix preds,targs; if(i_model == 3) { targs = np::sliceMatrixCols(xbad_data,2); preds = np::sliceMatrixCols(xbad_data,0,2); } else if(i_model == 4) { targs = np::sliceMatrixCols(xtainted_data,2); preds = np::sliceMatrixCols(xtainted_data,0,2); } else { targs = np::sliceMatrixCols(xdata,2); preds = np::sliceMatrixCols(xdata,0,2); } if(!models[i_model].train(preds,targs)) { Print(" failed to train i_model at shift ", i_model); cleanup(model_pairs); cleanup(models); return; } err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { vector testvec,testin,testtarg; for(int j=0; j<nsamps; j++) { testvec = test[i].Row(j); testtarg = np::sliceVector(testvec,2); testin = np::sliceVector(testvec,0,2); output_vector = models[i_model].classify(testin) ; if(output_vector.ArgMax() != testtarg.ArgMax()) err_score += 1.0 ; } } classification_err_raw[i_model] += err_score / (10 * nsamps) ; } int i_model = 0; for(int i=0 ; i<n_classes-1 ; i++) { for(int j=i+1 ; j<n_classes ; j++) { ntrain_pair[i_model] = 0 ; for(int z=0 ; z<nsamps ; z++) { if((xdata[z][2+i]> 0.5) || (xdata[z][2+j] > 0.5)) ++ntrain_pair[i_model] ; } nh_g = (n_hid < int(ntrain_pair[i_model]) - 1) ? n_hid : int(ntrain_pair[i_model]) - 1; model_pairs[i_model] = new CMLPC(2, 1, ulong(nh_g+1),0) ; matrix training; matrix preds,targs; ulong msize=0; for(int z=0 ; z<nsamps ; z++) { inputdata[0] = xdata[z][0] ; inputdata[1] = xdata[z][1] ; if(xdata[z][2+i]> 0.5) inputdata[2] = 1.0 ; else if(xdata[z][2+j] > 0.5) inputdata[2] = 0.0 ; else continue ; training.Resize(msize+1,inputdata.Size()); training.Row(inputdata,msize++); } preds = np::sliceMatrixCols(training,0,2); targs = np::sliceMatrixCols(training,2); model_pairs[i_model].train(preds,targs); ++i_model ; } } err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(average_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_average += err_score / (10 * nsamps) ; /* median_ensemble */ err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(median_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_median += err_score / (10 * nsamps) ; /* maxmax_ensemble */ err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(maxmax_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_maxmax += err_score / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(maxmin_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) // If predicted class not true class err_score += 1.0 ; // Count this misclassification } } classification_err_maxmin += err_score / (10 * nsamps) ; matrix preds,targs; err_score_1 = err_score_2 = err_score_3 = 0.0 ; preds = np::sliceMatrixCols(xdata,0,2); targs = np::sliceMatrixCols(xdata,2); intersection_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); ulong class_ = intersection_ensemble.classify(rowtest,models) ; output_vector = intersection_ensemble.proba(); if(output_vector[rowtarg.ArgMax()] < 0.5) { err_score_1 += 1.0 ; err_score_2 += 1.0 ; err_score_3 += 1.0 ; } else { if(class_ > 3) err_score_3 += 1.0 ; if(class_ > 2) err_score_2 += 1.0 ; if(class_ > 1) err_score_1 += 1.0 ; } } } classification_err_intersection_1 += err_score_1 / (10 * nsamps) ; classification_err_intersection_2 += err_score_2 / (10 * nsamps) ; classification_err_intersection_3 += err_score_3 / (10 * nsamps) ; union_rule.fit(preds,targs,models); err_score_1 = err_score_2 = err_score_3 = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); ulong clss = union_rule.classify(rowtest,models) ; output_vector = union_rule.proba(); if(output_vector[rowtarg.ArgMax()] < 0.5) { err_score_1 += 1.0 ; err_score_2 += 1.0 ; err_score_3 += 1.0 ; } else { if(clss > 3) err_score_3 += 1.0 ; if(clss > 2) err_score_2 += 1.0 ; if(clss > 1) err_score_1 += 1.0 ; } } } classification_err_union_1 += err_score_1 / (10 * nsamps) ; classification_err_union_2 += err_score_2 / (10 * nsamps) ; classification_err_union_3 += err_score_3 / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(majority_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_majority += err_score / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(borda_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_borda += err_score / (10 * nsamps) ; err_score = 0.0 ; logit_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(logit_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_logit += err_score / (10 * nsamps) ; err_score = 0.0 ; logitsep_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(logitsep_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_logitsep += err_score / (10 * nsamps) ; err_score = 0.0 ; localacc_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(localacc_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_localacc += err_score / (10 * nsamps) ; err_score = 0.0 ; fuzzyint_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(fuzzyint_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_fuzzyint += err_score / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(pairwise_ensemble.classify(ulong(n_classes),rowtest,model_pairs,ntrain_pair) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_pairwise += err_score / (10 * nsamps) ; cleanup(model_pairs); } err_score = 0.0 ; PrintFormat("Test Config: Classification Difficulty - %8.8lf\nNumber of classes - %5d\nNumber of component models - %5d\n Sample Size - %5d", ClassificationDifficultyFactor,NumClasses,NumModels,NumSamples); PrintFormat("%5d Replications:", nreps_done) ; for(int i_model=0 ; i_model<nmodels ; i_model++) { PrintFormat(" %.8lf", classification_err_raw[i_model] / nreps_done) ; err_score += classification_err_raw[i_model] / nreps_done ; } PrintFormat(" Mean raw error = %8.8lf", err_score / nmodels) ; PrintFormat(" average_ensemble error = %8.8lf", classification_err_average / nreps_done) ; PrintFormat(" median_ensemble error = %8.8lf", classification_err_median / nreps_done) ; PrintFormat(" maxmax_ensemble error = %8.8lf", classification_err_maxmax / nreps_done) ; PrintFormat(" maxmin_ensemble error = %8.8lf", classification_err_maxmin / nreps_done) ; PrintFormat(" majority_ensemble error = %8.8lf", classification_err_majority / nreps_done) ; PrintFormat(" borda_ensemble error = %8.8lf", classification_err_borda / nreps_done) ; PrintFormat(" logit_ensemble error = %8.8lf", classification_err_logit / nreps_done) ; PrintFormat(" logitsep_ensemble error = %8.8lf", classification_err_logitsep / nreps_done) ; PrintFormat(" localacc_ensemble error = %8.8lf", classification_err_localacc / nreps_done) ; PrintFormat(" fuzzyint_ensemble error = %8.8lf", classification_err_fuzzyint / nreps_done) ; PrintFormat(" pairwise_ensemble error = %8.8lf", classification_err_pairwise / nreps_done) ; PrintFormat(" intersection_ensemble error 1 = %8.8lf", classification_err_intersection_1 / nreps_done) ; PrintFormat(" intersection_ensemble error 2 = %8.8lf", classification_err_intersection_2 / nreps_done) ; PrintFormat(" intersection_ensemble error 3 = %8.8lf", classification_err_intersection_3 / nreps_done) ; PrintFormat(" Union error 1 = %8.8lf", classification_err_union_1 / nreps_done) ; PrintFormat(" Union error 2 = %8.8lf", classification_err_union_2 / nreps_done) ; PrintFormat(" Union error 3 = %8.8lf", classification_err_union_3 / nreps_done) ; cleanup(models); } //+------------------------------------------------------------------+
A continuación se muestran ejemplos de los resultados obtenidos al ejecutar el script. Estos son los resultados en los que la tarea de clasificación se estableció en el nivel de dificultad más alto.
ClassificationDifficultyFactor=0.0 DM 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 0.00000000 RP 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes - 3 QI 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models - 3 EK 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Sample Size - 10 MN 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 1000 Replications: CF 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 0.66554000 HI 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 0.66706000 DP 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 0.66849000 II 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Mean raw error = 0.66703000 JS 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) average_ensemble error = 0.66612000 HR 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) median_ensemble error = 0.66837000 QF 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) maxmax_ensemble error = 0.66704000 MD 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) maxmin_ensemble error = 0.66586000 GI 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) majority_ensemble error = 0.66772000 HR 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) borda_ensemble error = 0.66747000 MO 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) logit_ensemble error = 0.66556000 MP 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) logitsep_ensemble error = 0.66570000 JD 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) localacc_ensemble error = 0.66578000 OJ 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) fuzzyint_ensemble error = 0.66503000 KO 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) pairwise_ensemble error = 0.66799000 GS 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 1 = 0.96686000 DP 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 2 = 0.95847000 QE 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 3 = 0.95447000 OI 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 1 = 0.99852000 DM 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 2 = 0.97931000 JR 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 3 = 0.01186000
A continuación se muestran los resultados de la prueba en la que la dificultad de clasificación fue moderada.
LF 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 1.00000000 IG 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes - 3 JP 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models - 3 FQ 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Sample Size - 10 KH 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 1000 Replications: NO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 0.46236000 QF 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 0.45818000 II 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 0.45779000 FR 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Mean raw error = 0.45944333 DI 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) average_ensemble error = 0.44881000 PH 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) median_ensemble error = 0.45564000 JO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) maxmax_ensemble error = 0.46763000 GS 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) maxmin_ensemble error = 0.44935000 GP 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) majority_ensemble error = 0.45573000 PI 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) borda_ensemble error = 0.45593000 DF 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) logit_ensemble error = 0.46353000 FO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) logitsep_ensemble error = 0.46726000 ER 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) localacc_ensemble error = 0.46096000 KP 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) fuzzyint_ensemble error = 0.45098000 OD 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) pairwise_ensemble error = 0.66485000 IJ 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 1 = 0.93533000 RO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 2 = 0.92527000 OL 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 3 = 0.92527000 OR 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 1 = 0.99674000 KG 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 2 = 0.97231000 NK 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 3 = 0.00877000
El último conjunto de resultados ilustra los resultados de una prueba realizada en la que la dificultad de clasificación se configuró para que fuera relativamente fácil.
PL 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 10.00000000 CN 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes - 3 PK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models - 3 LH 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Sample Size - 10 EQ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 1000 Replications: MD 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 0.02905000 LO 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 0.02861000 CF 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 0.02879000 IK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Mean raw error = 0.02881667 RN 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) average_ensemble error = 0.02263000 PQ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) median_ensemble error = 0.02956000 QD 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) maxmax_ensemble error = 0.03426000 KJ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) maxmin_ensemble error = 0.02263000 IO 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) majority_ensemble error = 0.02956000 HP 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) borda_ensemble error = 0.02956000 KM 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) logit_ensemble error = 0.03171000 OE 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) logitsep_ensemble error = 0.04840000 GK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) localacc_ensemble error = 0.03398000 FO 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) fuzzyint_ensemble error = 0.02263000 QM 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) pairwise_ensemble error = 0.65277000 CQ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 1 = 0.96303000 DF 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 2 = 0.96167000 IK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 3 = 0.96167000 IK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 1 = 0.98620000 CP 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 2 = 0.95624000 LD 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 3 = 0.00000000
Todo el código que aparece en el texto adjunto al artículo. En la tabla siguiente se ofrece una descripción de cada archivo fuente.
| Nombre del archivo | Descripción del archivo |
|---|---|
| MQL5/include/np.mqh | Esta es una colección de funciones utilitarias para manipular vectores y matrices. |
| MQL5/include/nom2ord.mqh | Este archivo contiene clases para codificar datos categóricos. |
| MQL5/include/multilayerperceptron.mqh | Proporciona la definición de la clase CMlp que representa una red neuronal de avance. |
| MQL5/include/logistic.mqh | Contiene la definición de la clase Clogit que implementa la regresión logística. |
| MQL5/include/ensemble.mqh | Contiene definiciones para diversas implementaciones de metamodelos. |
| MQL5/scripts/ClassificationEnsemble_Demo.mq5 | Script que compara el rendimiento de los clasificadores de conjunto definidos en ensemble.mqh. |
| MQL5/scripts/PairWise_Ensemble_Demo.mq5 | Script de demostración que muestra cómo aplicar la clase CPairWise para el acoplamiento por pares. |
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/16838
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Dominando los registros (Parte 2): Formateo de registros
Dominando los registros (Parte 2): Formateo de registros
 Desarrollo de asesores expertos autooptimizables en MQL5 (Parte 3): Estrategias dinámicas de seguimiento de tendencias y reversión a la media
Desarrollo de asesores expertos autooptimizables en MQL5 (Parte 3): Estrategias dinámicas de seguimiento de tendencias y reversión a la media
 Cambiando a MQL5 Algo Forge (Parte 4): Trabajamos con versiones y lanzamientos
Cambiando a MQL5 Algo Forge (Parte 4): Trabajamos con versiones y lanzamientos
 Operar con noticias de manera sencilla (Parte 6): Ejecución de operaciones (III)
Operar con noticias de manera sencilla (Parte 6): Ejecución de operaciones (III)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso