De principiante a experto: sistema de análisis autogeométrico

Contenido:

1. Introducción
2. Antecedentes
3. Resumen general
4. Implementación
5. Pruebas y resultados
6. Conclusión

Introducción

El debate de hoy tiene como objetivo abordar el reto que supone analizar los patrones de velas japonesas utilizando enfoques geométricos. En nuestro reciente artículo, De principiante a experto: programando velas japonesas, nos centramos en identificar patrones simples de velas japonesas, que suelen estar compuestos por unas pocas velas. Sin embargo, cuando se trabaja con secuencias más largas de velas japonesas, el reconocimiento de patrones se vuelve más complejo, ya que la consistencia tiende a disminuir en series largas.

Sin embargo, una conclusión clara es que aún podemos identificar los principales máximos y mínimos dentro de los datos. Conectar estos puntos puede ayudarnos a evaluar las tendencias de manera más eficaz.

Cuando empezamos a aprender sobre el comercio de divisas, muchos recursos educativos nos presentaron la idea de las formaciones triangulares y otros patrones geométricos en la evolución de los precios del mercado. Y, efectivamente, la geometría está presente en los mercados: puede ofrecer un resumen simplificado y visual de lo que está haciendo el mercado.

La mayoría de los operadores están acostumbrados a identificar estas formas manualmente dibujando líneas de tendencia o colocando objetos geométricos en los gráficos. Hoy, nuestro objetivo es dar un paso más allá aprovechando MQL5 para automatizar este proceso, eliminando la necesidad de intervención manual y permitiendo un análisis más rápido y consistente.

Antecedentes

La ventaja de la programación orientada a objetos (OOP) reside en su potente capacidad para modelar y resolver problemas computacionales del mundo real de manera eficiente. MQL5, un lenguaje derivado de C++, hereda esta fortaleza y se erige como un valioso activo dedicado al desarrollo de algoritmos de trading. Teniendo en cuenta el problema que nos ocupa, ya contamos con una ventaja significativa gracias a los beneficios estructurales y modulares que ofrece la POO.

En esta sección definiremos brevemente los términos clave relacionados con nuestro tema antes de explorar los métodos tradicionales utilizados para identificar formas geométricas en el trading. Aunque existen muchas formas en el análisis técnico, nos centraremos en dos ejemplos comunes: los rectángulos y los triángulos.

¿Qué es la geometría?

La geometría es una rama de las matemáticas que se ocupa de las propiedades y relaciones del espacio. Esto incluye el estudio de distancias, formas, tamaños, ángulos y las posiciones relativas de las figuras. La geometría proporciona un marco sólido para interpretar el mundo físico, ya que nos permite modelar y analizar las relaciones espaciales.

¿Por qué es importante la geometría en el contexto del trading?

La geometría proporciona un marco visual y estructural para comprender e interpretar el comportamiento del mercado. Los operadores suelen basarse en patrones y formas que surgen de la evolución de los precios, y estos patrones son intrínsecamente geométricos. Ayuda en el reconocimiento de patrones, y aquí hay una lista de patrones comunes conocidos por la mayoría de los operadores:

• Triángulo (ascendente, descendente, simétrico)
• Rectángulos (zonas de consolidación)
• Canales (líneas de tendencia paralelas)
• Cabeza y hombros, techos y suelos dobles: todos dependen de la simetría geométrica

Estos patrones ayudan a los comerciantes a:

• Identificar posibles rupturas o reversiones
• Medir la fuerza de la tendencia
• Establecer puntos de entrada y salida

En esta tabla, he reunido consideraciones clave para aplicar el análisis geométrico a los datos de precios del mercado.

Aspecto	El papel de la geometría
Claridad visual	Ayuda a simplificar datos complejos del mercado en formatos reconocibles
Apoyo a la toma de decisiones	Las formas guían las entradas, salidas y configuraciones comerciales
Objetividad	Reduce las conjeturas mediante el uso de una lógica espacial precisa
Automatización	Permite la detección algorítmica de patrones y niveles clave
Psicología del mercado	Las formas a menudo reflejan el comportamiento colectivo del comerciante (por ejemplo, los triángulos muestran compresión)

Echemos un vistazo a cómo se aplican tradicionalmente las geometrías de triángulo y rectángulo en el trading. Ofreceré una descripción general de lo que los diferentes patrones de triángulo suelen sugerir sobre la acción del precio, pero no profundizaré en estrategias comerciales específicas. Esto se debe a que he observado que muchas de las reglas comúnmente aceptadas a menudo se vuelven invalidadas en condiciones reales del mercado. Si bien estos patrones funcionan hasta cierto punto, es recomendable prestar mucha atención al comportamiento de los precios antes de la formación de las estructuras geométricas.

Por ejemplo, aunque generalmente se espera que un triángulo ascendente resulte en una ruptura alcista, he visto numerosos casos en los que ocurre lo contrario. Estas formas a menudo representan puntos de decisión en el mercado, no garantías. Por lo tanto, si bien el patrón puede sugerir un cierto movimiento direccional, es fundamental alinear su interpretación con el contexto de precios real que precede al patrón. Confiar únicamente en las expectativas de los libros de texto sin el contexto del mercado puede llevar a conclusiones engañosas.

Triángulo

Un triángulo es una forma geométrica fundamental definida por tres lados y tres esquinas (vértices). En el mercado de divisas, los patrones triangulares indican posibles continuaciones o reversiones de tendencias. Los principales tipos de patrones triangulares son:

1. Triángulo simétrico:

Indica un período de consolidación con volatilidad decreciente; a menudo precede a una ruptura en cualquier dirección.

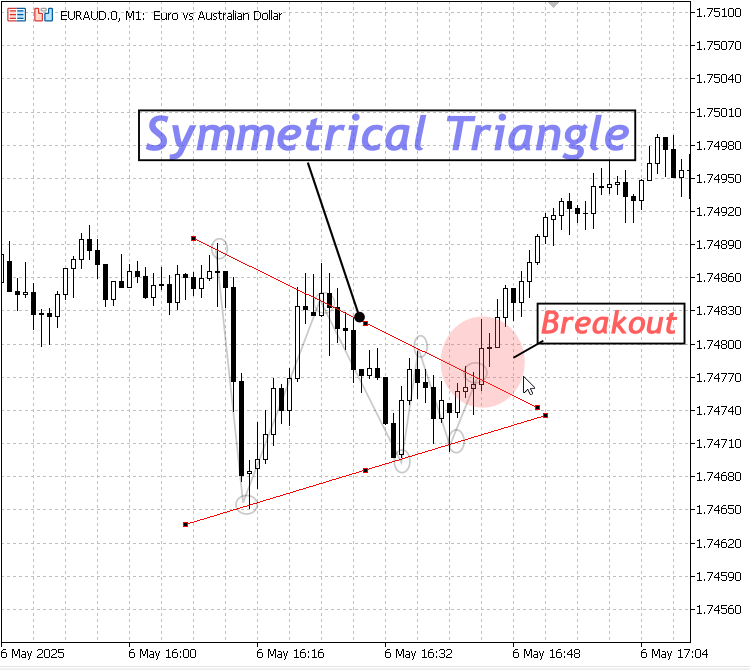
Triángulo simétrico

2. Triángulo ascendente:

Caracterizado por un nivel de resistencia plano o ligeramente inclinado y un soporte ascendente; típicamente un patrón alcista que indica una posible ruptura hacia arriba.

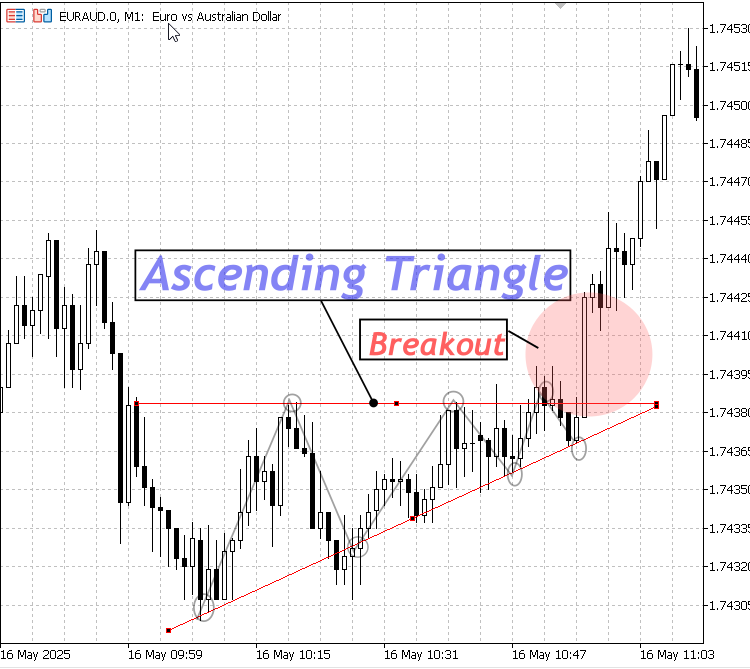
Triángulo ascendente

3. Triángulo descendente:

Presenta una línea de soporte plana o ligeramente inclinada y una resistencia decreciente; generalmente bajista, lo que indica una ruptura hacia abajo.

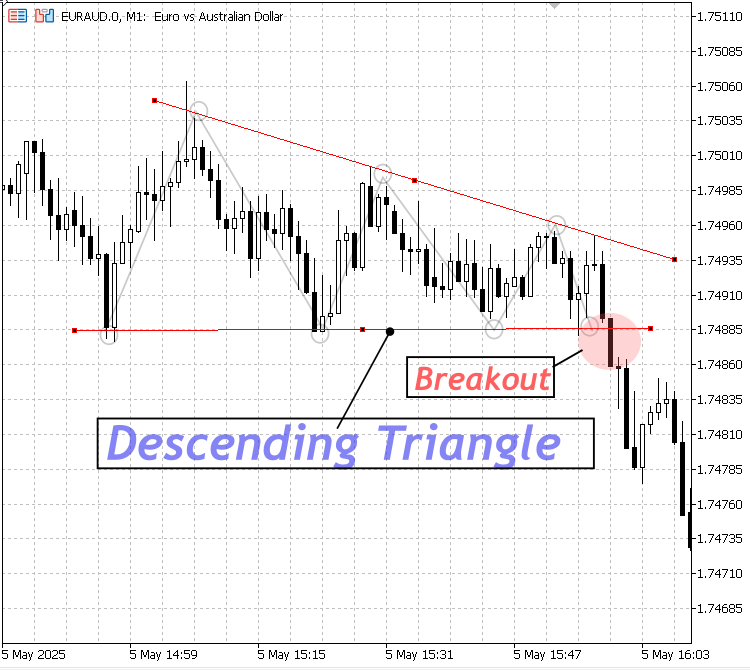
Triángulo descendente

Rectángulo

Un rectángulo es una forma geométrica de cuatro lados con lados opuestos iguales y paralelos. Tiene ángulos rectos (cada uno de 90 grados) en cada esquina. En forex y análisis técnico, un rectángulo (también llamado rango de negociación o zona de consolidación) es un patrón gráfico donde el precio se mueve lateralmente dentro de niveles horizontales de soporte y resistencia. Indica un período de indecisión antes de que el mercado potencialmente continúe en la tendencia anterior o se revierta. Está disponible entre las herramientas de análisis de mercado en la terminal Meta Trader 5.

Estas son las características principales:

• El precio oscila entre una línea de resistencia superior clara y una línea de soporte inferior.
• El patrón parece un rectángulo o un cuadro en el gráfico.
• Las rupturas por encima de la resistencia o por debajo del soporte a menudo señalan el comienzo de una nueva tendencia.

Este concepto también se puede ilustrar utilizando la herramienta de línea paralela incorporada, alineada horizontalmente para representar los niveles de soporte y resistencia. Dado que consta de dos líneas paralelas, resalta efectivamente el rango de precios durante la consolidación. Sin embargo, el rectángulo sigue siendo la opción preferida para marcar zonas de consolidación porque "enmarca" visualmente el período específico en el que el precio se movió lateralmente. Es importante recordar que la consolidación es una fase temporal: eventualmente, el mercado saldrá de ese rango y continuará su tendencia o revertirá su dirección.

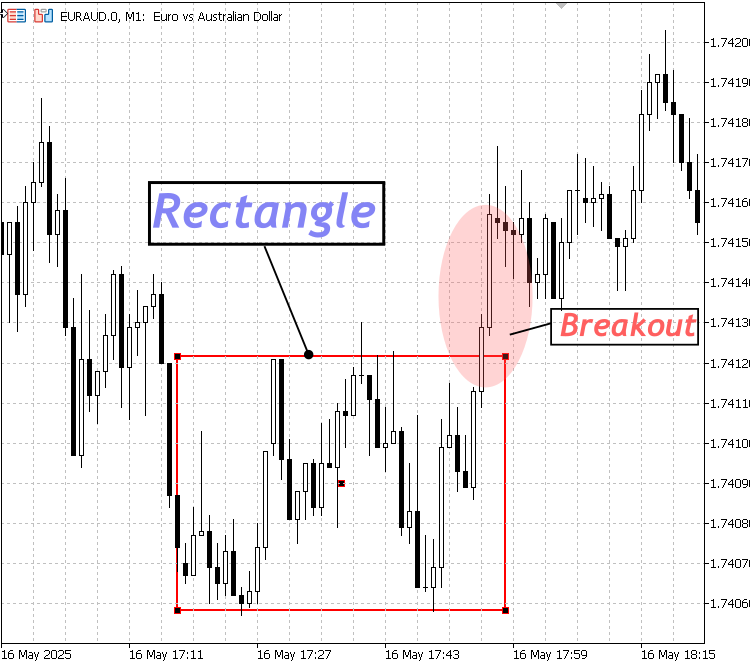
Estructura rectangular

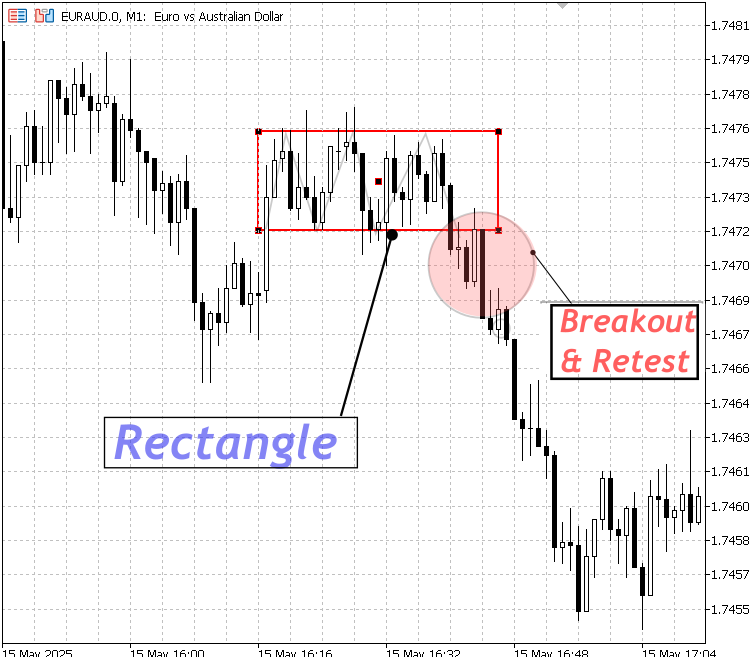
Rotura por debajo de una estructura rectangular

Resumen general

Ahora que hemos sentado las bases teóricas de nuestra discusión, aquí hay una descripción general de la implementación práctica. Utilizaremos técnicas de programación modular para construir componentes para un sistema de detección de estructuras geométricas. En concreto, desarrollaremos clases separadas para detectar formaciones de triángulos y rectángulos en la estructura del mercado. Estos son solo los ejemplos iniciales: el enfoque es extensible y nos permite agregar soporte para otras formas según sea necesario. Esta es una de las ventajas clave de utilizar las características de programación modular y orientada a objetos de MQL5, que nos permiten abordar problemas complejos del mundo real con un código limpio y fácil de mantener.

Los archivos de encabezado que creamos en esta sección se pueden integrar fácilmente en el Asesor Experto o indicador principal. Además, se pueden reutilizar en múltiples proyectos, lo que promueve la coherencia y la eficiencia del desarrollo.

En mi enfoque, cada forma geométrica requiere un conjunto de puntos de referencia en los datos de precios. Normalmente necesitamos dos puntos altos y dos puntos bajos. Estos puntos están conectados con líneas para formar formas. Por ejemplo, dos puntos forman una línea, y un triángulo puede formarse mediante dos líneas que convergen en un punto en el futuro. Por otro lado, un rectángulo se puede identificar cuando hay dos toques en los niveles de resistencia y soporte. Una vez cumplidas estas condiciones, se puede dibujar la forma geométrica conectando los puntos de referencia apropiados.

Para facilitar su comprensión, he incluido algunas ilustraciones a continuación que demuestran cómo se pueden construir estas formas en el gráfico utilizando lógica informática. Normalmente necesitamos al menos cuatro puntos clave para delinear cada forma. En las imágenes, comenzamos identificando los puntos a, b, c, y d, que sirven como anclajes fundamentales para nuestra estructura de formas. Desde estos puntos se puede proyectar la forma con antelación. Las líneas rojas punteadas representan expectativas teóricas, que indican cómo podría responder el mercado a los límites previstos de la forma. La forma en que el precio interactúa con estas líneas puede revelar pistas importantes sobre la acción futura del precio, como posibles rupturas o rebotes.

Detección teórica de un triángulo

En la ilustración del triángulo anterior, los puntos de oscilación a a d se identifican como puntos de referencia a partir de los cuales se puede construir un triángulo, con las líneas convergentes que se unen en el punto X. Los puntos e y f representan toques futuros teóricos; son especulativos y pueden no desarrollarse exactamente como se muestra. Su propósito es ayudarnos a conceptualizar el patrón para que podamos traducir la idea en código. El mismo concepto se aplica a la ilustración del rectángulo a continuación, donde la estructura se detecta utilizando una lógica similar; sin embargo, la diferencia clave es que sus lados son paralelos.

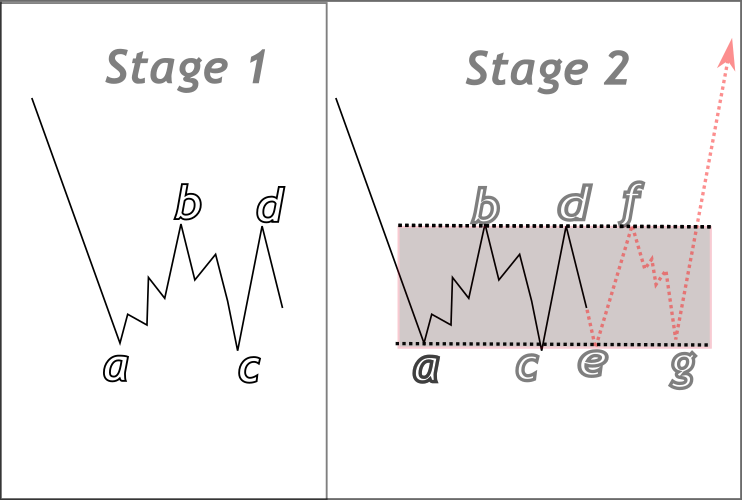
Detección de estructura rectangular

Implementación

En esta etapa comienza el desarrollo propiamente dicho. Comenzaremos creando un archivo de encabezado llamado GeometricPatternDetector.mqh, que contendrá todas las clases necesarias para detectar patrones geométricos. Una vez que el encabezado esté listo, procederemos a desarrollar un asesor experto que demuestre cómo utilizar las clases de manera eficaz. Ahora, sigamos los siguientes pasos para comprender cómo encaja todo.

Incluyendo los encabezados necesarios

En la parte superior de GeometricPatternDetector.mqh incorporamos tres bibliotecas MQL5 esenciales para dotar a nuestro detector de todas las herramientas que necesita. En primer lugar, incluimos Arrays\ArrayObj.mqh para poder utilizar CArrayObj, una clase de matriz dinámica y orientada a objetos, para almacenar nuestros pivotes de swing y los resultados de los patrones sin tener que lidiar con punteros sin procesar ni con la gestión manual de la memoria.

A continuación, Indicators\Indicators.mqh incorpora las funciones de indicadores integradas en MetaTrader, como iATR, CopyHigh, CopyLow y CopyTime, lo que nos permite obtener datos históricos de precios y calcular el rango verdadero promedio (Average True Range, ATR) sin problemas. Por último, Math\Stat\Math.mqh proporciona constantes matemáticas como M_PI y funciones de utilidad como MathArctan, que utilizamos para calcular pendientes, ángulos y tolerancias de planitud en nuestros algoritmos de detección de patrones. En conjunto, estos elementos crean la base para un código robusto, legible y fácil de mantener.

#include <Arrays\ArrayObj.mqh>       // For CArrayObj: dynamic arrays of objects 
#include <Indicators\Indicators.mqh> // For iATR, CopyHigh, CopyLow, CopyTime
#include <Math\Stat\Math.mqh>        // For M_PI, MathArctan, and other math utilities

Clases de contenedor

El encabezado GeometricPatternDetector.mqh comienza definiendo dos clases contenedoras simples: SwingPoint y PatternResult. Ambos heredan de la base CObject de MQL5. La clase SwingPoint contiene la marca de tiempo, el precio y un indicador booleano que indica si el pivote es alto o bajo. Este diseño nos permite recopilar y gestionar los pivotes de mercado individuales en una única matriz de objetos.

La clase PatternResult encapsula toda la información necesaria para describir un patrón detectado, es decir, el símbolo, el marco temporal, el tipo de patrón, los tres «vértices» que lo definen y el punto en el que debe colocarse una etiqueta. Al empaquetar estos elementos de datos en objetos, el código del detector permanece limpio y coherente, basándose en CArrayObj para el almacenamiento en lugar de matrices paralelas manuales de primitivas.

// SwingPoint: holds one market pivot
class SwingPoint : public CObject {
public:
   datetime time;
   double   price;
   bool     isHigh;
   SwingPoint(datetime t=0,double p=0.0,bool h=false)
     : time(t), price(p), isHigh(h) {}
};

// PatternResult: holds the details of one detected pattern
class PatternResult : public CObject {
public:
   string            symbol;
   ENUM_TIMEFRAMES   timeframe;
   ENUM_PATTERN_TYPE type;
   datetime          detectionTime;
   datetime          labelTime;
   double            labelPrice;
   datetime          vertex1Time;
   double            vertex1Price;
   datetime          vertex2Time;
   double            vertex2Price;
   datetime          vertex3Time;
   double            vertex3Price;
   PatternResult(const string _s,const ENUM_TIMEFRAMES _tf,const ENUM_PATTERN_TYPE _t,
                 datetime lt,double lp,
                 datetime v1t,double v1p,
                 datetime v2t,double v2p,
                 datetime v3t,double v3p)
     : symbol(_s), timeframe(_tf), type(_t), detectionTime(TimeCurrent()),
       labelTime(lt), labelPrice(lp),
       vertex1Time(v1t), vertex1Price(v1p),
       vertex2Time(v2t), vertex2Price(v2p),
       vertex3Time(v3t), vertex3Price(v3p) {}
};

Estructura de clases del detector

En el núcleo del encabezado se encuentra la clase CGeometricPatternDetector . Su sección privada declara variables miembro para almacenar los objetos pivote, los parámetros de configuración (como el swing lookback, el multiplicador ATR y los puntos de contacto mínimos) y el estado necesario para evitar dibujos duplicados (nombres y hash del último triángulo y rectángulo, junto con sus tiempos de detección).

Se declaran de forma privada cuatro métodos auxiliares: IsNewBar, UpdateSwingPoints, CalculateATR y GetSwingHash. Estas utilidades se encargan de identificar nuevas barras, extraer pivotes de oscilación a partir de datos recientes de máximos y mínimos, calcular una medida de sensibilidad del mercado mediante ATR y generar una clave de cadena única para cada conjunto de cuatro pivotes. Juntos, admiten las dos rutinas principales de detección pública, DetectTriangle y DetectRectangle, así como un método Update que lo une todo, además de los métodos GetLastPattern y ClearPatterns para recuperar resultados y limpiar recursos.

class CGeometricPatternDetector {
private:
   CArrayObj   m_swings;
   int         m_swingLookback;
   double      m_atrMultiplier;
   int         m_minTouchPoints;

   string      m_lastTriangle;
   string      m_lastSwingHash;
   datetime    m_lastTriangleTime;

   string      m_lastRectangle;
   string      m_lastRectangleHash;
   datetime    m_lastRectangleTime;

   bool    IsNewBar(const string sym,const ENUM_TIMEFRAMES tf);
   void    UpdateSwingPoints(const string sym,const ENUM_TIMEFRAMES tf);
   double  CalculateATR(const string sym,const ENUM_TIMEFRAMES tf,const int period=14);
   string  GetSwingHash(SwingPoint *p1,SwingPoint *p2,SwingPoint *p3,SwingPoint *p4);

public:
   CGeometricPatternDetector(int swingLookback=3,double atrMultiplier=1.5,int minTouchPoints=2);
   ~CGeometricPatternDetector();

   void Update(const string sym,const ENUM_TIMEFRAMES tf);
   void DetectTriangle(const string sym,const ENUM_TIMEFRAMES tf);
   void DetectRectangle(const string sym,const ENUM_TIMEFRAMES tf);
   ENUM_PATTERN_TYPE GetLastPattern();
   void ClearPatterns();

   CArrayObj m_currentPatterns;
};

Extracción del punto de giro

El método de extracción de puntos de oscilación, UpdateSwingPoints, se invoca en cada nueva barra. Copia una ventana de máximos, mínimos y marcas de tiempo del gráfico, y luego designa la barra central de esa ventana como un máximo oscilante si su precio supera a los dos vecinos, o como un mínimo oscilante si su precio es inferior a los dos vecinos. Cada pivote confirmado se envuelve en un objeto SwingPoint y se añade a la matriz m_swings.

Cuando la matriz supera una capacidad fija, se descartan las entradas más antiguas. Esta lista dinámica de pivotes constituye la base para la detección tanto de triángulos como de rectángulos, lo que garantiza que solo se tengan en cuenta los giros más recientes y significativos del mercado.

void CGeometricPatternDetector::UpdateSwingPoints(const string sym,const ENUM_TIMEFRAMES tf)
{
   int bars = m_swingLookback*2 + 1;
   double highs[], lows[];
   datetime times[];
   ArraySetAsSeries(highs,true);
   ArraySetAsSeries(lows,true);
   ArraySetAsSeries(times,true);

   if(CopyHigh(sym,tf,0,bars,highs)<bars ||
      CopyLow(sym,tf,0,bars,lows)<bars   ||
      CopyTime(sym,tf,0,bars,times)<bars)
   {
      Print("Error: Failed to copy price/time data");
      return;
   }

   int mid = m_swingLookback;
   datetime t = times[mid];
   double h = highs[mid], l = lows[mid];

   bool isH = true;
   for(int i=1; i<=m_swingLookback; i++)
      if(h<=highs[mid-i] || h<=highs[mid+i]) { isH=false; break; }
   if(isH) {
      m_swings.Add(new SwingPoint(t,h,true));
      Print("Swing High detected at ",TimeToString(t)," Price: ",h);
   }

   bool isL = true;
   for(int i=1; i<=m_swingLookback; i++)
      if(l>=lows[mid-i] || l>=lows[mid+i]) { isL=false; break; }
   if(isL) {
      m_swings.Add(new SwingPoint(t,l,false));
      Print("Swing Low detected at ",TimeToString(t)," Price: ",l);
   }

   while(m_swings.Total()>50) {
      delete (SwingPoint*)m_swings.At(0);
      m_swings.Delete(0);
   }
}

CalculateATR envuelve el indicador ATR integrado en MQL5 para proporcionar una unidad de magnitud sensible al mercado, mientras que GetSwingHash concatena cuatro tiempos y precios pivote en una clave de cadena. El valor ATR mide las tolerancias tanto para la «planitud» en triángulos como para la alineación en rectángulos. La cadena hash garantiza que cada conjunto de pivotes único solo se extraiga una vez por período de bloqueo.

double CGeometricPatternDetector::CalculateATR(const string sym,const ENUM_TIMEFRAMES tf,const int period)
{
   int h = iATR(sym,tf,period);
   if(h==INVALID_HANDLE) { Print("ATR handle error"); return 0; }
   double buf[]; ArraySetAsSeries(buf,true);
   if(CopyBuffer(h,0,0,1,buf)!=1) { Print("ATR copy error"); return 0; }
   return buf[0];
}

string CGeometricPatternDetector::GetSwingHash(SwingPoint *p1,SwingPoint *p2,SwingPoint *p3,SwingPoint *p4)
{
   return TimeToString(p1.time)+"*"+DoubleToString(p1.price,8)+"*"
        + TimeToString(p2.time)+"*"+DoubleToString(p2.price,8)+"*"
        + TimeToString(p3.time)+"*"+DoubleToString(p3.price,8)+"*"
        + TimeToString(p4.time)+"_"+DoubleToString(p4.price,8);
}

Lógica de detección de triángulos

La rutina de detección de triángulos busca estrictamente cuatro oscilaciones consecutivas en el orden de bajo a alto y de bajo a alto. Después de aplicar un intervalo mínimo para cada tramo, calcula las pendientes de los lados inferior y superior dividiendo las diferencias de precio por las diferencias de tiempo. Una tolerancia basada en el ATR determina si la parte superior o inferior del triángulo es lo suficientemente plana como para clasificarse como descendente o ascendente; si ninguno de los dos lados es lo suficientemente plano, el patrón se clasifica como simétrico.

A continuación, se cruzan analíticamente las dos líneas laterales para encontrar el vértice del triángulo en el futuro. Se dibuja un único objeto OBJ_TRIANGLE utilizando los dos puntos de pivote y el vértice calculado, y se crea y almacena un objeto PatternResult. Para evitar el parpadeo, el detector compara un hash de los cuatro pivotes con el último patrón dibujado y bloquea los redibujados de la misma forma durante un número fijo de barras.

void CGeometricPatternDetector::DetectTriangle(const string sym,const ENUM_TIMEFRAMES tf)
{
   int tot = m_swings.Total();
   if(tot < 4) return;
   ulong barSec = PeriodSeconds(tf);
   ulong minSpan = (ulong)m_swingLookback * barSec;

   for(int i=0; i<=tot-4; i++)
   {
      SwingPoint *p1 = (SwingPoint*)m_swings.At(i);
      SwingPoint *p2 = (SwingPoint*)m_swings.At(i+1);
      SwingPoint *p3 = (SwingPoint*)m_swings.At(i+2);
      SwingPoint *p4 = (SwingPoint*)m_swings.At(i+3);

      if(!( !p1.isHigh && p2.isHigh && !p3.isHigh && p4.isHigh )) continue;
      if((ulong)(p2.time-p1.time)<minSpan ||
         (ulong)(p3.time-p2.time)<minSpan ||
         (ulong)(p4.time-p3.time)<minSpan) continue;

      double m_low  = (p3.price - p1.price) / double(p3.time - p1.time);
      double m_high = (p4.price - p2.price) / double(p4.time - p2.time);
      double tolFlat = CalculateATR(sym,tf,14) * m_atrMultiplier;

      bool lowerFlat = MathAbs(p3.price-p1.price) < tolFlat;
      bool upperFlat = MathAbs(p4.price-p2.price) < tolFlat;

      ENUM_PATTERN_TYPE type;
      if(lowerFlat && m_high < 0)             type = PATTERN_TRIANGLE_DESCENDING;
      else if(upperFlat && m_low > 0)         type = PATTERN_TRIANGLE_ASCENDING;
      else                                    type = PATTERN_TRIANGLE_SYMMETRICAL;

      double denom = m_low - m_high;
      if(MathAbs(denom)<1e-12) continue;
      double num = (p2.price - p1.price) + (m_low*p1.time - m_high*p2.time);
      double tx  = num/denom;
      double px  = p1.price + m_low*(tx-p1.time);

      datetime latest = MathMax(p1.time,p2.time);
      if(tx<=latest || tx>TimeCurrent()+barSec*50) continue;

      if(StringLen(m_lastTriangle)>0)
         ObjectDelete(0,m_lastTriangle);

      string base = "GPD_"+sym+"_"+EnumToString(tf)+"_"+TimeToString(TimeCurrent(),TIME_SECONDS);
      long cid    = ChartID();
      m_lastTriangle = base+"_T";

      ObjectCreate(cid,m_lastTriangle,OBJ_TRIANGLE,0,
                   p1.time,p1.price,
                   p2.time,p2.price,
                   tx,      px);
      ObjectSetInteger(cid,m_lastTriangle,OBJPROP_COLOR,clrOrange);
      ObjectSetInteger(cid,m_lastTriangle,OBJPROP_WIDTH,2);
      ObjectSetInteger(cid,m_lastTriangle,OBJPROP_FILL,false);

      m_lastSwingHash    = GetSwingHash(p1,p2,p3,p4);
      m_lastTriangleTime = TimeCurrent();
      m_currentPatterns.Add(new PatternResult(
         sym,tf,type,
         latest,(p2.price+p4.price)/2.0,
         p1.time,p1.price,
         p2.time,p2.price,
         (datetime)tx,px
      ));

      ChartRedraw(cid);
      break;
   }
}

Lógica de detección de rectángulos

La detección de rectángulos sigue una secuencia de pivotes similar, pero aplica restricciones más estrictas. En primer lugar, identifica cuatro oscilaciones en el mismo patrón de mínimo-máximo a mínimo-máximo, exigiendo que cada oscilación (de mínimo a máximo y la segunda de mínimo a máximo) abarque al menos cinco barras y supere un umbral de magnitud escalado según el ATR. La parte inferior del rectángulo se alinea con la media de los dos mínimos, siempre que se encuentren dentro de la tolerancia ATR. Si los dos máximos también se alinean dentro de esa tolerancia, el máximo se establece en su promedio; de lo contrario, se utiliza una altura mínima igual a una unidad ATR, de modo que el rectángulo permanece visible.

El rectángulo se dibuja utilizando OBJ_RECTANGLE, abarcando desde el primer momento de pivote hasta exactamente veinte barras más tarde, lo que evita un crecimiento ilimitado. Un hash pivot único garantiza que cada rectángulo distinto se dibuje solo una vez por período de bloqueo, y sus detalles se registran en un PatternResult.

void CGeometricPatternDetector::DetectRectangle(const string sym,const ENUM_TIMEFRAMES tf)
{
   int tot = m_swings.Total();
   if(tot < 4) return;

   ulong barSec    = PeriodSeconds(tf);
   ulong minSpan5  = 5 * barSec;                        
   double tolATR   = CalculateATR(sym,tf,14) * m_atrMultiplier;

   for(int i=0; i<=tot-4; i++)
   {
      SwingPoint *a = (SwingPoint*)m_swings.At(i);
      SwingPoint *b = (SwingPoint*)m_swings.At(i+1);
      SwingPoint *c = (SwingPoint*)m_swings.At(i+2);
      SwingPoint *d = (SwingPoint*)m_swings.At(i+3);

      if(!( !a.isHigh && b.isHigh && !c.isHigh && d.isHigh )) continue;
      if((ulong)(b.time - a.time) < minSpan5 ||
         (ulong)(d.time - c.time) < minSpan5) continue;
      if(MathAbs(b.price - a.price) < tolATR ||
         MathAbs(d.price - c.price) < tolATR) continue;
      if(MathAbs(a.price - c.price) > tolATR) continue;

      bool highAligned = MathAbs(b.price - d.price) < tolATR;
      double lowP  = (a.price + c.price) / 2.0;
      double highP = highAligned ? (b.price + d.price)/2.0 : lowP + tolATR;

      datetime leftT  = MathMin(a.time, c.time);
      datetime rightT = leftT + (datetime)(20 * barSec);

      string rh = TimeToString(leftT,TIME_SECONDS) + "_" +
                  DoubleToString(lowP,8) + "_" +
                  DoubleToString(highP,8);
      datetime lockT = m_lastRectangleTime + (datetime)(40 * barSec);
      if(rh == m_lastRectangleHash && TimeCurrent() < lockT) return;

      if(StringLen(m_lastRectangle) > 0)
         ObjectDelete(0,m_lastRectangle);

      string base = "GPD_"+sym+"_"+EnumToString(tf)+"_"+TimeToString(TimeCurrent(),TIME_SECONDS);
      long cid    = ChartID();
      m_lastRectangle = base+"_Rect";

      ObjectCreate(cid,m_lastRectangle,OBJ_RECTANGLE,0,
                   leftT,   highP,
                   rightT,  lowP);
      ObjectSetInteger(cid,m_lastRectangle,OBJPROP_COLOR, clrBlue);
      ObjectSetInteger(cid,m_lastRectangle,OBJPROP_WIDTH, 2);
      ObjectSetInteger(cid,m_lastRectangle,OBJPROP_FILL,  false);

      m_currentPatterns.Add(new PatternResult(
         sym,tf,PATTERN_RECTANGLE,
         leftT,(highP+lowP)/2.0,
         leftT,highP,
         leftT,lowP,
         rightT,lowP
      ));
      m_lastRectangleHash = rh;
      m_lastRectangleTime = TimeCurrent();

      ChartRedraw(cid);
      break;
   }
}

Uso del encabezado con el asesor experto

Integrar este encabezado en un Asesor Experto es muy sencillo. Simplemente lo incluimos, instanciamos un CGeometricPatternDetector con nuestros parámetros preferidos y llamamos a su método Update(Symbol(), _Period) en el controlador de eventos OnTick . Después de cada actualización, GetLastPattern revela si se ha detectado un nuevo triángulo o rectángulo, y puede inspeccionar detector.m_currentPatterns para recuperar todos los detalles, emitir alertas o colocar etiquetas en el gráfico..

El EA no necesita conocer la geometría subyacente ni la lógica de pivote; simplemente controla el detector y reacciona ante los resultados de alto nivel. Esta separación (declaración en el encabezado, implementación detallada en el mismo archivo y uso sencillo en el EA) demuestra cómo el diseño orientado a objetos en MQL5 encapsula la complejidad y produce código reutilizable y fácil de mantener. Veamos los pasos detallados a continuación.

Inclusiones de encabezado y estado global

En la parte superior de GeometryAnalyzerEA.mq5, incluimos nuestro encabezado de detector para que el asesor experto pueda acceder a la clase CGeometricPatternDetector y sus tipos compatibles. Inmediatamente después, instanciamos un único objeto detector con los parámetros elegidos: tres barras de retrospectiva para los pivotes, un multiplicador ATR de 1,5 para la tolerancia y dos puntos de contacto mínimos para los patrones. También declaramos tres variables globales: lastAlerted recuerda el tipo del último patrón que alertamos para no repetirlo en la misma barra, lastBarTime rastrea cuándo llega una nueva barra y lastLabelName contiene el nombre de la etiqueta de texto que colocamos para que pueda eliminarse cuando aparezca un nuevo patrón.

#include <GeometricPatternDetector.mqh>

//–– detector instance & state
CGeometricPatternDetector  detector(3, 1.5, 2);
ENUM_PATTERN_TYPE          lastAlerted    = PATTERN_NONE;
datetime                   lastBarTime    = 0;
string                     lastLabelName  = "";

Inicialización y limpieza

La función OnInit se ejecuta una vez cuando se inicia el EA. Aquí simplemente imprimimos un mensaje para confirmar la inicialización, aunque también se podría iniciar un temporizador o asignar recursos si fuera necesario. Por el contrario, OnDeinit se ejecuta cuando se elimina el EA o se cierra el gráfico. En esa rutina, borramos todos los patrones dibujados mediante detector.ClearPatterns() y eliminamos cualquier etiqueta de texto restante por su nombre. Por último, registramos el motivo de la desinicialización, lo que facilita el diagnóstico de por qué se detuvo el EA.

int OnInit()
{
   Print("GeometryAnalyzerEA initialized");
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
   detector.ClearPatterns();
   if(StringLen(lastLabelName) > 0)
      ObjectDelete(0, lastLabelName);
   Print("GeometryAnalyzerEA deinitialized, reason=", reason);
}

Detección de una nueva barra

Dentro de OnTick, el primer paso es determinar si el tick entrante pertenece a una barra recién formada. Obtenemos la hora de apertura de la barra actual y la comparamos con nuestra lastBarTime almacenada. Si la barra es nueva, restablecemos lastAlerted para que los patrones se activen de nuevo y eliminamos la etiqueta de texto anterior para mantener el gráfico limpio. Si la barra no es nueva, simplemente volvemos y no hacemos nada más, asegurándonos de que la detección de patrones solo se ejecute una vez por barra.

void OnTick()
{
   datetime curBar = iTime(Symbol(), _Period, 0);
   bool isNewBar  = (curBar != lastBarTime);
   if(isNewBar)
   {
      lastBarTime = curBar;
      lastAlerted = PATTERN_NONE;
      if(StringLen(lastLabelName) > 0)
      {
         ObjectDelete(0, lastLabelName);
         lastLabelName = "";
      }
   }
   if(!isNewBar)
      return;
   // …
}

Ejecutar el detector

Una vez que hemos confirmado una nueva barra, llamamos al método Update del detector, pasando el símbolo y el marco temporal actuales. Esta única llamada actualiza los puntos de oscilación y ejecuta las rutinas de detección de triángulos y rectángulos en segundo plano. Después de que Update regrese, consultamos GetLastPattern() para ver si se encontró un patrón válido en esta barra. Si no aparece ningún patrón nuevo, o si coincide con el que ya hemos alertado, salimos antes de tiempo.

detector.Update(Symbol(), _Period);

ENUM_PATTERN_TYPE pattern = detector.GetLastPattern();
if(pattern == PATTERN_NONE || pattern == lastAlerted)
   return;
lastAlerted = pattern;

Manejo de un patrón detectado

Si aparece un nuevo patrón, recuperamos el PatternResult más reciente de la matriz de patrones del detector. A continuación, traducimos la enumeración del patrón a un nombre legible para los humanos y formateamos sus vértices para su registro. Los rectángulos reciben un tratamiento especial porque solo proporcionan tres puntos de esquina; aproximamos el cuarto para presentar un conjunto completo de coordenadas. Mostramos una ventana emergente de alerta y una declaración de impresión, en las que se indican el nombre del patrón, la hora, el precio y las coordenadas de las esquinas.

int count = detector.m_currentPatterns.Total();
PatternResult *pr = (PatternResult*)detector.m_currentPatterns.At(count - 1);

string name = (pattern == PATTERN_RECTANGLE) ? "Rectangle" :
              (pattern == PATTERN_TRIANGLE_ASCENDING)   ? "Ascending Triangle" :
              (pattern == PATTERN_TRIANGLE_DESCENDING)  ? "Descending Triangle" :
                                                         "Symmetrical Triangle";

Alert("GeometryAnalyzerEA: Detected ", name, " on ", Symbol(), " ", EnumToString(_Period));
Print("GeometryAnalyzerEA: ", name,
      " @", TimeToString(pr.labelTime, TIME_SECONDS),
      " Price=", pr.labelPrice);

Dibujando etiquetas

Por último, colocamos una etiqueta de texto en el gráfico en el momento y el precio designados por el patrón. Se genera un nombre de objeto único combinando el nombre del patrón con la hora de la etiqueta. Mediante funciones de objetos de gráfico, dibujamos OBJ_TEXT y configuramos sus propiedades (contenido del texto, color, tamaño de fuente y fondo) para que destaque claramente en el gráfico. Registramos el nombre de la última etiqueta para que pueda eliminarse en el siguiente compás nuevo antes de dibujar una nueva etiqueta. Una llamada para volver a dibujar el gráfico garantiza una representación inmediata.

   lastLabelName = name + "_" + TimeToString(pr.labelTime, TIME_SECONDS);
   long chartId = ChartID();
   if(ObjectCreate(chartId, lastLabelName, OBJ_TEXT, 0, pr.labelTime, pr.labelPrice))
   {
      ObjectSetString(chartId, lastLabelName, OBJPROP_TEXT,     name);
      ObjectSetInteger(chartId, lastLabelName, OBJPROP_COLOR,    clrOrangeRed);
      ObjectSetInteger(chartId, lastLabelName, OBJPROP_FONTSIZE, 12);
      ObjectSetInteger(chartId, lastLabelName, OBJPROP_BACK,     true);
   }
   ChartRedraw(chartId);
}

Pruebas y resultados

Para evaluar rápidamente el rendimiento del EA, utilizamos el Probador de estrategias para obtener una vista previa de su comportamiento en datos históricos. Los resultados fueron prometedores, ya que los patrones se detectaron correctamente y las formas se dibujaron según lo esperado. Además, tuve la oportunidad de observar el EA funcionando en un gráfico en vivo, donde tuvo un rendimiento notablemente bueno. Las señales de patrón se activaron sin problemas junto con la representación de formas en tiempo real, lo que confirmó la solidez de la integración. Ahora, echa un vistazo a la presentación que aparece a continuación.

Visualización del Probador de estrategias: GeometricAnalyzerEA

A continuación se muestra un registro que muestra la detección de un triángulo ascendente durante las pruebas.

2025.05.20 13:40:54.241 2025.01.14 18:45:00   Alert: GeometryAnalyzerEA: Detected Ascending Triangle on AUDJPY.0 PERIOD_M1
2025.05.20 13:40:54.241 2025.01.14 18:45:00   GeometryAnalyzerEA: Ascending Triangle @14:03:00 Price=97.45599999999999 → Vertices: (1736863200@97.381), (1736863380@97.448), (1736873819@97.912)
2025.05.20 13:40:54.242 2025.01.14 18:46:00   Swing High detected at 2025.01.14 18:43 Price: 97.789

Conclusión

En conclusión, hemos utilizado con éxito MQL5 para desarrollar un sistema automatizado capaz de detectar estructuras de mercado triangulares y rectangulares. Estos patrones geométricos, reconocidos desde hace tiempo en el análisis técnico, proporcionan información significativa sobre el comportamiento del mercado, especialmente a la hora de identificar posibles zonas de continuación o reversión. Al centrarnos en formas bien definidas, como triángulos ascendentes y rectángulos, demostramos cómo la geometría puede traducir los movimientos de los precios en estructuras visuales y algorítmicas que son tanto prácticas como fiables.

El enfoque que implementamos sienta una base sólida para construir sistemas analíticos más complejos. La clase GeometricPatternDetector es modular y reutilizable: se puede integrar en otros proyectos y ampliar para mejorar la precisión y la flexibilidad de la detección.

Aunque nuestro sistema dibuja con precisión las formas en el gráfico, hay margen para perfeccionar la lógica de detección de estructuras con el fin de gestionar los casos extremos y mejorar la precisión del reconocimiento de patrones. Este proyecto demuestra cómo los enfoques algorítmicos pueden simplificar la detección de patrones complejos del mercado, agilizando lo que de otro modo sería un proceso manual muy intrincado.

Este viaje ha sido un proceso de aprendizaje continuo. A lo largo del camino, hemos visto cómo el desarrollo basado en clases en MQL5 no solo mejora la modularidad, sino que también promueve la reutilización del código y la abstracción de la interfaz. Esto permite a otros desarrolladores, o incluso a los usuarios finales, trabajar con una interfaz limpia y de alto nivel sin necesidad de comprender la lógica de detección de bajo nivel.

Para aquellos de nosotros que construimos este tipo de sistemas, es esencial dominar la implementación interna. Pero gracias al diseño encapsulado, otros pueden seguir beneficiándose de la funcionalidad sin tener que profundizar en el código subyacente. Con esta estructura en marcha, ahora podemos desarrollar y ampliar con confianza el sistema para detectar cualquier patrón del mercado simplemente diseñando las clases adecuadas.

El siguiente avance lógico sería integrar la lógica de ejecución de órdenes basada en patrones confirmados, como ejecutar órdenes de compra al romper un triángulo ascendente, colocar stop-loss en puntos de oscilación recientes y establecer take-profits dinámicos utilizando la altura del patrón. Las mejoras más avanzadas podrían incluir la confirmación de patrones con indicadores de volumen u osciladores, la aplicación de análisis multitemporal para la validación y la implementación de un sistema de clasificación para priorizar las configuraciones de alta calidad.

Archivos adjuntos:

Archivo	Descripción
GeometricPatternDetector.mqh	Este archivo de encabezado contiene la implementación completa basada en clases de la lógica de detección de patrones geométricos. Define estructuras de datos para puntos de oscilación y resultados de patrones, gestiona la detección de puntos de oscilación, calcula la sensibilidad del mercado utilizando ATR e incluye rutinas para identificar triángulos y rectángulos. El archivo está diseñado para su integración modular en asesores expertos.
GeometryAnalyzerEA.mq5	Este asesor experto muestra el uso práctico del encabezado de detección de patrones. Inicializa y actualiza la clase `CGeometricPatternDetector` en cada nueva barra, obtiene los resultados de los patrones y anota visualmente los patrones detectados en el gráfico. Sirve como un ejemplo sencillo y real de cómo integrar el reconocimiento de patrones orientado a objetos en una estrategia comercial.