MetaTrader 5 / 示例
English Русский Español Deutsch 日本語
preview
MQL5中用于预测与分类评估的重采样技术

MQL5中用于预测与分类评估的重采样技术

MetaTrader 5 — 示例 |
146 0
Francis Dube
Francis Dube

概述

机器学习模型的性能评估通常分为两个独立阶段：在一个数据集上进行训练，在另一个数据集上进行测试。然而，当因资源限制或物流难题而难以收集多个数据集时，则需采用替代方法。

其中一种方法便是运用重采样技术来评估预测或分类模型的性能。尽管该方法可能存在潜在的缺陷，但已被证明能够提供可靠结果。本文将探讨一种新颖的模型质量评估方法，该方法利用单一数据集同时作为训练集和验证集。应用这些方法的主要原因在于测试数据的可用性有限。

因此，从业者必须采用复杂的重采样算法，以生成与更直接方法所产生的性能指标相当的结果。这些技术需要大量的计算资源，并可能增加模型开发过程的复杂性。尽管存在这种权衡，但在某些情况下，采用基于重采样的评估策略仍具有价值，因为其益处超过了成本。


误差分解

为便于阐述本文提出的算法概念，引入了一套记号系统。该记号框架主要处理将模型误差分解为构成要素的问题。考虑一个数据集T，该数据集源自一个具有未知分布F的总体。此数据集包含n个观测值，每个观测值由一个预测变量x（可为标量或向量值）和一个被预测变量y（为标量）组成。为强调预测变量与被预测变量之间的内在依赖关系，采用复合术语t（用于训练）来表示这对变量（x, y）。因此，数据集中的第i个观测值表示为t_i = (x_i, y_i)。尽管此记号代表一个数值预测框架，但分类问题可通过将y_i解释为第i个观测值的类别成员来解决。

完整数据集用T表示。当使用T作为训练集训练模型时，所得的训练模型记为M_T。将此训练模型M_T应用于预测变量x的特定值，以生成对应被预测变量的估计值，即得到模型的预测，记为M_T(x)。为简洁起见，通用模型预测可缩写为M。在评估预测模型的效能时，通常需要量化模型预测M与被预测变量观测值y之间的差异。此差异被正式定义为误差度量，记为Ef[y, M]。回归问题中常用的误差度量是均方误差，其使用平方差，如下方程所示。在分类问题中，Ef[y, M]可定义为二元函数，如果y等于M则赋值为零，否则赋值为一。

误差度量

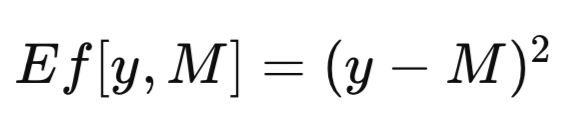
当将训练好的模型应用于其训练所用的同一数据集时，所有训练样本上的平均误差被称为表观误差。尽管传统方法通过最小化该表观误差来训练模型，但本文提出的方法并未施加此类约束。该方法允许对任意度量指标进行优化，随后采用独立标准评估训练后模型的质量。如下文定义的表观误差，仅取决于模型在训练数据上的表现以及对每个预测值应用Ef[]函数的结果，与训练方法无关。

表观误差

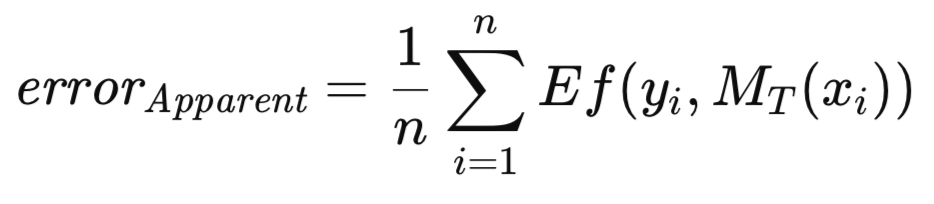
众所周知，由于模型是在用于训练的同一数据集上进行评估的，表观误差会表现出乐观偏差，这种现象有时也被称为训练偏差。为减轻这种偏差，当有足够数据时，会在独立数据集上评估训练好的模型。这一过程有助于估计训练好的模型在应用于总体时的预期误差。这种在给定模型已在训练集上训练的条件下得出的预期误差，被称为预测误差。此处强调的是对特定训练好的模型未来预期性能的评估。预测误差的正式表达式的方程形式如下所示。

预测误差

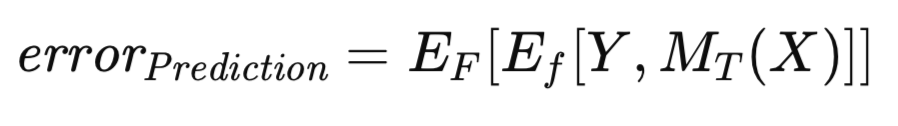
还有一个相关但概念上截然不同的误差度量值得探讨。如前所述，预测误差是基于在特定数据集上训练得到的特定模型而定的。然而，我们可以将期望扩展到涵盖所有可能训练集的集合。具体而言，鉴于训练集由从未知分布中抽取的n个观测值组成，我们可以评估在该特定训练数据集上训练的模型所关联的预测误差，并可能通过独立验证集对其进行近似估算。现在，考虑这样一种情形：抽取一个新的训练集，并重新进行训练过程。不可避免地，我们会得到一个略有不同的预测误差。因此，有必要制定一种度量，以捕捉跨所有潜在训练集范围的预期预测误差。这种度量被称为总体误差，其正式定义如下。

总体误差

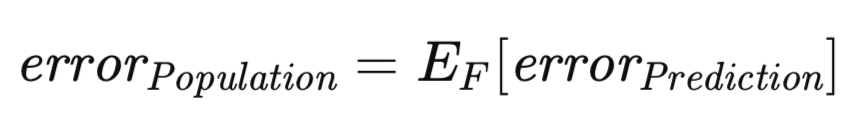
一个公认的原则是，对于任何给定的训练集，表观误差极有可能低估预测误差。这种差异源于模型倾向于过度拟合训练数据的特定特征，从而损害了其在更广泛的总体中的泛化能力。预测误差与表观误差之间的差值幅度被定义为超额误差。

超额误差

在此背景下，预期超额误差尤为重要。鉴于预测误差和表观误差均取决于特定训练集，因此有必要考虑所有可能训练集集合上超额误差的期望值，这与总体误差的推导方法类似。其正式表达式的方程形式如下所示。

预期超额误差

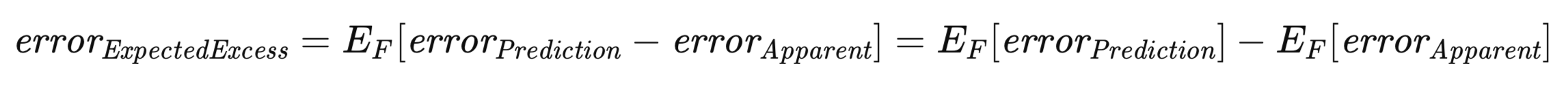
上述方程凸显了预期超额误差在概念上的双重性。一方面，它可以被视为在所有可能的训练集上，每个单独训练集的预测误差与表观误差之差的期望值。这种解释与该概念的直观理解相一致。另一方面，它也可以表示为总体误差与预期表观误差之差。



交叉验证：方法与局限性

交叉验证是学术界广为认可的一种技术。在本文讨论的算法中，交叉验证因其概念简单、易于实现且通常计算效率较高而备受关注。它具有一个显著优势，即能够提供模型预期未来性能的近乎无偏估计。

此外，其广泛的适用性使其能够应用于多种模型训练算法，这是其他方法所不具备的特点。然而，交叉验证存在一个显著局限性：其内在方差往往较大，有时甚至达到不可接受的程度。这意味着对原始数据集随机抽样引入的随机变化高度敏感。

具体而言，实验者收集样本、训练模型，随后使用交叉验证评估模型预期未来性能时，如果使用独立样本重复该过程，可能会观察到截然不同的结果。尽管估计的近乎无偏性是一个理想特性，但往往被方差的大小所掩盖。关键在于，从业者经常低估这种变异性。

尽管存在用于类似任务的更优方法，但交叉验证仍因其简单性以及在替代方法不可行场景下的适用性而被广泛使用。尽管如此，鉴于其普遍性和偶尔的必要性，有必要对交叉验证过程进行详细阐述。

交叉验证的基本原理从概念上讲非常简单。它涉及将数据集划分为两个不同的子集：一个训练集，用于模型参数估计；一个验证集，用于独立模型评估，这与数据充足时采用的程序相类似。

然而，与将大部分数据分配给验证集已获得稳健的性能估计不同，交叉验证使用极小的验证集，将大部分观测值分配给训练集。具体而言，通常采用单个观测值作为验证集是常见做法。

在采用这种划分方式训练和评估模型后，验证集被重新整合到数据集中，并指定不同的观测值作为验证集。这一过程迭代进行，直到每个观测值都曾作为验证点一次。所有迭代中的平均测试误差构成交叉验证误差估计。

交叉验证最普遍的变体涉及逐个排除单个观测值。这些算法应易于适应排除多个观测值的情况。鉴于M_T表示在完整数据集T上训练的模型，设M_T(i)表示在排除第i个观测值的数据集T上训练的模型。那么，模型预期未来误差的交叉验证估计的正式表示方式如下。

交叉验证误差估计

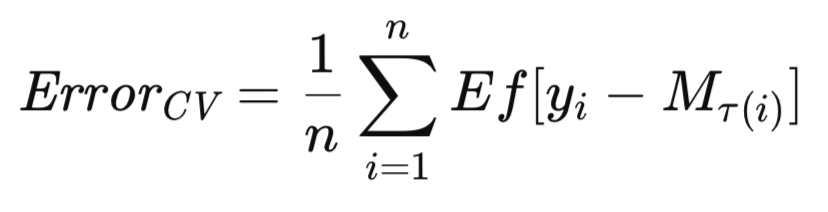
本节将介绍交叉验证算法，并附有解释性说明。本文末尾提供了对比性能评估结果。所有用于估计预期误差的算法均在头文件error_variance_estimation.mqh中呈现。交叉验证算法以cross_validation()方法的形式实现。此例程与用于实现其他误差估计算法的例程在结构和函数参数上相似。这些参数包括：

  • 该方法的头两个必需参数是训练数据集的矩阵。第一个矩阵包含预测变量，第二个矩阵包含对应的目标值。
  • 该例程的第三个参数是实现IModel接口的模型实例。这代表正在评估的预测模型。
  • 传递给cross_validation()方法的最后一个参数存储计算得到的最终误差度量值。如果发生错误，该方法将返回布尔值false。
//+------------------------------------------------------------------+
//| estimate error variance using cross validation testing           |
//+------------------------------------------------------------------+
bool CErrorVar::cross_validation(matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   out_err = 0.0;
   vector test;
   double test_target;
   matrix preds,targs;

   for(ulong i = 0; i<predictors.Rows(); i++)
     {
      test = predictors.Row(i);
      test_target = targets[i][0];
      
      predictors.SwapRows(i,(predictors.Rows()-1));
      targets.SwapRows(i,(targets.Rows()-1));
      
      preds = np::sliceMatrixRows(predictors,0,long(predictors.Rows()-1));
      targs = np::sliceMatrixRows(targets,0,long(targets.Rows()-1));

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ");
         return false;
        }

      out_err += error_fun(test_target,model.forecast(test));
      
      predictors.SwapRows(i,(predictors.Rows()-1));
      targets.SwapRows(i,(targets.Rows()-1));
     }

   out_err/=double(predictors.Rows());

   return true;
  }

调用cross_validation()会触发一个遍历训练数据集的循环。训练数据集中的最后一个位置始终用作测试点。该循环每次将其他样本逐个交换到预测变量矩阵和目标值矩阵的这个位置中。一旦数据划分完成，模型就会在未参与训练的单个样本上进行训练和测试。其误差会被累加，最终作为整个循环的结果返回。

交叉验证的优缺点


基于自助法（Bootstrap）的总体误差估计

本节阐述了一种用于估计总体误差的基础自助法算法。需要指出的是，该算法通常并不推荐用于实际应用，因为后续章节将详细介绍的E0和E632算法通常性能更优。尽管如此，此处介绍的直接自助法仍作为构建更复杂算法的基础原理。因此，全面理解其运作机制对于理解后续算法至关重要。

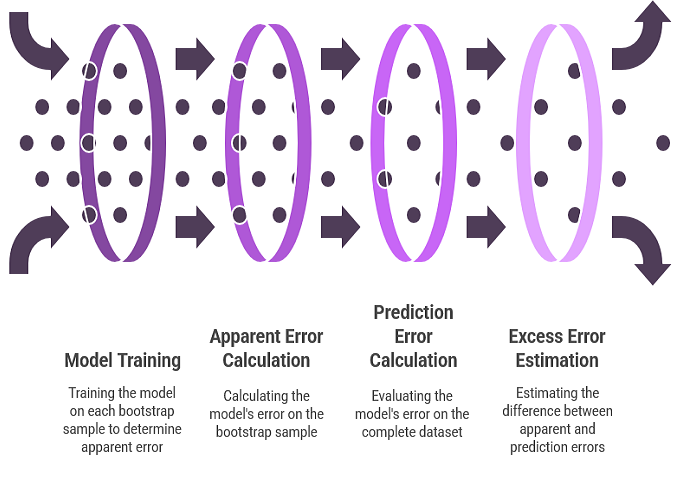
在当前的情境中，我们假设存在一个总体F，训练集中的观测值均从该总体中随机抽样得到。模型在训练集T上进行训练和评估，得出表观误差。该误差本质上过于乐观，预计总体误差将超过表观误差，超出部分即为超额误差。然而，在缺乏独立验证集的情况下，我们主要关注的超额误差和总体误差均无法直接观测。我们仅能获取乐观的表观误差。尽管如此，仍可运用自助法来估计超额误差，进而将其与表观误差相加，以粗略估计总体误差。

利用自助法估计超额误差的过程与估计参数偏差的过程类似。以经验分布函数替代未知的总体分布，并抽取大量自助样本。针对每个自助样本，对模型进行训练。模型在自助样本上的误差代表该样本的表观误差。模型在完整数据集上的误差代表预测误差，因为经验分布实际上充当了整个总体。这两个误差之差即为该自助样本的超额误差。通过大量自助重复实验，计算超额误差的平均值，即可估计预期超额误差。

自助法误差估计过程

为强化上述算法的严谨性，现引入一系列定义与方程。设B表示通过自助采样（从原始数据集中）生成的训练集。具体而言，B是通过从T中有放回地随机选取n个观测值构建而成的。随后，利用B对模型进行训练。该模型的预测误差通过计算其在生成自助样本的总体（在此情境下即原始数据集）中所有观测值上的平均误差来确定。其正式表达式的方程形式如下所示。

自助数据集的预测误差

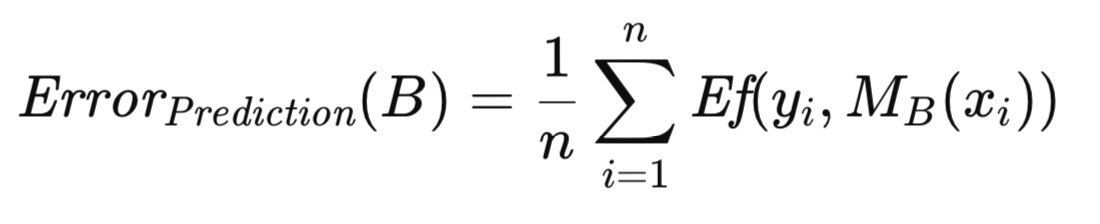
设ki表示原始数据集，T中第i个观测值在自助样本集B中出现的频次。与自助样本集B相关的表观误差，通过对模型在构成B的观测值上的误差求平均来计算，具体方程如下所示。

自助数据集的表观误差

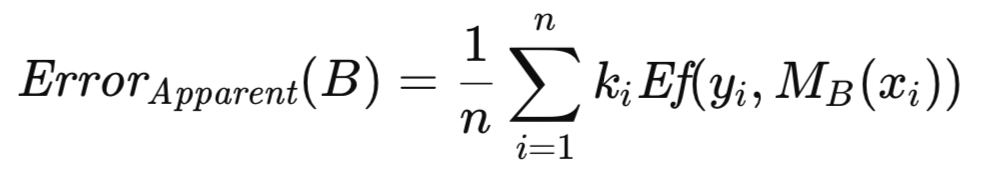
与自助样本集B相关的超额误差，被定义为其预测误差与表观误差之差。由于存在共同的误差项，如果分别计算预测误差与表观误差后再相减，计算过程将存在冗余。因此，通过提取公共量可得到一个更高效的计算式。该计算式需针对大量（数量级为数百至数千）自助重复样本逐一进行评估。这些重复样本的平均超额误差可提供预期超额误差的估计值，将该估计值与全样本的表观误差相加，即可得到总体误差的近似值。

自助数据集的超额误差

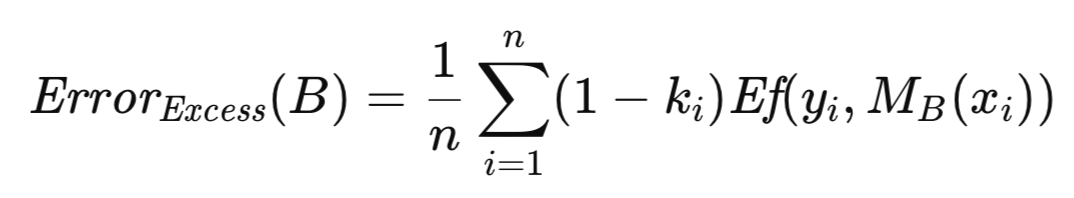
使用boot_strap()方法实现用于误差估计的自助法技术。除交叉验证实现中列出的参数外，该方法还包含一个额外参数，用于指定自助重复抽样的次数。该例程首先借助MQL5中Alglib库实现的随机数生成器实例，初始化一个随机数生成器。利用该随机数生成器，从原始训练集中随机选取一个行索引作为自助样本，并将其置于矩阵变量preds（预测变量）和targs（目标变量）中。随后，使用该自助样本集训练模型，并对其进行测试，以累加超额误差。

//+------------------------------------------------------------------+
//| estimate error variance using ordinary bootstrap                 |
//+------------------------------------------------------------------+
bool CErrorVar::boot_strap(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   double err,apparent,excess;
   excess = 0.0;
   ulong nsize = predictors.Rows();
   ulong count[];
   ulong k;

   ArrayResize(count,int(nsize));

   vector predicted(nsize);

   CHighQualityRandStateShell rstate;
   CHighQualityRand::HQRndRandomize(rstate.GetInnerObj());

   matrix preds = predictors;
   matrix targs = targets;

   for(ulong boot = 0; boot<nboot; boot++)
     {
      ArrayInitialize(count,0);
      //---
      for(ulong i=0; i<nsize; i++)
        {
         k=(int)(CAlglib::HQRndUniformR(rstate)*nsize);
         //---
         if(k>=nsize)
            k=nsize-1;
         //---
         preds.Row(predictors.Row(k),i);
         targs.Row(targets.Row(k),i);
         ++count[k];
        }

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ", boot);
         return false;
        }

      for(ulong i=0; i<nsize; i++)
        {
         predicted[i] = model.forecast(predictors.Row(i));
         err = error_fun(targets[i][0],predicted[i]);
         excess+=(1.0 - double(count[i]))*err;
        }
     }

   excess/=double(nsize*nboot);

自助操作完成后，利用原始训练数据集计算表观误差。最终误差估计值为超额误差与表观误差的累加结果。

if(!model.train(predictors,targets))
     {
      Print(__FUNCTION__," failed to train model ");
      return false;
     }
   apparent = 0.0;
   for(ulong i=0; i<nsize; i++)
     {
      predicted[i] = model.forecast(predictors.Row(i));
      err = error_fun(targets[i][0],predicted[i]);
      apparent+=err;
     }
   apparent/=double(nsize);
   out_err = apparent+excess;
   return true;
  }


埃弗龙（Efron）的总体误差E0估计量

自助样本中训练案例重复出现所引发的一个显著挑战是，可能导致某些模型类别失效。具体而言，概率神经网络和广义回归神经网络对此尤为敏感。除非平滑常数足够大，否则与训练案例完全相同的测试案例将产生近乎完美的预测，从而加剧乐观偏差问题。为了缓解这一问题，布拉德利·埃弗龙（Bradley Efron）提出了一个简单直接的解决方案：防止重复伪影。这就涉及通过标准重采样程序生成自助训练集。然而，对于每个自助重复实验，模型仅在训练集中未出现的原始观测值上进行评估。这些被排除观测值的平均误差随后被用作总体误差的估计值。该方法被指定为总体误差的E0估计量。

学术文献中提出了两种计算E0的不同方法。最初的方法是将所有误差求和后除以评估案例的总数。本文采用的正是此方法。后续对E0性质的理论研究提出了一种替代算法，该算法将平均过程分解为两个阶段。首先，对于每个原始观测值，将所有不包含该观测值的自助重复实验的误差求和，并除以此类重复实验的数量，从而得到该观测值的平均误差。随后，将所有观测值的平均误差求和，并除以观测值的总数，得到总体平均误差。尽管后一种方法计算复杂度增加，但与前一种方法渐近等价，且实证评估表明其性能差异可忽略不计。因此，为简化起见，本文选择最初的方法。

埃弗龙E0误差估计量



为了更清晰地描述该算法，现引入附加符号表示。与前文一致，T表示原始数据集，B表示自助样本。设C为T中未包含于B的观测值集合，count(C)表示集合C的基数（即观测值数量）。则埃弗龙原始的总体误差E0估计量的正式表达如下：

E0估计误差

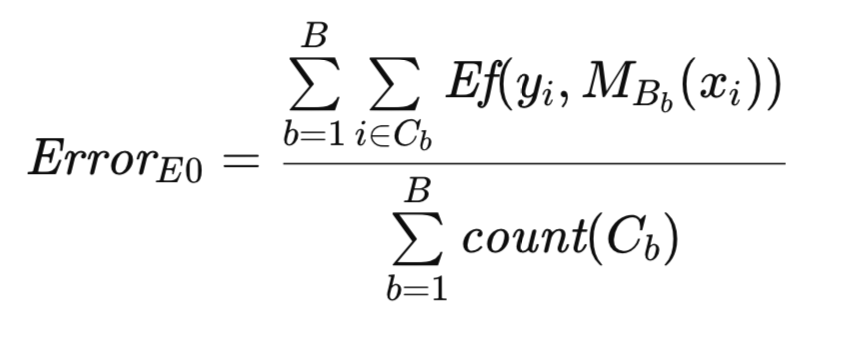
E0估计量的算法实现与前文所述的自助法流程存在相似之处。两种方法在生成自助样本并用于模型训练的环节上保持一致。然而，在此情境下，计数数组作为二元指示器，用于表示观测值是否存在，而非像前述流程中那样作为频次计数器。该算法通过efrons_0()方法实现。  

//+------------------------------------------------------------------+
//| estimate error variance using efron's E0 bootstrap               |
//+------------------------------------------------------------------+
bool CErrorVar::efrons_0(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   out_err = 0.0;
   ulong tot = 0;
   ulong nsize = predictors.Rows();
   ulong count[];
   ulong k;

   ArrayResize(count,int(nsize));

   vector predicted(nsize);

   CHighQualityRandStateShell rstate;
   CHighQualityRand::HQRndRandomize(rstate.GetInnerObj());

   matrix preds = predictors;
   matrix targs = targets;

   for(ulong boot = 0; boot<nboot; boot++)
     {
      ArrayInitialize(count,0);
      //---
      for(ulong i=0; i<nsize; i++)
        {
         k=(int)(CAlglib::HQRndUniformR(rstate)*nsize);
         //---
         if(k>=nsize)
            k=nsize-1;
         //---
         preds.Row(predictors.Row(k),i);
         targs.Row(targets.Row(k),i);
         ++count[k];
        }

      if(!model.train(preds,targs))
        {
         Print(__FUNCTION__," failed to train model ", boot);
         continue;//return false;
        }

      for(ulong i=0; i<nsize; i++)
        {
         if(count[i])
            continue;
         predicted[i] = model.forecast(predictors.Row(i));
         out_err+= error_fun(targets[i][0],predicted[i]);
         ++tot;
        }
     }

   if(tot)
      out_err/=double(tot);
   else
     {
      Print(__FUNCTION__, " zero denominator ");
      return false;
     }
   return true;
  }


埃弗龙的总体误差 E632估计量

如前所述，E0估计量具备诸多理想特性，通常推荐用于实际应用。其避免对训练集中已出现的观测值进行评估的特性，确保了其与各类模型类型的兼容性。此外，其方差处于合理范围内，反映了当前方法论的发展水平。

然而，E0估计量存在适度的保守偏差，倾向于高估真实总体误差。需要指出的是，只要该偏差不过度，通常认为其比低估问题的危害更小。如普通自助法所示，低估因易引发无根据的乐观情绪而更具危害性。采用E0方法通常可确保实际总体误差更可能低于计算值。这种内在的保守性虽然总体有利，但是可能因过度悲观导致错误拒绝模型。E632估计量旨在通过减轻E0的固有保守偏差来解决此问题。

考虑将表观误差（通过评估训练集获得的误差）作为总体误差估计量的固有局限性。评估过程本身存在偏差，因为仅对训练中使用的观测值进行评估。该子集无法代表整个总体，与训练集过度相似，导致乐观偏差。

相反，E0估计量表现出相反的偏差。通过刻意排除训练观测值进行评估，测试集无法代表总体，与训练集过度相异。在实际场景中，与训练观测值相同或高度相似的观测值必然会出现。E0排除这些观测值导致悲观偏差。

埃弗龙E632误差估计量



E632算法试图在上述两种极端情况之间寻求平衡。更公平的方法包括：以反映实际发生概率的方式，同时从训练集内外抽取样本对模型进行评估。或者，可针对抽样差异进行校正调整。随着样本量增大，任意给定观测值出现在自助样本中的概率趋近于1 − 1/e ≈ 0.632。埃弗龙的启发式方法提出，将总体误差估计为E0与表观误差的加权和，权重由上述抽样概率决定。其提出的E632估计量正式表达式的方程形式如下所示。

E632误差估计量

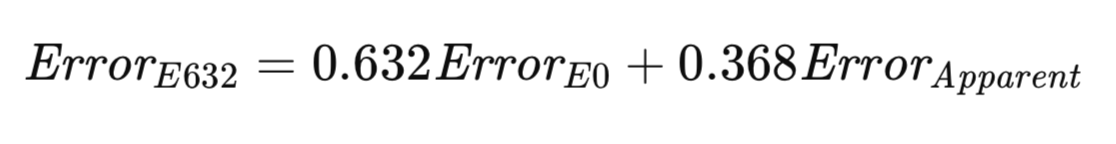
E632算法的实现按照efrons_632()方法提供，具体实现将在稍后展示。 

//+------------------------------------------------------------------+
//| estimate error variance using efron's E632 bootstrap             |
//+------------------------------------------------------------------+
bool CErrorVar::efrons_632(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err)
  {
   double apparent;

   if(!efrons_0(nboot,predictors,targets,model,out_err))
      return false;


   if(!model.train(predictors,targets))
     {
      Print(__FUNCTION__," failed to train model ");
      return false;
     }

   apparent = 0.0;
   
   vector predicted(predictors.Rows());

   for(ulong i=0; i<predictors.Rows(); i++)
     {
      predicted[i] = model.forecast(predictors.Row(i));
      apparent+= error_fun(targets[i][0],predicted[i]);
     }

   apparent/=double(predictors.Rows());

   out_err = 0.632*out_err + 0.368*apparent;

   return true;
  }

截至目前，本文讨论的所有算法均作为CErrorVar类的成员实现。该类还定义了error_fun()方法，用于计算预测值（作为第二个参数传入）与对应目标值（作为第一个参数传入）之间的误差。 

//+------------------------------------------------------------------+
//|  class for estimating error variance                             |
//+------------------------------------------------------------------+
class CErrorVar
  {
public:
                     CErrorVar(void);
                    ~CErrorVar(void);

   virtual double    error_fun(const double truevalue,const double predictedvalue);
   virtual bool      cross_validation(matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      boot_strap(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      efrons_0(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
   virtual bool      efrons_632(ulong nboot,matrix &predictors, matrix &targets, IModel & model,double &out_err);
  };
//+------------------------------------------------------------------+
//| constructor                                                      |
//+------------------------------------------------------------------+
CErrorVar::CErrorVar(void)
  {
  }
//+------------------------------------------------------------------+
//| destructor                                                       |
//+------------------------------------------------------------------+
CErrorVar::~CErrorVar(void)
  {
  }
//+------------------------------------------------------------------+
//| calculate the error                                              |
//+------------------------------------------------------------------+
double CErrorVar::error_fun(const double truevalue,const double predictedvalue)
  {
   return pow(truevalue-predictedvalue,2.0);
  }

下一部分将展示如何仅使用训练数据集，运用这些算法来估计已训练模型的误差。


预测误差估计量的对比分析

本文已介绍了一系列用于估计预测模型总体误差的方法。需要注意以下关键考量因素：

  • 交叉验证：该技术以实现简便、计算高效著称。其适用性广泛，可应用于多种模型类别，并能提供近乎无偏的估计。然而，在训练过程不稳定的场景中，其方差可能较高。因此，除非缺乏替代方法，否则通常不建议将交叉验证作为首选方法。尽管有效，但并非最优选择。
  • 普通自助法：该方法通常被视为最不理想的选择。它不适用于无法处理重复训练观测值或因训练集中存在测试观测值而受影响的模型。此外，该方法显著倾向于低估真实总体误差。因此，其优势并不突出。
  • E0估计量：在训练过程允许重复观测值的场景中，E0估计量通常是首选。其适用性广泛，因避免评估训练观测值而适用于多种模型。在不稳定的学习条件下（如涉及随机训练过程的模型），该方法表现出鲁棒性。在稳定的学习环境中，其方差与交叉验证相近；在不稳定环境中，其方差显著降低。此外，该方法计算效率高，因为计算E632估计量所需的表观误差可与E0估计同时完成。然而，必须承认的是，从业者可能更倾向于选择具有保守偏差的E0，而非方差可能更高但偏差更小的E632估计量。

为实证评估这些估计量，我们使用根据模型（y = x_1 - x_2 + 误差）生成的人工数据进行了模拟研究。在该模型中，预测变量x_1和x_2，服从标准正态分布，误差项服从均值为0、方差由用户指定的正态分布。我们使用普通线性模型拟合数据集，并利用本文介绍的算法估计总体均方误差。同时，该拟合模型还在独立测试数据上进行了评估，以确定其真实误差。此过程针对用户指定的试验次数重复进行，并计算误差估计的平均值和标准差。这一功能在脚本ErrorVarianceEstimation_NumericalPredictionDemo.mq5中实现。

//+------------------------------------------------------------------+
//|              ErrorVarianceEstimation_NumericalPredictionDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<error_variance_estimation.mqh>
#include<OLS.mqh>
//--- input parameters
input ulong      NumSamples=15;
input ulong      NumBootStraps = 1000;
input ulong      NumReplications = 100;
input double     Variance = 1.0;
//---
//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//| ordinary least squares class                                     |
//+------------------------------------------------------------------+
class COrdReg:public IModel
  {
private:
   OLS*              m_ols;
public:
                     COrdReg(void)
     {
      m_ols = new OLS();
     }
                    ~COrdReg(void)
     {
      if(CheckPointer(m_ols) == POINTER_DYNAMIC)
         delete m_ols;
     }
   bool              train(matrix &predictors,matrix& targets)
     {
      return m_ols.Fit(targets.Col(0),predictors);
     }
   double            forecast(vector &predictors)
     {
      return m_ols.Predict(predictors);
     }
  };
//---
ulong nreplications, itry, nsamps, nboots, divisor, ndone;
vector computed_err_cv, computed_err_boot, predictions;
vector computed_err_E0, computed_err_E632 ;
double temperr,sum_observed_error, mean_computed_err, var_computed_err,dfactor,dif;
matrix xdata, testdata,trainpreds,traintargs,testpreds,testtargs;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nboots = NumBootStraps;
   nsamps = NumSamples ;
   nreplications = NumReplications ;
   dfactor = Variance ;

   if((nsamps <= 3)  || (nreplications <= 0) || (dfactor < 0.0) || nboots<=0)
     {
      Alert(" Invalid inputs ");
      return;
     }

   double std = sqrt(dfactor) ;

   divisor = 1000000 / (nsamps * nboots) ;  // This is for progress reports only
   if(divisor < 2)
      divisor = 2 ;

   xdata = matrix::Zeros(nsamps,3);

   sum_observed_error = mean_computed_err = var_computed_err = 0.0;
   computed_err_cv = vector::Zeros(nreplications);
   computed_err_E0 = vector::Zeros(nreplications);
   computed_err_E632 = vector::Zeros(nreplications);
   computed_err_boot = vector::Zeros(nreplications);

   testdata = matrix::Zeros(nsamps*10,3);
   predictions = vector::Zeros(nsamps*10);

   CErrorVar errorvar;
   COrdReg regmodel;

   for(ulong irep = 0; irep<nreplications; irep++)
     {
      ndone = irep + 1 ;

      for(ulong i =0; i<nsamps; i++)
        {
         xdata[i][0] = normal(rngstate);
         xdata[i][1] = normal(rngstate);
         xdata[i][2] = xdata[i][0] - xdata[i][1] + std * normal(rngstate);
        }


      for(ulong j =0; j<testdata.Rows(); j++)
        {
         testdata[j][0] = normal(rngstate);
         testdata[j][1] = normal(rngstate);
         testdata[j][2] = testdata[j][0] - testdata[j][1] + std *normal(rngstate);
        }

      trainpreds = np::sliceMatrixCols(xdata,0,2);
      traintargs = np::sliceMatrixCols(xdata,2);

      if(!regmodel.train(trainpreds,traintargs))
        {
         Print(" fitting first model failed ");
         return;
        }

      testpreds=np::sliceMatrixCols(testdata,0,2);
      testtargs=np::sliceMatrixCols(testdata,2);
      temperr = 0.0;
      for(ulong i = 0;i<testpreds.Rows(); i++)
        {
         predictions[i] = regmodel.forecast(testpreds.Row(i));
         temperr += errorvar.error_fun(testtargs[i][0],predictions[i]);
        }

      sum_observed_error += temperr/double(10*nsamps);

      if(!errorvar.cross_validation(trainpreds,traintargs,regmodel,computed_err_cv[irep]) ||
         !errorvar.boot_strap(nboots,trainpreds,traintargs,regmodel,computed_err_boot[irep]) ||
         !errorvar.efrons_0(nboots,trainpreds,traintargs,regmodel,computed_err_E0[irep]) ||
         !errorvar.efrons_632(nboots,trainpreds,traintargs,regmodel,computed_err_E632[irep])
        )
        {
         Print(" error variance calculation failed ");
         return;
        }
      //---
     }
//---
   PrintFormat("Number of Iterations %d   Observed error = %.5lf",ndone, sum_observed_error / double(ndone)) ;
//---
   PrintFormat("CV: computed error  mean=%10.5lf      std=%10.5lf",computed_err_cv.Mean(), computed_err_cv.Std()) ;
//---
   PrintFormat("BOOT: computed error  mean=%10.5lf      std=%10.5lf",computed_err_boot.Mean(), computed_err_boot.Std()) ;
//---
   PrintFormat("E0: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E0.Mean(), computed_err_E0.Std()) ;
//---
   PrintFormat("E632: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E632.Mean(), computed_err_E632.Std()) ;
  }
//+------------------------------------------------------------------+

采用方差为1.0、样本量为15个观测值、自助法迭代次数为1000次的设置。结果如下：

MJ      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    Number of Iterations 100   Observed error = 1.18380
RF      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    CV: computed error  mean=   1.18825      std=   0.53117
PK      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    BOOT: computed error  mean=   1.12521      std=   0.48780
IR      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E0: computed error  mean=   1.38168      std=   0.63579
NO      0       12:40:47.575    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E632: computed error  mean=   1.18647      std=   0.52380

正如预期的那样，普通自助法低估了真实误差。相反，E0估计量则显著高估了误差。尽管这种高估可能被视为局限性，但需注意，E0估计量同时也表现出最高的标准差。这种高估程度主要归因于样本量过小。然而，其可接受性仍需主观判断。为进一步评估误差估计量的性能，我们将模拟研究重复进行，并将样本量增加至100个观测值——这一规模对于许多实际应用场景更具代表性。结果如下：

KG      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    CV: computed error  mean=   1.01810      std=   0.24132
LH      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    BOOT: computed error  mean=   1.01672      std=   0.14194
PS      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E0: computed error  mean=   1.01989      std=   0.14441
IP      0       12:43:23.483    ErrorVarianceEstimation_NumericalPredictionDemo (Gold RSI Trend Up Index,H1)    E632: computed error  mean=   1.01855      std=   0.14099

该实验结果表明，四种方法均表现出令人满意的性能。值得注意的是，E0估计量仍存在轻微误差高估现象。而其余三种算法的误差低估程度可忽略不计。尽管E0估计量的标准差最高，但差异幅度极小。在整体估计质量较高的场景下，E0估计量产生的轻微误差高估，相较于其他方法中观察到的微不足道的误差低估而言更可取——尤其考虑到误差低估对模型选择与评估的潜在负面影响。

前述案例揭示了不同总体误差估计方法间的某些差异。然而，可能在无意中让人产生这样一种印象：交叉验证在有效性方面始终可以与其他方法相媲美。这种认知源于实验采用了平滑的误差函数，特别是简单模型的均方误差，从而营造了稳定的学习环境。

相比之下，分类任务通常具有内在的不稳定性。数据中的微小扰动可能导致误差率发生剧烈且显著的波动。本节将通过一个案例来探讨这一现象。用于估计总体误差的算法与前文保持一致。主要修改涉及预测误差函数的定义及用于对比评估的主程序结构。

测试脚本ErrorVarianceEstimation_ClassificationDemo.mq5生成了具有中等正相关性的二元数据。 

//+------------------------------------------------------------------+
//|                   ErrorVarianceEstimation_ClassificationDemo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<error_variance_estimation.mqh>
#include<OLS.mqh>
//--- input parameters
input ulong      NumSamples=15;
input ulong      NumBootStraps = 1000;
input ulong      NumReplications = 100;
input double     PredictionDifficultyLevel = 0.0;
//---
//+------------------------------------------------------------------+
//|  normal(rngstate)                                                |
//+------------------------------------------------------------------+
double normal(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndNormal(state);
  }
//+------------------------------------------------------------------+
//|   unifrand(rngstate)                                             |
//+------------------------------------------------------------------+
double unifrand(CHighQualityRandStateShell &state)
  {
   return CAlglib::HQRndUniformR(state);
  }
//+------------------------------------------------------------------+
//| ordinary least squares class                                     |
//+------------------------------------------------------------------+
class COrdReg:public IModel
  {
private:
   OLS*              m_ols;
public:
                     COrdReg(void)
     {
      m_ols = new OLS();
     }
                    ~COrdReg(void)
     {
      if(CheckPointer(m_ols) == POINTER_DYNAMIC)
         delete m_ols;
     }
   bool              train(matrix &predictors,matrix& targets)
     {
      return m_ols.Fit(targets.Col(0),predictors);
     }
   double            forecast(vector &predictors)
     {
      return m_ols.Predict(predictors);
     }
  };
//+------------------------------------------------------------------+
//| error variance for classification models                         |
//+------------------------------------------------------------------+
class CErrorVarC:public CErrorVar
  {
public:
                     CErrorVarC(void)
     {
     }
                    ~CErrorVarC(void)
     {
     }

   virtual double    error_fun(const double truevalue,const double predictedvalue)
     {
      if(truevalue*predictedvalue>0.0)
         return 0.0;
      else
         return 1.0;
     }


  };
//---
ulong nreplications, itry, nsamps, nboots, divisor, ndone;
vector computed_err_cv, computed_err_boot, predictions;
vector computed_err_E0, computed_err_E632 ;
double temperr,sum_observed_error, mean_computed_err, var_computed_err,dfactor,dif;
matrix xdata, testdata,trainpreds,traintargs,testpreds,testtargs;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CHighQualityRandStateShell rngstate;
   CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj());
//---
   nboots = NumBootStraps;
   nsamps = NumSamples ;
   nreplications = NumReplications ;
   dfactor = PredictionDifficultyLevel ;

   if((nsamps <= 3)  || (nreplications <= 0) || (dfactor < 0.0) || nboots<=0)
     {
      Alert(" Invalid inputs ");
      return;
     }

   double std = sqrt(dfactor) ;

   divisor = 1000000 / (nsamps * nboots) ;  // This is for progress reports only
   if(divisor < 2)
      divisor = 2 ;

   xdata = matrix::Zeros(nsamps,3);

   sum_observed_error = mean_computed_err = var_computed_err = 0.0;
   computed_err_cv = vector::Zeros(nreplications);
   computed_err_E0 = vector::Zeros(nreplications);
   computed_err_E632 = vector::Zeros(nreplications);
   computed_err_boot = vector::Zeros(nreplications);

   testdata = matrix::Zeros(nsamps*10,3);
   predictions = vector::Zeros(nsamps*10);

   CErrorVarC errorvar;
   COrdReg olsmodel;

   for(ulong irep = 0; irep<nreplications; irep++)
     {
      ndone = irep + 1 ;

      for(ulong i =0; i<nsamps; i++)
        {
         xdata[i][0] = normal(rngstate);
         xdata[i][1] = 0.7071 * xdata[i][0]  +  0.7071 * normal(rngstate);
         if(CAlglib::HQRndUniformR(rngstate)>0.5)
           {
            xdata[i][0] -=dfactor;
            xdata[i][1] +=dfactor;
            xdata[i][2] = 1.0;
           }
         else
           {
            xdata[i][0] +=dfactor;
            xdata[i][1] -=dfactor;
            xdata[i][2] = -1.0;
           }
        }


      for(ulong j =0; j<testdata.Rows(); j++)
        {
         testdata[j][0] = normal(rngstate);
         testdata[j][1] = 0.7071 * testdata[j][0]  +  0.7071 * normal(rngstate);
         if(CAlglib::HQRndUniformR(rngstate)>0.5)
           {
            testdata[j][0] -=dfactor;
            testdata[j][1] +=dfactor;
            testdata[j][2] = 1.0;
           }
         else
           {
            testdata[j][0] +=dfactor;
            testdata[j][1] -=dfactor;
            testdata[j][2] = -1.0;
           }
        }

      trainpreds = np::sliceMatrixCols(xdata,0,2);
      traintargs = np::sliceMatrixCols(xdata,2);

      if(!olsmodel.train(trainpreds,traintargs))
        {
         Print(" fitting first model failed ");
         return;
        }

      testpreds=np::sliceMatrixCols(testdata,0,2);
      testtargs=np::sliceMatrixCols(testdata,2);
      temperr = 0.0;
      for(ulong i = 0;i<testpreds.Rows(); i++)
        {
         predictions[i] = olsmodel.forecast(testpreds.Row(i));
         temperr += errorvar.error_fun(testtargs[i][0],predictions[i]);
        }

      sum_observed_error += temperr/double(10*nsamps);

      if(!errorvar.cross_validation(trainpreds,traintargs,olsmodel,computed_err_cv[irep]) ||
         !errorvar.boot_strap(nboots,trainpreds,traintargs,olsmodel,computed_err_boot[irep]) ||
         !errorvar.efrons_0(nboots,trainpreds,traintargs,olsmodel,computed_err_E0[irep]) ||
         !errorvar.efrons_632(nboots,trainpreds,traintargs,olsmodel,computed_err_E632[irep])
        )
        {
         Print(" error variance calculation failed ");
         return;
        }
     }

   PrintFormat("Number of Iterations %d   Observed error = %.5lf",ndone, sum_observed_error / double(ndone)) ;
//---
   PrintFormat("CV: computed error  mean=%10.5lf      std=%10.5lf",computed_err_cv.Mean(), computed_err_cv.Std()) ;
//---
   PrintFormat("BOOT: computed error  mean=%10.5lf    std=%10.5lf",computed_err_boot.Mean(), computed_err_boot.Std()) ;
//---
   PrintFormat("E0: computed error  mean=%10.5lf      std=%10.5lf",computed_err_E0.Mean(), computed_err_E0.Std()) ;
//---
   PrintFormat("E632: computed error  mean=%10.5lf    std=%10.5lf",computed_err_E632.Mean(), computed_err_E632.Std()) ;
  }
//+--------------------------------------------------------------------+

当设置“预测难度系数”（PredictionDifficultyLevel）为1.0时，数据的散点图将呈现椭圆形分布，其长轴方向为右上倾斜。脚本中的“预测难度系数”参数用于控制不同类别簇之间的分离程度，该值越大，类别区分越容易。反之，该参数值越低，模型推断类别归属的难度就越高。

测试数据集的散点图

生成两个不同类别，其数据分布分别沿与长轴垂直的方向按用户指定幅度偏移。采用线性模型拟合数据，其中一类预测变量赋值为-1.0，另一类赋值为+1.0。如果真实值与预测值符号相同，则预测误差定义为0.0；反之如果相反，则误差定义为1.0。这种二元误差度量反映了分类问题的本质特征。

开展两项独立的实验评估。首个实验采用15个观测值的样本量、1000次自助法重复、100次试验，且设置类别分离度为0。该配置模拟了无区分性信息的场景，因为两类分布完全相同。如预期所示，观察到的平均误差约为0.5。实验结果如下：

OO      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) Number of Iterations 100   Observed error = 0.50267
PS      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) CV: computed error  mean=   0.50267      std=   0.18389
KM      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) BOOT: computed error  mean=   0.45214    std=   0.11748
EQ      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E0: computed error  mean=   0.50517      std=   0.10845
RF      0       10:35:04.051    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E632: computed error  mean=   0.45196    std=   0.09941

交叉验证再次展现了其近乎无偏的特性。这一结果在预期之中，因为模型缺乏预测能力时，任意观测值被误分类的概率均为50%。类似逻辑同样适用于E0估计量。尽管E0通常被认为存在悲观偏差，但这种特性仅在模型具备一定有效性时才会显现。在此场景下，E0强制排除测试观测值对训练集的影响呈中性。

然而，这种中性特性并不适用于E632估计量。由于E632同时包含无偏成分和强乐观偏差成分，其整体表现出显著的乐观偏差。这种潜在的偏差需谨慎考量。该实验还凸显了交叉验证的主要缺陷：其方差较高。交叉验证估计量的标准差显著高于E0估计量。如常见情况所示，E632估计量的标准差最低。然而，这一优势被E632固有的强乐观偏差所削弱。

我们还开展了第二项实验，使模型具备一定预测能力（将PredictionDifficultyLevel参数提升至1.0）。实验结果如下：

GM      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) Number of Iterations 100   Observed error = 0.00747
NM      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) CV: computed error  mean=   0.00533      std=   0.01909
RO      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) BOOT: computed error  mean=   0.00716    std=   0.01766
OG      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E0: computed error  mean=   0.01012      std=   0.01878
FD      0       10:38:15.306    ErrorVarianceEstimation_ClassificationDemo (Gold RSI Trend Up Index,H1) E632: computed error  mean=   0.00820    std=   0.01869

本实验表明，E632估计量效果最优。其偏差低且标准差最小。然而，E0估计量虽标准差稍高，却展现出其特有的（且常被视为可取的）悲观偏差特性。结合前次实验结果，在选择E0与E632估计量时，需谨慎权衡这一因素。再次强调，交叉验证的标准差最高，而普通自助法存在可能引发风险的乐观偏差。

关于应用所提到的算法评估分类性能的注意事项。生成自助分类数据集时存在显著局限性。部分自助样本可能仅包含单一类别实例，导致分类算法出现问题，甚至完全失效。欲采用所述技术的读者需警惕此类潜在风险。


结论

粗略浏览本文内容可能会让人觉得，用于估计模型总体误差的重采样技术，虽然在概念上颇具吸引力，但是过于复杂且实际效用有限。像这样得出此类结论实在可惜，因为本文所介绍的重采样方法具有显著优势，值得认真考量。

具体而言，这些方法解决了模型评估中的一个根本性难题：对独立数据集的需求。传统方法需获取独立数据集，这一过程往往存在操作障碍，某些情况下甚至难以实现。

本文讨论的重采样技术则无需满足此要求。整个数据集可同时用于模型训练和未来性能评估，从而实现了数据利用的最大化。这一能力标志着方法论的重大进步，不应被轻易忽视。


文件名
文件描述
MQL5/include/error_variance_estimation.mqh 包含本文所述的定义误差估计算法的头文件。
MQL5/include/imodel.mqh 该头文件包含用于与机器学习模型交互的接口定义。
MQL5/include/np.mqh 该头文件包含用于与机器学习模型交互的接口定义。
MQL5/include/OLS.mqh 该头文件定义了实现普通最小二乘模型的OLS类。
MQL5/scripts/ErrorVarianceEstimation_NumericalPredictionDemo.mq5 通过演示脚本展示误差估计算法在数值预测中的实际应用价值。
MQL5/scripts/ErrorVarianceEstimation_ClassificationDemo.mq5 用于展示误差估计算法在数据分类中实用性的演示脚本。

本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/17446

注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

本文由网站的一位用户撰写，反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责，也不对因使用所述解决方案、策略或建议而产生的任何后果负责。

该作者的其他文章

前往讨论
探索达瓦斯箱体突破策略中的高级机器学习技术 探索达瓦斯箱体突破策略中的高级机器学习技术
达瓦斯箱体突破策略由尼古拉斯·达瓦斯（Nicolas Darvas）提出，是一种技术交易方法：当股价突破预设的"箱体"区间上沿时，视为潜在买入信号，表明强劲的上升动能。本文将以该策略为例，探讨三种高级机器学习技术的应用。其中包括：利用机器学习模型直接生成交易信号（而非仅过滤交易）；采用连续型信号（而非离散型信号）；使用基于不同时间框架训练的模型进行交易验证。
市场模拟（第四部分）：创建 C_Orders 类（一） 市场模拟（第四部分）：创建 C_Orders 类（一）
在本文中，我们将开始创建 C_Orders 类，以便能够向交易服务器发送订单。我们将循序渐进地进行，目标是通过消息系统详细说明这一过程的具体实现方式。
市场模拟（第五部分）：创建 C_Orders 类（二） 市场模拟（第五部分）：创建 C_Orders 类（二）
在本文中，我将解释 Chart Trade 如何与 EA 交易一起处理平仓请求，以关闭用户的所有未平仓头寸。这听起来简单，但你需要知道如何应对一些复杂情况。
交易中的神经网络：配备注意力机制（MASAAT）的智代融汇（终章） 交易中的神经网络：配备注意力机制（MASAAT）的智代融汇（终章）
在上一篇文章中，我们讲述了多智代自适应框架 MASAAT，其用一组智代的融汇在不同数据尺度下对多模态时间序列进行交叉分析。今天我们将继续实现该框架方法的 MQL5 版本，并将这项工作带至逻辑完结。