
Redes neuronales en el trading: Modelos bidimensionales del espacio de enlaces (Final)
Introducción
En el artículo anterior, presentamos el framework Quimera, un modelo de espacio de estados bidimensional (2D-SSM) basado en transformaciones lineales a lo largo del eje temporal y del eje de variables analizadas. El framework integra modelos de espacio de estados a lo largo de los dos ejes, así como sus mecanismos de interacción.
Los modelos de espacio de estados (SSM) se utilizan ampliamente en el análisis de series temporales porque permiten modelizar dependencias complejas. Sin embargo, los SSM tradicionales solo tienen en cuenta el eje temporal, lo cual limita su aplicación a problemas multivariantes. Chimera amplía este concepto incorporando el eje de características al proceso de modelado.
El framework funciona con una forma de 2D-SSM discretizada introduciendo los pasos de muestreo Δ1 y Δ2. El primer parámetro afecta a las dependencias temporales y el segundo a las relaciones entre variables. Los valores más pequeños de Δ1 ayudan a considerar las tendencias a largo plazo, mientras que los valores más grandes enfatizan los cambios estacionales. Del mismo modo, la discretización por variables regula el nivel de detalle del análisis.
Para recuperar correctamente los procesos, los autores del framework introducen restricciones estructurales en las matrices A1, A2 (dependencias temporales) y A3, A4 (relaciones intervariables) La naturaleza causal de 2D-SSM limita la transferencia de información a lo largo del eje de características, por lo que Quimera usa dos módulos para analizar las interdependencias con las características antecedentes y consecuentes del entorno analizado.
La flexibilidad del framework Quimera permite el uso de los parámetros Bi, Ci y Δi tanto independientemente de los datos de origen como en función de los propios datos de origen. El uso de parámetros dependientes del contexto hace que el modelo se adapte mejor a las condiciones de los sistemas multidimensionales complejos.
El framework usa una pila 2D-SSM con transformaciones no lineales entre capas, aproximándose a una arquitectura de modelo profundo. Permite descomponer las series temporales en componentes de tendencia y estacionales, ofreciendo un análisis preciso de los patrones.
A continuación se muestra la visualización del framework Chimera realizada por el autor.
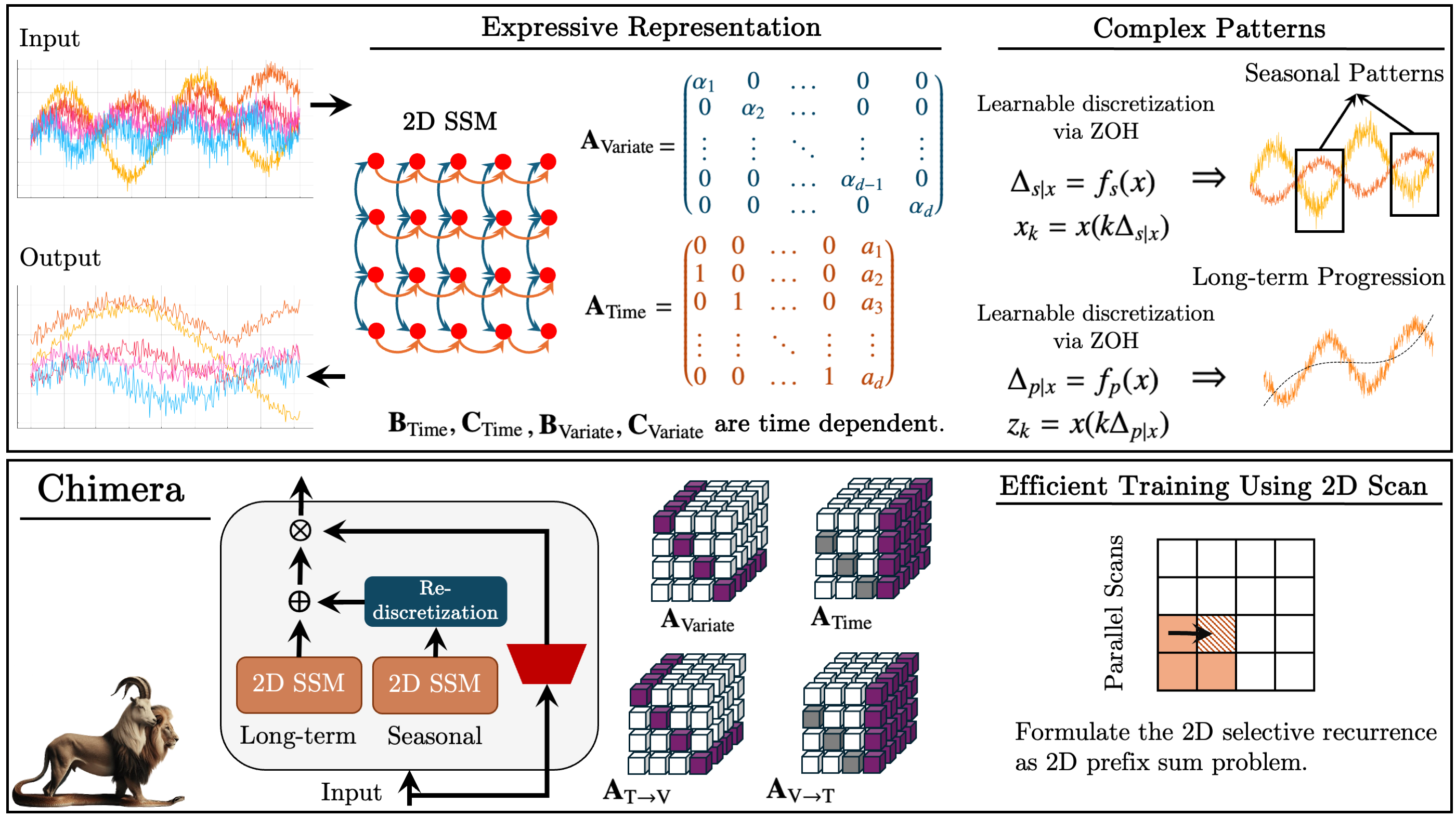
En la parte práctica del artículo, desarrollamos la arquitectura necesaria para realizar nuestra propia visión de los enfoques propuestos mediante MQL5 y comenzamos a trabajar en su implementación. Asimismo, revisamos los cambios introducidos en el programa OpenCL. También desarrollamos la estructura del objeto 2D-SSM y presentamos su método de inicialización. En la actualidad, continuamos construyendo algoritmos para aplicar los planteamientos propuestos en nuestros propios modelos.
El objeto 2D-SSM
El artículo anterior lo concluimos considerando el método de inicialización del objeto CNeuron2DSSMOCL, en el que pretendemos implementar la funcionalidad de construcción y entrenamiento de 2D-SSM. La estructura de este mecanismo se resume a continuación:
class CNeuron2DSSMOCL : public CNeuronBaseOCL { protected: uint iWindowOut; uint iUnitsOut; CNeuronBaseOCL cHiddenStates; CLayer cProjectionX_Time; CLayer cProjectionX_Variable; CNeuronConvOCL cA; CNeuronConvOCL cB_Time; CNeuronConvOCL cB_Variable; CNeuronConvOCL cC_Time; CNeuronConvOCL cC_Variable; CNeuronConvOCL cDelta_Time; CNeuronConvOCL cDelta_Variable; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool feedForwardSSM2D(void); //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradientsSSM2D(void); virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuron2DSSMOCL(void) {}; ~CNeuron2DSSMOCL(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuron2DSSMOCL; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); //--- virtual bool Clear(void) override; };
Proseguimos por donde lo dejamos. Hoy veremos primero el algoritmo de construcción del método de pasada directa feedForward de este objeto.
bool CNeuron2DSSMOCL::feedForward(CNeuronBaseOCL *NeuronOCL) { CNeuronBaseOCL *inp = NeuronOCL; CNeuronBaseOCL *x_time = NULL; CNeuronBaseOCL *x_var = NULL;
En los parámetros del método obtenemos el puntero al objeto de datos de origen, que guardaremos inmediatamente en una variable local. Aquí declararemos dos variables locales más, para almacenar punteros a los objetos de proyección de los datos de origen en el contexto del tiempo y las características. En esta fase, todavía tendremos que elaborar estas proyecciones.
Permítame recordarle que para formar las proyecciones anteriores, creamos dos secuencias internas en el método de inicialización; los punteros a sus objetos se almacenaron en los arrays dinámicos cProjectionX_Time y cProjectionX_Variable. Ahora podemos usarlos para obtener las proyecciones necesarias.
En primer lugar, generaremos la proyección en el contexto del tiempo. Ya hemos almacenado el puntero al objeto de datos de origen en una variable local. A continuación, crearemos un ciclo de enumeración secuencial de los objetos del modelo de proyección en el contexto del tiempo.
//--- Projection Time int total = cProjectionX_Time.Total(); for(int i = 0; i < total; i++) { x_time = cProjectionX_Time.At(i); if(!x_time || !x_time.FeedForward(inp)) return false; inp = x_time; }
En el cuerpo del ciclo, primero obtendremos un puntero al siguiente objeto de la secuencia. Luego comprobaremos la pertinencia del puntero obtenido. Y después de pasar con éxito el punto de control, llamaremos al método de pasada directa de objetos, transmitiéndole el puntero al objeto de datos de origen.
A continuación, guardaremos el puntero al objeto actual en la variable local de los datos de origen y pasaremos a la siguiente iteración del ciclo.
Una vez completadas todas las iteraciones del ciclo, en la variable de proyección local de los datos de origen en el contexto temporal se escribirá un puntero al último objeto de la secuencia correspondiente. El búfer de este objeto contendrá la proyección que necesitamos.
Del mismo modo, obtendremos una proyección de los datos de origen en el contexto de las características.
//--- Projection Variable inp = NeuronOCL; total = cProjectionX_Variable.Total(); for(int i = 0; i < total; i++) { x_var = cProjectionX_Variable.At(i); if(!x_var || !x_var.FeedForward(inp)) return false; inp = x_var; }
Para obtener cuatro proyecciones de los dos estados ocultos, solo tendremos que llamar al método de pasada directa del objeto de las proyecciones correspondientes. En sus parámetros, transmitiremos el puntero al objeto que contiene el tensor de estado oculto concatenado.
if(!cA.FeedForward(cHiddenStates.AsObject())) return false;
El resto de parámetros de nuestro 2D-SSM dependerán del contexto. Por ese motivo, a continuación generaremos los parámetros del modelo basándonos en las proyecciones correspondientes de los datos de entrada. Para ello, buscaremos secuencialmente en los objetos de generación de parámetros del modelo y llamaremos a sus métodos de pasada directa pasando los punteros a los objetos de las proyección correspondientes de los datos de origen.
if(!cB_Time.FeedForward(x_time) || !cB_Variable.FeedForward(x_var)) return false; if(!cC_Time.FeedForward(x_time) || !cC_Variable.FeedForward(x_var)) return false; if(!cDelta_Time.FeedForward(x_time) || !cDelta_Variable.FeedForward(x_var)) return false;
En esta fase, hemos terminado nuestro trabajo de preparación de los parámetros del modelo bidimensional del espacio de estados. Solo nos queda generar los nuevos valores del estado oculto y los resultados del modelo. Como ya sabe, en el último artículo los procesos anteriores se pusieron en un kernel aparte que creamos en el lado del programa OpenCL. Y ahora bastará con llamar al método-envoltorio del kernel dado. Pero antes, conviene señalar que la generación de un nuevo estado oculto eliminará los valores actuales que necesitaremos para realizar las operaciones de pasada inversa. Por lo tanto, primero sustituiremos los punteros a los objetos de búfer de datos y, a continuación, llamaremos al método-envoltorio feedForwardSSM2D.
if(!cHiddenStates.SwapOutputs()) return false; //--- return feedForwardSSM2D(); }
La próxima etapa de nuestro trabajo consistirá en construir los algoritmos de pasada inversa para nuestro objeto. Aquí le propongo examinar el método de distribución de gradientes de error calcInputGradients. En los parámetros de este método obtendremos el puntero al mismo objeto de datos de origen, solo que esta vez tendremos que pasarle el gradiente de error según la influencia de los datos de origen en el resultado global del modelo.
bool CNeuron2DSSMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
La transferencia de datos solo será posible si existe un puntero válido al objeto. Por lo tanto, el primer paso del algoritmo será comprobar el puntero recibido, lo que impedirá el acceso a recursos liberados o no inicializados. Este enfoque resultará fundamental para garantizar la estabilidad del proceso de cálculo y evitar fallos en el procesamiento de datos.
Una vez superado con éxito el bloque de control, comenzarán las operaciones de distribución del gradiente de error. Este proceso se realizará desde el nivel de resultados del objeto hacia los datos de origen, siguiendo el mecanismo de propagación inversa del error según el flujo de datos de la pasada directa, pero en orden inverso.
Finalizaremos el método de pasada directa llamando al método-envoltorio del kernel de generación de estados ocultos y cálculo de los resultados 2D-SSM. En consecuencia, el proceso de propagación del gradiente de error se iniciará llamando a un método-envoltorio similar, pero para el kernel que realiza la propagación del error. Dentro de este kernel, el gradiente se distribuirá correctamente entre los elementos 2D-SSM según su contribución a la formación de los resultados del modelo.
if(!calcInputGradientsSSM2D()) return false;
Debemos considerar que en esta fase solo se realizará la distribución de los valores de gradiente entre los componentes estructurales del modelo. Sin embargo, el ajuste directo de los valores a las derivadas de las funciones de activación de los objetos no se realizará dentro del kernel especificado. Por ello, antes de propagar el gradiente de error a través de los objetos internos del modelo, deberemos comprobar la presencia de las funciones de activación en estos objetos. En caso necesario, deberán efectuarse las correcciones de valor correspondientes para considerar los efectos de las transformaciones no lineales en los gradientes transmitidos. Esto garantizará que cada parámetro del modelo se actualice para reflejar la contribución real a la generación de la señal de salida.
//--- Deactivation CNeuronBaseOCL *x_time = cProjectionX_Time[-1]; CNeuronBaseOCL *x_var = cProjectionX_Variable[-1]; if(!x_time || !x_var) return false; if(x_time.Activation() != None) if(!DeActivation(x_time.getOutput(), x_time.getGradient(), x_time.getGradient(), x_time.Activation())) return false; if(x_var.Activation() != None) if(!DeActivation(x_var.getOutput(), x_var.getGradient(), x_var.getGradient(), x_var.Activation())) return false; if(cB_Time.Activation() != None) if(!DeActivation(cB_Time.getOutput(), cB_Time.getGradient(), cB_Time.getGradient(), cB_Time.Activation())) return false; if(cB_Variable.Activation() != None) if(!DeActivation(cB_Variable.getOutput(), cB_Variable.getGradient(), cB_Variable.getGradient(), cB_Variable.Activation())) return false; if(cC_Time.Activation() != None) if(!DeActivation(cC_Time.getOutput(), cC_Time.getGradient(), cC_Time.getGradient(), cC_Time.Activation())) return false; if(cC_Variable.Activation() != None) if(!DeActivation(cC_Variable.getOutput(), cC_Variable.getGradient(), cC_Variable.getGradient(), cC_Variable.Activation())) return false; if(cDelta_Time.Activation() != None) if(!DeActivation(cDelta_Time.getOutput(), cDelta_Time.getGradient(), cDelta_Time.getGradient(), cDelta_Time.Activation())) return false; if(cDelta_Variable.Activation() != None) if(!DeActivation(cDelta_Variable.getOutput(), cDelta_Variable.getGradient(), cDelta_Variable.getGradient(), cDelta_Variable.Activation())) return false; if(cA.Activation() != None) if(!DeActivation(cA.getOutput(), cA.getGradient(), cA.getGradient(), cA.Activation())) return false;
A continuación, pasaremos al proceso de distribución del gradiente de error a través de los objetos internos de nuestro 2D-SSM. Y en primer lugar, necesitaremos distribuir los valores del gradiente a través de los objetos de generación de parámetros del modelo dependientes del contexto. Permítame recordarle que se forman a partir de las correspondientes proyecciones de los datos de origen.
Y aquí deberemos prestar atención al hecho de que los objetos de las proyecciones de los datos de origen participan en el proceso principal de formación de los resultados del modelo y ya han recibido los valores de los gradientes de error durante las operaciones anteriores. Para conservar los valores obtenidos anteriormente, sustituiremos los punteros a los búferes de datos correspondientes.
//--- Gradient to projections X CBufferFloat *grad_x_time = x_time.getGradient(); CBufferFloat *grad_x_var = x_var.getGradient(); if(!x_time.SetGradient(x_time.getPrevOutput(), false) || !x_var.SetGradient(x_var.getPrevOutput(), false)) return false;
A continuación, haremos descender sucesivamente el gradiente de error a través de los objetos de formación de parámetros dependientes del contexto y, en cada paso, sumaremos los valores resultantes con los valores acumulados anteriormente.
//--- B -> X if(!x_time.calcHiddenGradients(cB_Time.AsObject()) || !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1)) return false; if(!x_var.calcHiddenGradients(cB_Variable.AsObject()) || !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1)) return false;
//--- C -> X if(!x_time.calcHiddenGradients(cC_Time.AsObject()) || !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1)) return false; if(!x_var.calcHiddenGradients(cC_Variable.AsObject()) || !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1)) return false;
//--- Delta -> X if(!x_time.calcHiddenGradients(cDelta_Time.AsObject()) || !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1)) return false; if(!x_var.calcHiddenGradients(cDelta_Variable.AsObject()) || !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1)) return false;
Y después de transferir con éxito los gradientes de error de todos los flujos de información, retornaremos los punteros a los objetos al estado inicial.
if(!x_time.SetGradient(grad_x_time, false) || !x_var.SetGradient(grad_x_var, false)) return false;
En esta fase, hemos obtenido los valores de los gradientes de error en el nivel de proyección de los datos de origen en ambos contextos. A continuación tendremos que pasar los gradientes por los correspondientes modelos de proyección interna. Para ello, crearemos ciclos de iteración inversa de los objetos de las secuencias correspondientes.
//--- Projection Variable int total = cProjectionX_Variable.Total() - 2; for(int i = total; i >= 0; i--) { x_var = cProjectionX_Variable[i]; if(!x_var || !x_var.calcHiddenGradients(cProjectionX_Variable[i + 1])) return false; }
//--- Projection Time total = cProjectionX_Time.Total() - 2; for(int i = total; i >= 0; i--) { x_time = cProjectionX_Time[i]; if(!x_time || !x_time.calcHiddenGradients(cProjectionX_Time[i + 1])) return false; }
Nótese que al pasar el gradiente de error a través de los modelos internos de las proyecciones de contexto, nos hemos detenido en la primera capa de cada una de las secuencias. Aquí debemos decir que nuestras dos secuencias de proyección generan sus valores a partir de los datos de origen recibidos en los parámetros del método desde un programa externo. Y ahora tendremos que pasar el gradiente de error al objeto de datos de origen desde ambos modelos de proyección interna.
Como es habitual en estos casos, primero transmitiremos el gradiente de error a través de un flujo de información.
//--- Projections -> inputs if(!NeuronOCL.calcHiddenGradients(x_var.AsObject())) return false;
Y luego sustituiremos los punteros a los objetos de búfer de gradiente y pasaremos los errores a través del segundo flujo de información.
grad_x_time = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(x_time.getPrevOutput(), false) || !NeuronOCL.calcHiddenGradients(x_time.AsObject()) || !SumAndNormilize(grad_x_time, NeuronOCL.getGradient(), grad_x_time, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(grad_x_time, false)) return false; //--- return true; }
Por último, sumaremos los valores de ambos flujos de información y devolveremos los punteros a los búferes de datos al estado inicial.
Tenga en cuenta que no pasaremos el gradiente de error al nivel del objeto de estado oculto, ya que este objeto solo se utiliza para el almacenamiento de datos y no contiene parámetros entrenables.
Ahora que hemos distribuido los valores del gradiente de error entre todos los objetos internos, solo quedará devolver el resultado lógico de las operaciones al programa que realiza la llamada y finalizar el método.
Con esto concluye nuestro análisis de los algoritmos de construcción de los métodos del objeto CNeuron2DSSMOCL. Podrá leer el código completo de este objeto y todos sus métodos por sí mismo en el archivo adjunto.
Módulo Quimera
La siguiente etapa de nuestro trabajo será la construcción del módulo Quimera. Los autores del framework proponen el uso de dos 2D-SSM paralelos con distintos niveles de muestreo y enlaces residuales. La combinación de dos modelos independientes de espacio de estados que operen a distintos niveles de discretización posibilitará un análisis más profundo de las dependencias y permitirá construir modelos predictivos muy eficaces adaptados a datos multiescala.
El uso de 2D-SSM con distintos parámetros de muestreo permitirá un análisis diferenciado de las series temporales. El modelo de alta frecuencia identificará patrones a largo plazo, mientras que el de baja frecuencia se centrará en reconocer los ciclos estacionales. Esta separación mejorará la precisión de las predicciones, ya que cada uno de los modelos se adaptará a una parte diferente de los datos, minimizando la pérdida de información y los errores causados por una agregación excesiva de características temporales. La incorporación del módulo de discretización permitirá comparar los resultados de ambos modelos.
Una ventaja adicional del módulo Quimera es el uso de enlaces residuales, que garantizarán una transferencia eficaz de información entre los niveles del modelo. Estos permiten almacenar el gradiente y transmitirlo durante la propagación inversa del error, evitando que se desvanezca. Esto resulta especialmente importante a la hora de entrenar modelos profundos, en los que el descenso de gradiente suele encontrar problemas de inestabilidad numérica. El modelo sigue siendo más resistente a la pérdida de información cuando se transfieren datos entre capas, mientras que el proceso de aprendizaje se vuelve más estable, incluso cuando se trata de series temporales largas.
Implementaremos el mecanismo propuesto dentro del objeto CNeuronChimera, cuya estructura se muestra a continuación.
class CNeuronChimera : public CNeuronBaseOCL { protected: CNeuron2DSSMOCL caSSM[2]; CNeuronConvOCL cDiscretization; CLayer cResidual; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; //--- virtual bool calcInputGradients(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; public: CNeuronChimera(void) {}; ~CNeuronChimera(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronChimera; } //--- virtual bool Save(int const file_handle); virtual bool Load(int const file_handle); //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau); virtual void SetOpenCL(COpenCLMy *obj); //--- virtual bool Clear(void) override; };
En la estructura presentada podemos ver el conjunto habitual de métodos redefinidos y varios objetos internos cuya funcionalidad no es difícil de adivinar por sus nombres.
Todos los objetos internos se declaran estáticamente, lo cual permite dejar vacíos el constructor y el destructor de la clase. La inicialización de todos los objetos, a su vez, se realizará en el método Init.
bool CNeuronChimera::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window_in, uint window_out, uint units_in, uint units_out, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_out * window_out, optimization_type, batch)) return false; SetActivationFunction(None);
En los parámetros del método obtendremos una serie de constantes que nos permitirán interpretar sin ambigüedades la arquitectura del objeto creado. Debemos tener en cuenta que la lista de parámetros se heredará al completo del método similar del objeto CNeuron2DSSMOCL descrito anteriormente, e indicará la arquitectura de uno de los 2D-SSM internos.
El algoritmo del método de inicialización comenzará, como es habitual, llamando al método homónimo de la clase padre. En este caso, se tratará de una capa básica completamente conectada.
Y luego, inicializaremos los objetos internos. Como ya hemos mencionado, utilizaremos 2 modelos bidimensionales de espacio de estados con distintos niveles de detalle. En la estructura del objeto, los modelos internos se representarán como un array caSSM. Y para inicializar los objetos del array especificado, organizaremos un ciclo.
int index = 0; for(int i = 0; i < 2; i++) { if(!caSSM[i].Init(0, index, OpenCL, window_in, (i + 1)*window_out, units_in, units_out, optimization, iBatch)) return false; index++; }
Para inicializar el primer modelo de espacio de estados, se utilizarán los parámetros recibidos de un programa externo. Y el segundo modelo obtendrá 2 veces la dimensionalidad del espacio de características de los resultados, lo que permitirá capturar dependencias más complejas. Y como ambos modelos funcionan con el mismo conjunto de datos de entrada, los parámetros clave de su configuración permanecerán inalterados, lo que garantizará la integridad y coherencia de la estructura.
A continuación, inicializaremos una capa de discretización adicional que creará una proyección de los resultados del segundo modelo en el subespacio del primer modelo. Se trata de una capa convolucional regular que reducirá el espacio de características a un tamaño determinado.
if(!cDiscretization.Init(0, index, OpenCL, 2 * window_out, 2 * window_out, window_out, units_out, 1, optimization, iBatch)) return false; cDiscretization.SetActivationFunction(None);
Para evitar la pérdida de datos, desactivaremos la función de activación de este objeto.
Tras inicializar los objetos de flujo de información para los dos modelos de espacio de estados, organizaremos los enlaces residuales. En esta fase, surge el problema de sumar tensores que pueden diferir en tamaño a lo largo de uno o varios ejes. Para resolver el problema, deberemos realizar una proyección preliminar de los datos de origen en un subespacio de resultados determinado. Para ello, crearemos un modelo interno de proyección de datos similar a los modelos de proyección contextual comentados anteriormente. Este planteamiento permitirá correlacionar correctamente las dimensionalidades de los datos, garantizando la estabilidad de la arquitectura y la precisión del procesamiento de la dependencia temporal.
En primer lugar, prepararemos un array dinámico para registrar los punteros a los objetos modelo y declararemos variables locales para el almacenamiento temporal de estos punteros.
//--- Residual cResidual.Clear(); cResidual.SetOpenCL(OpenCL); CNeuronConvOCL *conv = NULL; CNeuronTransposeOCL *transp = NULL;
Luego crearemos un objeto de transposición de datos, seguido de una capa convolucional de proyección de secuencias unitarias en una dimensionalidad determinada de la serie temporal.
transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, units_in, window_in, optimization, iBatch) || !cResidual.Add(transp)) { delete transp; return false; } index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, units_in, units_in, units_out, window_in, 1, optimization, iBatch) || !cResidual.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Este enfoque nos permitirá preservar las dependencias estructurales dentro de las secuencias unitarias individuales de las series temporales multivariantes analizadas.
Les seguirán otro bloque de objeto de transposición y una capa de convolución, que realizarán la proyección de los datos de origen a lo largo del eje de características.
index++; transp = new CNeuronTransposeOCL(); if(!transp || !transp.Init(0, index, OpenCL, window_in, units_out, optimization, iBatch) || !cResidual.Add(transp)) { delete transp; return false; } index++; conv = new CNeuronConvOCL(); if(!conv || !conv.Init(0, index, OpenCL, window_in, window_in, window_out, units_out, 1, optimization, iBatch) || !cResidual.Add(conv)) { delete conv; return false; } conv.SetActivationFunction(None);
Obsérvese que ninguna de las dos capas convolucionales utiliza funciones de activación, lo cual permite proyectar los datos de origen con una pérdida mínima de información.
A la salida del objeto, planeamos realizar la suma de los tres flujos de información. Y, como solemos hacer en estos casos, el gradiente de error se transmitirá íntegramente a través de todas las líneas troncales. Para eliminar operaciones innecesarias de copiado de datos, sincronizaremos los punteros a los búferes de gradiente de error. Sin embargo, cabe señalar que las capas convolucionales utilizadas para la proyección de datos pueden tener funciones de activación. Claro está, en este caso no las hemos usado y podríamos haber obviado esta función. Pero para construir una solución más universal, no haremos la vista gorda con esto. Por lo tanto, transferiremos el gradiente de error a las capas convolucionales solo después de corregir la derivada de la función de activación real.
if(!SetGradient(caSSM[0].getGradient(), true)) return false; //--- return true; }
Ahora todo lo que deberemos hacer es devolver el resultado lógico de las operaciones al programa que realiza la llamada y finalizar el método.
Una vez completado el método de inicialización, construiremos los algoritmos de pasada directa dentro del método feedForward.
bool CNeuronChimera::feedForward(CNeuronBaseOCL *NeuronOCL) { for(uint i = 0; i < caSSM.Size(); i++) { if(!caSSM[i].FeedForward(NeuronOCL)) return false; }
El algoritmo de pasada directa es bastante sencillo. En los parámetros del método obtendremos el puntero al objeto de datos de origen, que pasaremos a los modelos internos de espacio de estados. Para ello, organizaremos un ciclo de 2D-SMM internos y llamaremos a sus métodos de pasada directa uno a uno.
Tras realizar todas las iteraciones del ciclo, proyectaremos los resultados obtenidos de forma comparable.
if(!cDiscretization.FeedForward(caSSM[1].AsObject())) return false;
A continuación, deberemos obtener una proyección de los datos de origen en el subespacio de resultados. Para ello, organizaremos un ciclo de iteración secuencial de objetos del modelo de proyección interna con llamada de los métodos de pasada directa de los objetos correspondientes.
CNeuronBaseOCL *inp = NeuronOCL; CNeuronBaseOCL *current = NULL; for(int i = 0; i < cResidual.Total(); i++) { current = cResidual[i]; if(!current || !current.FeedForward(inp)) return false; inp = current; }
Por último, solo nos quedará sumar los resultados de los tres flujos de información y, a continuación, normalizar los datos.
if(!SumAndNormilize(caSSM[0].getOutput(), cDiscretization.getOutput(), Output, 1, false, 0, 0, 0, 1) || !SumAndNormilize(Output, current.getOutput(), Output, cDiscretization.GetFilters(), true, 0, 0, 0, 1)) return false; //--- return true; }
Después, devolveremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.
Sin embargo, la aparente simplicidad del algoritmo del método de pasada directa oculta el uso de tres flujos de información, lo que impone algunas dificultades en la organización del proceso de distribución del gradiente de error. Organizaremos este proceso dentro del método calcInputGradients.
bool CNeuronChimera::calcInputGradients(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
En los parámetros del método obtendremos el puntero al objeto de los datos de origen, al que esta vez tendremos que pasar el gradiente de error según su influencia en el resultado final del modelo. En el cuerpo del método comprobaremos directamente la relevancia del puntero obtenido. Ya hemos comentado anteriormente por qué esto es necesario.
A continuación, ajustaremos el gradiente de error obtenido de los objetos posteriores a la función de activación de la capa de proyección de los resultados del segundo 2D-SSM, y lo reduciremos al nivel del modelo especificado.
if(!DeActivation(cDiscretization.getOutput(), cDiscretization.getGradient(), Gradient, cDiscretization.Activation())) return false; if(!caSSM[1].calcHiddenGradients(cDiscretization.AsObject())) return false;
Del mismo modo, ajustaremos el gradiente de error mediante la derivada de la función de activación de la última capa del modelo de proyección interna de los datos de origen y lo haremos descender secuencialmente sobre los objetos de la secuencia especificada.
CNeuronBaseOCL *residual = cResidual[-1]; if(!residual) return false; if(!DeActivation(residual.getOutput(), residual.getGradient(), Gradient, residual.Activation())) return false; for(int i = cResidual.Total() - 2; i >= 0; i--) { residual = cResidual[i]; if(!residual || !residual.calcHiddenGradients(cResidual[i + 1])) return false; }
Llegados a este punto, deberemos transmitir el gradiente de error a la capa de datos de origen en las tres líneas troncales. Y recordamos que durante la transferencia del gradiente de error se borrarán los datos previamente almacenados. Afortunadamente, ya hemos aprendido a combatir dicho problema. Primero transferiremos el gradiente de error desde el modelo de espacio de estados.
if(!NeuronOCL.calcHiddenGradients(caSSM[0].AsObject())) return false;
A continuación, sustituiremos el puntero al búfer de datos y transferimos el gradiente de error en la segunda línea troncal, tras lo cual sumaremos los datos de los dos flujos de información.
CBufferFloat *temp = NeuronOCL.getGradient(); if(!NeuronOCL.SetGradient(residual.getPrevOutput(), false) || !NeuronOCL.calcHiddenGradients(caSSM[1].AsObject()) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1)) return false;
Del mismo modo, añadiremos los valores del tercer flujo de información.
if(!NeuronOCL.calcHiddenGradients((CObject*)residual) || !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1) || !NeuronOCL.SetGradient(temp, false) ) return false; //--- return true; }
Y solo después de sumar los datos de todos los flujos de información, retornaremos los punteros a los objetos al estado inicial.
Después retornaremos el resultado lógico de las operaciones al programa que realiza la llamada y finalizaremos el método.
Con esto concluirá la revisión de los algoritmos para implementar el framework Chimera utilizando las herramientas MQL5. Encontrará el código completo de los objetos presentados y todos sus métodos en el archivo adjunto.
Arquitectura del modelo
Anteriormente hemos presentado una descripción detallada de la implementación de los enfoques propuestos por los autores del framework Quimera mediante MQL5. Sin embargo, los autores del framework recomiendan usar una arquitectura consistente en una pila de objetos similares con la organización de no-linealidades entre ellos. La aplicación de una arquitectura de este tipo contribuirá a crear un sistema flexible y adaptable que pueda responder dinámicamente a los cambios del entorno operativo. Por lo tanto, nos centraremos un poco en la arquitectura de los modelos entrenados.
Digamos de entrada que, como parte de este experimento, implementaremos los enfoques de Quimera en un framework de aprendizaje multitarea.
La arquitectura de los modelos entrenados se representará en el método CreateDescriptions.
bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&probability) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; }
En los parámetros del método obtendremos los punteros a 2 arrays dinámicos, en los que guardaremos la descripción de la arquitectura de los modelos. En el cuerpo del método, verificaremos la relevancia de los punteros obtenidos y, de ser necesario, crearemos nuevas instancias de objetos.
En primer lugar, describiremos la arquitectura del Actor, que incluye un bloque codificador del estado del entorno. Tenemos previsto introducir los datos de origen de la descripción del entorno en la entrada del modelo. Los trasladaremos a una capa totalmente conectada de tamaño suficiente.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
A continuación vendrá la capa de normalización por lotes, en la que se realizará el procesamiento inicial de los datos de origen y se les dará una forma comparable.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Los datos procesados se introducirán en el primer módulo Chimera, a cuya salida esperamos obtener una secuencia temporal multivariante de 64 elementos con 16 características cada uno.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronChimera; //--- Window { int temp[] = {BarDescr, 16}; //In, Out if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } //--- Units { int temp[] = {HistoryBars, 64}; //In, Out if(ArrayCopy(descr.units, temp) < int(temp.Size())) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
A continuación, una capa de convolución con activación SoftPlus creará la no-linealidad.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = 64; descr.window = 16; descr.step = 16; descr.window_out = 16; descr.activation = SoftPlus; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Añadimos 2 módulos Quimera más de la misma forma con la adición de no-linealidad entre ellos.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronChimera; //--- Window { int temp[] = {16, 32}; //In, Out if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } //--- Units { int temp[] = {64, 32}; //In, Out if(ArrayCopy(descr.units, temp) < int(temp.Size())) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = 32; descr.window = 32; descr.step = 32; descr.window_out = 16; descr.activation = SoftPlus; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronChimera; //--- Window { int temp[] = {16, 32}; //In, Out if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } //--- Units { int temp[] = {32, 16}; //In, Out if(ArrayCopy(descr.units, temp) < int(temp.Size())) return false; } descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Al hacerlo, de forma similar al framework ResNeXt, reduciremos la longitud de la secuencia y aumentaremos proporcionalmente el espacio de características.
Le seguirá una cabeza de decisión formada por tres capas consecutivas totalmente conectadas.
//--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 512; descr.batch = 1e4; descr.activation = TANH; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 256; descr.activation = TANH; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = NActions; descr.activation = SoftPlus; descr.batch = 1e4; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Normalizaremos sus resultados utilizando la capa de normalización de datos por lotes.
//--- layer 10 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Al igual que en los modelos anteriores, añadiremos un módulo de gestión de riesgos a la salida del Actor.
//--- layer 11 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronMacroHFTvsRiskManager; //--- Windows { int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description if(ArrayCopy(descr.windows, temp) < int(temp.Size())) return false; } descr.count = 10; descr.window_out = 16; descr.step = 4; // Heads descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 12 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = NActions / 3; descr.window = 3; descr.step = 3; descr.window_out = 3; descr.activation = SIGMOID; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
El modelo para estimar las probabilidades de la dirección del próximo movimiento de los precios se mantendrá casi sin cambios desde el artículo anterior. Solo hemos realizado modificaciones puntuales en las funciones de activación de la capa oculta utilizadas. Por lo tanto, no nos detendremos en su descripción. En el archivo adjunto encontrará una descripción completa de la arquitectura de los modelos. También se presenta el código completo de los programas de entrenamiento y prueba del modelo, que hemos trasladado de trabajos anteriores sin modificaciones.
Simulación
Tras completar la aplicación de nuestra propia visión de los planteamientos propuestos por los autores del framework Quimera, pasaremos a la fase final de nuestro trabajo: entrenar y probar los modelos con datos históricos reales.
Para entrenar los modelos, utilizaremos la muestra de entrenamiento recogida durante el entrenamiento de los modelos anteriormente comentados. Permítame recordarle que las trayectorias se recogen en los datos históricos del par de divisas EURUSD para todo el año 2024, y el marco temporal M1. Los parámetros de todos los indicadores analizados se han usado por defecto. En el enlace encontrará una descripción detallada del proceso de preparación de las muestras de entrenamiento.
Los modelos entrenados se han probado en el simulador de estrategias de MetaTrader 5 con los datos históricos de enero de 2025, manteniendo los demás parámetros de entrenamiento del modelo. Ahora le presentaremos los resultados de las pruebas.
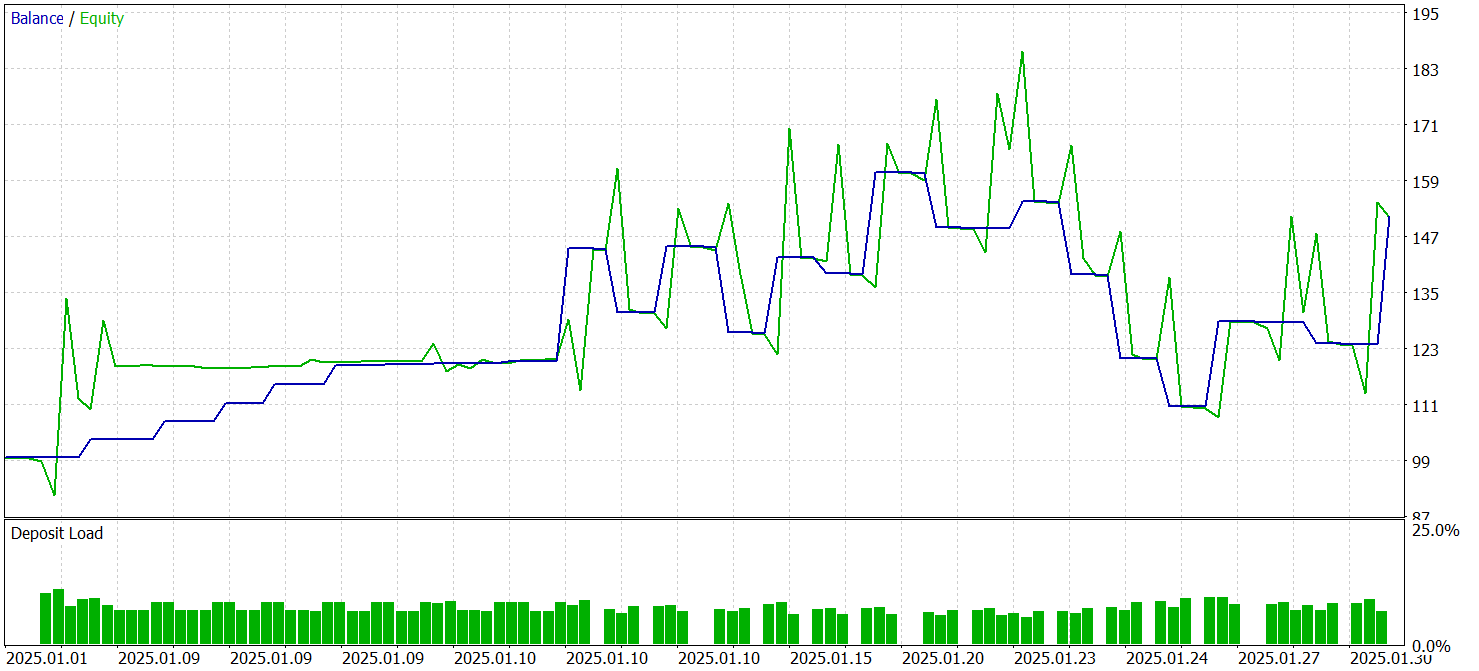
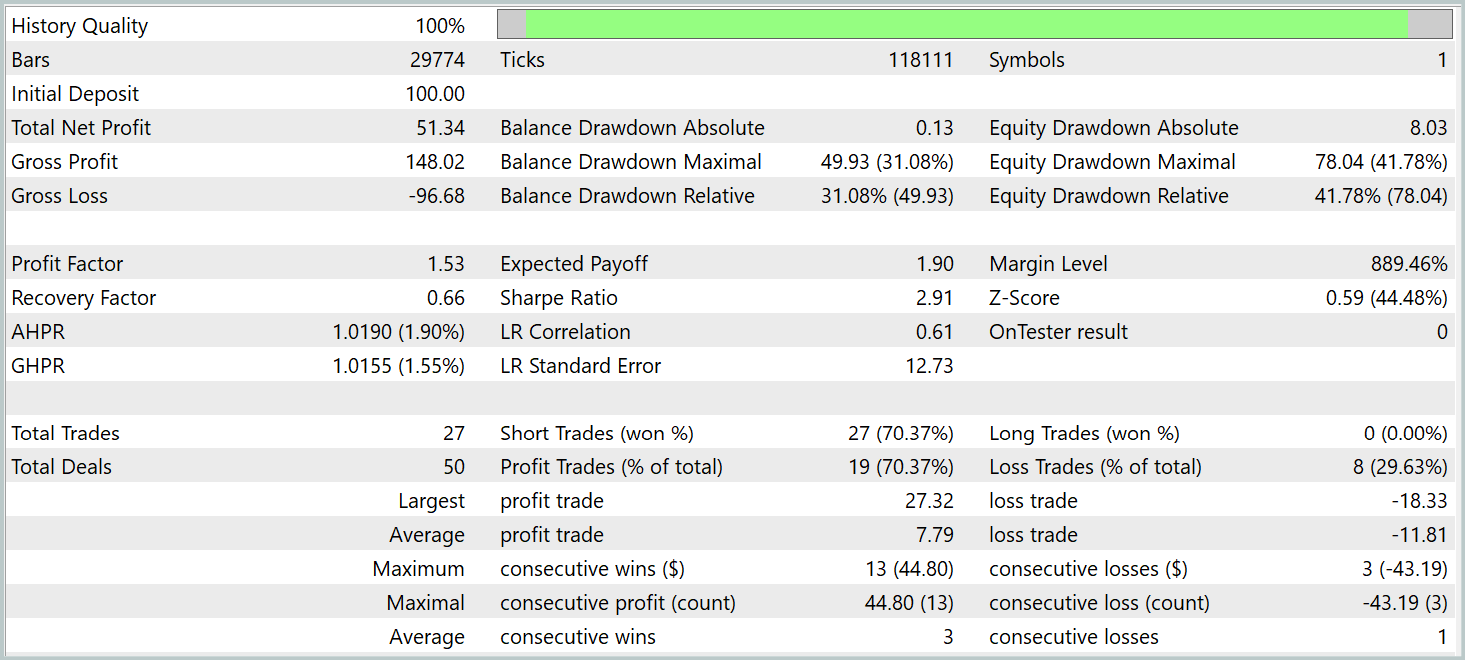
Según los resultados de las pruebas, el modelo ha sido capaz de obtener beneficios. En este caso, más del 70% de las operaciones se han cerrado con beneficios. El indicador del factor de beneficio se ha fijado en 1,53.
Pero debemos considerar un par de puntos. Hemos probado los modelos en el marco temporal M1. Al mismo tiempo, el modelo solo ha realizado 27 transacciones, lo que resulta bastante poco para una negociación de alta frecuencia en el marco temporal mínimo. Además, el modelo solo ha abierto posiciones cortas, lo que también plantea dudas.
El tiempo de mantenimiento de la posición es igualmente cuestionable. La posición más rápida, si se me permite decirlo, se ha cerrado casi una hora después de la apertura. Y el tiempo medio de mantenimiento de la posición es de más de 14 horas. Y esto, probando el modelo en el marco temporal M1.
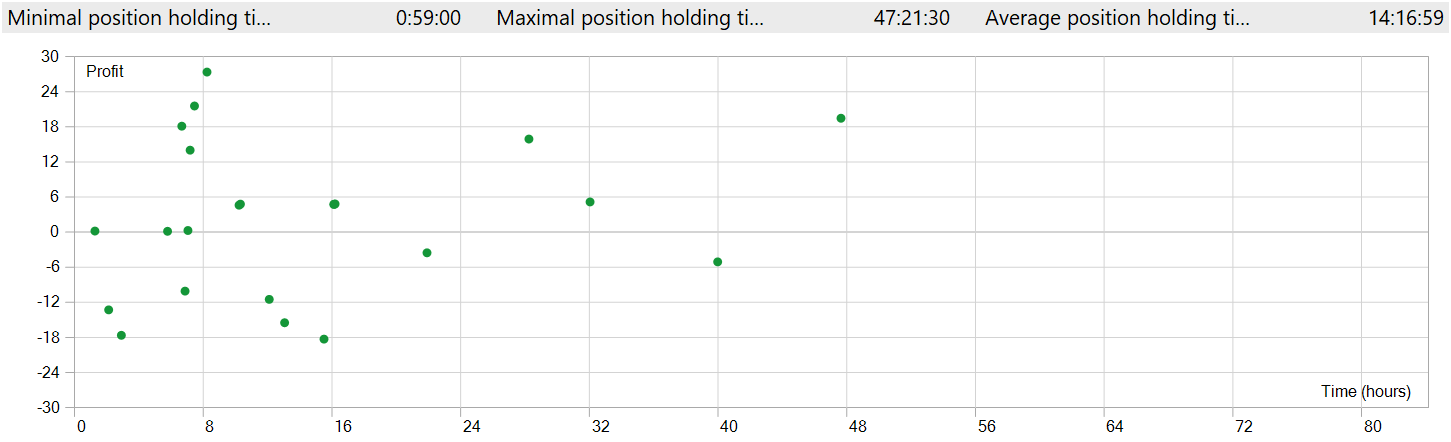
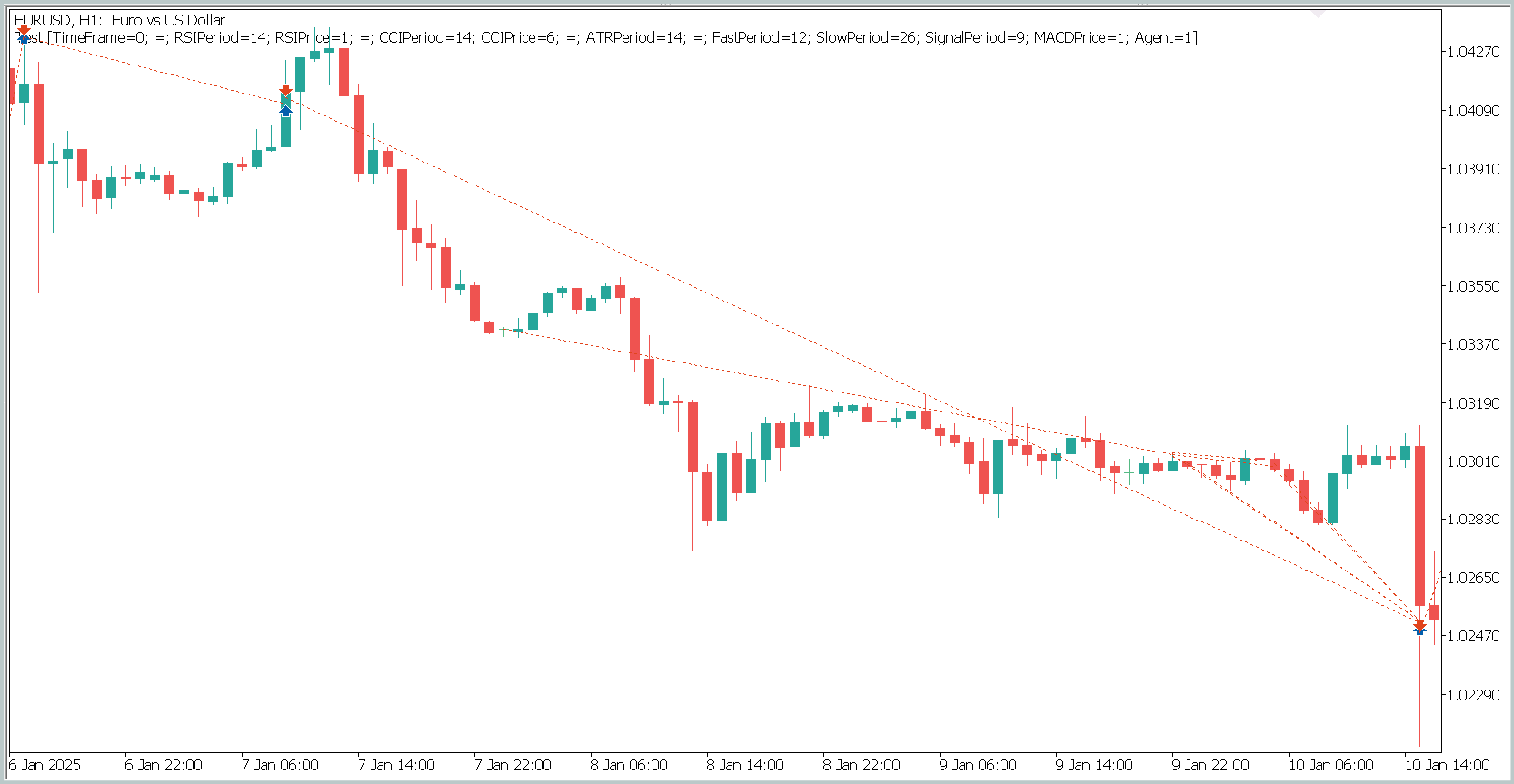
Para mostrar la apertura y el cierre de una posición en una ventana del gráfico, ha sido necesario aumentar el marco temporal. Desde este punto de vista, vemos un comercio claro en la dirección de la tendencia global. Esto, por supuesto, no encaja en la comprensión de la negociación de alta frecuencia en el marco temporal M1. Sin embargo, está claro que el modelo que hemos aplicado es capaz de captar las tendencias a largo plazo ignorando las fluctuaciones a corto plazo.
Conclusión
Hoy nos hemos familiarizado con el framework Chimera, basado en un modelo bidimensional de espacio de estados. Este enfoque introduce técnicas innovadoras para la modelización multivariante de series temporales, lo que permite considerar relaciones complejas tanto en contextos temporales como de características.
En la parte práctica de nuestro trabajo, hemos implementado nuestra propia visión de los enfoques propuestos usando MQL5. El modelo que hemos construido se ha entrenado y probado con datos históricos reales. Los resultados de la prueba han sido un tanto sorprendentes. Durante el periodo de prueba, el modelo ha sido capaz de generar beneficios. Solo que, contrariamente a lo esperado, hemos observado una negociación en la dirección de la tendencia global con una posición larga, aunque la prueba del modelo se ha realizado en el marco temporal M1.
Enlaces
- Chimera: Effectively Modeling Multivariate Time Series with 2-Dimensional State Space Models
- Otros artículos de la serie
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor experto para recopilar ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento de modelos |
| 4 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 5 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema y la arquitectura del modelo |
| 6 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código del programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/17241
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Cómo funciones centenarias pueden actualizar nuestras estrategias comerciales
Cómo funciones centenarias pueden actualizar nuestras estrategias comerciales
 Simulación de mercado (Parte 08): Sockets (II)
Simulación de mercado (Parte 08): Sockets (II)
 Redefiniendo los indicadores de MQL5 y MetaTrader 5
Redefiniendo los indicadores de MQL5 y MetaTrader 5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso