Нейросети в трейдинге: Двухмерные модели пространства связей (Окончание)

MetaTrader 5 — Торговые системы | 18 февраля 2025, 13:55

511

Dmitriy Gizlyk

Введение

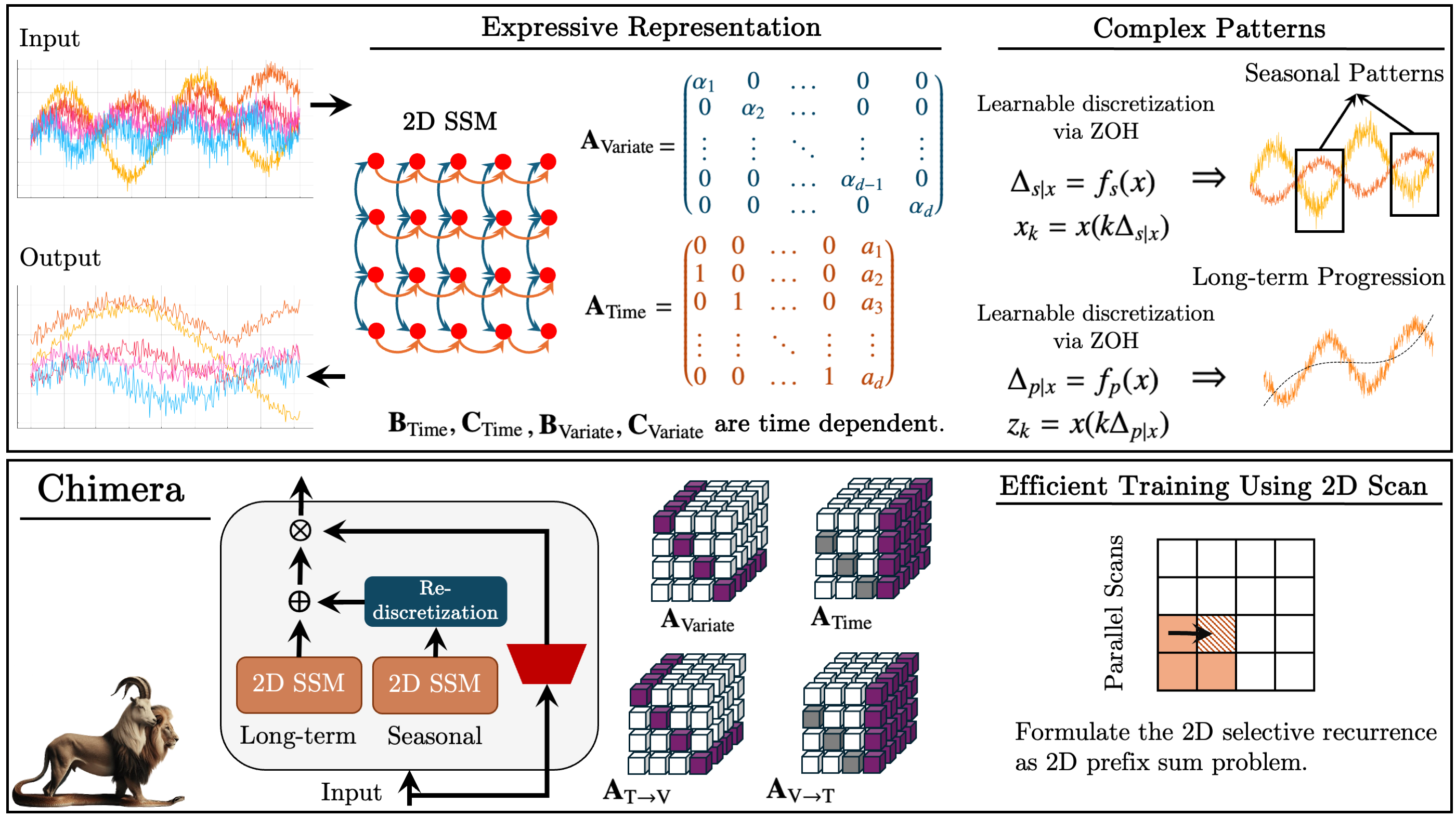
В предыдущей статье мы познакомились с фреймворком Chimera — это двухмерная модель пространства состояний (2D-SSM), основанная на линейных преобразованиях вдоль осей времени и анализируемых переменных. Он объединяет модели пространства состояний по двум осям и механизмы их взаимодействия.

Модели пространства состояний (SSM) широко применяются в анализе временных рядов, так как позволяют моделировать сложные зависимости. Однако, традиционные SSM учитывают только временную ось, что ограничивает их применение в решении многомерных задач. Chimera расширяет эту концепцию, включая ось признаков в процесс моделирования.

Фреймворк работает с дискретизированной формой 2D-SSM, вводя шаги дискретизации Δ1 и Δ2. Первый параметр влияет на временные зависимости, а второй — на межпеременные связи. Меньшие значения Δ1 помогают учитывать долгосрочные тренды, тогда как большие акцентируют сезонные изменения. Аналогично, дискретизация по переменным регулирует степень детализации анализа.

Для корректного восстановления процессов авторы фреймворка вводят структурные ограничения на матрицы A1, A2 (временные зависимости) и A3, A4 (межпеременные связи). Причинно-следственная природа 2D-SSM ограничивает передачу информации по оси признаков, поэтому в Chimera используются два модуля для анализа взаимозависимостей с предшествующими и последующими признаками анализируемой окружающей среды.

Гибкость фреймворка Chimera позволяет использование как независимых от исходных данных параметров Bi, Ci и Δi, так и в качестве функции исходных данных. Использование контекстно-зависимых параметров делает модель более адаптивной к условиям сложных многомерных систем.

Фреймворк использует стек 2D-SSM с нелинейными преобразованиями между слоями, приближаясь к архитектуре глубоких моделей. Он позволяет разложить временные ряды на трендовые и сезонные компоненты, обеспечивая точный анализ закономерностей.

Ниже представлена авторская визуализация фреймворка Chimera.

Авторская визуализация фреймворка Chimera

В практической части статьи была разработана архитектура реализации собственного видения предложенных подходов средствами MQL5 и начата работа по их имплементации. Рассмотрены изменения, внесенные в OpenCL-программу. Разработана структура объекта 2D-SSM и представлен метод его инициализации. Сегодня мы продолжаем построение алгоритмов внедрения предложенных подходов в собственные модели.

Объект 2D-SSM

Предыдущую статью мы завершили на рассмотрении метода инициализации объекта CNeuron2DSSMOCL, в котором намерены реализовать функционал построения и обучения 2D-SSM. Структура данного объекта представлена ниже.

class CNeuron2DSSMOCL  :  public CNeuronBaseOCL
  {
protected:
   uint                 iWindowOut;
   uint                 iUnitsOut;
   CNeuronBaseOCL       cHiddenStates;
   CLayer               cProjectionX_Time;
   CLayer               cProjectionX_Variable;
   CNeuronConvOCL       cA;
   CNeuronConvOCL       cB_Time;
   CNeuronConvOCL       cB_Variable;
   CNeuronConvOCL       cC_Time;
   CNeuronConvOCL       cC_Variable;
   CNeuronConvOCL       cDelta_Time;
   CNeuronConvOCL       cDelta_Variable;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      feedForwardSSM2D(void);
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradientsSSM2D(void);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuron2DSSMOCL(void)  {};
                    ~CNeuron2DSSMOCL(void)  {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window_in, uint window_out, uint units_in, uint units_out, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuron2DSSMOCL; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      Clear(void) override;
  };

Продолжаем начатую работу. И сегодня первым мы рассмотрим алгоритм построения метода прямого прохода данного объекта feedForward.

bool CNeuron2DSSMOCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL *inp = NeuronOCL;
   CNeuronBaseOCL *x_time = NULL;
   CNeuronBaseOCL *x_var = NULL;

В параметрах метода получаем указатель на объект исходных данных, который сразу сохраняем в локальной переменной. Тут же мы объявим еще две локальные переменные, для хранения указателей на объекты проекции исходных данных в контексте времени и признаков. На данном этапе нам еще предстоит сформировать эти проекции.

Напомню, что для формирования указанных проекций, в методе инициализации были созданы две внутренние последовательности, указатели на объекты которых сохранили в динамических массивах cProjectionX_Time и cProjectionX_Variable. Теперь мы можем воспользоваться ими для получения необходимых проекций.

Вначале генерируем проекцию в контексте времени. Указатель на объект исходных данных мы уже сохранили в локальной переменной. Далее, создаем цикл последовательного перебора объектов модели проекции в контексте времени.

//--- Projection Time
   int total = cProjectionX_Time.Total();
   for(int i = 0; i < total; i++)
     {
      x_time = cProjectionX_Time.At(i);
      if(!x_time ||
         !x_time.FeedForward(inp))
         return false;
      inp = x_time;
     }

В теле цикла мы сначала получаем указатель на очередной объект последовательности. Проверяем актуальность полученного указателя. И после успешного прохождения точки контроля вызываем метод прямого прохода объекта, передав ему указатель на объект исходных данных.

Затем сохраняем указатель на текущий объект в локальную переменную исходных данных и переходим к следующей итерации цикла.

После завершения всех итераций цикла, в локальной переменной проекции исходных данных в контексте времени будет записан указатель на последний объект соответствующей последовательности. В буфере данного объекта и будет необходимая нам проекция.

Аналогичным образом получаем проекцию исходных данных в контексте признаков.

//--- Projection Variable
   inp = NeuronOCL;
   total = cProjectionX_Variable.Total();
   for(int i = 0; i < total; i++)
     {
      x_var = cProjectionX_Variable.At(i);
      if(!x_var ||
         !x_var.FeedForward(inp))
         return false;
      inp = x_var;
     }

Для получения четырех проекций двух скрытых состояний, нам достаточно вызвать один метод прямого прохода объекта соответствующих проекций. В его параметрах мы передаем указатель на объект, содержащий конкатенированный тензор скрытых состояний.

   if(!cA.FeedForward(cHiddenStates.AsObject()))
      return false;

Остальные параметры нашей 2D-SSM являются контекстно-зависимыми. Поэтому далее мы сгенерируем параметры модели на основе соответствующих проекций исходных данных. С этой целью последовательно перебираем объекты генерации параметров модели и вызываем их методы прямого прохода с передачей указателей на объекты соответствующих проекций исходных данных.

if(!cB_Time.FeedForward(x_time) ||
   !cB_Variable.FeedForward(x_var))
   return false;
if(!cC_Time.FeedForward(x_time) ||
   !cC_Variable.FeedForward(x_var))
   return false;
if(!cDelta_Time.FeedForward(x_time) ||
   !cDelta_Variable.FeedForward(x_var))
   return false;

На этом этапе мы завершили работу по подготовке параметров двухмерной модели пространства состояний. И нам остается сгенерировать новые значения скрытого состояния и результаты работы модели. Как вы знаете, в прошлой статье указанные процессы были вынесены в отдельный кернел, который мы создали на стороне OpenCL-программы. И теперь достаточно вызвать метод-обертку данного кернела. Но прежде стоит обратить внимание, что генерация нового скрытого состояния удалит текущие значения, которые нам потребуются для выполнения операций обратного прохода. Поэтому мы сначала осуществим подмену указателей на объекты буферов данных, а затем вызываем метод-обертку feedForwardSSM2D.

   if(!cHiddenStates.SwapOutputs())
      return false;
//---
   return feedForwardSSM2D();
  }

Следующим этапом нашей работы будет построение алгоритмов обратного прохода нашего объекта. Здесь я предлагаю посмотреть на метод распределения градиента ошибки calcInputGradients. В параметрах данного метода мы получаем указатель на тот же объект исходных данных, только на этот раз нам предстоит передать в него градиент ошибки в соответствии с влиянием исходных данных на общий результат работы модели.

bool CNeuron2DSSMOCL::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

Передача данных возможна только при наличии валидного указателя на объект. Поэтому первым этапом алгоритма является проверка полученного указателя, что позволяет предотвратить обращение к освобождённым или неинициализированным ресурсам. Такой подход критичен для обеспечения стабильности вычислительного процесса и предотвращения сбоев при обработке данных.

После успешного прохождения контрольного блока, начинаются операции распределения градиента ошибки. Данный процесс осуществляется от уровня результатов работы объекта в направлении исходных данных, следуя механизму обратного распространения ошибки, в соответствии с потоком данных прямого прохода, но в обратном порядке.

Метод прямого прохода мы завершили вызовом метода-обёртки кернела генерации скрытых состояний и вычисления результатов работы 2D-SSM. Соответственно, процесс распространения градиента ошибки начинается вызовом аналогичного метода-обёртки, но для кернела, выполняющего распределение погрешностей. Внутри данного кернела градиент корректно распределяется между элементами 2D-SSM, в соответствии с их вкладом в формирование результатов работы модели.

if(!calcInputGradientsSSM2D())
   return false;

Важно учитывать, что на данном этапе осуществляется исключительно распределение градиентных значений между структурными компонентами модели. Однако, непосредственная корректировка значений на производные функций активации объектов не выполняется в рамках указанного кернела. Поэтому, перед распространением градиента ошибки через внутренние объекты модели, необходимо проверить наличие функций активации в этих объектах. При необходимости, следует осуществить соответствующую коррекцию значений, чтобы учесть влияние нелинейных преобразований на передаваемые градиенты. Это гарантирует, что каждый параметр модели будет обновлён с учётом реального вклада в формирование выходного сигнала.

//--- Deactivation
   CNeuronBaseOCL *x_time = cProjectionX_Time[-1];
   CNeuronBaseOCL *x_var = cProjectionX_Variable[-1];
   if(!x_time || !x_var)
      return false;
   if(x_time.Activation() != None)
      if(!DeActivation(x_time.getOutput(), x_time.getGradient(), x_time.getGradient(), x_time.Activation()))
         return false;
   if(x_var.Activation() != None)
      if(!DeActivation(x_var.getOutput(), x_var.getGradient(), x_var.getGradient(), x_var.Activation()))
         return false;
   if(cB_Time.Activation() != None)
      if(!DeActivation(cB_Time.getOutput(), cB_Time.getGradient(), cB_Time.getGradient(), cB_Time.Activation()))
         return false;
   if(cB_Variable.Activation() != None)
      if(!DeActivation(cB_Variable.getOutput(), cB_Variable.getGradient(), cB_Variable.getGradient(),
                                                                           cB_Variable.Activation()))
         return false;
   if(cC_Time.Activation() != None)
      if(!DeActivation(cC_Time.getOutput(), cC_Time.getGradient(), cC_Time.getGradient(), cC_Time.Activation()))
         return false;
   if(cC_Variable.Activation() != None)
      if(!DeActivation(cC_Variable.getOutput(), cC_Variable.getGradient(), cC_Variable.getGradient(), 
                                                                           cC_Variable.Activation()))
         return false;
   if(cDelta_Time.Activation() != None)
      if(!DeActivation(cDelta_Time.getOutput(), cDelta_Time.getGradient(), cDelta_Time.getGradient(), 
                                                                           cDelta_Time.Activation()))
         return false;
   if(cDelta_Variable.Activation() != None)
      if(!DeActivation(cDelta_Variable.getOutput(), cDelta_Variable.getGradient(), cDelta_Variable.getGradient(), 
                                                                                   cDelta_Variable.Activation()))
         return false;
   if(cA.Activation() != None)
      if(!DeActivation(cA.getOutput(), cA.getGradient(), cA.getGradient(), cA.Activation()))
         return false;

Далее мы переходим к процессу распределения градиентов ошибки через внутренние объекты нашей 2D-SSM. И прежде всего, нам необходимо распределить значения градиента через объекты генерации контекстно-зависимых параметров модели. Напомню, что они формируются на основании соответствующих проекций исходных данных.

И тут следует обратить внимание, что объекты проекций исходных данных участвуют в основном процессе формирования результатов работы модели и уже получили значения градиентов ошибки при выполнении предшествующих операций. С целью сохранения ранее полученных значений, мы осуществляем подмену указателей на соответствующие буферы данных.

//--- Gradient to projections X
   CBufferFloat *grad_x_time = x_time.getGradient();
   CBufferFloat *grad_x_var = x_var.getGradient();
   if(!x_time.SetGradient(x_time.getPrevOutput(), false) ||
      !x_var.SetGradient(x_var.getPrevOutput(), false))
      return false;

Далее мы последовательно спускаем градиент ошибки через объекты формирования контекстно-зависимых параметров и на каждом этапе суммируем полученные значения с ранее накопленными.

//--- B -> X
   if(!x_time.calcHiddenGradients(cB_Time.AsObject()) ||
      !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1))
      return false;
   if(!x_var.calcHiddenGradients(cB_Variable.AsObject()) ||
      !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1))
      return false;

//--- C -> X
   if(!x_time.calcHiddenGradients(cC_Time.AsObject()) ||
      !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1))
      return false;
   if(!x_var.calcHiddenGradients(cC_Variable.AsObject()) ||
      !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1))
      return false;

//--- Delta -> X
   if(!x_time.calcHiddenGradients(cDelta_Time.AsObject()) ||
      !SumAndNormilize(grad_x_time, x_time.getGradient(), grad_x_time, iWindowOut, false, 0, 0, 0, 1))
      return false;
   if(!x_var.calcHiddenGradients(cDelta_Variable.AsObject()) ||
      !SumAndNormilize(grad_x_var, x_var.getGradient(), grad_x_var, iWindowOut, false, 0, 0, 0, 1))
      return false;

А после успешной передачи градиентов ошибки от всех информационных потоков, возвращаем указатели на объекты в исходное состояние.

if(!x_time.SetGradient(grad_x_time, false) ||
   !x_var.SetGradient(grad_x_var, false))
   return false;

На данном этапе мы получили значения градиентов ошибки на уровне проекций исходных данных в обоих контекстах. Далее нам предстоит провести градиенты через соответствующие внутренние модели проекций. Для этого создаем циклы обратного перебора объектов соответствующих последовательностей.

//--- Projection Variable
   int total = cProjectionX_Variable.Total() - 2;
   for(int i = total; i >= 0; i--)
     {
      x_var = cProjectionX_Variable[i];
      if(!x_var ||
         !x_var.calcHiddenGradients(cProjectionX_Variable[i + 1]))
         return false;
     }

//--- Projection Time
   total = cProjectionX_Time.Total() - 2;
   for(int i = total; i >= 0; i--)
     {
      x_time = cProjectionX_Time[i];
      if(!x_time ||
         !x_time.calcHiddenGradients(cProjectionX_Time[i + 1]))
         return false;
     }

Обратите внимание, что, проводя градиент ошибки через внутренние модели контекстных проекций, мы остановились на первом слое каждой из последовательностей. Здесь надо сказать, что обе наши последовательности проекций генерируют свои значения на основании исходных данных, получаемых в параметрах метода от внешней программы. И теперь нам предстоит передать градиент ошибки в объект исходных данных от обоих внутренних моделей проекции.

Как обычно в подобных случаях, мы сначала передаем градиент ошибки по одному информационному потоку.

//--- Projections -> inputs
   if(!NeuronOCL.calcHiddenGradients(x_var.AsObject()))
      return false;

А затем осуществляем подмену указателей на объекты буферов градиентов и проводим погрешности через второй информационный поток.

   grad_x_time = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(x_time.getPrevOutput(), false) ||
      !NeuronOCL.calcHiddenGradients(x_time.AsObject()) ||
      !SumAndNormilize(grad_x_time, NeuronOCL.getGradient(), grad_x_time, 1, false, 0, 0, 0, 1) ||
      !NeuronOCL.SetGradient(grad_x_time, false))
      return false;
//---
   return true;
  }

В завершении, суммируем значения обоих информационных потоков и возвращаем указатели на буферы данных в исходное состояние.

Следует обратить внимание, что мы не проводим градиент ошибки до уровня объекта скрытого состояния, так как данный объект используется лишь для хранения данных и не содержит обучаемых параметров.

Теперь, когда мы распределили значения градиента ошибки между всеми внутренними объектами, остается вернуть логический результат выполнения операций вызывающей программе и завершить работу метода.

На этом мы завершаем рассмотрение алгоритмов построения методов объекта CNeuron2DSSMOCL. С полным кодом данного объекта и всех его методов вы можете самостоятельно ознакомиться во вложении.

Модуль Chimera

Следующим этапом нашей работы является построение модуля Chimera. Авторы фреймворка предлагают использование двух параллельных 2D-SSM с различными уровнями дискретизации и остаточными связями. Объединение двух независимых моделей пространства состояний, работающих с разным уровнем дискретизации, способствует более глубокому анализу зависимостей и позволяет строить высокоэффективные прогнозные модели, адаптированные к многомасштабным данным.

Применение 2D-SSM с разными параметрами дискретизации позволяет проводить дифференцированный анализ временных рядов. Высокочастотная модель выявляет долгосрочные закономерности, тогда как низкочастотная модель ориентирована на распознавание сезонных циклов. Такое разделение улучшает точность прогнозов, поскольку каждая из моделей адаптируется к своей части данных, минимизируя потери информации и ошибки, вызванные избыточной агрегацией временных признаков. Добавление модуля дискретизации позволяет привести результаты работы двух моделей в сопоставимый вид.

Дополнительным преимуществом модуля Chimera является использование остаточных связей, которые обеспечивают эффективную передачу информации между уровнями модели. Они позволяют сохранять и передавать градиент в ходе обратного распространения ошибки, предотвращая его затухание. Это особенно важно при обучении глубоких моделей, где градиентный спуск часто сталкивается с проблемами численной нестабильности. Модель остаётся более устойчивой к потере информации при передаче данных между слоями, а процесс обучения становится более стабильным, даже при работе с длинными временными рядами.

Предложенный механизм мы реализуем в рамках объекта CNeuronChimera, структура которого представлена ниже.

class CNeuronChimera    :  public CNeuronBaseOCL
  {
protected:
   CNeuron2DSSMOCL    caSSM[2];
   CNeuronConvOCL     cDiscretization;
   CLayer             cResidual;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronChimera(void) {};
                    ~CNeuronChimera(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window_in, uint window_out, uint units_in, uint units_out,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronChimera; }
   //---
   virtual bool      Save(int const file_handle);
   virtual bool      Load(int const file_handle);
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau);
   virtual void      SetOpenCL(COpenCLMy *obj);
   //---
   virtual bool      Clear(void) override;
  };

В представленной структуре мы видим уже привычный набор переопределяемых методов и несколько внутренних объектов, о функционале которых не сложно догадаться по их наименованию.

Все внутренние объекты объявлены статично, что позволяет оставить пустыми конструктор и деструктор класса. А инициализация всех объектов осуществляется в методе Init.

bool CNeuronChimera::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window_in, uint window_out, uint units_in, uint units_out,
                          ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_out * window_out, optimization_type, batch))
      return false;
   SetActivationFunction(None);

В параметрах метода получаем ряд констант, позволяющих однозначно интерпретировать архитектуру создаваемого объекта. Следует отметить, что список параметров полностью перенесен из аналогичного метода описанного выше объекта CNeuron2DSSMOCL и указывает на архитектуру одной из внутренних 2D-SSM.

Алгоритм метода инициализации, как обычно, начинается с вызова одноименного метода родительского класса. В данном случае это базовый полносвязный слой.

А затем, переходим к инициализации внутренних объектов. Как было сказано выше, мы используем 2 двухмерных модели пространства состояний с различным уровнем детализации. В структуре объекта внутренние модели представлены в виде массива caSSM. И для инициализации объектов указанного массива, мы организуем цикл.

int index = 0;
for(int i = 0; i < 2; i++)
  {
   if(!caSSM[i].Init(0, index, OpenCL, window_in, (i + 1)*window_out, units_in, units_out, optimization, iBatch))
      return false;
   index++;
  }

Для инициализации первой модель пространства состояний используются параметры, полученные от внешней программы. А вторая модель получает увеличенную в 2 раза размерность признакового пространства результатов, что позволяет захватывать более сложные зависимости. А поскольку обе модели оперируют единым набором исходных данных, ключевые параметры их конфигурации остаются неизменными, обеспечивая целостность и согласованность структуры.

Далее инициализируем слой дополнительной дискретизации, который создает проекцию результатов второй модели в подпространстве первой. Это обычный сверточный слой, который понижает пространство признаков до заданного размера.

   if(!cDiscretization.Init(0, index, OpenCL, 2 * window_out, 2 * window_out, window_out, units_out, 1,
                                                                                 optimization, iBatch))
      return false;
   cDiscretization.SetActivationFunction(None);

С целью исключения потери данных, мы отключаем функцию активации для данного объекта.

После инициализации объектов информационных потоков для двух моделей пространства состояний, переходим к организации остаточных связей. На данном этапе возникает проблема суммирования тензоров, которые могут отличаться размерами по одной или нескольким осям. Для решения указанной проблемы, требуется предварительная проекция исходных данных в заданное подпространство результатов. С этой целью создается внутренняя модель проекции данных, аналогичная моделям контекстных проекций, рассмотренным ранее. Такой подход позволяет корректно согласовать размерности данных, обеспечивая стабильность архитектуры и точность обработки временных зависимостей.

Вначале мы подготовим динамический массив для записи указателей на объекты модели и объявим локальные переменные временного хранения этих указателей.

//--- Residual
   cResidual.Clear();
   cResidual.SetOpenCL(OpenCL);
   CNeuronConvOCL *conv = NULL;
   CNeuronTransposeOCL *transp = NULL;

Создаем объект транспонирования данных, за которым следует сверточный слой проекции унитарных последовательностей в заданную размерность временного ряда.

   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, units_in, window_in, optimization, iBatch) ||
      !cResidual.Add(transp))
     {
      delete transp;
      return false;
     }
   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, units_in, units_in, units_out, window_in, 1, optimization, iBatch) ||
      !cResidual.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

Такой подход позволяет нам сохранить структурные зависимости внутри отдельных унитарных последовательностей анализируемого многомерного временного ряда.

За ними следует еще один блок из объекта транспонирования и сверточного слоя, которые осуществляют проекцию исходных данных по оси признаков.

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, window_in, units_out, optimization, iBatch) ||
      !cResidual.Add(transp))
     {
      delete transp;
      return false;
     }
   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window_in, window_in, window_out, units_out, 1, optimization, iBatch) ||
      !cResidual.Add(conv))
     {
      delete conv;
      return false;
     }
   conv.SetActivationFunction(None);

Обратите внимание, что оба сверточных слоя не используют функции активации, что позволяет осуществить проекцию исходных данных с минимальной потерей информации.

На выходе объекта мы планируем осуществить суммирование трех информационных потоков. И, как мы обычно поступаем в таких случаях, градиент ошибки будем передавать в полном объеме по всем магистралям. С целью исключения излишних операций копирования данных, мы осуществим синхронизацию указателей на буферы градиентов ошибки. Однако, стоит обратить внимание, что сверточные слои, используемые для проекции данных, могут иметь функции активации. Конечно, в данном случае мы не использовали их и могли бы пренебречь этой особенностью. Но с целью построения более универсального решения, мы все же не будем закрывать на это глаза. Поэтому, в сверточные слои будем передавать градиент ошибки, только после корректировки на производную актуальной функции активации.

   if(!SetGradient(caSSM[0].getGradient(), true))
      return false;
//---
   return true;
  }

Теперь нам остается лишь вернуть логический результат выполнения операций вызывающей программе и завершить работу метода.

После завершения работы над методом инициализации, мы переходим к построению алгоритмов прямого прохода в рамках метода feedForward.

bool CNeuronChimera::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   for(uint i = 0; i < caSSM.Size(); i++)
     {
      if(!caSSM[i].FeedForward(NeuronOCL))
         return false;
     }

Алгоритм прямого прохода довольно прост. В параметрах метода получаем указатель на объект исходных данных, который передаем во внутренние модели пространства состояний. Для этого организуем цикл перебора внутренних 2D-SMM и поочередно будем вызывать их методы прямого прохода.

После выполнения всех итераций цикла, осуществляем проекцию полученных результатов в сопоставимый вид.

   if(!cDiscretization.FeedForward(caSSM[1].AsObject()))
      return false;

Далее нам необходимо получить проекцию исходных данных в подпространство результатов. Для этого, организуем цикл последовательного перебора объектов внутренней модели проекции с вызовом методов прямого прохода соответствующих объектов.

   CNeuronBaseOCL *inp = NeuronOCL;
   CNeuronBaseOCL *current = NULL;
   for(int i = 0; i < cResidual.Total(); i++)
     {
      current = cResidual[i];
      if(!current ||
         !current.FeedForward(inp))
         return false;
      inp = current;
     }

И в завершении, нам остается сложить результаты трех информационных потоков с последующей нормализацией данных.

   if(!SumAndNormilize(caSSM[0].getOutput(), cDiscretization.getOutput(), Output, 1, false, 0, 0, 0, 1) ||
      !SumAndNormilize(Output, current.getOutput(), Output, cDiscretization.GetFilters(), true, 0, 0, 0, 1))
      return false;
//---
   return true;
  }

После чего, возвращаем логический результат выполнения операций вызывающей программе и завершаем работу метода.

Однако, за кажущейся простотой алгоритма метода прямого прохода скрывается использование трех информационных потоков, что накладывает некоторые сложности на организацию процесса распределения градиента ошибки. Данный процесс мы организуем в рамках метода calcInputGradients.

bool CNeuronChimera::calcInputGradients(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;

В параметрах метода получаем указатель на объект исходных данных, в который на это раз нам предстоит передать градиент ошибки, в соответствии с его влиянием на итоговый результат работы модели. И в теле метода мы сразу проверяем актуальность полученного указателя. Необходимости осуществления такого контроля обсуждалась выше.

Далее мы корректируем градиент ошибки, полученный от последующих объектов, на функцию активации слоя проекции результатов второй 2D-SSM, и спускаем его до уровня указанной модели.

   if(!DeActivation(cDiscretization.getOutput(), cDiscretization.getGradient(), Gradient, cDiscretization.Activation()))
         return false;
   if(!caSSM[1].calcHiddenGradients(cDiscretization.AsObject()))
      return false;

Аналогичным образом корректируем градиент ошибки на производную функции активации последнего слоя внутренней модели проекции исходных данных и последовательно спускаем его по объектам указанной последовательности.

   CNeuronBaseOCL *residual = cResidual[-1];
   if(!residual)
      return false;
   if(!DeActivation(residual.getOutput(), residual.getGradient(), Gradient, residual.Activation()))
         return false;
   for(int i = cResidual.Total() - 2; i >= 0; i--)
     {
      residual = cResidual[i];
      if(!residual ||
         !residual.calcHiddenGradients(cResidual[i + 1]))
         return false;
     }

На данном этапе мы подошли к шагу передачи градиента ошибки на уровень исходных данных по всем трем магистралям. И мы помним, что во время передачи градиента ошибки, удаляются ранее сохраненные данные. К счастью, мы уже научились бороться с указанной проблемой. Сначала передаем градиент ошибки от одной модели пространства состояний.

   if(!NeuronOCL.calcHiddenGradients(caSSM[0].AsObject()))
      return false;

Затем осуществляем подмену указателя на буфер данных и осуществляем передачу градиента ошибки по второй магистрали, с последующим суммирование данных двух информационных потоков.

   CBufferFloat *temp = NeuronOCL.getGradient();
   if(!NeuronOCL.SetGradient(residual.getPrevOutput(), false) ||
      !NeuronOCL.calcHiddenGradients(caSSM[1].AsObject()) ||
      !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1))
      return false;

Аналогичным образом добавляем значения третьего информационного потока.

   if(!NeuronOCL.calcHiddenGradients((CObject*)residual) ||
      !SumAndNormilize(temp, NeuronOCL.getGradient(), temp, 1, false, 0, 0, 0, 1) ||
      !NeuronOCL.SetGradient(temp, false)
     )
      return false;
//---
   return true;
  }

И только после суммирования данных всех информационных потоков, мы возвращаем указатели на объекты в исходное состояние.

Логический результат выполнения операций возвращаем вызывающей программе и завершаем работу метода.

На этом мы завершаем рассмотрение алгоритмов имплементации фреймворка Chimera средствами MQL5. С полным кодом представленных объектов и всех их методов вы можете ознакомиться во вложении.

Архитектура модели

Выше было представлено детальное описание реализации подходов, предложенных авторами фреймворка Chimera, средствами MQL5. Однако, авторы фреймворка рекомендуют использовать архитектуру, состоящую из стека подобных объектов с организацией нелинейностей между ними. Применение подобной архитектуры способствует созданию гибкой и адаптивной системы, способной динамически реагировать на изменения в условиях эксплуатации. Поэтому мы немного остановимся на архитектуре обучаемых моделей.

Сразу скажем, что в рамках данного эксперимента мы имплементировали подходы Chimera в фреймворк многозадачного обучения.

Архитектура обучаемых моделей представлена в методе CreateDescriptions.

bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&probability)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!probability)
     {
      probability = new CArrayObj();
      if(!probability)
         return false;
     }

В параметрах метода получаем указатели на 2 динамических массива, в которые нам предстоит сохранить описание архитектуры моделей. В теле метода мы проверяем актуальность полученных указателей и, при необходимости, создаем новые экземпляры объектов.

Вначале мы опишем архитектуру Актера, который включает и блок энкодера состояния окружающей среды. На вход модели мы планируем подавать необработанные исходные данные описания состояния окружающей среды. Их мы перенесем в полносвязный слой достаточного размера.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

За ним следует слой пакетной нормализации, в котором осуществляется первичная обработка исходных данных и приведение их в сопоставимый вид.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Обработанные данные поступают в первый модуль Chimera, на выходе которого мы ожидаем получить многомерную временную последовательность из 64 элементов по 16 признаков в каждом.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronChimera;
//--- Window
     {
      int temp[] = {BarDescr, 16}; //In, Out
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
//--- Units
     {
      int temp[] = {HistoryBars, 64}; //In, Out
      if(ArrayCopy(descr.units, temp) < int(temp.Size()))
         return false;
     }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

За ним следует сверточный слой с функцией активации SoftPlus для создания нелинейности.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = 64;
   descr.window = 16;
   descr.step = 16;
   descr.window_out = 16;
   descr.activation = SoftPlus;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Аналогичным образом добавляем еще 2 модуля Chimera с добавлением нелинейности между ними.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronChimera;
//--- Window
     {
      int temp[] = {16, 32}; //In, Out
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
//--- Units
     {
      int temp[] = {64, 32}; //In, Out
      if(ArrayCopy(descr.units, temp) < int(temp.Size()))
         return false;
     }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = 32;
   descr.window = 32;
   descr.step = 32;
   descr.window_out = 16;
   descr.activation = SoftPlus;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronChimera;
//--- Window
     {
      int temp[] = {16, 32}; //In, Out
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
//--- Units
     {
      int temp[] = {32, 16}; //In, Out
      if(ArrayCopy(descr.units, temp) < int(temp.Size()))
         return false;
     }
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

При этом, по аналогии с фреймворком ResNeXt, мы уменьшаем длину последовательности и пропорционально увеличиваем пространство признаков.

Далее следует голова принятия решений из трех последовательных полносвязных слоев.

//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 512;
   descr.batch = 1e4;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = 256;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions;
   descr.activation = SoftPlus;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Результаты их работы нормализуем с помощью слоя пакетной нормализации данных.

//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Как и в ранее рассмотренных моделях, на выходе Актера добавляем модуль риск менеджмента.

//--- layer 11
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMacroHFTvsRiskManager;
//--- Windows
     {
      int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
   descr.count = 10;
   descr.window_out = 16;
   descr.step = 4;                              // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 12
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = NActions / 3;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 3;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Модель оценки вероятностей направления предстоящего ценового движения перенесена из предыдущей статьи практически без изменений. Внесены лишь точечные правки в части используемых функций активации скрытых слоев. Поэтому, позвольте не останавливаться на её описании. А полное описание архитектуры моделей вы найдете во вложении. Там же представлен полный код программ обучения и тестирования моделей, которые перенесены из предыдущей работы без изменений.

Тестирование

После завершения реализации собственного видения подходов, предложенных авторами фреймворка Chimera, мы переходим к заключительному этапу нашей работы — обучению и тестированию моделей на реальных исторических данных.

Для обучения моделей мы использовали обучающую выборку, собранную в процессе обучения ранее рассмотренных моделей. Напомню, что траектории собраны на исторических данных валютной пары EURUSD за весь 2024 год, таймфрейм M1. Параметры всех анализируемых индикаторов используются по умолчанию. С подробным описанием процесса подготовки обучающей выборки можно ознакомиться по ссылке.

Тестирование обученных моделей проводилось в тестере стратегий MetaTrader 5 на исторических данных Января 2025 года с сохранением прочих параметров обучения модели. Результаты тестирования представлены ниже.

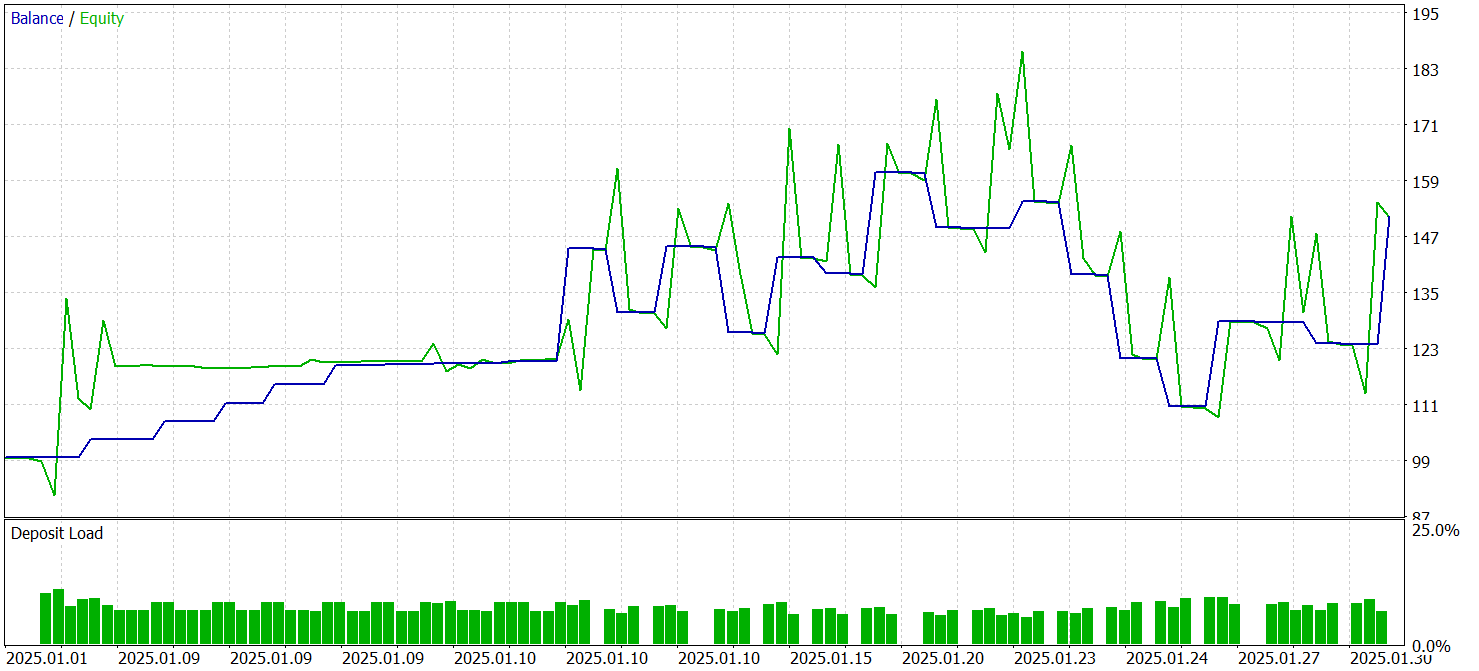
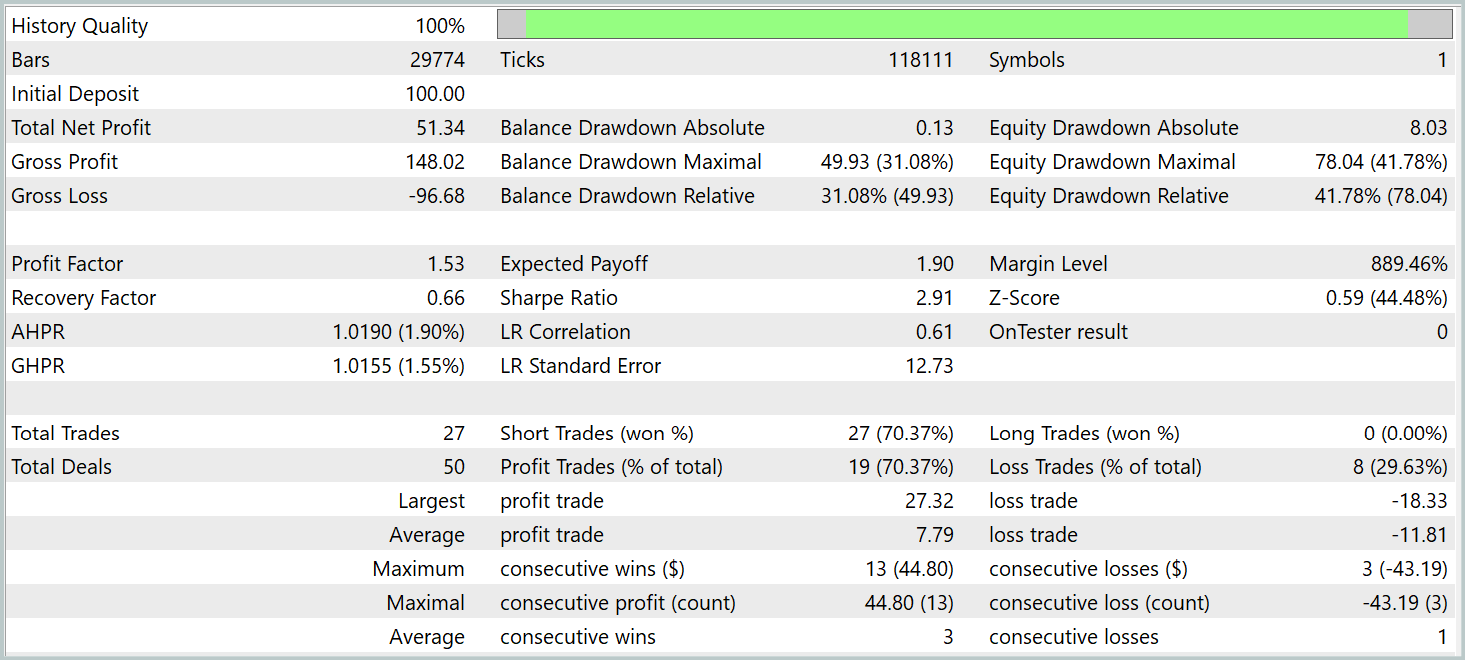
Результаты тестирования модели Chimera

По результатам тестирования модель смогла получить прибыль. При этом более 70% сделок были закрыты с прибылью. Показатель профит-фактора зафиксирован на уровне 1.53.

Но следует обратить внимание на пару моментов. Мы проводили тестирование моделей на таймфрейме M1. При этом модель совершила только 27 сделок, что довольно мало для высокочастотной торговли на минимальном таймфрейме. Более того, модель открывала только короткие позиции, что так же вызывает вопросы.

Время удержания позиции так же вызывает вопросы. Самая быстрая позиция, если можно так сказать, была закрыта почти через час после открытия. А среднее время удержания позиции составляет более 14 часов. И это — при тестировании модели на таймфрейме M1.

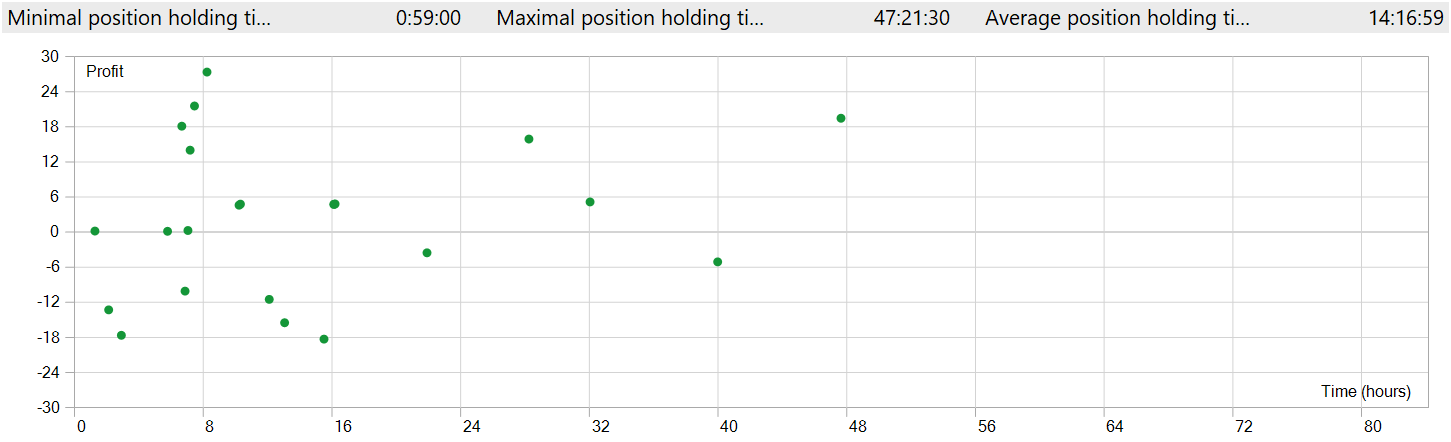
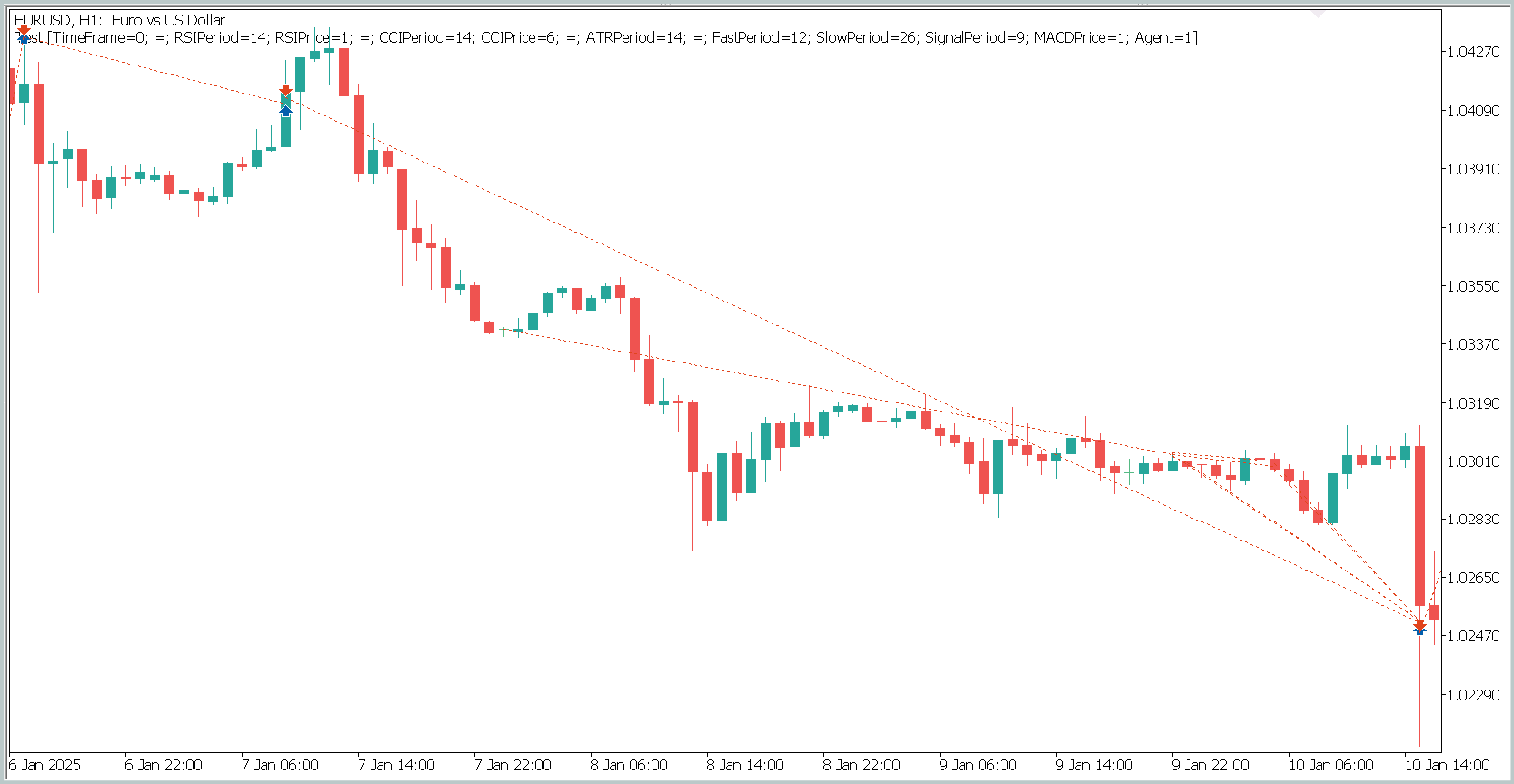
Результаты тестирования модели Chimera

Чтобы отобразить в одном окне графика открытие и закрытие позиции потребовалось увеличить таймфрейм. В таким виде мы видим явную торговлю в направлении глобального тренда. Это, конечно, не укладывается в понимание высокочастотной торговли на таймфрейме M1. Однако, очевидно, что реализованная нами модель способна захватывать долгосрочные тренды, игнорируя краткосрочные колебания.

Заключение

Мы познакомились с фреймворком Chimera, основанном на двухмерной модели пространства состояний. Этот подход внедряет инновационные методики для моделирования многомерных временных рядов, позволяя учитывать сложные взаимосвязи как в контексте времени, так и признаков.

В практической части нашей работы было реализовано собственное видение предложенных подходов средствами MQL5. Построенная нами модель была обучена и протестирована на реальных исторических данных. Результаты тестирования оказались несколько неожиданными. За период тестирования модель смогла сгенерировать прибыль. Только вопреки ожиданиям, мы увидели торговлю в направлении глобального тренда с длительным удержанием позиции, хотя тестирование модели осуществлялось на таймфрейме M1.

Ссылки

Программы, используемые в статье

#	Имя	Тип	Описание
1	Research.mq5	Советник	Советник сбора примеров
2	ResearchRealORL.mq5	Советник	Советник сбора примеров методом Real-ORL
3	Study.mq5	Советник	Советник обучения моделей
4	Test.mq5	Советник	Советник для тестирования модели
5	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
6	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
7	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы

Прикрепленные файлы |

Загрузить ZIP

MQL5.zip (2458.9 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Построение модели для ограничения диапазона сигналов по тренду (Часть 8): Разработка советника (I)

В этой статье мы разработаем наш первый советник на MQL5 на основе индикатора, который мы создали в предыдущей статье. Мы рассмотрим все функции, необходимые для автоматизации процесса, включая управление рисками. Это позволит перейти от ручного выполнения сделок к автоматизированным системам.

От начального до среднего уровня: Массивы и строки (II)

В этой статье я покажу, что хотя мы всё еще находимся на очень базовой стадии программирования, мы уже можем реализовать несколько интересных приложений. В данном случае мы создадим довольно простой генератор паролей. Таким образом мы сможем применить некоторые концепции, которые объяснялись до этого. Кроме того, мы рассмотрим, как можно разработать решения для некоторых конкретных проблем.

Разработка системы репликации (Часть 68): Настройка времени (I)

Сегодня мы продолжим работу над тем, чтобы заставить указатель мыши сообщать нам об оставшемся времени бара в периоды низкой ликвидности. Хотя на первый взгляд кажется, что всё просто, на самом деле эта задача гораздо сложнее. Это связано с некоторыми препятствиями, которые нам придется преодолеть. Поэтому важно, чтобы вы хорошо усвоили материал из первой части данной серии, чтобы понять следующие части.

Фибоначчи на Форекс (Часть I): Проверяем отношения цены и времени

Как рынок ходит по отношениям, основанным на числах Фибоначчи? Эта последовательность, где каждое следующее число равно сумме двух предыдущих (1, 1, 2, 3, 5, 8, 13, 21...), не только описывает рост популяции кроликов. Рассмотрим гипотезу Пифагора о том, что все в мире подчиняется определенным соотношениям чисел...