您应当知道的 MQL5 向导技术（第 45 部分）：蒙特卡洛强化学习

概述

本文通过研究另一种算法（即蒙特卡洛），继续我们对强化学习的研究。该算法非常相似，事实上可以说包括 Q-学习 和 SARSA ，既可开启政策，亦可关闭政策。不过，它的与众不同之处在于对局次的强调。这些只是我们在本文中讲述的一种批量处理强化学习周期更新的方式，这样 Q-映射 的 Q-值的更新频率就会降低。

使用蒙特卡洛算法，Q-值仅在局次完成后才会更新。一个局次是一次批量循环。至于本文，我们把输入参数 “m_episodes_size” 赋值给到循环次数，并且它是可优化或可调整的。蒙特卡洛之所以对市场波动非常稳健，因为它能更好地模拟广泛的可能市场场景，令交易者能判定不同策略在各种条件下的表现。这种可变性有助于交易者理解潜在的权衡、风险、和回报，令他们能够制定更明智的决策。

有一种论调，这种优势源于其“长期绩效洞察力”，这与倾向于专注短期成果的传统方法形成鲜明对比。这意味着蒙特卡洛模拟要执行的更新不会太频繁，因为它们在一局中只发生一次，这就避免了市场噪音，而 Q-学习 和 SARSA 必然会遇到市场噪音，在于它们执行更新更频繁。评估一段时间内的累积回报，来评估交易策略的长期表现，这便是蒙特卡洛努力达成的目标。通过分析其中的多个轮次，交易者能够深入洞察其策略的整体盈利能力和可持续性。

蒙特卡洛算法基于单个轮次中多个周期的“状态-动作”对的平均回报来计算“动作-估值”。这令交易者更好地基于历史表现评估哪些动作（例如，买入或卖出）最有可能产生有利的成果。Q-值的更新源自这些 Q-值具有的奖励分量，判定如下：

其中：

• R t+1 , R t+2 ,…,R T 是时间 t 之后每一步获得的奖励。
• γ /gamma 是折扣系数 (0 ≤ γ ≤ 1)，它按照未来奖励的“折扣”程度（即价值低于即时奖励）来设置。
• T 代表轮次结束时的时间步长（终结状态或以周期为单位的轮次大小）。

考虑这些总体奖励，暗指由上面所示 Q-值更新，往往会令所提到的蒙特卡洛更具可适性。这种固有的可适性，令交易者能够基于不断变化的市场条件调整策略。这种可适性在金融市场中至关重要，因为趋势能够迅速变化，过去的表现或许并不总能预测未来结果。在上一篇涵盖 SARSA 的强化学习文章中，我们将强化学习当作一个独立的模型，即经过训练来预测价格动作，它不像传统的其它机器学习模型那样只能协助训练，我们将其视为监督学习和无监督学习之外的第三种训练形式。我们在本文中遵循类似的方式。

因此，策略的可适性，在蒙特卡洛下，将在许多方面取决于 Q-映射和状态的选择。在上一篇文章中所见，由于强化学习算法也是智能交易系统的主要预测模型，通过自定义信号类，我们用过三种跨短期和长期横向范围的环境状态来创建包含 9 个选项的网格/矩阵。这些捕获的状态只是简单地看涨、横盘、和看跌，而且相对简单/粗糙。然而，它有被打造成更加复杂、及对市场更敏感的潜力，不仅要增加其整体维度，还要为其增加更多参考因素。当它与蒙特卡洛结伴时，可适性就会强化。

回顾交易中的强化学习（RL）

强化学习（RL）旨在动态环境中运行，譬如金融市场，其中它基于当前状态（这些状态由市场价格、或指标等定义）采取动作（例如买入、抛售、持有），不断与“周围环境”互动。由代理人采取的每一个动作都会影响环境状态，从而导致新的观察、和潜在的奖励。

交易者可为其 Q-映射采用的附加状态集示例，可以包括基于技术指标的状态。这些可以包括移动平均线，如其短期均线大于长期均线，则为看涨状态，而若短期均线低于长期均线，则意味着看跌状态，均衡意味着中性状态。

由于我们已将短期和长期前景合并到一个数轴上，这意味着我们现在有机会引入另一个数轴，其可涵盖除了均线指标读数之外的不同量值。另一个可用的指标读数是相对强弱指数（RSI）。有了它，我们就能考虑超买状态（RSI > 70）是潜在的卖出信号，而超卖状态（RSI < 30）可能是买入信号，以及无信号时的过渡状态。

或者，在基于指标的状态下，我们能看看布林带，其价格接近或高于上轨可能是看跌状态，而价格处于或低于下轨可能是看涨状态，而第三个中性状态则暗示任何位置。

除了技术指标状态外，市场波动还可作为环境状态矩阵的替代轴呈现。据此，衡量将基于价格标准差或 ATR 等指标，一个就可示意高波动性、低波动性、和温和三种可能的状态；可以添加更多的等级，以便令算法能对市场更加敏感。这种状态设置（或数轴）将有助于指导代理人进行积极交易、亦或保守交易。对于股票也可以考虑基于交易量的状态，配以类似的等级。

除了我们在过去文章中用过的价格走势看跌和看涨趋势之外，我们也正在考虑它还可充当的状态，更具体的价格走势形态，像是突破支撑位/阻力位。再者，它可能适用于看涨和看跌信号的头肩形态，任何其它拉扯形态。在最近的价格动作中识别出这样的类形态，将令代理人能够预测延续或逆转。

Q-映射状态的另一个可能数轴或许是基于时间的状态。回想一下，该数轴将与另一个数轴配对，例如上面的价格动作、或提到的技术指标，以便可以推断出在每个时间段内哪个价格动作更可靠。可能的时间状态可以包括市场开盘/收盘、交易时段，甚至周内的几天。基于情绪的状态是另一个轴，可以形成环境状态矩阵。衡量这些情绪将取决于特定指标的经济新闻日历读数，给出提供各种可能性。这些状态的梯度范围应从正面到中性再到负面，内部状态可根据感兴趣的粒度添加。协同情绪状态，特别是配以这些方法，能帮助代理人对影响市场的外部事件做出反应。

与此类似的替代方案是基于经济事件的状态。然而，还可以考虑与这两者不同的东西，如基于投资组合的状态。该类别在外汇之外非常适用，它呈现了许多潜在的数轴。首先是敞口级别，即根据股票与债券的相对敞口，为一个投资组合评级。梯度范围可分别从一端的 90-10，到另一端的 10-90。这样一条数轴可与时间、或任何其它不同但相关的指标配对，以便投资组合绩效（与代理人-奖励保持一致）可以指导 Q-值更新过程。

另一种基于投资组合的状态选项是风险等级。这可以参考每项投资的资本配置百分比，状态级别从少量 < 0.5%，到上限 10% 不等。再次，可以将其与另一个投资组合的特定量值进行比较或配对，并且涵盖一个不错的数据集进行优化，这应当能提供一个 Q-映射，指导何时采用什么样的风险等级。另一种替代可能是回撤状态，总之，这些基于投资组合的状态将令代理人参考更广泛的金融境况，而不仅是孤立的市场信号。

我还可提到宏观趋势状态，原理相似，但更重要的是，这里分享的例子并不详尽。环境状态的选择能定义一个人的策略使之走得更长久，并为他提供优势，这取决于它的独特性，以及不仅在测试上投入的努力，而且在交叉验证方面投入的努力。

除了环境状态之外，每个动作后的奖励信号，也能以指示其动作成功或失败的形式向代理人提供反馈。奖励可以根据损益（正如我们迄今为止一直在应用的那样）、风险调整后的回报、或任何其它相关的绩效量值来量化，其可引导代理人采取更有利的动作。回想一下，奖励是更新 Q-映射的 Q-值的关键组成部分。

大概强化学习更出名的是在做出预测时平衡探索与开发。纸面上，代理人经常采用探索策略来发现可能产生更好奖励的新动作，同时交替利用先前已被证明成功的已知动作。由输入参数 epsilon 控制的探索和开发的平衡，对于代理人避免局部最优，并随时间推移继续改进其决策至关重要。

尽管，通过反复试验，选择合适动作的 ε-贪婪方式包括随机选择；代理人从环境中的经验中学习，并再以往结果的基础上调整其动作选择政策。据每一次经验，代理人对哪些动作会带来积极奖励的理解，令其能够在类似的未来状况下做出更好的选择。

这种改进要归功于代理人的 Q-映射值或政策。该映射代表了一种将状态与动作配对的策略，并根据观察到的奖励持续更新每个状态的动作。该政策的改进是以强化学习算法为指导，旨在随时间推移最大化累积奖励。

这些是我们在前三篇关于强化学习文章中所研究的基本层面；然而，强化内仍有更多创新概念。其中之一是价值函数估算，代理人通常估算价值函数，它能预测给定状态、或“状态-动作”对的预期回报。通过近似价值函数，代理人能够估测不同动作的潜在长期收益，从而促进更佳决策。

时域信用分配是另一个概念，代理人将过去采取的行动与未来得到的奖励联系起来。这种纸面方式令代理人了解其先前的动作如何影响未来的结果，这可导致更佳规划、或先发设定某些政策，即覆盖默认的“动作-状态”配对。

另一个是自适应学习率，这是我们在过去这篇文章中处置多层感知器时研究的主题。在执行 Q-值更新时，这些也可作为初值参与。代理人能在基于“状态-动作”值的不确定性进行调整时运用它们，若代理人不确定时，启用更激进的更新，若信心慢慢之时，则启用更保守的更新。这种适应性能帮助代理人在不同的市场条件下有效地学习。

其它值得注意的与强化学习相关的思路包括：跨状态泛化，以便提高效率，及超越眼前奖励的长期策略发展。

蒙特卡洛算法

蒙特卡洛方法采用的学习方式与我们早期研究的强化学习算法不同，它从完整的经验局次中学习，等到一局结束才“学习”，但该期间获得的多个奖励积分按整体方式取得。因此，这需要多次缓冲奖励值，如此这般在局次完结时，所有过去的奖励值才可访问。我们利用 MQL5 实现这一点，在自定义信号类的 GetOutput 函数内，如下所示：

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalMC::GetOutput(Cql *QL, vector &Rewards)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      for(int i = m_episode_cycles - 1; i > 0; i--)
      {  Rewards[i] = Rewards[i - 1];
      }
      Rewards[0] = QL.GetReward(_reward_max, _reward_min, _reward_float);
      QL.transition_act = 1;
      if(Rewards[m_episode_cycles - 1] != -1.0)
      {  double _reward = Rewards[m_episode_cycles - 1];
         for(int i = m_episode_cycles - 2; i >= 0; i--)
         {  _reward += pow(QL.THIS.gamma, m_episode_cycles - 1 - i) * Rewards[i];
         }
         if(m_policy)
         {  QL.SetOnPolicy(_reward, _in_e);
         }
         else if(!m_policy)
         {  QL.SetOffPolicy(_reward, _in_e);
         }
      }
   }
}

对比之下，Q-学习使用时域差（TD）学习方法，即取的每个动作后（或每个周期之后）更新的估算值，使用后续状态动作值的引导。这类似于 SARSA，但此处是用从下一个状态采取的动作完成更新估值，提供了一种开启政策学习的方式。

蒙特卡洛更新机制基于在一局中跨多个周期据状态采取行动后观察到的平均回报。每个“状态-动作”对仅在局次完成后才会更新，如此反映真实的长期回报。因此，本次更新中所用奖励值是加权总和，如上分享的公式所示，以及上面 GetOutput 函数中的 MQL5 代码。

然而，Q-学习采用下一个状态（关闭政策）的最大未来奖励来更新当前状态的动作值，这可导致更积极的学习，在于它会参考一局内每个周期步骤的最可能成果。类似地，SARSA 会基于下一个状态（开启政策）中采取的实际动作来更新值，将代理人的当前政策合并到学习过程之中，这能导致比 Q-学习略多保守一些的更新，但仍比蒙特卡洛更激进。

蒙特卡洛，原则上，依靠在一局中经由多个循环对环境进行完整探索，去学习最优动作，从而在进行更新之前对“状态-动作”对进行彻底采样。这是通过一种 ε-贪婪的方式，我们在关于 Q-学习的讲述文章中引入了该方法，其中更新会受到代理人未采取动作的影响。

SARSA 在平衡勘探和开发的方式上也遵循 ε-贪婪，不过它会基于下一个状态实际采取的动作更新值，令其对代理人的当前政策和探索选择更敏感。蒙特卡洛与这两者的不同之处在于，除了在一局中只更新一次之外，它既可开启政策，亦可关闭政策。为此，我们据蒙特卡洛创建的自定义信号类有一个输入参数 m_on_policy，其是布尔值，顾名思义，它指导是否开启、或关闭政策状态。

该自定义信号类的接口如下所示：

//+------------------------------------------------------------------+
//| MCs CSignalMC.                                                   |
//| Purpose: MonteCarlo for Reinforcement-Learning.                  |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
class CSignalMC   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   int                           m_episode_cycles;    // Episode Size

public:
   void                          CSignalMC(void);
   void                          ~CSignalMC(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }
   void                          QL_EpisodeCycles(int value)
   {  m_episode_cycles = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   void              GetOutput(Cql *QL, vector &Rewards);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   vector            REWARDS_BUY, REWARDS_SELL;
};

蒙特卡洛的收敛速度往往较慢，在于它需要完整局次进行更新，这在局次较长、或奖励稀少的环境中或许不一定有效。这与 Q-学习算法形成鲜明对比，Q-学习算法因其引导性质，在大多数情况下收敛得更快，但必然不稳定，因为它可以在具有非平稳奖励、或高方差环境中振荡或发散。在某些情况下，SARSA 被吹捧成比 Q-学习更稳定，因为它在更新期间参考代理人的实际政策，这往往会出品更平滑的学习曲线。

当来到采样效率，蒙特卡洛的采样效率通常较低，因为它需要完整局次才能获取更新，这在具有较大“状态-动作”空间的环境中可能是一个主要缺陷。另一方面，Q-学习的采样效率更高，在于它每一步都会更新数值，从而允许基于即时反馈快速修正。事实上，有论调说它比 SARSA 更有效，因为后者或许需要比 Q-学习更多的样本，因为它对当前的政策和所用的探索正策很敏感。

蒙特卡洛非常适合可以明确定义局次的环境，长期回报往往比短期突增更重要，譬如交易模拟。对于价值、或长期“投资的“交易者”，显然会如此设置作为关键策略。Q-学习在具有清晰奖励结构、和明确状态转换的环境中非常有效，令其成为日内交易等任务的理想选择。而在学习需要密切反映代理人政策的状况下， SARSA 会受益，例如在动态、或部分可观察的环境中，其中适应性至关重要，例如波段交易。

在自定义信号类中实现蒙特卡洛

我们运用蒙特卡洛强化学习作为根模型和信号发生器来实现了自定义信号。实现这一点的主要步骤已在上面的类接口和 GetOutput 函数中分享。以下是做多条件和做空条件函数：

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalMC::LongCondition(void)
{  int result = 0;
   GetOutput(QL_BUY, REWARDS_BUY);
   if(QL_BUY.transition_act == 0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalMC::ShortCondition(void)
{  int result = 0;
   GetOutput(QL_SELL, REWARDS_SELL);
   if(QL_SELL.transition_act == 2)
   {  result = 100;//printf(__FUNCSIG__);
   }
   return(result);
}

该实现的完整源代码附在底部，有关在向导中用它来汇编智能系统的指南，可在这里和这里找到。马尔可夫决策过程是使用 Q-映射所固有的，无论如何，有一个输入参数提供了在执行 Q-值更新时使用马尔可夫加权的选项。此外，我们能够优化是否使用政策、ε 的大小，我们的参数指导我们探索与利用的程度，以及局次中的周期数量。我们依据 GBPUSD 货币对 2022 年 H1 时间帧运行优化。以下是我们的结果：

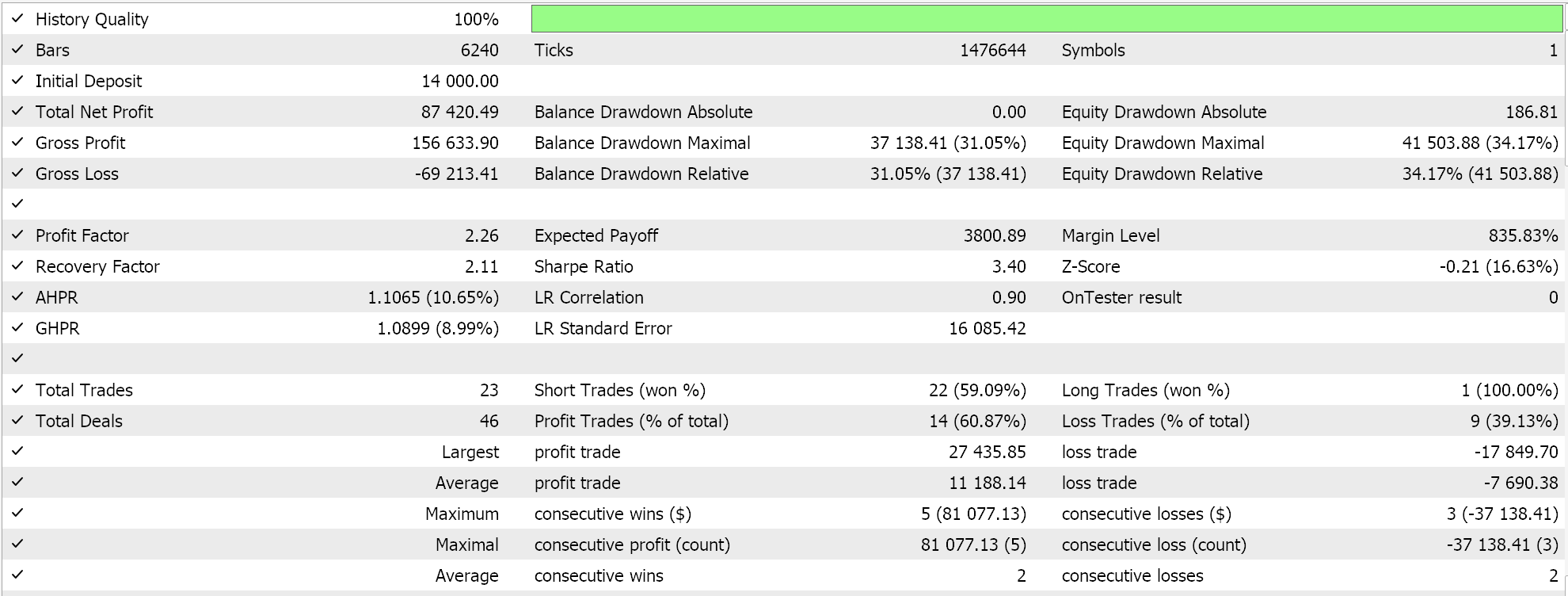
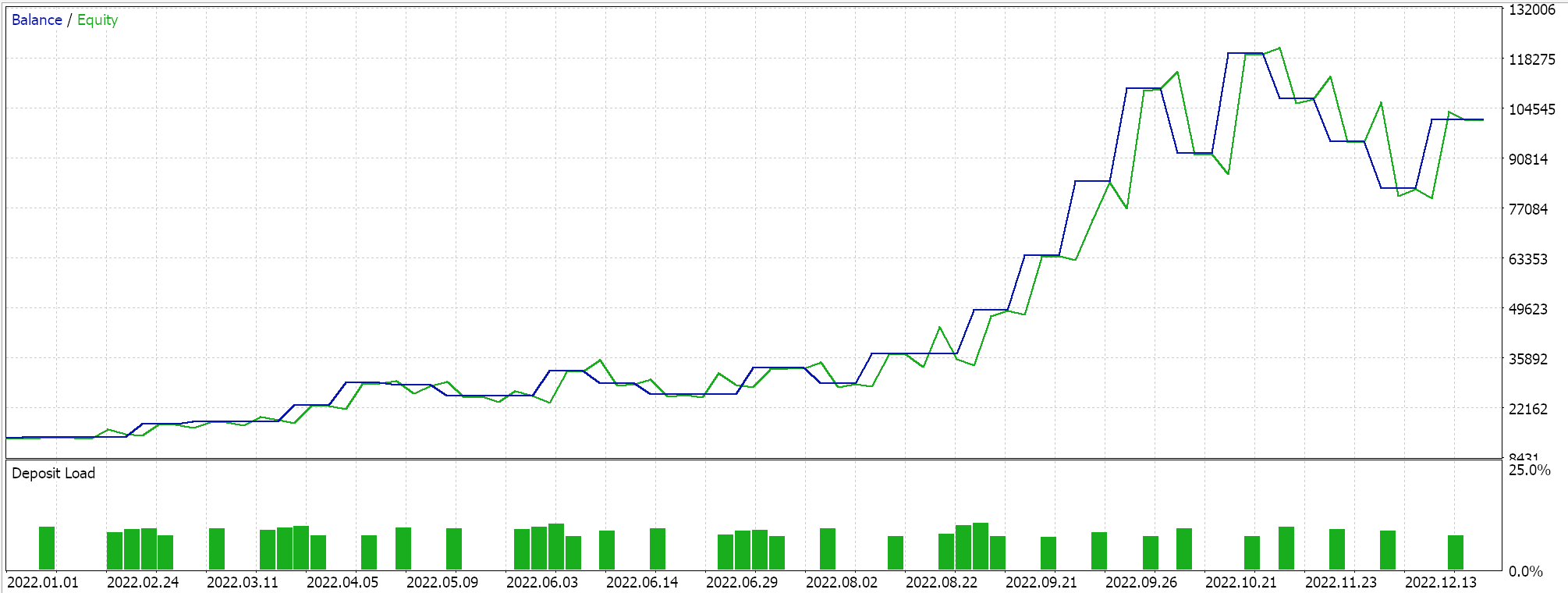
结论和其它注意事项

总之，我们研究了强化学习的蒙特卡洛算法，它从 Q-学习和 SARSA 中汲取了许多特征，这两种算法我们之前分别在这里和这里讲述过，并呈现了一种更加动态、且适应性更强的学习方式，它仍然专注于其环境的长期特征和属性。除了使用更多定制的环境矩阵外，如本文中列出的一些备选方案中强调的，还可以利用具有 3 个以上选项的替代动作量表。

在实现蒙特卡洛（MC）时，还有一些值得一提的其它注意事项。MC 计算更新奖励值的方式，在偏差和方差之间进行权衡。在一个局次里周期数较少的实例中，往往存在高偏差和低方差，而周期数较多的较长局次往往具有相反的特征。因此，取决于个人的意向，这是在开发 Q-映射时需要考虑的事情，因为高偏差往往会令模型更适应短期行动，而高方差将更适合算法捕捉长期特征和属性。

当使用多个 n 步回报时，通过不同时间点的多个奖励，对状态-行动空间进行更精细的探索，意味着通过不同的可能回报范围（在我们的自定义信号类中由输入参数 m_episode_cycles 控制），我们可以优调交易策略的信号强度。这种粒度导致在判定入场点和离场点时，能做出更细致的决策，从而可优化两者，并调整其信号的时间和强度。