Reimaginando las estrategias clásicas en MQL5 (Parte III): Previsión del FTSE 100

La Inteligencia Artificial (IA) ofrece infinitos casos de uso potencial en la estrategia del inversor moderno. Lamentablemente, ningún inversor tiene tiempo suficiente para analizar cuidadosamente cada estrategia antes de decidir a cuál confiarle su capital. En esta serie de artículos, lo ayudaremos a recorrer el amplio panorama de posibles estrategias basadas en IA, para ayudarlo a identificar una estrategia que se adapte a su perfil de inversionista.

Descripción general de la estrategia comercial

La Bolsa de Valores de Londres (London Stock Exchange, LSE) es una de las bolsas de valores más antiguas del mundo desarrollado. Fue fundada en 1801 y es la principal bolsa de valores del Reino Unido. Se considera parte de las 3 grandes junto con la Bolsa de Valores de Nueva York y la Bolsa de Valores de Tokio. La Bolsa de Valores de Londres es la bolsa de valores más grande de Europa y, según su sitio web oficial, la capitalización de mercado total actual de todas las empresas que cotizan en la bolsa es de aproximadamente 4,4 billones de libras esterlinas.

El Financial Times Stock Exchange (FTSE) 100 es un índice derivado de la LSE que sigue a las 100 empresas más grandes que cotizan en la LSE. A estas empresas se las suele denominar acciones de primera línea y se las considera inversiones relativamente seguras dada la reputación ganada por las empresas a lo largo del tiempo y su historial comprobado. Podemos aprovechar nuestro conocimiento de cómo se calcula el índice FTSE 100 y, potencialmente, crear una nueva estrategia comercial que pronostique el precio de cierre futuro del FTSE 100, considerando el precio de cierre actual del índice, así como el desempeño de 10 grandes acciones que figuran en el índice.

Descripción general de la metodología

Construimos nuestro Asesor Experto impulsado por IA completamente en MQL5. Esto nos da flexibilidad porque nuestro modelo puede utilizarse en diferentes marcos temporales sin necesidad de ajustarlo constantemente. Además, podemos ajustar dinámicamente los parámetros del modelo, como por ejemplo hasta qué punto en el futuro debe pronosticar el modelo. Nuestro modelo utilizó 12 entradas en total para pronosticar el precio de cierre futuro del FTSE 100, 20 pasos en el futuro.

Realizamos una estandarización Z para normalizar y escalar cada una de las entradas de nuestro modelo utilizando los valores de media y desviación estándar de la columna. Nuestro objetivo era el precio de cierre futuro del índice FTSE 100 en 20 pasos en el futuro, y creamos un modelo de regresión lineal múltiple para pronosticar el precio de cierre futuro del índice.

No todos los modelos de aprendizaje automático son iguales; esto es especialmente evidente en las tareas relacionadas con la previsión. Consideremos árboles de decisión; los algoritmos de árboles generalmente funcionan dividiendo los datos en grupos y luego, cuando se requiere que el modelo haga una predicción, simplemente devuelve la media del grupo que mejor coincida con los datos de entrada actuales. Por lo tanto, los algoritmos basados en árboles no realizan extrapolación, es decir, no poseen la capacidad de mirar hacia adelante y hacer una predicción hacia el futuro. Por lo tanto, si a un modelo basado en árboles se le dieran 5 entradas similares de 5 momentos diferentes, podría pronosticar el mismo precio de cierre para los 5 si fueran lo suficientemente similares, mientras que nuestro modelo de regresión lineal es capaz de extrapolación y puede darnos un pronóstico sobre el precio de cierre futuro de un valor.

Diseño inicial como script

Inicialmente construiremos nuestra idea como un script simple en MQL5 para que podamos apreciar cómo las piezas de nuestro sistema funcionan juntas. Comenzaremos definiendo nuestras variables globales.

//+------------------------------------------------------------------+
//|                                                        UK100.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+

//1) ADM.LSE  - Admiral
//2) AAL.LSE  - Anglo American
//3) ANTO.LSE - Antofagasta
//4) AHT.LSE  - Ashtead
//5) AZN.LSE  - AstraZeneca
//6) ABF.LSE  - Associated British Foods
//7) AV.LSE   - Aviva
//8) BARC.LSE - Barclays
//9) BP.LSE   - BP
//10) BKG.LSE - Berkeley Group 
//11) UK100   - FTSE 100 Index

//+-------------------------------------------------------------------+
//| Global variables                                                  |
//+-------------------------------------------------------------------+
int fetch = 2000;
int look_ahead = 20;
double mean_values[11],std_values[11];
string list_of_companies[11] = {"ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"};
vector intercept = vector::Ones(fetch);
matrix target = matrix::Zeros(1,fetch);
matrix coefficients;
matrix input_matrix = matrix::Zeros(12,fetch);

La primera tarea que completaremos es obtener y normalizar los datos de entrada. Almacenaremos los datos de entrada en una matriz y los datos de destino se mantendrán en su propia matriz.

void OnStart()
  {
//--- Fetch the target
target.CopyRates("UK100",PERIOD_CURRENT,COPY_RATES_CLOSE,1,fetch);

//--- Fill in the input matrix
for(int i = 0; i < 11; i++)
   {
      //--- Add the symbol to market watch
      SymbolSelect(list_of_companies[i],true);
      //--- Fetch historical data
      vector temp = vector::Zeros(fetch);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,1+look_ahead,fetch);
      //--- Store the mean value and standard deviation, also scale the data
      mean_values[i] = temp.Mean();
      std_values[i] = temp.Std();
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i);
   }
//--- Add the intercept
input_matrix.Row(intercept,11);

//--- Show the input data
Print("Input data:");
Print(input_matrix);

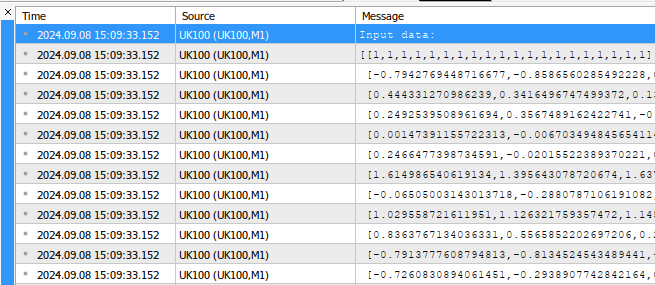
Figura 1: Un ejemplo de la salida generada por nuestro script.

Después de obtener nuestros datos de entrada, ahora podemos proceder a calcular los parámetros de nuestro modelo. Afortunadamente, los coeficientes de un modelo de regresión lineal múltiple se pueden calcular mediante una fórmula de forma cerrada. Podemos observar un ejemplo de los coeficientes del modelo a continuación.

//--- Calculating coefficient values
coefficients = target.MatMul(input_matrix.PInv());

//--- Display the coefficient values
Print("UK100 Coefficients:");
Print(coefficients.Transpose());

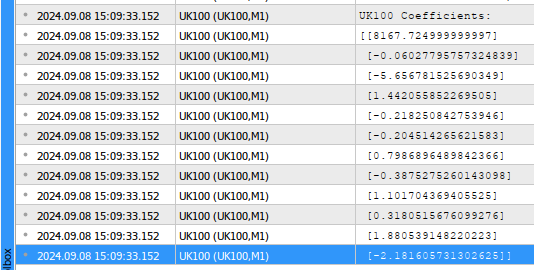
Figura 2: Nuestros parámetros del modelo.

Interpretemos los resultados juntos, el primer valor del coeficiente representa el valor promedio del objetivo cuando todas las entradas del modelo son 0. Ésta es la definición matemática del parámetro de sesgo. Sin embargo, en nuestra aplicación comercial, esto tiene muy poco sentido intuitivo. Técnicamente hablando, si todas las acciones del FTSE 100 estuvieran valoradas en 0 libras esterlinas, entonces el valor futuro promedio del FTSE 100 también sería 0 libras esterlinas. El segundo término del coeficiente representa el cambio marginal en el valor futuro del FTSE 100, asumiendo que todas las demás acciones cierran al mismo precio. Por lo tanto, cada vez que las acciones de Admiral aumentan en una unidad, observamos que el precio de cierre futuro del índice parece caer ligeramente.

Obtener una predicción de nuestro modelo es tan simple como multiplicar el precio actual de cada acción por su valor de coeficiente calculado y sumar todos estos productos. Ahora que tenemos una idea de cómo podemos construir nuestro modelo, estamos listos para comenzar a construir nuestro Asesor Experto.

Implementando nuestro Asesor Experto

Comenzaremos definiendo las entradas que el usuario puede cambiar para alterar el comportamiento del programa.

//+------------------------------------------------------------------+
//|                                                  FTSE 100 AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| User inputs                                                      |
//+------------------------------------------------------------------+
input int look_ahead = 20;       // How far into the future should we forecast?
input int rsi_period = 20;       // The period of our RSI
input int profit_target = 20;     // After how much profit should we close our positions?
input bool ai_auto_close = true; // Should the AI automatically close positions?

Luego importaremos la biblioteca comercial para ayudarnos a administrar nuestras posiciones.

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

Ahora definiremos algunas variables globales que necesitaremos en todo nuestro Asesor Experto.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
double position_profit = 0;
int fetch = 20;
matrix coefficients;
matrix input_matrix = matrix::Zeros(12,fetch);
double mean_values[11],std_values[11],rsi_buffer[1];
string list_of_companies[11] = {"ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"};
ulong open_ticket;

Ahora definiremos una función para obtener nuestros datos de entrenamiento. Recuerde que nuestro objetivo es obtener los datos de entrenamiento y luego normalizarlos y estandarizarlos antes de agregarlos a la matriz de entrada.

//+------------------------------------------------------------------+
//| This function will fetch our training data                       |
//+------------------------------------------------------------------+
void fetch_training_data(void)
  {
//--- Fetch the target
   target.CopyRates("UK100",PERIOD_CURRENT,COPY_RATES_CLOSE,1,fetch);

//--- Add the intercept
   input_matrix.Row(intercept,0);

//--- Fill in the input matrix
   for(int i = 0; i < 11; i++)
     {
      //--- Add the symbol to market watch
      SymbolSelect(list_of_companies[i],true);
      //--- Fetch historical data
      vector temp = vector::Zeros(fetch);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,1+look_ahead,fetch);
      //--- Store the mean value and standard deviation, also scale the data
      mean_values[i] = temp.Mean();
      std_values[i] = temp.Std();
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i+1);
     }
  }

Después de obtener nuestros datos de entrenamiento, también debemos definir una función para ajustar los coeficientes de nuestro modelo.

//+---------------------------------------------------------------------+
//| This function will fit our multiple linear regression model         |
//+---------------------------------------------------------------------+
void model_fit(void)
  {
//--- Calculating coefficient values
   coefficients = target.MatMul(input_matrix.PInv());
  }

Una vez que hayamos entrenado y ajustado nuestro modelo, finalmente podremos obtener predicciones de nuestro modelo. Primero buscaremos y normalizaremos los datos actuales del mercado de nuestro modelo para comenzar. Después de obtener los datos, aplicamos la fórmula de regresión lineal para obtener un pronóstico de nuestro modelo. Luego, finalmente, almacenaremos el pronóstico del modelo como un indicador binario para ayudarnos a realizar un seguimiento de posibles reversiones.

//+---------------------------------------------------------------------+
//| This function will fetch a prediction from our model                |
//+---------------------------------------------------------------------+
void model_predict(void)
  {
//--- Add the intercept
   intercept = vector::Ones(1);
   input_matrix.Row(intercept,0);

//--- Fill in the input matrix
   for(int i = 0; i < 11; i++)
     {
      //--- Fetch historical data
      vector temp = vector::Zeros(1);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,0,1);
      //--- Normalize and scale the data
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i+1);
     }

//--- Calculate the model forecast
   forecast = (
                 (1 * coefficients[0,0]) +
                 (input_matrix[0,1] * coefficients[0,1]) +
                 (input_matrix[0,2] * coefficients[0,2]) +
                 (input_matrix[0,3] * coefficients[0,3]) +
                 (input_matrix[0,4] * coefficients[0,4]) +
                 (input_matrix[0,5] * coefficients[0,5]) +
                 (input_matrix[0,6] * coefficients[0,6]) +
                 (input_matrix[0,7] * coefficients[0,7]) +
                 (input_matrix[0,8] * coefficients[0,8]) +
                 (input_matrix[0,9] * coefficients[0,9]) +
                 (input_matrix[0,10] * coefficients[0,10]) +
                 (input_matrix[0,11] * coefficients[0,11])
              );
//--- Store the model's state
//--- Whenever the system and model state aren't the same, we may have a potential reversal
   if(forecast > iClose("UK100",PERIOD_CURRENT,0))
     {
      model_state = 1;
     }

   else
      if(forecast < iClose("UK100",PERIOD_CURRENT,0))
        {
         model_state = -1;
        }
  }
//+------------------------------------------------------------------+

También necesitaremos una función encargada de obtener datos actuales del mercado desde nuestro terminal.

//+------------------------------------------------------------------+
//| Update our market data                                           |
//+------------------------------------------------------------------+
void update_market_data(void)
  {
//--- Update the bid and ask prices
   bid = SymbolInfoDouble("UK100",SYMBOL_BID);
   ask = SymbolInfoDouble("UK100",SYMBOL_ASK);
//--- Update the RSI readings
   CopyBuffer(rsi_handler,0,1,1,rsi_buffer);
  }

Ahora crearemos funciones que analizarán el sentimiento del mercado para ver si concuerda con nuestro modelo. Siempre que nuestro modelo sugiera que compremos, primero verificaremos el cambio en el precio en el marco temporal semanal durante 1 ciclo comercial, si los niveles de precios se han apreciado, entonces también verificaremos si nuestro indicador RSI sugiere un sentimiento de mercado alcista. Si este es el caso, entonces configuraremos nuestra posición de compra. De lo contrario, nos marcharemos sin fijar ninguna posición.

//+------------------------------------------------------------------+
//| Check if we have an opportunity to sell                          |
//+------------------------------------------------------------------+
void check_sell(void)
  {
   if(iClose("UK100",PERIOD_W1,0) < iClose("UK100",PERIOD_W1,12))
     {
      if(rsi_buffer[0] < 50)
        {
         Trade.Sell(0.3,"UK100",bid,0,0,"FTSE 100 AI");
         //--- Remeber the ticket
         open_ticket = PositionGetTicket(0);
         //--- Whenever the system and model state aren't the same, we may have a potential reversal
         system_state = -1;
        }
     }
  }

//+------------------------------------------------------------------+
//| Check if we have an opportunity to buy                           |
//+------------------------------------------------------------------+
void check_buy(void)
  {
   if(iClose("UK100",PERIOD_W1,0) > iClose("UK100",PERIOD_W1,12))
     {
      if(rsi_buffer[0] > 50)
        {
         Trade.Buy(0.3,"UK100",ask,0,0,"FTSE 100 AI");
         //--- Remeber the ticket
         open_ticket = PositionGetTicket(0);
         //--- Whenever the system and model state aren't the same, we may have a potential reversal
         system_state = 1;
        }
     }
  }

Al inicializar nuestra aplicación, primero prepararemos nuestro indicador RSI. A partir de ahí, lo validaremos. Si se supera esta prueba procederemos a crear nuestro modelo de regresión lineal múltiple. Comenzamos obteniendo los datos de entrenamiento y luego calculamos los coeficientes de nuestro modelo. Finalmente, validaremos las entradas del usuario para garantizar que el usuario haya definido una medida para controlar los niveles de riesgo.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Prepare the technical indicator
   rsi_handler = iRSI(Symbol(),PERIOD_CURRENT,rsi_period,PRICE_CLOSE);

//--- Validate the indicator handler
   if(rsi_handler == INVALID_HANDLE)
     {
      //--- We failed to load the indicator
      Comment("Failed to load the RSI indicator");
      return(INIT_FAILED);
     }

//--- This function will fetch our training data and scaling factors
   fetch_training_data();

//--- This function will fit our multiple linear regression model
   model_fit();

//--- Ensure the user's inputs are valid
   if((ai_auto_close == false && profit_target == 0))
     {
      Comment("Either set AI auto close true, or define a profit target!")
      return(INIT_FAILED);
     }

//--- Everything went well
   return(INIT_SUCCEEDED);
  }

Siempre que nuestro Asesor Experto no esté en uso, liberaremos los recursos que ya no utilizamos. En particular, eliminaremos el indicador RSI y el Asesor Experto del gráfico principal.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we are no longer using
   IndicatorRelease(rsi_handler);
   ExpertRemove();
  }

Finalmente, cada vez que recibamos precios actualizados, primero seleccionaremos el símbolo FTSE 100, antes de obtener los datos de mercado actualizados y los valores de los indicadores técnicos. A partir de ahí, podemos obtener una nueva predicción de nuestro modelo y tomar acción. Si nuestro sistema no tiene posiciones abiertas, verificaremos si el sentimiento actual del mercado se alinea con las predicciones de nuestros modelos antes de abrir cualquier posición. Si ya tenemos posiciones abiertas, probaremos si hay posibles reversiones, estas se pueden detectar fácilmente por incidencias en las que el estado de nuestro modelo y el estado del sistema no son los mismos.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Since we are dealing with a lot of different symbols, be sure to select the UK1OO (FTSE100)
//--- Select the symbol
   SymbolSelect("UK100",true);

//--- Update market data
   update_market_data();

//--- Fetch a prediction from our AI model
   model_predict();

//--- Give the user feedback
   Comment("Model forecast: ",forecast,"\nPosition Profit: ",position_profit);



//--- Look for a position
   if(PositionsTotal() == 0)
     {
      //--- We have no open positions
      open_ticket = 0;

      //--- Check if our model's prediction is validated
      if(model_state == 1)
        {
         check_buy();
        }

      else
         if(model_state == -1)
           {
            check_sell();
           }
     }

//--- Do we have a position allready?
   if(PositionsTotal() > 0)
     {

      //--- Should we close our positon manually?
      if(PositionSelectByTicket(open_ticket))
        {
         if((profit_target > 0) && (ai_auto_close == false))
           {
            //--- Update the position profit
            position_profit = PositionGetDouble(POSITION_PROFIT);
            if(profit_target < position_profit)
              {
               Trade.PositionClose("UK100");
              }
           }
        }

      //--- Should we close our positon using a hybrid approach?
      if(PositionSelectByTicket(open_ticket))
        {
         if((profit_target > 0) && (ai_auto_close == true))
           {
            //--- Update the position profit
            position_profit = PositionGetDouble(POSITION_PROFIT);
            //--- Check if we have passed our profit target or if we are expecting a reversal
            if((profit_target < position_profit) || (model_state != system_state))
              {
               Trade.PositionClose("UK100");
              }
           }
        }


      //--- Are we closing our system just using AI?
      else
         if((system_state != model_state) &&
            (ai_auto_close == true) &&
            (profit_target == 0))
           {
            Trade.PositionClose("UK100");
           }
     }
  }
//+------------------------------------------------------------------+

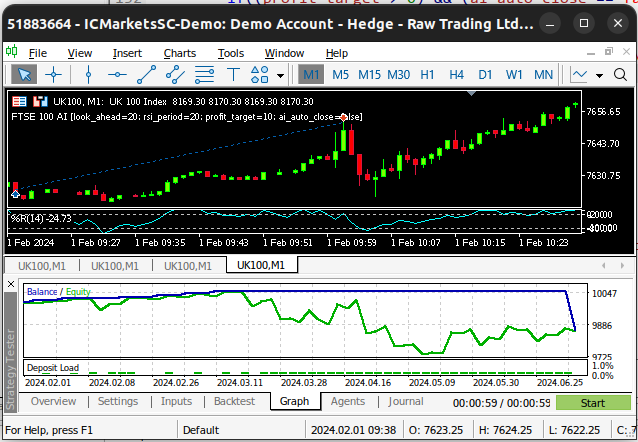
Figura 3: Prueba retrospectiva de nuestro Asesor Experto.

Optimizando nuestro Asesor Experto

Hasta ahora, nuestra aplicación comercial parece ser inestable, podemos intentar mejorar la estabilidad de nuestra aplicación comercial utilizando ideas establecidas por el economista estadounidense Harry Markowitz. A Markowitz se le atribuye la conceptualización de los fundamentos de la Teoría Moderna de Carteras (Modern Portfolio Theory, MPT) tal como la conocemos hoy. En esencia, se dio cuenta de que el rendimiento de cualquier activo individual es insignificante en comparación con el rendimiento de la cartera completa de un inversor.

Figura 4: Una fotografía del premio Nobel Harry Markowitz.

Intentemos aplicar algunas de las ideas de Markowitz, con la esperanza de estabilizar el rendimiento de nuestra aplicación comercial. Comenzaremos importando las bibliotecas que necesitamos.

#Import the libraries we need
import pandas            as pd
import numpy             as np
import seaborn           as sns
import MetaTrader5       as mt5
import matplotlib.pyplot as plt
from   scipy.optimize    import  minimize

Necesitamos crear una lista de las acciones que vamos a mantener bajo consideración.

#Create the list of stocks
stocks = ["ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"]

Inicializar el terminal.

#Initialize the terminal
if(!mt5.initialize()):
    print('Failed to load the MT5 Terminal')

True

Ahora necesitamos crear un marco de datos para almacenar los retornos de cada símbolo.

#Create a dataframe to store our returns
amount  = 10000
returns = pd.DataFrame(columns=stocks,index=np.arange(0,amount))

Obtenga los datos que necesitamos de nuestro terminal MetaTrader 5.

#Fetch the data
for stock in stocks:
     temp = pd.DataFrame(mt5.copy_rates_from_pos(stock,mt5.TIMEFRAME_M1,0,amount))
     returns[[stock]] = temp[['close']]

Para esta tarea, utilizaremos los rendimientos de cada acción, en lugar del precio de cierre normal.

#Store the data as returns
returns = returns.pct_change()
returns.dropna(inplace=True)

De forma predeterminada, debemos multiplicar cada entrada por 100 para obtener el porcentaje de retorno real.

#Let's look at our dataframe
returns = returns * (10.0 ** 2)

Veamos ahora los datos que tenemos.

returns

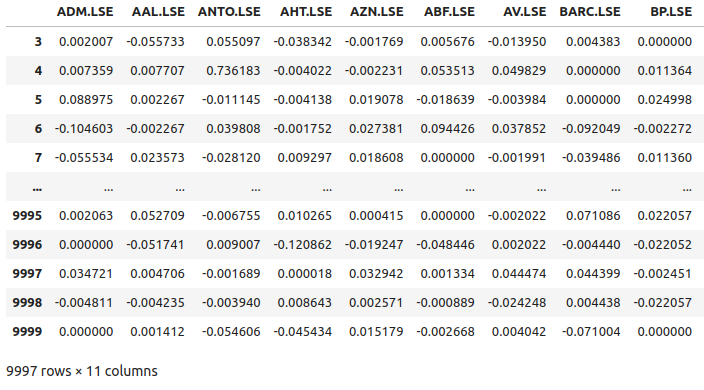
Figura 5: Algunos de los rendimientos de las acciones de nuestra cesta de acciones FTSE 100.

Grafiquemos ahora los rendimientos del mercado de cada acción que tenemos. Podemos ver claramente que ciertas acciones como Ashtead Group (AHT.LSE) tienen colas fuertes y contundentes que se desvían del rendimiento promedio de la cartera de las 11 acciones que tenemos. En esencia, el algoritmo de Markowitz nos ayudará a seleccionar empíricamente menos acciones que tengan alta varianza y más acciones que tengan menor varianza. El enfoque de Markowitz es analítico y elimina cualquier conjetura del proceso por nuestra parte.

#Let's visualize our market returns
returns.plot()

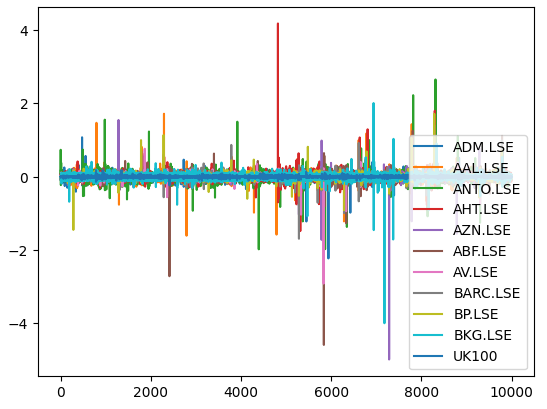
Figura 6: Los rendimientos del mercado de nuestra cesta de acciones FTSE 100.

Observemos si hay niveles de correlación significativos en nuestros datos. Desafortunadamente no encontramos niveles de correlación significativos que nos pareciera interesantes.

#Let's analyze the correlation coefficients
fig, ax = plt.subplots(figsize=(8,8)) 
sns.heatmap(returns.corr(),annot=True,linewidths=.5, ax=ax)

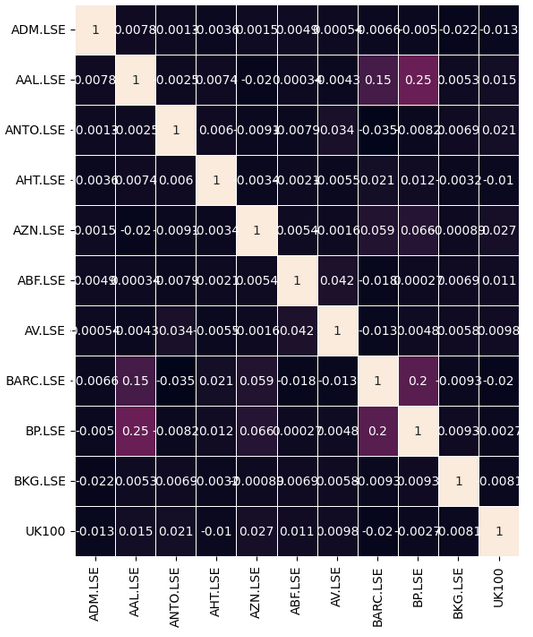
Figura 7: Nuestro mapa de calor (heat-map) de correlación del FTSE 100.

Algunas relaciones no serán fáciles de encontrar y requerirán algunos pasos de preprocesamiento para descubrirlas. En lugar de simplemente buscar correlación directamente entre la cesta de acciones que tenemos, también podemos buscar correlación entre los valores actuales de cada acción y el valor futuro del símbolo UK100. Esta es una técnica clásica conocida como correlación adelanto-retraso.

Comenzaremos empujando nuestra cesta de acciones 20 puestos hacia atrás, y empujando el símbolo UK100 20 puestos hacia adelante.

# Let's also analyze for lead-lag correlation
look_ahead  = 20
lead_lag    = pd.DataFrame(columns=stocks,index=np.arange(0,returns.shape[0] - look_ahead))
for stock in stocks:
    if stock == 'UK100':
        lead_lag[[stock]] = returns[[stock]].shift(-20)
    else:
        lead_lag[[stock]] = returns[[stock]].shift(20)

# Returns
lead_lag.dropna(inplace=True)

Veamos si hubo algún cambio en la matriz de correlación. Lamentablemente no obtuvimos ninguna mejora con este procedimiento.

#Let's see if there are any stocks that are correlated with the future UK100 returns
fig, ax = plt.subplots(figsize=(8,8)) 
sns.heatmap(lead_lag.corr(),annot=True,linewidths=.5, ax=ax)

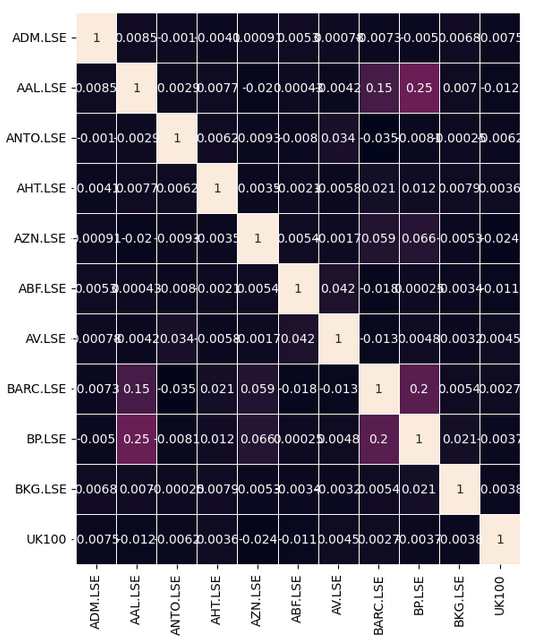
Figura 8: Nuestro mapa de calor (heat-map) de la correlación adelanto-retraso

Intentemos ahora minimizar la varianza de toda nuestra cartera. Modeloremos nuestra cartera de tal manera que se nos permita comprar y vender diferentes acciones para minimizar el riesgo de nuestra cartera. Para lograr nuestro objetivo, utilizaremos la biblioteca de optimización de SciPy. Tendremos 11 pesos diferentes a optimizar, cada peso representa la asignación de capital que se debe realizar a cada respectiva acción. El coeficiente de cada peso simbolizará si debemos comprar, coeficiente positivo, o vender, coeficiente negativo, cada acción en particular. Para ser más específicos, queremos estar seguros de que todos nuestros coeficientes estén entre -1 y 1 inclusive, o en notación de intervalo [-1,1].

Además de esto, nos gustaría utilizar todo el capital que tenemos y no más. Por lo tanto, debemos establecer restricciones a nuestro procedimiento de optimización. En concreto, debemos asegurar que la suma de todos los pesos de la cartera sea igual a 1. Esto significará que hemos asignado todo el capital que tenemos. Recuerde que algunos de nuestros coeficientes serán negativos, lo que puede dificultar que la suma de todos nuestros coeficientes sea igual a 1. Por lo tanto, debemos modificar esta restricción para considerar solo los valores absolutos de cada peso. En otras palabras, si almacenamos nuestros 11 pesos en un vector, queremos asegurarnos de que la norma L1 sea igual a 1.

Para comenzar, primero inicializaremos nuestros pesos con valores aleatorios y calcularemos la covarianza de nuestra matriz de retornos.

#Let's attempt to minimize the variance of the portfolio
weights = np.array([0,0,0,0,0,0,-1,1,1,0,0])
covariance = returns.cov()

Ahora hagamos un seguimiento de los niveles de varianza iniciales.

#Store the initial portfolio variance
initial_portfolio_variance = np.dot(weights.T,np.dot(covariance,weights))
initial_portfolio_variance

0.011959689589562724

Al realizar la optimización, buscamos las entradas óptimas para una función que resulten en la salida más baja de la función. Esta función se conoce como función de costo. Nuestra función de costo será la varianza de la cartera bajo los pesos actuales. Afortunadamente, esto es fácil de calcular utilizando comandos de álgebra lineal.

#Cost function
def cost_function(x):
    return(np.dot(x.T,np.dot(covariance,x)))

Ahora definiremos nuestras restricciones que especifican que los pesos de nuestra cartera deben ser iguales a 1.

#Constraints
def l1_norm(x):
    return(np.sum(np.abs(x))) - 1

constraints = {'type': 'eq', 'fun':l1_norm}

SciPy espera que le proporcionemos una estimación inicial al realizar la optimización.

#Initial guess
initial_guess = weights

Recordemos que queremos que todos nuestros pesos estén entre -1 y 1, pasamos estas instrucciones a SciPy usando una tupla de límites.

#Add bounds
bounds =   [(-1,1)] * 11

Ahora minimizaremos la varianza de nuestra cartera utilizando el algoritmo de programación de mínimos cuadrados secuenciales (Sequential Least Squares Programming, SLSQP). El algoritmo SLSQP fue desarrollado originalmente por el destacado ingeniero alemán Dieter Kraft en la década de 1980. La rutina original se implementó en FORTRAN. El artículo científico original de Kraft en el que se describe el algoritmo puede consultarse en este enlace, aquí. SLSQP es un algoritmo cuasi-Newton, lo que significa que estima la segunda derivada (matriz hessiana) de la función objetivo para encontrar el óptimo de la función objetivo.

#Minimize the portfolio variance
result = minimize(cost_function,initial_guess,method="SLSQP",constraints=constraints,bounds=bounds)

Hemos realizado con éxito este procedimiento de optimización, veamos nuestros resultados.

result

 message: Optimization terminated successfully
 success: True
  status: 0
     fun: 0.0004706570068070814
       x: [ 5.845e-02 -1.057e-01  8.800e-03  2.894e-02 -1.461e-01
            3.433e-02 -2.625e-01  6.867e-02  1.653e-01  3.450e-02
            8.675e-02]
     nit: 12
     jac: [ 3.820e-04 -9.886e-04  3.242e-05  4.724e-04 -1.544e-03
            4.151e-04 -1.351e-03  5.850e-04  8.880e-04  4.457e-04
            4.392e-05]
    nfev: 154
    njev: 12

Almacenemos los pesos óptimos que nuestro solucionador SciPy encontró para nosotros.

#Store the optimal weights
optimal_weights = result.x

Validemos que no se violó la restricción de la norma L1. Tenga en cuenta que, debido a la precisión flotante de la memoria limitada de las computadoras, nuestros pesos no sumarán con precisión 1.

#Validating the weights add up to one
np.sum(np.abs(optimal_weights))

0.9999999998893961

Almacene la nueva varianza de la cartera.

#Store the new portfolio variance
otpimal_variance = cost_function(optimal_weights)

Crear un marco de datos que nos permita comparar nuestro desempeño.

#Portfolio variance
portfolio_var = pd.DataFrame(columns=['Old Var','New Var'],index=[0])

Guarde nuestros niveles de varianza en un marco de datos.

portfolio_var.iloc[0,0] = initial_portfolio_variance * (10.0 ** 7)
portfolio_var.iloc[0,1] = otpimal_variance * (10.0 ** 7)

Grafique la varianza de nuestra cartera. Como podemos ver, nuestros niveles de varianza han disminuido significativamente.

portfolio_var.plot.bar()

Figura 9: Varianza de nuestra nueva cartera.

Obtengamos ahora el número de posiciones que debemos abrir en cada mercado en función de nuestros pesos óptimos. Nuestros datos sugieren que siempre que abramos 1 posición larga en el símbolo UK100, no deberíamos abrir ninguna posición en Admiral Group (ADM.LSE) y deberíamos abrir 2 posiciones cortas equivalentes en Anglo-American (AAL.LSE).

int_weights = (optimal_weights / optimal_weights[-1]) // 1
int_weights

array([ 0., -2.,  0.,  0., -2.,  0., -4.,  0.,  1.,  0.,  1.])

Actualización de nuestro Asesor Experto

Ahora podemos centrar nuestra atención en actualizar nuestro algoritmo comercial, para aprovechar nuestra nueva comprensión del mercado FTSE 100. Carguemos primero los pesos óptimos que hemos calculado con SciPy.

int    optimization_weights[11] = {0,-2,0,0,-2,0,-4,0,1,0,1};

También necesitamos un ajuste para activar nuestro procedimiento de optimización, estableceremos un límite de pérdidas. Siempre que la pérdida de nuestra operación abierta sea mayor que nuestro límite de pérdida, abriremos operaciones en otros mercados FTSE 100 para intentar minimizar nuestros niveles de riesgo.

input double  loss_limit = 20;        // After how much loss should we optimize our portfolio?

Definamos ahora la función que será encargada de llamar al procedimiento para minimizar los niveles de riesgo de nuestra cartera. Recuerde que solo realizaremos esta rutina si la cuenta ha superado su límite de pérdidas o está en riesgo de superar su umbral de capital.

      //--- Should we optimize our portfolio variance using the optimal weights we have calculated
      if((loss_limit > 0))
        {
         //--- Update the position profit
         position_profit = AccountInfoDouble(ACCOUNT_EQUITY) - AccountInfoDouble(ACCOUNT_BALANCE);
         //--- Check if we have passed our profit target or if we are expecting a reversal
         if(((loss_limit * -1) < position_profit))
           {
            minimize_variance();
           }
        }
        

Esta función realmente realizará la optimización de la cartera, la función iterará a través de nuestra lista de acciones y luego verificará el número y tipo de posición que debe abrir.

//+------------------------------------------------------------------+
//| This function will minimize the variance of our portfolio        |
//+------------------------------------------------------------------+
void minimize_variance(void)
  {
   risk_minimized = true;

   if(!risk_minimized)
     {
      for(int i = 0; i < 11; i++)
        {
         string current_symbol = list_of_companies[i];

         //--- Add that stock to the portfolio to minimize our variance, buy
         if(optimization_weights[i] > 0)
           {
            for(int i = 0; i < optimization_weights[i]; i++)
              {
               Trade.Buy(0.3,current_symbol,ask,0,0,"FTSE Optimization");
              }
           }
         //--- Add that stock to the portfolio to minimize our variance, sell
         else
            if(optimization_weights[i] < 0)
              {
               for(int i = 0; i < optimization_weights[i]; i--)
                 {
                  Trade.Sell(0.3,current_symbol,bid,0,0,"FTSE Optimization");
                 }
              }
        }
     }
  }

Figura 10: Pruebas futuras de nuestro algoritmo.

Figura 11: Prueba retrospectiva de nuestro algoritmo.

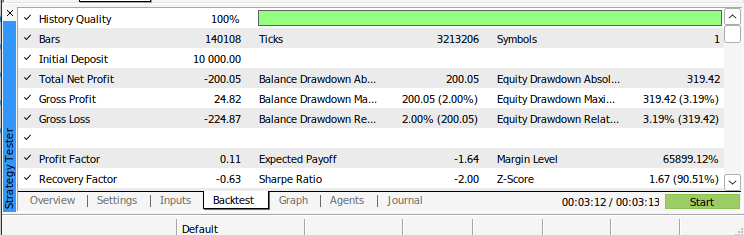
Figura 12: Resultados de las pruebas retrospectivas de nuestro algoritmo.

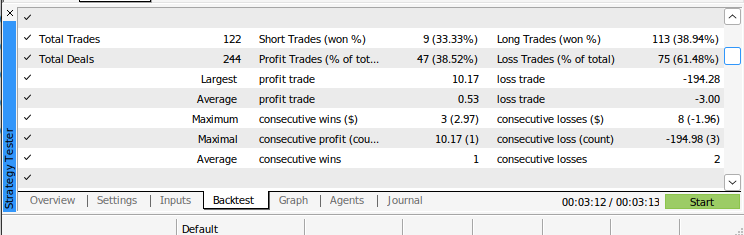
Figura 13: Resultados adicionales de las pruebas retrospectivas de nuestro algoritmo.

Conclusión

En este artículo, hemos demostrado cómo se puede construir un conjunto de análisis técnico y la IA sin problemas utilizando Python y MQL5, nuestra aplicación es capaz de ajustarse dinámicamente a todos los plazos disponibles en el terminal MetaTrader 5. Esbozamos los principios fundamentales de la optimización moderna de carteras utilizando algoritmos de optimización contemporáneos. Demostramos cómo minimizar el sesgo humano en el proceso de selección de cartera. Además, hemos mostrado cómo utilizar los datos del mercado para tomar decisiones óptimas. Todavía hay margen de mejora en nuestro algoritmo, por ejemplo, en futuros artículos demostraremos cómo optimizar 2 criterios simultáneamente, como optimizar los niveles de riesgo mientras se considera la tasa de retorno libre de riesgo.

Sin embargo, la mayoría de los principios que hemos descrito hoy seguirán siendo los mismos incluso cuando realicemos procedimientos de optimización más matizados: solo necesitaremos ajustar nuestras funciones de costos, restricciones e identificar el algoritmo de optimización apropiado para nuestras necesidades.